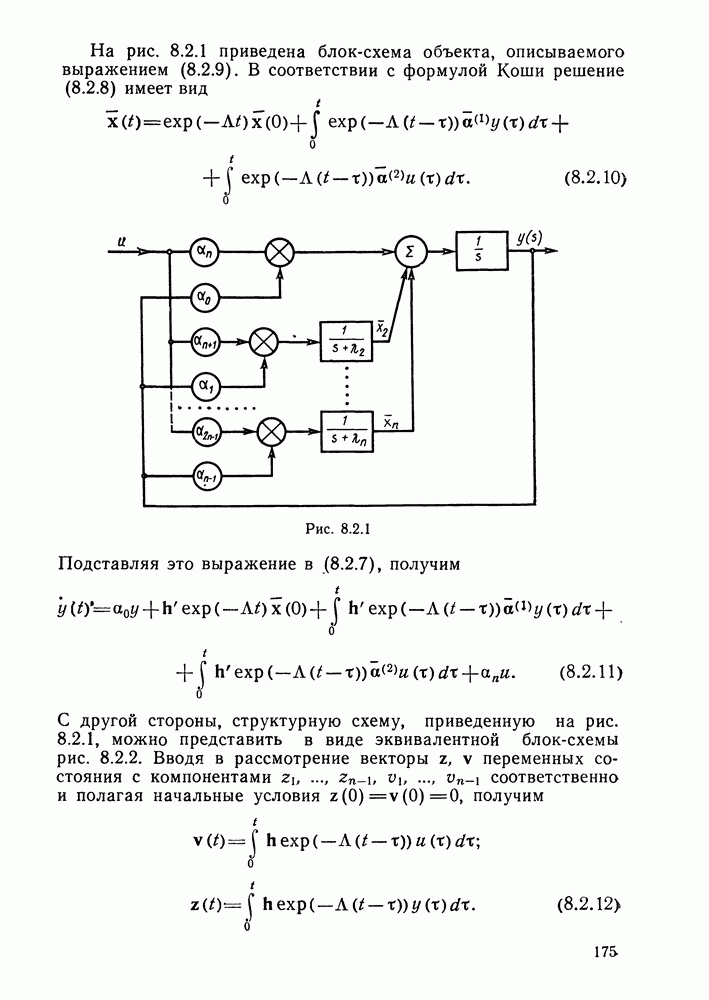
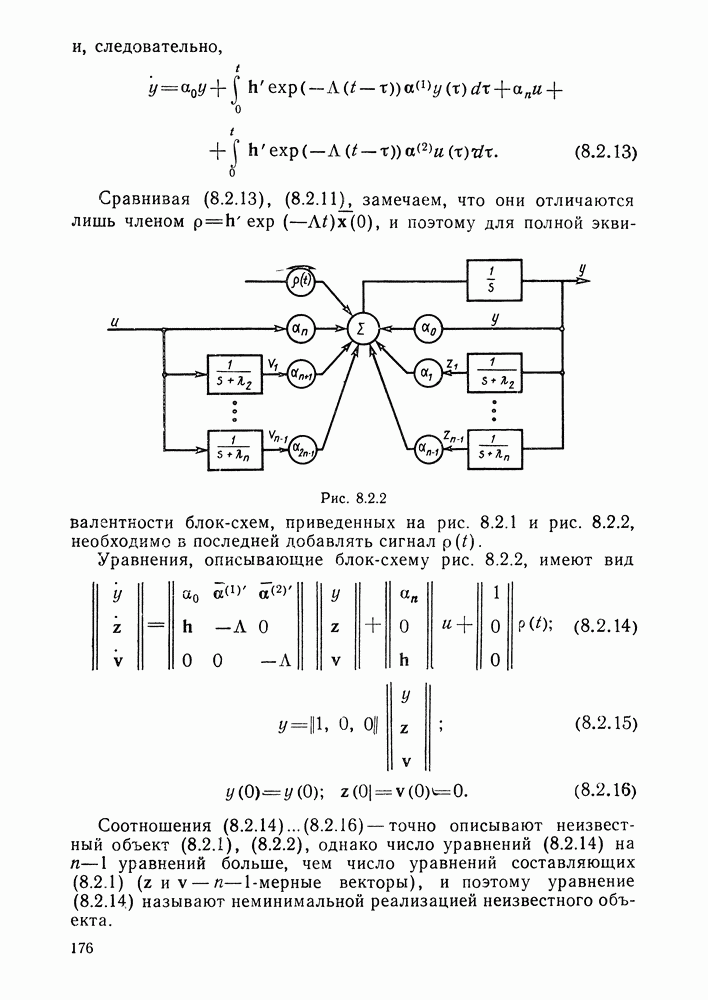
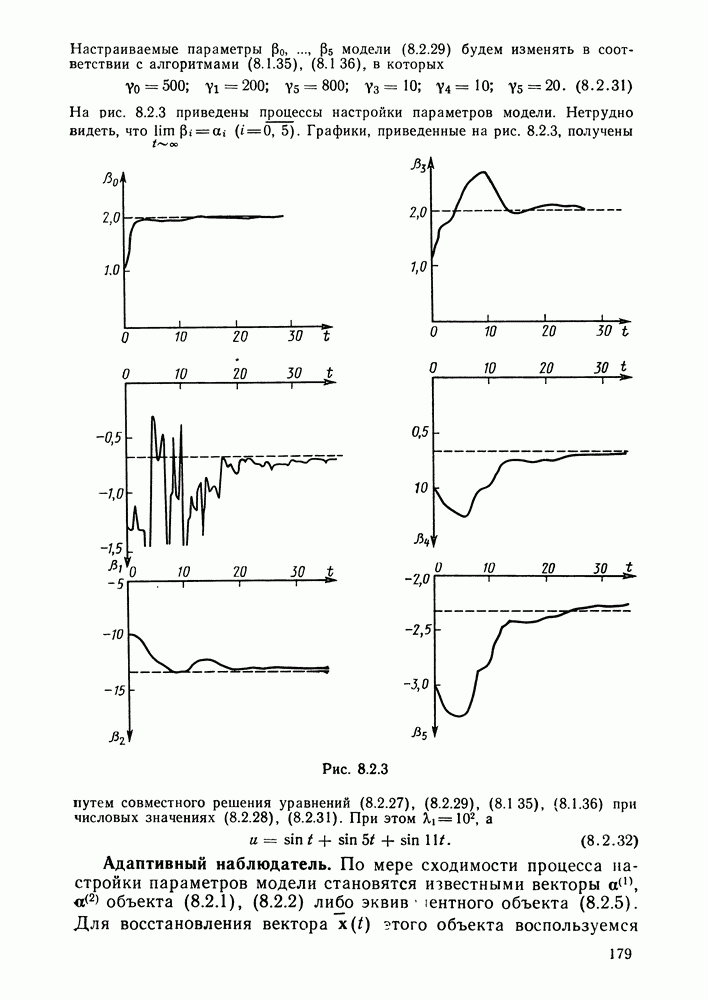
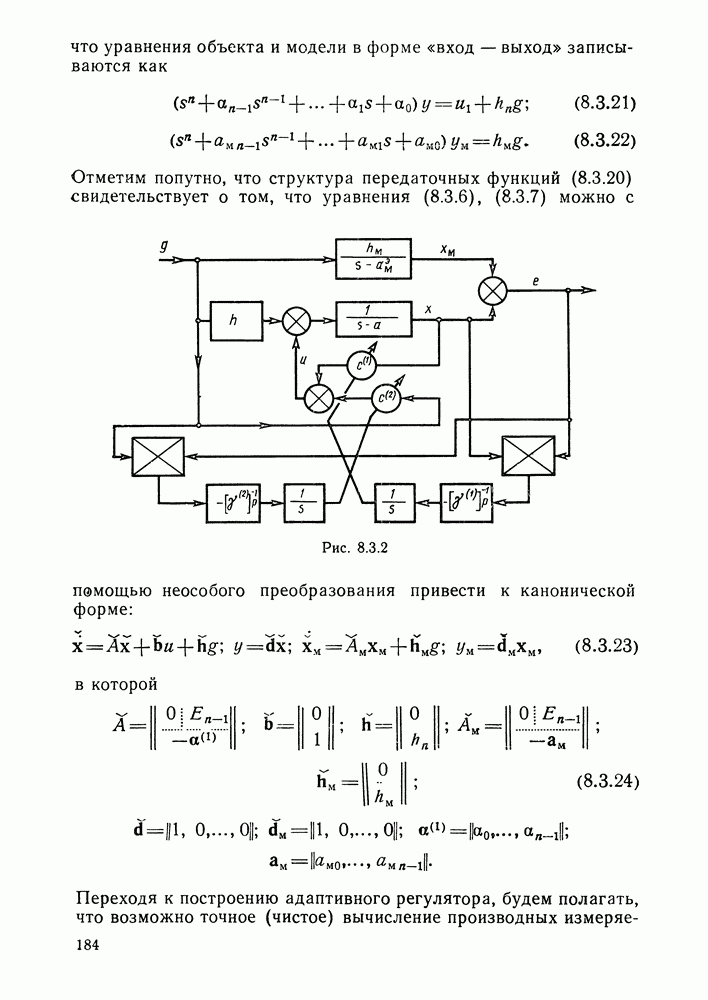
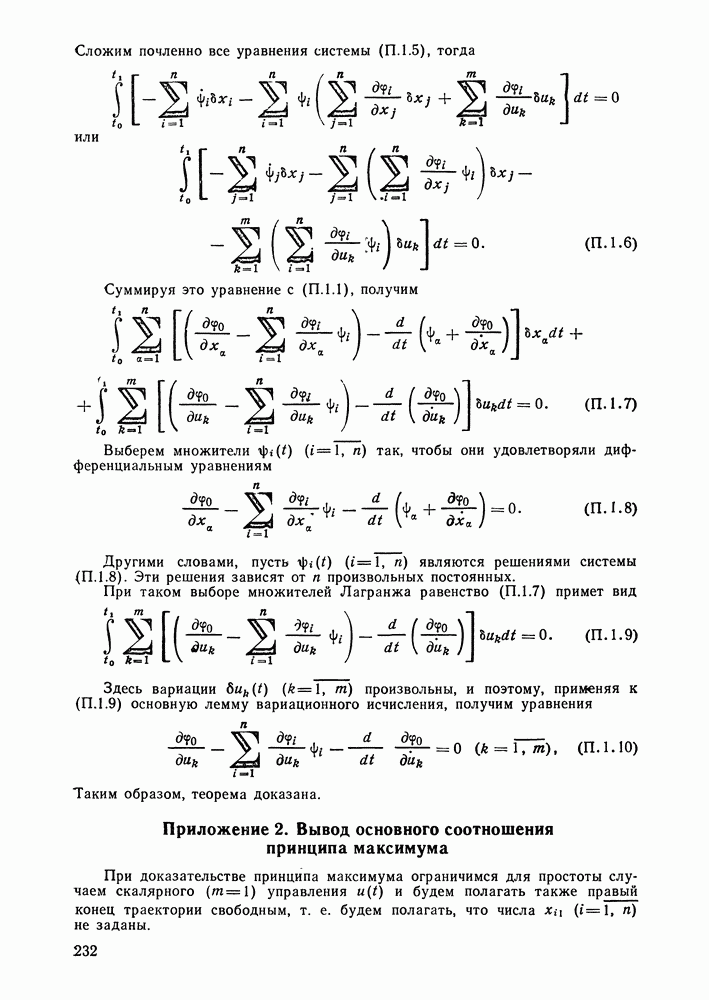
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4.1. Процедуры аналитического конструирования регуляторов
Аналитическое конструирование оптимальных регуляторов на основе метода динамического программирования.
Рассмотрим объект управления, возмущенное движение которого описывается в первом приближении уравнением
где А и В — заданные матрицы чисел размеров  соответственно.
соответственно.
Требуется найти матрицу чисел  (размеров
(размеров  ) уравнения регуляторов
) уравнения регуляторов

такую, чтобы на асимптотически устойчивых движениях системы (4.1.1), (4.1.2), возбужденных произвольными начальными отклонениями  , минимизировался функционал
, минимизировался функционал

где Q — заданная положительно-определенная матрица размеров  для всех
для всех  , это обозначается далее
, это обозначается далее  .
.
Матрицу С закона управления (4.1.2) иногда называют матрицей коэффициентов усиления регулятора.
Переходя к решению этой задачи об оптимальной стабилизации на основе метода динамического программирования, ограничимся вначале случаем  . В этом случае уравнения системы и функционал примут вид
. В этом случае уравнения системы и функционал примут вид


Тогда уравнения (2.3.8), (2.3.9) метода динамического программирования запишутся как

Предпоследнее равенство выражает необходимое условие экстремума правой части (4.1.4). Нетрудно проверить, что при этом управлении достигается ее минимум. Действительно,

Этот минимум — единственный и поэтому единственно управление вида (4.1.5). Правда, как будет показано ниже, уравнению (4.1.4) удовлетворяет не единственная функция v. Эта функция доопределяется из условия устойчивости системы (4.1.1), (4.1.2.).
Исключая и из (4.1.4) с помощью (4.1.5), получим нелинейное уравнение в частных производных:

Решение этого уравнения при краевом условии

будем искать в виде

Подставляя это выражение в (4.1.6), получим

Отсюда следует алгебраическое уравнение для определения  известного коэффициента
известного коэффициента  в (4.1.7):
в (4.1.7):

Из двух решений

этого уравнения выбираем первое исходя из условия положительности функции  , обеспечивающего асимптотическую устойчивость синтезируемой системы, а следовательно, и выполнение краевого условия
, обеспечивающего асимптотическую устойчивость синтезируемой системы, а следовательно, и выполнение краевого условия  .
.
На основе (4.1.5) получаем

и, таким образом, искомое число

В общем случае  уравнения (4.1.9), (4.1.11) аналитического конструирования регуляторов имеют вид
уравнения (4.1.9), (4.1.11) аналитического конструирования регуляторов имеют вид

где  — симметричная матрица чисел размеров
— симметричная матрица чисел размеров  .
.
Вывод этих уравнений приведен в приложении 4. Матричное уравнение (4.1.12) имеет два названия: первое — матричное алгебраическое уравнение Риккати (смысл такого названия станет ясен несколько позже), второе — уравнение Лурье (А. И. Лурье получил уравнение вида (4.1.12) при исследовании абсолютной устойчивости систем регулирования [4.2]).
Таким образом, процедура 4.1.1 аналитического конструирования регуляторов (процедура АКОР) состоит из трех операций: 1) решение системы нелинейных алгебраических уравнений; 2) выделение из всего множества этих решений матрицы  (численный метод нахождения
(численный метод нахождения  приведен ниже); 3) вычисление искомой матрицы коэффициентов усиления регулятора по формуле
приведен ниже); 3) вычисление искомой матрицы коэффициентов усиления регулятора по формуле

Убедимся непосредственно, что матрица С, определяемая соотношением (4.1.14), обеспечивает асимптотическую устойчивость системы (4.1.1), (4.1.2). Для исследования устойчивости системы  воспользуемся прямым методом Ляпунова. Примем в качестве функции Ляпунова
воспользуемся прямым методом Ляпунова. Примем в качестве функции Ляпунова  и вычислим полную производную этой функции:
и вычислим полную производную этой функции:

Учитывая, что матрица С определяется выражением (4.1.14), получим, с учетом того, что  удовлетворяет (4.1.12),
удовлетворяет (4.1.12),

Если объект (4 1.1) полностью управляем и  , то среди решений системы (4.1.12.) всегда найдется и при том единственная положительно-определенная матрица
, то среди решений системы (4.1.12.) всегда найдется и при том единственная положительно-определенная матрица  .
.
Напомним, что условием полной управляемости объекта (4.1.1) является равенство

которое будем называть условием управляемости пары  . Если матрица Q — неотрицательно-определенная матрица
. Если матрица Q — неотрицательно-определенная матрица  , то ее всегда можно представить в виде
, то ее всегда можно представить в виде

где  — матрица размеров
— матрица размеров  (
( — ранг матрицы Q). Среди решений (4.1.12) по-прежнему существует [4.6] единственная матрица
— ранг матрицы Q). Среди решений (4.1.12) по-прежнему существует [4.6] единственная матрица  , если Q в функционале (4.1.3) неотрицательно-определенная матрица, удовлетворяющая условию полной управляемости пары (
, если Q в функционале (4.1.3) неотрицательно-определенная матрица, удовлетворяющая условию полной управляемости пары ( ):
):

Требование полной управляемости пар  для существования и единственности
для существования и единственности  можно ослабить, заменив его условием стабилизируемости этих пар [4.6].
можно ослабить, заменив его условием стабилизируемости этих пар [4.6].
Пример 4.1.1. Уравнение процедуры аналитического конструирования регулятора гирорамы. Осуществим первый этап (составление уравнений (4.1.12), (4.1.13.) аналитического конструирования регулятора гирорамы.
Опишем вначале физическое содержание задачи стабилизации гирорамы [4.3], поскольку на примере решения этой задачи будут иллюстрироваться результаты, приведенные в этой и следующих главах.

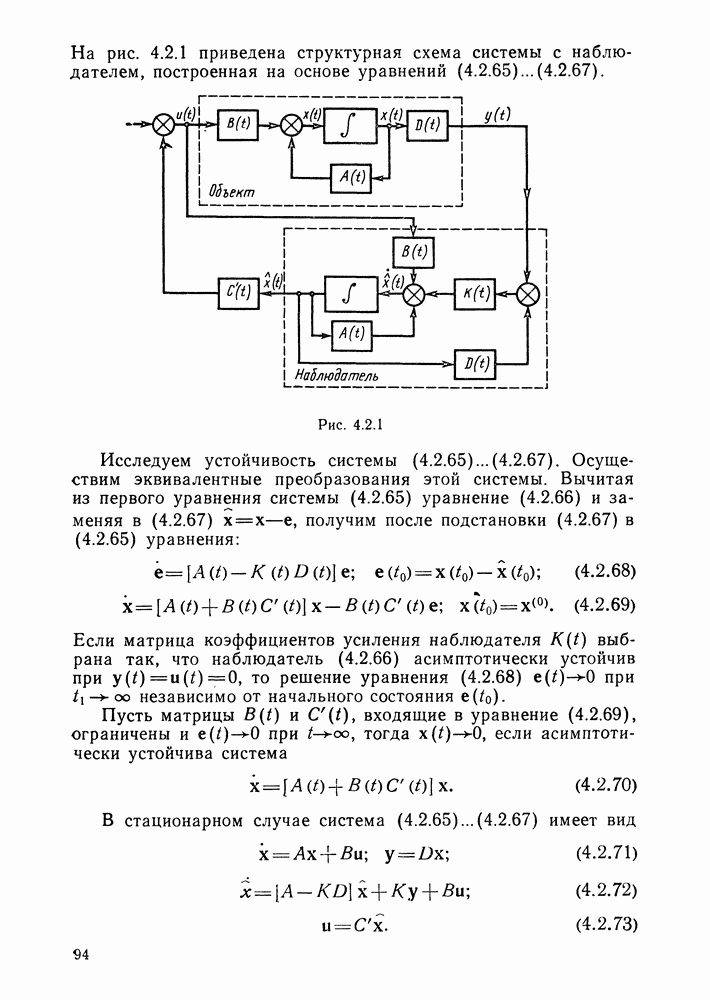
Рис. 4.1.1.

Рис. 4.1.2.
Рассмотрим трехстепенной гироскоп в кардановом подвесе (рис. 4.1.1). Его уравнения имеют вид [4.4]:

 — угол поворота наружной рамы относительно оси
— угол поворота наружной рамы относительно оси  ;
;  — угол поворота внутреннего кольца карданова подвеса относительно оси ОХ (угол прецессии);
— угол поворота внутреннего кольца карданова подвеса относительно оси ОХ (угол прецессии);  — момент инерции наружной рамы (кольца) относительно оси
— момент инерции наружной рамы (кольца) относительно оси  ;
;  — экваториальный момент инерции гироскопа;
— экваториальный момент инерции гироскопа;  — моменты инерции внутреннего кольца карданова подвеса относительно осей OZ, ОХ, OY соответственно, при этом
— моменты инерции внутреннего кольца карданова подвеса относительно осей OZ, ОХ, OY соответственно, при этом  ;
;  — кинетический момент гироскопа;
— кинетический момент гироскопа;  — моменты относительно осей ОХ и OY соответственно;
— моменты относительно осей ОХ и OY соответственно;  — коэффициенты демпфирования.
— коэффициенты демпфирования.
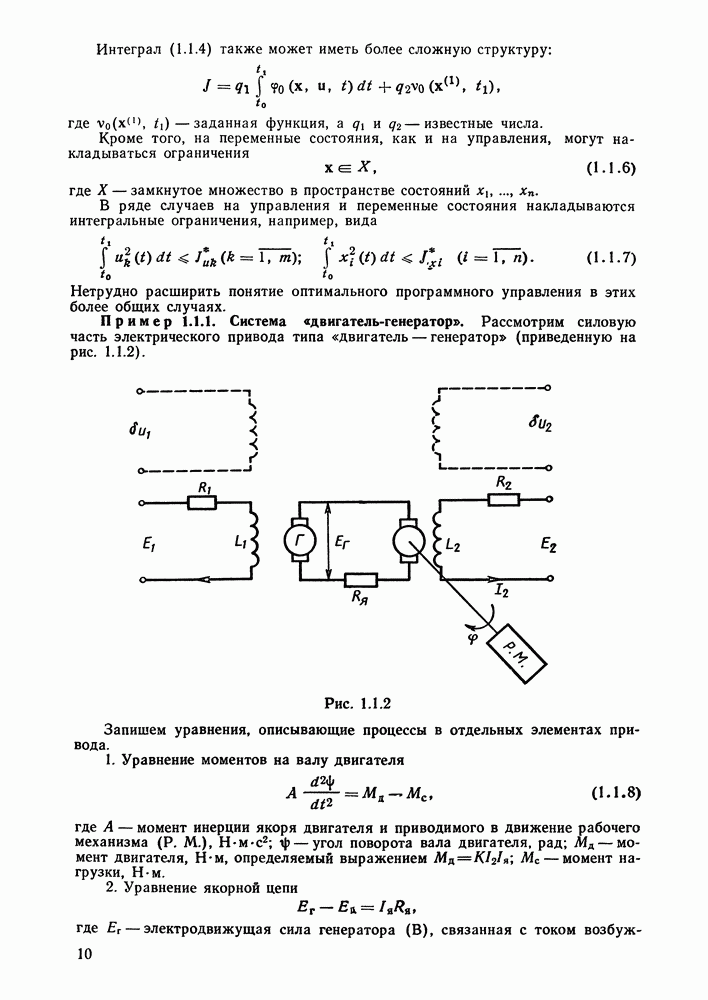
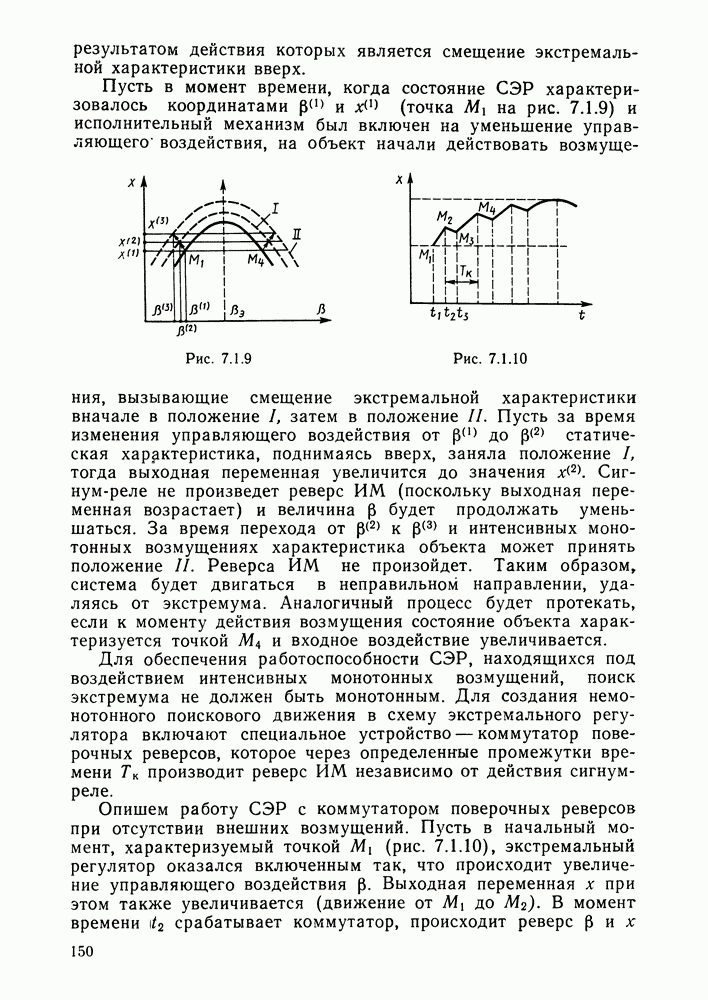
Гироскоп в кардановом подвесе используется (если установить на оси OY датчик угла) для измерения углов поворота движущегося объекта (например, ракеты) относительно оси OY. Однако из-за вредных моментов по этой оси (трения, дисбаланса и т. п.) гироскоп начинает «прецессировать» относительно оси ОХ, т. е. ось OZ начинает поворачиваться в направлении оси OY, и гироскоп теряет свойство быть индикатором поворота летательного аппарата. Явление прецессии следует непосредственно из уравнения (4.1.17), если в нем пренебречь всеми слагаемыми в левой части, кроме последнего слагаемого (так как  ). Прецессию можно измерить, установив на оси ОХ датчик угла. Усилим этот сигнал и подадим его на двигатель, который развивает полезный момент, равный и противоположный по знаку вредному. Тогда прецессия прекратится и гироскоп будет сохранять свои функции. Гироскоп в кардановом подвесе с системой стабилизации угла прецессии называется гирорамой. Ее схема приведена на рис. 4.1.2, где ДУП — датчик угла прецессии, ДМ — датчик момента (двигатель).
). Прецессию можно измерить, установив на оси ОХ датчик угла. Усилим этот сигнал и подадим его на двигатель, который развивает полезный момент, равный и противоположный по знаку вредному. Тогда прецессия прекратится и гироскоп будет сохранять свои функции. Гироскоп в кардановом подвесе с системой стабилизации угла прецессии называется гирорамой. Ее схема приведена на рис. 4.1.2, где ДУП — датчик угла прецессии, ДМ — датчик момента (двигатель).
Запишем уравнения (4.1.16), (4.1.17) в форме Коши.
Пренебрегая значениями  по сравнению с полагая
по сравнению с полагая  и вводя обозначения
и вводя обозначения

запишем (4.1.16), (4.1.17) в виде

Разлагая правые части этих уравнений в ряд Тейлора в окрестности точки  , получим уравнения первого приближения
, получим уравнения первого приближения

где и пропорционально моменту, развиваемому датчиком моментов, a  пропорционально вредному моменту по оси
пропорционально вредному моменту по оси  .
.
Полагая пока  , будем искать управление
, будем искать управление

при котором на движениях гирорамы (возбужденных начальными отклонениями) минимизируется функционал

Переходя к решению этой задачи, запишем уравнения (4.1.12), (4.1.13) процедуры АКОР. Первое из этих уравнений имеет вид

Это матричное уравнение можно записать в виде системы уравнений

(Из-за симметричности матрицы А число этих уравнений не  ).
).
На основе уравнений (4.1.13) получим

Таким образом, аналитическое конструирование регулятора гирорамы (системы стабилизации гирорамы) сводится к решению алгебраических уравнений (4.1.23) и нахождению искомых параметров регулятора (4.1.21) по формулам (4.1.24.).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
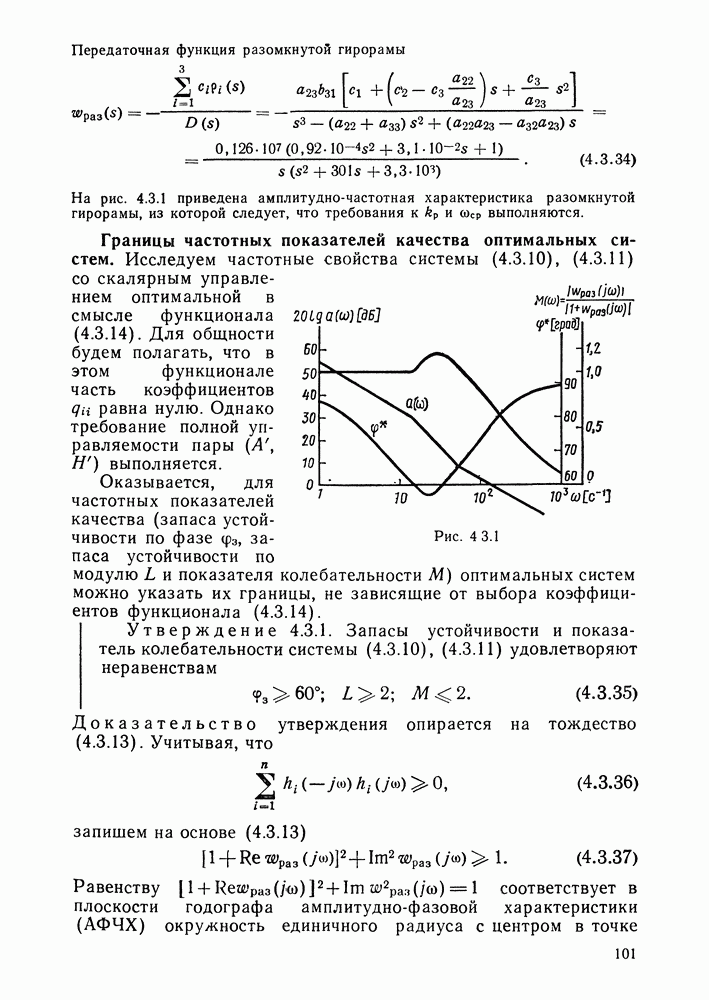
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
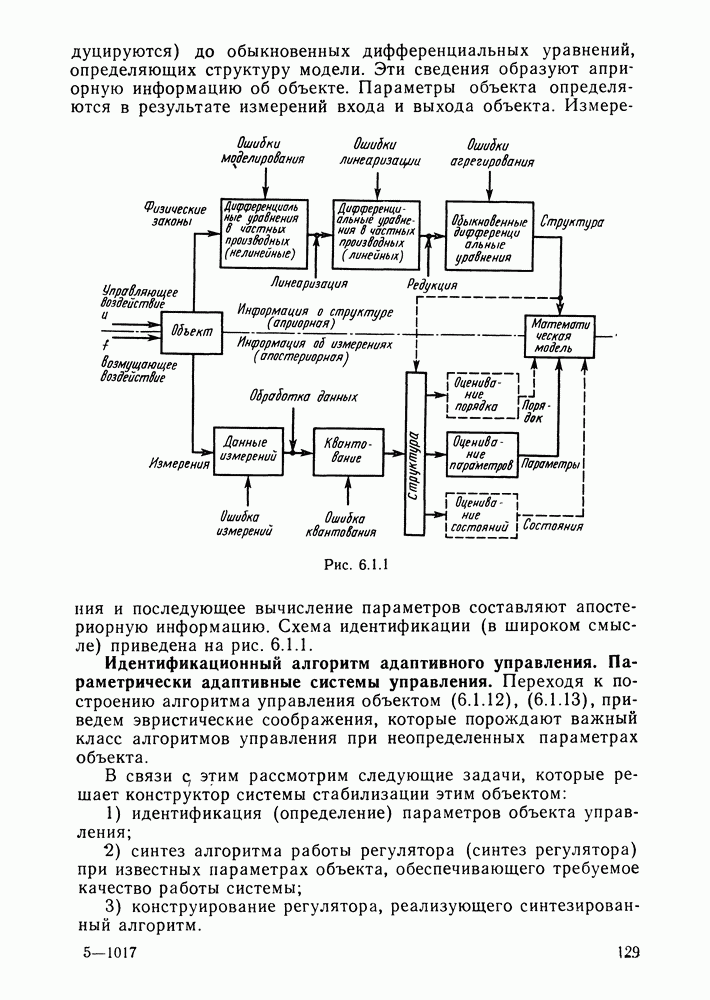
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
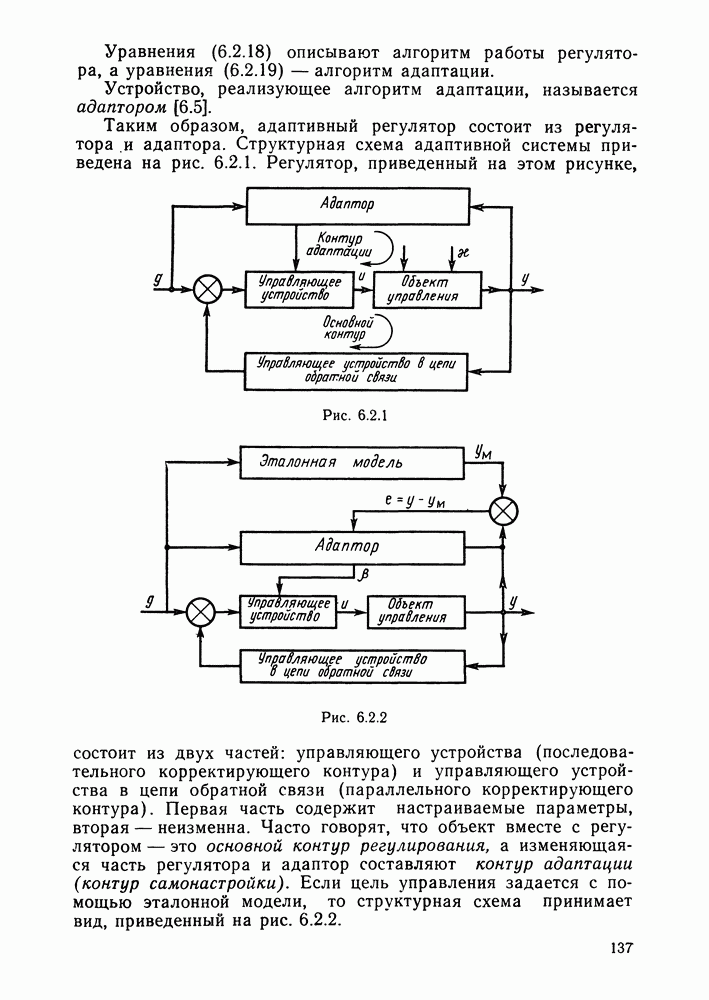
- § 6.2. Структура адаптивных систем
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
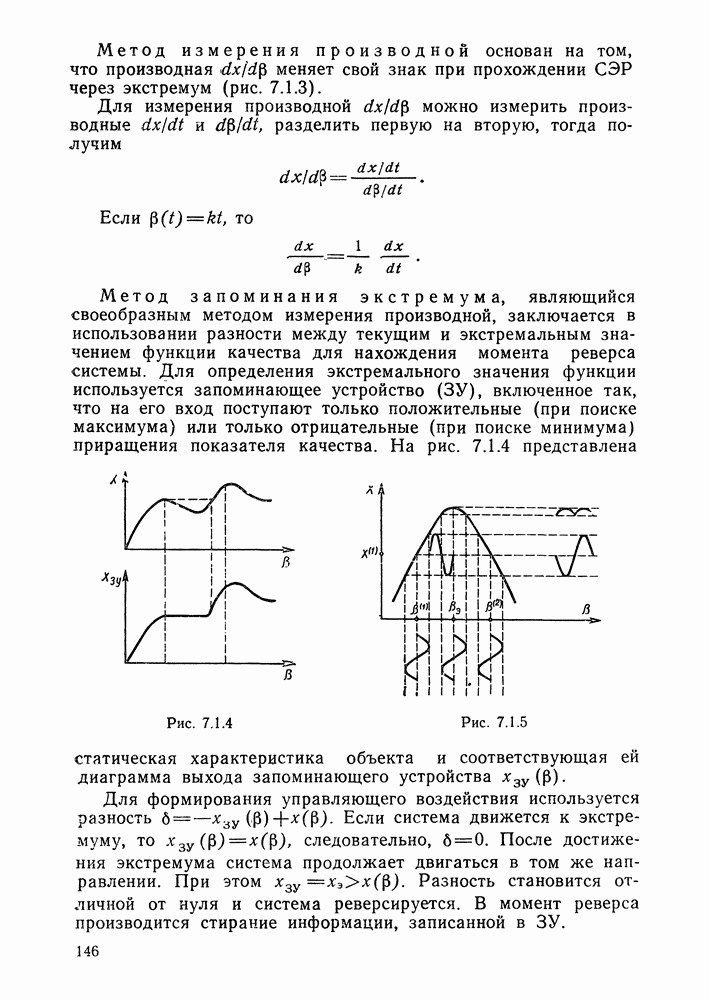
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
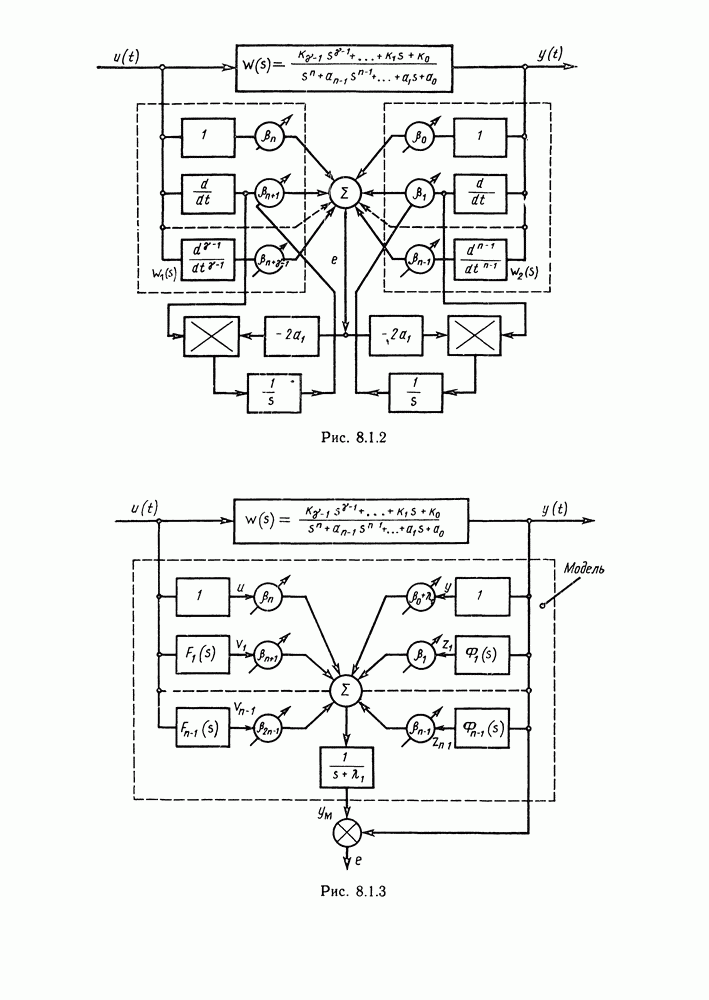
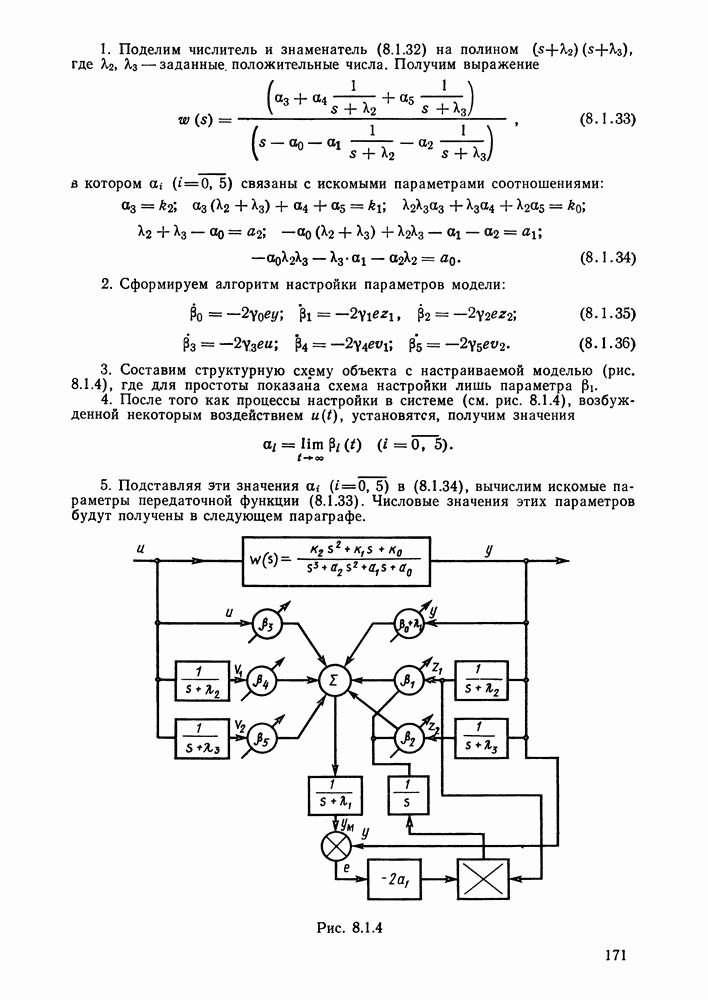
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
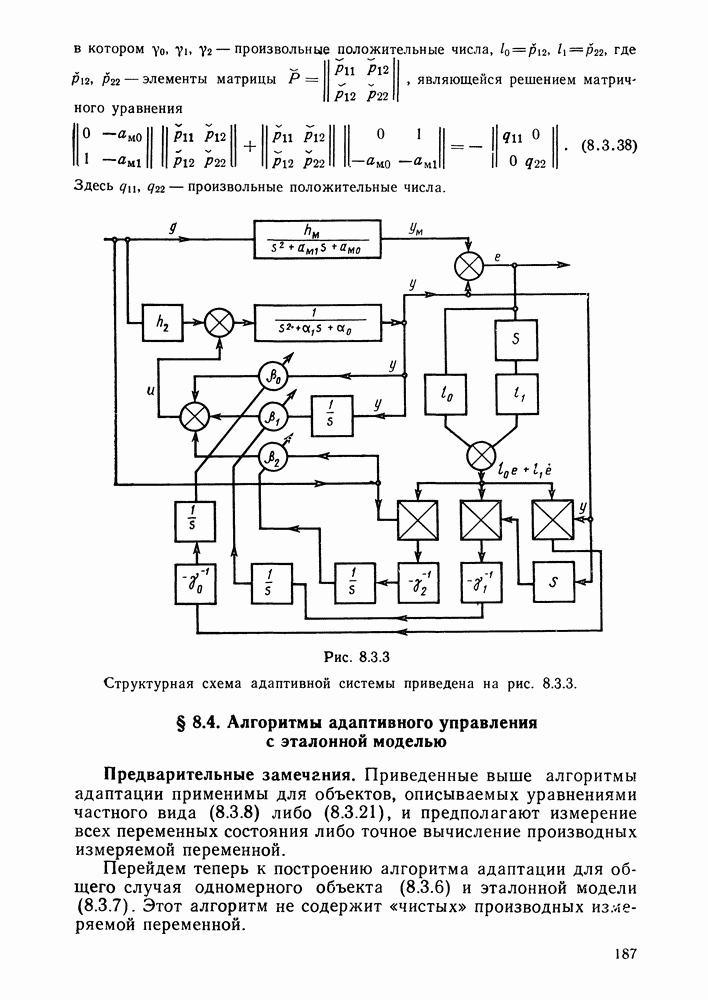
- § 8.3. Адаптивные системы с эталонной моделью
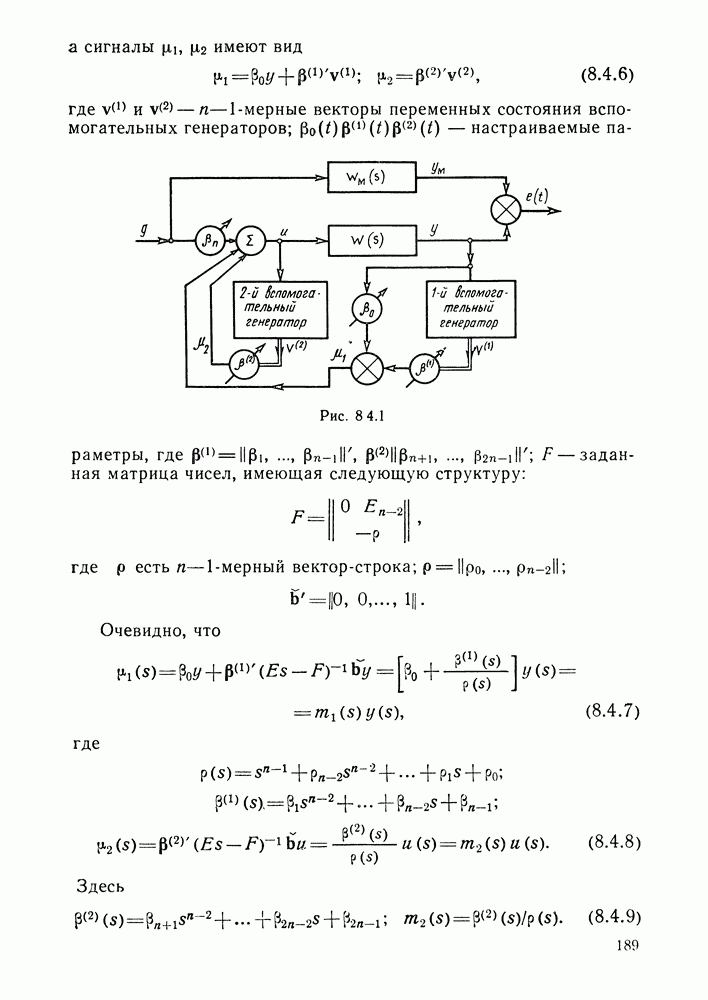
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
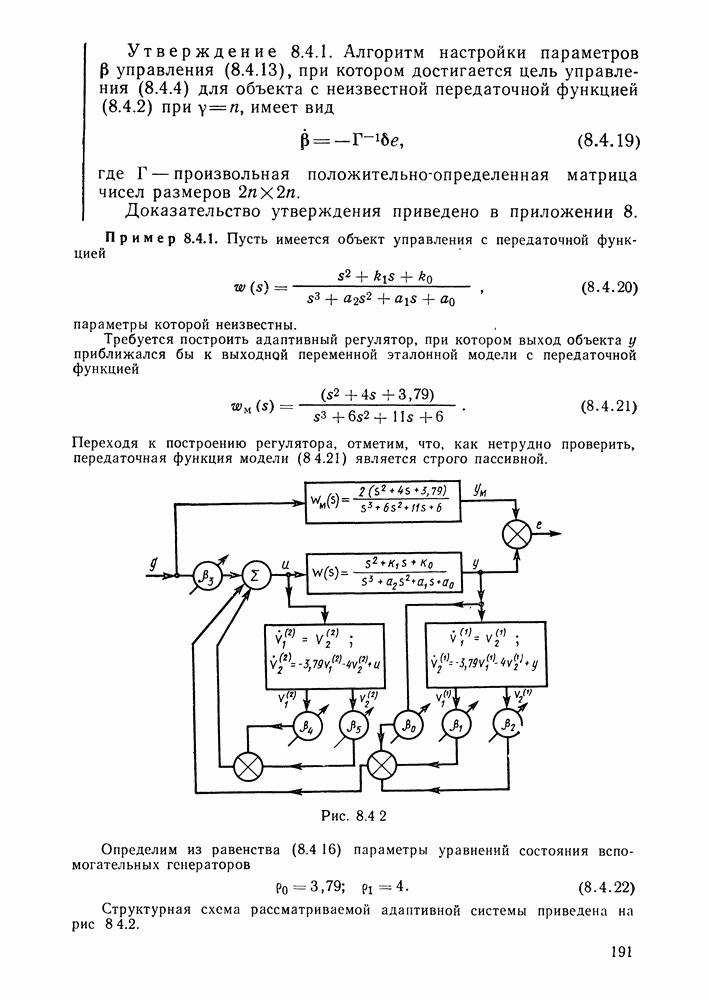
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
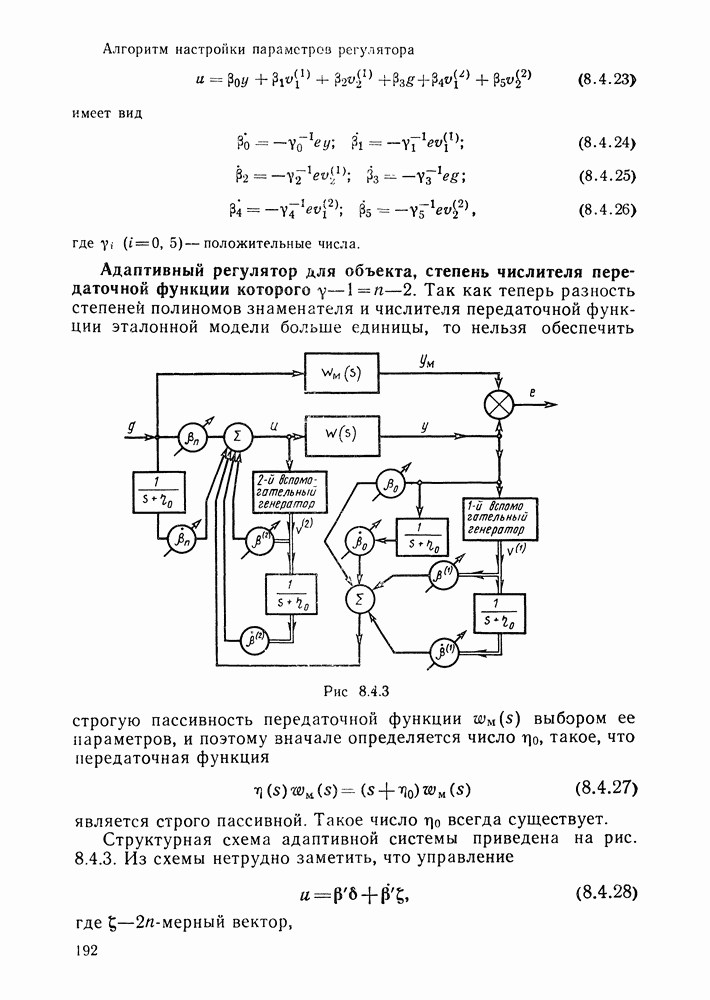
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ