| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
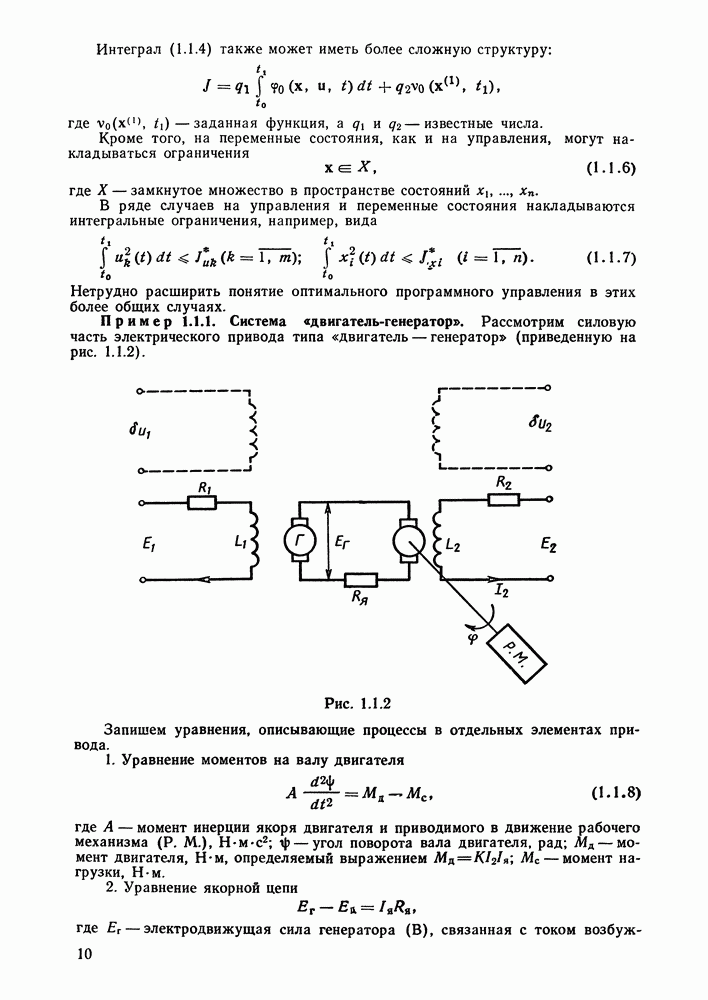
Точность и качество оптимальных систем.
Возвращаясь к общему случаю, исследуем зависимость точности и качества оптимальной системы (4.3.1), (4.3.2) от коэффициентов функционала (4.3.3).
Вначале введем понятие о точности и качестве этой системы. Для этого необходим  -мерный вектор
-мерный вектор  регулируемых переменных, связанных с вектором
регулируемых переменных, связанных с вектором  соотношением
соотношением

где N — заданная матрица чисел размеров  .
.
Пусть к объекту (4.3.1) приложено внешнее возмущение  . Тогда уравнение объекта примет вид
. Тогда уравнение объекта примет вид

где W — заданная матрица чисел размеров  .
.
В качестве  -мерного вектора
-мерного вектора  обычно принимают типовые возмущения: ступенчатые, гармонические, импульсные и т. п.
обычно принимают типовые возмущения: ступенчатые, гармонические, импульсные и т. п.
Так, ступенчатые возмущения

Точность системы (4.3.1), (4.3.2), (4.3.39) определяется значением вектора установившихся ошибок по регулируемым переменным [4.15].
При ступенчатых возмущениях он называется вектором статических ошибок, компоненты которого

Качество рассматриваемой системы определяется временем регулирования  и перерегулированием
и перерегулированием  по каждой из регулируемых переменных при ступенчатых внешних воздействиях.
по каждой из регулируемых переменных при ступенчатых внешних воздействиях.
Время регулирования по  регулируемой переменной находится как обычно (это время, через которое
регулируемой переменной находится как обычно (это время, через которое  попадает в пятипроцентную трубку в окрестности
попадает в пятипроцентную трубку в окрестности  ), а
), а

Требования к точности и качеству системы (4.3.1), (4.3.2), (4.3.38) выражаются соотношениями:

где  — заданные числа.
— заданные числа.
Теперь введем в рассмотрение функционал, содержащий регулируемые переменные:

Производные компонент вектора  в этом функционале можно исключить, используя соотношение
в этом функционале можно исключить, используя соотношение  . Для того чтобы избежать произведений
. Для того чтобы избежать произведений  и и в подынтегральном выражении, далее будем полагать, что
и и в подынтегральном выражении, далее будем полагать, что

В этом случае функционал (4.3.43) принимает стандартный вид

где

 -мерный вектор внешних возмущений и пусть он приложен к объекту в местах приложения управления. Это означает, что матрицы В и W в (4.3.40) совпадают:
-мерный вектор внешних возмущений и пусть он приложен к объекту в местах приложения управления. Это означает, что матрицы В и W в (4.3.40) совпадают:

При этом условии и выполнении (4.3.46) можно установить в явной форме связь между точностью и качеством системы, с одной стороны, и коэффициентами функционала, в смысле которого эта система  с другой. В конструктивной форме эта связь выражается [4.15] следующим образом.
с другой. В конструктивной форме эта связь выражается [4.15] следующим образом.
Утверждение 4.3.2. Пусть нужно построить закон управления (4.3.2) для объекта (4.3.39), (4.3.40), такой, чтобы эта система удовлетворяла требованиям (4.3.43), (4.3.44) к точности и качеству. Для этого достаточно использовать процедуру АКОР для объекта (4.3.1) и функционал (4.3.45). Для обеспечения требований (4.3.43) к точности коэффициенты этого функционала выбираются из соотношений

где  —
—  -мерный вектор чисел с компонентами (4.3.41). Требования (4.3.44) к времени регулирования будут выполнены, если при достаточно больших
-мерный вектор чисел с компонентами (4.3.41). Требования (4.3.44) к времени регулирования будут выполнены, если при достаточно больших  принять
принять

При этом переходные процессы по регулируемым переменным будут носить апериодический характер.
Доказательство первой части утверждения [соотношения (4.3.50)] опирается на связь между вектором регулируемых переменных и внешним возмущением и на условие оптимальности (4.3.8). Указанная связь имеет вид

Действительно, преобразуя (4.3.40) по Лапласу при нулевых начальных условиях, получим, используя (4.3.39), (4.3.49),

Исключим из этого выражения сумму  . Для этого на основе (4.3.2), (4.3.40) запишем
. Для этого на основе (4.3.2), (4.3.40) запишем  . Отсюда, прибавляя к обеим частям вектор f, получим соотношение
. Отсюда, прибавляя к обеим частям вектор f, получим соотношение  , подставляя которое в (4.3.53) приходим к (4.3.52). Эту зависимость запишем в виде
, подставляя которое в (4.3.53) приходим к (4.3.52). Эту зависимость запишем в виде

Отсюда следует, что

Теперь воспользуемся условием оптимальности (4.3.8), которое с учетом структуры матрицы в функционале (4.3.47) представим как

При выводе последнего выражения использовалось очевидное тождество

Подставляя (4.3.55) в (4.3.54) и пренебрегая при достаточно больших  слагаемым
слагаемым

получим

Учитывая, что  , и умножая (4.3.56) на
, и умножая (4.3.56) на  , а также полагая, что
, а также полагая, что  , найдем
, найдем

Если выбрать  в соответствии с соотношением (4.3.50), то, как следует из (4.3.57), статические ошибки в системе будут не более
в соответствии с соотношением (4.3.50), то, как следует из (4.3.57), статические ошибки в системе будут не более  .
.
Обоснование второй части утверждения (соотношения (4.3.51) и апериодичности переходных процессов по регулируемым переменным) опирается на (4.3.56) и гипотезу, которую приведем ниже.
Соотношение (4.3.56) в развернутой форме имеет вид

При

(с точностью до указанного при построении (4.3.56) слагаемого) выражение (4.3.58) превращается в тождество. Оригинал изображения (4.3.59)

Отсюда следует, что время регулирования  m), а переходный процесс апериодический. Такой вывод опирается на гипотезу, что решение (4.3.59) уравнения (4.3.58) единственно.
m), а переходный процесс апериодический. Такой вывод опирается на гипотезу, что решение (4.3.59) уравнения (4.3.58) единственно.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
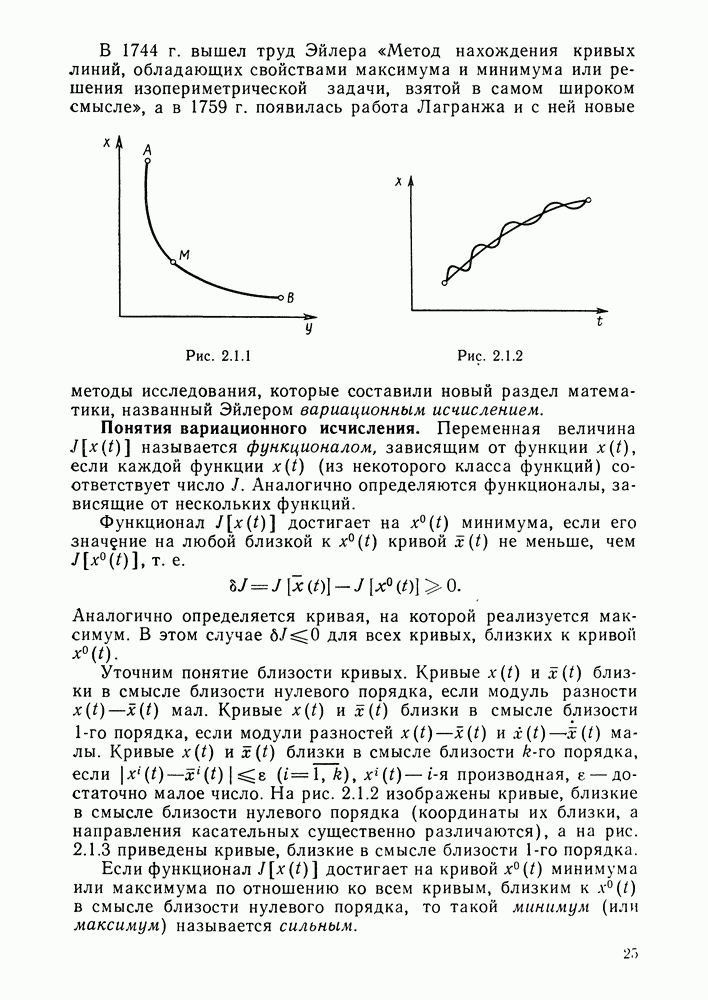
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
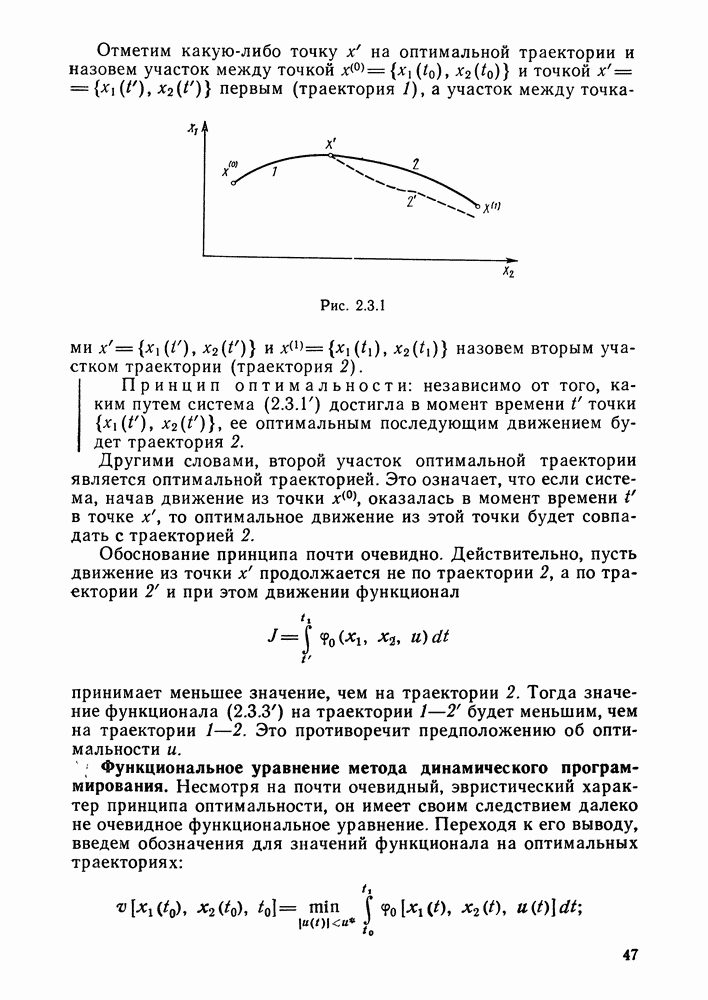
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
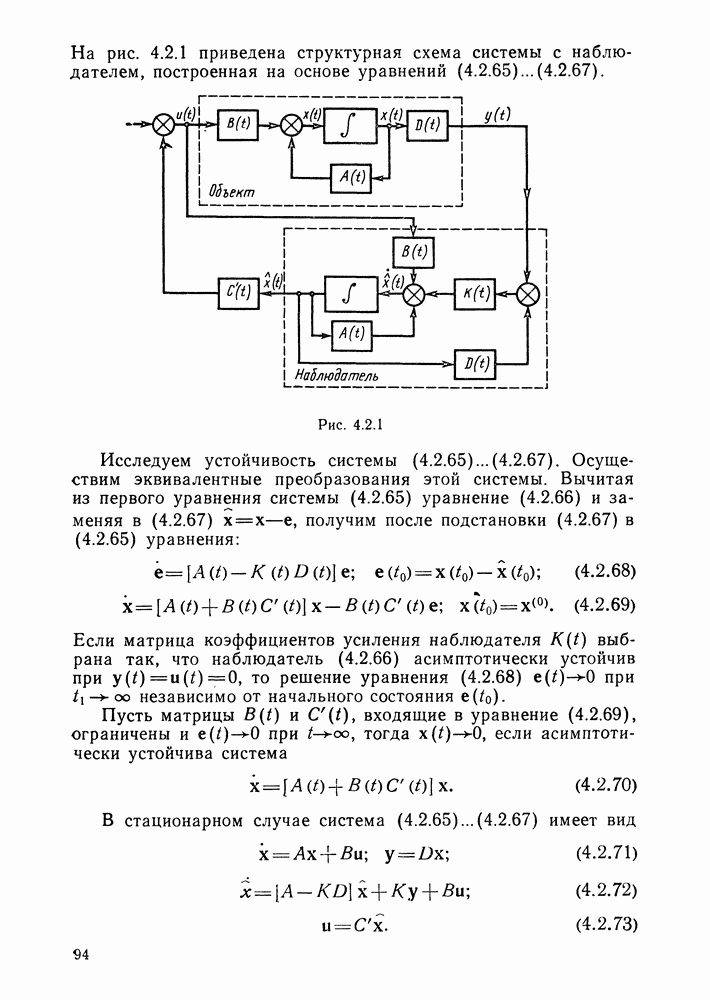
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
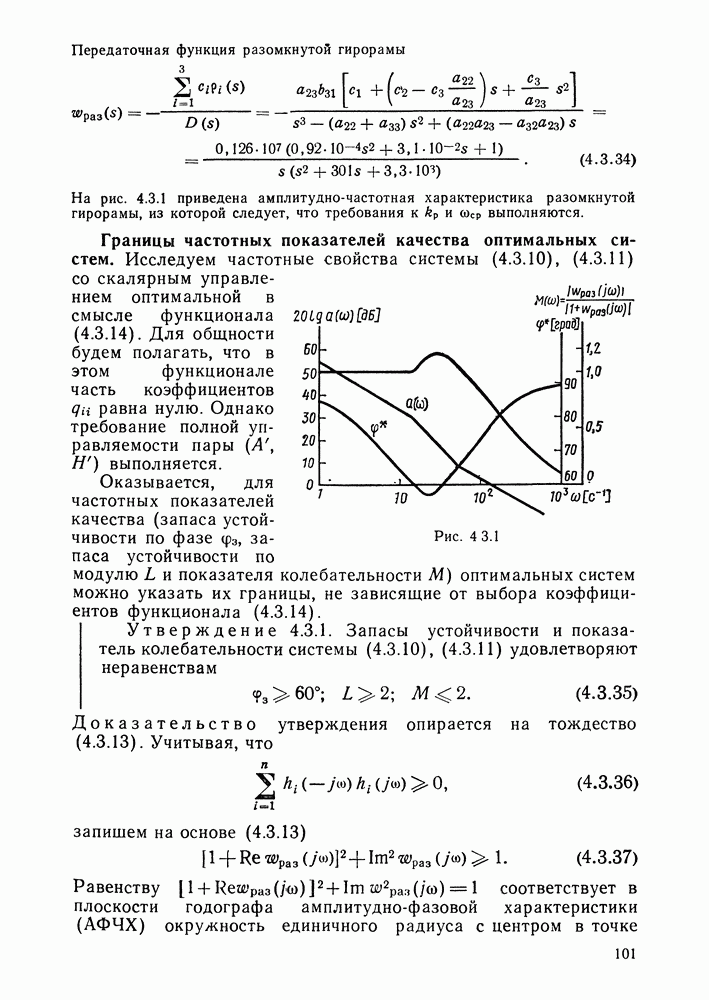
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
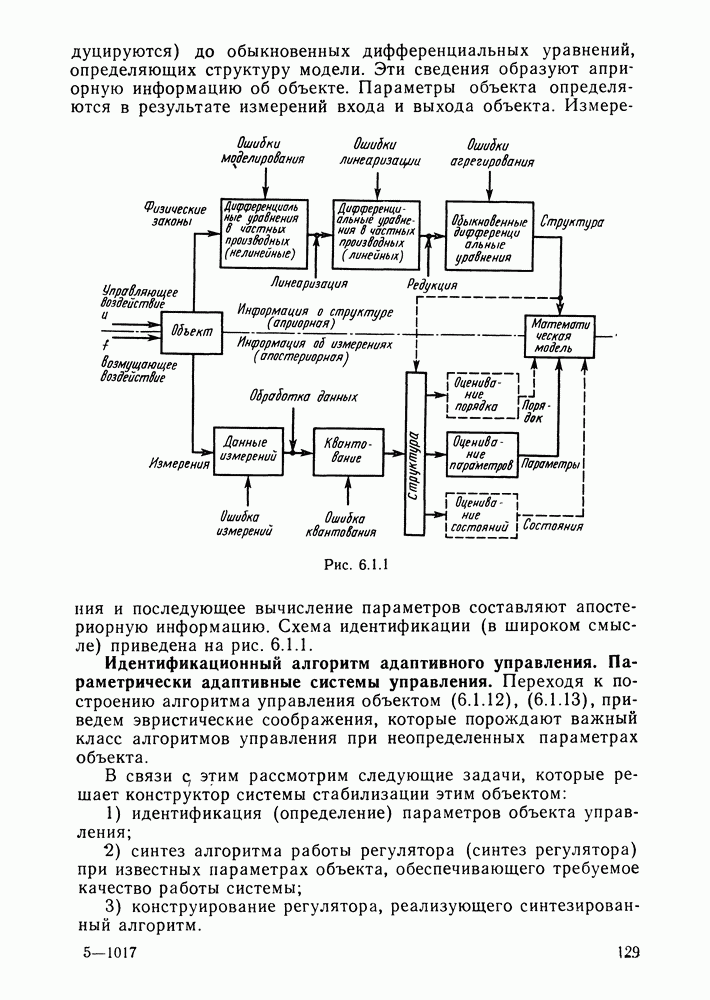
- Понятие об идентификации.
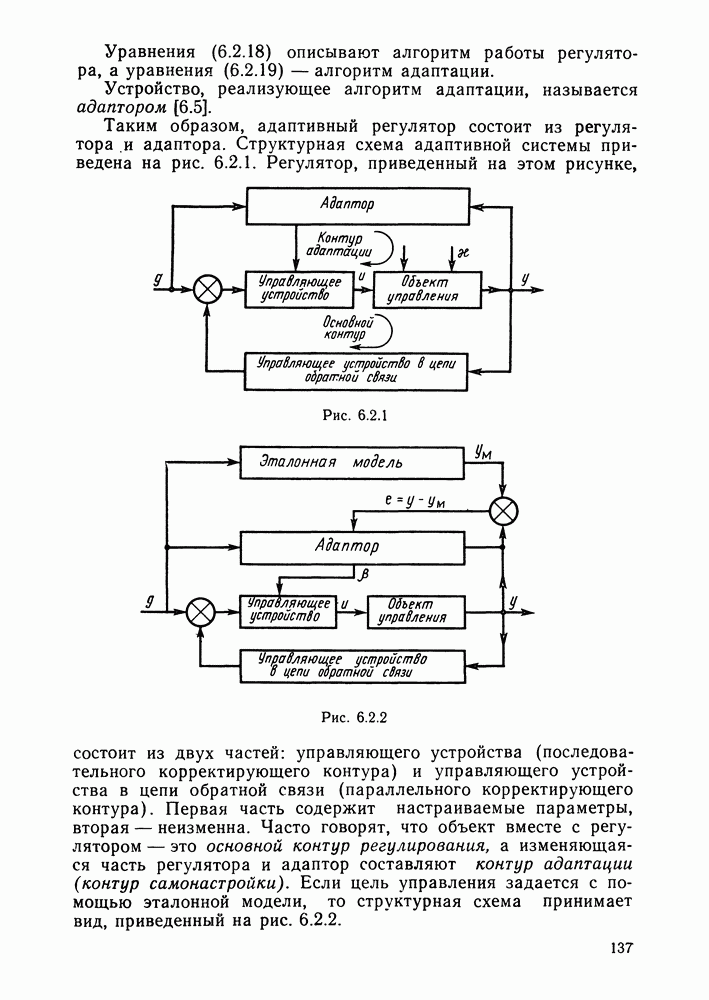
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
- § 8.3. Адаптивные системы с эталонной моделью
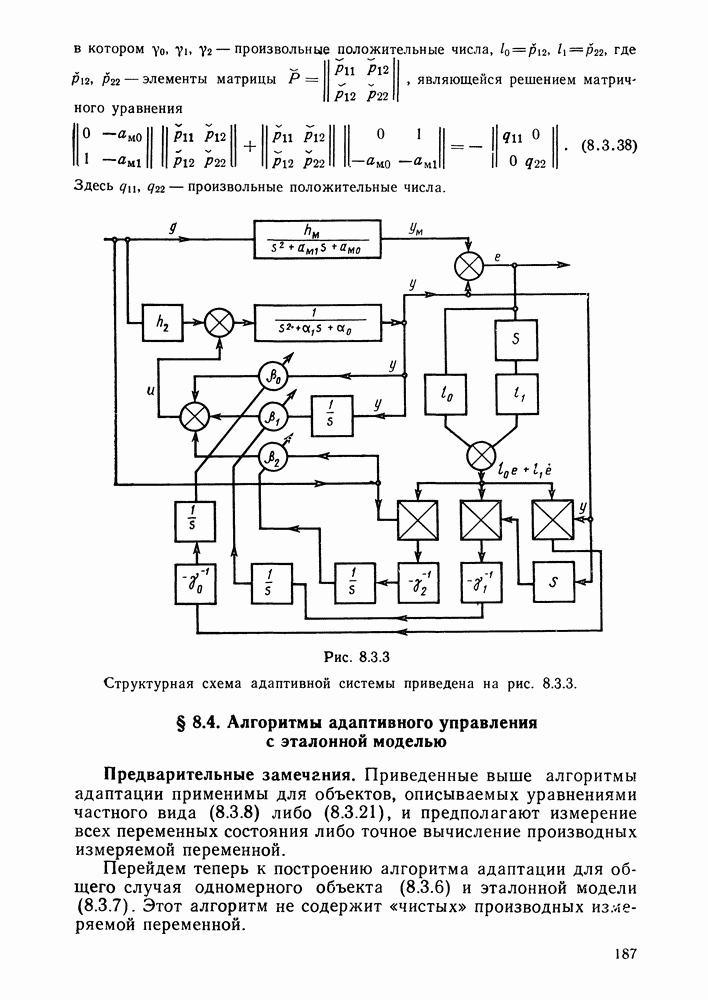
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
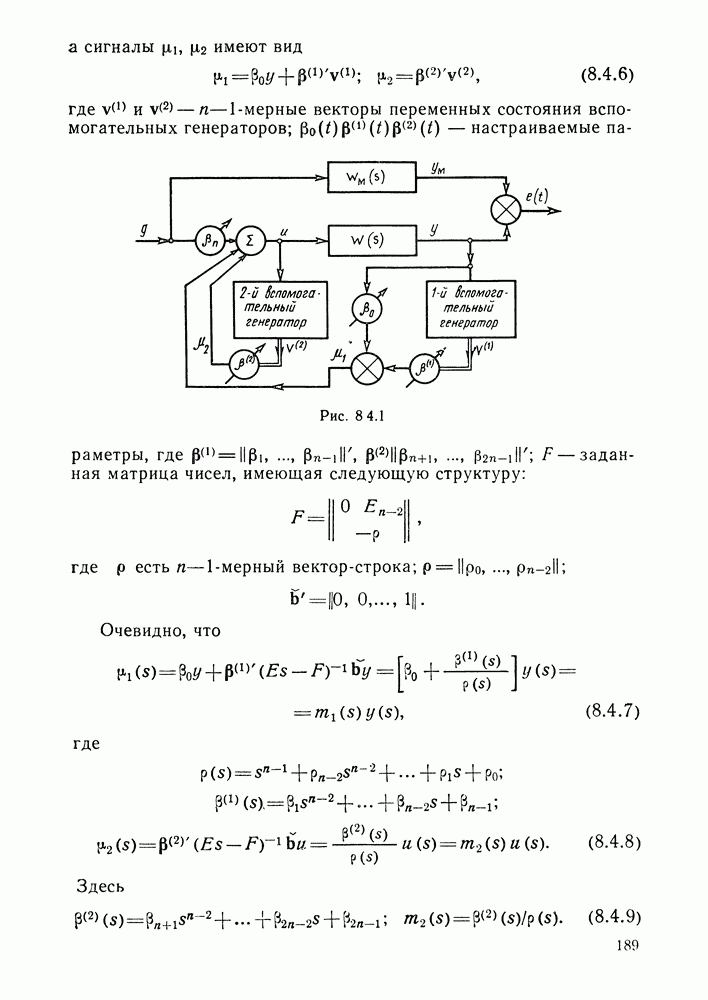
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
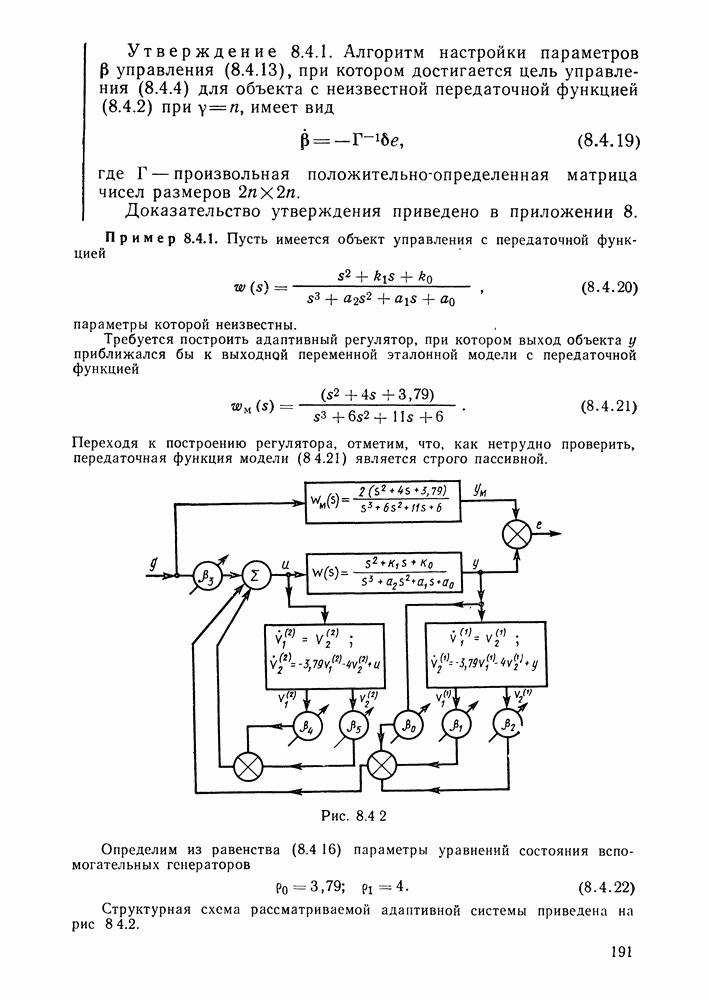
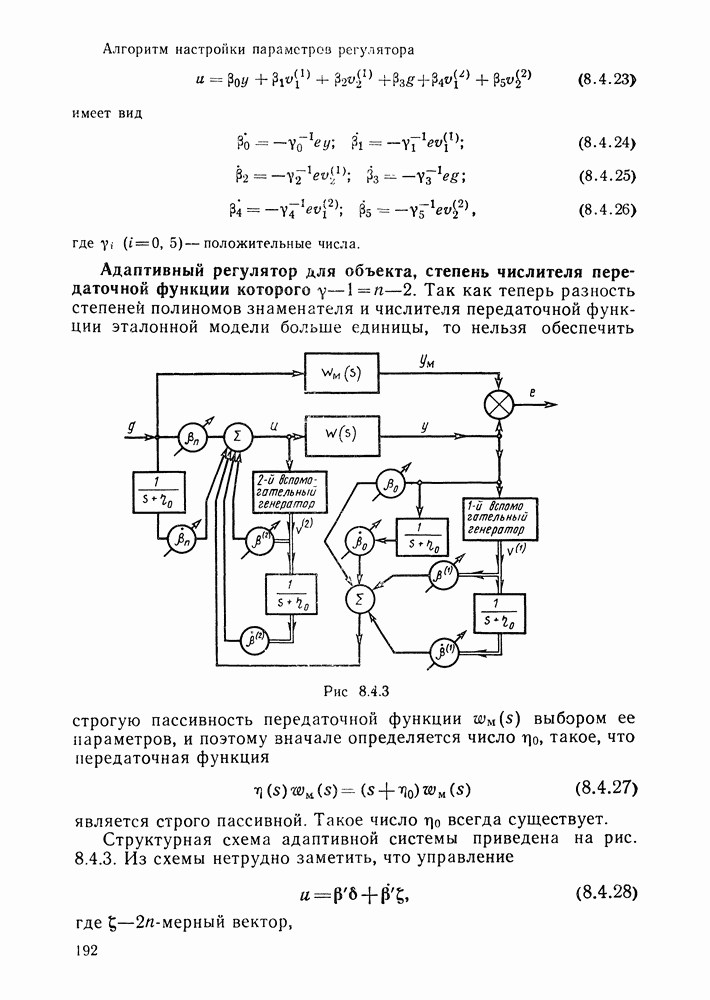
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ