| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
1. Найдем вначале уравнения для ошибки  ) наблюдения. Для этого вычтем из уравнения объекта (5.2.1) уравнение наблюдателя (5.2.6), тогда получим
) наблюдения. Для этого вычтем из уравнения объекта (5.2.1) уравнение наблюдателя (5.2.6), тогда получим

2 Теперь вычислим значение критерия (5.2.7) на решениях  . В связи с этим введем обозначения
. В связи с этим введем обозначения

где  - математическое ожидание;
- математическое ожидание;  — матрица дисперсий ошибок наблюдения.
— матрица дисперсий ошибок наблюдения.
Нетрудно видеть, что

Отсюда следует, что

Матрица  называется матрицей моментов второго порядка. Элементы матрицы
называется матрицей моментов второго порядка. Элементы матрицы  определяются выражениями
определяются выражениями

Таким образом,  можно записать в виде
можно записать в виде

Утверждение  . Среднее значение квадрата ошибка восстановления (5.2.7) выражается через математическое ожидание и матрицу дисперсий ошибок наблюдения следующим образом:
. Среднее значение квадрата ошибка восстановления (5.2.7) выражается через математическое ожидание и матрицу дисперсий ошибок наблюдения следующим образом:

Доказательство этого соотношения получаем, если с учетом  запишем
запишем

Далее для простоты полагаем  .
.
3. Переходя к минимизации критерия (5.2.7), заметим что в соответствии с  второе слагаемое достигает минимума, когда
второе слагаемое достигает минимума, когда  . Найдем условия, при которых выполняется это равенство. В соответствии с формулой Коши (1.3.18) решение уравнения
. Найдем условия, при которых выполняется это равенство. В соответствии с формулой Коши (1.3.18) решение уравнения  имеет вид
имеет вид

где  - нормированная фундаментальная матрица решений однородного уравнения
- нормированная фундаментальная матрица решений однородного уравнения

Принимая во внимание, что  , получим на основе
, получим на основе 

Это означает, что  является решением уравнения
является решением уравнения

Если задать начальное условие наблюдателя

то  и, следовательно, решение уравнения
и, следовательно, решение уравнения 

Таким образом, доказано соотношение (5.2.11).
4. Найдем условия, при которых достигает минимума первое слагаемое в выражении  . Для этого построим вначале уравнение, которому удовлетворяет матрица дисперсий ошибок восстановления
. Для этого построим вначале уравнение, которому удовлетворяет матрица дисперсий ошибок восстановления  . Такое уравнение нетрудно записать, если воспользоваться следующим утверждением [4.7].
. Такое уравнение нетрудно записать, если воспользоваться следующим утверждением [4.7].
Утверждение  . Если
. Если  — решение уравнения
— решение уравнения

(где  "белый шум" интенсивности
"белый шум" интенсивности  - стохастический вектор, не зависящий от
- стохастический вектор, не зависящий от  со средним
со средним  и матрицей дисперсий
и матрицей дисперсий  матрица дисперсий
матрица дисперсий

удовлетворяет матричному дифференциальному уравнению

Для доказательства этого утверждения запишем вначале в соответствии с 

Для вычисления значения матрицы  воспользуемся выражением для решения уравнения
воспользуемся выражением для решения уравнения  :
:

Тогда

Второе и третье слагаемые в этом выражении равны нулю, так как векторы  независимы и
независимы и  .
.
Преобразуем последнее слагаемое с учетом (5.1.3)

Подставляя  , получим с учетом
, получим с учетом 

Аналогично  получим
получим

(Нетрудно видеть, что  ). Дифференцируя это равенство с учетом соотношения
). Дифференцируя это равенство с учетом соотношения

и равенства

получим (П 6 14), и таким образом, утверждение  доказано.
доказано.
Используя это утверждение, запишем уравнение для матрицы дисперсий ошибок восстановления

5. Сформулируем одно утверждение, касающееся свойств решений матричного дифференциального уравнения Риккати (4.1.28).
Отметим вначале, что в соответствии с (2.3.11) функция

являющаяся решением уравнения метода динамического программирования, возникшего в связи с задачей о минимуме функционала (4.1.26) на связях (4.1.25), позволяет вычислить значение функционала (4.1.26) на оптимальных траекториях. Это значение

Вычислим значение функционала (4.1.26) при неоптимальном управлении

где  - произвольная, но фиксированная матрица функций времени, заданных на интервале
- произвольная, но фиксированная матрица функций времени, заданных на интервале  .
.
Объект, замкнутый управлением  , описывается уравнением
, описывается уравнением

где

а функционал (4.1.26) принимает вид

где

Итак, необходимо вычислить значение функционала  на решениях уравнения
на решениях уравнения  .
.
Не фиксируя пока  , будем искать значение функционала (П 6.29) как
, будем искать значение функционала (П 6.29) как

Из этого выражения следует, в частности, что

Дифференцируя обе части  с учетом
с учетом  , получим
, получим

Отсюда следует уравнение

Это уравнение с учетом  примет вид
примет вид

Из  получим значение функционала
получим значение функционала 

Очевидно, что

так как  — значение этого функционала при оптимальном управлении.
— значение этого функционала при оптимальном управлении.
Из  следует, что
следует, что  поскольку вектор
поскольку вектор  произвольный. Кроме того, используя произвольность
произвольный. Кроме того, используя произвольность  , заключаем, что
, заключаем, что

Таким образом, доказано следующее утверждение.
Утверждение  . Матричное уравнение
. Матричное уравнение  с краевым условием
с краевым условием  имеет решение, удовлетворяющее неравенству
имеет решение, удовлетворяющее неравенству  . Это неравенство обращается в равенство, если
. Это неравенство обращается в равенство, если

Если функционал (4.1.26) имеет вид  , то уравнение
, то уравнение  принимает вид
принимает вид

а матрица

6. Введем (полагая дальше для простоты  ) в рассмотрение дифференциальное уравнение для некоторой матрицы
) в рассмотрение дифференциальное уравнение для некоторой матрицы  (размеров
(размеров  ), которое получается
), которое получается  уравнения
уравнения  обращением времени путем введения
обращением времени путем введения  и последующей замены
и последующей замены  на
на  :
:

Очевидно, что решения уравнений  связаны равенством
связаны равенством

Применим теперь утверждение  к уравнению
к уравнению  . Матрица
. Матрица  достигает минимума, если матрица
достигает минимума, если матрица

Действительно, уравнение  совпадает с уравнением
совпадает с уравнением  , если в последнем положить
, если в последнем положить  ,
,

и тогда на основе  получаем
получаем  . Подставляя
. Подставляя  , получим уравнение для наименьшего значения матрицы
, получим уравнение для наименьшего значения матрицы  :
:

Решения уравнений  удовлетворяют условию
удовлетворяют условию

Обращая время в уравнении  , заключаем, что
, заключаем, что

где  - решение уравнения (5.2.9), которое совпадает с
- решение уравнения (5.2.9), которое совпадает с  после обращения времени.
после обращения времени.
Из  следует
следует

и поэтому матрица  , совпадающая при
, совпадающая при  с матрицей (5.2.8), минимизирует наблюдатель, и таким образом, утверждение 5.2.2 доказано.
с матрицей (5.2.8), минимизирует наблюдатель, и таким образом, утверждение 5.2.2 доказано.
Отметим, что полученный результат не зависит от конкретного момента времени t, который выбран для минимизации критерия (5.2.7) и выбора матрицы  , поэтому матрица (5.2.8) минимизирует (5.2.7) одновременно для всех
, поэтому матрица (5.2.8) минимизирует (5.2.7) одновременно для всех  и любых знакоопределенных матриц
и любых знакоопределенных матриц  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
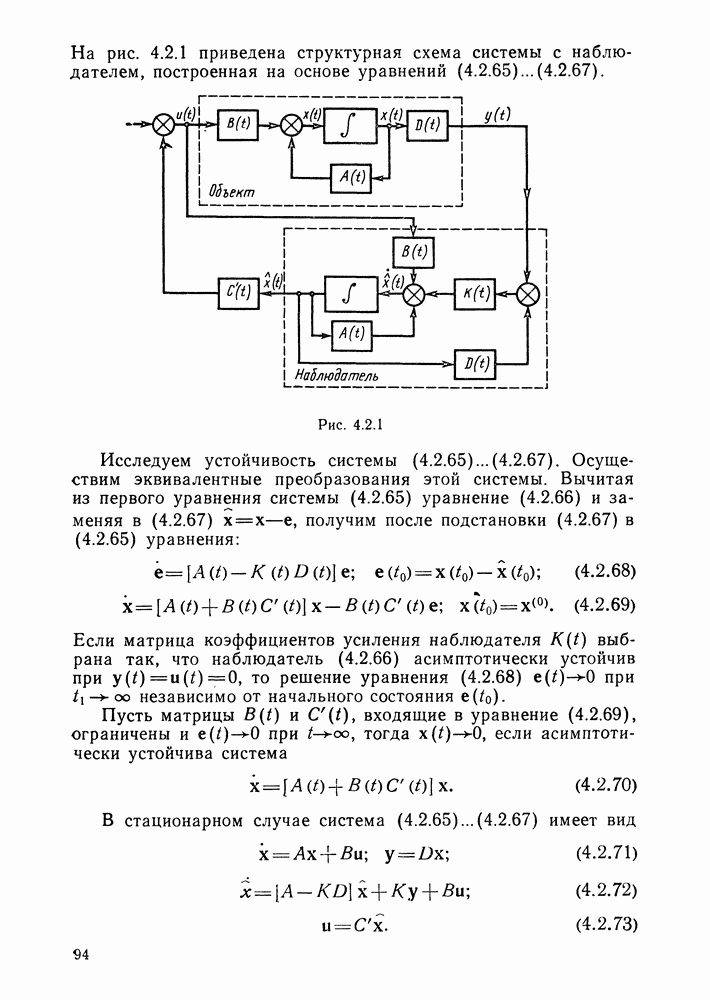
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
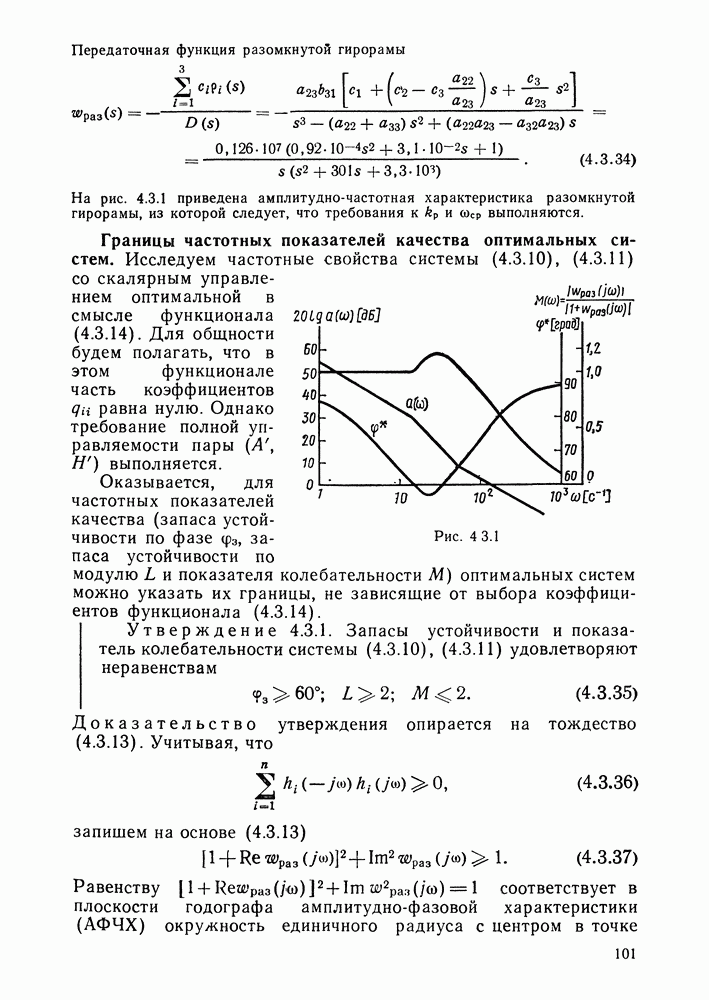
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
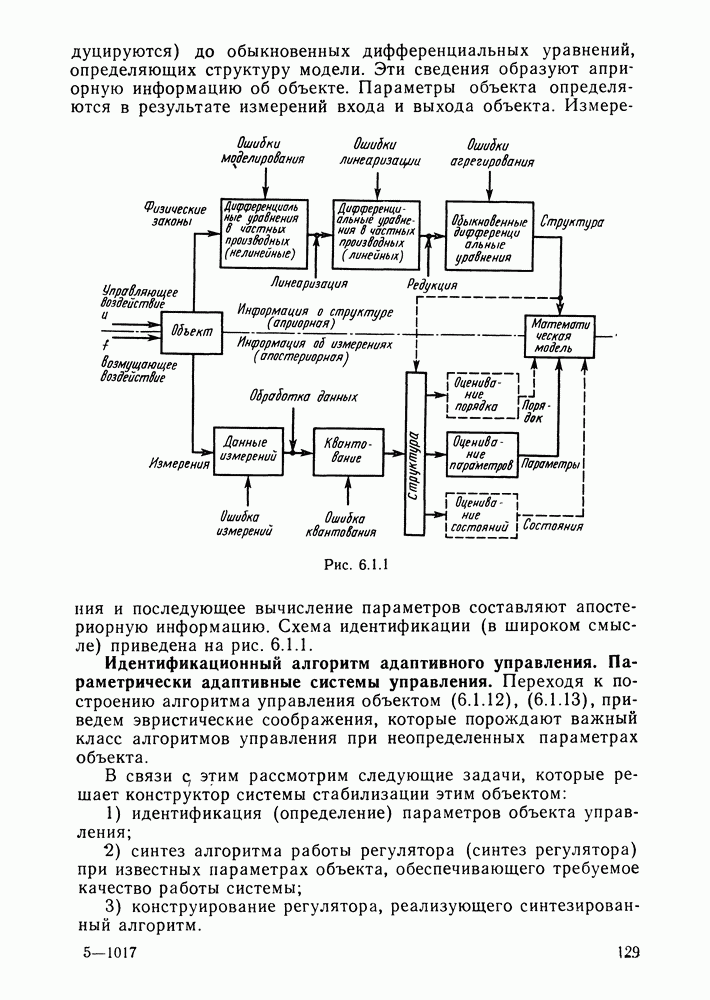
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
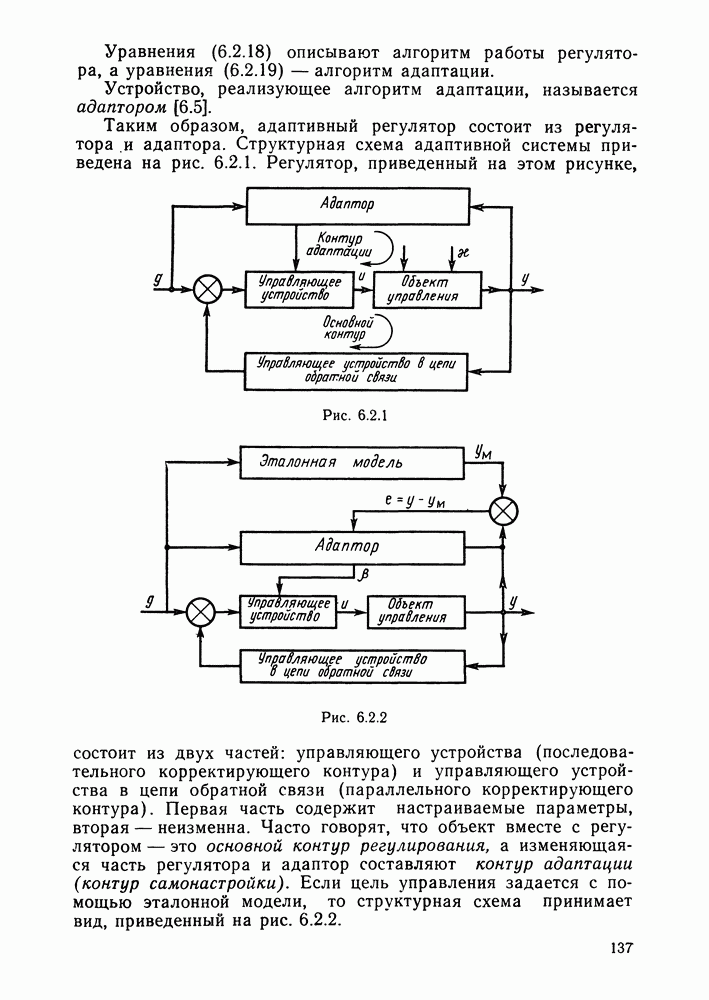
- § 6.2. Структура адаптивных систем
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
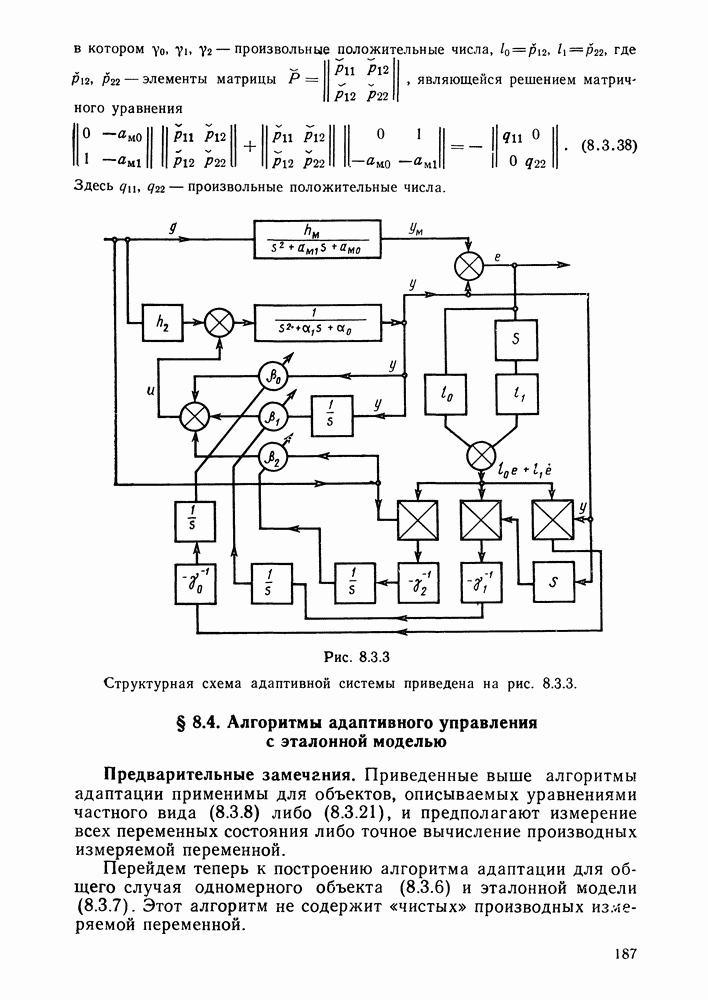
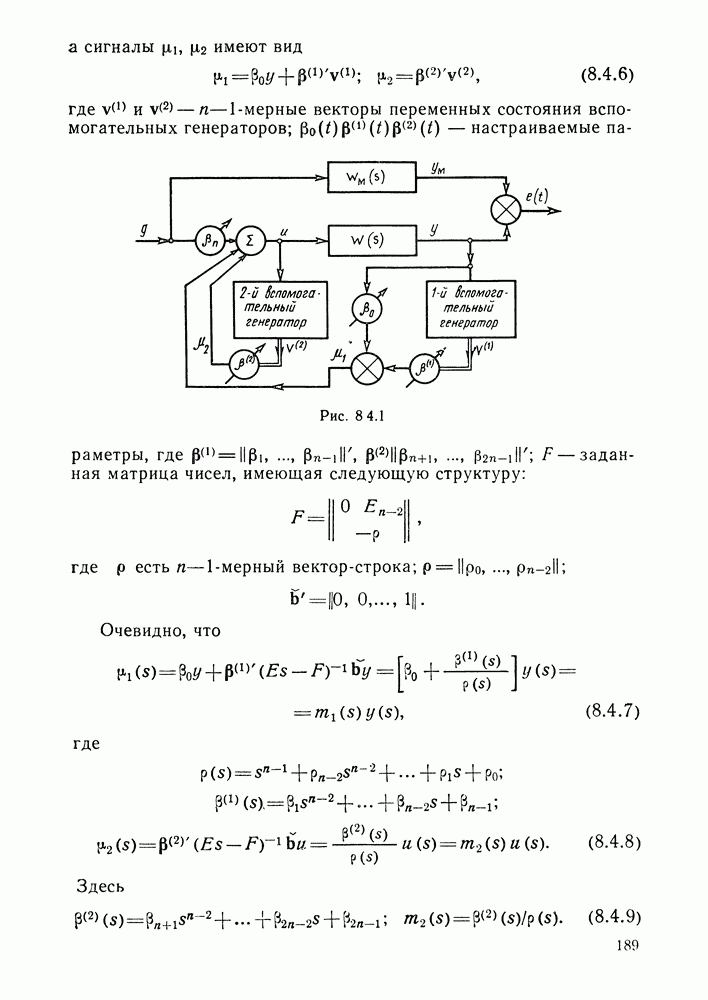
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
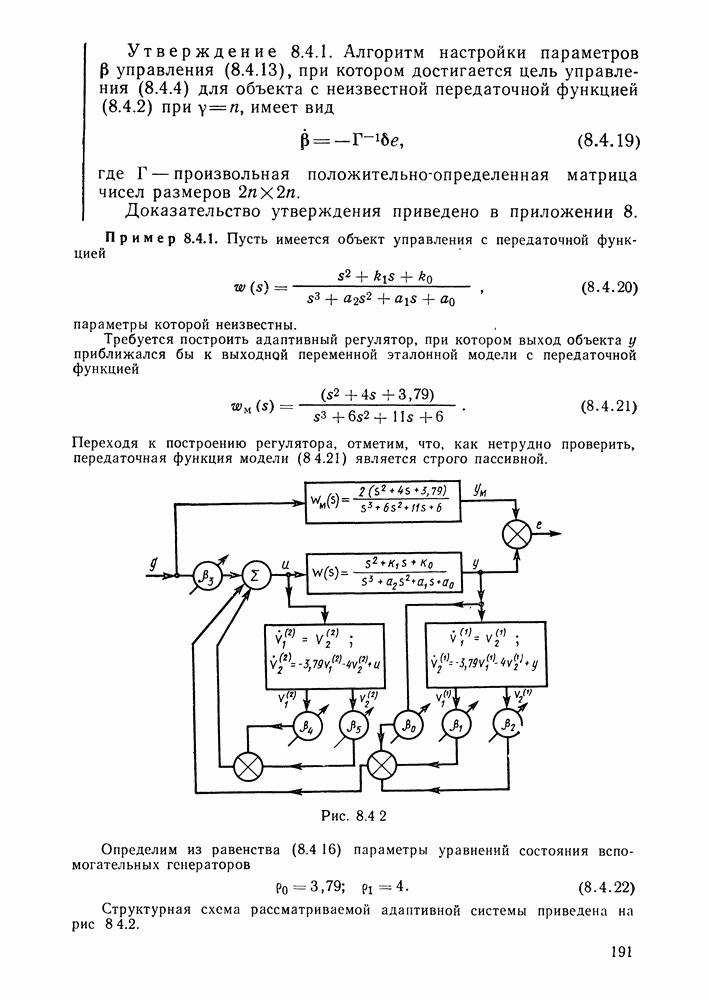
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
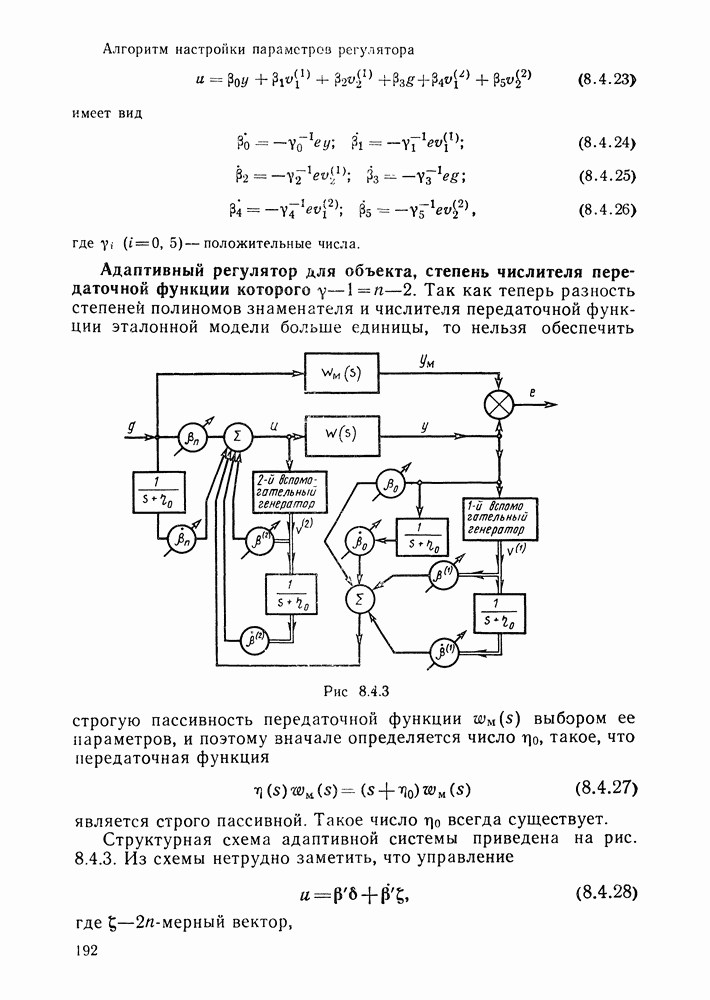
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ