| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
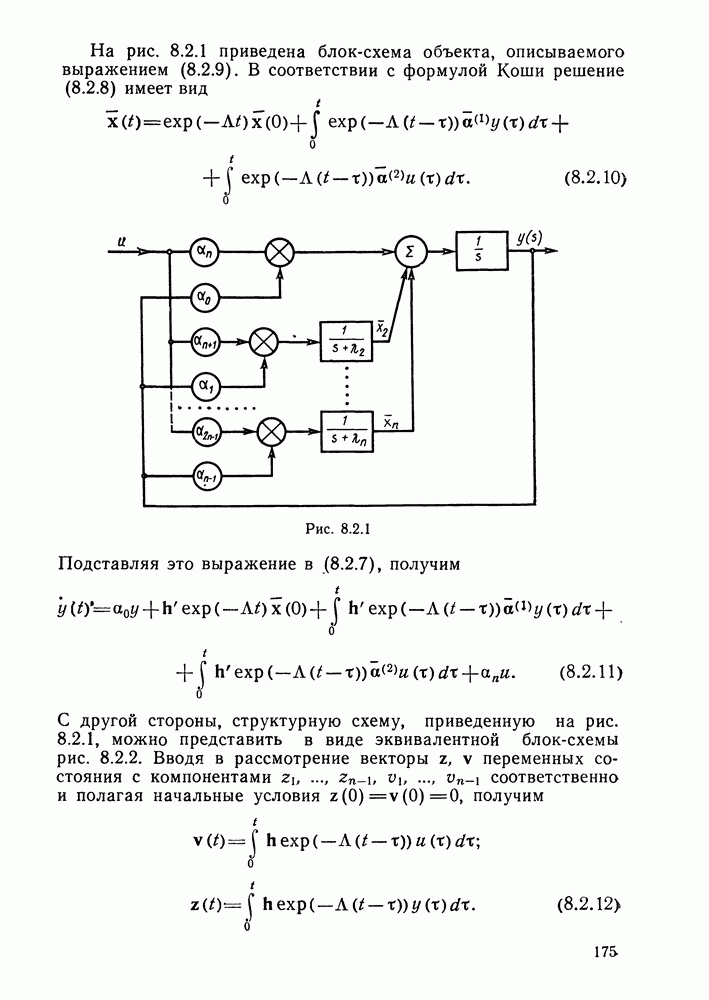
Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
Рассмотрим объект управления, описываемый уравнениями
 (5.3.10)
(5.3.10)
где  - последовательности некоррелированных векторных стохастических величин с нулевым средним и заданными матрицами дисперсий
- последовательности некоррелированных векторных стохастических величин с нулевым средним и заданными матрицами дисперсий  . Здесь
. Здесь

Пусть  — случайный вектор, некоррелированный с векторами
— случайный вектор, некоррелированный с векторами  , при этом
, при этом

где  известны.
известны.
Требуется найти уравнение устройства восстановления (наблюдения, фильтрации), выходами которого является оценка  неизмеряемого вектора состояний
неизмеряемого вектора состояний  .
.
При этом критерий
 (5.3.12)
(5.3.12)
(где  - заданные положительно-определенные матрицы,
- заданные положительно-определенные матрицы,  ) должен принимать наименьшее значение.
) должен принимать наименьшее значение.
Утверждение 5.3.2. Оптимальный в смысле критерия (5.3.12) наблюдатель (устройство восстановления, фильтрации) для объекта (5.3.10), (5.3.11) описывается уравнением
 (5.3.13)
(5.3.13)
в котором матрицы  определяются рекуррентными соотношениями:
определяются рекуррентными соотношениями:
 (5.3.14)
(5.3.14)
при начальном условии  .
.
Начальное условие для наблюдателя (5.3.13)
 (5.3.17)
(5.3.17)
Матрицы  размеров
размеров  являются матрицами дисперсий ошибки восстановления
являются матрицами дисперсий ошибки восстановления  . Для оптимального наблюдения среднее значение
. Для оптимального наблюдения среднее значение
 (5.3.18)
(5.3.18)
Доказательство этого утверждения аналогично непрерывному случаю [4.7].
Часто применяют оптимальные наблюдатели вида (5.3.13), в которых вместо  используется
используется  . Такой наблюдатель описывается уравнениями
. Такой наблюдатель описывается уравнениями
 (5.3.19)
(5.3.19)
где
 (5.3.20)
(5.3.20)
В стационарном случае уравнения объекта (5.3.10), (5.3.11) принимают вид

и оптимальный наблюдатель описывается уравнениями
 (5.3.23)
(5.3.23)
где
 (5.3.24)
(5.3.24)
 — матрица чисел (размеров
— матрица чисел (размеров  ), являющаяся решением уравнения
), являющаяся решением уравнения
 (5.3.25)
(5.3.25)
Матрица  находится как установившееся решение уравнения
находится как установившееся решение уравнения
 (5.3.26)
(5.3.26)
при  . Иными словами:
. Иными словами:

Пример 5.3.1. Рассмотрим гирораму, описываемую уравнениями 
 (5.3.27)
(5.3.27)
с параметрами из примера 4.1.2 и  , где
, где  -случайный гауссовский процесс типа «белый шум» с нулевым математическим ожиданием и параметром ковариационной функции
-случайный гауссовский процесс типа «белый шум» с нулевым математическим ожиданием и параметром ковариационной функции  .
.
Пусть процесс измерения  датчиком угла прецессии сопровождается случайной гауссовской помехой
датчиком угла прецессии сопровождается случайной гауссовской помехой  типа «белый шум» с нулевым математическим ожиданием и параметром ковариационной функции
типа «белый шум» с нулевым математическим ожиданием и параметром ковариационной функции  .
.
Таким образом,
 (5.3.28)
(5.3.28)
Пусть начальное состояние гирорамы
 (5.3.29)
(5.3.29)
Требуется построить наблюдатель (фильтр) переменных  , восстанавливающий значения этих переменных в моменты времени
, восстанавливающий значения этих переменных в моменты времени  , при
, при  . При этом сумма дисперсий ошибок восстановления
. При этом сумма дисперсий ошибок восстановления
 (5.3.30)
(5.3.30)
должна быть наименьшей для каждого момента времени  .
.
Переходя к решению этой задачи, запишем дискретную модель гирорамы
 (5.3.31)
(5.3.31)
значения параметров  , которой определены (4.1.94).
, которой определены (4.1.94).
В соответствии с (5 3.23). уравнения оптимального наблюдения имеют вид:
 (5.3.33)
(5.3.33)
Неизвестные параметры  в этих уравнениях определяются на основе (5 3 24):
в этих уравнениях определяются на основе (5 3 24):
 (5.3.36)
(5.3.36)
Для нахождения чисел  будем на основе (5.3.26) вычислять последовательно
будем на основе (5.3.26) вычислять последовательно  (при этом
(при этом  в силу (5.3.29)),
в силу (5.3.29)),  . После некоторого числа шагов, когда
. После некоторого числа шагов, когда  , примем
, примем
 (5.3.37)
(5.3.37)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
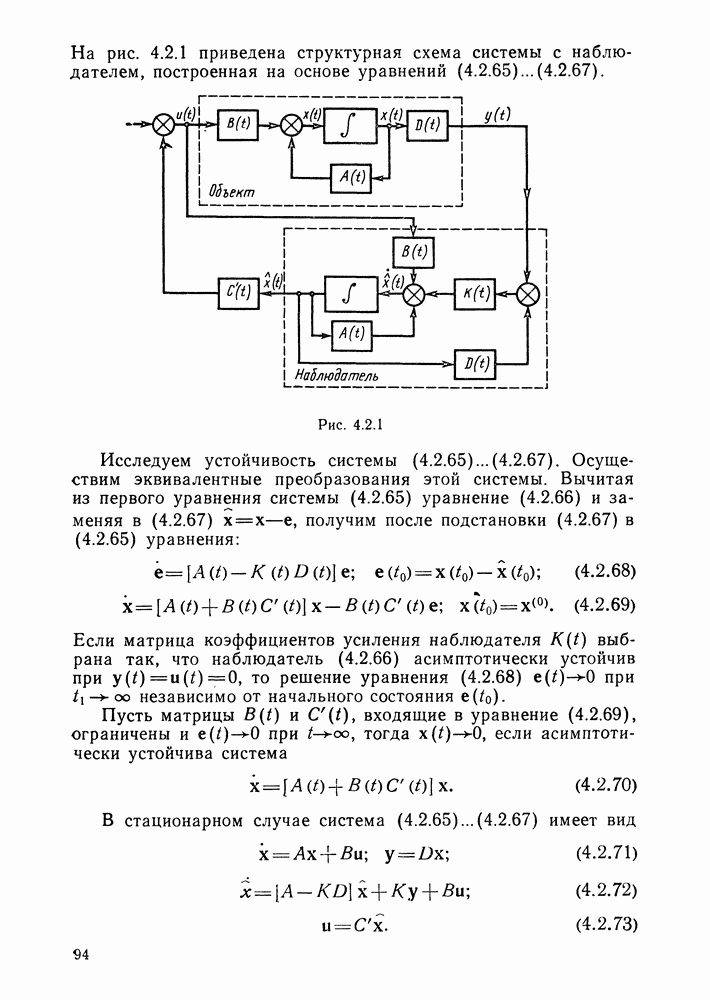
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
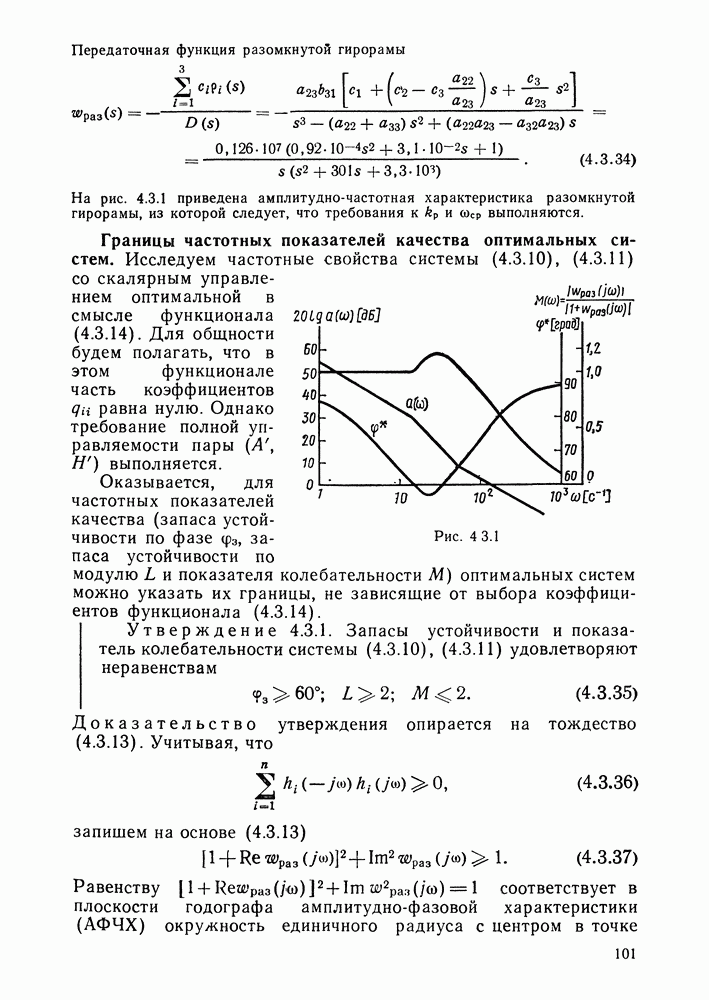
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
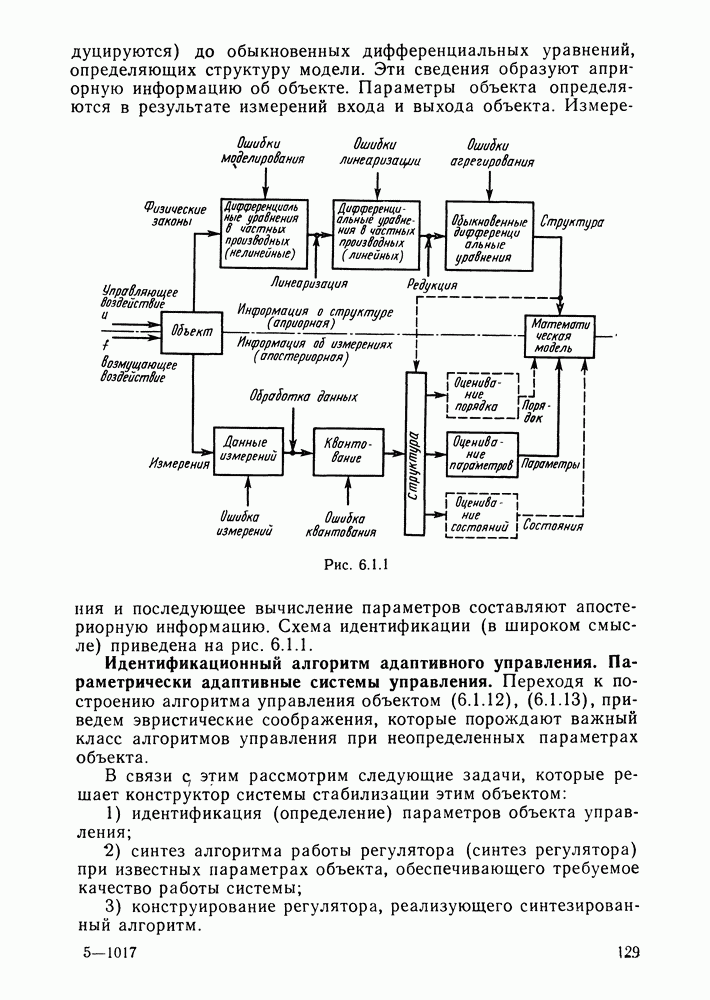
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
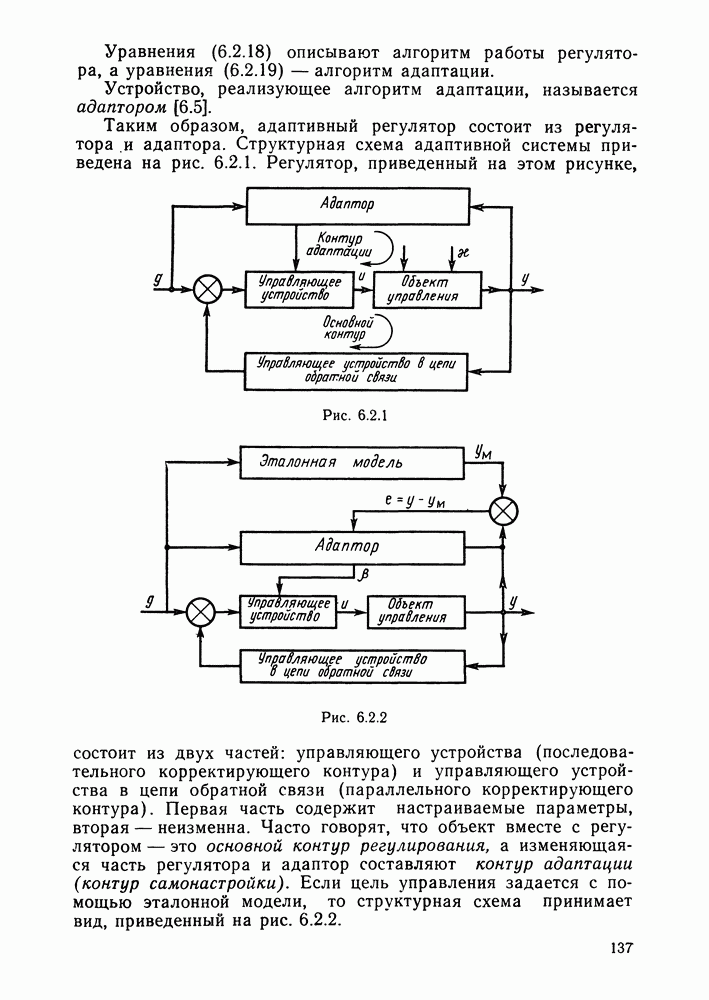
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
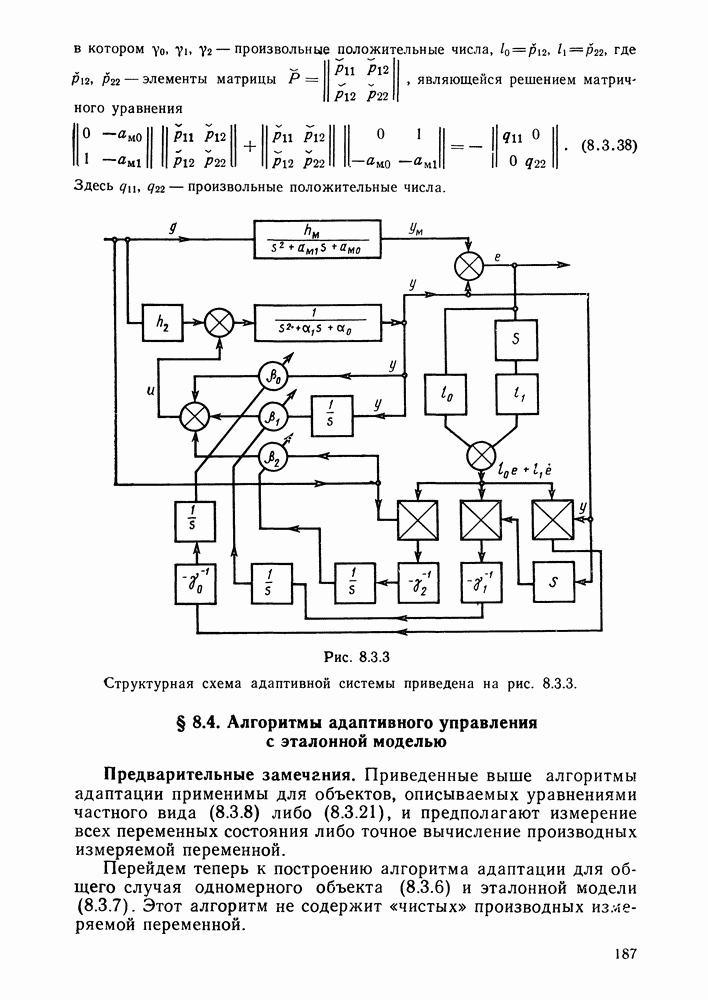
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
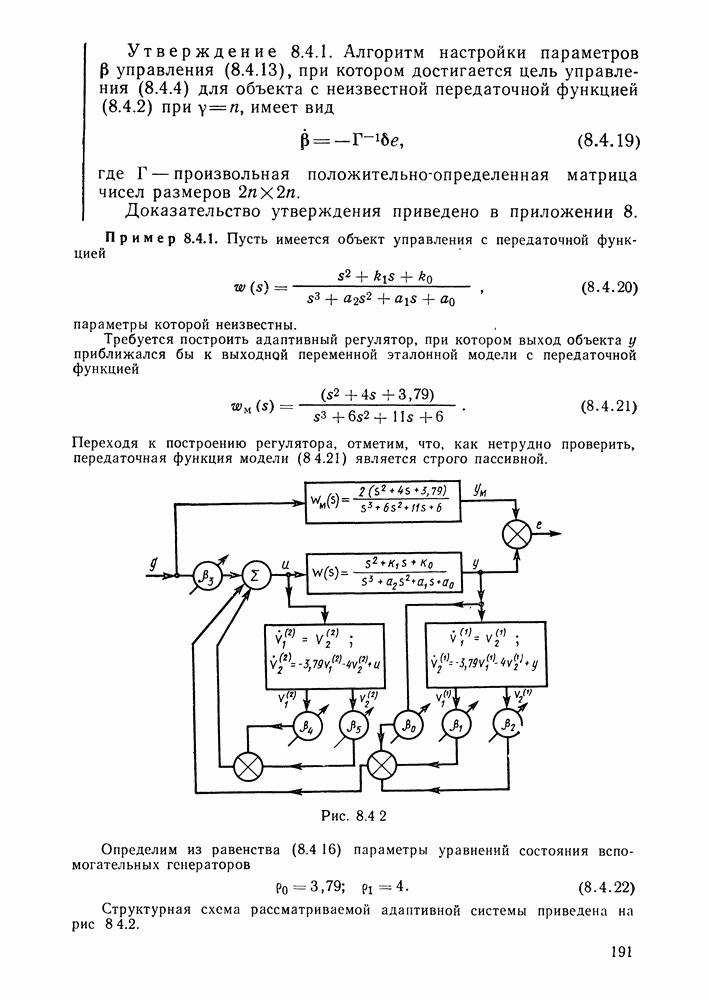
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
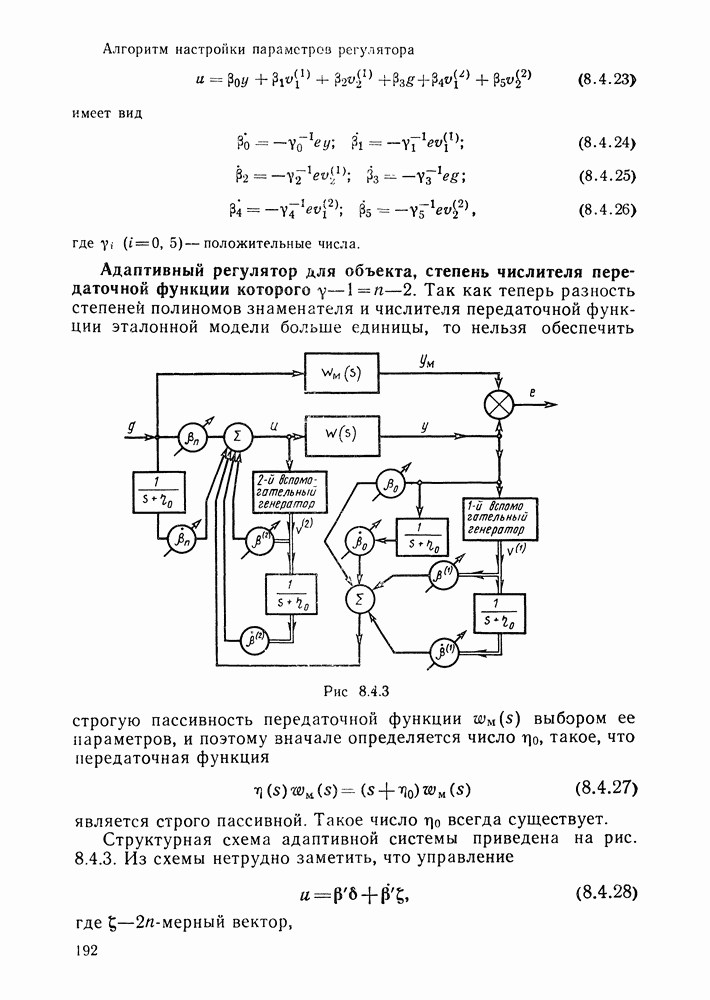
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ