6. Негэнтропийный принцип в применении к каналу с шумом

В предыдущих главах мы подчеркивали тот принцип, что получение любой информации о физической системе оплачивается соответствующим количеством отрицательной энтропии, отбираемой у системы, и обратно, что всякая информация, запасенная или переданная физической системой, соответствует увеличению негэнтропии системы.

Принцип может быть проверен на обсуждаемых примерах. Мы обсудим посвященную этому вопросу работу Рэймонда и покажем, как она должна быть исправлена в отношении ошибочного численного множителя 1/4.

Кабель, по которому мы передаем сообщение, имеет первоначально температуру Т. При нормальных условиях он имеет энтропию и уровень шума, соответствующий средней мощности в полосе шириной v и для определенного направления распространения (см. (11.17) и (17.8а)):

Здесь Рэймонд вводит неправильный множитель 4 в свое равенство (4), что приводит к множителю 1/4 в его равенстве (5).

При передаче сообщения мы используем на протяжении некоторого времени среднюю мощность Р, но не тепло. Энтропия кабеля вначале не меняется, но если мы не приняли сообщения и оставили его в кабеле, то оно будет распространяться туда и обратно и постепенно затухать вследствие эффекта Джоуля в сопротивлениях, пока вся энергия не превратится в тепло. Это конечное состояние соответствует энтропии S большей, чем исходная энтропия . Негэнтропия , введенная вначале в кабель в процессе передачи сигнала, представляется разностью

Эту величину мы и должны вычислить.

Предположим сначала очень сильную связь между сигналами и физической системой (кабелем). Это есть предположение Рэймонда, «что теплоемкость замкнутой системы настолько велика, что изменением температуры при действии устройства связи можно пренебречь». Это ведет к окончательной энтропии

откуда с помощью (17.41)

Негэнтропия представляет информацию, текущую со скоростью в секунду, и, следовательно, пропускная способность (в секунду) равна

Сравнивая этот результат с формулой Шеннона (17.15):

мы видим, что обе формулы согласуются только при очень малых отношениях , когда можно ограничиться первым членом в разложении логарифма.

Формула Шеннона была получена в специальных предположениях, не соответствующих только что рассмотренной модели. Шеннон имел в виду кабель без потерь, без омического сопротивления. Это означает отсутствие связи между электрическими токами, текущими по кабелю, и самим физическим кабелем. Предполагается, что источник шума находится вне кабеля и действует независимо. Здесь нет прямого механизма, приводящего в конце концов к увеличению энтропии, которое мы обнаружили в нашем предыдущем примере. Если мы примем представление об отсутствии связи между сигналами и кабелем, то мы должны предположить какой-либо иной механизм рассеяния. Увеличение энтропии может происходить вследствие искажения сигнала или из-за нерегулярного изменения интервалов между импульсами тока и интенсивности импульсов.

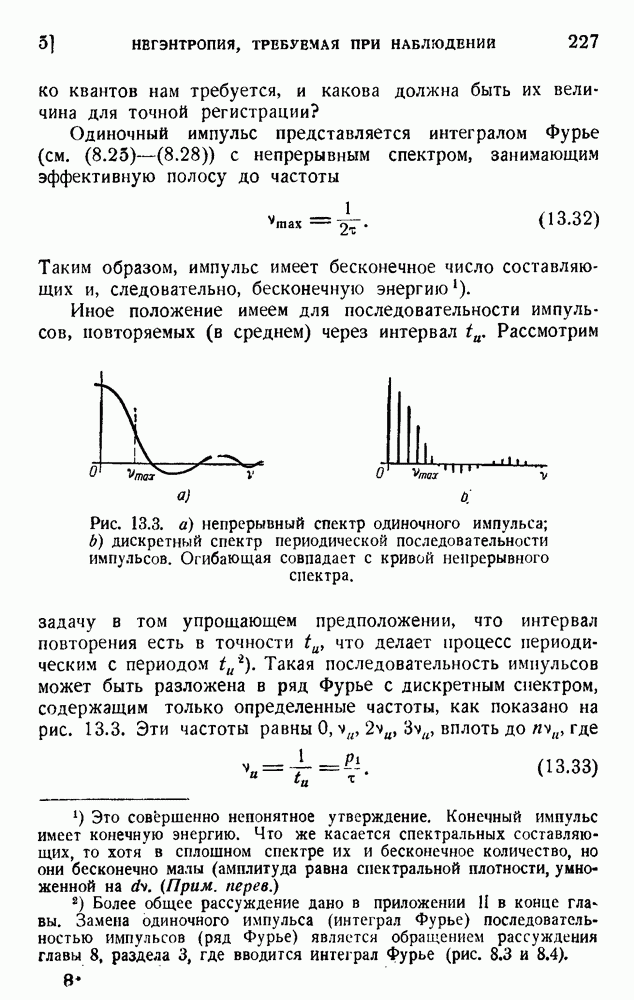
Начальное состояние есть организованная система импульсов, несущих желаемую информацию, а конечное состояние есть дезорганизованная беспорядочная последовательность импульсов, расположенных случайно и не несущих разборчивой информации. Система имеет колебательных степеней свободы (ячейка раздела 1), и случайное распределение энергии соответствует температуре Т (см. (17.8))

Если теперь предположить, что энергия постепенно нарастает ступенями , то увеличение энтропии есть

Начальное состояние соответствует только мощности шума длительностью . Конечный уровень энергии получается после того, как вся добавочная энергия распределена случайным образом между n осцилляторами и добавлена к энергии шума

Отсюда имеем для негэнтропии

Это дает пропускную способность канала (на единицу времени)

что совпадает с формулой Шеннона (17.46). Различие между нашим предыдущим результатом (17.45) и новым (17.50) обусловлено тем, что первоначальная модель поддерживалась при постоянной температуре Т, тогда как в новой модели наблюдается повышение температуры, пропорциональное увеличению случайной энергии причем равенство (17.47) все время соблюдается. Это повышение температуры уменьшает разность энтропий (17.48) и приводит к меньшей пропускной способности канала.

Логарифм появляется здесь таким же образом, как известный член в энтропии идеального газа (см. (12.12)). Ситуация в этой задаче очень сходна с той, которую мы ранее обнаружили в разделе 7 главы 13 (см. (13.55)), когда нашли, что информация растет как логарифм некоторой величины F, тогда как изменение энтропии Д S есть линейная функция F. В проблеме связи мы имеем сходные формулы: информация (или пропускная способность канала С, формулы (17.46) и (17.50)) есть логарифм величины

тогда как изменение энтропии (см. (17.44)) пропорционально в модели Рэймонда, представляющей реальную физическую систему с рассеянием.

В заключение нужно подчеркнуть физическое значение этого рассуждения: формула Шеннона действительно дает предел, соответствующий оптимальным условиям с наибольшей эффективностью преобразования негэнтропии в информацию. Это следует из того факта, что вычисления, основанные на информации (раздел 3) и на негэнтропии (см. (17.50)), дают совпадающие результаты при условии, что все величины измеряются в одной системе единиц.

Если информация измеряется в двоичных единицах, а энтропия — в термодинамических единицах, то каждая двоичная единица соответствует термодинамических единиц. Это снова доказывает (см. главу 14), что одна двоичная единица информации никогда не может быть получена за негэнтропийную цену меньшую, чем .