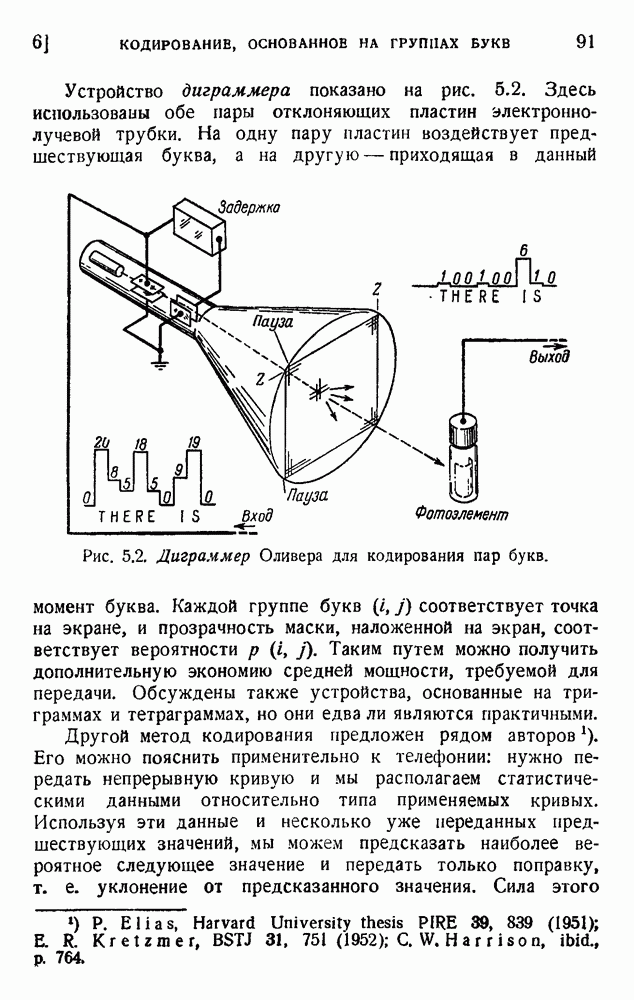
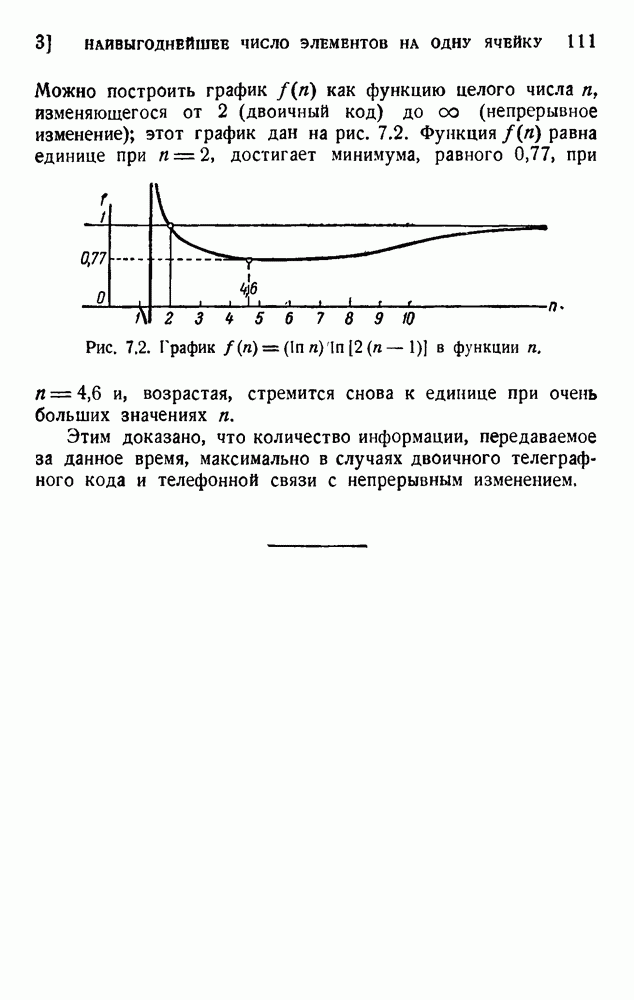
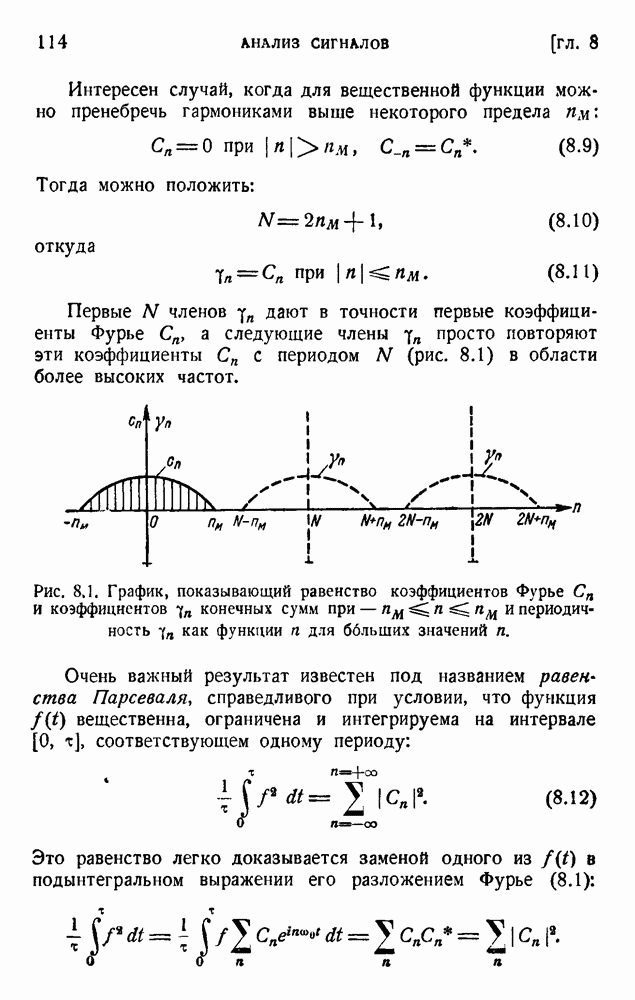
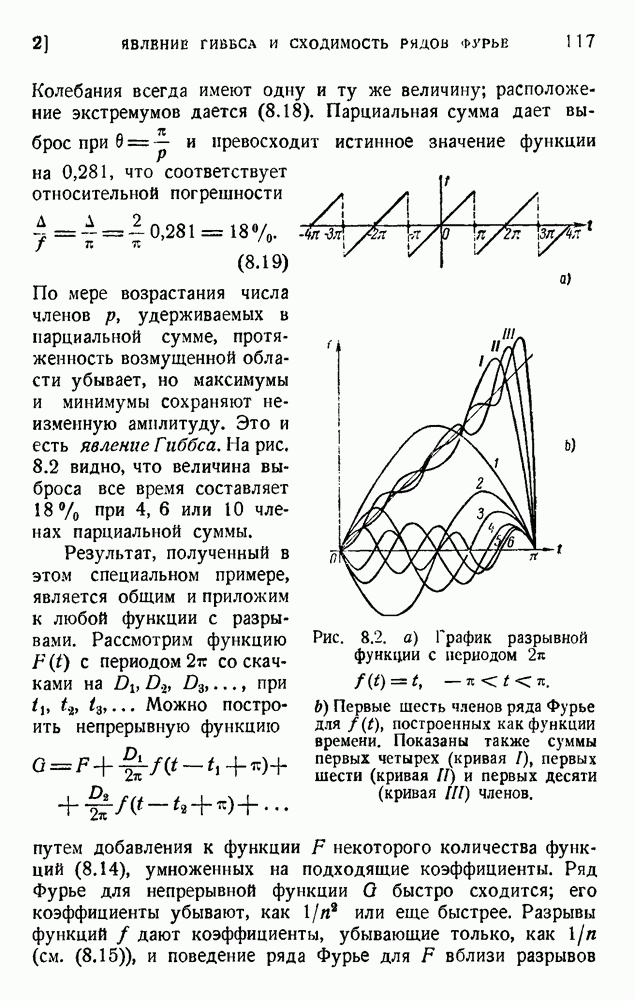
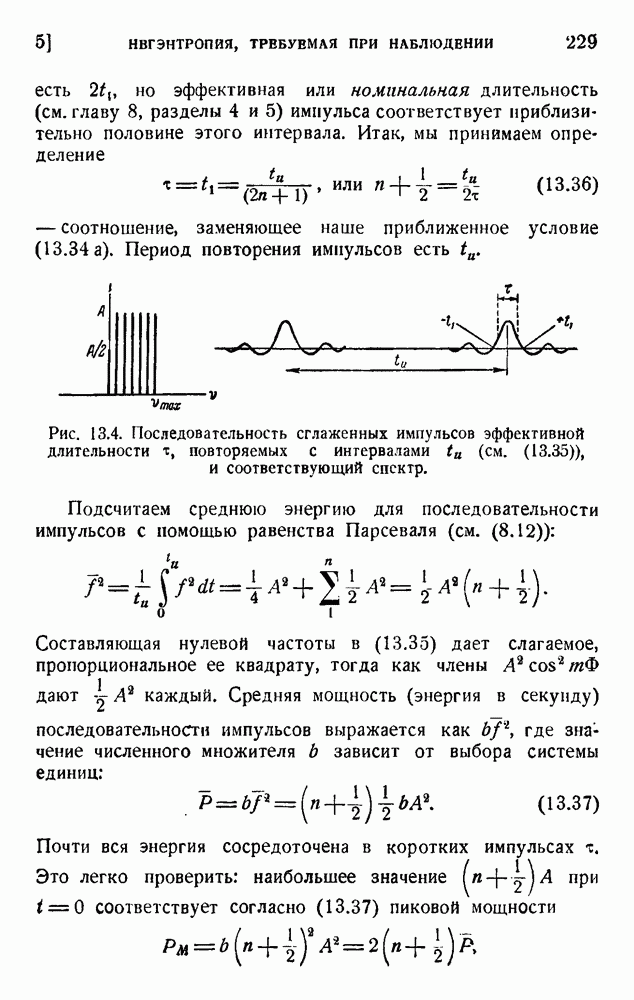
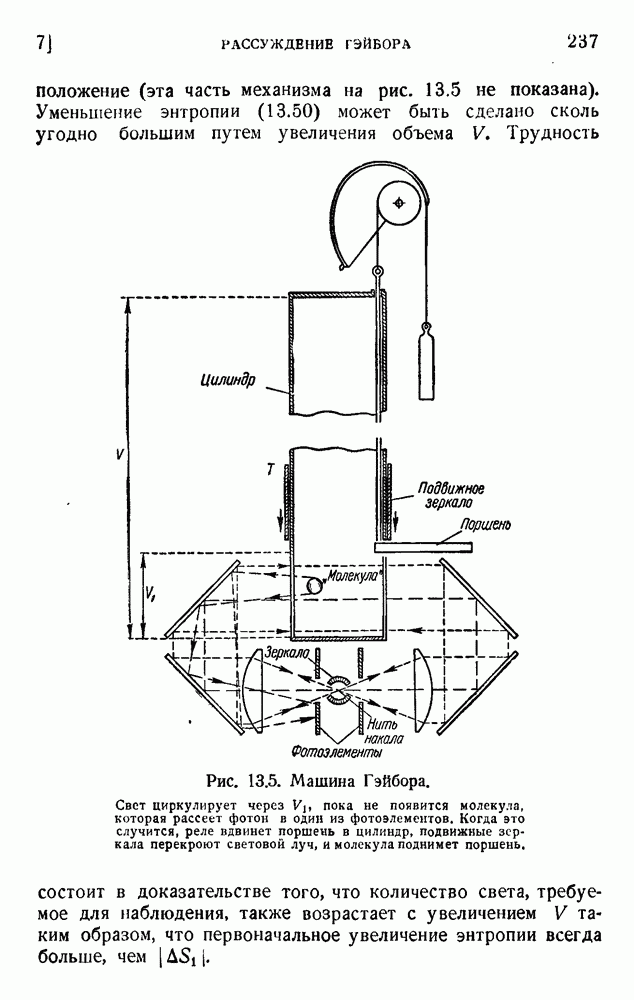
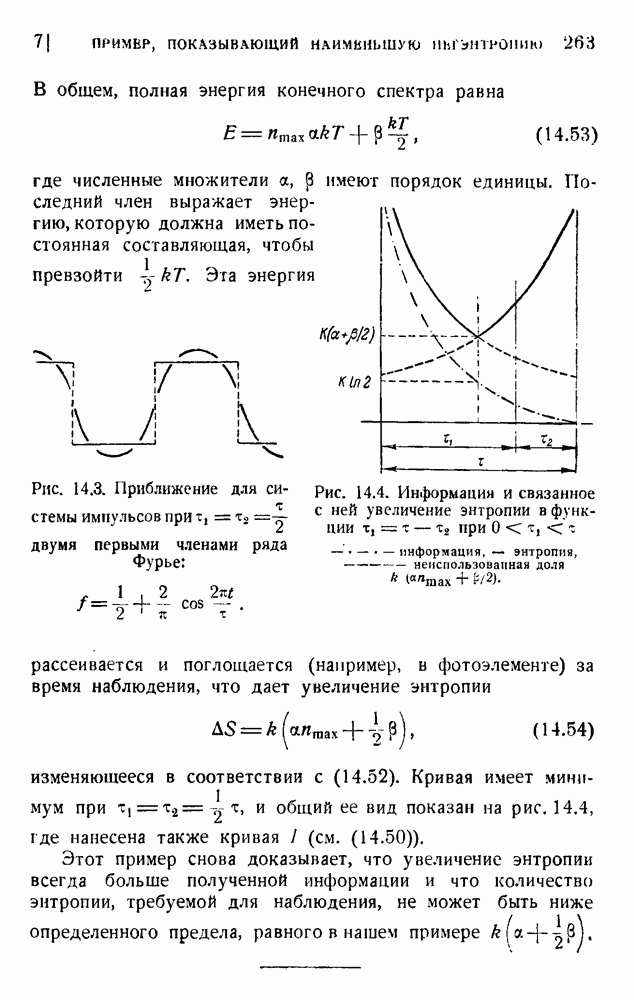
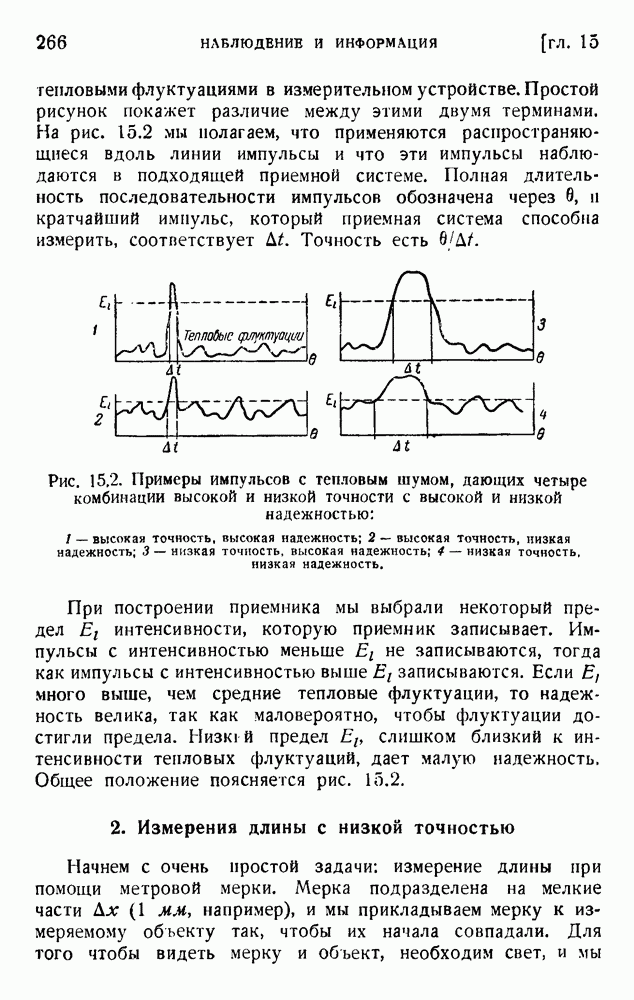
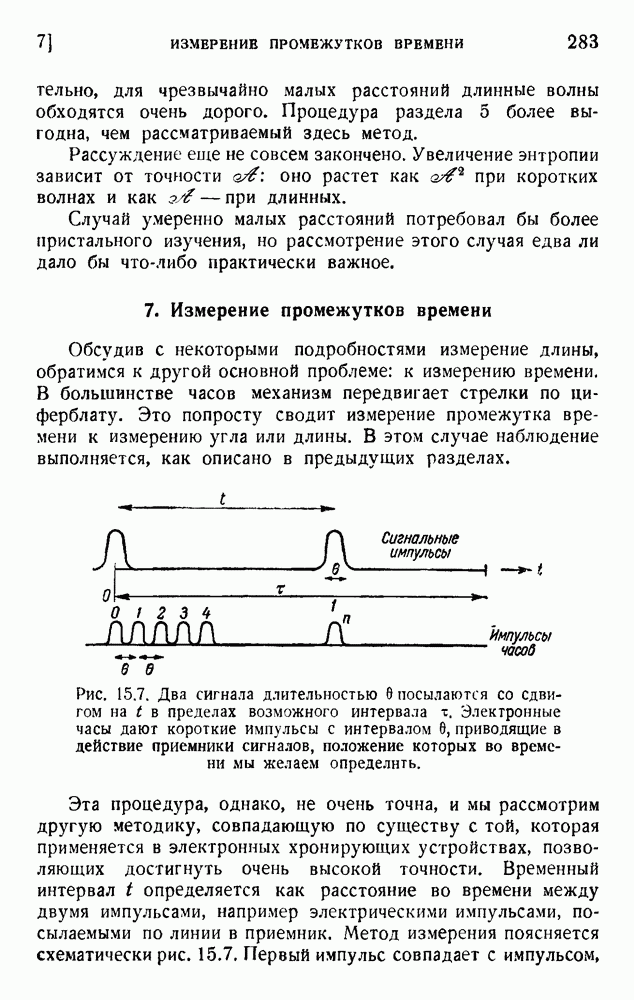
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Вычислительная машина как математический элемент
Интересно исследовать роль вычислительной машины, когда она работает с входными данными, полученными из эксперимента. Эти данные являются результатом наблюдений над некоторой физической системой, и серия наблюдений дает обычно непрерывную функцию  Так как всякая физическая система имеет конечную ширину полосы, то это относится также и к f(t).
Так как всякая физическая система имеет конечную ширину полосы, то это относится также и к f(t).
2) Общие положения этого раздела наводят на следующие размышления. Итак, машина не создает информации; иначе говоря, никакая последовательность математических и логических действий не приводит к появлению новой информации (мы оставляем в стороне интереснейший вопрос о том, какова же действительная природа какого-либо источника информации). Следовательно, решение поставленной задачи не дает нам новой информации. Новая информация не содержится также ни в таблицах, ни в справочниках и т. п. Это уже может показаться странным, хотя несомненным образом вытекает из принятых определений. Но в таком случае ощущается настоятельная необходимость введения еще какой-то новой категории, — может быть, не информации, — которая выражала бы эффект, т. е. полезный результат работы вычислительной машины. Большая вычислительная машина стоит дорого и затрачивает значительную мощность, превращая ее в тепло. (Известно, что только проблема охлаждения машины представляет немалые технические трудности.) Что же мы получаем от машины? Мы получаем от нее результат переработки информации по заданной программе. Этот результат имеет определенную ценность, и мы могли бы ввести количественную меру еще не названной величины, характеризующей полезный эффект машины. Эта количественная мера, очевидно, связана со сложностью обработки и могла бы быть непосредственно выражена числом элементарных арифметических действий в двоичной системе счисления. (Заметим, что практической характеристикой машины является именно число элементарных операций в секунду. Мы обсуждаем, однако, принципиальную сторону дела.)
До введения определенной величины, характеризующей полезный результат работы вычислительной машины, невозможна никакая разумная оценка эффективности машины. {Прим. переа.)
Цифровая вычислительная машина работает с дискретными сигналами. Операция отсчитывания в точности соответствует задаче, обсужденной в разделах 6 и 7 главы 8. Если мы хотим использовать всю информацию, содержащуюся в непрерывной функции, то мы должны взять отсчеты с интервалом

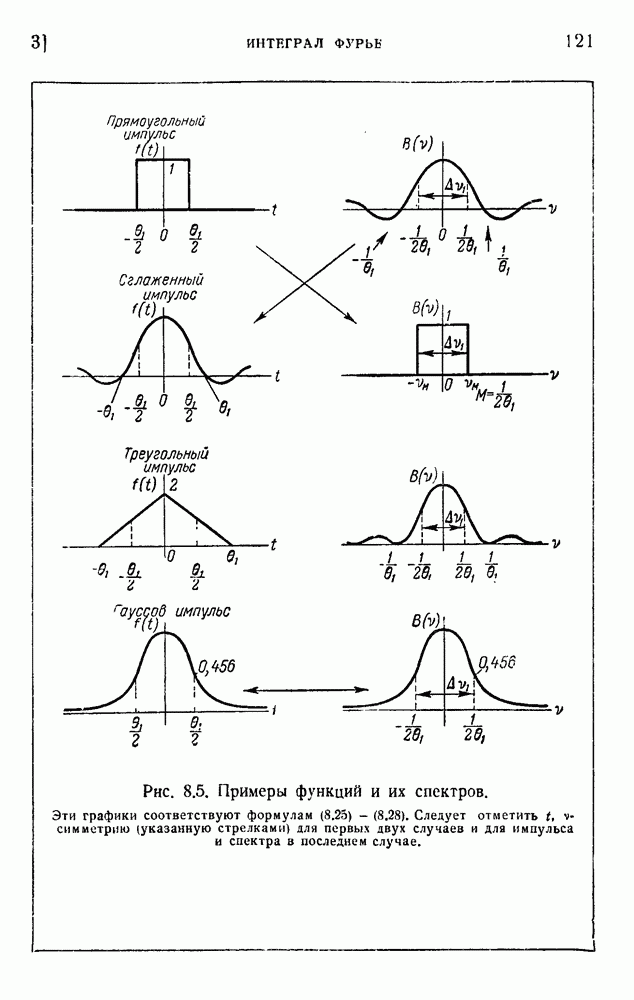
Исходная функция  практически определена только на конечном промежутке времени
практически определена только на конечном промежутке времени  , но для получения точной математической задачи мы должны установить поведение функции от —
, но для получения точной математической задачи мы должны установить поведение функции от —  до
до  как мы сделали в разделе 6 главы 8. Предположим снова, что мы имеем периодическую функцию с периодом
как мы сделали в разделе 6 главы 8. Предположим снова, что мы имеем периодическую функцию с периодом  , удовлетворяющую условию (8.52). На вход машины поступают N отсчетов
, удовлетворяющую условию (8.52). На вход машины поступают N отсчетов  и если
и если  велико, то мы имеем:
велико, то мы имеем:

(см. (8.51)). По этим отсчетам мы можем найти коэффициенты Фурье, и наоборот (см. 8.63) и (8.63а)):

Машина обрабатывает отсчеты  и дает выходные значения
и дает выходные значения

Вообще говоря, функции F представляющие программу вычисления, могут быть очень сложными. Если, однако, мы ограничим свое рассуждение линейной математической задачей, то операция будет представлена матрицей 

и эта матрица выражает программу вычисления. Мы имеем N различных значений  на входе, но мы можем иметь иное число
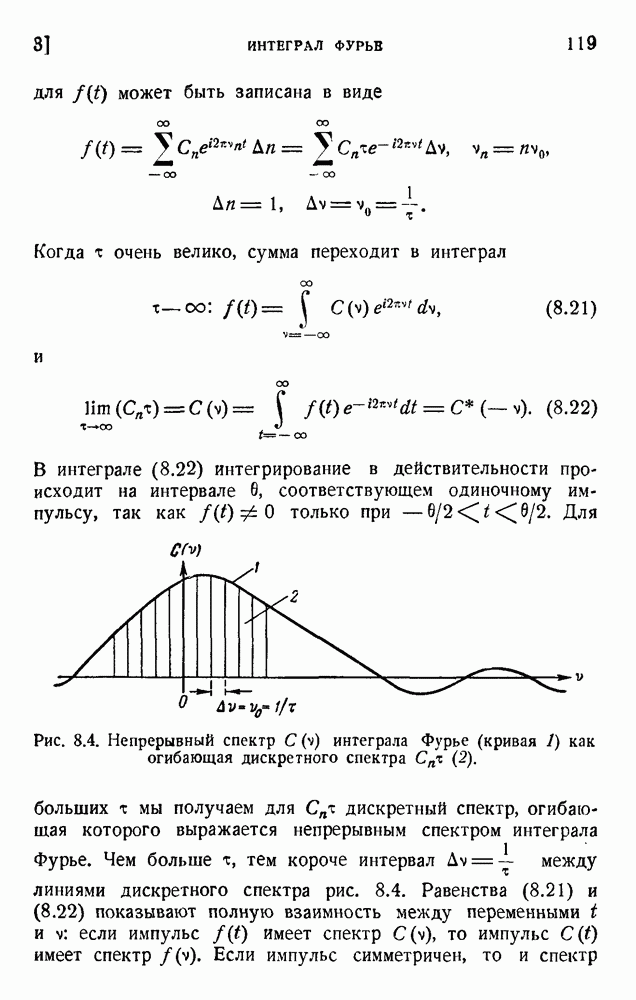
на входе, но мы можем иметь иное число  значений
значений  на выходе. Возможно также, что имеется некоторая избыточность как во входных, так и в выходных данных. Если мы не хотим изменять ширину полосы системы в целом, то наши
на выходе. Возможно также, что имеется некоторая избыточность как во входных, так и в выходных данных. Если мы не хотим изменять ширину полосы системы в целом, то наши  выходных данных потребуют иной длительности
выходных данных потребуют иной длительности  для непрерывной функции на выходе
для непрерывной функции на выходе

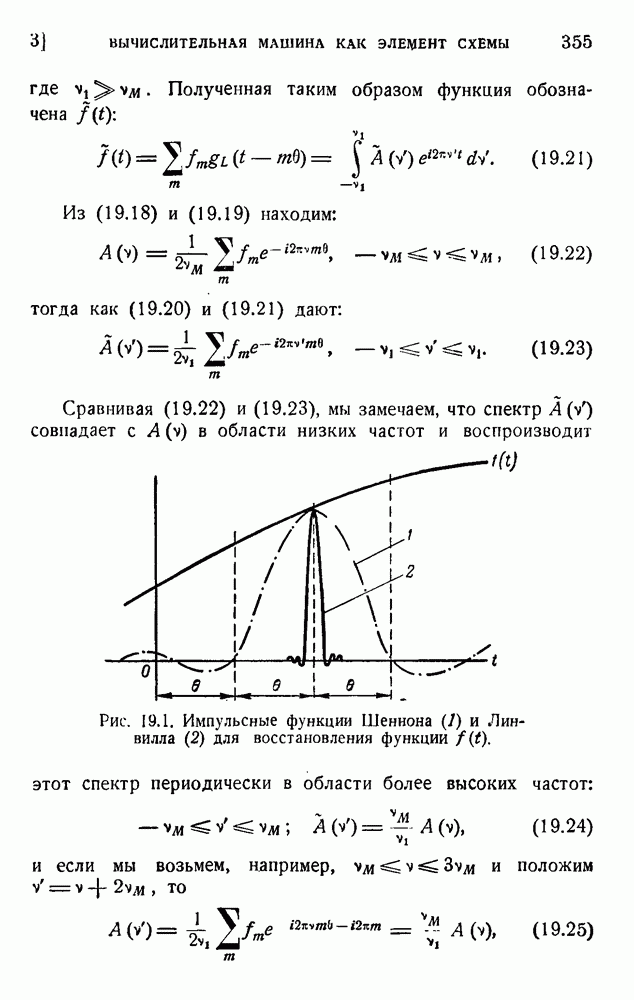
которая восстанавливается по правилам главы 8 (см. (8.60)) и может быть снова разложена в ряд Фурье (как в (8.58))

Соотношение между коэффициентами Фурье а и отсчетами выходной функции в точности такое же, как в (19.3)

Из (19.4)-(19.9) мы можем непосредственно получить соотношение между входным спектром  и выходным спектром а
и выходным спектром а  предполагая линейное вычисление, представляемое матрицей
предполагая линейное вычисление, представляемое матрицей  :
:

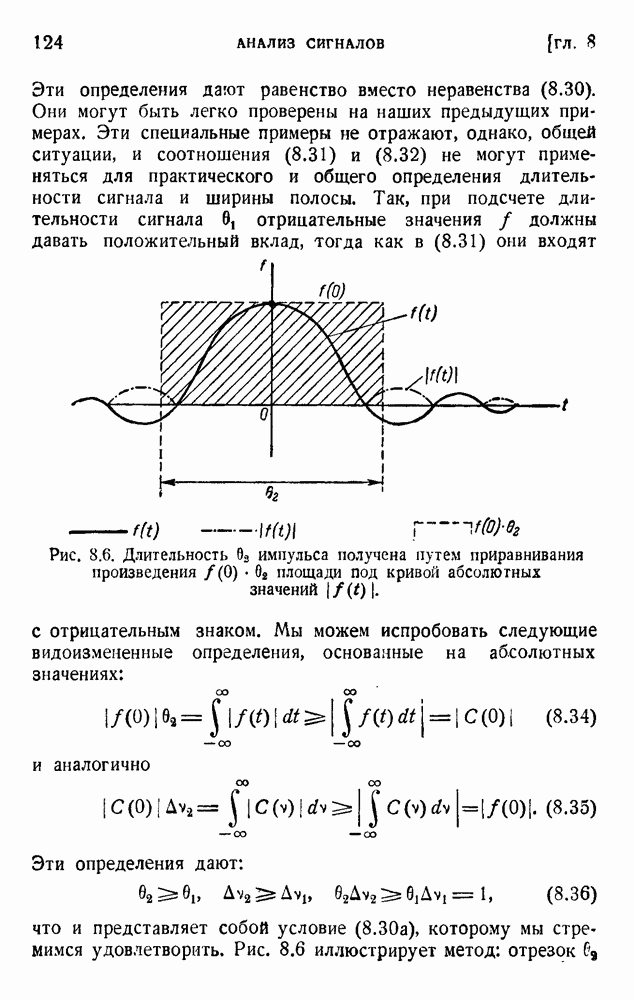
Если мы положим, что число выходных данных равно числу N входных данных, то формула упрощается. Матрица М есть квадратная матрица и

где  Величина
Величина  есть положительное или отрицательное целое число, а коэффициенты а выходного спектра являются рациональными функциями аргумента
есть положительное или отрицательное целое число, а коэффициенты а выходного спектра являются рациональными функциями аргумента

Эти формулы полностью подкрепляют точку зрения, развитую в предыдущем разделе: машина обрабатывает информацию, но не производит никакой новой информации. Операция может выполняться в обратном порядке, если матрица несингулярна и может быть обращена. Это значит, что обратная матрица J может быть найдена

Обозначим через Лиц элементы этой обратной матрицы, представляющей программу обратного действия машины. Условия (19.13) означают:

и обратное действие машины представляется соотношением, сходным с (19.11):

Доказательство нетрудно и использует (19.14) совместно с (8.63b):

Подставляя (19.11) в (19.15), получаем (при  ):
):

Суммирование по  в последнем экспоненциальном множителе и использование (19.16) дает
в последнем экспоненциальном множителе и использование (19.16) дает  откуда
откуда  Затем мы вычисляем сумму
Затем мы вычисляем сумму

и получаем  в соответствии с (19.14). Последний шаг состоит в суммировании
в соответствии с (19.14). Последний шаг состоит в суммировании  по
по  , что дает
, что дает  согласно (19.16), так что окончательно мы получаем:
согласно (19.16), так что окончательно мы получаем:

что и требовалось доказать.
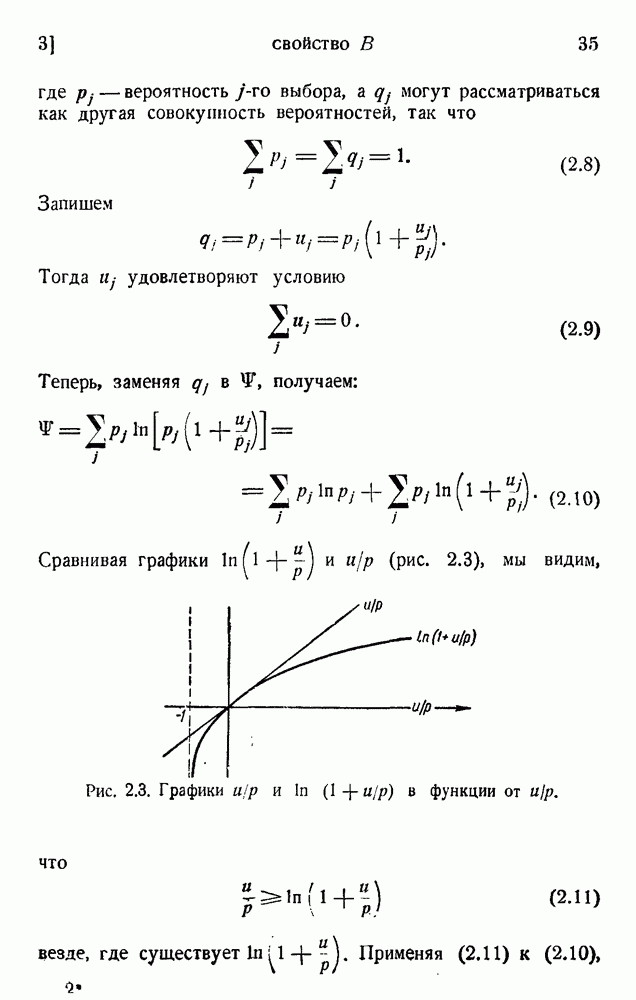
Мы получили полное представление машины, работающей по линейной обратимой программе, причем информация не теряется, но и не создается заново. Небольшая потеря информации будет обусловлена округлением ошибок вычисления. Вычисление по линейной программе, представляемой прямоугольной матрицей М, будет терять информацию, если  вводить избыточность, если
вводить избыточность, если  Нелинейные программы (см. (19.5)) исследовать труднее.
Нелинейные программы (см. (19.5)) исследовать труднее.
Мы обсудим в следующем разделе несколько иную задачу, соответствующую возможному использованию вычислительной машины.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
- 4. Информация и алфавит
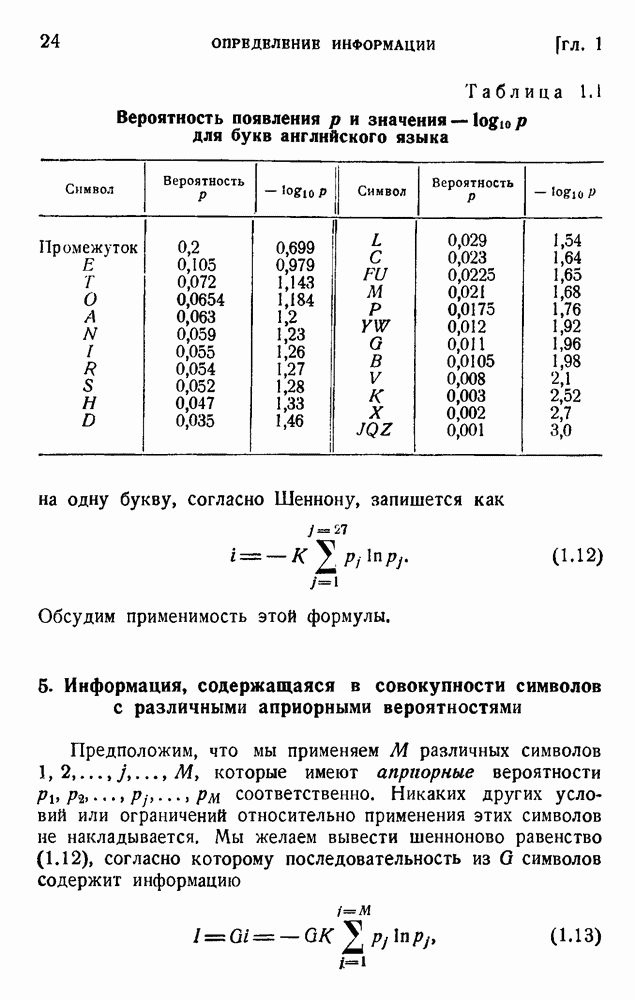
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
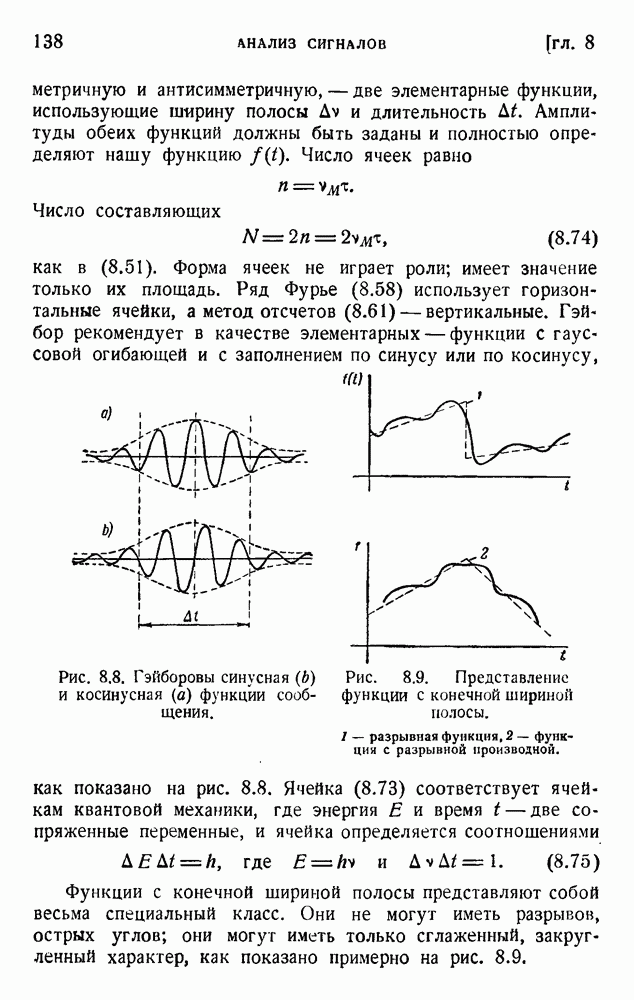
- 2. Корреляция в языке
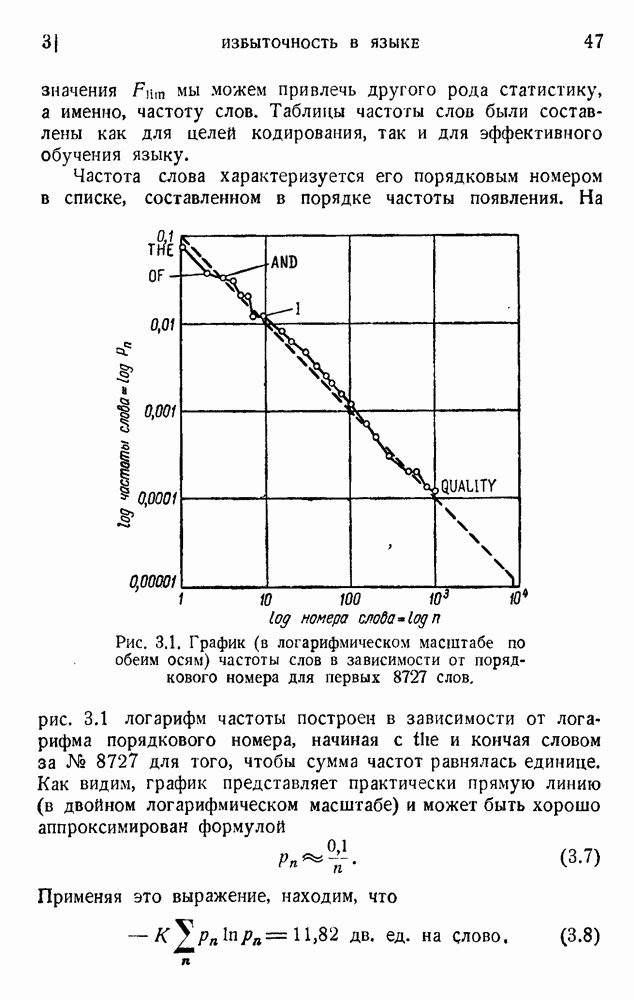
- 3. Избыточность в языке
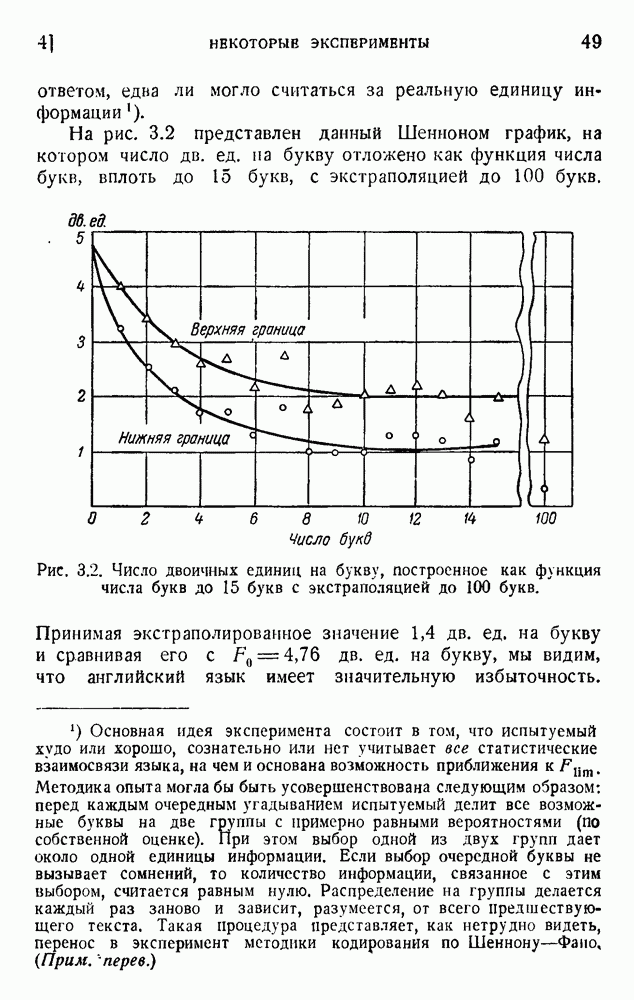
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
- 10. Проблемы статистики слов
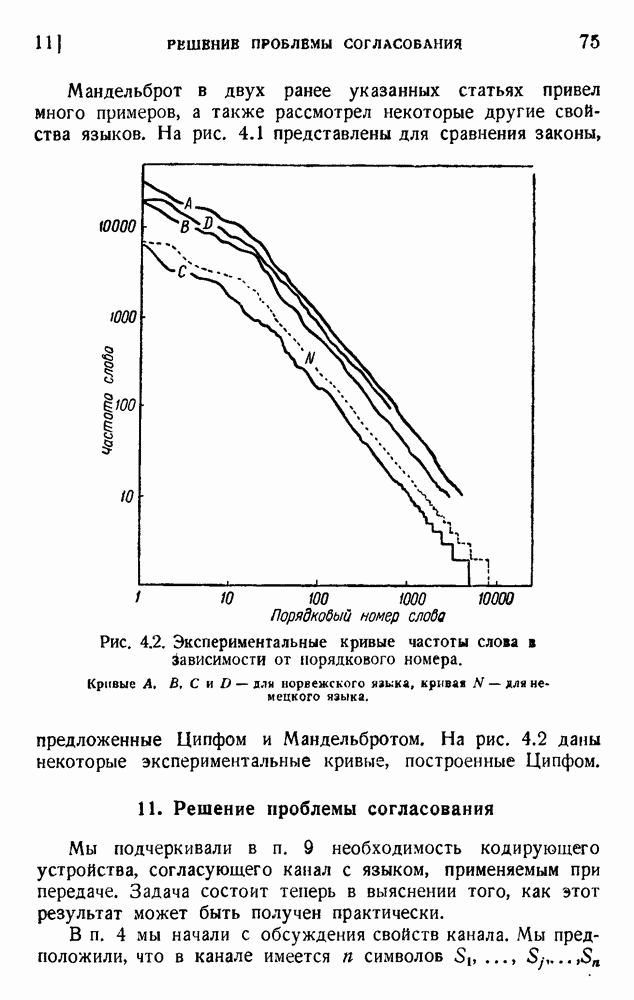
- 11. Решение проблемы согласования
- Приложение
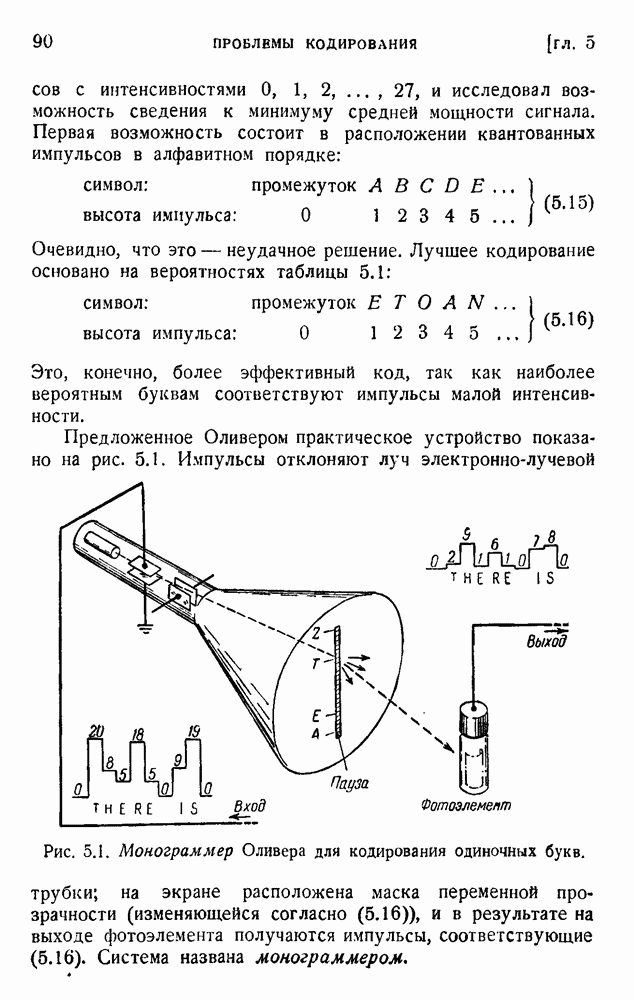
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
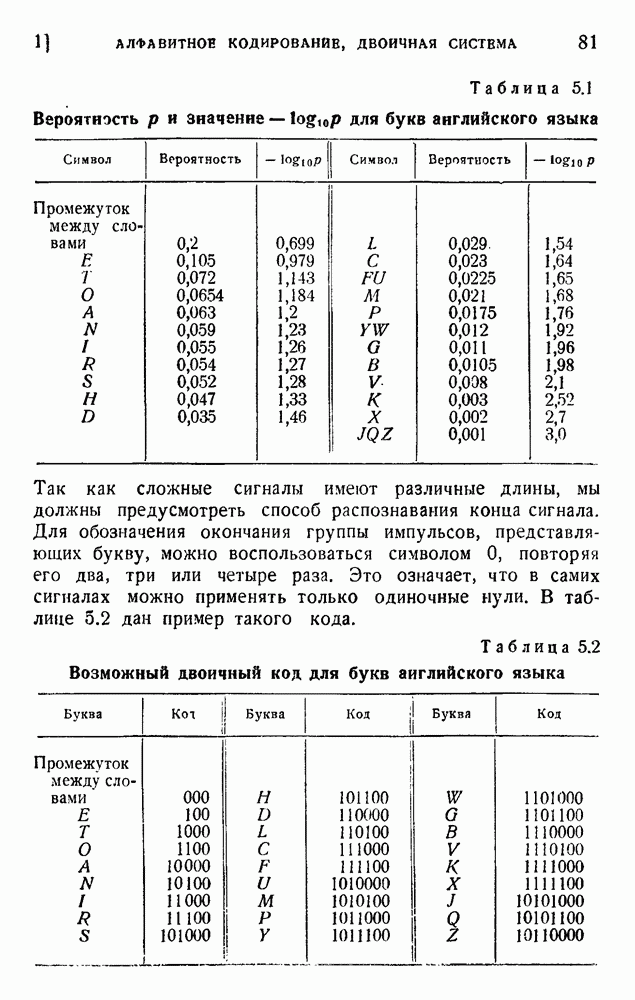
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
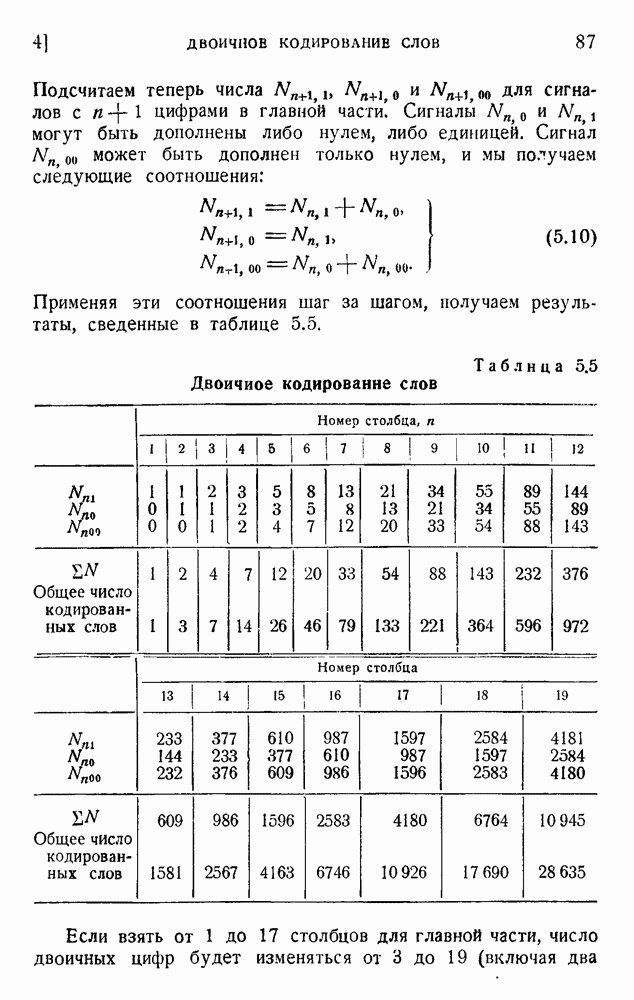
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
- 1. Ряд Фурье
- 2. Явление Гиббса и сходимость рядов Фурье
- 3. Интеграл Фурье
- 4. Роль конечной ширины полосы частот
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
- 7. Метод отсчетов Шеннона
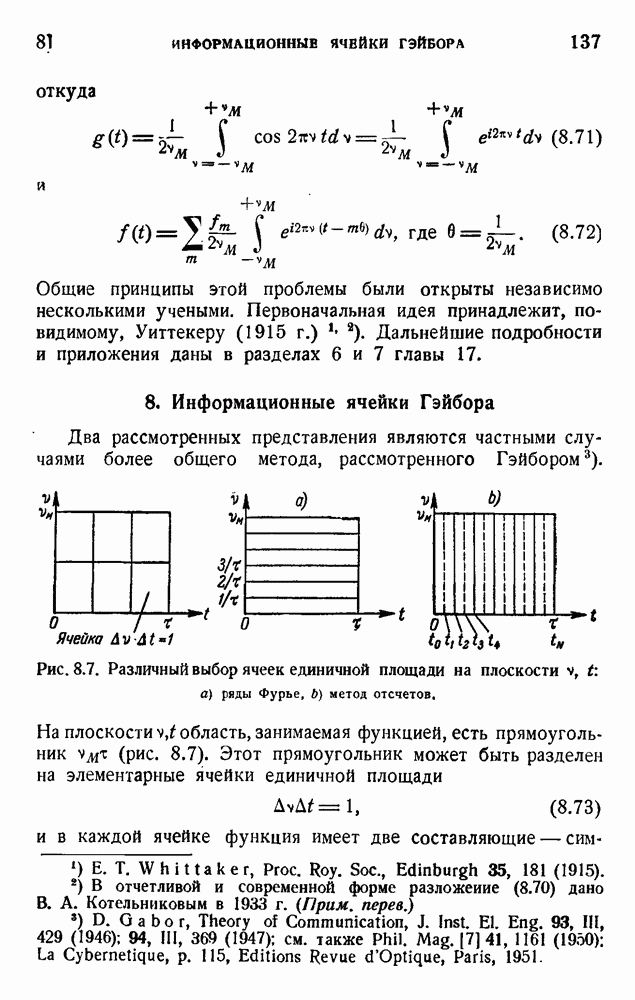
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
- 10. Линейные преобразования и фильтры
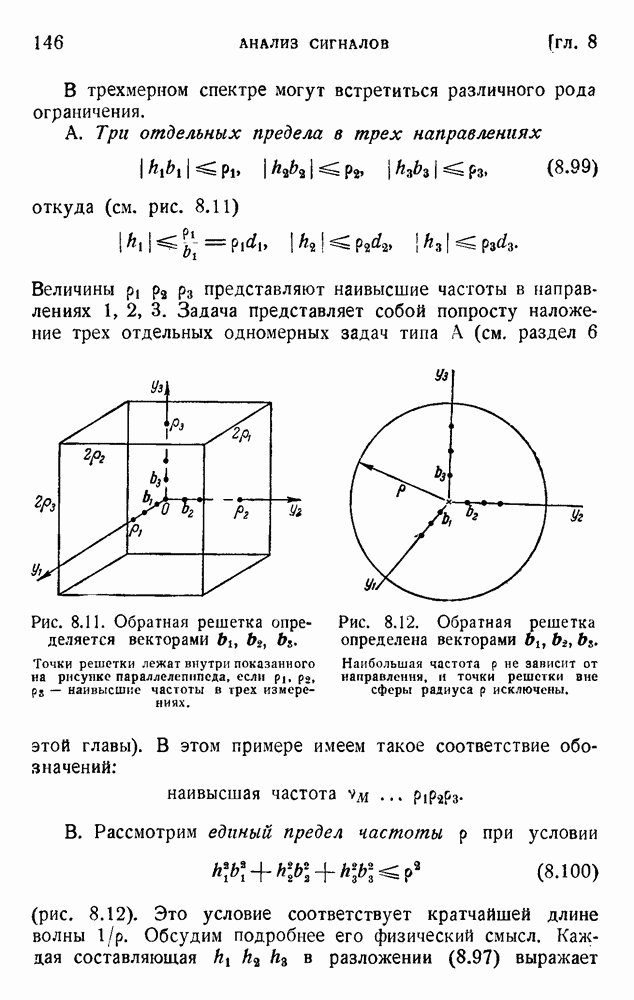
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
- 1. Тепловое движение
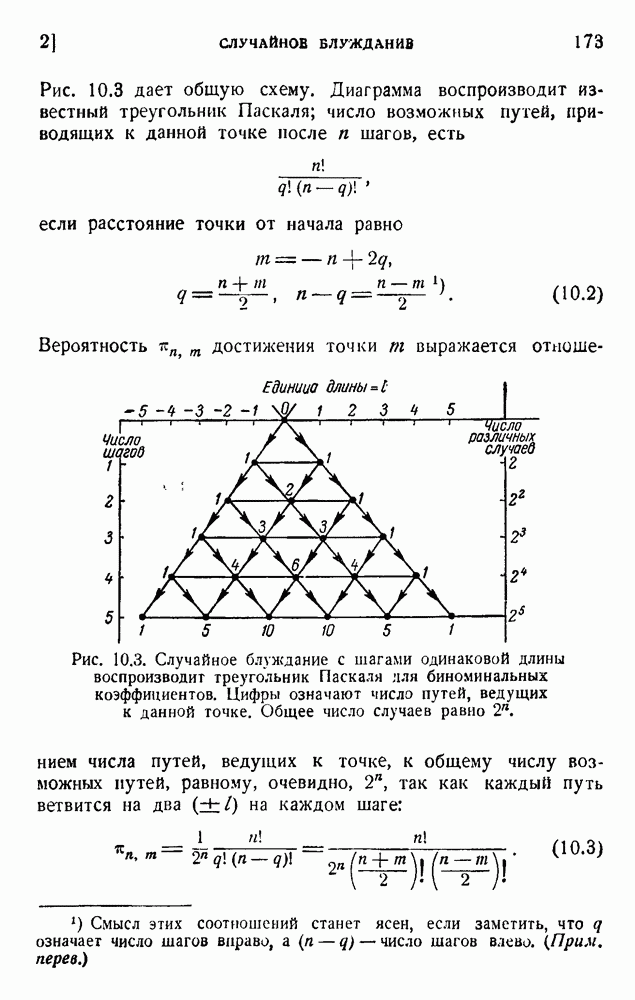
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
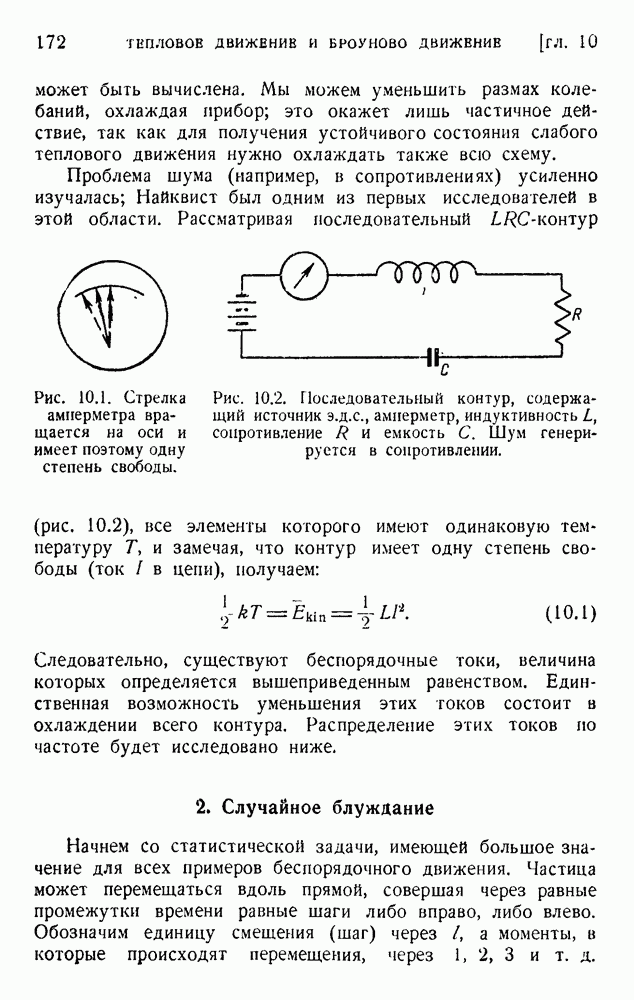
- 5. Тепловое движение в электрической цепи
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
- 5. Тепловое движение в выпрямителе
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
- 5. Негэнтропия, требуемая при наблюдении
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
- 4. Пределы евклидовой геометрии
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
- 6. Проблемы семантической информации