| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
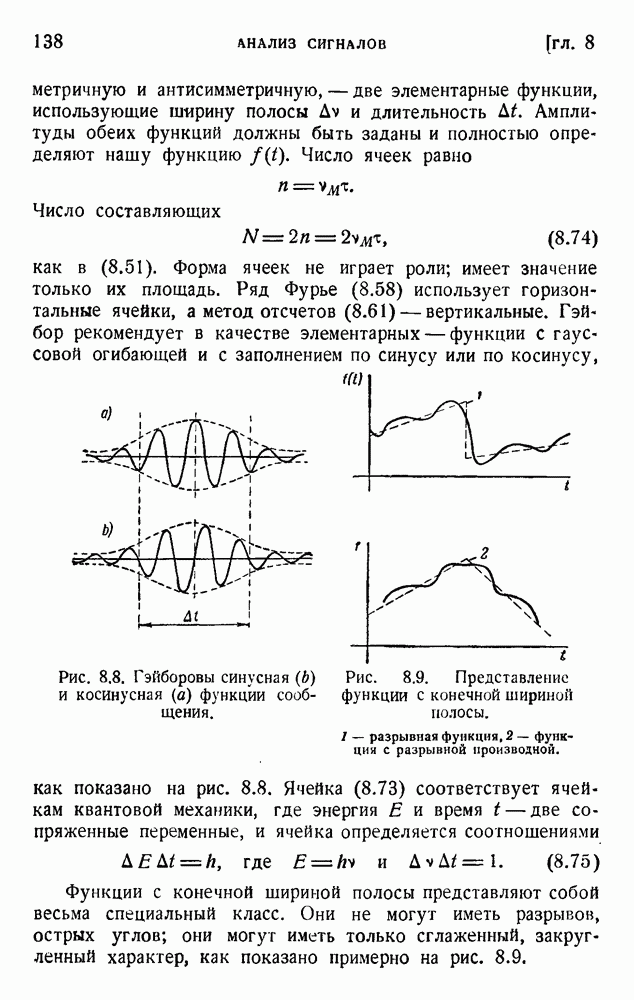
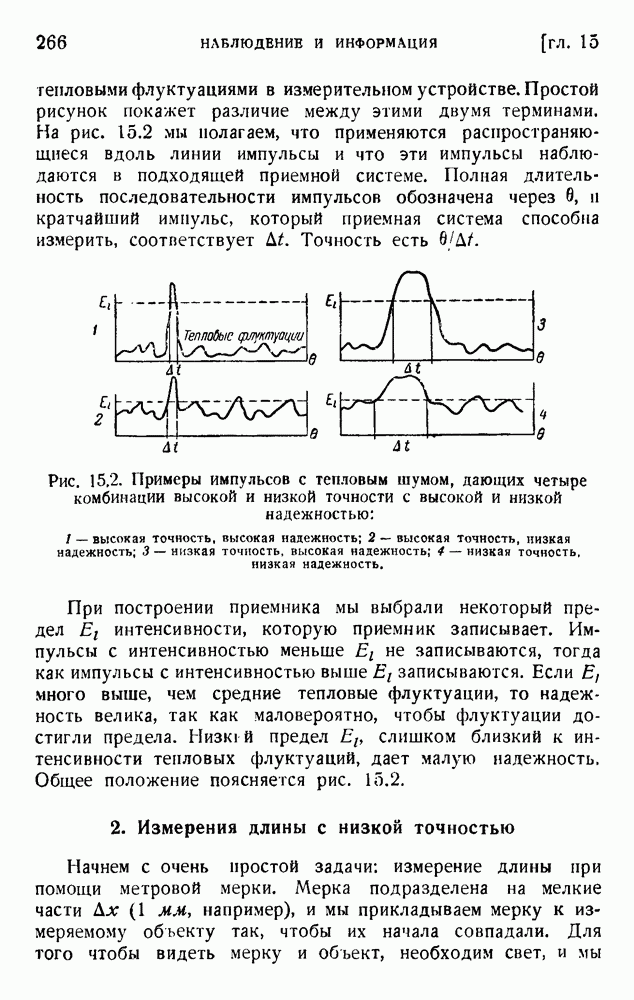
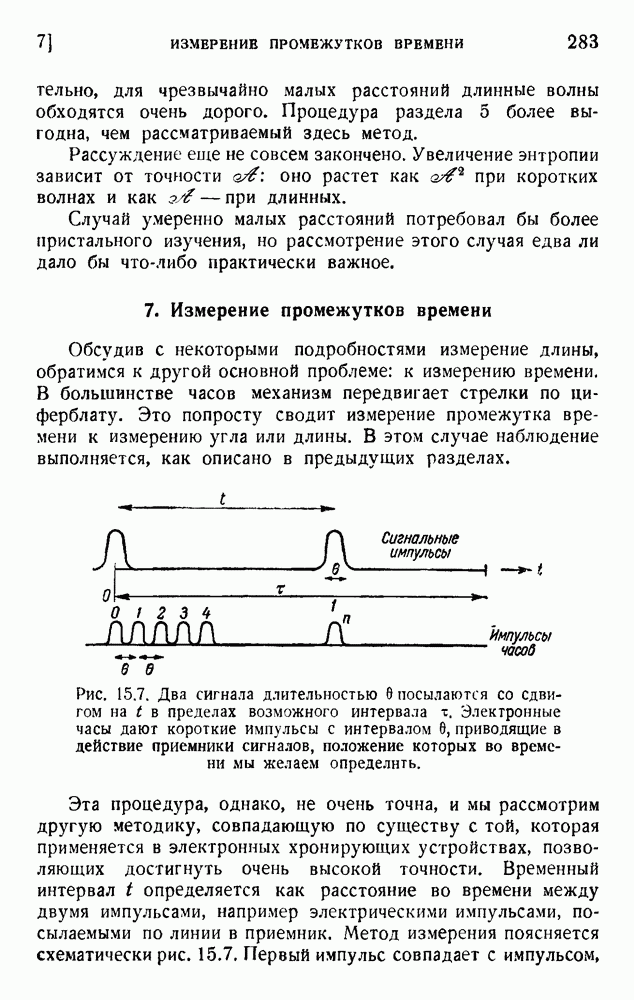
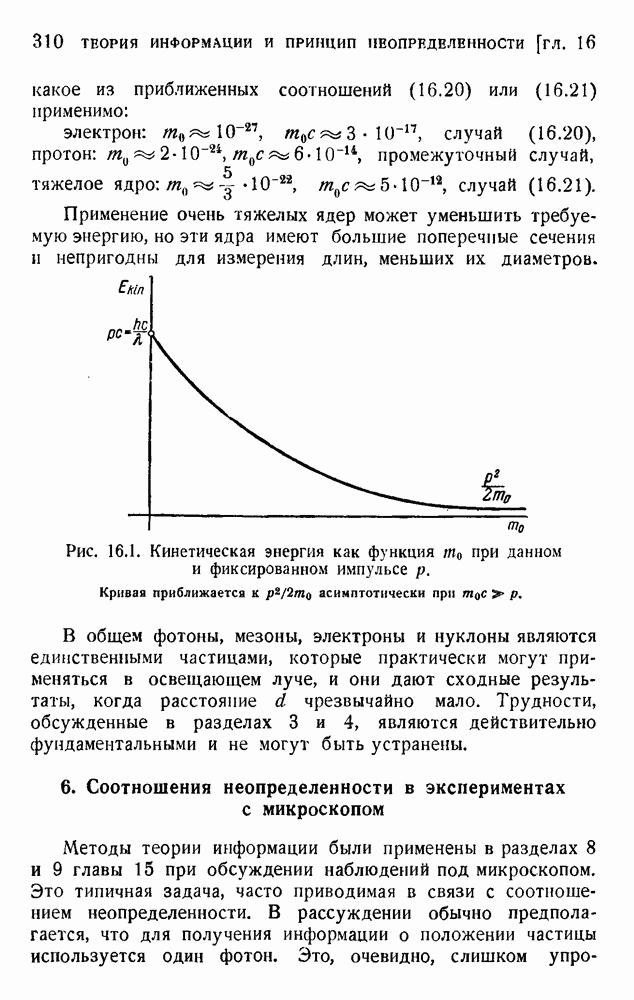
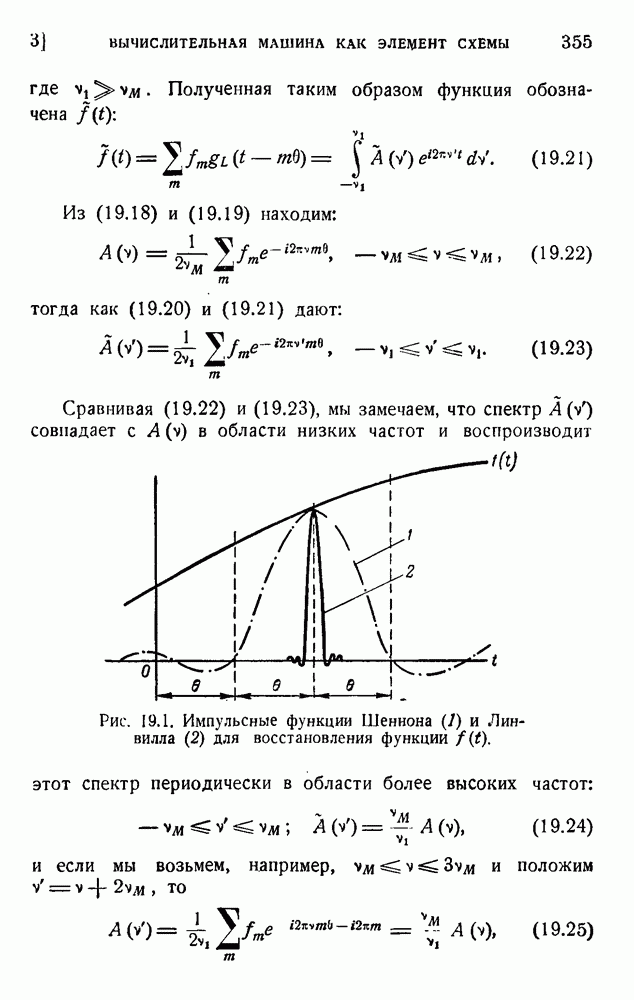
4. Статистическое толкование энтропии
Величина, названная энтропией, формально определена равенством (9.1), и мы показали на нескольких примерах, что она находится в обратном соответствии качеству энергии. Второе начало устанавливает, что энтропия должна всегда возрастать, тогда как энергия всегда теряет свое качество (деградация энергии Кельвина).
Ясное истолкование этих общих свойств дано Гиббсом, Максвеллом, Больцманом и завершено Планком. Основание этого объяснения найдено в атомной структуре материи и квантовых законах устойчивости атомов, молекул и кристаллов. Атомы так малы, что количество их в любом кусочке вещества, с которым мы экспериментируем, ошеломляюще велико. Грамм-атом вещества содержит около  атомов. Вместе с тем мы совершенно не в состоянии следить за движением отдельных атомов. Единственные свойства, которые
атомов. Вместе с тем мы совершенно не в состоянии следить за движением отдельных атомов. Единственные свойства, которые
мы можем практически наблюдать, — это средние статистические величины.
Статистическая теория термодинамики, основанная на этих общих замечаниях, представляет собой одну из наиболее разработанных глав физики. Как будет показано, энтропия связана с вероятностью. Можно создать искусственно замкнутую изолированную систему с очень маловероятной структурой. Если предоставить эту систему самой себе, то она будет эволюционировать в сторону более вероятной структуры. Вероятность имеет естественную тенденцию к возрастанию, как и энтропия. Точное соотношение дается известной формулой Больцмана — Планка:

где  — постоянная Больцмана, S — энтропия рассматриваемой системы, Р — статистический вес (число элементарных комплексий.
— постоянная Больцмана, S — энтропия рассматриваемой системы, Р — статистический вес (число элементарных комплексий.
Рассмотрим, прежде всего, точный смысл числа Р, чтобы пояснить связь с теорией вероятностей. Согласно квантовой теории атомы и молекулы могут существовать лишь в виде конечного числа различных структур. На атомном уровне нет непрерывности, есть только дискретные стабильные (или метастабильные) структуры, и система атомов внезапно перескакивает от одной системы к другой, поглощая или излучая при этом энергию. Каждая из этих дискретных конфигураций квантованной физической системы называется микросостоянием (комплексна Планка).
Рассмотрим теперь физическую систему: кусок кристалла, или газ в сосуде при определенных условиях в отношении объема, давления, полной энергии, температуры, химического строения. Макроскопические переменные — это те величины, которые мы можем измерить в лаборатории. Их недостаточно, чтобы полностью определить состояние системы. Имеется огромное число микроскопических переменных, которые невозможно в точности измерить: положения и скорости всех отдельных атомов, квантовые состояния этих атомов или
молекулярных структур и т. д. Все эти неизвестные величины дают системе возможность принимать большое число разнообразных квантовых структур, или микросостояний. Общее число Р этих микросостояний мы и ввели в (9.15) и связали с энтропией системы. Это число чрезвычайно велико, но, конечно, и (9.15) имеет определенный смысл.
В нашем рассуждении понадобится еще одно важное соотношение — известное соотношение между энергией и частотой

где  — начальная энергия,
— начальная энергия,  — окончательная энергия системы, излучающей колебание с частотой
— окончательная энергия системы, излучающей колебание с частотой  — постоянная Планка.
— постоянная Планка.

Рис. 9.1. Два тела  и
и  с энергиями
с энергиями  и соответственно соприкасаются. Они могут обмениваться только теплом. Система
и соответственно соприкасаются. Они могут обмениваться только теплом. Система  заключена в изолирующий контейнер V.
заключена в изолирующий контейнер V.
Излучение испускается, когда физическая система теряет энергию, и поглощается, когда система получает энергию. Так как уровни энергии дискретны, частоты излучения (или поглощения) образуют прерывистый спектр, типичный для рассматриваемых атомных или молекулярных систем.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
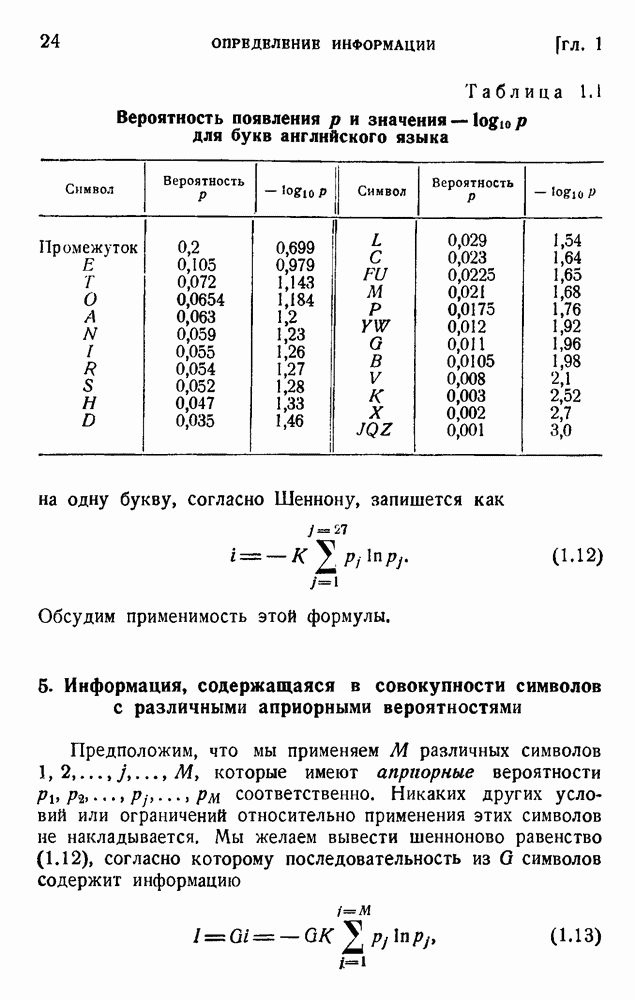
- 4. Информация и алфавит
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
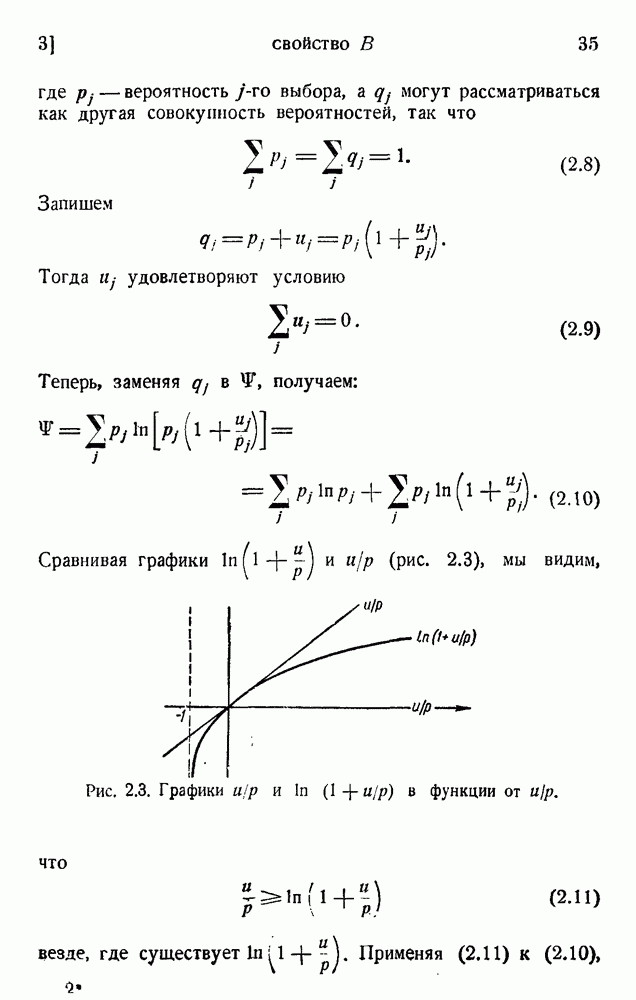
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
- 2. Корреляция в языке
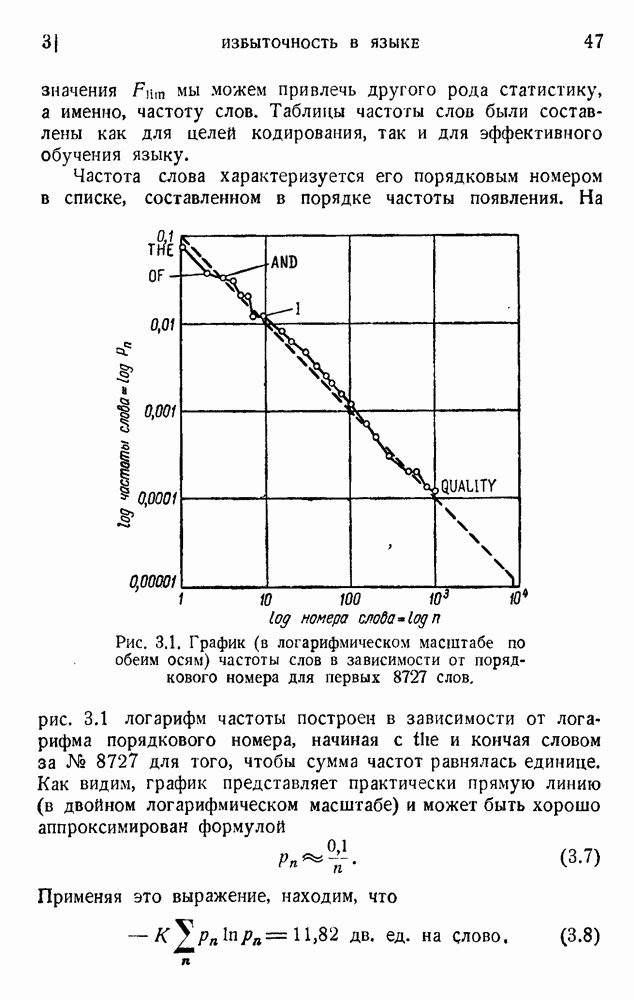
- 3. Избыточность в языке
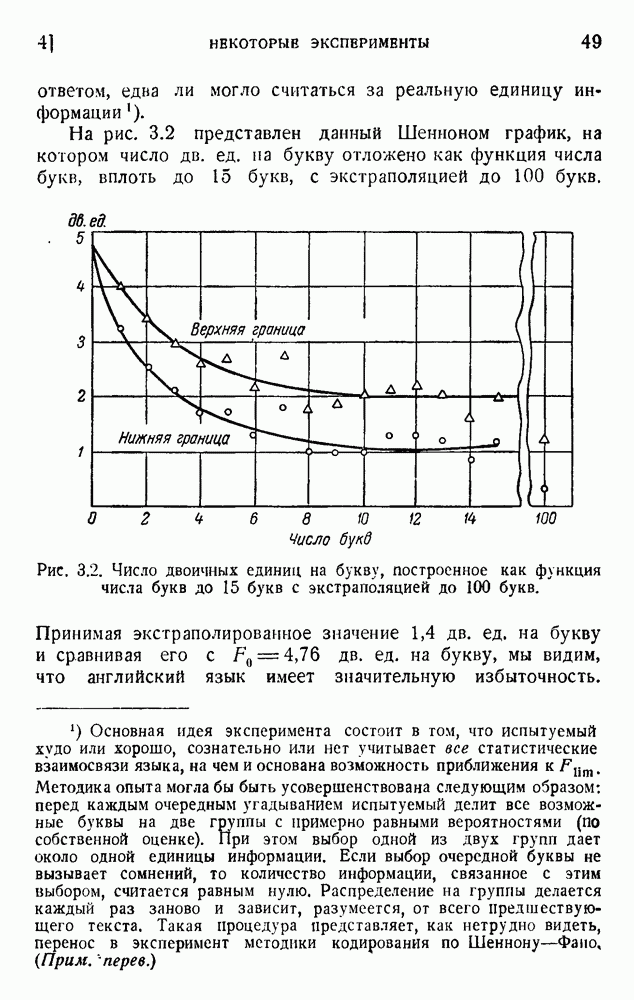
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
- 10. Проблемы статистики слов
- 11. Решение проблемы согласования
- Приложение
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
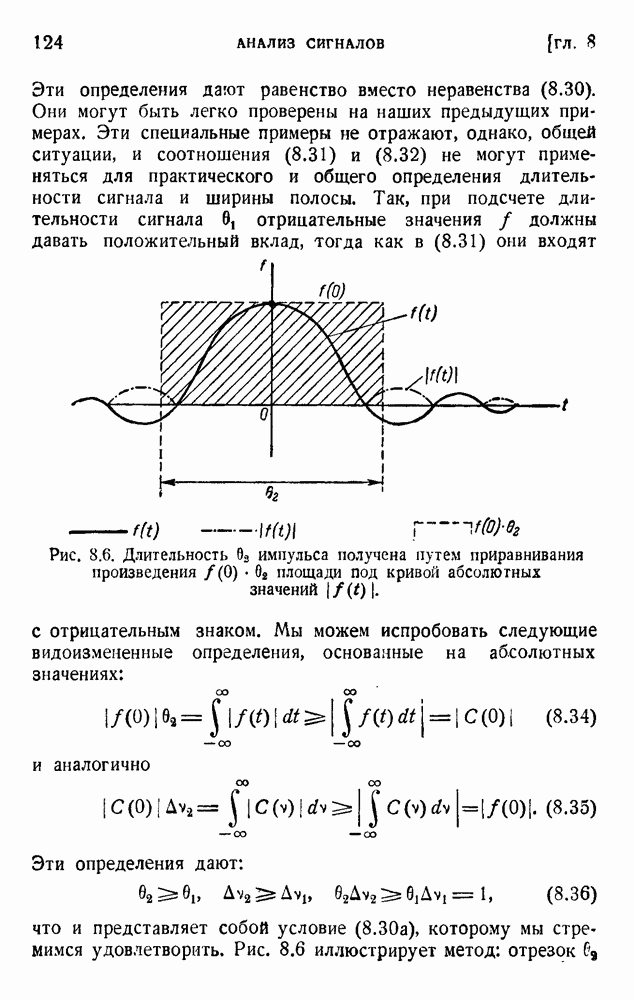
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
- 1. Ряд Фурье
- 2. Явление Гиббса и сходимость рядов Фурье
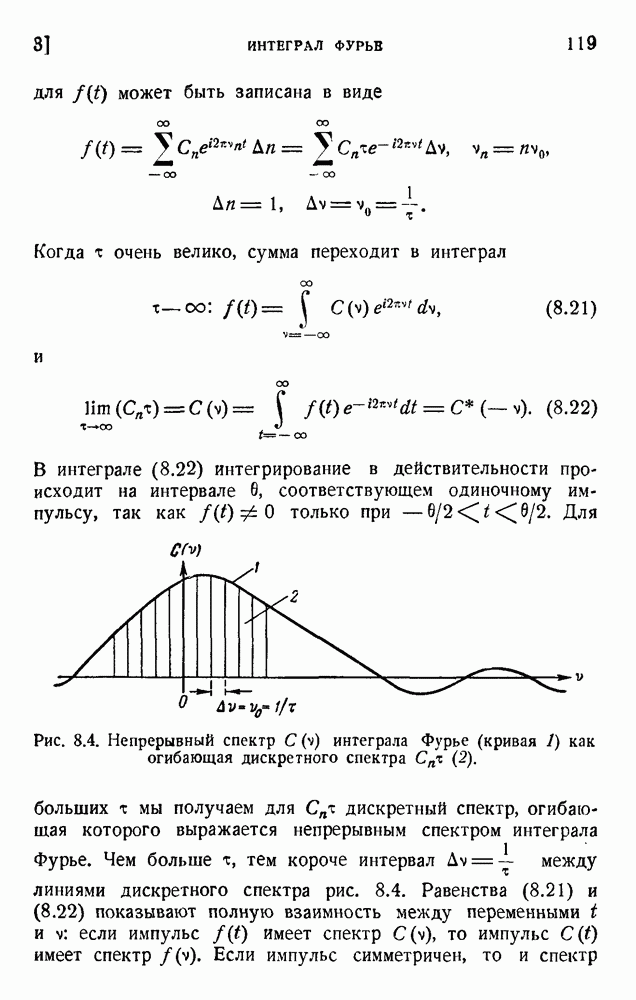
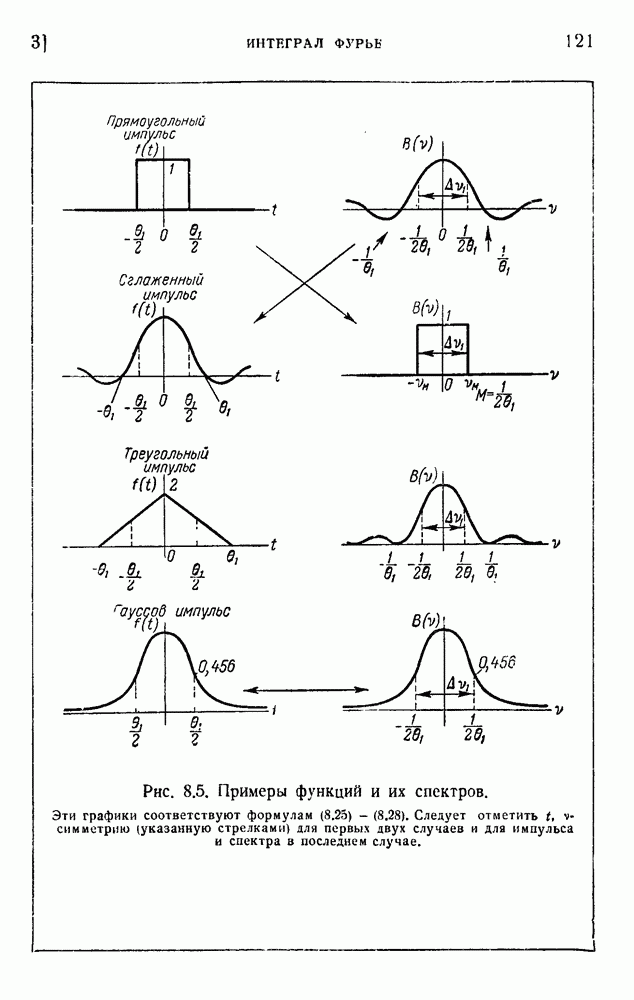
- 3. Интеграл Фурье
- 4. Роль конечной ширины полосы частот
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
- 7. Метод отсчетов Шеннона
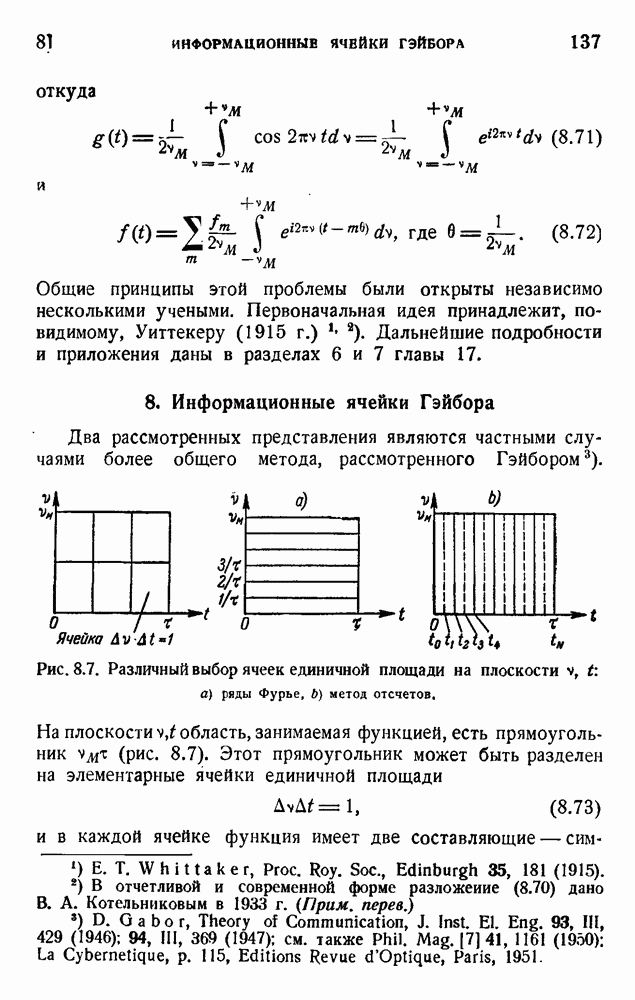
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
- 10. Линейные преобразования и фильтры
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
- 1. Тепловое движение
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
- 5. Тепловое движение в электрической цепи
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
- 5. Тепловое движение в выпрямителе
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
- 5. Негэнтропия, требуемая при наблюдении
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
- 4. Пределы евклидовой геометрии
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
- 6. Проблемы семантической информации