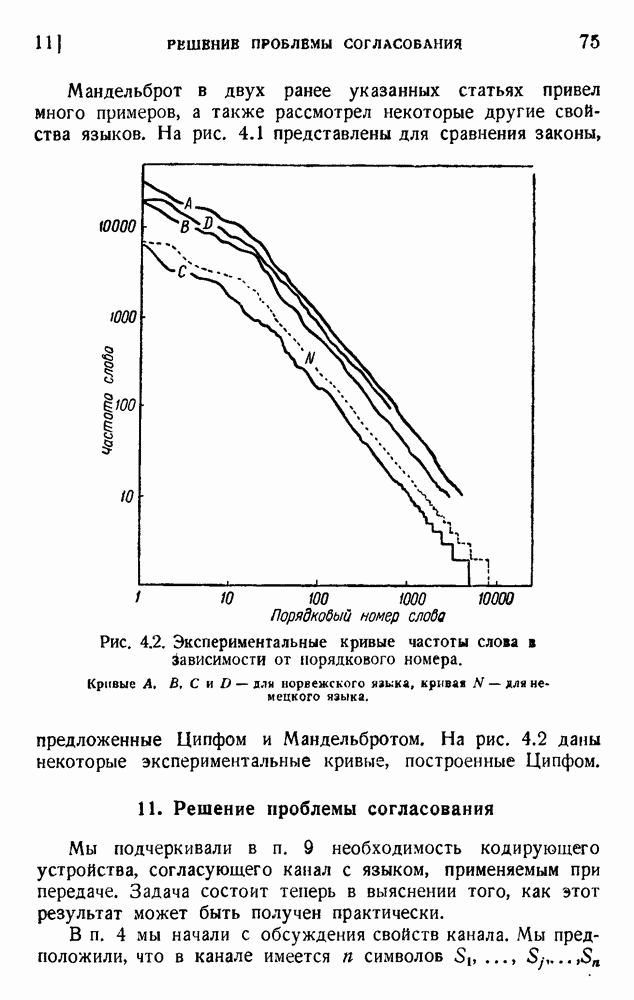
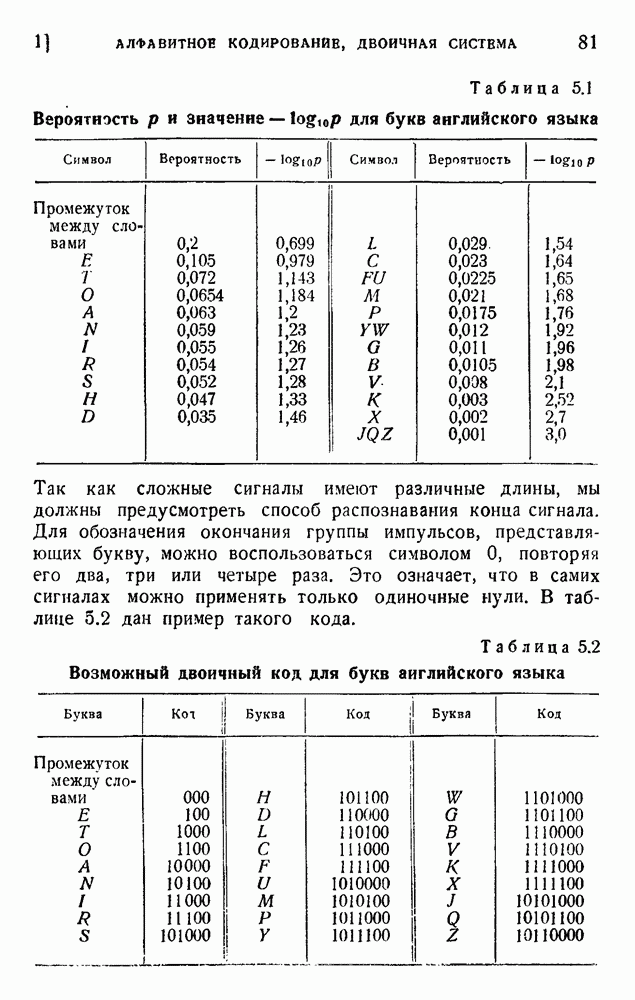
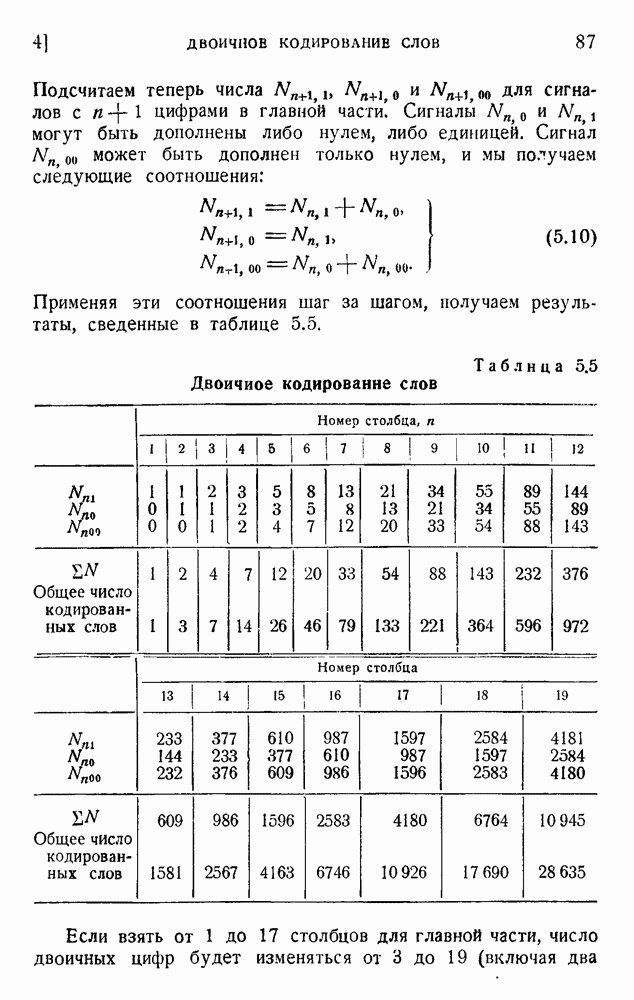
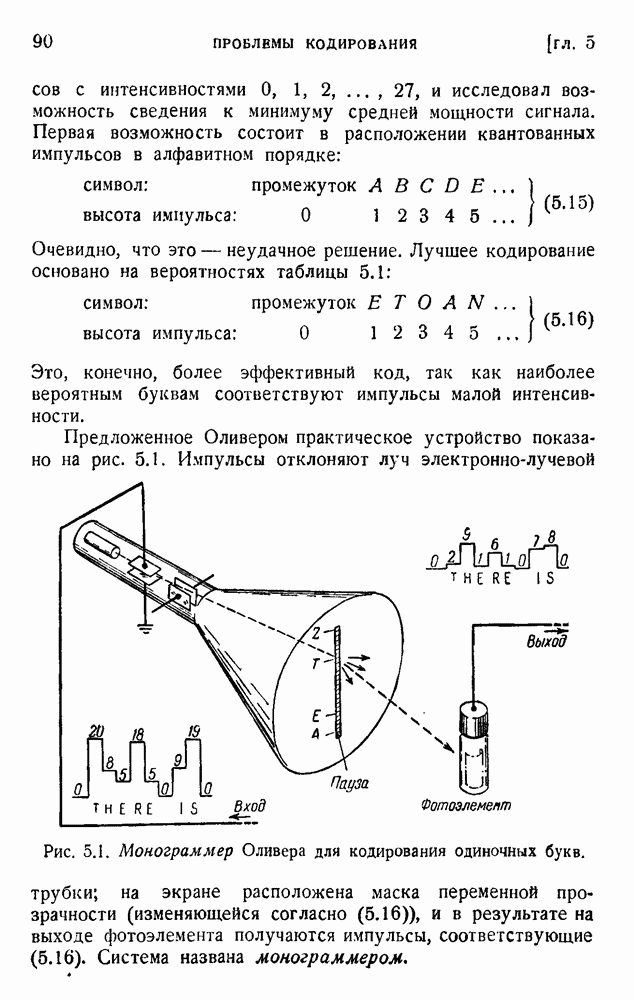
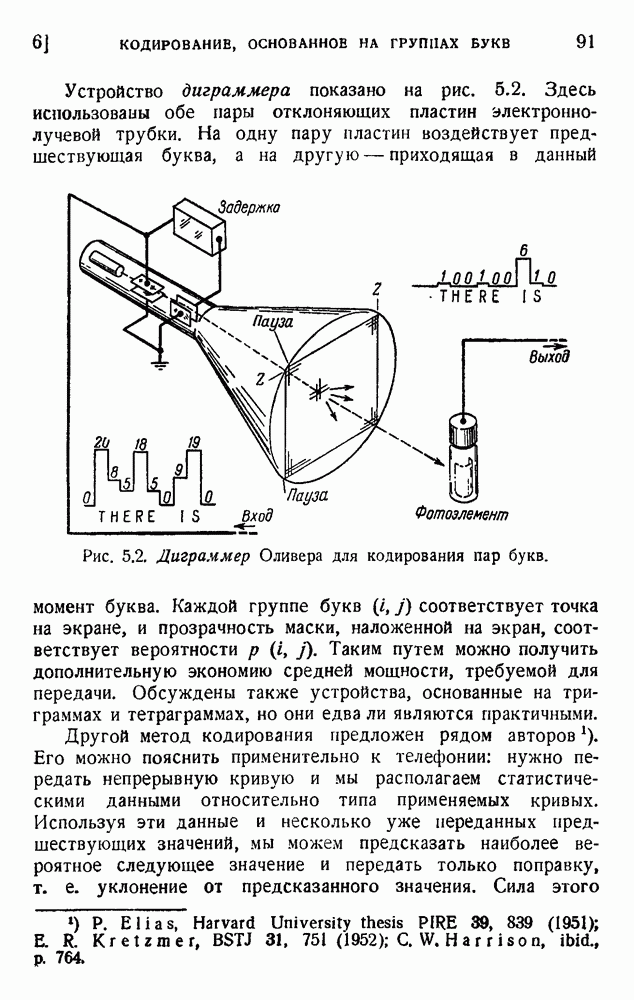
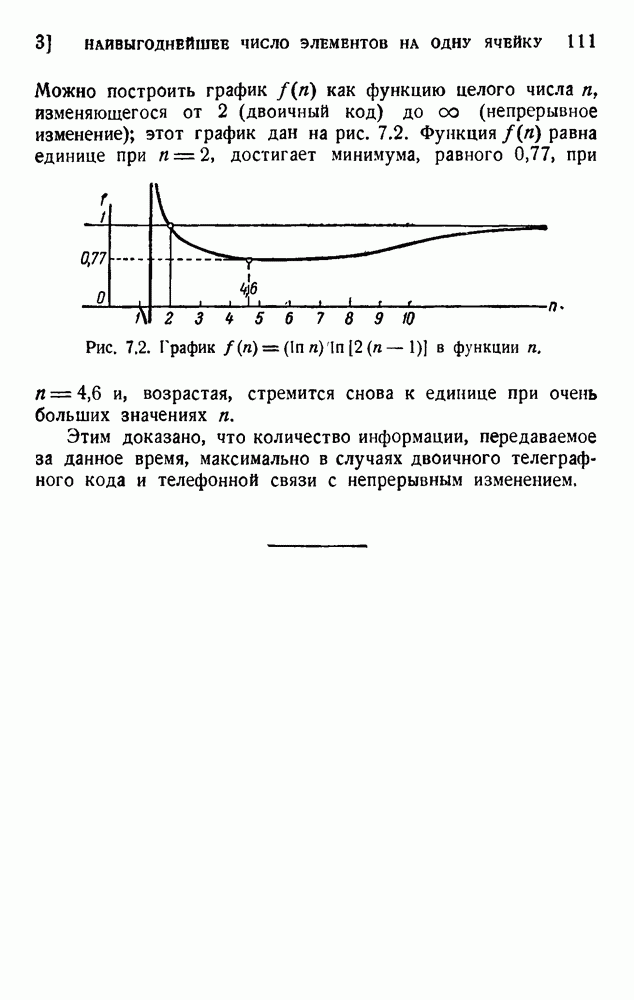
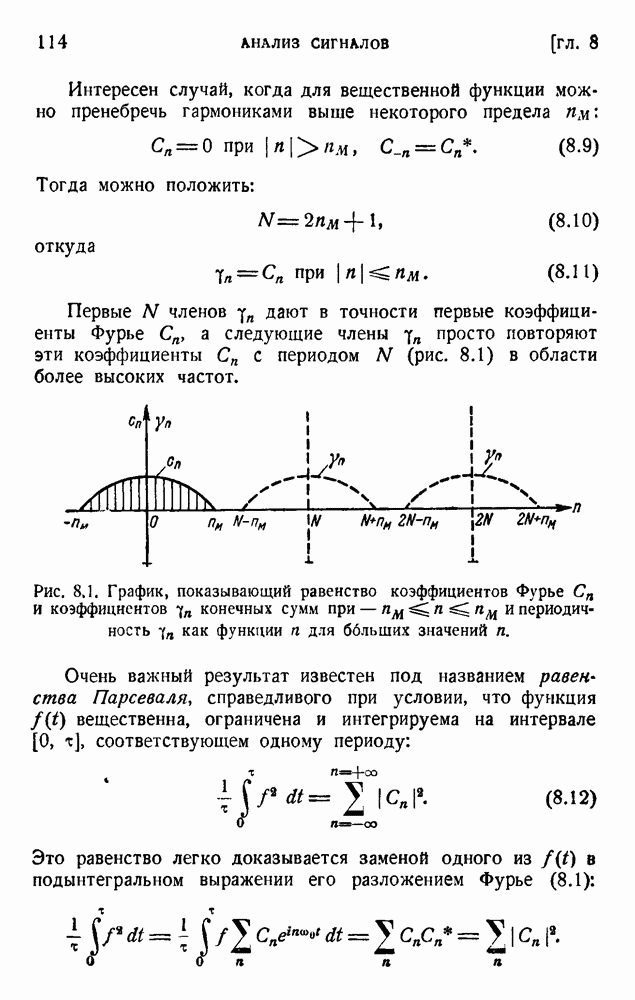
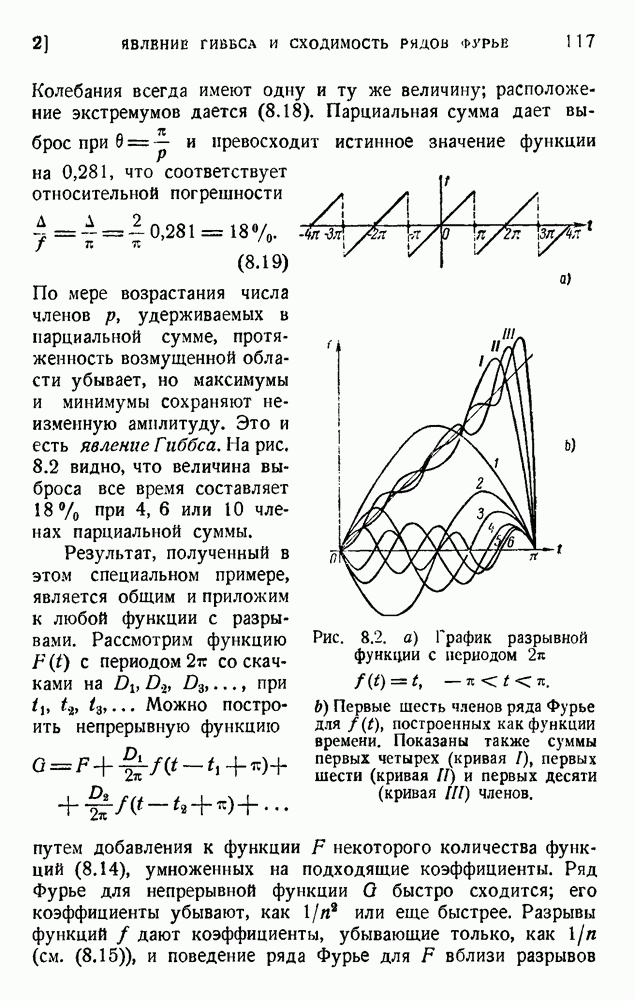
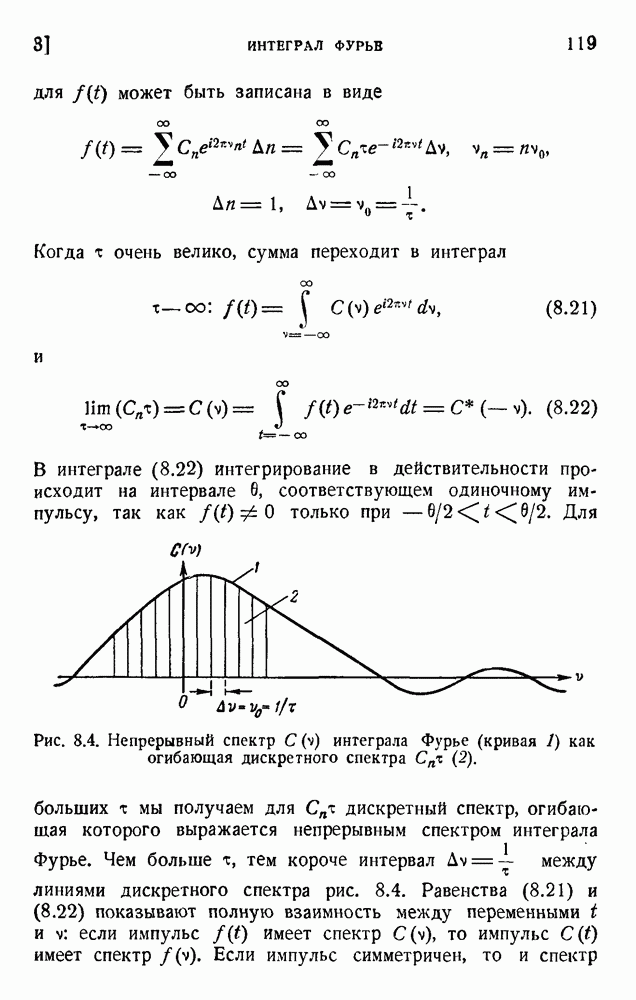
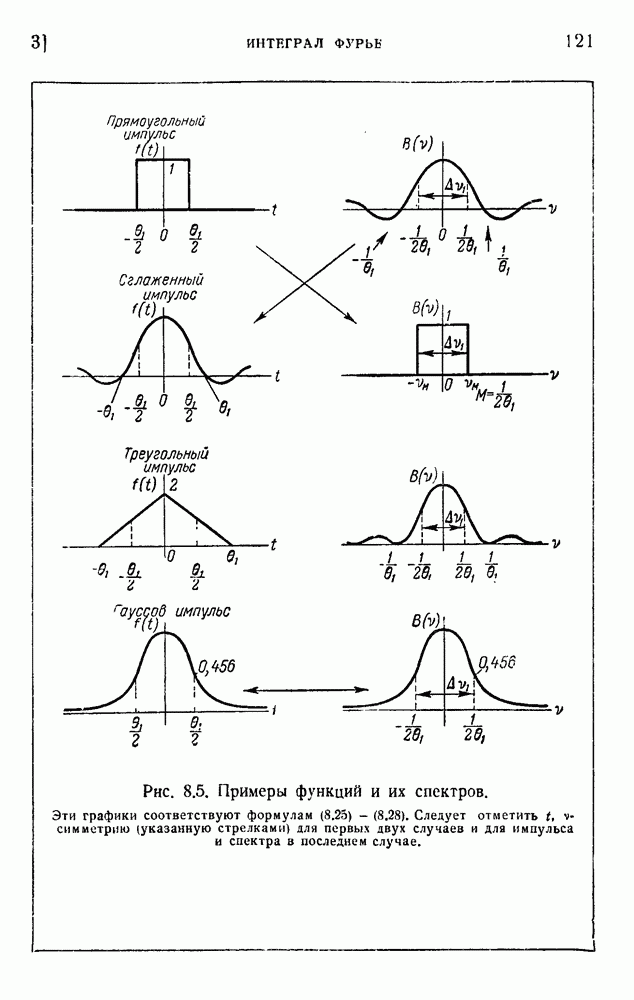
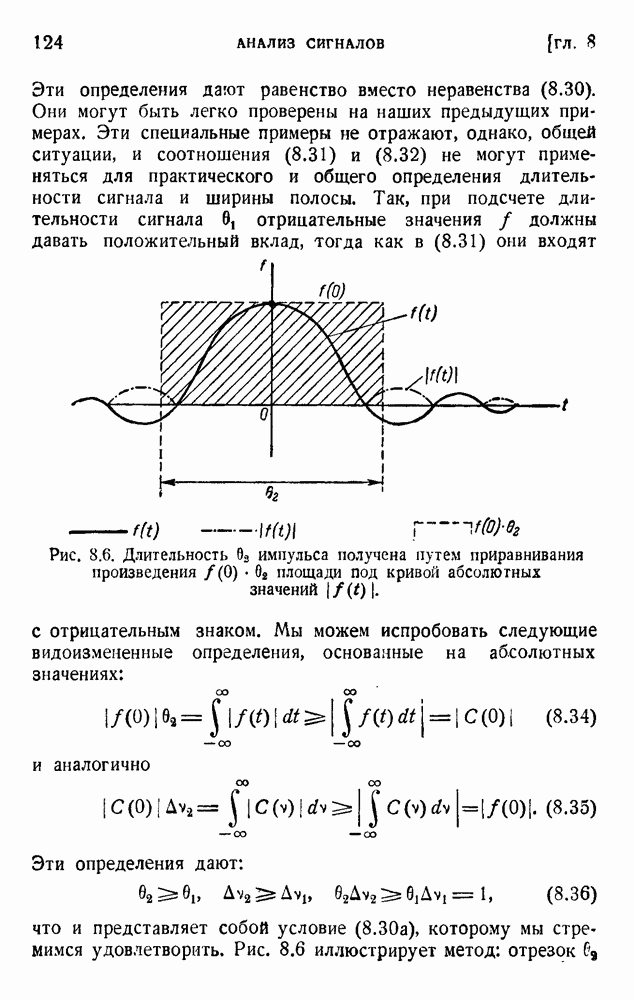
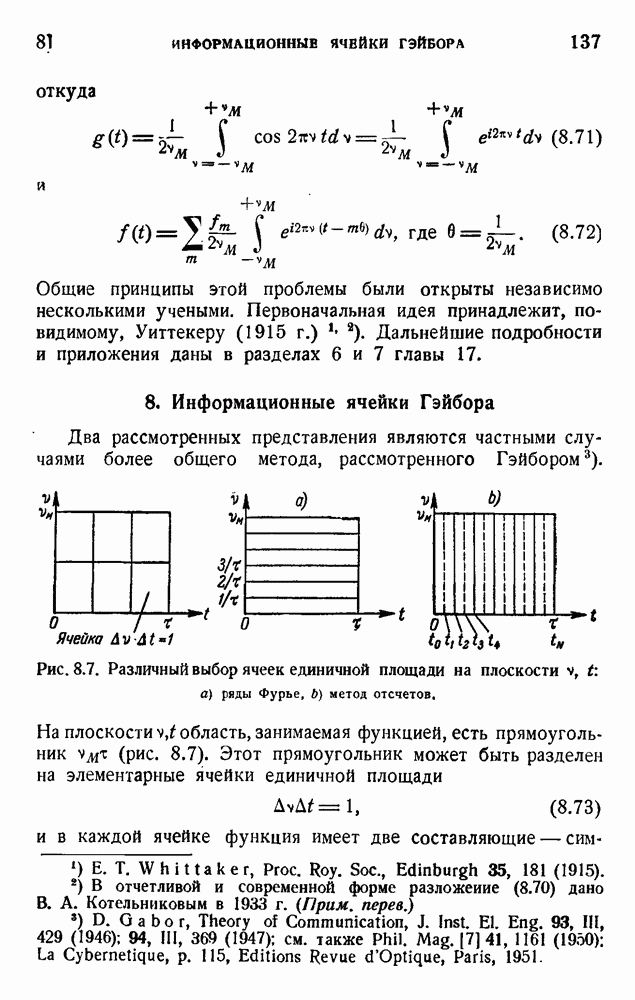
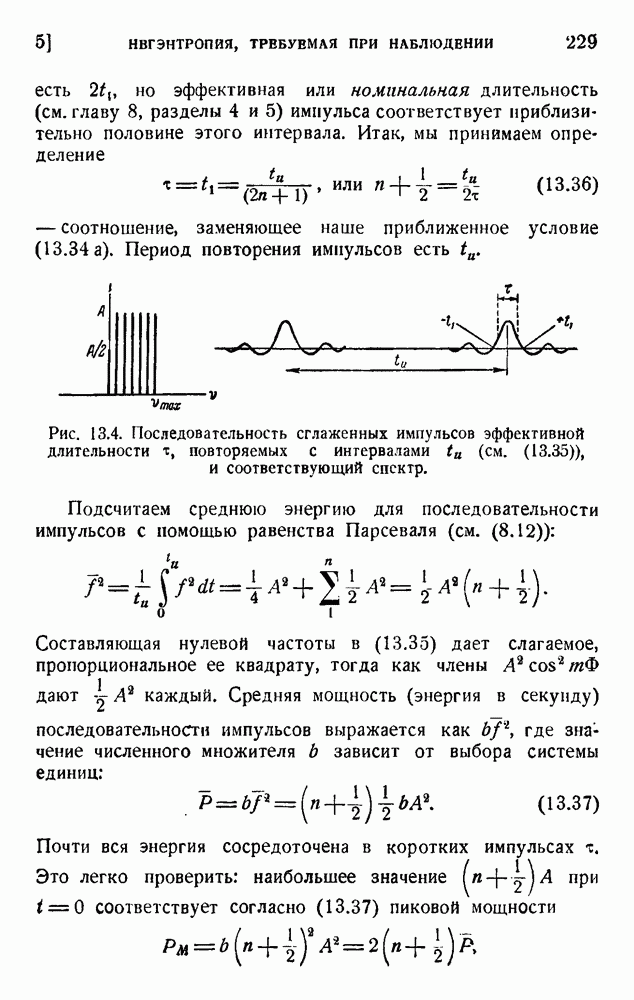
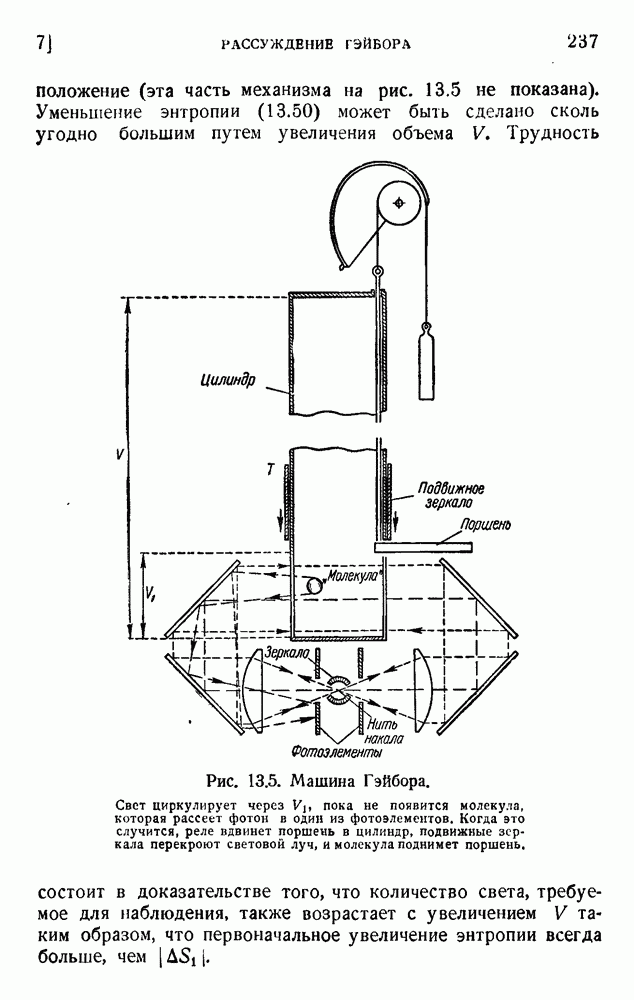
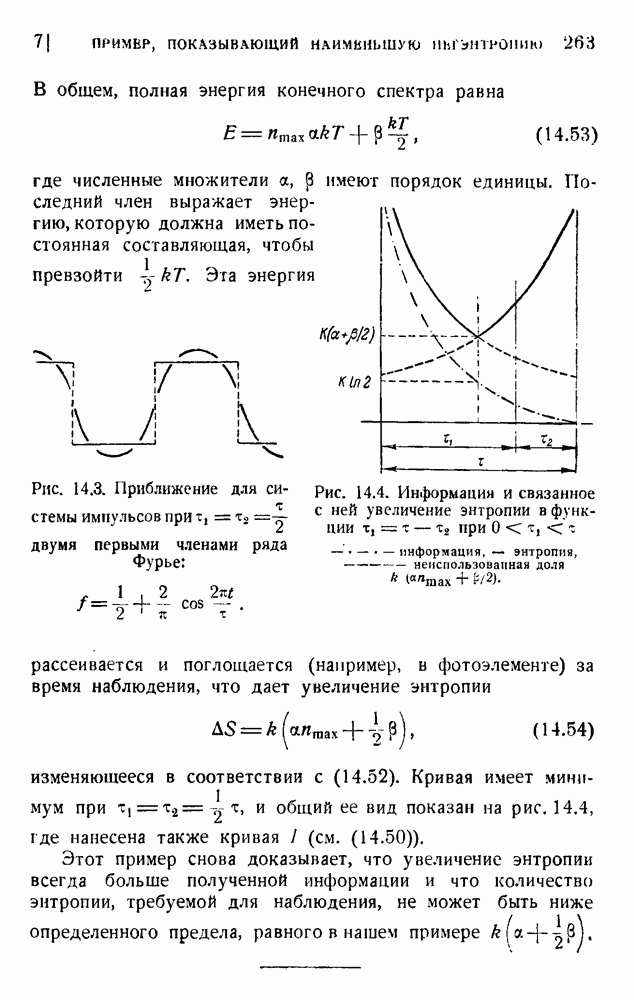
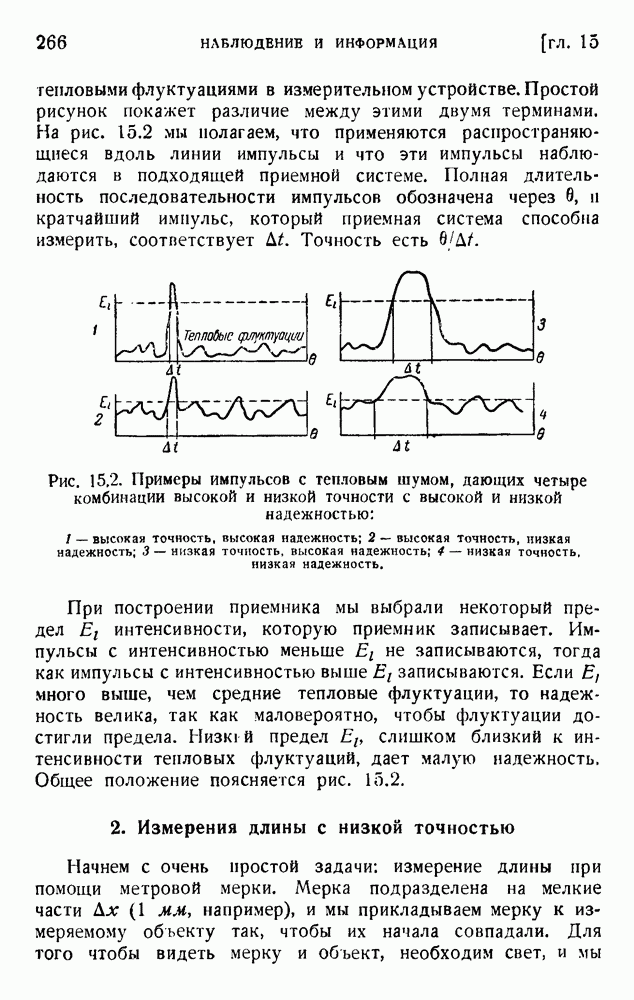
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
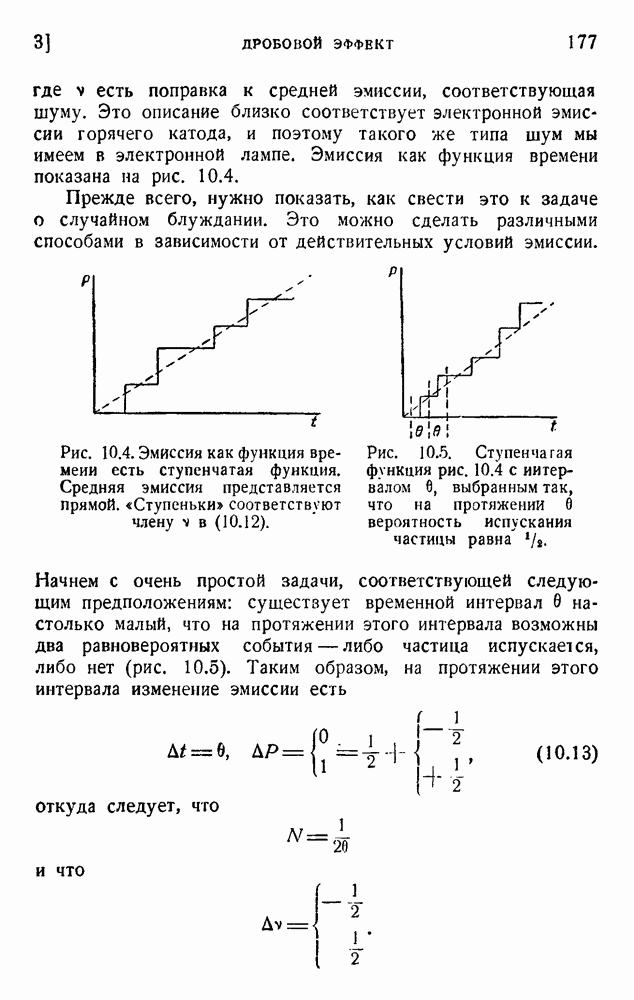
4. Броуново движение
Вернемся к обсуждению броунова движения; будем следовать трактовке Лоренца. Напомним некоторые численные значения:


Рис. 10.6. Координаты x, у и z частицы, погруженной в вязкую жидкость.
Рассмотрим частицу, погруженную в среду с координатами, показанными на рис. 10.6. Мы ограничимся рассмотрением движения только вдоль оси  . Так как движение случайно, то движение в направлении оси х не зависимо от движений в направлениях у и z.
. Так как движение случайно, то движение в направлении оси х не зависимо от движений в направлениях у и z.
Вводя коэффициент вязкого трения w, запишем уравнение движения частицы с массой 
 (10.17)
(10.17)
где  означает случайную силу, действующую на частицу. Сила
означает случайную силу, действующую на частицу. Сила  должна быть случайной, так как на протяжении любого промежутка времени (разумно выбранной малости) будет происходить очень большое число случайных столкновений частицы с молекулами жидкости.
должна быть случайной, так как на протяжении любого промежутка времени (разумно выбранной малости) будет происходить очень большое число случайных столкновений частицы с молекулами жидкости.
Рассмотрим теперь временной интервал  , настолько малый, чтобы изменение скорости
, настолько малый, чтобы изменение скорости  частицы на протяжении этого интервала было мало. Тогда полный импульс силы, действующей на частицу за время
частицы на протяжении этого интервала было мало. Тогда полный импульс силы, действующей на частицу за время  , равен
, равен
 (10.18)
(10.18)
Скорость частицы равна  при
при  и
и  при
при  ; интегрирование (10.17) по интервалу
; интегрирование (10.17) по интервалу  дает:
дает:
 (10.19)
(10.19)
Перегруппировывая члены, имеем:
 (10.20)
(10.20)
Так как  полностью случайна, можно считать:
полностью случайна, можно считать:
 (10.21)
(10.21)
но надо учесть, что  не равно нулю. Возведем (10.20) в квадрат:
не равно нулю. Возведем (10.20) в квадрат:

и заметим, что t очень мало, так что

Усредняя затем (10.22) и учитывая, что мы положили X
равным нулю, найдем среднее значение  :
:

Наша система (частица + жидкость) имеет температуру Т, и к ней применимы соотношения кинетической теории, именно:

Поэтому

Подставляя (10.24) в (10.23) и разрешая относительно X получаем для этой величины
 (10.25)
(10.25)
Итак, средний квадрат импульса силы не равен нулю. Далее, переписывая (10.23) в виде

мы замечаем, что  представляет потерю кинетической энергии частицы при ее движении в вязкой среде, тогда как
представляет потерю кинетической энергии частицы при ее движении в вязкой среде, тогда как  представляет компенсирующую энергию, доставляемую частице случайными столкновениями с молекулами.
представляет компенсирующую энергию, доставляемую частице случайными столкновениями с молекулами.
Итак, мы наблюдаем передачу энергии в двух направлениях:
Кинетическая энергия частицы — движение молекул.
Движение молекул кинетическая энергия частицы.
Далее, мы видим, что если вязкое трение велико, то и компенсирующий перенос энергии велик. Большое вязкое трение означает сильную связь между частицей и окружающей ее вязкой жидкостью, а следовательно, и мощные столкновения, соответствующие большим случайным импульсам X. Работа случайных сил производится за счет энергии теплового движения (т. е. теплоты) и снова превращается в теплоту через посредство вязкого трения.
Для нахождения среднеквадратичного смещения частицы мы несколько упростим рассуждение, предположив, что при  а при
а при  Предположим также, что после момента
Предположим также, что после момента  силы, действующие на частицу, отсутствуют; иначе говоря, мы выделяем одно из столкновений и рассматриваем его, а также каждое из других столкновений как индивидуальное событие. Тогда после
силы, действующие на частицу, отсутствуют; иначе говоря, мы выделяем одно из столкновений и рассматриваем его, а также каждое из других столкновений как индивидуальное событие. Тогда после  движение затухает, и мы можем записать:
движение затухает, и мы можем записать:
 (10.26)
(10.26)
Разрешая относительно  , находим;
, находим;

Но так как  мало, мы можем взять пределы для экспоненциальной функции 0 и
мало, мы можем взять пределы для экспоненциальной функции 0 и  ; поэтому из (10.20) при
; поэтому из (10.20) при  получаем:
получаем:
 (10.27)
(10.27)
Величина  представляет смещение частицы вследствие импульса X, полученного в момент
представляет смещение частицы вследствие импульса X, полученного в момент  . Это есть вид случайного блуждания, так как
. Это есть вид случайного блуждания, так как  потому, что
потому, что  . Но
. Но  ; возводя в квадрат и усредняя (10.27), получаем:
; возводя в квадрат и усредняя (10.27), получаем:

Подстановка (10.25) в (10.28) дает:
 (10.29)
(10.29)
Для большего промежутка времени t, содержащего много малых интервалов  , квадраты смещений суммируются как независимые величины, и мы имеем:
, квадраты смещений суммируются как независимые величины, и мы имеем:
 (10.30)
(10.30)
Этот результат был проверен экспериментально путем наблюдения зависимости от времени положений коллоидальных частиц в суспензии.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
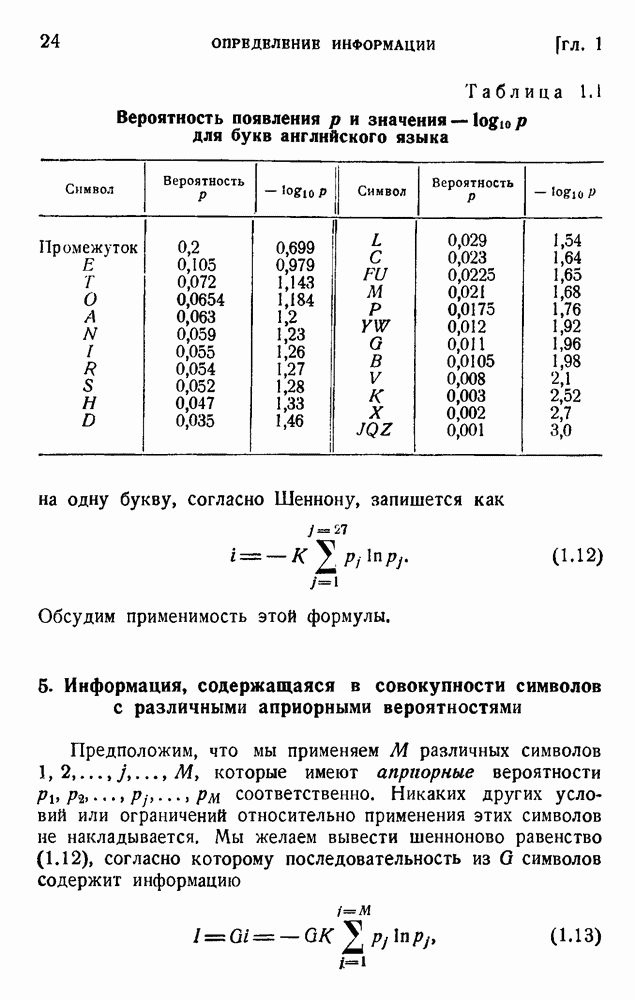
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
- 4. Информация и алфавит
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
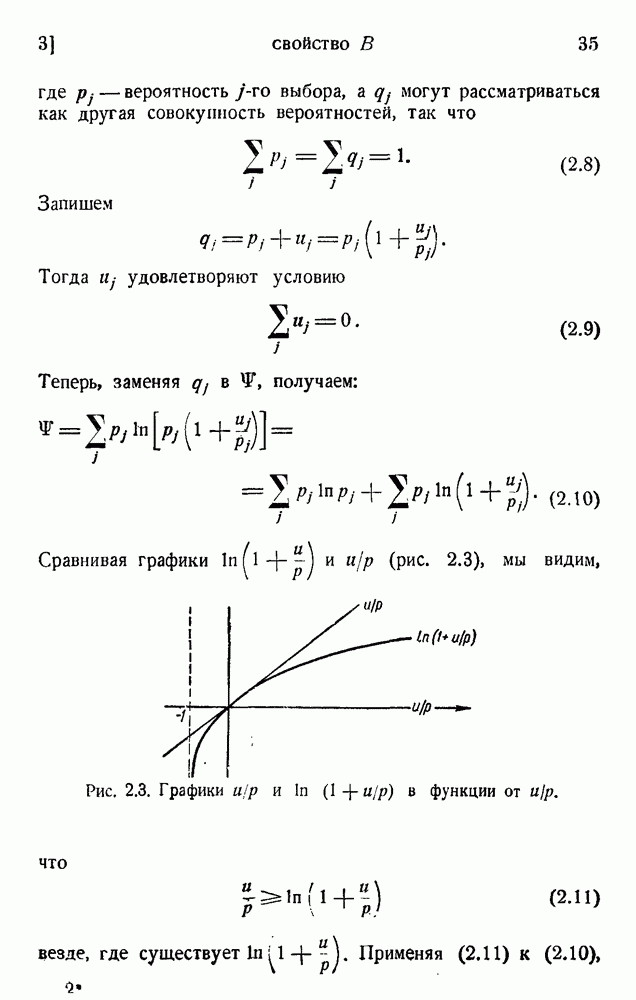
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
- 2. Корреляция в языке
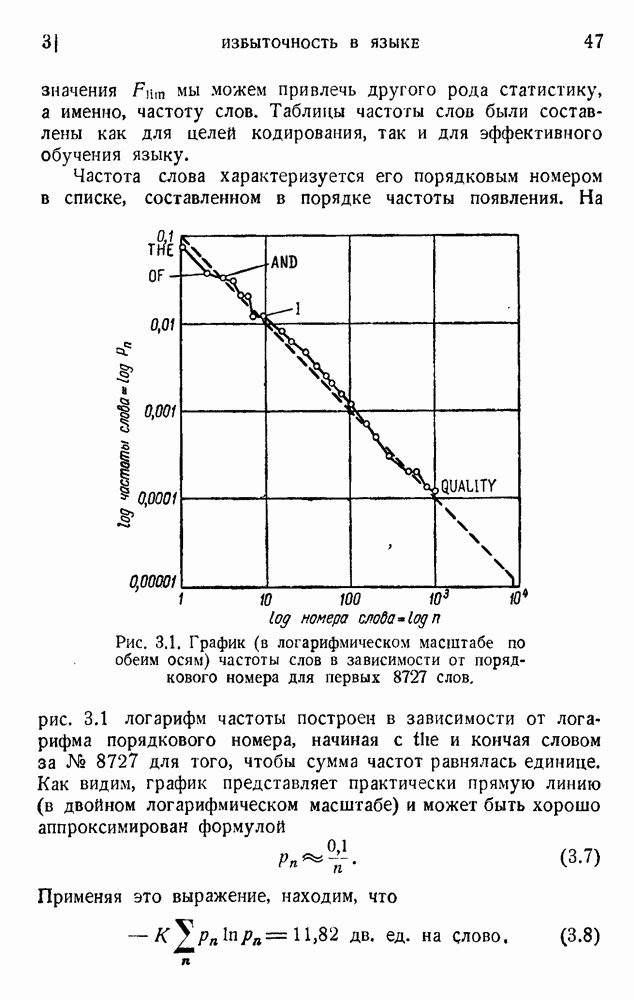
- 3. Избыточность в языке
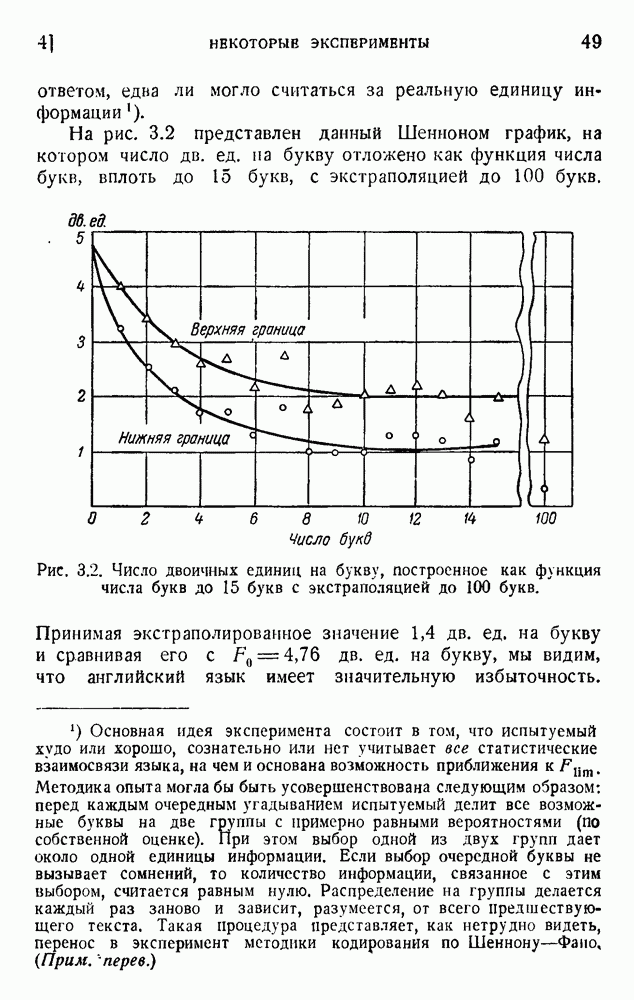
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
- 10. Проблемы статистики слов
- 11. Решение проблемы согласования
- Приложение
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
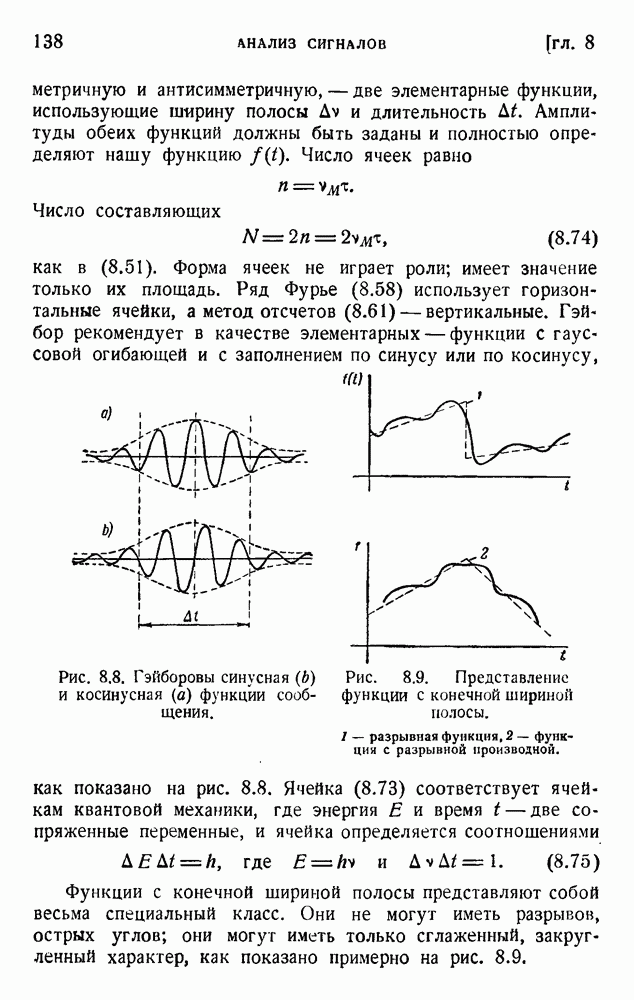
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
- 1. Ряд Фурье
- 2. Явление Гиббса и сходимость рядов Фурье
- 3. Интеграл Фурье
- 4. Роль конечной ширины полосы частот
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
- 7. Метод отсчетов Шеннона
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
- 10. Линейные преобразования и фильтры
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
- 1. Тепловое движение
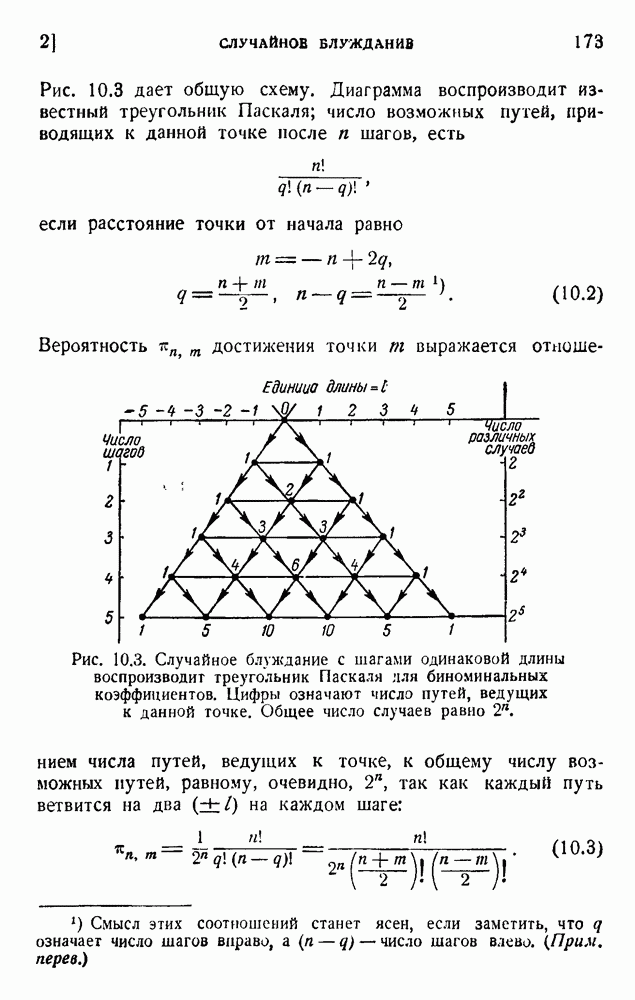
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
- 5. Тепловое движение в электрической цепи
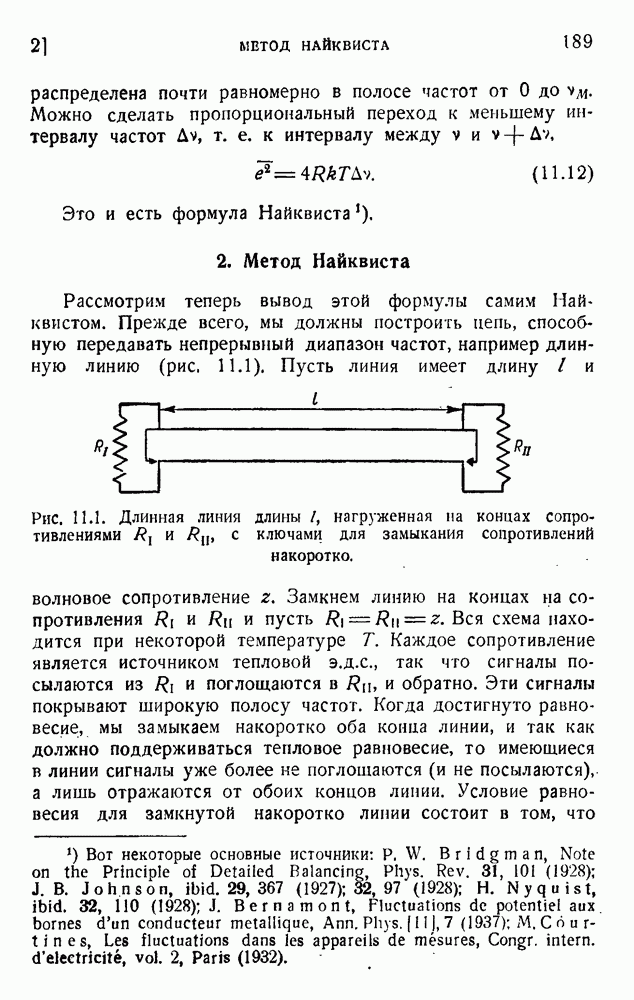
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
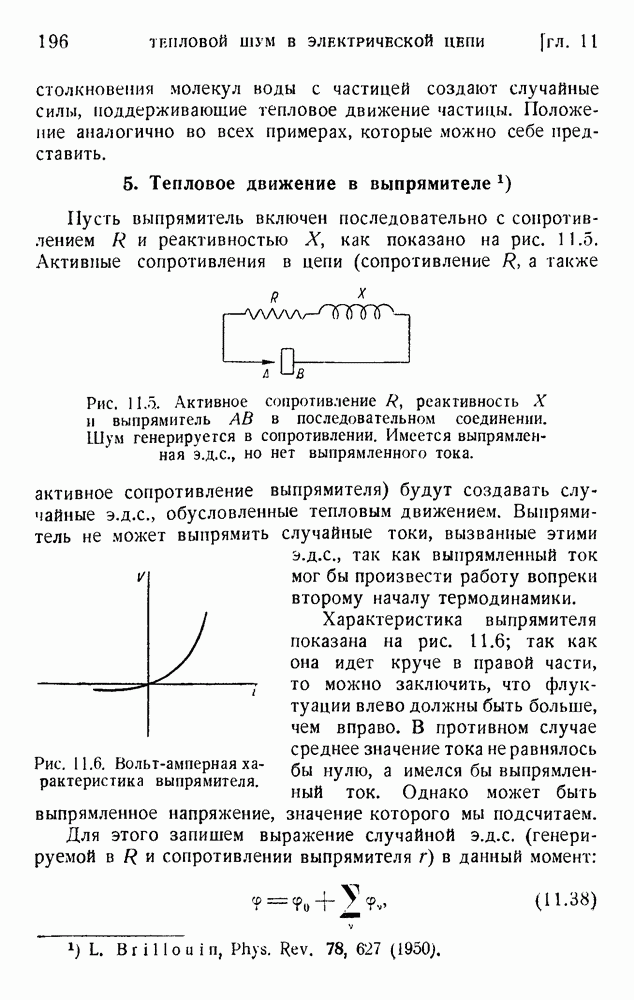
- 5. Тепловое движение в выпрямителе
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
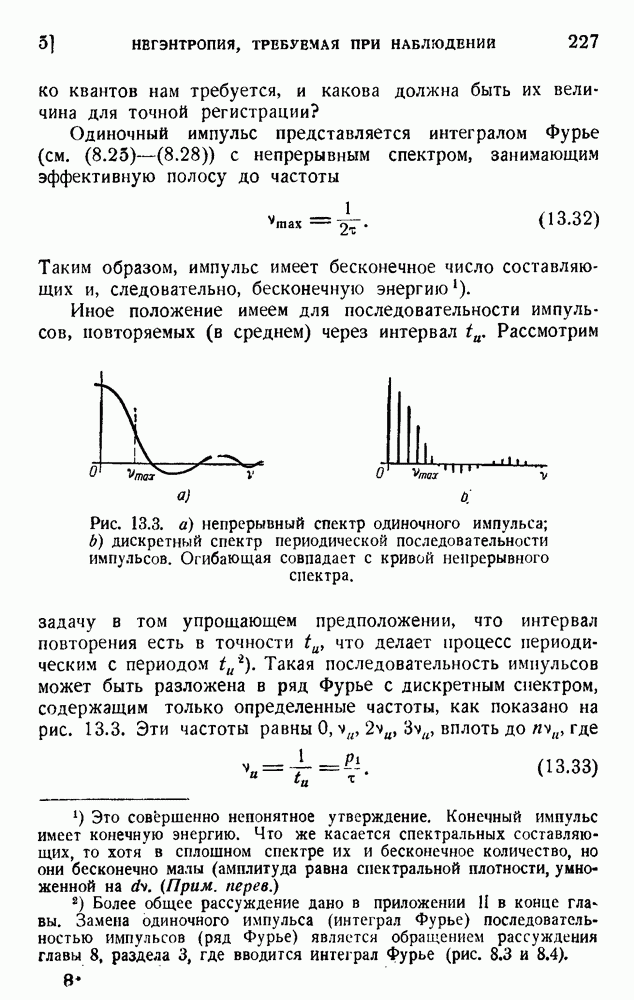
- 5. Негэнтропия, требуемая при наблюдении
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
- 4. Пределы евклидовой геометрии
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
- 6. Проблемы семантической информации