| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Примеры проблем, выходящих за рамки данной теории
Существующая теория полностью игнорирует ценность передаваемой и обрабатываемой информации. Это обстоятельство настойчиво подчеркивалось на протяжении всей книги. Многие другие авторы недооценивали, по-видимому, важность этого ограничения, что повело ко многим недоразумениям по поводу возможностей существующей теории. Только игнорируя человеческую ценность информации мы смогли построить научную теорию информации, основанную на статистике, и была показана полезность этой теории. Существует, однако, много проблем, которые нельзя разрешить методами этой теории. Цель этого раздела состоит в том, чтобы вкратце поставить некоторые из этих вопросов и показать, что все они сводятся к одной и той же общей проблеме: как ввести в теорию элемент ценности информации.
Надобность в этом новом элементе возникает всякий раз, когда информация рассматривается как основание для предсказания и для практического применения. Сперва подытожим кратко существующее положение: положим, например, что посылаемая телеграмма закодирована двоичным кодом (0 или 1) и содержит n двоичных цифр. Если кодирование не имеет избыточности, то телеграмма содержит всего n двоичных единиц информации. Вопрос о том, имеет телеграмма значение для получателя или нет, не рассматривается.
На научной конференции в Милане в апреле 1954 г. д-р Куфиньяль (Париж) поставил следующий вопрос: после того как телеграмма послана, автор добавляет одну двоичную цифру со следующим значением:
0: все неверно; не обращайте на телеграмму внимания,
1: телеграмма правильная; можете ею воспользоваться.
С точки зрения информации это означает добавление одной двоичной единицы, так что всего получается  единица вместо n. Практически же положение иное:
единица вместо n. Практически же положение иное:
0 («нет») — разрушает всю ценность содержащейся в телеграмме информации,
1 («да») — попросту добавляет избыточность.
Мы можем, следовательно, сказать, что «нет» (0) несет отрицательную информацию, равную по абсолютной величине полной информации в телеграмме. С точки зрения существующей теории информация всегда положительна и никогда не является отрицательной. Здесь ясно обнаруживается различие между статистической мерой информации и практической ценностью этой информации для получателя.
Коды с самопроверкой и самоисправлением, рассмотренные в главе 6, соответствуют практическим задачам, очень сходным с рассмотренной выше. К телеграмме, содержащей n двоичных знаков, мы добавляем 0 или 1 так, чтобы число единиц было всегда четно. Приемник проверяет общее число единиц. Если оно нечетно, то может быть 1, 3, 5, ... ошибок. Если оно четно, то либо ошибок нет, либо имеется 2, 4, 6, ... ошибок. Первый случай, очевидно, соответствует сигналу «нет» в задаче Куфиньяля.
Дополнительные сигналы для проверки или исправления не добавляют никакой информации. По существующей теории эти сигналы просто добавляют избыточность. Здесь речь идет, однако, о практической ценности информации.
Вместо того чтобы разделять утверждения на истинные и ложные («да» или «нет», см. выше), мы можем условиться указывать вероятность р того, что сообщение является истинным. Выберем шкалу с  значениями, и пусть число
значениями, и пусть число  соответствует
соответствует  , что означает, что утверждение в среднем истинно в
, что означает, что утверждение в среднем истинно в  случаях из 8 и ложно в
случаях из 8 и ложно в  случаях из 8. С информационной точки зрения это означает добавление к телеграмме трех двоичных единиц информации, что дает в общем
случаях из 8. С информационной точки зрения это означает добавление к телеграмме трех двоичных единиц информации, что дает в общем  вместо n. Поскольку рассматривается ценность информации для получателя, разумно считать, что ценность выражается произведением
вместо n. Поскольку рассматривается ценность информации для получателя, разумно считать, что ценность выражается произведением  Во многих случаях, однако, информация вовсе не представляет интереса для получателя, если вероятность ошибки превосходит некоторый установленный минимум, например
Во многих случаях, однако, информация вовсе не представляет интереса для получателя, если вероятность ошибки превосходит некоторый установленный минимум, например  ; в этом случае практическая ценность будет равна нулю для вероятностей 0, 1/8, 2/8, 3/8 и принимать некоторые возрастающие значения, когда вероятности составляют 4/8, 5/8, 6/8, 7/8, 1.
; в этом случае практическая ценность будет равна нулю для вероятностей 0, 1/8, 2/8, 3/8 и принимать некоторые возрастающие значения, когда вероятности составляют 4/8, 5/8, 6/8, 7/8, 1.
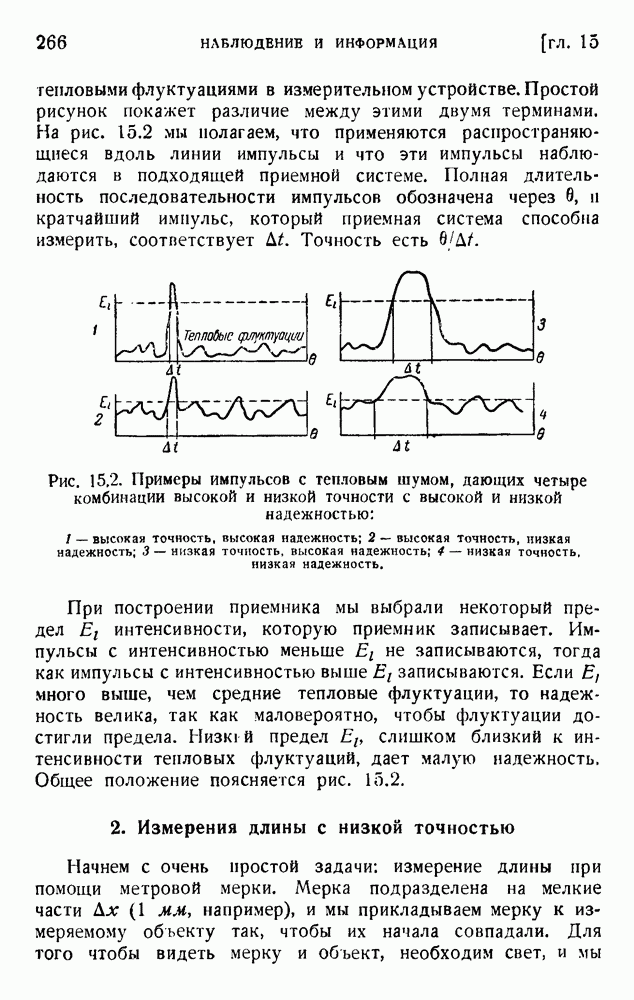
Вопрос о надежности физического наблюдения обсуждался в главе 14. Всякое физическое измерение содержит возможность ошибок. Надежность  экспериментального метода была определена через вероятность
экспериментального метода была определена через вероятность  ошибки, обусловленной тепловыми флуктуациями, и вероятность -
ошибки, обусловленной тепловыми флуктуациями, и вероятность - -правильного наблюдения. Эта задача, очень сходная с предыдущей, была дополнена предположением, что наименьшее рассматриваемое значение есть
-правильного наблюдения. Эта задача, очень сходная с предыдущей, была дополнена предположением, что наименьшее рассматриваемое значение есть  , что дает вероятность правильного наблюдения, равную 0,5.
, что дает вероятность правильного наблюдения, равную 0,5.
Вычислительные машины рассматривались в главе 19, и было показано, что вычисление очень сходно с переводом, кодированием и декодированием. В лучшем случае вычисление сохраняет всю информацию, содержащуюся во входных (исходных) данных, но обычно некоторое количество информации теряется за счет приближений, вводимых вычислительной процедурой. С информационной точки зрения вычисление не добавляет никакой новой информации, а лишь повторяет уже имеющуюся информацию на другом языке и, возможно, с некоторыми потерями. Но вычисление, как и декодирование, и перевод, конечно, увеличивают практическую ценность информации и ее значение для получателя. Вопрос об информации, содержащейся в программе вычисления, является другим аспектом проблемы, до сих пор не исследованным, хотя он и был поставлен на миланской конференции.
Весьма важным для практического применения является вопрос о циркуляции информации в каналах с обратной связью, или без нее. Положительная обратная связь обладает свойствами, существенно отличными от отрицательной. По нашему определению информация есть положительная величина, которая никогда не может стать отрицательной. Следовательно, в каналах с обратной связью мы снова имеем дело не с самой информацией, а с ее ценностью. Вопрос о том, как определить ценность в такого рода задачах, остается открытым. По-видимому, единственное заключение, которое мы пока что можем сделать (и которое не имеет большого практического значения), состоит в следующем: рассмотрим рис. 20.1, на котором входной канал С, дает в среднем  дв. ед. в секунду (пропускная способность
дв. ед. в секунду (пропускная способность  ). Эта информация проходит по
). Эта информация проходит по  , и некоторая доля
, и некоторая доля 
возвращается обратно по цепи обратной связи. Канал  должен быть в состоянии передать
должен быть в состоянии передать

так что его пропускная способность есть

и выходной канал имеет пропускную способность

Это, однако, не затрагивает хорошо известных проблем цепей с обратной связью. К задаче такого рода могли бы быть применены методы Линвилла и Зальцера, рассмотренные в главе 19.

Рис. 20.1. Схематическое представление пропускных способностей в цепи с обратной связью.
Большое число задач показывает важность обсуждения практической ценности информации для получателя. В то время как мера информации, как она определена в настоящее время, является абсолютной, ценность информации, конечно, относительна для некоторого получателя. Предполагается, что эти вопросы можно обсуждать с эмпирической точки зрения, пытаясь в каждом случае найти разумное определение ценности, а затем сравнивая различные задачи, с целью обнаружить общие свойства различных определений и выяснить, может ли быть развита теория, применимая к различным частным случаям. Такое обсуждение, вероятно, сделало бы теорию информации значительно более ценной для практических применений и могло бы открыть новые важные направления исследований.
Во всяком случае, одно непосредственно очевидно: любой критерий ценности ведет к оценке получаемой информации. Это равносильно отбору информации, имеющей определенную меру качества. Некоторая часть информации может быть признана важной и сохранена со всей ее ценностью, тогда как другая часть может считаться не имеющей ценности и
быть отброшена. Эта задача очень сходна с процессом фильтрации. Фильтр является хорошо известным в обшей теории элементом и обладает двумя важными свойствами: он необратим и он уменьшает общее количество информации. Мы можем установить следующее положение: относительная ценность информации для некоторого данного получателя меньше или равна абсолютной информации. Это уже является отправной точкой, действительной в общем случае, и задача состоит в установлении общего определения различных методов фильтрации, применяемых для оценки. относительной ценности информации.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
- 4. Информация и алфавит
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
- 2. Корреляция в языке
- 3. Избыточность в языке
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
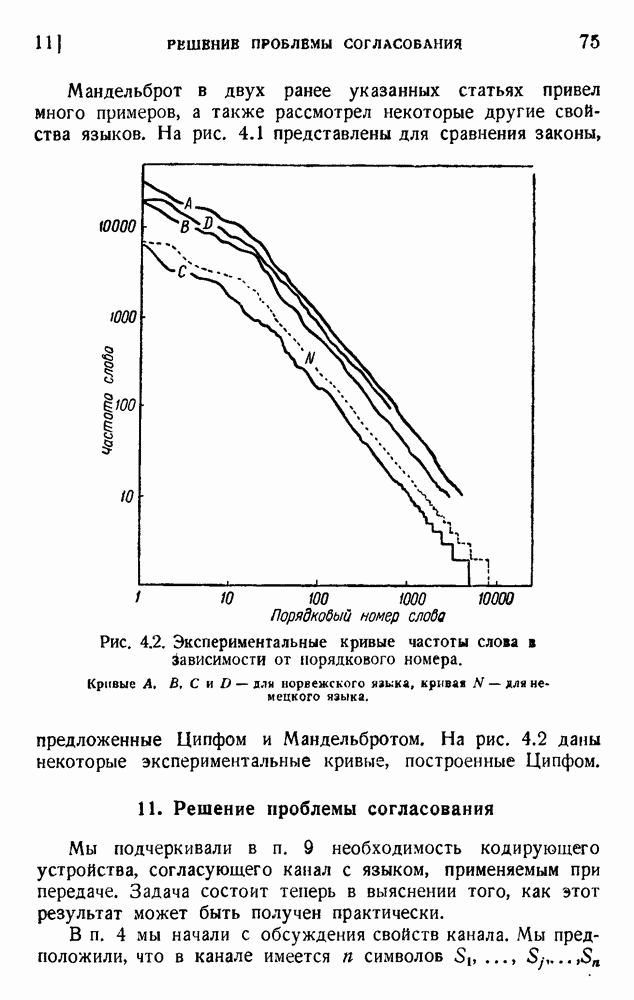
- 10. Проблемы статистики слов
- 11. Решение проблемы согласования
- Приложение
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
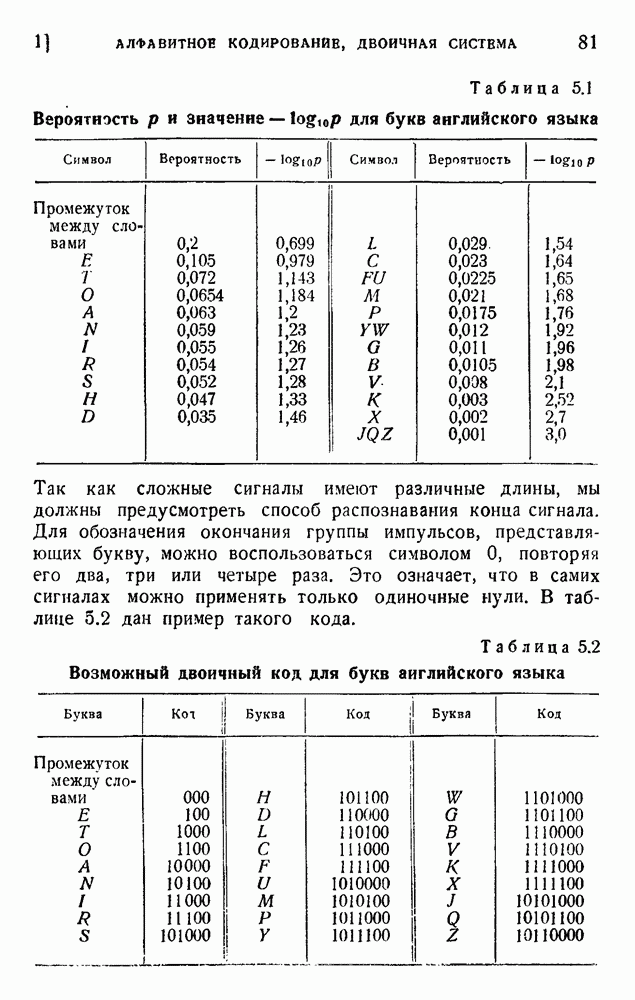
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
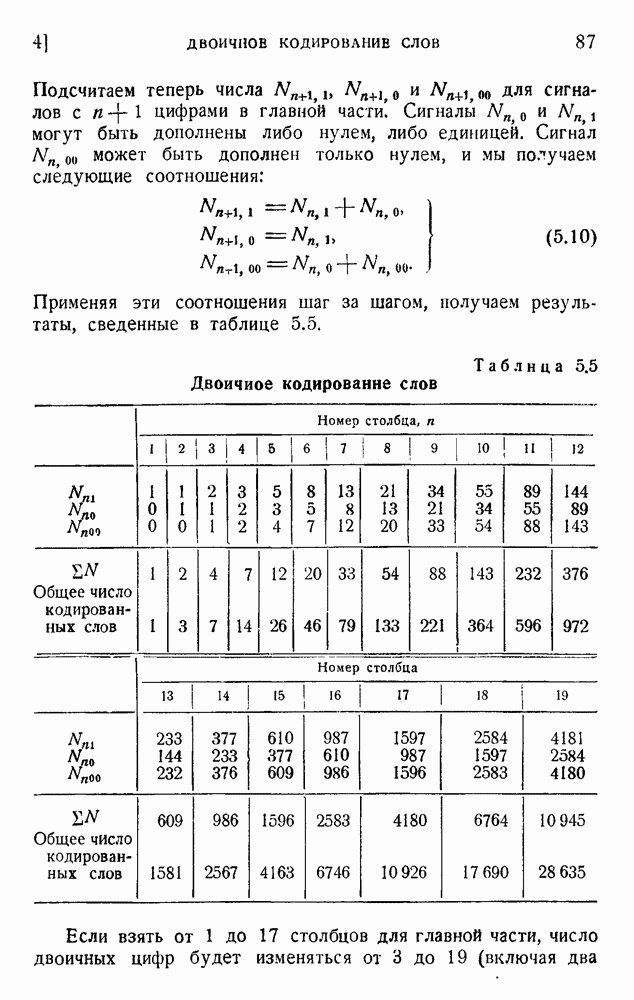
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
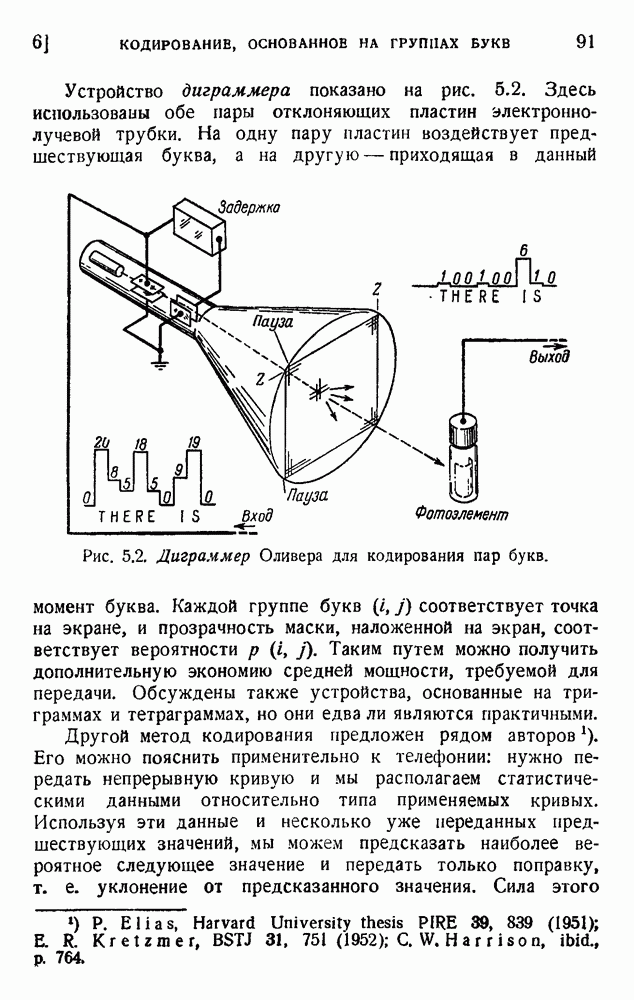
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
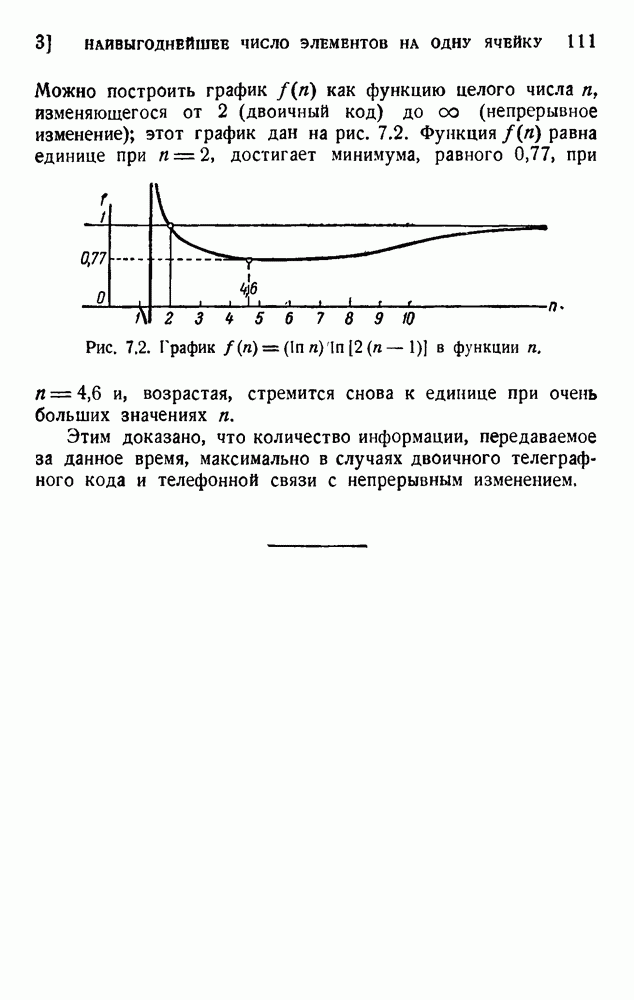
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
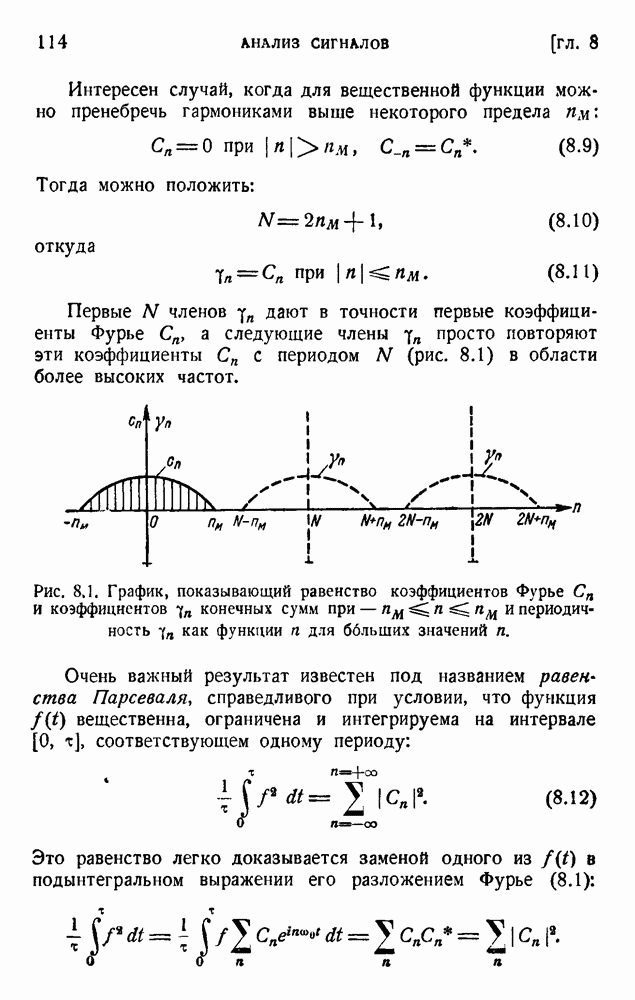
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
- 1. Ряд Фурье
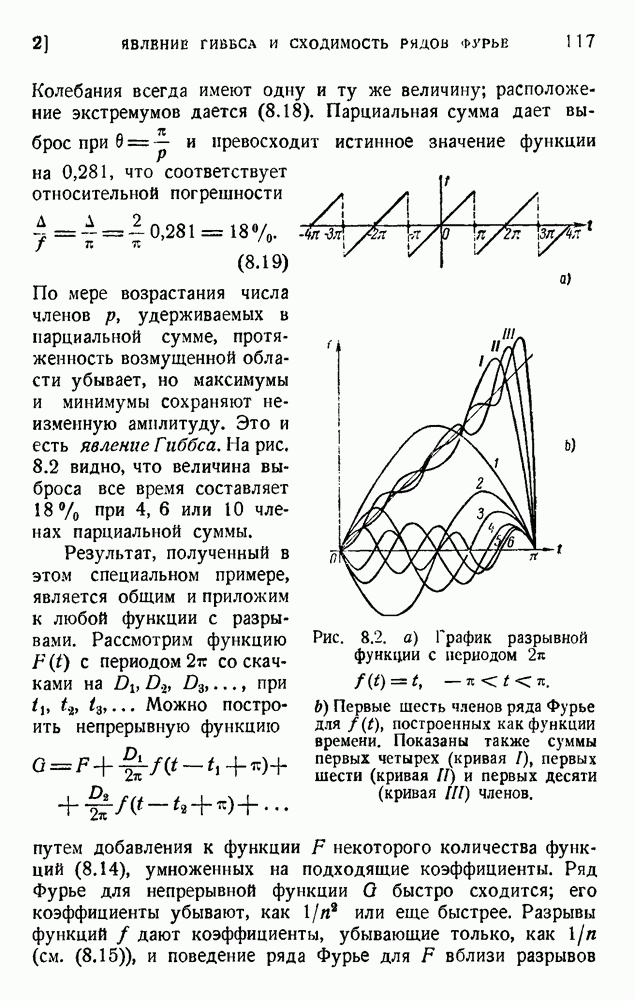
- 2. Явление Гиббса и сходимость рядов Фурье
- 3. Интеграл Фурье
- 4. Роль конечной ширины полосы частот
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
- 7. Метод отсчетов Шеннона
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
- 10. Линейные преобразования и фильтры
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
- 1. Тепловое движение
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
- 5. Тепловое движение в электрической цепи
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
- 5. Тепловое движение в выпрямителе
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
- 5. Негэнтропия, требуемая при наблюдении
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
- 4. Пределы евклидовой геометрии
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
- 6. Проблемы семантической информации