| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
В разделах 2 и 3 мы обсуждали очень простой пример, в котором эксперимент был основан на наблюдении одного-единственного осциллятора, и мы нашли предел  увеличения энтропии, когда перонтность правильного наблюдения считается равной 1/2. Этот предел был получен для
увеличения энтропии, когда перонтность правильного наблюдения считается равной 1/2. Этот предел был получен для
низких частот. Если включить и случай высокой частоты (раздел 3), то результаты могут быть представлены следующим образом: увеличение энтропии при отдельном наблюдении равно  — низкие частоты
— низкие частоты  ,
,

На практике в излучении черного тела высокие частоты не возбуждаются и одного кванта  достаточно для надежного наблюдения.
достаточно для надежного наблюдения.
Нужно отметить, что в рассуждениях предыдущих разделов предполагалось, что наблюдение состоит в отсчете значения энергии в резонаторе выше  . Считается, что отрицательный отсчет, т. е. наблюдение низкой энергии резонатора, не дает какой-либо информации в силу соображений, приведенных в разделе 6 главы 13 в связи с обсуждением тепловой машины Силарда. Основное соображение, на основании которого мы ограничиваемся только информацией, полученной из положительных результатов (т. е. наблюдений высокой энергии в обнаруживающем приборе), состоит в том, что неясно, как определить надежность отрицательного отсчета.
. Считается, что отрицательный отсчет, т. е. наблюдение низкой энергии резонатора, не дает какой-либо информации в силу соображений, приведенных в разделе 6 главы 13 в связи с обсуждением тепловой машины Силарда. Основное соображение, на основании которого мы ограничиваемся только информацией, полученной из положительных результатов (т. е. наблюдений высокой энергии в обнаруживающем приборе), состоит в том, что неясно, как определить надежность отрицательного отсчета.
Рассмотрим теперь более сложную задачу, в которой эксперимент требует наблюдений над я осцилляторами. В некоторых случаях наблюдения с помощью я приемников делаются одновременно, но при иных обстоятельствах мы можем делать наблюдения последовательно. Для наблюдения может требоваться, чтобы только один резонатор обладал в данный момент энергией выше определенного предела  , однако в иных экспериментальных устройствах наблюдение может быть основано на высоких значениях энергии в некотором числе
, однако в иных экспериментальных устройствах наблюдение может быть основано на высоких значениях энергии в некотором числе  резонаторов:
резонаторов:

Предполагается, что все резонаторы поддерживаются в термостате при постоянной температуре Т; мы рассмотрим сначала случай низких частот  . Задача состоит в определении предела
. Задача состоит в определении предела  , который дает общую вероятность
, который дает общую вероятность
правильного наблюдения, равную 1/2, и вероятность, равную 1/2, для ложного наблюдения, обусловленного флуктуациями.
Возьмем произвольный предел  и рассмотрим случай одного из
и рассмотрим случай одного из  осцилляторов. Из (14.5а) имеем следующие вероятности:
осцилляторов. Из (14.5а) имеем следующие вероятности:
 (14.21а)
(14.21а)
— вероятность того, что тепловые флуктуации дают данному резонатору энергию больше  , тогда как
, тогда как

есть вероятность того, что тепловые флуктуации дают резонатору энергию ниже  . Для случая, когда наблюдение ведется над
. Для случая, когда наблюдение ведется над  резонаторами, нетрудно вычислить следующую таблицу вероятностей, зависящих от тепловых флуктуаций.
резонаторами, нетрудно вычислить следующую таблицу вероятностей, зависящих от тепловых флуктуаций.
Таблица 14.1

Сумма вероятностей для этих различных случаев должна, очевидно, равняться единице:

Уточним теперь экспериментальные условия наблюдения. Положим прежде всего, что наблюдение дает положительный результат, когда какой-либо из  осцилляторов обладает энергией большей, чем
осцилляторов обладает энергией большей, чем  Вероятность того, что это происходит не благодаря флуктуациям, равна а вероятность того, что один осциллятор (или более) поднят на уровень выше
Вероятность того, что это происходит не благодаря флуктуациям, равна а вероятность того, что один осциллятор (или более) поднят на уровень выше  тепловыми флуктуациями, составляет 1 — Таким образом, вероятность правильного наблюдения есть
тепловыми флуктуациями, составляет 1 — Таким образом, вероятность правильного наблюдения есть  , так как наблюдаемая энергия выше
, так как наблюдаемая энергия выше  должна в этом случае быть результатом поглощения энергии внешнего источника. Вероятность ложного наблюдения, являющегося результатом флуктуаций, есть
должна в этом случае быть результатом поглощения энергии внешнего источника. Вероятность ложного наблюдения, являющегося результатом флуктуаций, есть  . Требуя, чтобы вероятность правильного наблюдения равнялась 1/2, получаем условие
. Требуя, чтобы вероятность правильного наблюдения равнялась 1/2, получаем условие
 (14.22)
(14.22)
или
 (14.22а)
(14.22а)
При  мы получаем наш прежний результат (14.15):
мы получаем наш прежний результат (14.15):

При увеличении  должно возрастать, так как с увеличением
должно возрастать, так как с увеличением  правая часть (14.22а) убывает. Следовательно, и
правая часть (14.22а) убывает. Следовательно, и  убывает. Логарифмируя (14.22), получим асимптотическое выражение для
убывает. Логарифмируя (14.22), получим асимптотическое выражение для 

или
 (14.23)
(14.23)
Значения коэффициента  даны в следующей таблице:
даны в следующей таблице:

В нашем эксперименте возбужденный резонатор получил свою избыточную энергию от внешнего источника, если наблюдение правильно, или, если наблюдение ложно, резонатор получил эту энергию от термостата. В любом случае эта избыточная энергия будет впоследствии поглощена термостатом, что приведет в случае правильного наблюдения к увеличению энтропии на

Это рассуждение в точности совпадает с предыдущим (см. (14.14) и (14.15)).
Нужно подчеркнуть, что в этой новой задаче вычисленное значение Д S представляет лишь нижний предел. Действительное увеличение может быть больше, чем  . Мы наблюдаем поглощение энергии от внешнего источника только тогда, когда оно достаточно для превышения резонатором уровня
. Мы наблюдаем поглощение энергии от внешнего источника только тогда, когда оно достаточно для превышения резонатором уровня  . Но многие другие резонаторы могут поглотить некоторую энергию от внешнего источника в меньших количествах, которые не поднимут энергию резонаторов выше
. Но многие другие резонаторы могут поглотить некоторую энергию от внешнего источника в меньших количествах, которые не поднимут энергию резонаторов выше  и ускользнут, таким образом, от нашего внимания. Эта поглощенная энергия также перейдет в термостат и даст дополнительное неизвестное увеличение энтропии. Итак, окончательно мы приходим к условию
и ускользнут, таким образом, от нашего внимания. Эта поглощенная энергия также перейдет в термостат и даст дополнительное неизвестное увеличение энтропии. Итак, окончательно мы приходим к условию
 (14.25)
(14.25)
Так как  есть возрастающая функция n, то нижний предел увеличения энтропии возрастает с числом необходимых для эксперимента резонаторов.
есть возрастающая функция n, то нижний предел увеличения энтропии возрастает с числом необходимых для эксперимента резонаторов.
Выражения (14.22), (14.22а), (14.23) и (14.24) для  были получены в предположении, что только один из резонаторов дает положительный отсчет. Эти выражения, однако, действительны в случае, когда мы получаем
были получены в предположении, что только один из резонаторов дает положительный отсчет. Эти выражения, однако, действительны в случае, когда мы получаем  положительных отсчетов, если мы потребуем, чтобы вероятность того, что все они истинны, равнялась 1/2. Это, как и ранее, означает, что, поскольку мы ограничиваемся флуктуациями, мы должны приравнять 1/2 вероятность того, что все
положительных отсчетов, если мы потребуем, чтобы вероятность того, что все они истинны, равнялась 1/2. Это, как и ранее, означает, что, поскольку мы ограничиваемся флуктуациями, мы должны приравнять 1/2 вероятность того, что все  резонаторов имеют энергию ниже
резонаторов имеют энергию ниже  . Таким образом, все предыдущие выражения для
. Таким образом, все предыдущие выражения для  сохраняют силу. Нужно, однако, видоизменить выражение (14.25) для увеличения энтропии, так как теперь термостатом должна быть поглощена
сохраняют силу. Нужно, однако, видоизменить выражение (14.25) для увеличения энтропии, так как теперь термостатом должна быть поглощена
энергия  . Итак,
. Итак,

или, если учесть неопределенность отрицательных отсчетов.

В этом рассуждении использована лишь небольшая часть таблицы 14.1. В других задачах, например, когда лишь некоторая доля положительных отсчетов считается истинной, понадобятся другие из приведенных вероятностей.
Иные соотношения получаются в случае высоких частот. Одного-единственного кванта  на каждый резонатор достаточно для надежного наблюдения, что и представляет, очевидно, необходимый минимум энергии. Эти частоты практически не встречаются в излучении черного тела. Поэтому мы берем
на каждый резонатор достаточно для надежного наблюдения, что и представляет, очевидно, необходимый минимум энергии. Эти частоты практически не встречаются в излучении черного тела. Поэтому мы берем

Суммируя результаты, мы видим, что эксперимент, требующий n одновременных наблюдений над n резонаторами, находящимися в термостате, соответствует увеличению энтропии на

для каждого резонатора, энергия которого превосходит причем

Промежуточный случай  должен исследоваться отдельно для каждой частной задачи.
должен исследоваться отдельно для каждой частной задачи.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
- 4. Информация и алфавит
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
- 2. Корреляция в языке
- 3. Избыточность в языке
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
- 10. Проблемы статистики слов
- 11. Решение проблемы согласования
- Приложение
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
- 1. Ряд Фурье
- 2. Явление Гиббса и сходимость рядов Фурье
- 3. Интеграл Фурье
- 4. Роль конечной ширины полосы частот
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
- 7. Метод отсчетов Шеннона
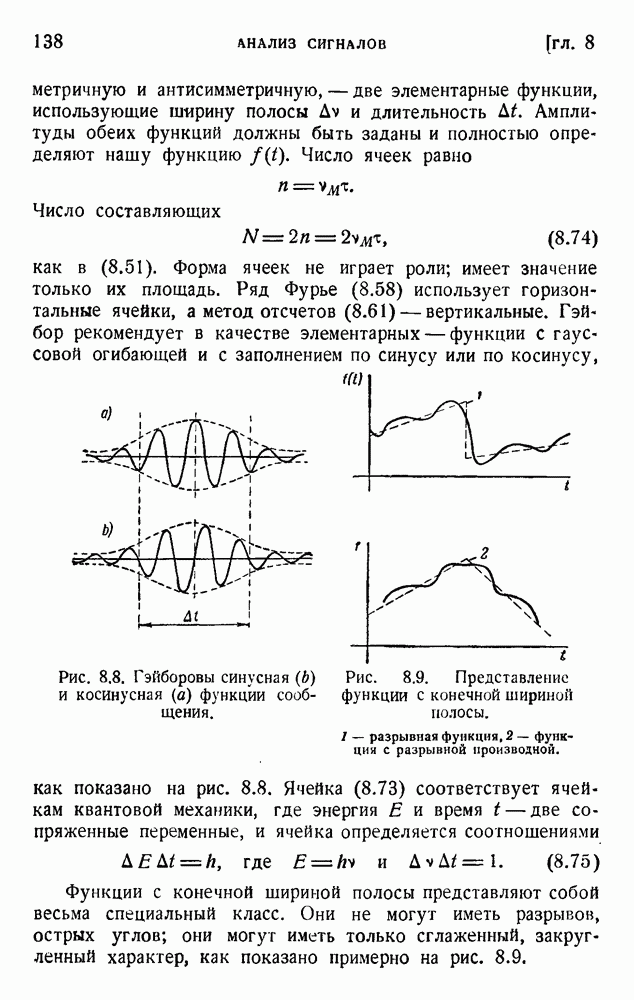
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
- 10. Линейные преобразования и фильтры
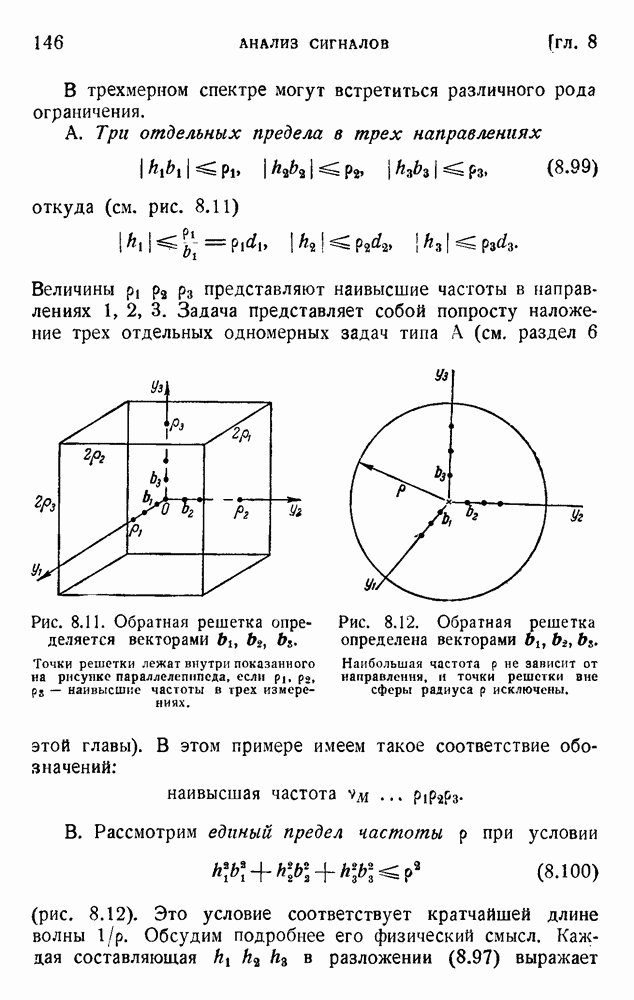
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
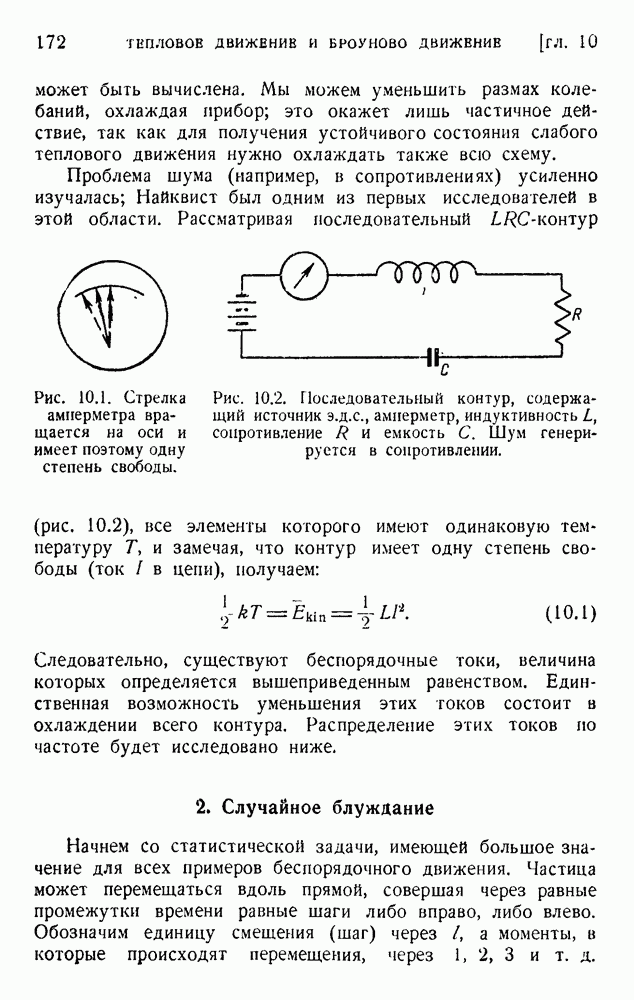
- 1. Тепловое движение
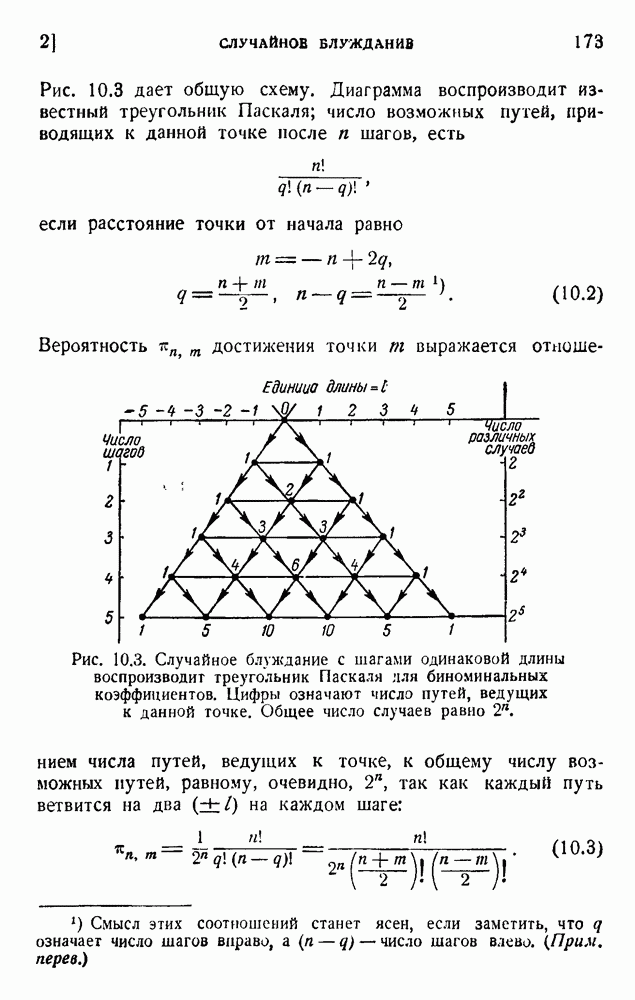
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
- 5. Тепловое движение в электрической цепи
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
- 5. Тепловое движение в выпрямителе
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
- 5. Негэнтропия, требуемая при наблюдении
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
- 4. Пределы евклидовой геометрии
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
- 6. Проблемы семантической информации