| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Двоичное кодирование слов
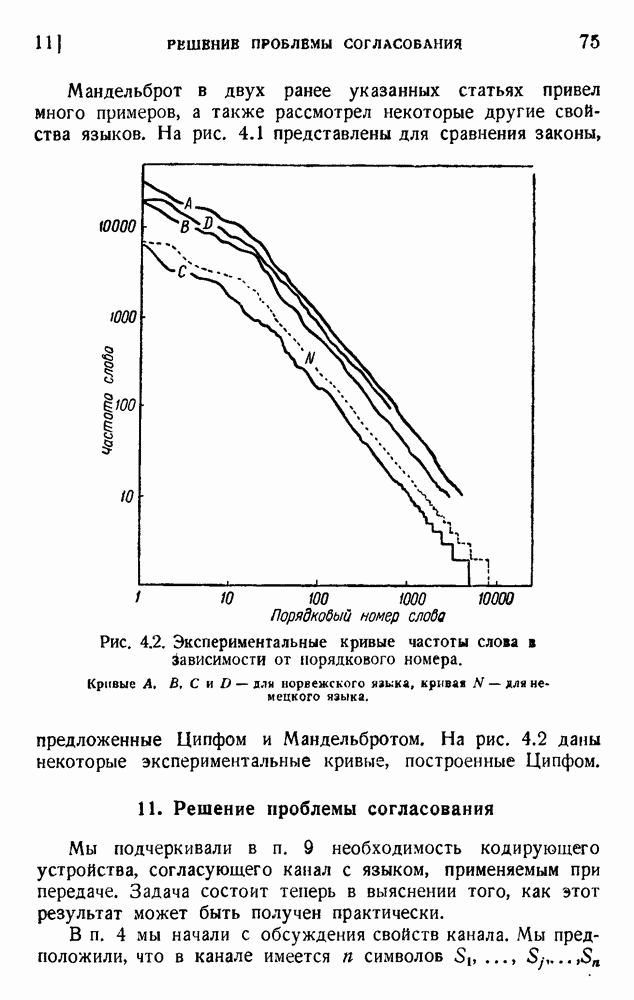
В главе 3 мы обсуждали исследование Шеннона избыточности английского языка. В одном из своих примеров Шеннон рассматривал частоту различных слов в языке и указал закон

устанавливающий вероятность появления слова, имеющего порядковый номер  . в списке, составленном в порядке убывающей частоты. Этот закон нельзя применять до бесконечности, так как сумма будет расходиться, и Шеннон предположил, что применяется только 8727 слов. Это число выбрано так, чтобы сумма вероятностей равнялась единице):
. в списке, составленном в порядке убывающей частоты. Этот закон нельзя применять до бесконечности, так как сумма будет расходиться, и Шеннон предположил, что применяется только 8727 слов. Это число выбрано так, чтобы сумма вероятностей равнялась единице):

В этих предположениях была подсчитана информация, оказавшаяся равной

так как среднее слово содержит 5,5 буквы при алфавите из 27 букв (26 букв плюс промежуток между словами). Цифра 2,14 дв. ед. на букву представляет значительную экономию по сравнению с обычным алфавитным кодированием, которое требует около 5 дв. ед. на букву.
Посмотрим, как можно использовать это преимущество. Рассмотрим сначала сигналы одинаковой длины. Применяя двоичные цифры 0 и 1 и беря постоянную длину, равную 13 цифрам, можем составить  различных сигналов, которыми можно закодировать 8192 слова, образующих словарь, достаточный для многих применений. Этот очень простой код дает 13 дв. ед. на слово или 2,36 дв. ед. на
различных сигналов, которыми можно закодировать 8192 слова, образующих словарь, достаточный для многих применений. Этот очень простой код дает 13 дв. ед. на слово или 2,36 дв. ед. на
букву, что уже очень близко к теоретическому пределу (см. (5.9)).
Можно получить лучший результат, применяя метод, обсужденный в п. 1 этой главы и иллюстрированный таблицей 5.2. Исключим кратные нули в главном сигнале и используем их только в окончании. Каждый сигнал начинается единицей и кончается группой 00,000, 0000,... Несколько таких комбинаций дано в таблице 5.4.
Таблица 5.4

В четвертом столбце комбинация 1001 опущена, так как она содержит два нуля подряд. По этой же причине опущены комбинации 10001.00; 10010.00; 10011.00 и 11001.00 в пятом столбце.
В последующем рассуждении мы опустим последние два нуля, появляющиеся в конце каждого сигнала. Предположим, что мы нашли все сигналы некоторого столбца (например, семь сигналов четвертого столбца с четырьмя цифрами в главной части каждого сигнала). Введем следующие обозначения:
n — номер столбца,
 — число сигналов, оканчивающихся единицей,
— число сигналов, оканчивающихся единицей,
 — число сигналов, оканчивающихся одним нулем,
— число сигналов, оканчивающихся одним нулем,
 — число сигналов, оканчивающихся группой нулей.
— число сигналов, оканчивающихся группой нулей.
Например, для четвертого столбца (не считая последних двух нулей после точки)

Подсчитаем теперь числа  и
и  для сигналов с
для сигналов с  цифрами в главной части. Сигналы
цифрами в главной части. Сигналы  могут быть дополнены либо нулем, либо единицей. Сигнал
могут быть дополнены либо нулем, либо единицей. Сигнал  может быть дополнен только нулем, и мы получаем следующие соотношения:
может быть дополнен только нулем, и мы получаем следующие соотношения:

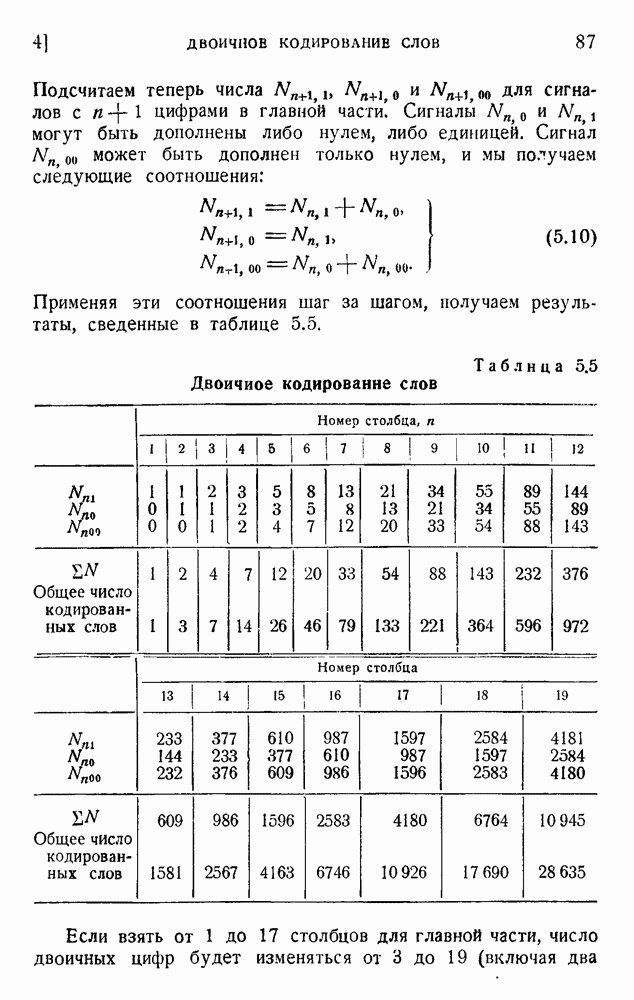
Применяя эти соотношения шаг за шагом, получаем результаты, сведенные в таблице 5.5.
Таблица 5.5. Двоичное кодирование слов

Если взять от 1 до 17 столбцов для главной части, число двоичных цифр будет изменяться от 3 до 19 (включая два
нуля, которые должны быть добавлены в конце каждого сигнала), что даст словарь, содержащий около 11 000 слов.
Подсчет среднего числа двоичных единиц на слово может быть выполнен без особых трудностей, если принять результаты Шеннона для вероятности последовательных слов. Такой подсчет дает около 12 дв. ед. на слово, что очень близко к теоретическому пределу 11,82. Такого родз кодирование является, по-видимому, наиболее экономичным из числа практически выполнимых.
Для практического применения код должен быть дополнен буквенным кодом. Буквы во всяком случае будут нужны для всех слов, не вошедших в словарь, в особенности для имен, географических названий и т. д. Если такие слова встречаются редко, можно оставить последние 27 символов кода для алфавита. Если же специальные слова встречаются очень часто, кодирование слов становится невыгодным.
Воспользуемся соотношениями (5.10) для вычисления вероятностей  сигналов, главная часть которых имеет окончание 1, 0 или 00. Имеем:
сигналов, главная часть которых имеет окончание 1, 0 или 00. Имеем:

Равенства (5.10) и (5.11), взятые совместно, определяют последовательные значения вероятностей. Когда  велико (например,
велико (например,  ), эти вероятности делаются независимыми от n, и легко получить
), эти вероятности делаются независимыми от n, и легко получить
 (5.12)
(5.12)
и равенства (5.10) принимают вид:

откуда

где  . Сравнение с точными цифрами таблицы 5.5 показывает, что эти соотношения дают хорошее приближение при
. Сравнение с точными цифрами таблицы 5.5 показывает, что эти соотношения дают хорошее приближение при  . При помощи этих формул можно провести более детальное исследование кода, предложенного в данном разделе,
. При помощи этих формул можно провести более детальное исследование кода, предложенного в данном разделе,
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
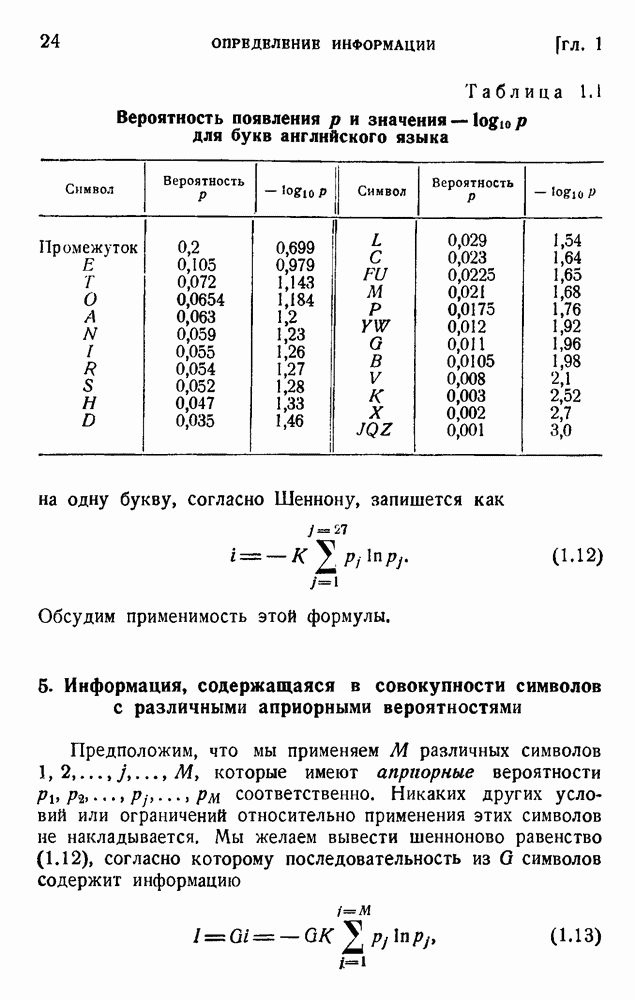
- 4. Информация и алфавит
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
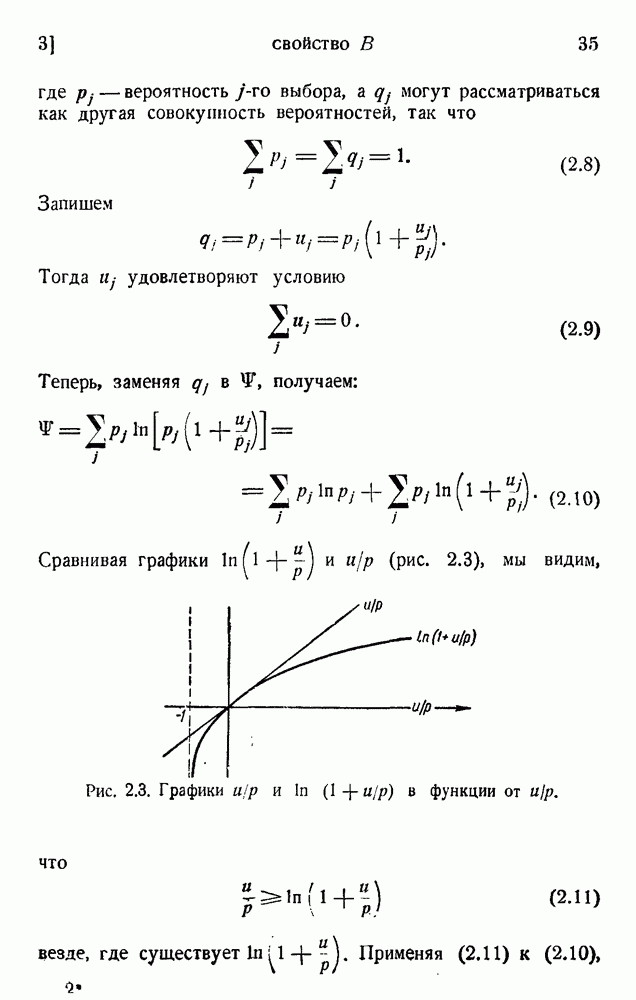
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
- 2. Корреляция в языке
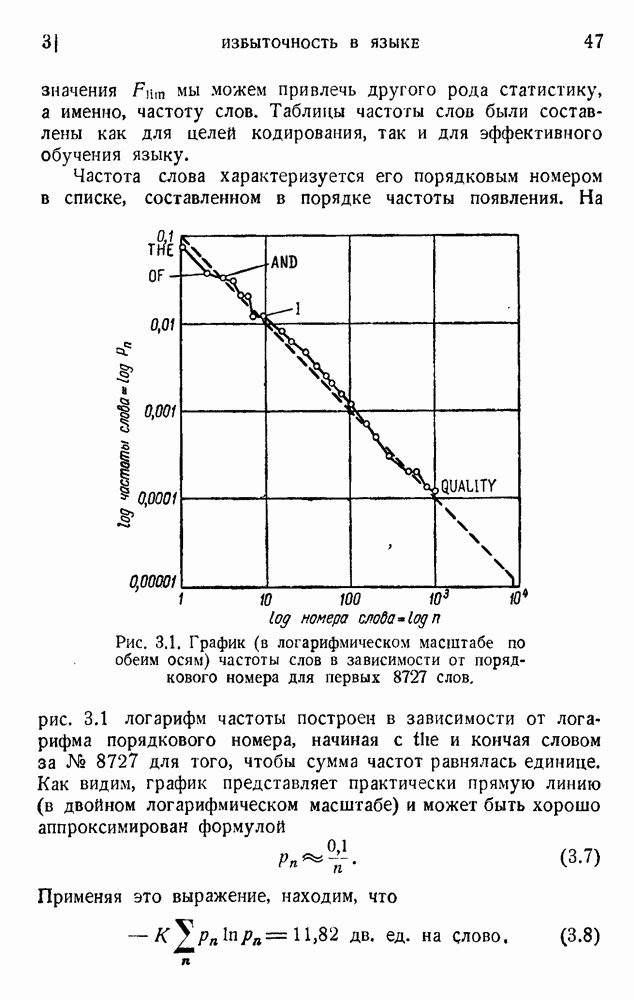
- 3. Избыточность в языке
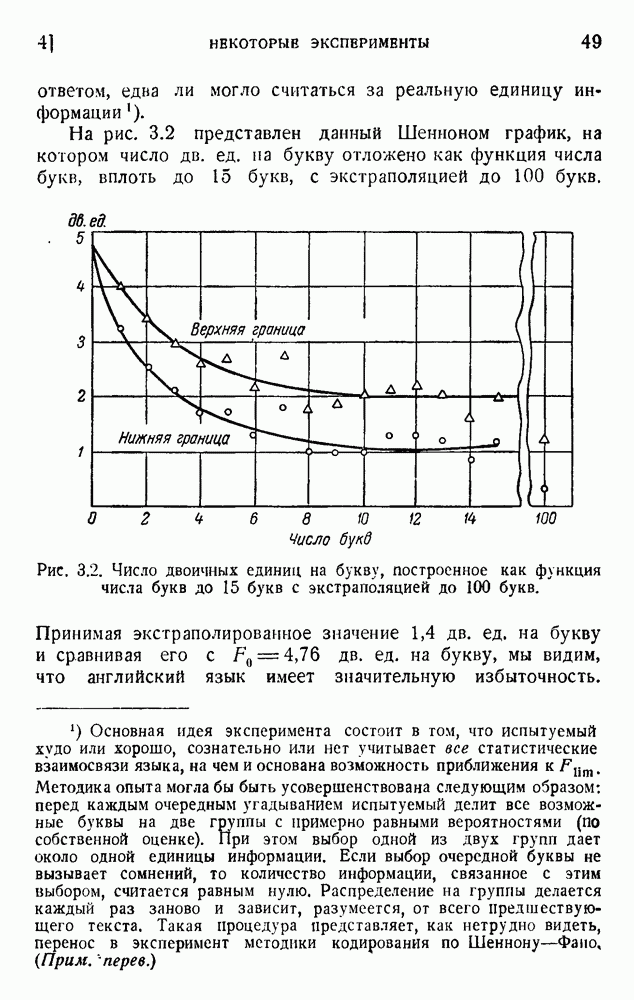
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
- 10. Проблемы статистики слов
- 11. Решение проблемы согласования
- Приложение
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
- 1. Ряд Фурье
- 2. Явление Гиббса и сходимость рядов Фурье
- 3. Интеграл Фурье
- 4. Роль конечной ширины полосы частот
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
- 7. Метод отсчетов Шеннона
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
- 10. Линейные преобразования и фильтры
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
- 1. Тепловое движение
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
- 5. Тепловое движение в электрической цепи
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
- 5. Тепловое движение в выпрямителе
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
- 5. Негэнтропия, требуемая при наблюдении
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
- 4. Пределы евклидовой геометрии
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
- 6. Проблемы семантической информации