6. Проблемы семантической информации

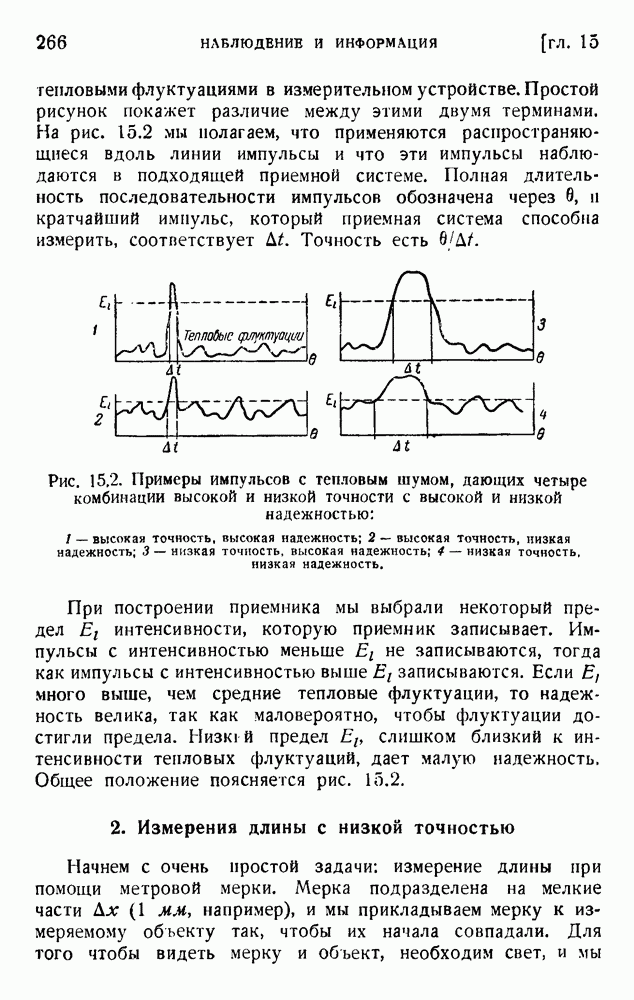
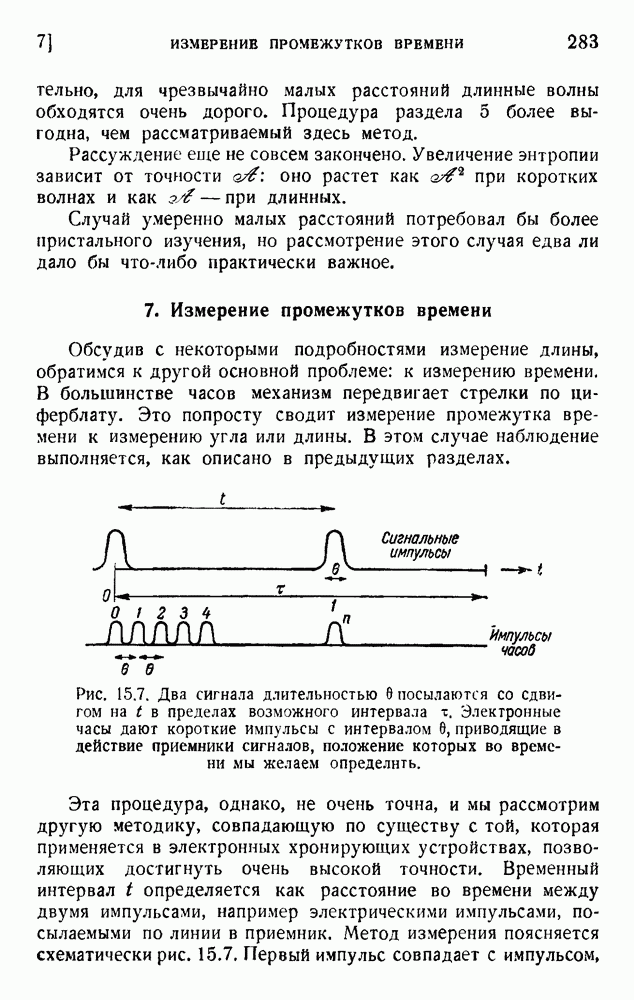
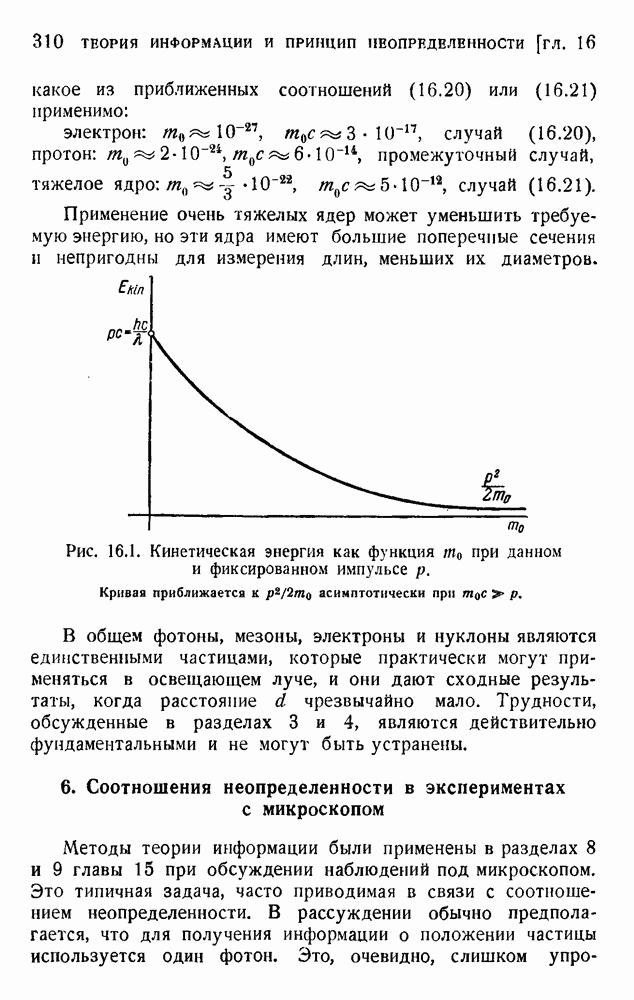
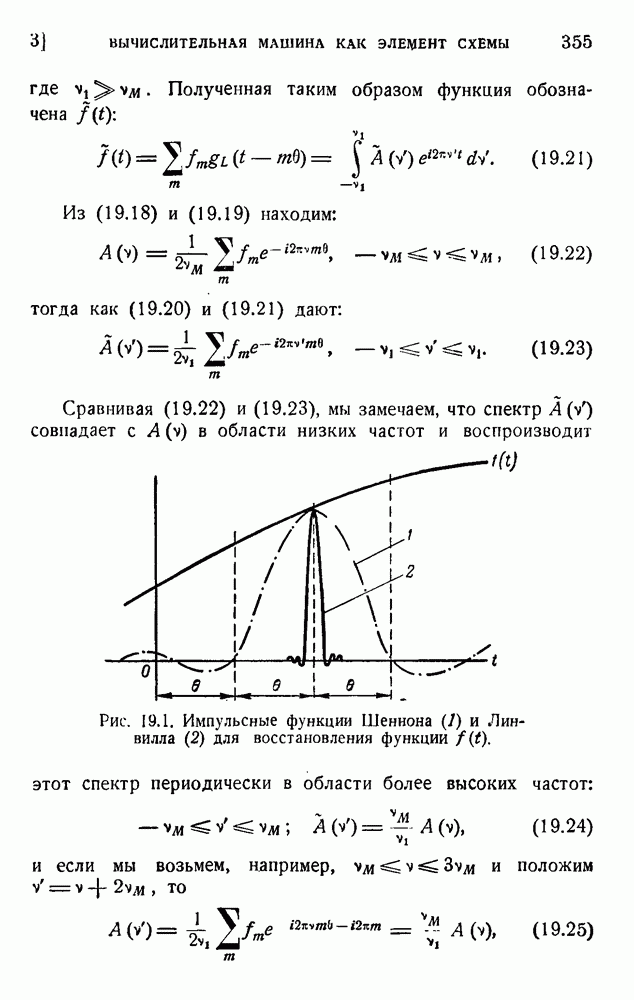
Развитая в этой книге теория основана исключительно на статистических данных. Согласно нашим определениям, предложения, встречающиеся очень редко, несут большое количество информации. Проблема ценности, кратко обсужденная в предыдущем разделе, не рассматривается в пашей теории. Мы полностью игнорировали также и другую проблему: проблему смысла. Вопрос о том, имеет ли сообщение смысл для отправителя или получателя, мы считали совершенно не относящимся к делу. Некоторые исследования семантических проблем выполнили недавно Билль во Франции и Карнап и Бар-Хиллель в США.

Работа Карнапа и Бар-Хиллеля основана на методах и символике символической логики. Мы дадим здесь краткий очерк их исследования, которое ограничено (отчасти ради простоты, а отчасти вследствие ограниченности методов индуктивной логики, на которой основывается большая часть рассуждений) предложениями на весьма простом языке. Они изучают несколько возможных определений меры информации, содержащейся в данном предложении, и анализируют преимущества и недостатки каждого из них. Их анализ исключает из рассмотрения вопросы оценки и интерпретации: они

игнорируют, будет ли сообщение истолковано получателем в соответствии с намерениями отправителя.

По всем приведенным определениям такое предложение, как , не имеет информации. Основание для этого состоит в предположении, что получатель сообщения располагает весьма возможными логическими выводами из структуры данной языковой системы, так что такого рода предложение является избыточным. Считается, что информацию содержат только такие предложения, хотя бы часть которых не определяется структурой языка.

Карнап и Бар-Хиллель берут за основу весьма простой язык, состоящий из конечного числа n существительных и прилагательных (называемых в их работе соответственно индивидуалами и предикатами) и одного-единственного глагола имеет или есть. Так, если а есть существительное, а Р — прилагательное, то Ра читается как «а имеет свойство Р» или, проще, «а есть Р».

В языке имеются следующие связи, которые могут быть использованы для построения более длинных предложений:

Выбор прилагательных в языке несколько ограничен. Прилагательные никак не должны перекрываться по смыслу; кроме того, одно прилагательное не должно ни в какой мере обусловливать применение или неприменение другого прилагательного. Словарь языка дополняется введением для каждого из прилагательных Р противоположного ему, или его отрицания, которое может быть обозначено ~Р, или новым символом, или зачастую и тем и другим.

Предложения в этом языке разделяются на логически ложные (противоречивые, как, например, ), фактуальные (логически неопределенные, как, например, Ра) и логически истинные (тавтологические, как, например, ).

Один очевидный метод определения информационного содержания предложения в этом языке состоит в следующем: имеется конечное число предложений, которые можно построить, и между этими предложениями существуют определенные логические соотношения. Информация некоторого частного предложения I может быть определена как подходящим образом выбранная функция числа предложений, обусловленных . Существуют по меньшей мере два пути к построению этого определения; мы отсылаем читателя за подробностями к книге Карнапа, так как эти определения находятся с нашей точкой зрения в весьма отдаленной связи.

Работа MIT содержит определения, более тесно связанные с теми, которыми мы пользовались. Эти определения основаны на особом виде фактуального предложения, а именно, на описании состояния, обозначаемом через Z. Описание состояния есть предложение, состоящее из конъюнкции простых (атомных) предложений и содержащее каждое из n существительных в соединении с каждым из прилагательных или с его отрицанием (но не с тем и другим одновременно). Имеется возможных соединений существительных с прилагательными, и так как каждое соединение может осуществляться двояким образом (т. е. либо с прилагательным, либо с его отрицанием), то всего имеется возможных описаний состояния. Описание состояния полностью определяет возможное состояние рассматриваемой системы, и в определения информации должны войти априорные вероятности описаний состояния. В структуре языка не содержится априори никакого основания для присвоения определенных вероятностей описаниям состояния, хотя некоторые свойства приемлемой совокупности вероятностей до некоторой степени ограничивают выбор. В задачах, обсуждавшихся в этой книге, свойства физической системы, которую мы желаем описать, указывают выбор вероятностей. Так, например, при обсуждении температур мы можем обозначить те, которые выше 40° F, как «высокие», а те, которые ниже 40° F, — как «низкие».

Очевидно, что вероятности «высоких» и «низких» температур на Северном полюсе и на экваторе будут различны.

Для предложения i (которое, вообще, не является описанием состояния) область (range) i, обозначаемая R(i), есть совокупность описаний состояния, в которых i сохраняет силу. На этом этапе могут быть введены определения информации, основанные на теории совокупности точек. Нас, однако, больше интересуют количественные определения, т. е. определения, дающие числовую меру информации. С этой целью мы вводим функцию меры, обладающую следующими свойствами:

A. Для каждого описания состояния Z существует мера такая, что

Эта величина может толковаться как априорная вероятность описания состояния Z.

B. Сумма , взятая по всем Z, равна единице.

C. Для всякого ложного предложения

Для всякого неложного предложения i мы определяем как сумму по всем Z, содержащимся в области .

E. Все существительные трактуются наравне, т. е. инвариантно при перестановке существительных, встречающихся в предложении i.

F. Все прилагательные трактуются наравне, т. е. инвариантно при перестановке прилагательных, встречающихся в I.

G. Любое прилагательное может быть заменено его отрицанием без изменения значения .

H. Если два предложения i и j не имеют общих прилагательных, то они считаются индуктивно-независимыми и

I. Число существительных, не входящих в предложение i, не должно влиять на значение m(i).

Такая функция меры называется собственной -функцией, и Карнап полагает, что ее можно рассматривать как вероятность, которую он называет: абсолютная логическая вероятность. Условия Е, F и G вводят связи между вероятностями различных описаний состояния, но не определяют их

единственным образом. Свойства могут быть использованы для вывода многих теорем и соотношений, необходимых для детальной разработки теории. Из числа этих соотношений мы воспользуемся следующим:

Так как не содержат общих описаний состояния (описание состояния не может быть связано как с , так и с его отрицанием) и каждое описание состояния находится либо в либо в (каждое описание состояния связано либо с , либо с его отрицанием), то

Простейшее определение информации через функцию меры названо Карнапом и Бар-Хиллелем мерой содержания (cont) и выражается как

Мера содержания обладает многими интересными свойствами и находится в качественном согласии с определениями, использованными в этой книге, в следующем смысле. Если мало, то относительно велико. Но малое означает, что принимаются сравнительно маловероятные описания состояния, так что есть мера редкости. Другое определение, мера информации, ближе к нашим определениям. Она выражается как

Так же как и для имеется качественное согласие этого определения с нашими. Далее, можно показать, что условие Н, которому удовлетворяет функция , приводит к аддитивности меры информации для конъюнкции индуктивно-независимых предложений. Рассмотрение нижеследующего специального случая сделает более ясной тесную связь между обоими определениями. Выберем функцию меры вида

для всех Z, где N — общее число описаний состояния. Мы предполагаем, таким образом, что все описания состояния равновероятны. Это предположение совместимо с условиями, наложенными на функцию меры. Если обозначать через число описаний состояния в области , то из определения имеем:

Это равенство совпадает с тем, которое применялось на протяжении книги, если мы отождествим описания состояния с равновероятными исходами в некоторой данной ситуации. Вначале имеются N возможных исходов (N описаний состояния). Знание предложения i уменьшает возможное число до , так что информация, даваемая предложением i, согласно нашим прежним определениям, равна

Для описания состояния содержит только Z, и

Карнап и Бар-Хиллель дают дальнейшую детальную разработку этих семантических определений и обсуждают приложения к различным вопросам заключения и дедукции.

В этом кратком очерке мы старались лишь показать связь между этими проблемами и теми, которым посвящена эта книга.