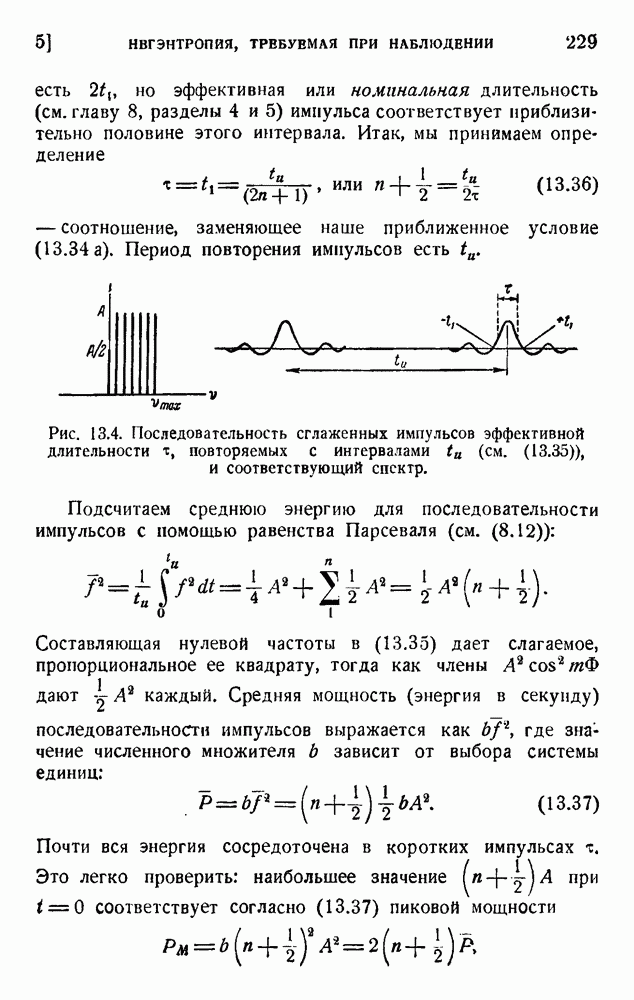
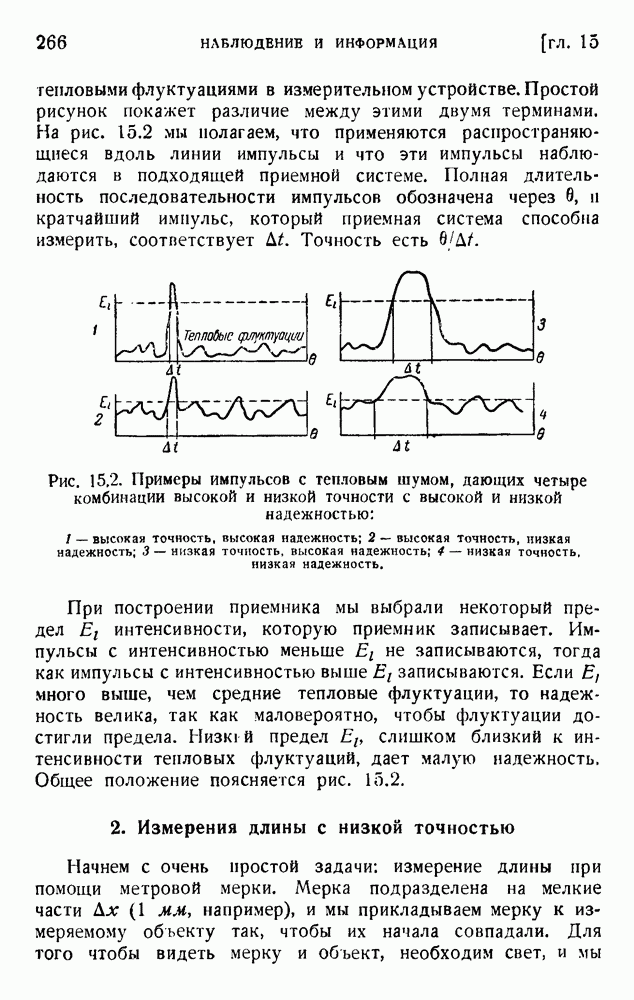
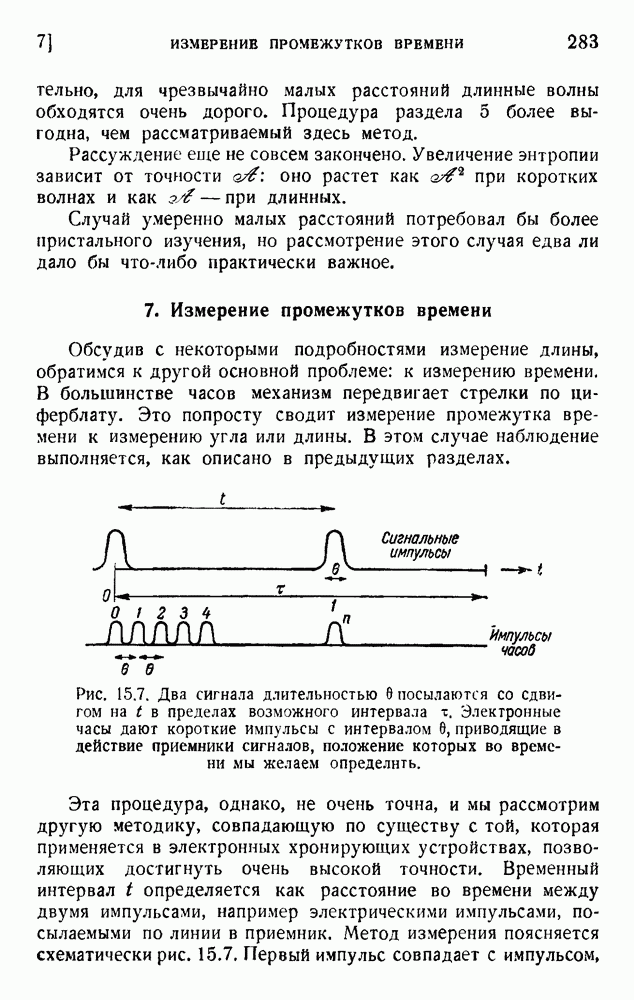
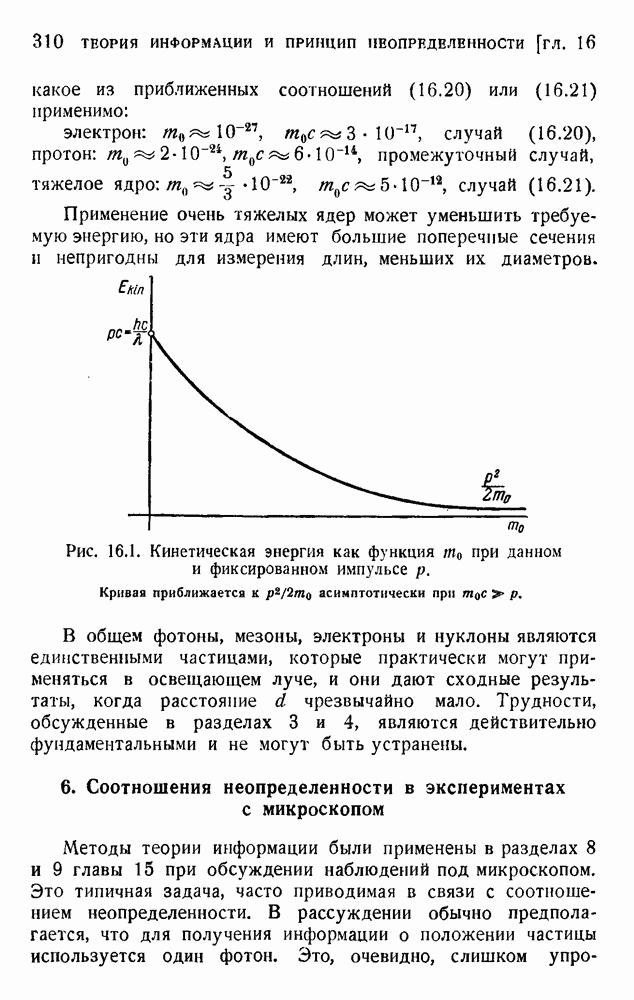
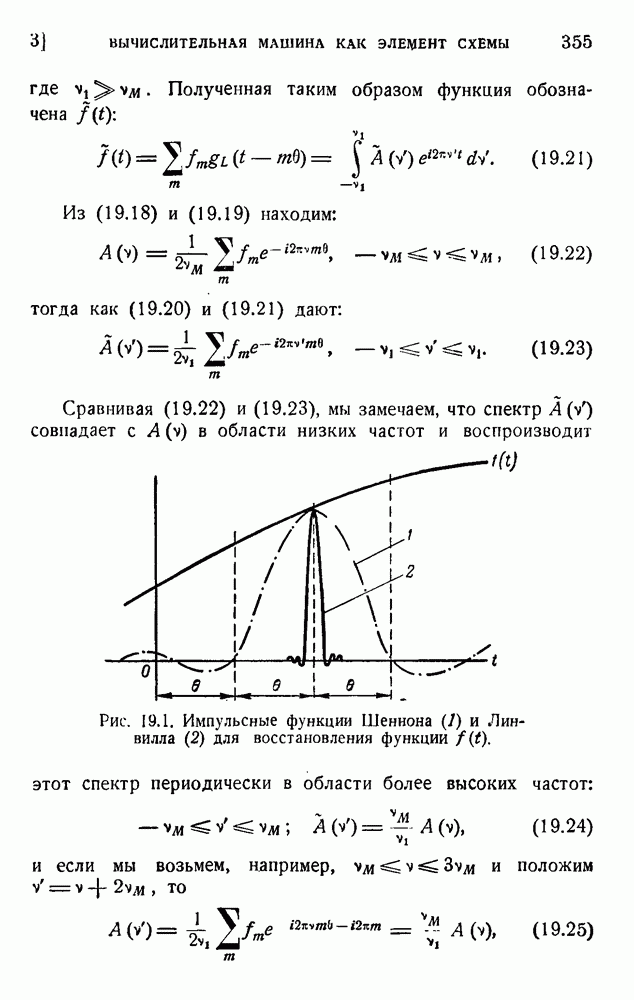
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
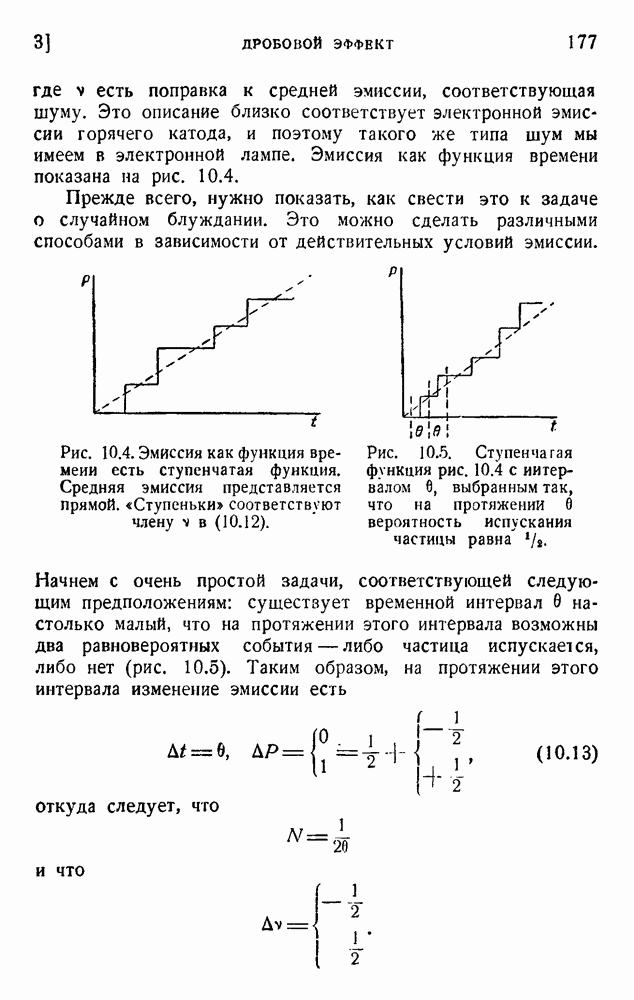
7. Рассуждение Гэйбора
Гэйбор исследовал сходную задачу, но с отличным способом действия машины. Изменяя порядок первых двух операций А и В, он предлагает действовать следующим образом:
A. Убедиться, что молекула находится в  (по Силарду — этап В).
(по Силарду — этап В).
B. Вдвинуть заслонку (по Силарду — этап А).
C. Двигать поршень.
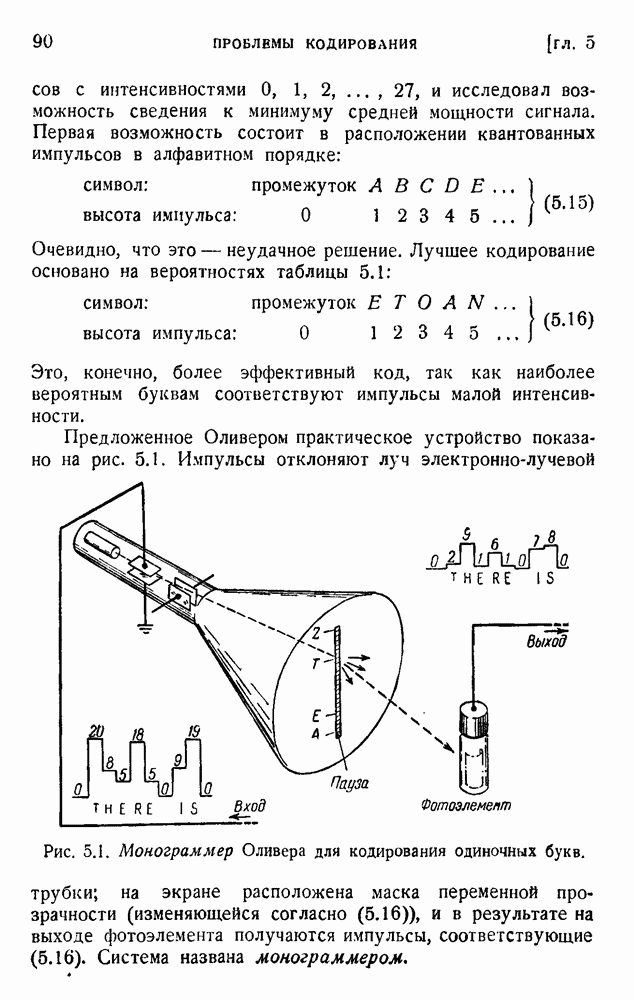
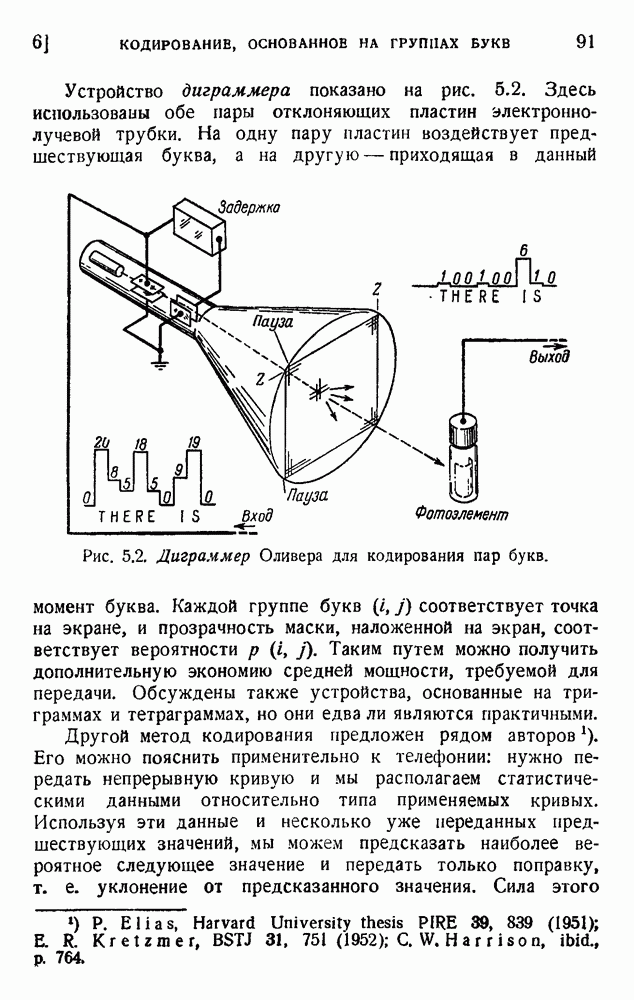
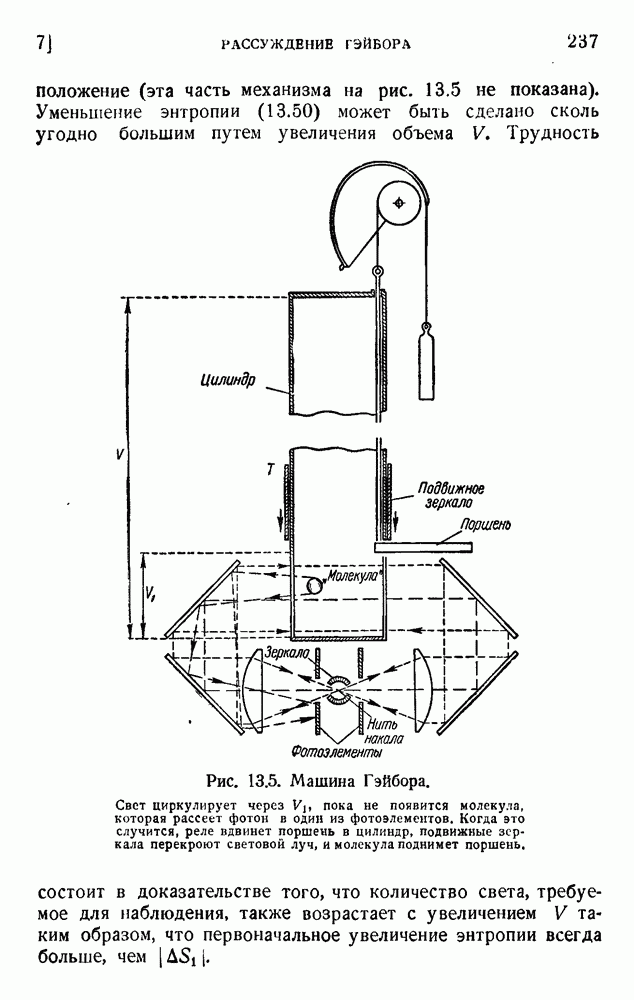
Гэйбор предполагает, что для получения информации применяется луч света, освещающий объем  . Эскиз всего устройства машины дан на рис. 13.5. Единственная молекула движется в цилиндре V, поддерживаемом при температуре Т. Нижняя часть цилиндра (объем
. Эскиз всего устройства машины дан на рис. 13.5. Единственная молекула движется в цилиндре V, поддерживаемом при температуре Т. Нижняя часть цилиндра (объем  ) имеет прозрачные стенки и освещается лучом от нагретой нити, излучающей определенную частоту v. Система зеркал и линз поддерживает циркуляцию света без поглощения до тех пор, пока некоторое количество света не будет рассеяно молекулой и поглощено фотоэлементом. Когда это случится, механизм приводится в действие посредством реле: поршень, лишенный трения, вводится в цилиндр; два зеркала, скользя вниз, перекрывают световой луч. Молекула постепенно поднимает поршень и совершает механическую работу.
) имеет прозрачные стенки и освещается лучом от нагретой нити, излучающей определенную частоту v. Система зеркал и линз поддерживает циркуляцию света без поглощения до тех пор, пока некоторое количество света не будет рассеяно молекулой и поглощено фотоэлементом. Когда это случится, механизм приводится в действие посредством реле: поршень, лишенный трения, вводится в цилиндр; два зеркала, скользя вниз, перекрывают световой луч. Молекула постепенно поднимает поршень и совершает механическую работу.
Изменение энтропии при введении поршня есть убывание:
 (13.50)
(13.50)
а при расширении происходит увеличение энтропии, восстанавливающее ее первоначальную величину. Когда расширение закончено, поршень выдвигается и возвращается в исходное
положение (эта часть механизма на рис. 13.5 не показана).
Уменьшение энтропии (13.50) может быть сделано сколь угодно большим путем увеличения объема V.

Рис. 13.5. Машина Гэйбора.
Свет циркулирует через пока не появится молекула, которая рассеет фотон в один из фотоэлементов. Когда это случится, реле вдвинет поршень в цилиндр, подвижные зеркала перекроют световой луч, и молекула поднимет поршень.
Трудность состоит в доказательстве того, что количество света, требуемое для наблюдения, также возрастает с увеличением V таким образом, что первоначальное увеличение энтропии всегда больше, чем  .
.
Рассмотрим первый этап действия, когда мы ожидаем, что молекула вступит в объем  и рассеет свет. Среднее время ожидания
и рассеет свет. Среднее время ожидания  пропорционально V, а вспышка рассеянного света имеет длительность
пропорционально V, а вспышка рассеянного света имеет длительность  , пропорциональную
, пропорциональную  . В общем, наше наблюдение должно дать двоякого рода информацию:
. В общем, наше наблюдение должно дать двоякого рода информацию:
A. Молекула находится в  вместо V.
вместо V.
B. Это происходит на протяжении интервала  всего времени
всего времени  .
.
Ситуация отличается от той, которую мы имели в опыте рис. 13.1, где положение определялось геометрией прибора, и единственное требуемое наблюдение относилось ко времени. Мы можем подсчитать общее количество информации с помощью (12.1):

где  — число равновероятных возможностей в общем случае,
— число равновероятных возможностей в общем случае,  — число равновероятных возможностей, когда дана информация
— число равновероятных возможностей, когда дана информация  . Здесь мы имеем, очевидно,
. Здесь мы имеем, очевидно,

Следовательно, количество информации в такого рода опыте равно

Информация  вдвое больше первоначального увеличения энтропии
вдвое больше первоначального увеличения энтропии  (см. (13.50)), определяющего негэнтропию, получаемую с помощью информации
(см. (13.50)), определяющего негэнтропию, получаемую с помощью информации  Эффективность преобразования информации в негэнтропию равна 1/2.
Эффективность преобразования информации в негэнтропию равна 1/2.
Подсчитаем теперь начальное увеличение энтропии, требуемое для получения этой информации. Во всем объеме полной длины L (пропорциональной V) мы должны образовать луч света, покрывающий только длину L, (пропорциональную  ). Это можно сделать надлежащим наложением некоторого числа собственных колебаний длины L. Эти собственные колебания имеют длины волн
). Это можно сделать надлежащим наложением некоторого числа собственных колебаний длины L. Эти собственные колебания имеют длины волн

и кратчайшая длина волны должна быть порядка  для того, чтобы длина
для того, чтобы длина  отчетливо определилась. Отсюда имеем для числа собственных колебаний в объеме
отчетливо определилась. Отсюда имеем для числа собственных колебаний в объеме

Для каждого из этих колебаний мы имеем вспышки  с повторением через интервал
с повторением через интервал  . Ситуация аналогична обсужденной в разделе 5 (см. (13.39) и (13.42)) и требует увеличения энтропии
. Ситуация аналогична обсужденной в разделе 5 (см. (13.39) и (13.42)) и требует увеличения энтропии

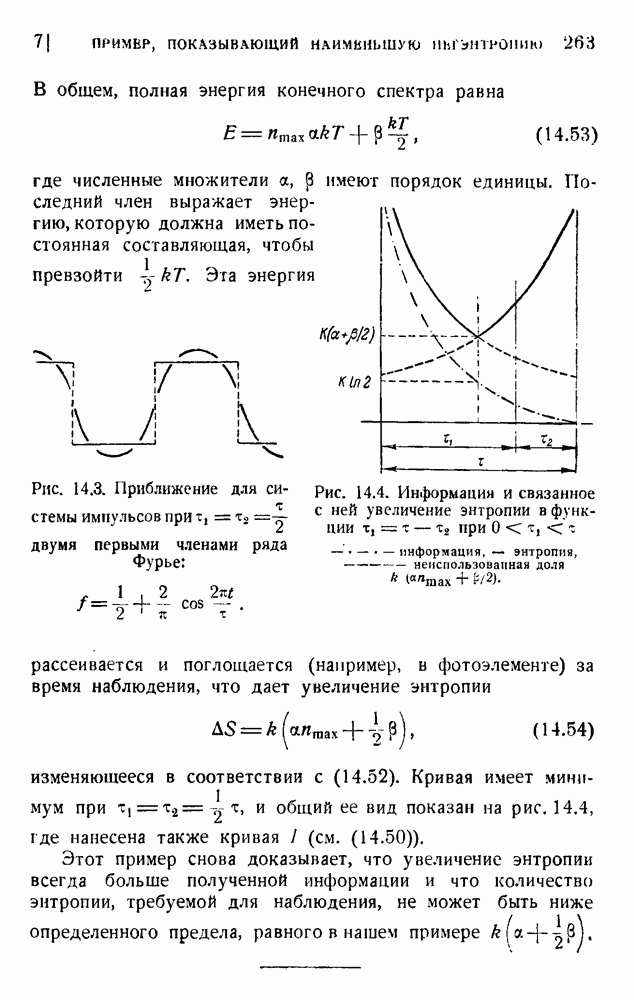
на каждый вид колебания. В общем, для полной энтропийной стоимости наблюдения получаем:
 (13.54)
(13.54)
Сравним этот результат с формулой (13.52) для информации:
 (13.55)
(13.55)
где

Это выражение всегда положительно. Когда  неограниченно убывает, F стремится к бесконечности, а следовательно, и скобка в (13.55). В этом заключается объяснение задачи Силарда. Дальнейшие подробности даны в главе 15.
неограниченно убывает, F стремится к бесконечности, а следовательно, и скобка в (13.55). В этом заключается объяснение задачи Силарда. Дальнейшие подробности даны в главе 15.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
- 4. Информация и алфавит
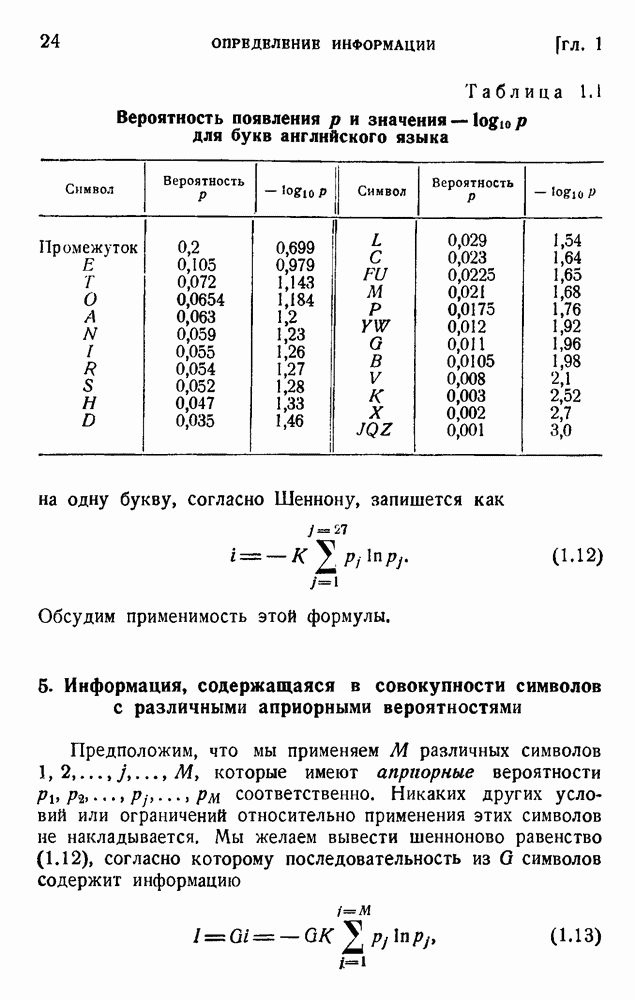
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
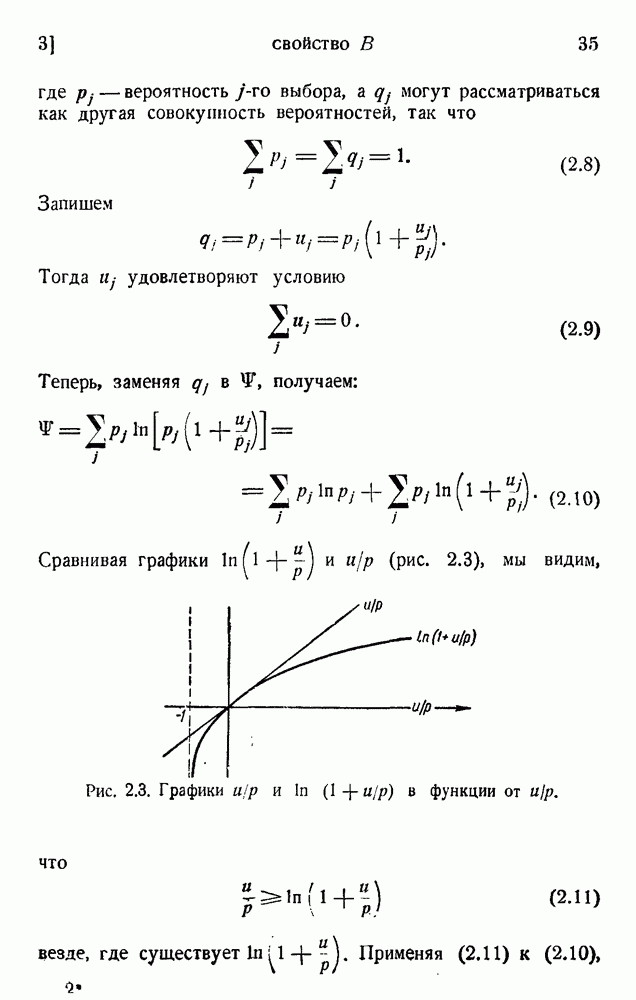
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
- 2. Корреляция в языке
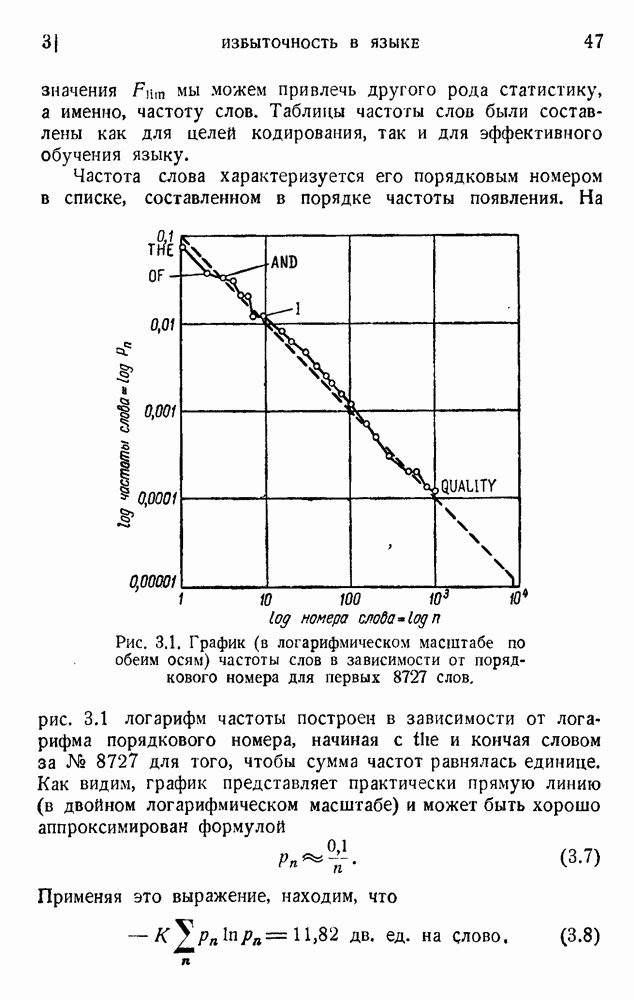
- 3. Избыточность в языке
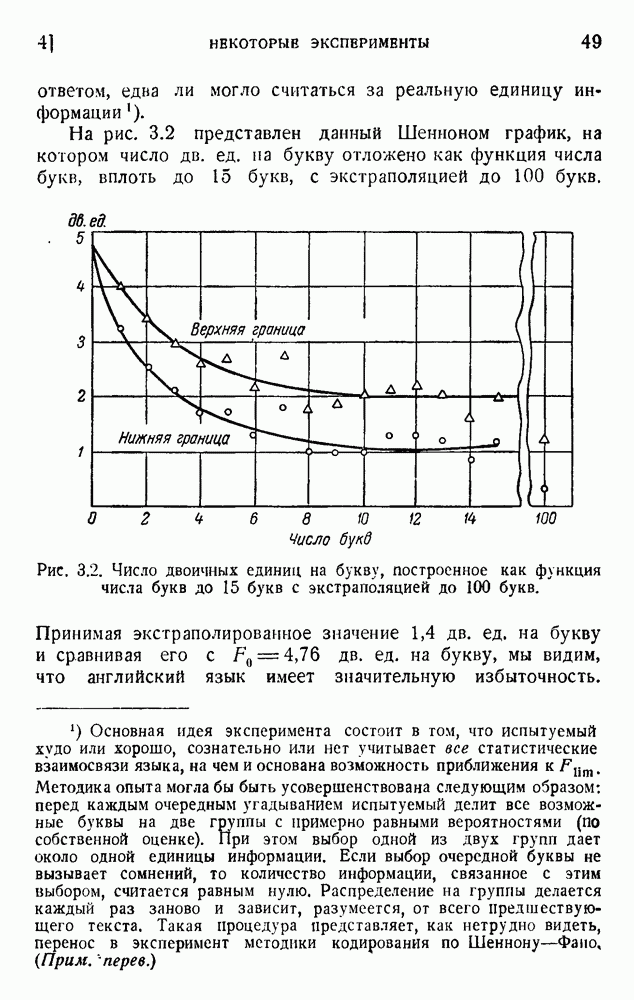
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
- 10. Проблемы статистики слов
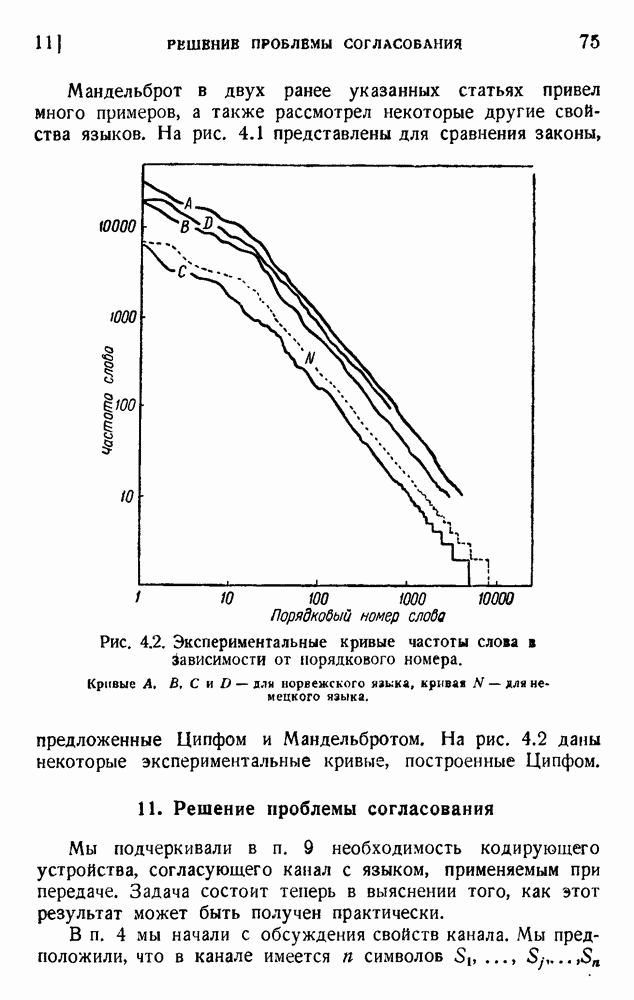
- 11. Решение проблемы согласования
- Приложение
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
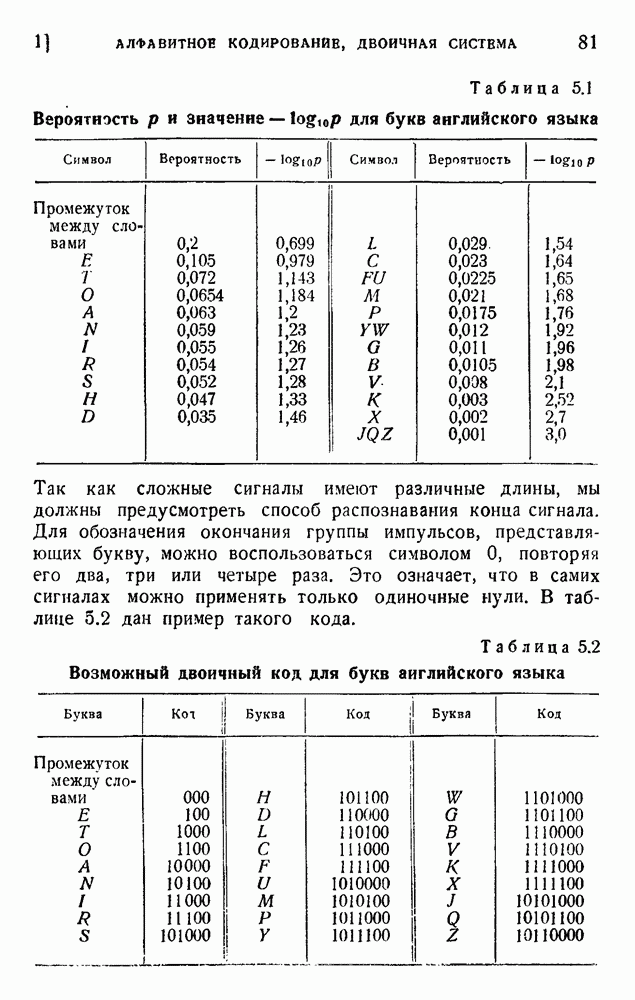
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
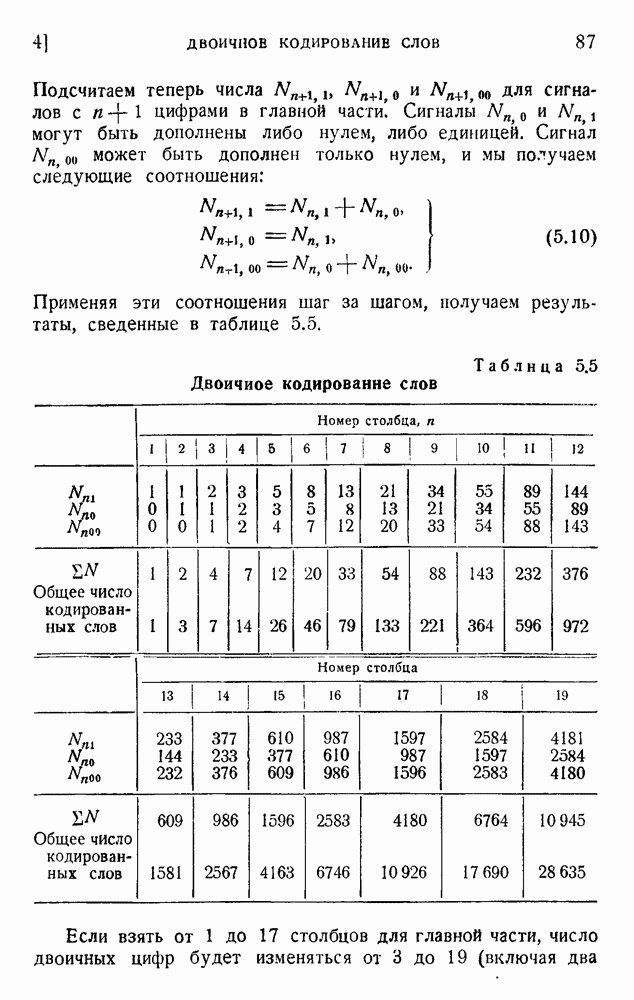
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
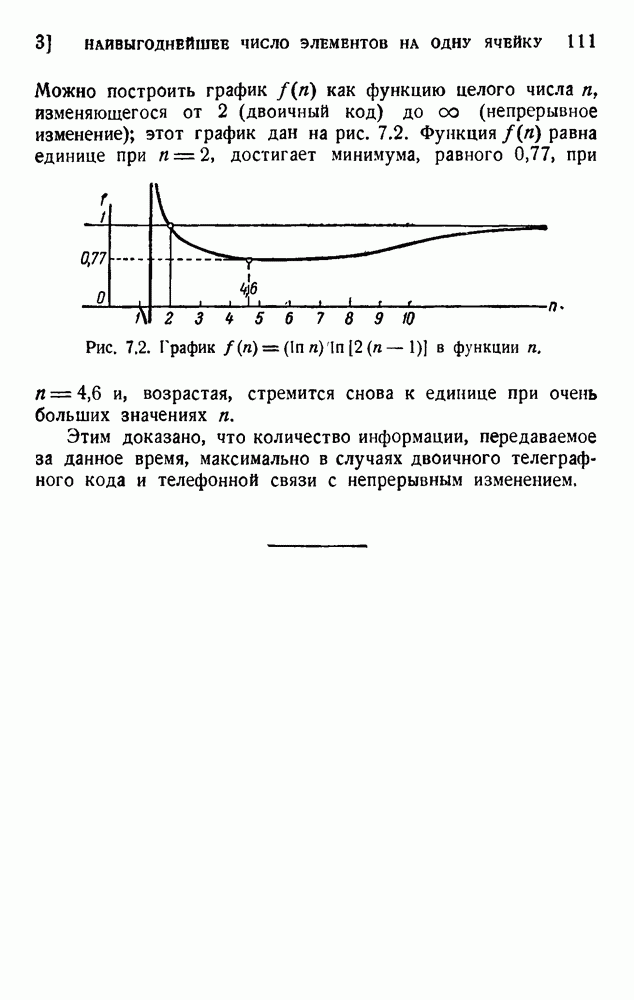
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
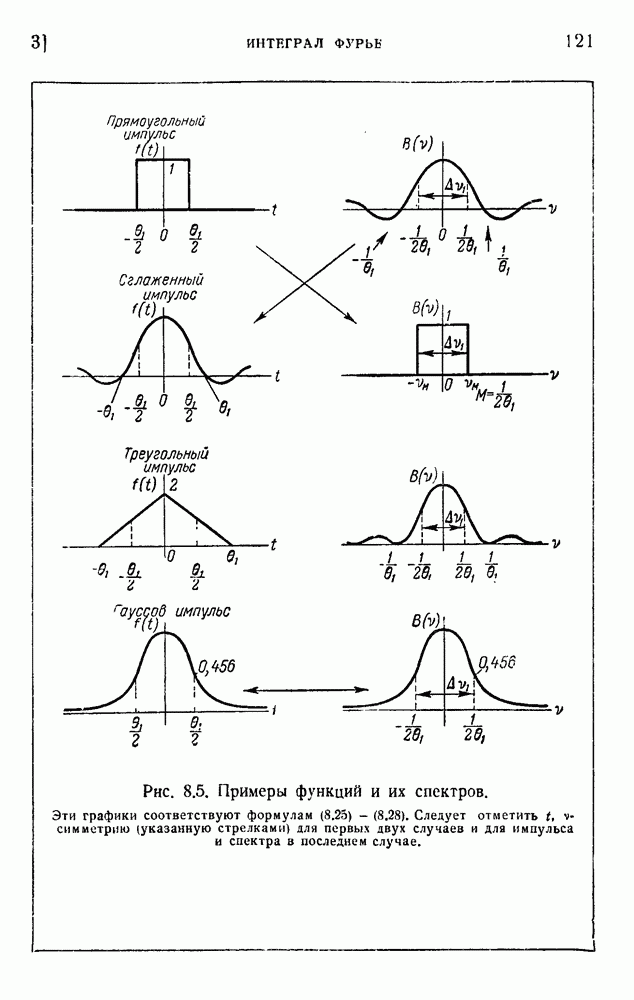
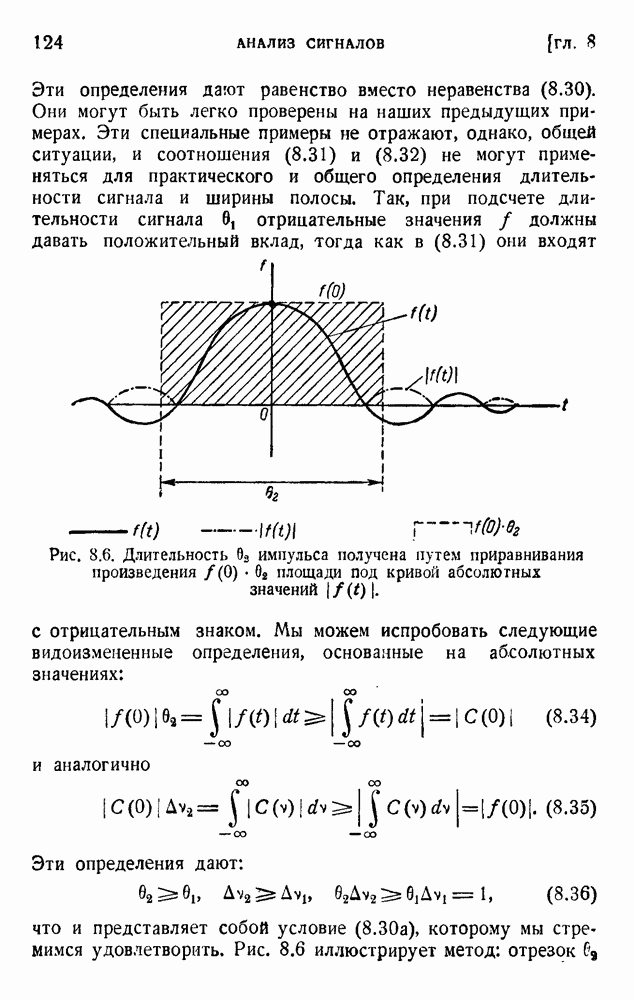
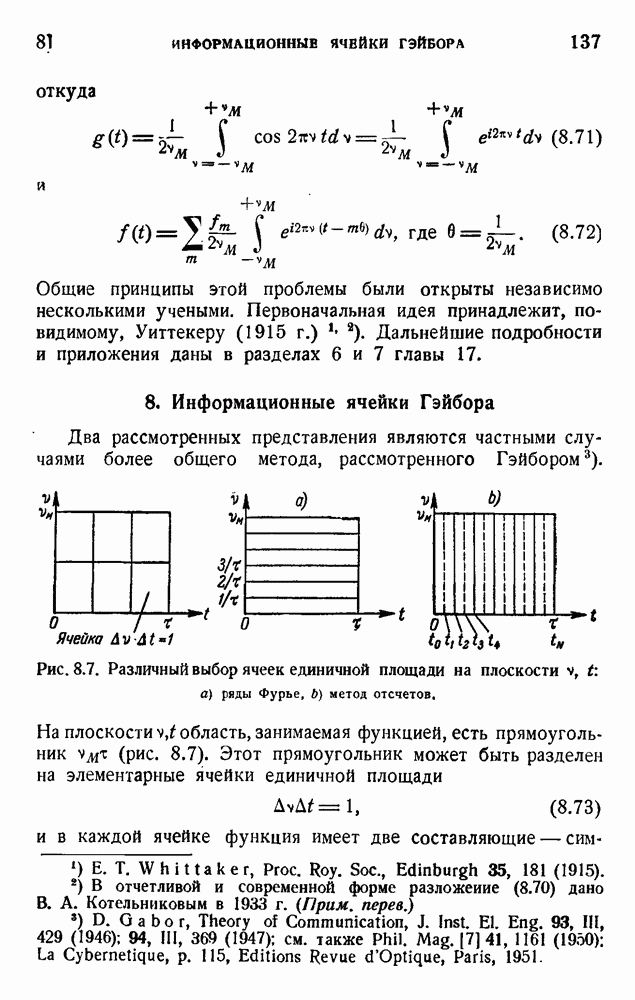
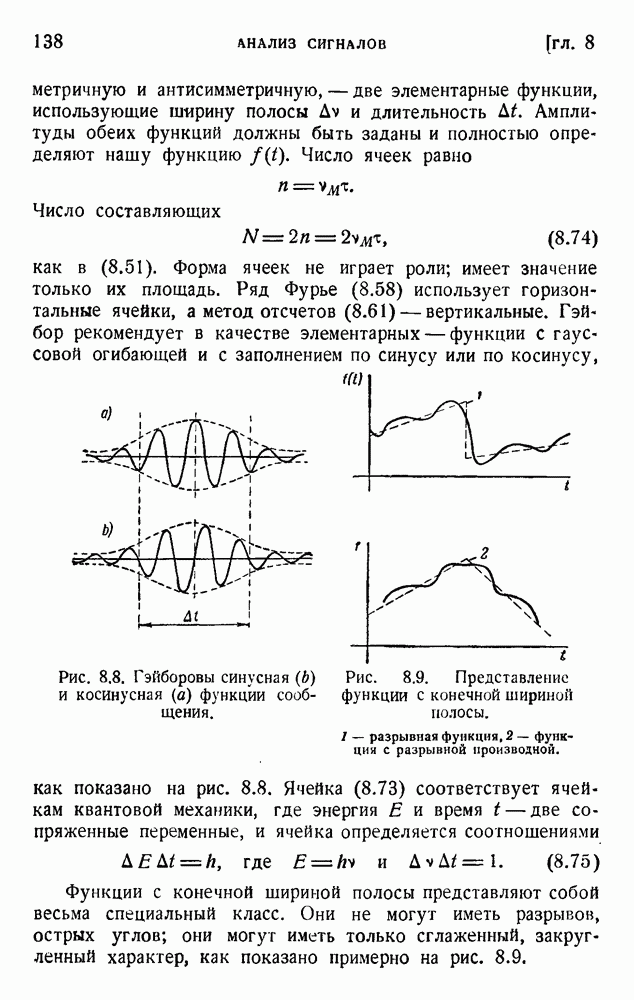
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
- 1. Ряд Фурье
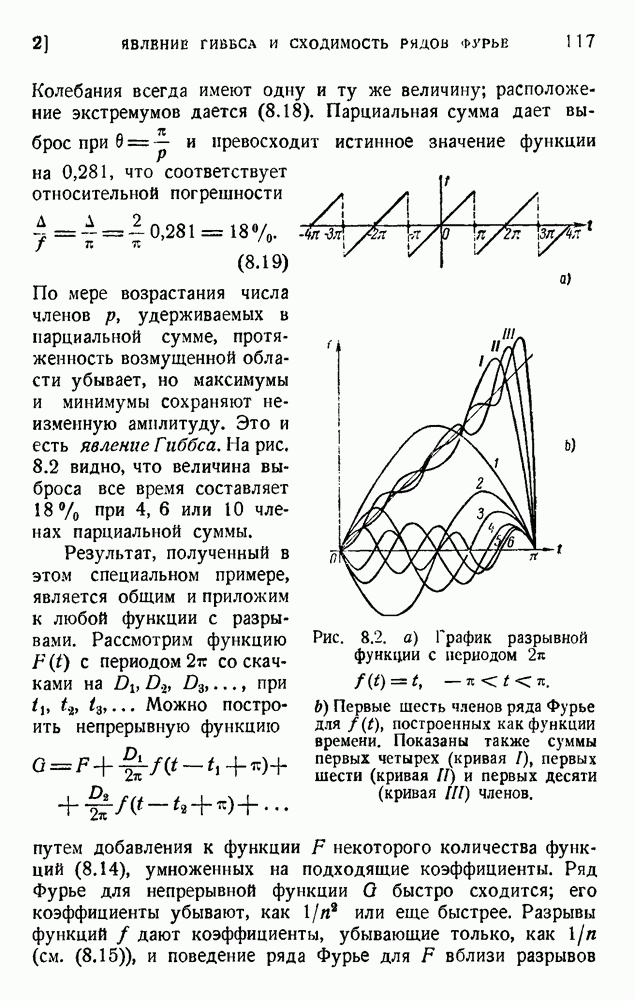
- 2. Явление Гиббса и сходимость рядов Фурье
- 3. Интеграл Фурье
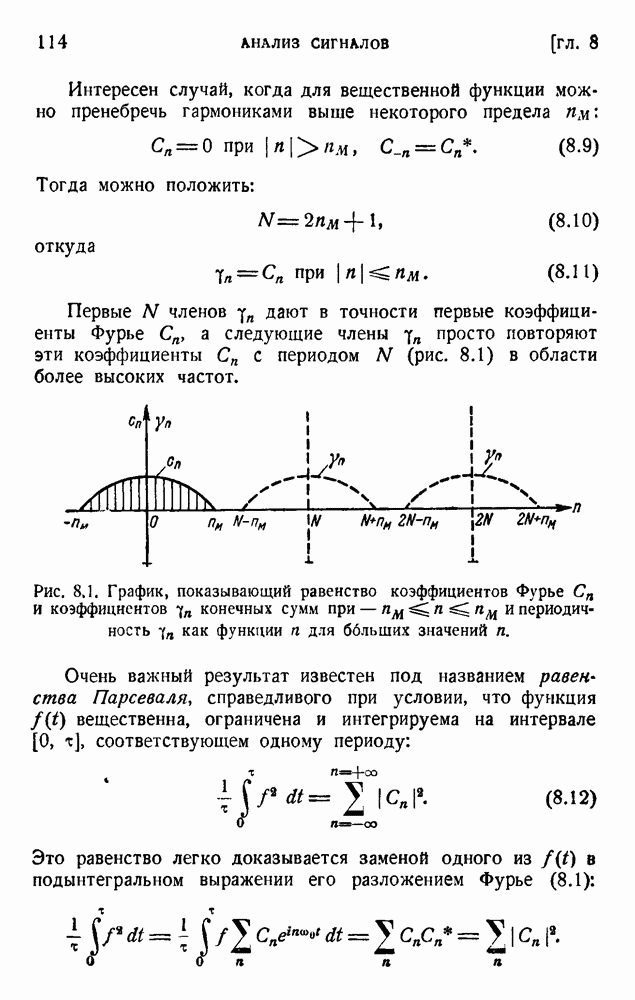
- 4. Роль конечной ширины полосы частот
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
- 7. Метод отсчетов Шеннона
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
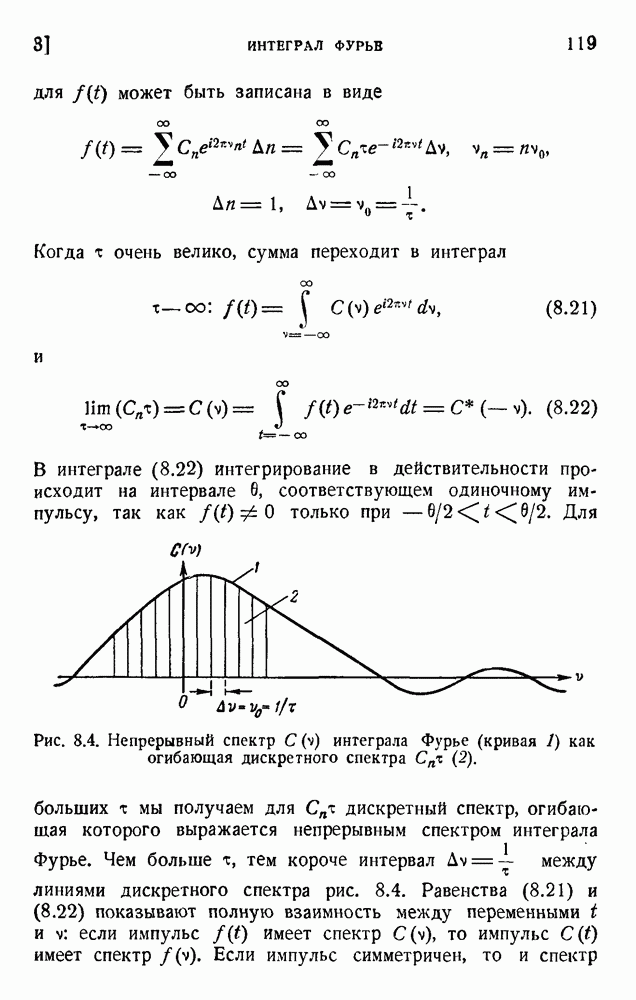
- 10. Линейные преобразования и фильтры
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
- 1. Тепловое движение
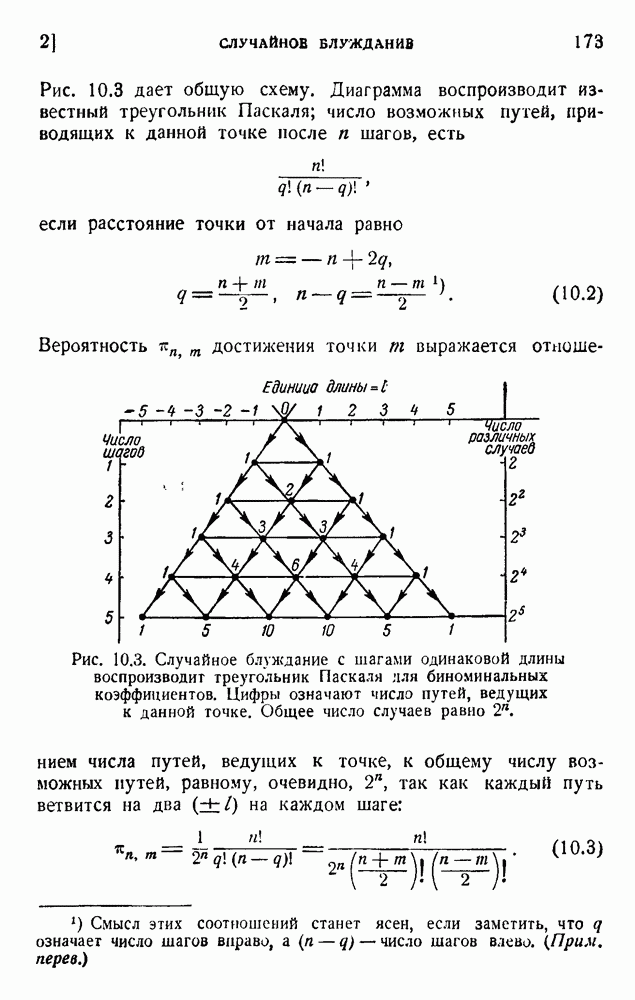
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
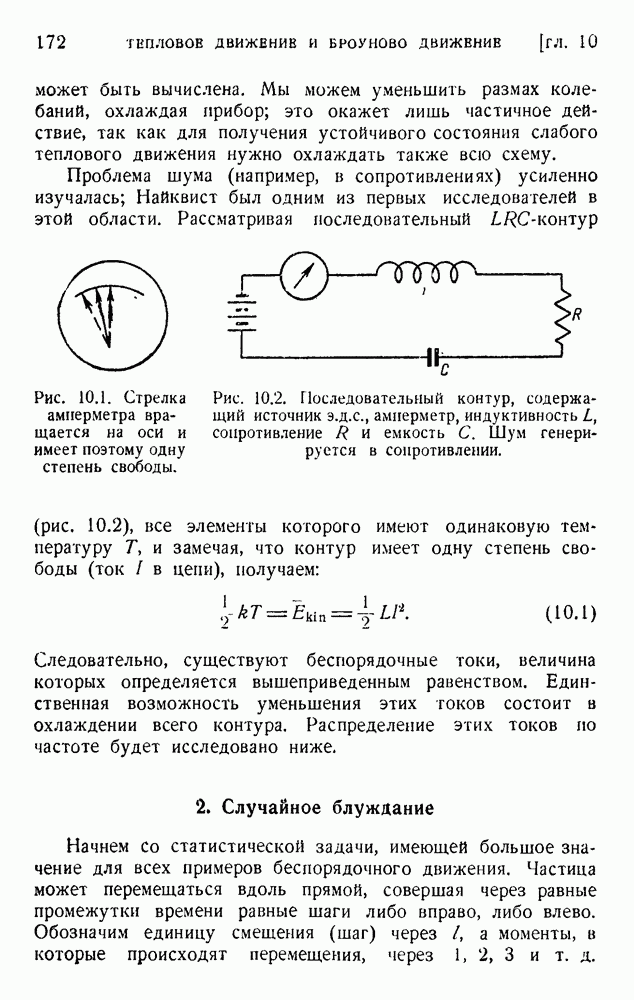
- 5. Тепловое движение в электрической цепи
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
- 5. Тепловое движение в выпрямителе
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
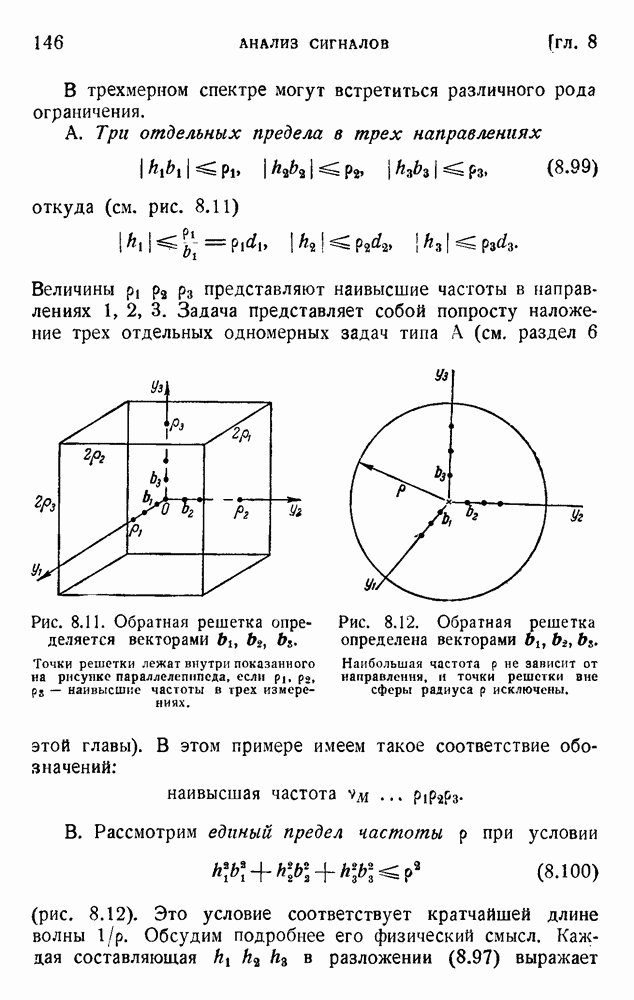
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
- 5. Негэнтропия, требуемая при наблюдении
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
- 4. Пределы евклидовой геометрии
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
- 6. Проблемы семантической информации