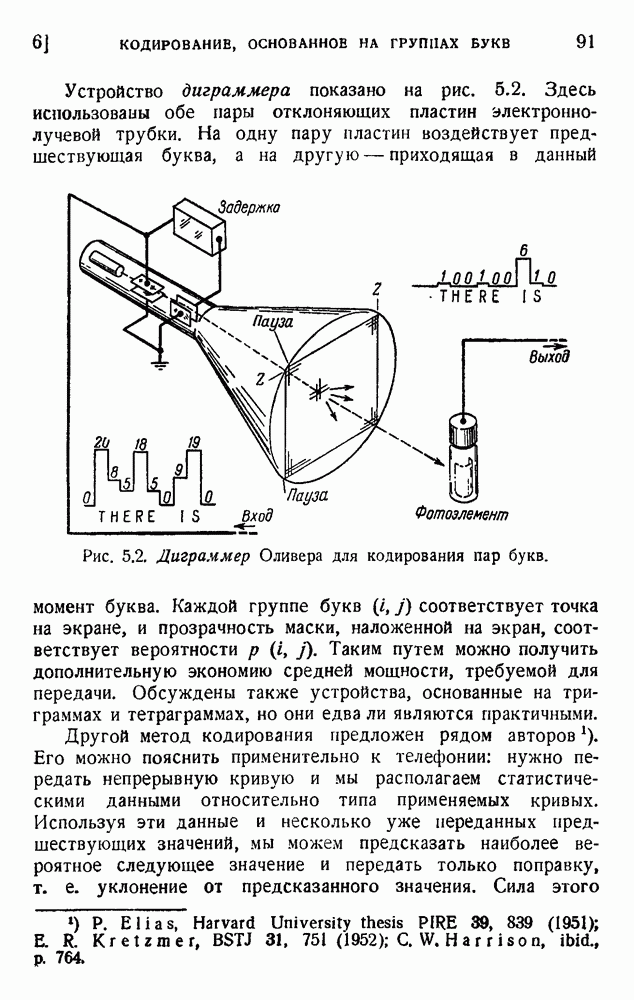
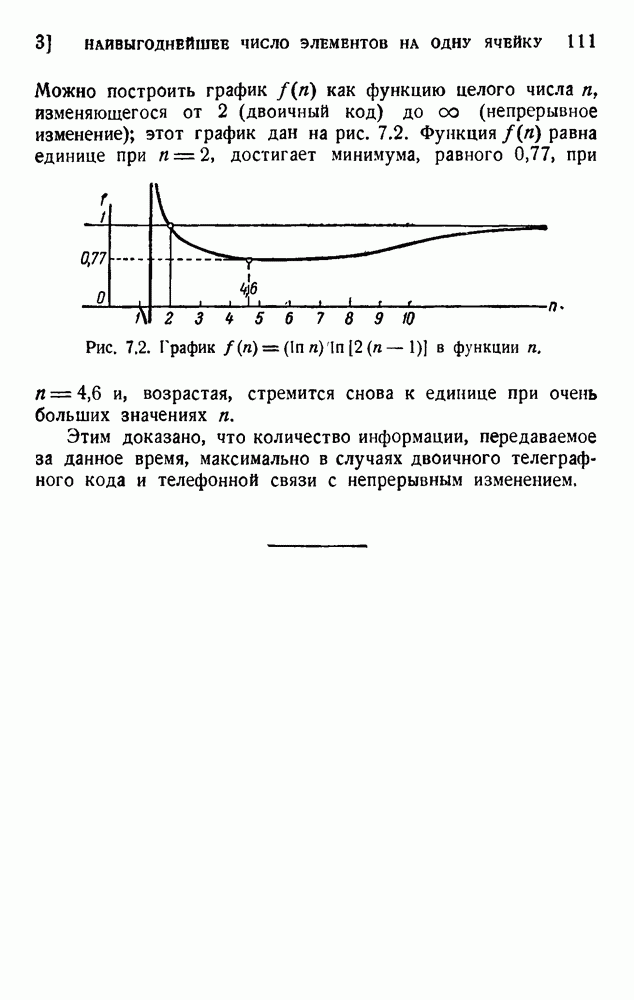
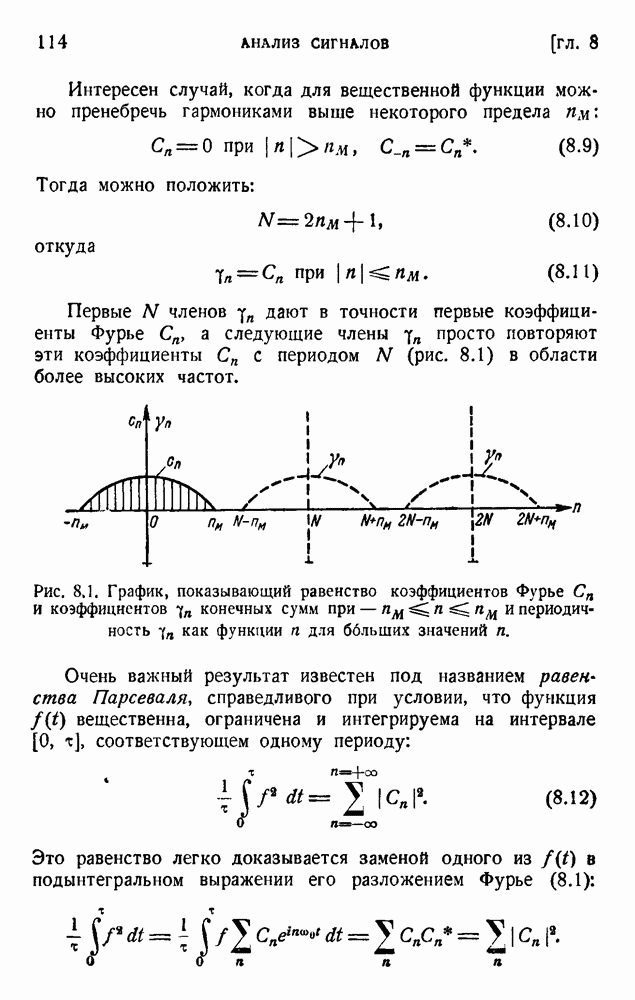
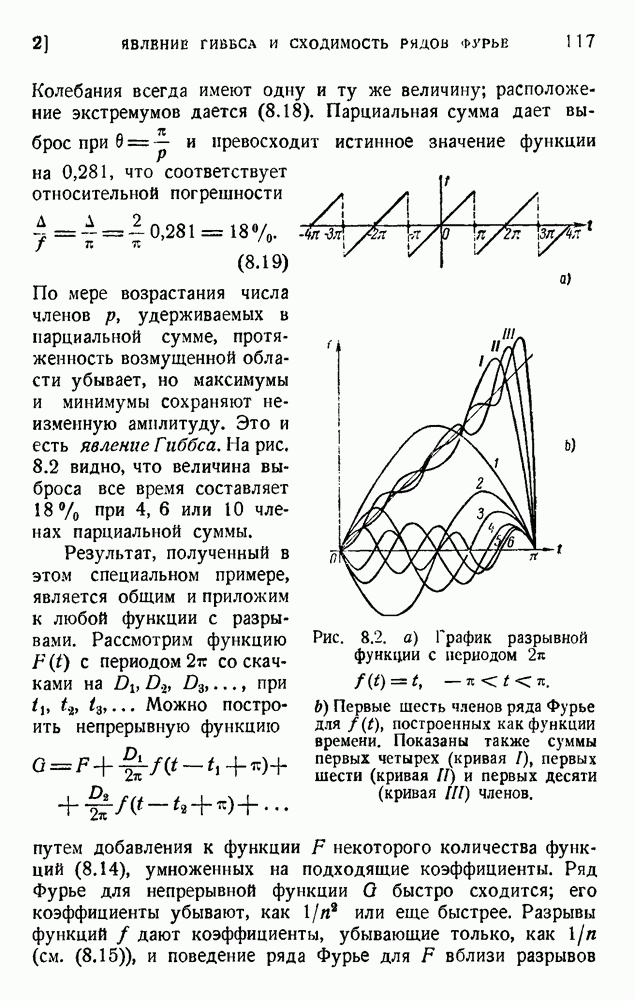
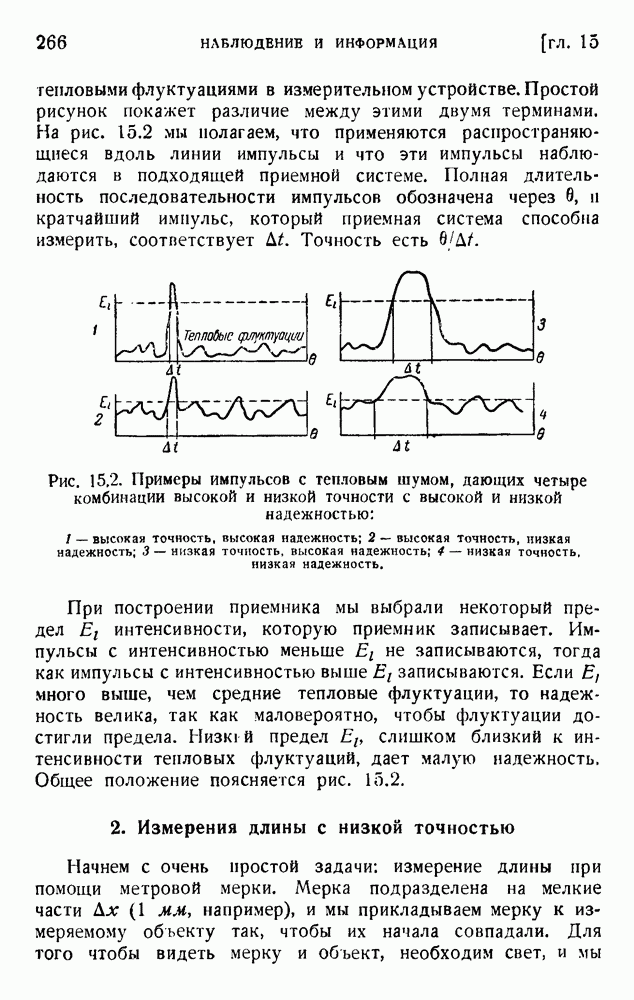
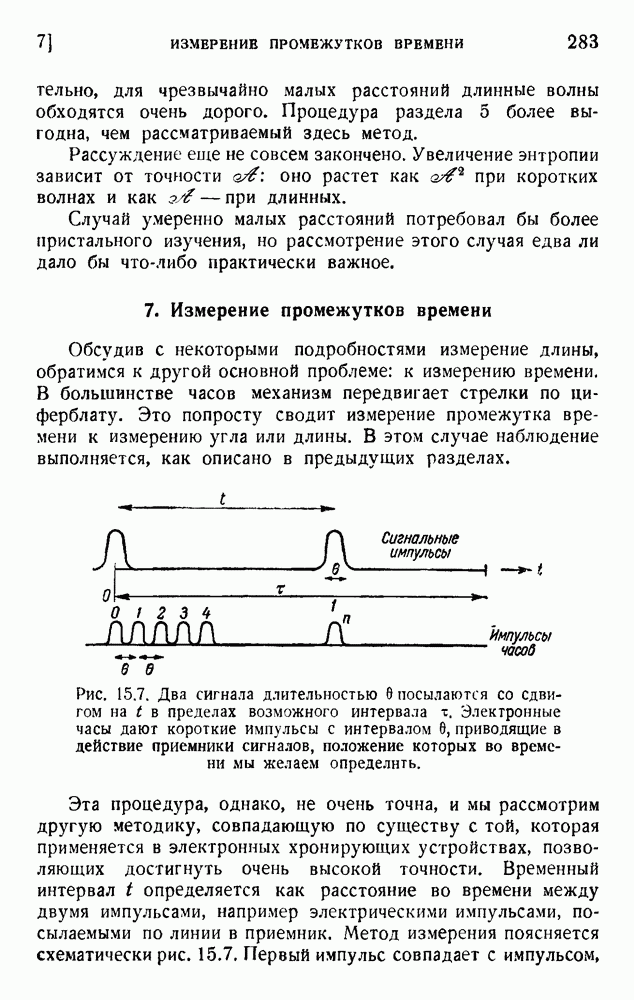
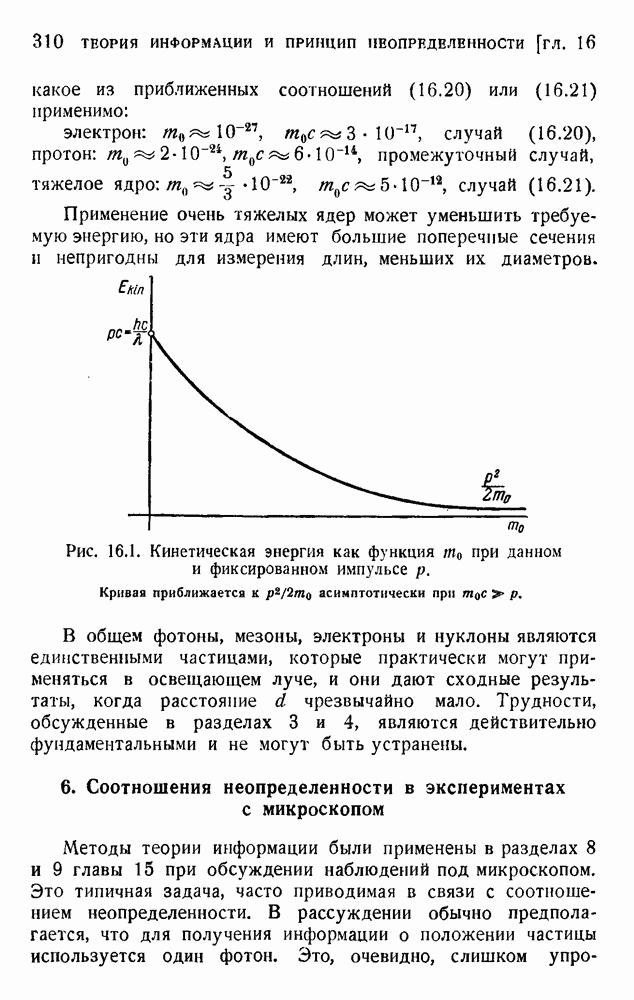
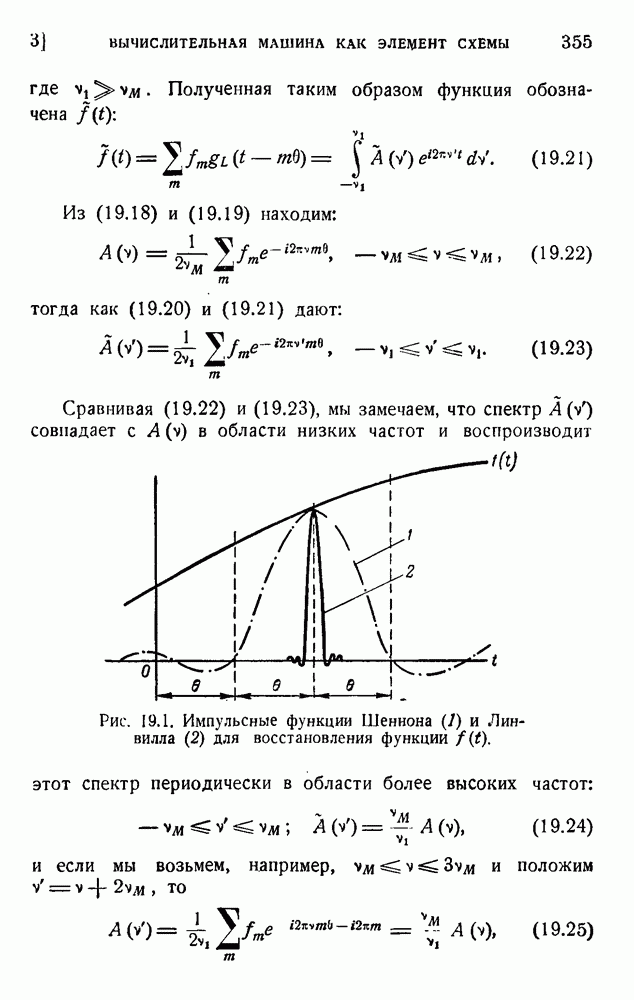
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
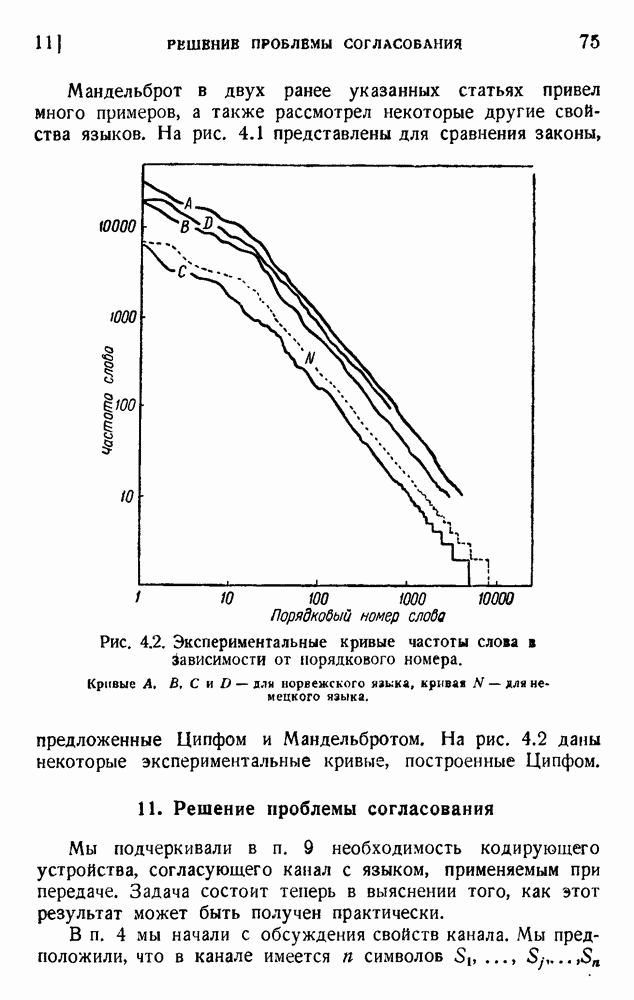
11. Решение проблемы согласования
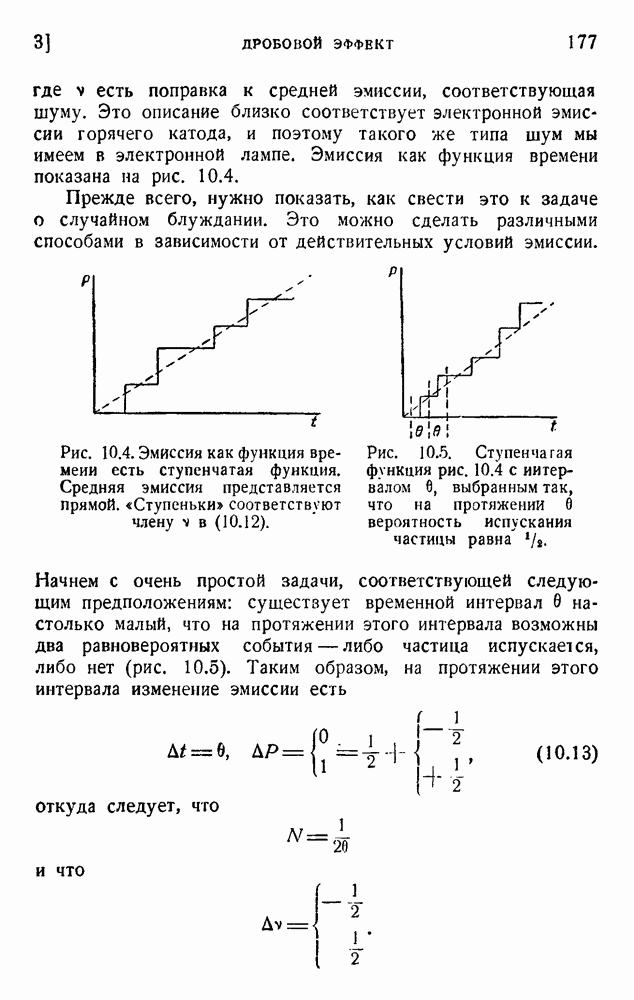
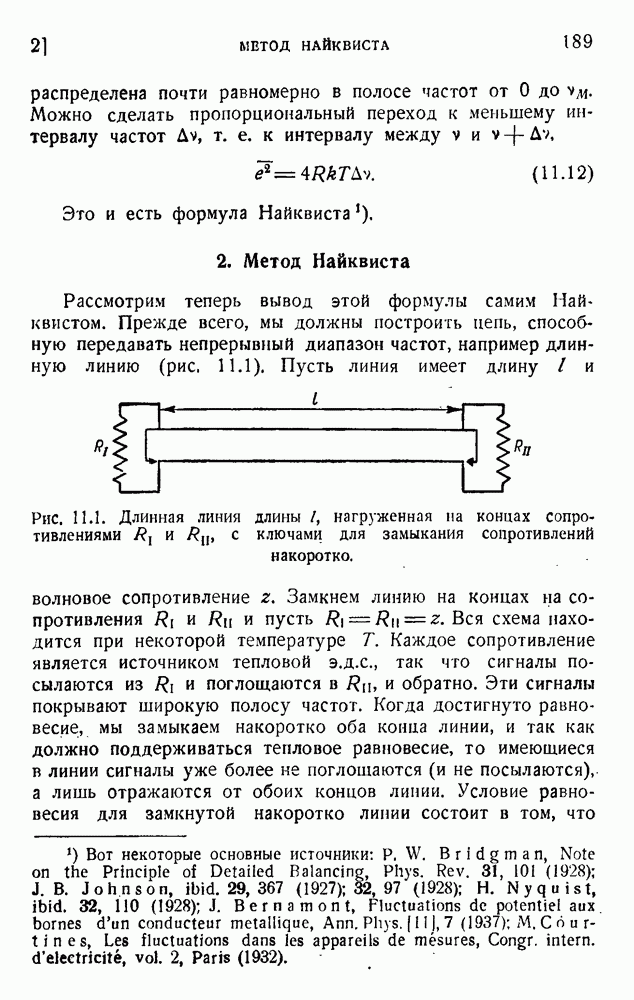
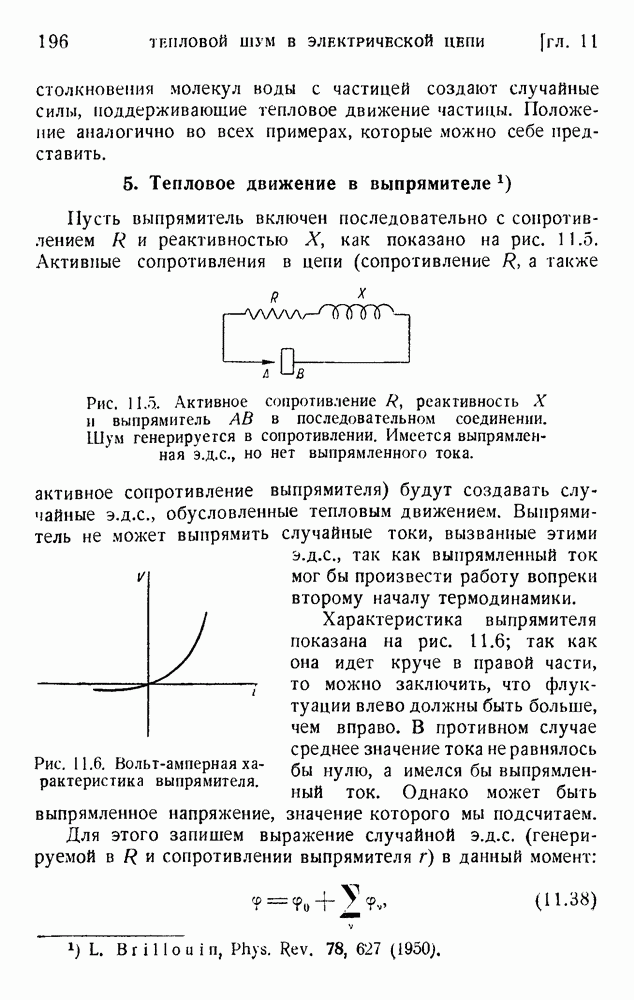
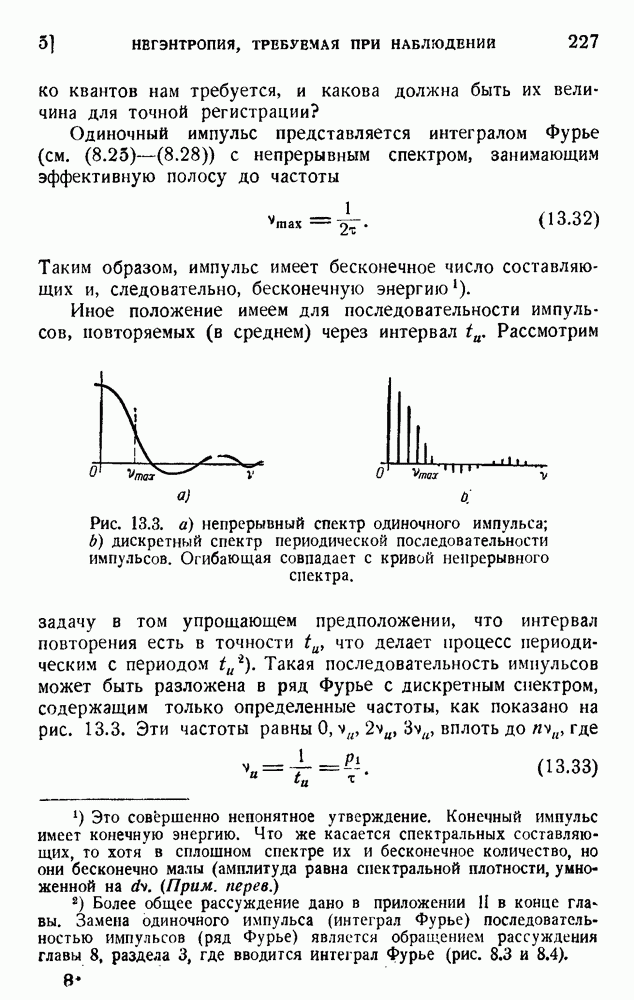
Мы подчеркивали в п. 9 необходимость кодирующего устройства, согласующего канал с языком, применяемым при передаче. Задача состоит теперь в выяснении того, как этот результат может быть получен практически.
В п. 4 мы начали с обсуждения свойств канала. Мы предположили, что в канале имеется n символов 
и что их относительные длительности равны  . Мы нашли, что средняя информация на символ максимальна (см. п. 8), когда вероятность
. Мы нашли, что средняя информация на символ максимальна (см. п. 8), когда вероятность  символа связана с его длительностью
символа связана с его длительностью  соотношением
соотношением

где  — постоянная.
— постоянная.
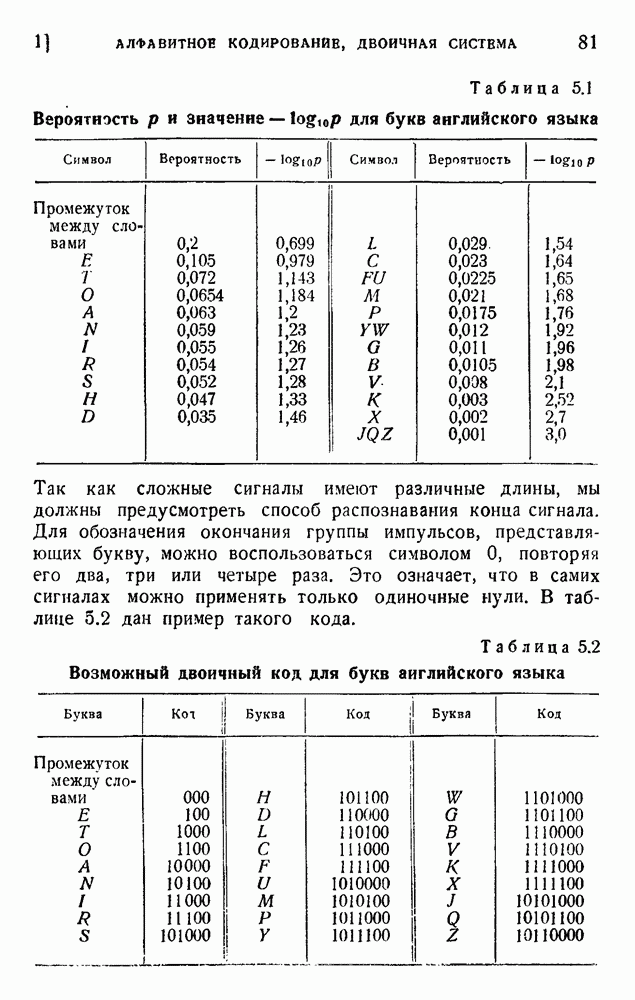
Рассмотрим теперь сообщение, написанное на языке, применяющем некоторое число v знаков Эти знаки могут быть буквами, группами букв, словами и т. д. В китайском языке, например, каждый знак соответствует слову. Для упрощения задачи предположим, что каждый знак  имеет определенную вероятность не зависящую от предшествующих знаков. Другими словами, мы игнорируем корреляцию между знаками, во избежание усложнения задачи.
имеет определенную вероятность не зависящую от предшествующих знаков. Другими словами, мы игнорируем корреляцию между знаками, во избежание усложнения задачи.
Рассмотрим сперва простейший возможный код, применяющий v символов (или групп символов, если и присваивающий кратчайшие символы наиболее вероятным знакам. При этом обычно условие (4.61) не выполняется и согласование получается неудовлетворительное.
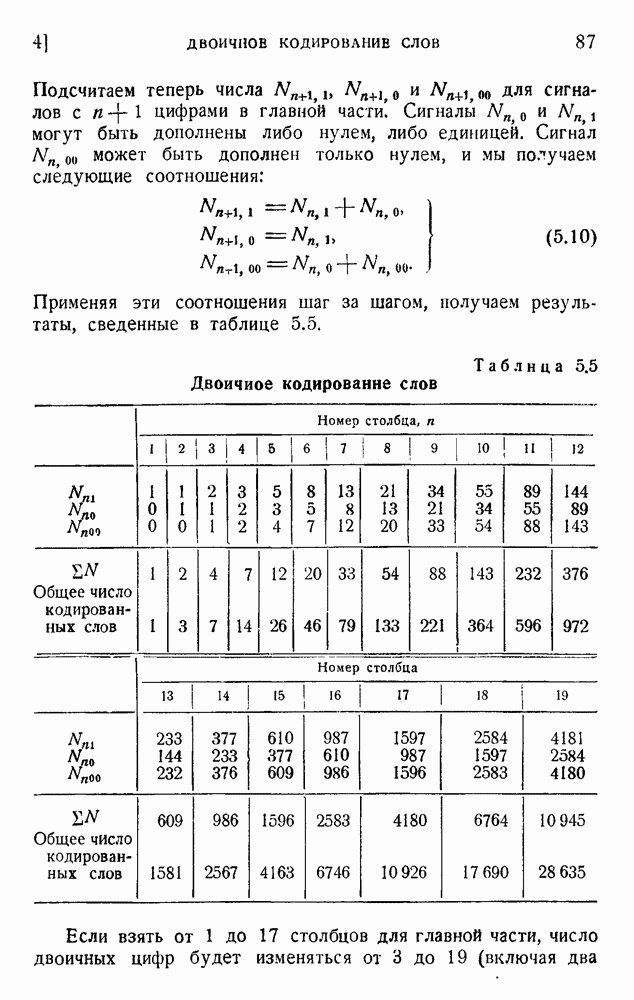
Мы получим значительно лучшее решение, кодируя группы знаков посредством групп символов, однако обсуждение такой системы требует предварительного исследования вероятностей групп знаков. Мы имеем:

Определим показатели вероятностей  :
:

(4.74) Группа символов  , имеет вероятность
, имеет вероятность

Мы имеем, таким образом, закон аддитивности показателей вероятностей 6. Найдем теперь число  групп знаков, имеющих определенную вероятность
групп знаков, имеющих определенную вероятность  Задача в точности совпадает с задачей, рассмотренной в п. 3, в которой нужно только заменить длительности
Задача в точности совпадает с задачей, рассмотренной в п. 3, в которой нужно только заменить длительности  показателями вероятностей
показателями вероятностей  и 0. Для длинных групп знаков мы
и 0. Для длинных групп знаков мы
перепишем результаты, выражаемые формулами (4.18) и (4.23):

где  — среднее число групп знаков при
— среднее число групп знаков при  — коэффициент, введенный вместо прежнего
— коэффициент, введенный вместо прежнего  . Аналогично
. Аналогично

где  — среднее число групп знаков при несравним теперь статистические свойства групп знаков и групп символов. Будем кодировать
— среднее число групп знаков при несравним теперь статистические свойства групп знаков и групп символов. Будем кодировать  групп знаков посредством
групп знаков посредством  групп символов, присваивая, таким образом, кратчайшие кодовые обозначения наиболее часто встречающимся группам знаков. Приравняем
групп символов, присваивая, таким образом, кратчайшие кодовые обозначения наиболее часто встречающимся группам знаков. Приравняем  и
и  и воспользуемся соотношениями (4.77) и (4.23):
и воспользуемся соотношениями (4.77) и (4.23):

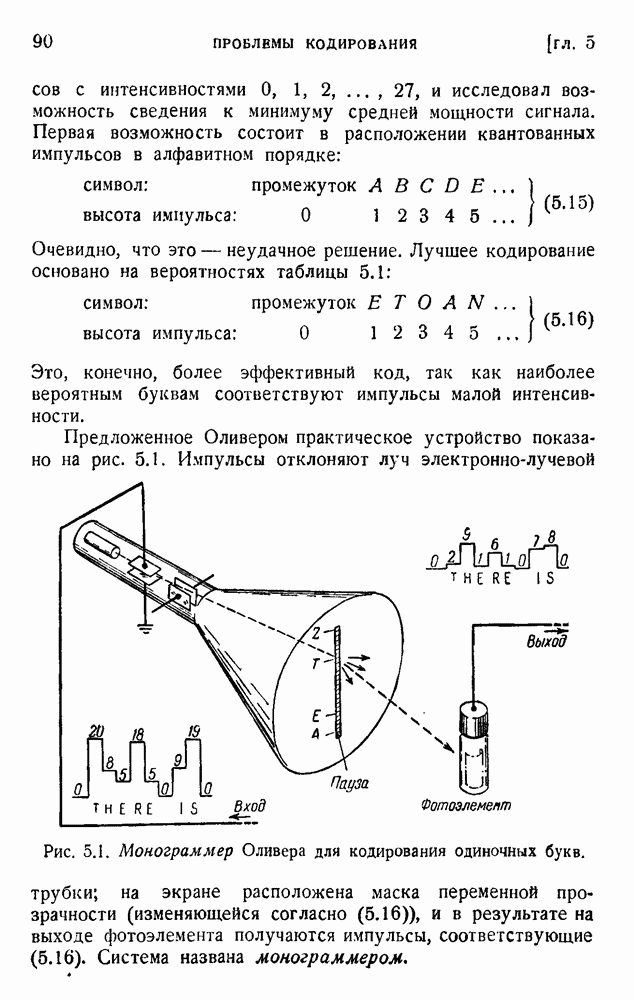
Эта упрощенная формула применима к длинным группам знаков и символов. При этом экспоненциальные члены в (4.78) будут много больше постоянных  которые можно опустить. Практическое условие запишется в виде
которые можно опустить. Практическое условие запишется в виде

Так как  и
и  велики, последний член можно отбросить и записать:
велики, последний член можно отбросить и записать:

Это соотношение выражает пропорциональность между показателем вероятности  и длительностью
и длительностью 
При таком кодировании символ  длительностью
длительностью  будет иметь среднюю вероятность
будет иметь среднюю вероятность

а это и есть экспоненциальный закон (4.61) оптимального кодирования. Условие (4.78) оставляет нам значительную свободу в выборе частного способа кодирования, однако мы смогли доказать возможность выполнения наших условий согласования языка с каналом. Хорошее согласование требует
кодирования длинных групп знаков и символов, а это означает задержку процесса кодирования на передающей стороне и декодирования на приемной стороне.
Более сложные задачи, учитывчюшие корреляцию между последовательными символами (и избыточность), могут быть решены методом, сходным с тем, который был применен для решения нашей упрощенной задачи.
Вернемся к условию (4.78). Мы предоставили длинные группы символов редким группам знаков и короткие группы символов часто встречающимся группам знаков. При применении групп символов различной длины возникает трудность, состоящая в том, что для обозначения места стыка соседних групп необходим особый символ. Этого можно избежать, применяя группы символов одинаковой длины. На первый взгляд это решение кажется неэкономичным. Можно, однако, показать, что оно не хуже того, которое обсуждалось выше. Возьмем вместо (4.78)

Так как  и
и  велики, мы можем пренебречь постоянной
велики, мы можем пренебречь постоянной

В этом выражении можно отбросить последний член, и мы придем снова к условию (4.80). Это иллюстрирует многообразие способов кодирования, дающих хорошее согласование.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
- 4. Информация и алфавит
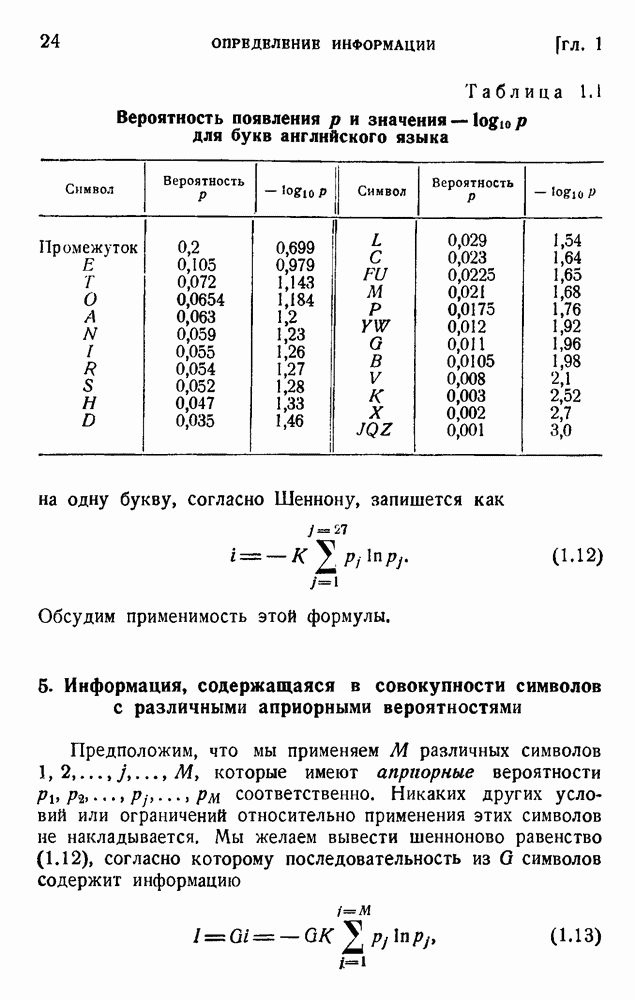
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
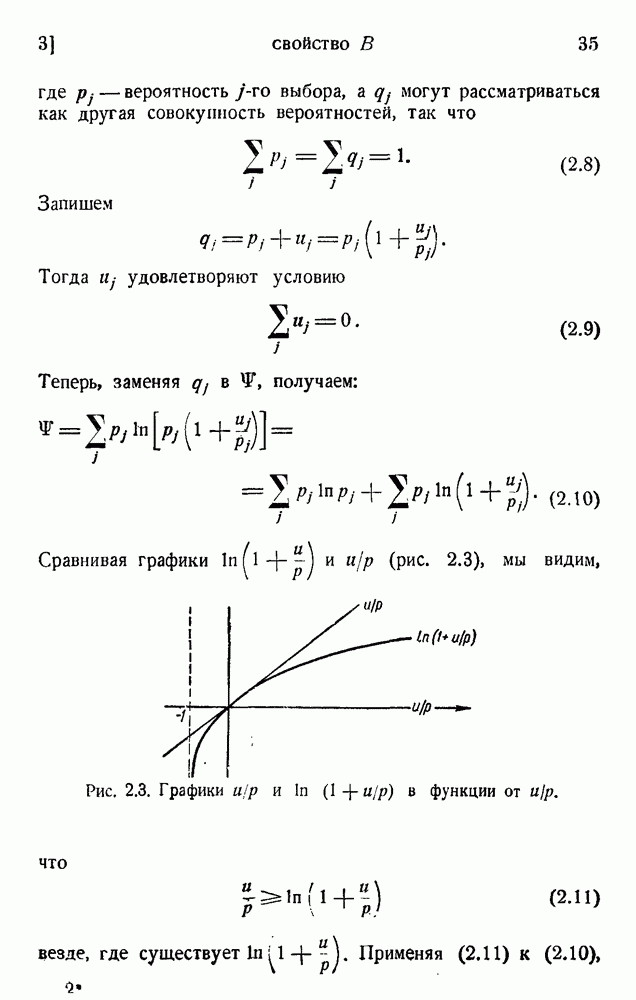
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
- 2. Корреляция в языке
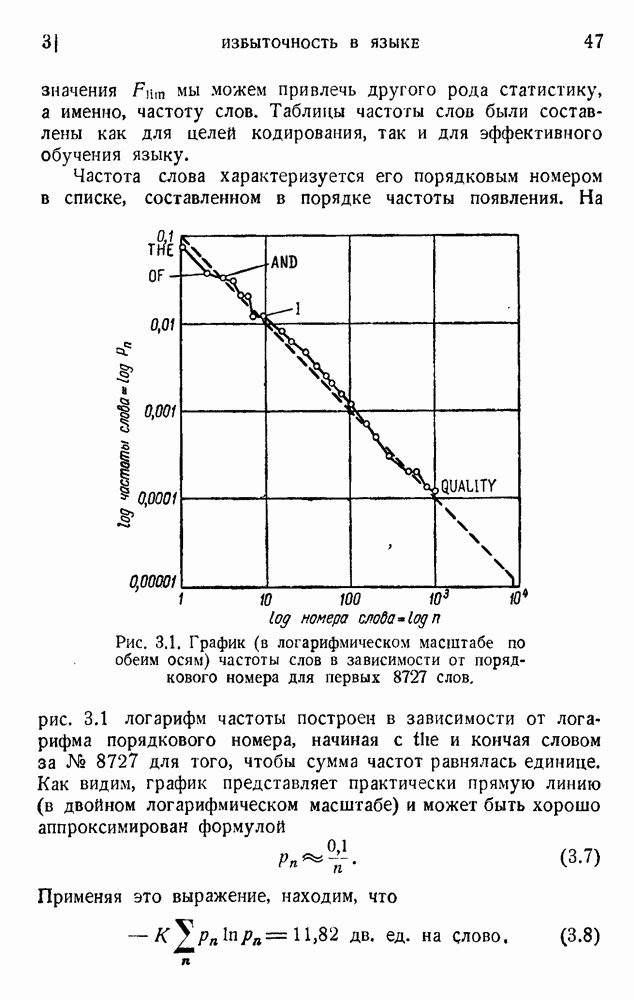
- 3. Избыточность в языке
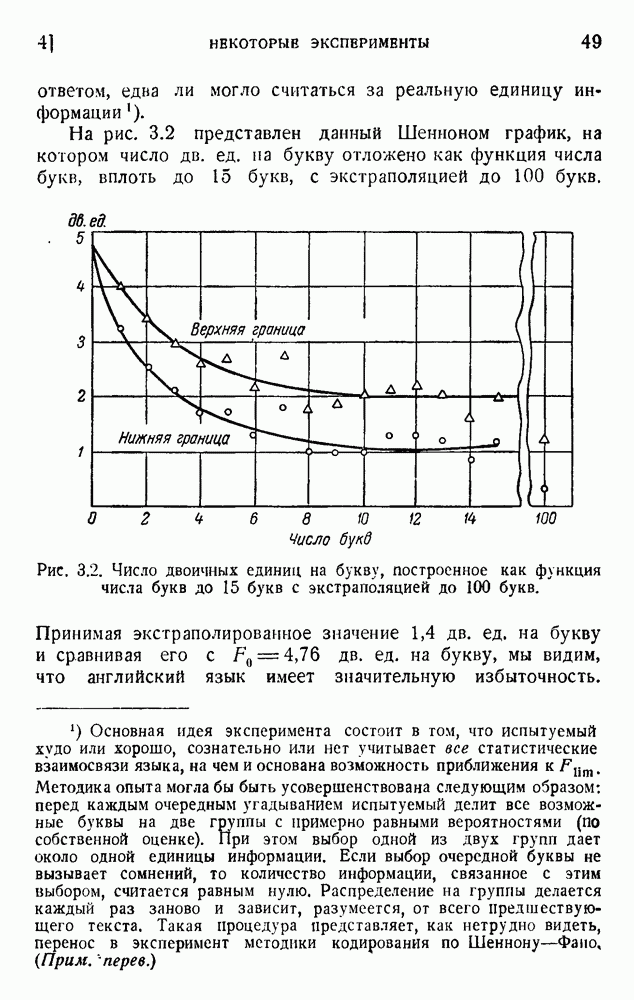
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
- 10. Проблемы статистики слов
- 11. Решение проблемы согласования
- Приложение
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
- 1. Ряд Фурье
- 2. Явление Гиббса и сходимость рядов Фурье
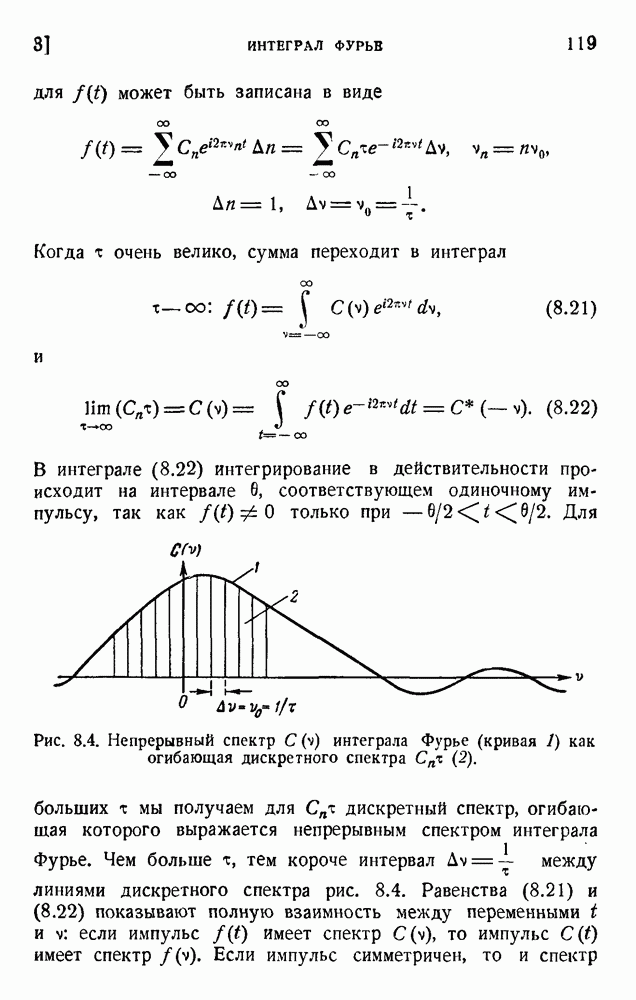
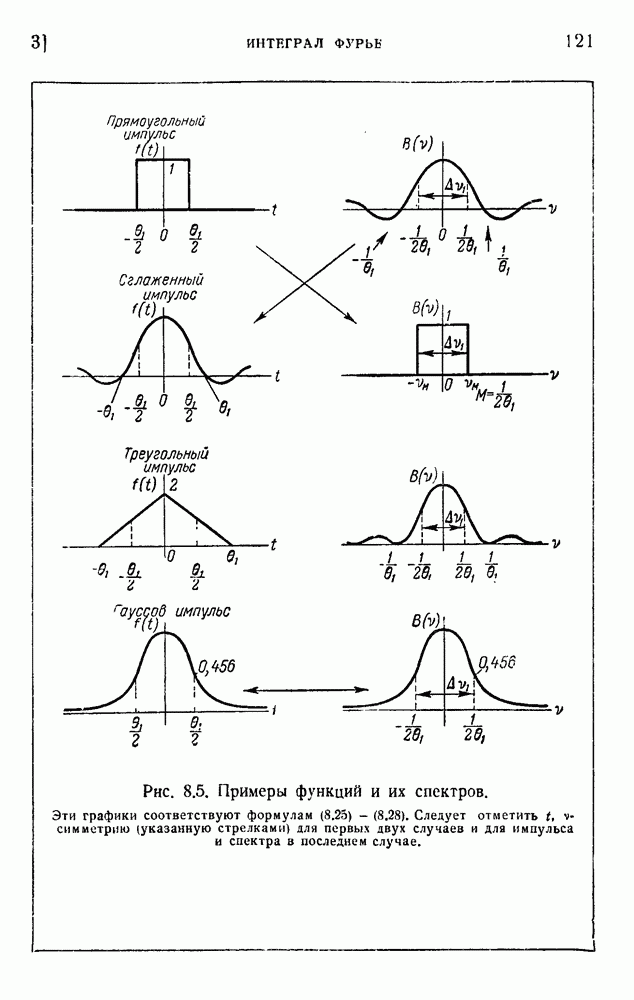
- 3. Интеграл Фурье
- 4. Роль конечной ширины полосы частот
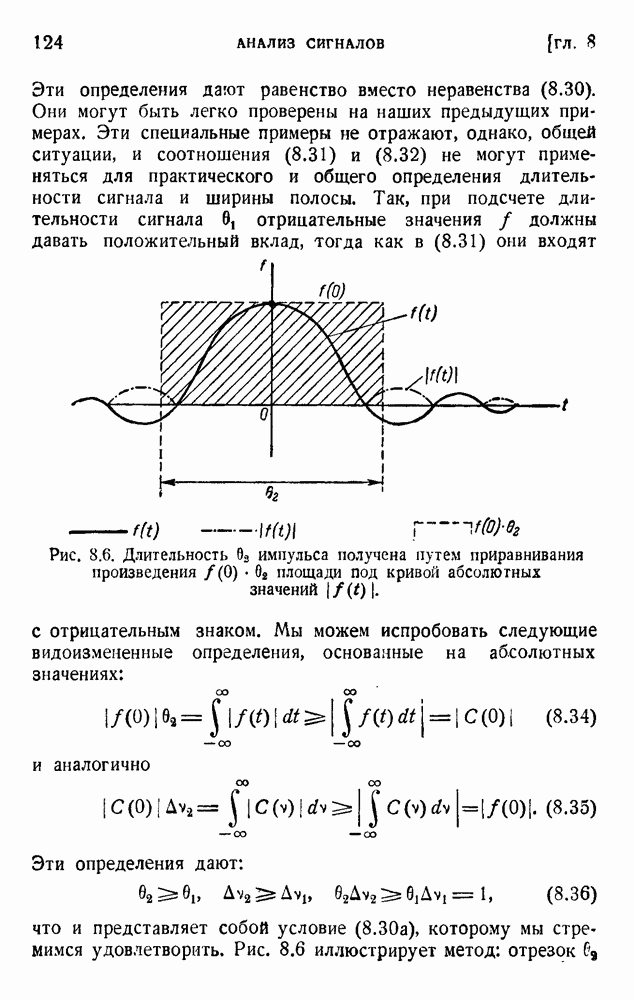
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
- 7. Метод отсчетов Шеннона
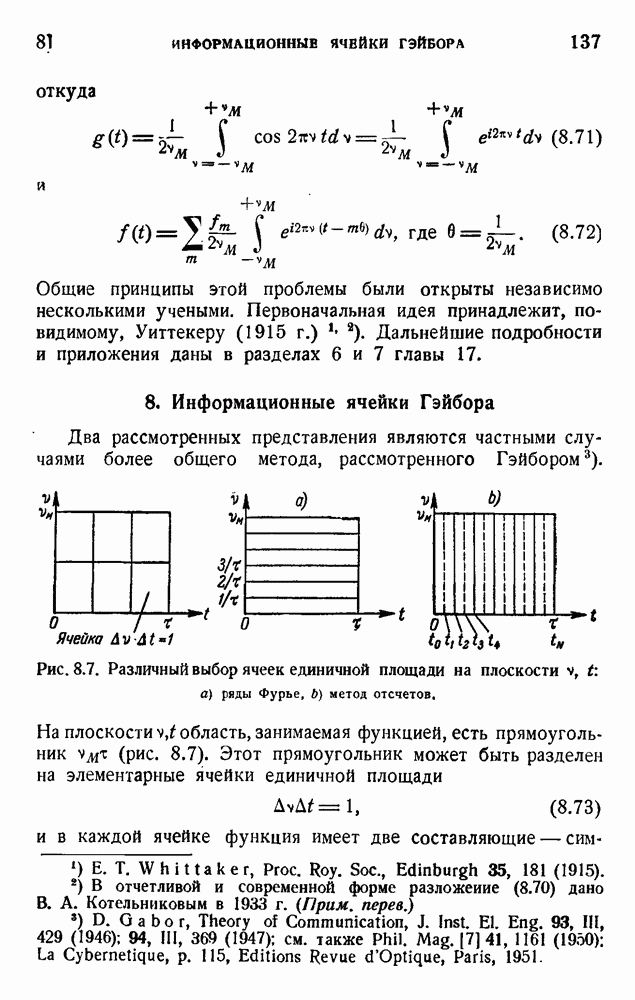
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
- 10. Линейные преобразования и фильтры
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
- 1. Тепловое движение
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
- 5. Тепловое движение в электрической цепи
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
- 5. Тепловое движение в выпрямителе
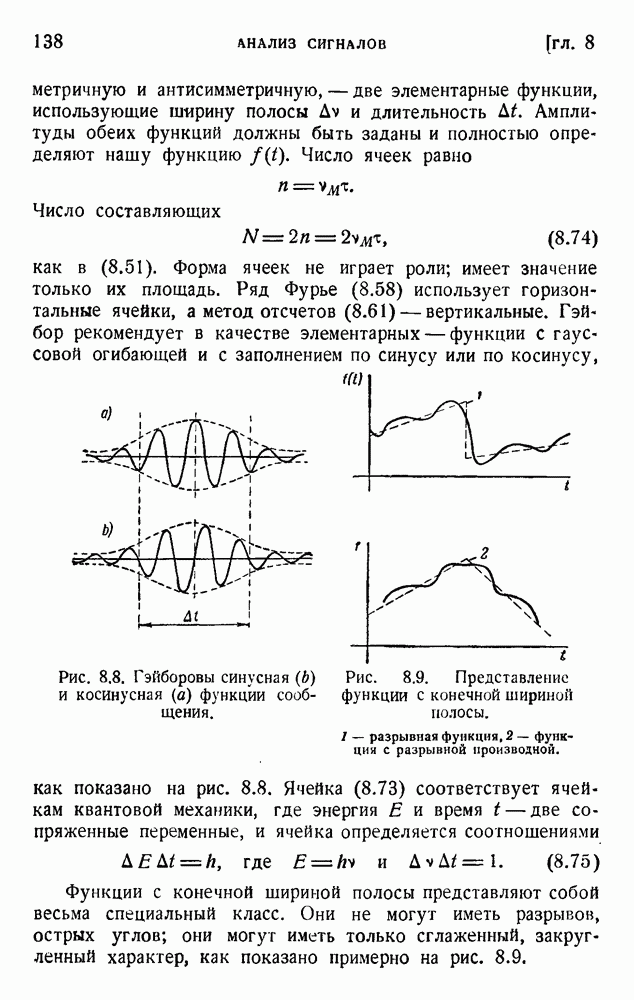
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
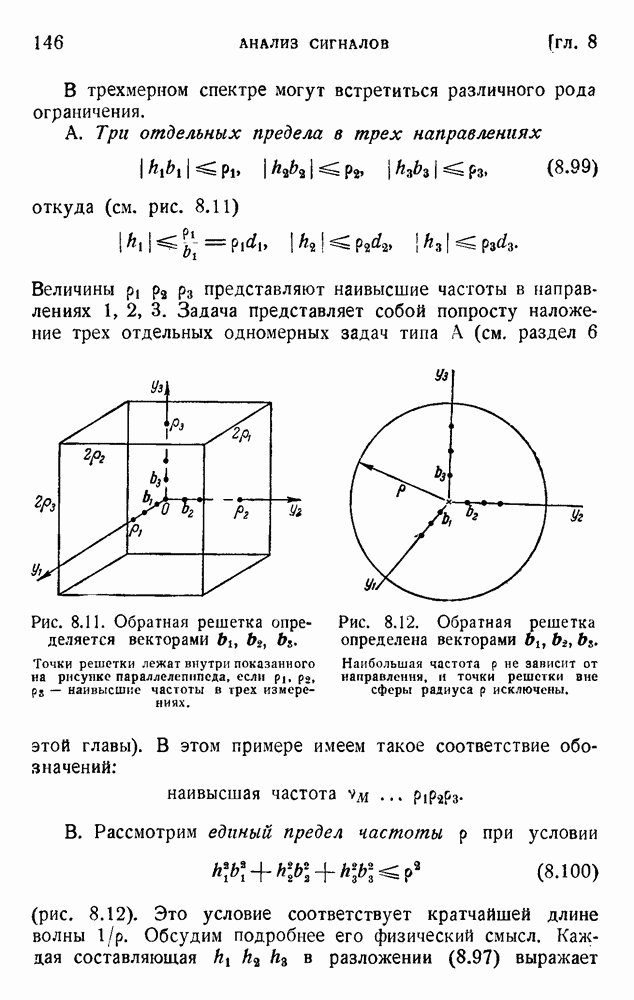
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
- 5. Негэнтропия, требуемая при наблюдении
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
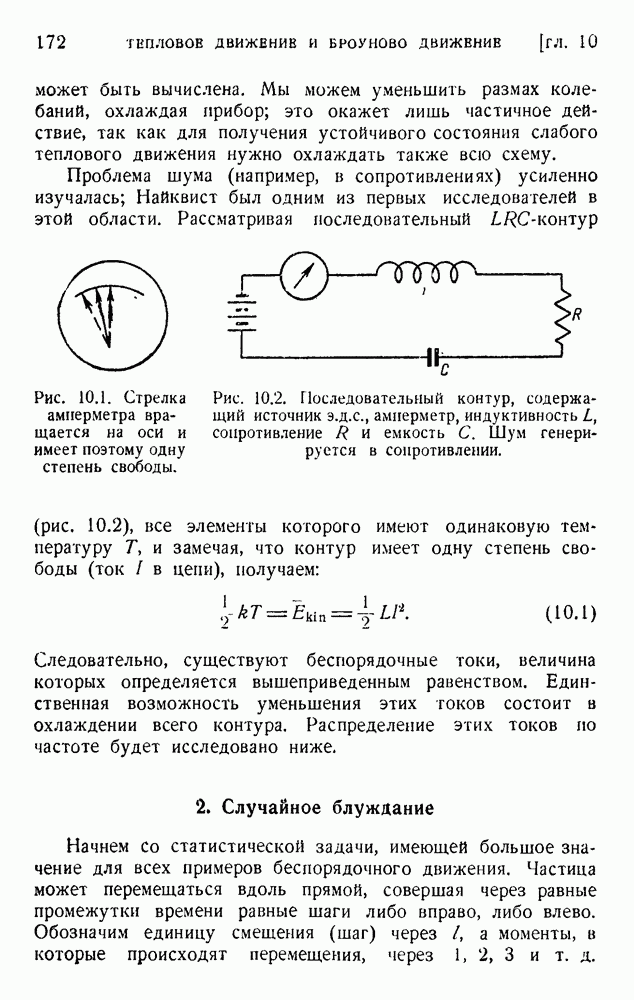
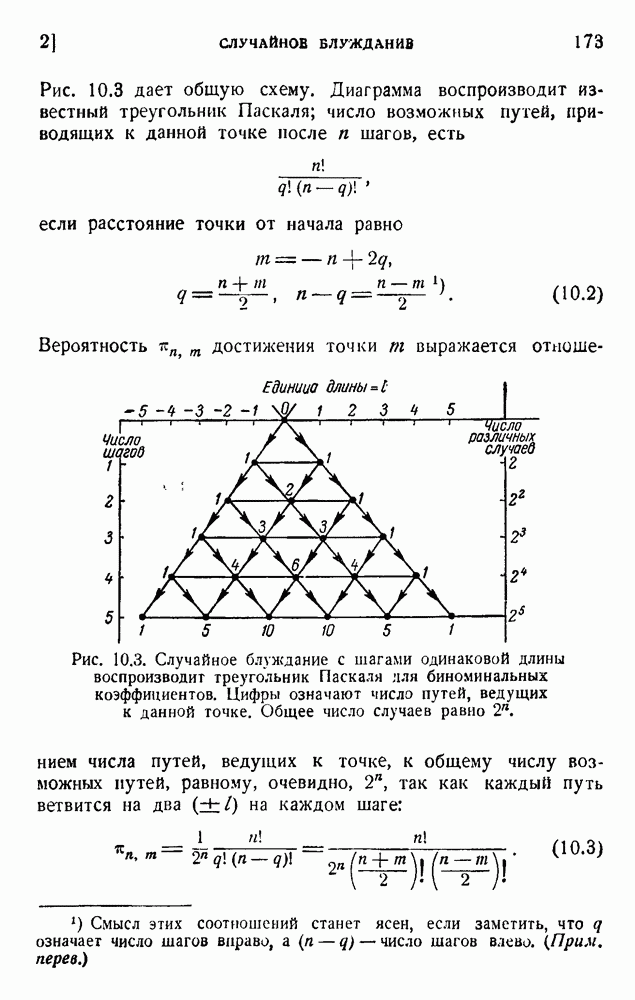
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
- 4. Пределы евклидовой геометрии
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
- 6. Проблемы семантической информации