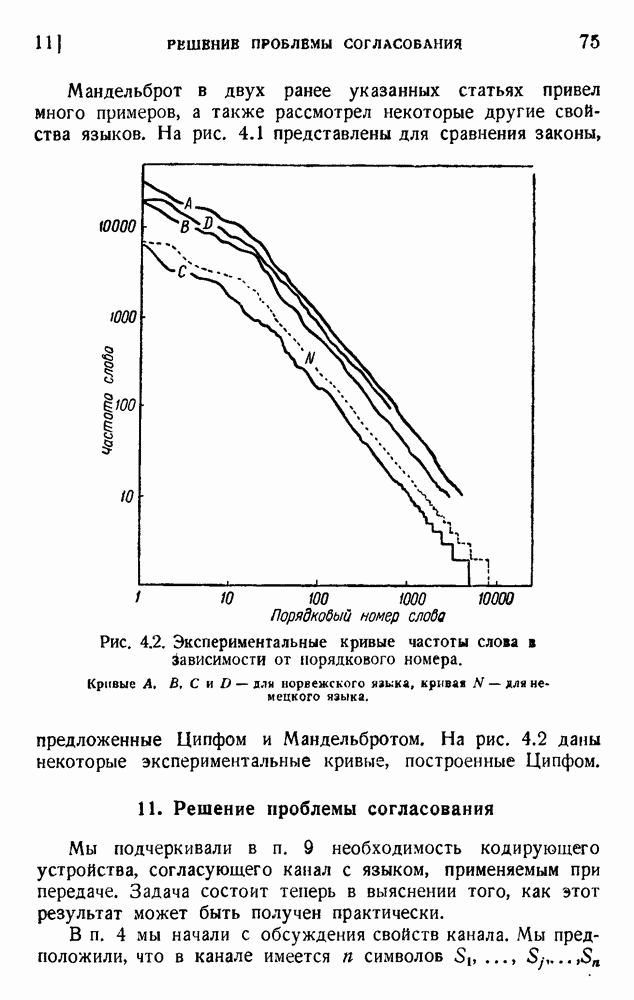
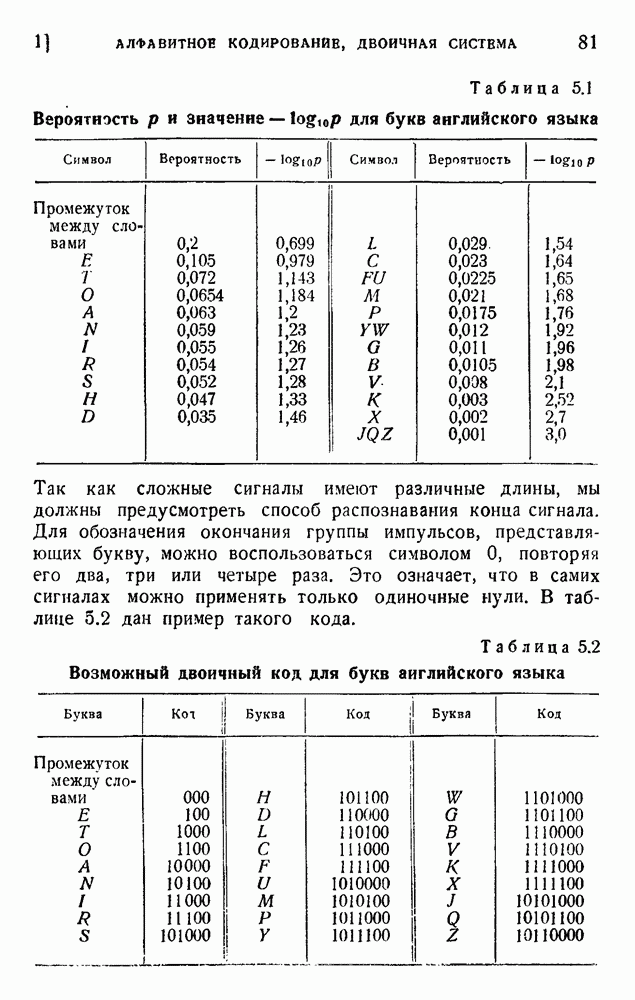
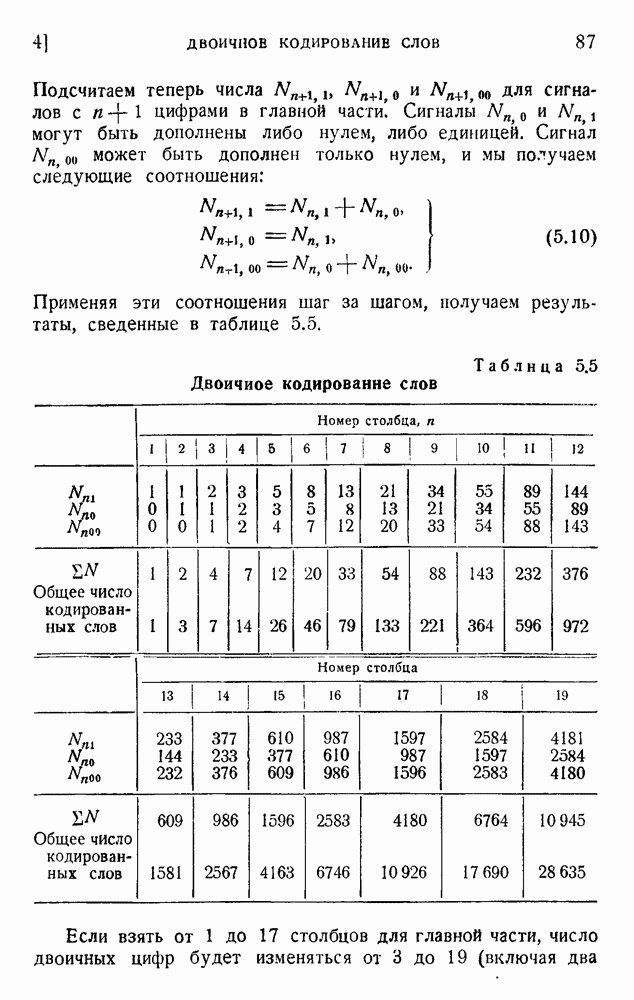
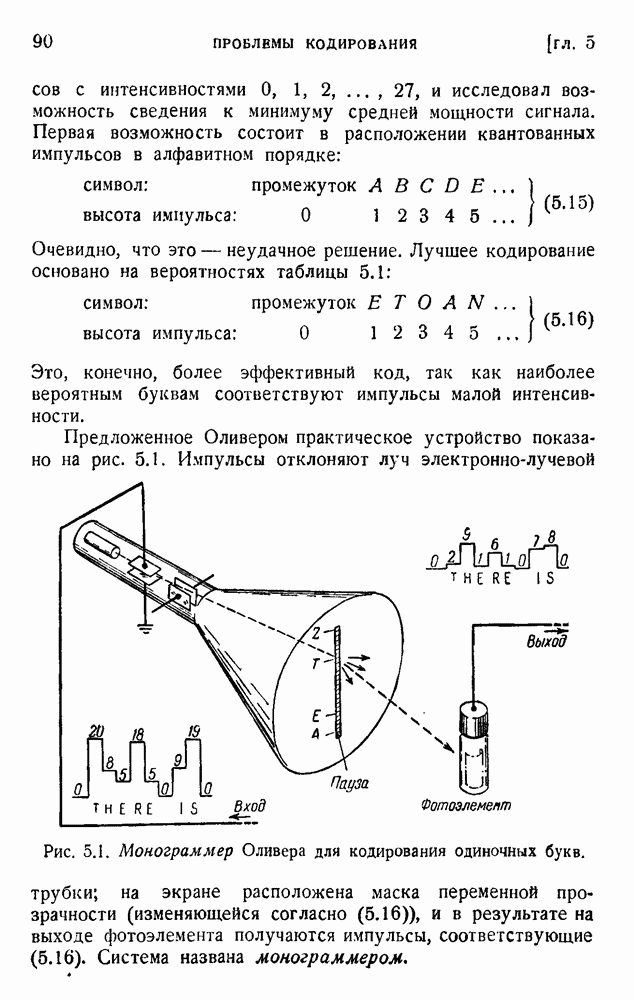
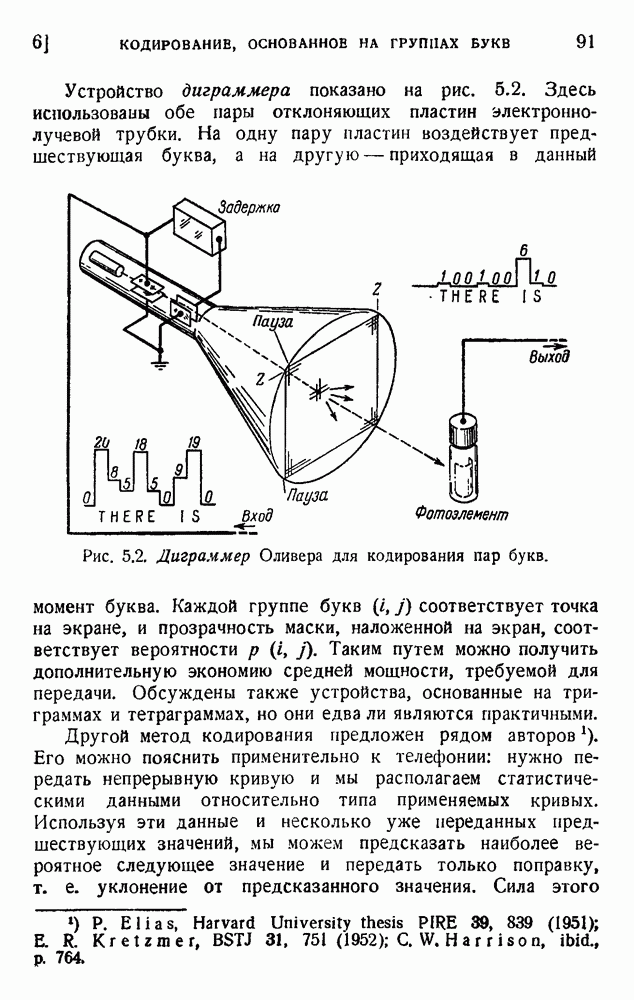
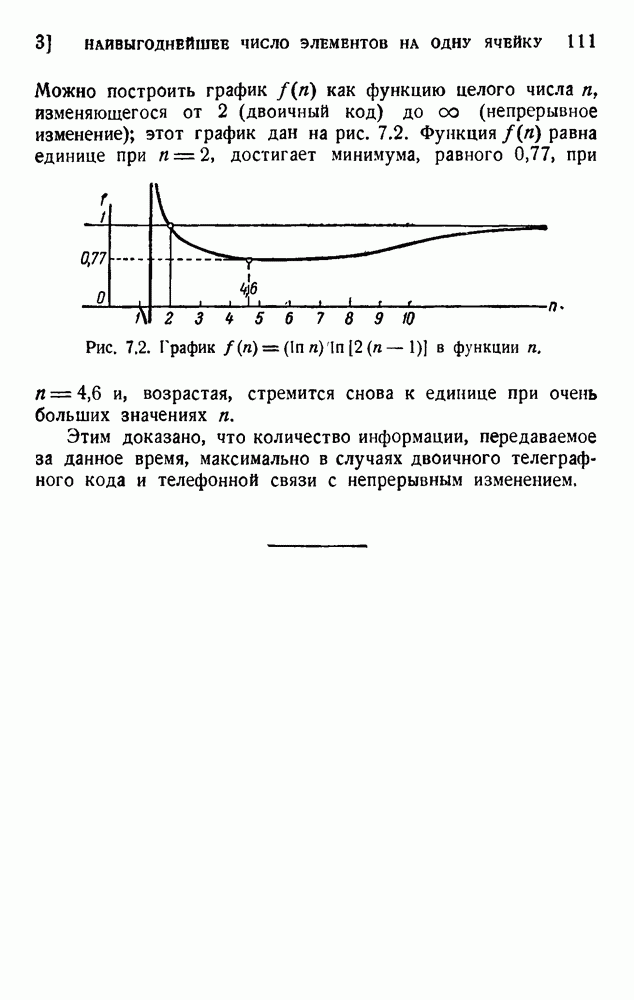
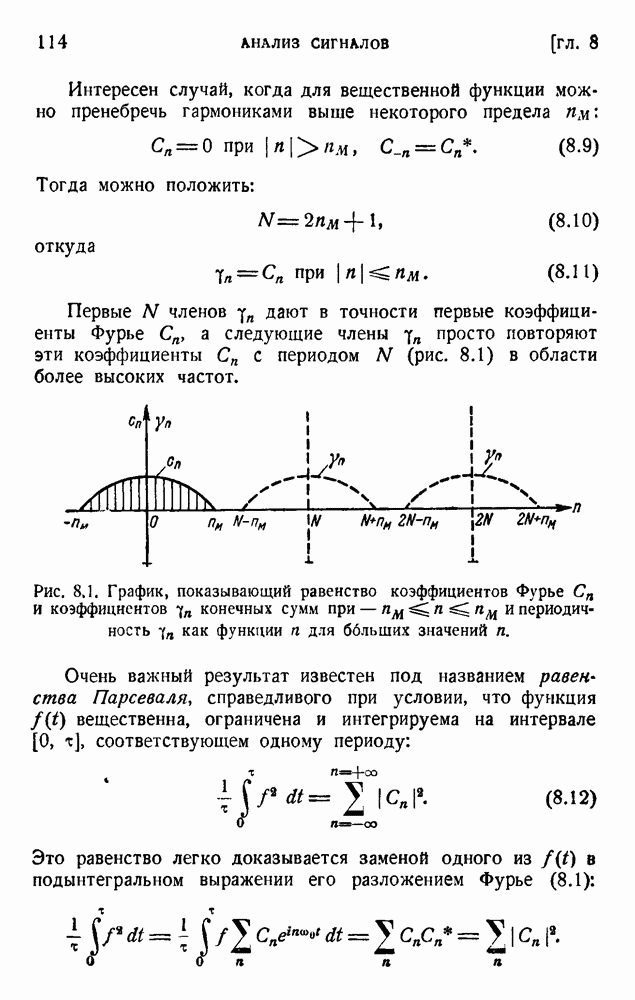
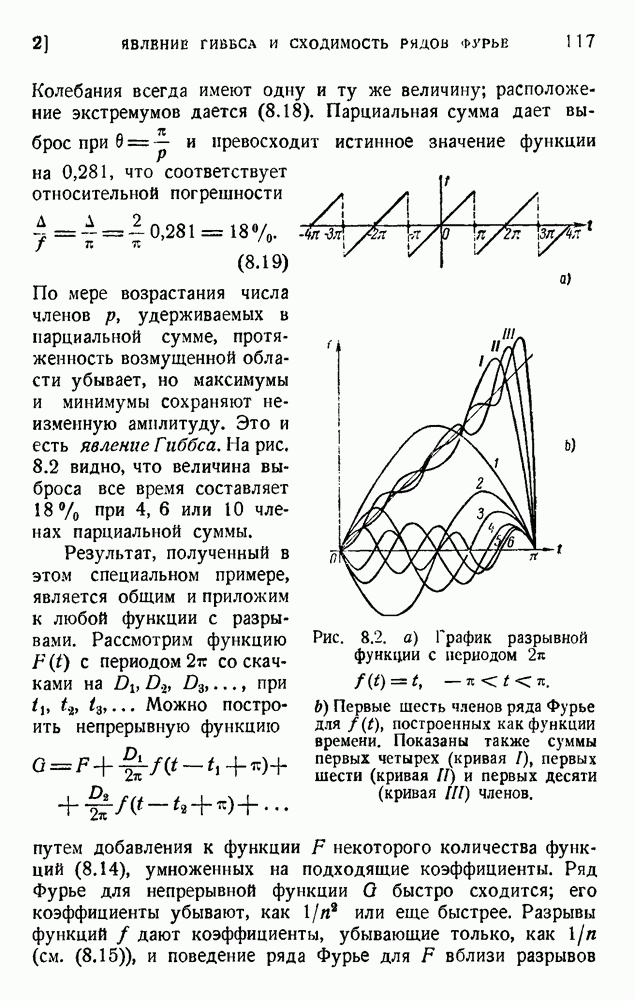
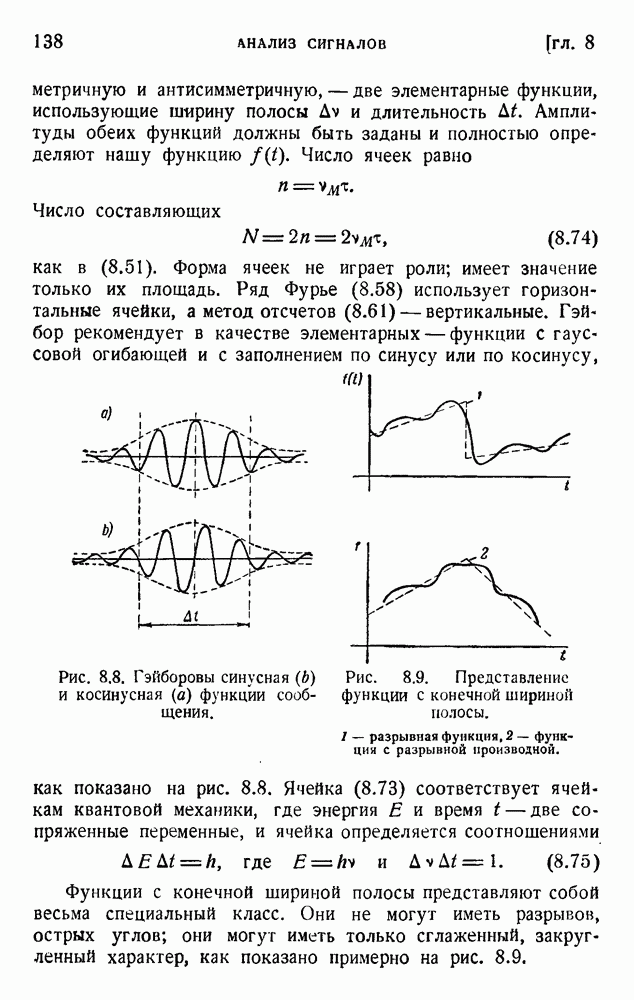
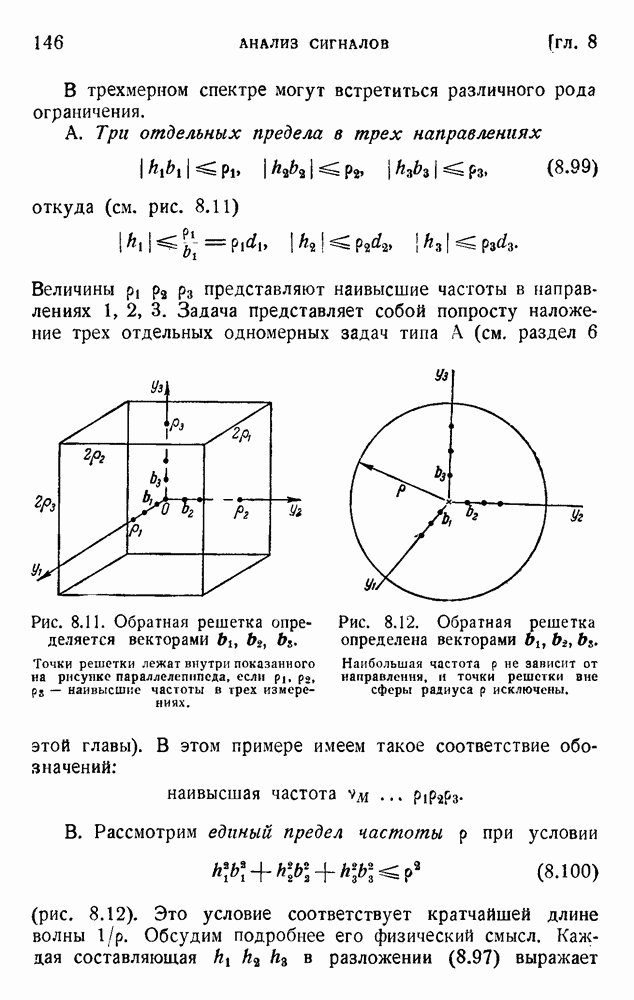
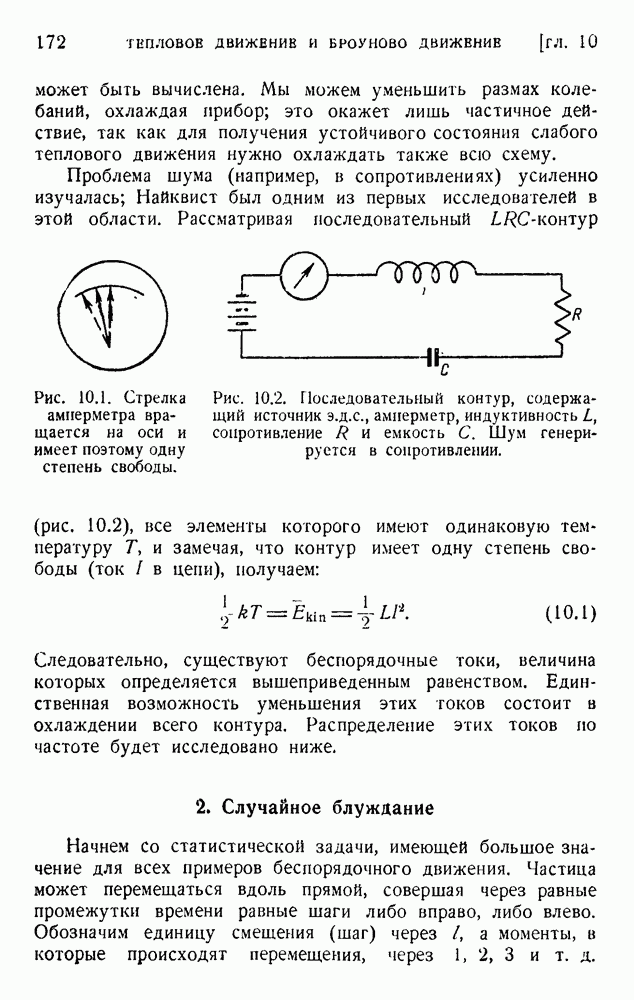
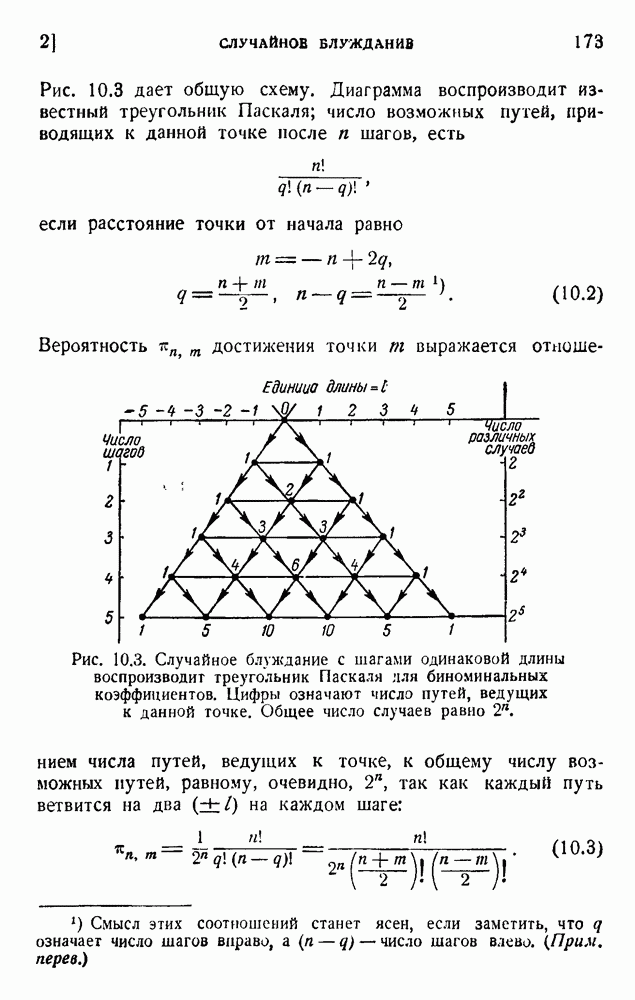
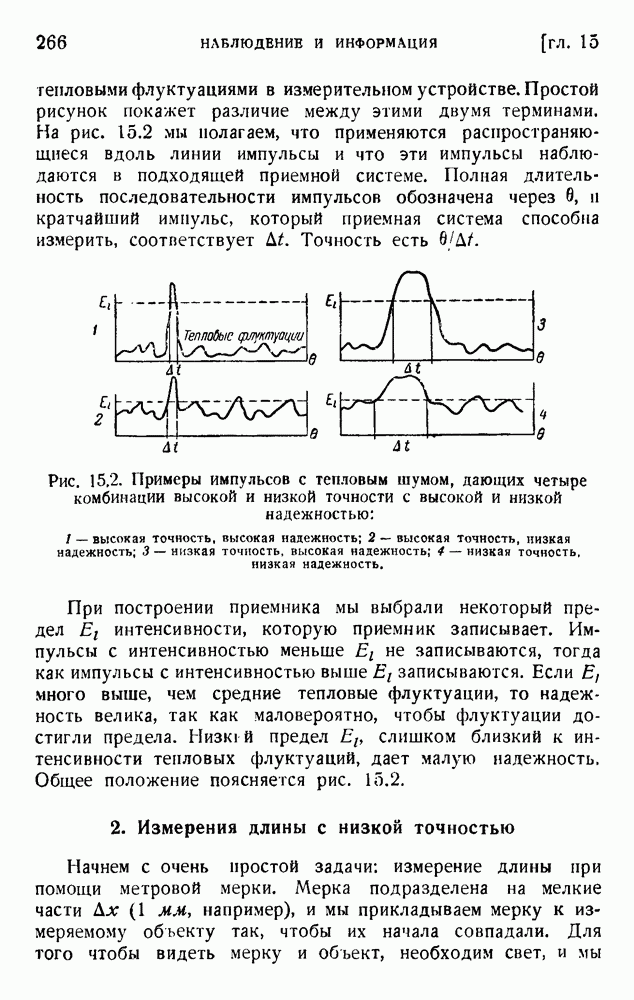
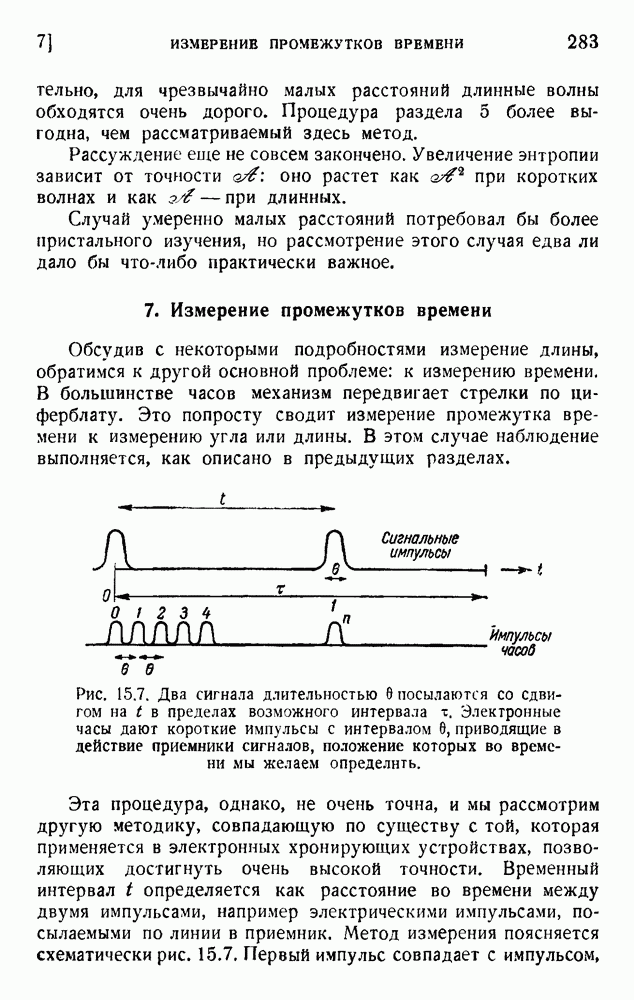
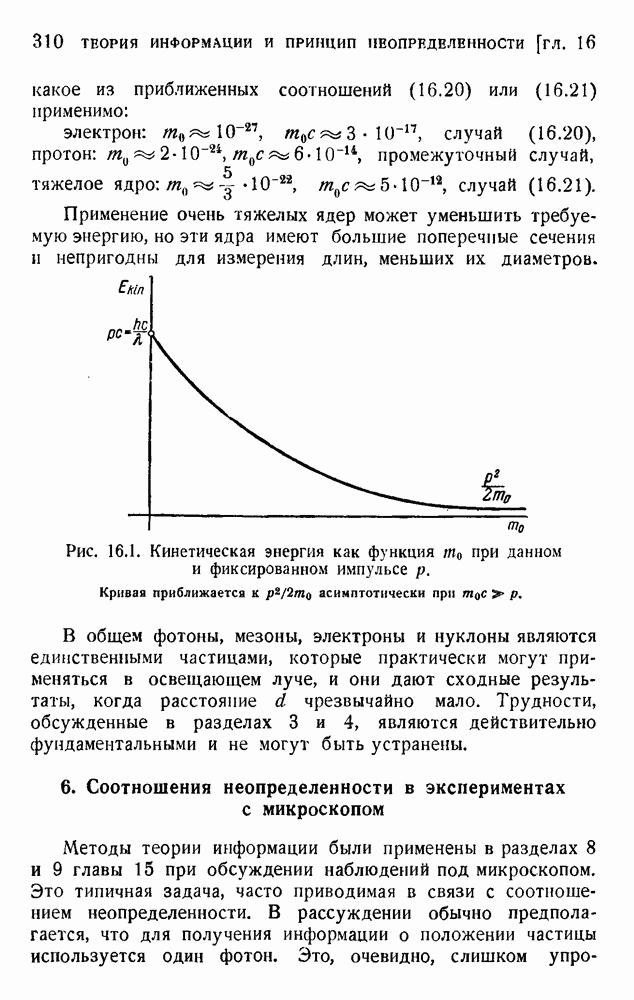
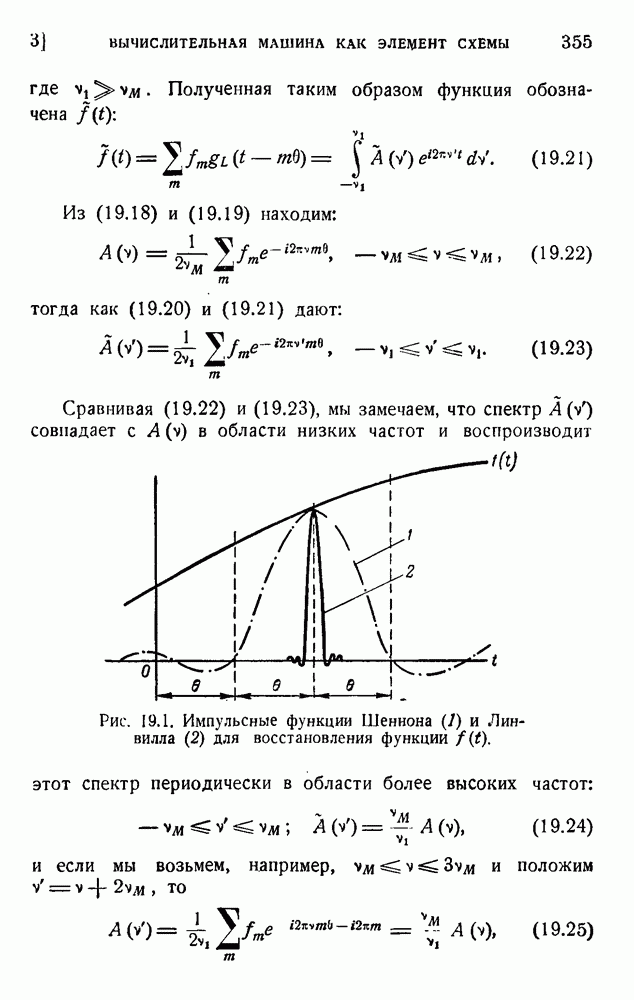
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Несколько типичных физических примеров
Рассмотрим несколько классических задач физики, чтобы показать, как возникает связанная информация и какую роль она играет. Это будет подходящим случаем для рассмотрения некоторых старых споров о значении энтропии и для разъяснения некоторых трудных вопросов.
Возьмем случай идеального одноатомного газа, заключенного в теплоизолированный сосуд объема V.
Когда достигнуто равновесное состояние, энтропия равна

где n — число атомов газа, m — масса атома, k и h — постоянные Больцмана и Планка соответственно, Е — полная энергия и g — число неразличимых состояний на основном уровне атома.
Если основное состояние не вырождено, то  . Это есть случай атома без момента количества движения в основном состоянии
. Это есть случай атома без момента количества движения в основном состоянии  . Если имеется момент количества движения у (спин плюс орбитальный момент), то имеется
. Если имеется момент количества движения у (спин плюс орбитальный момент), то имеется  состояний, предполагаемых равновероятными. Основное состояние предполагается достаточно низким, а температура не слишком высокой, так что возбуждение на высшие энергетические уровни не может иметь места.
состояний, предполагаемых равновероятными. Основное состояние предполагается достаточно низким, а температура не слишком высокой, так что возбуждение на высшие энергетические уровни не может иметь места.
Теоретическая формула хорошо согласуется с экспериментальными данными, но многие теоретические члены, совершенно необходимые для логической полноты, в действительности слишком малы, чтобы их можно было наблюдать в большинстве термодинамических экспериментов. Перепишем (12.12) следующим образом:
 (12.13)
(12.13)
Случай  соответствует атомам со спином 1/2 и с двумя ориентациями
соответствует атомам со спином 1/2 и с двумя ориентациями  . При
. При  мы имеем
мы имеем  и три ориентации
и три ориентации  . Все ориентации равновероятны, если внешнее поле отсутствует; небольшое внешнее поле расщепляет энергетические уровни и устраняет вырождение.
. Все ориентации равновероятны, если внешнее поле отсутствует; небольшое внешнее поле расщепляет энергетические уровни и устраняет вырождение.
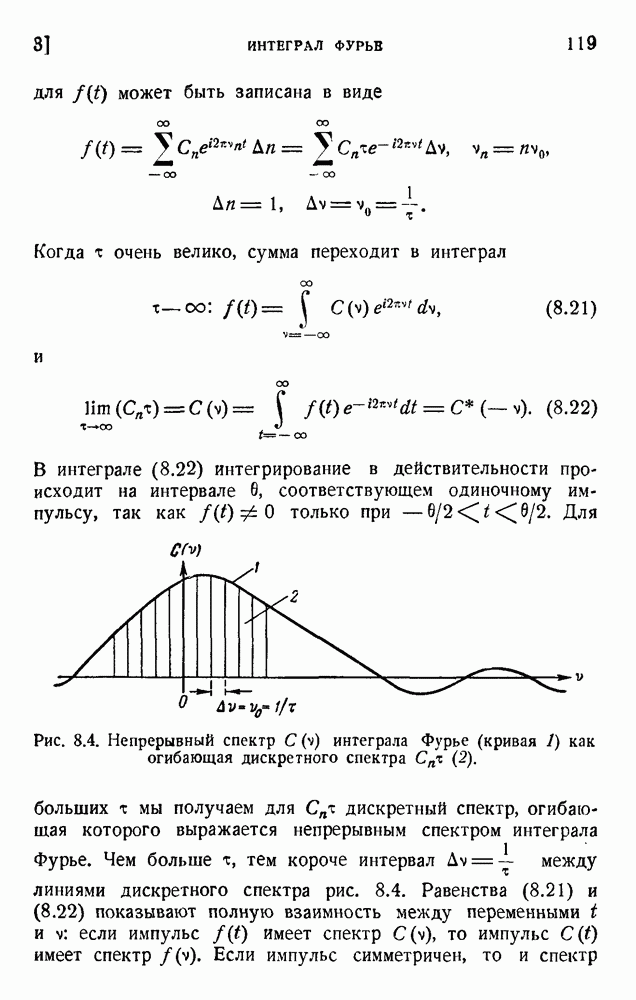
Разности между  очень малы и не могут непосредственно наблюдаться, так как мы не в состоянии изменить значение j для данного атома. Однако при радиоактивных превращениях мы можем наблюдать превращение атома с массой m и спином j в другой атом с массой m и спином
очень малы и не могут непосредственно наблюдаться, так как мы не в состоянии изменить значение j для данного атома. Однако при радиоактивных превращениях мы можем наблюдать превращение атома с массой m и спином j в другой атом с массой m и спином  и в этом случае эти величины имели бы физический смысл.
и в этом случае эти величины имели бы физический смысл.
Это рассуждение показывает, что можно говорить о различии в энтропии  только тогда, когда преобразование физически осуществимо. В противном случае это не имеет практического смысла. Предположим, что мы имеем дополнительную информацию о состоянии газа; например, нам удалось узнать, что в некоторый предшествующий момент газ занимал меньший объем
только тогда, когда преобразование физически осуществимо. В противном случае это не имеет практического смысла. Предположим, что мы имеем дополнительную информацию о состоянии газа; например, нам удалось узнать, что в некоторый предшествующий момент газ занимал меньший объем  . Так обстояло бы дело, если бы газ содержался в сосуде V, который мы внезапно соединили бы с другим объемом
. Так обстояло бы дело, если бы газ содержался в сосуде V, который мы внезапно соединили бы с другим объемом  :
:

Начальная энтропия S меньше энтропии S после расширения на величину, определяемую (12.12):
 (12.14)
(12.14)
где  есть информация. Когда мы впускаем газ в объем
есть информация. Когда мы впускаем газ в объем  между обоими сосудами возникают колебания плотности, и постепенно устанавливается равновесное состояние с плотностью, однородной во всем объеме V. Возрастание энтропии и потеря информации происходят совместно. Мы можем сказать, что газ постепенно «забывает» информацию).
между обоими сосудами возникают колебания плотности, и постепенно устанавливается равновесное состояние с плотностью, однородной во всем объеме V. Возрастание энтропии и потеря информации происходят совместно. Мы можем сказать, что газ постепенно «забывает» информацию).
В качестве другого примера рассмотрим диффузию газа. Чтобы упростить задачу, сохранив ее существенные черты, предположим, что имеются два газа с атомами одинаковой массы m при  атомов первого газа занимают первоначально объем
атомов первого газа занимают первоначально объем  атомов второго газа — объем
атомов второго газа — объем  :
:


Эти соотношения требуют, чтобы начальные концентрации составляющих и конечная концентрация были равны:

Кроме того, мы предполагаем равнораспределение энергий:
 (12.16)
(12.16)
и все  и условия, вместе взятые, требуют, чтобы в начальном состоянии давления и температуры обоих газов не различались. Введем для скобок в (12.12) обозначение
и условия, вместе взятые, требуют, чтобы в начальном состоянии давления и температуры обоих газов не различались. Введем для скобок в (12.12) обозначение

В силу наших предположений Q имеет одинаковое значение для обоих газов и сохраняет это значение на протяжении всего процесса смешивания газов. Отсюда имеем: до смешивания
 (12.17)
(12.17)
после смешивания

Необратимое возрастание энтропии равно
 (12.19)
(12.19)
Эта величина положительна, так как для  и
и  логарифм отрицателен. Мы имели в исходном состоянии некоторую информацию
логарифм отрицателен. Мы имели в исходном состоянии некоторую информацию  (связанную информацию) о системе:
(связанную информацию) о системе:
 (12.20)
(12.20)
и эта информация была потеряна в процессе диффузии газа. Можно сравнить (12.20) с формулой Шеннона (2.1) для информации. Газ в окончательно смешанном состоянии соответствует
ситуации с двумя символами с аириорными вероятностями  . Роль символа здесь играет один из видов атомов. Выбор некоторой частной комбинации символов дает информацию
. Роль символа здесь играет один из видов атомов. Выбор некоторой частной комбинации символов дает информацию  на символ (Шеннон). Начальное состояние газа соответствует отбору атомов 1 и помещению их в
на символ (Шеннон). Начальное состояние газа соответствует отбору атомов 1 и помещению их в  , тогда как атомы 2 помещаются в
, тогда как атомы 2 помещаются в  . Для этого требуется информация, выражаемая (12.20).
. Для этого требуется информация, выражаемая (12.20).
Рассмотрим теперь несколько видоизмененную задачу, предположив, что атомы имеют спин 1/2, причем атомы вида 1 имеют ориентацию  а вида
а вида  . Столкновения вызовут переходы между двумя видами атомов, и в окончательном состоянии будем иметь:
. Столкновения вызовут переходы между двумя видами атомов, и в окончательном состоянии будем иметь:
 (12.21)
(12.21)
с энтропией
 (12.22)
(12.22)
Мы снова теряем информацию и увеличиваем энтропию

Окончательная энтропия  равна энтропии
равна энтропии  (см. (12.13)) для газа со спином 1/2 с двумя равновероятными ориентациями. Наше рассуждение ясно показывает необходимость члена, зависящего от g, в формуле для энтропии и объясняет его физическое значение.
(см. (12.13)) для газа со спином 1/2 с двумя равновероятными ориентациями. Наше рассуждение ясно показывает необходимость члена, зависящего от g, в формуле для энтропии и объясняет его физическое значение.
Возрастание энтропии соответствует потере информации, как и в предыдущих примерах. Сравним нашу формулу с результатами главы 2. Мы нашли (см. (2.18)), что выбор одной возможности из двух с априорными вероятностями  дает информацию
дает информацию
 (12.24)
(12.24)
на символ. Эта величина достигает максимума при
 (12.25)
(12.25)
Если мы переходим от случая  к случаю 1/2, 1/2, то информация изменяется на
к случаю 1/2, 1/2, то информация изменяется на

на символ. Это в точности совпадает с (12.23).
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
- 4. Информация и алфавит
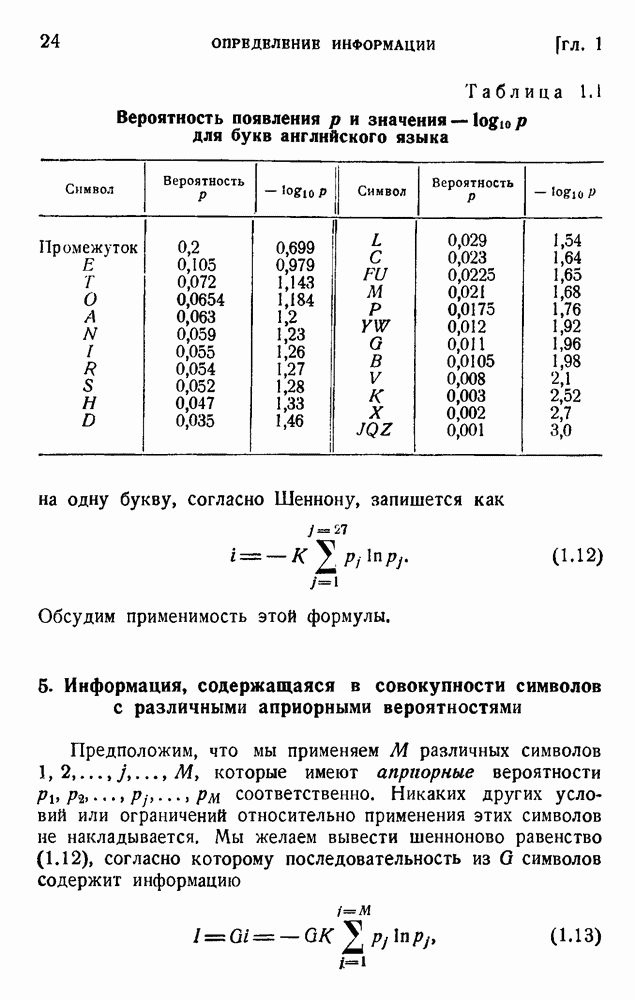
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
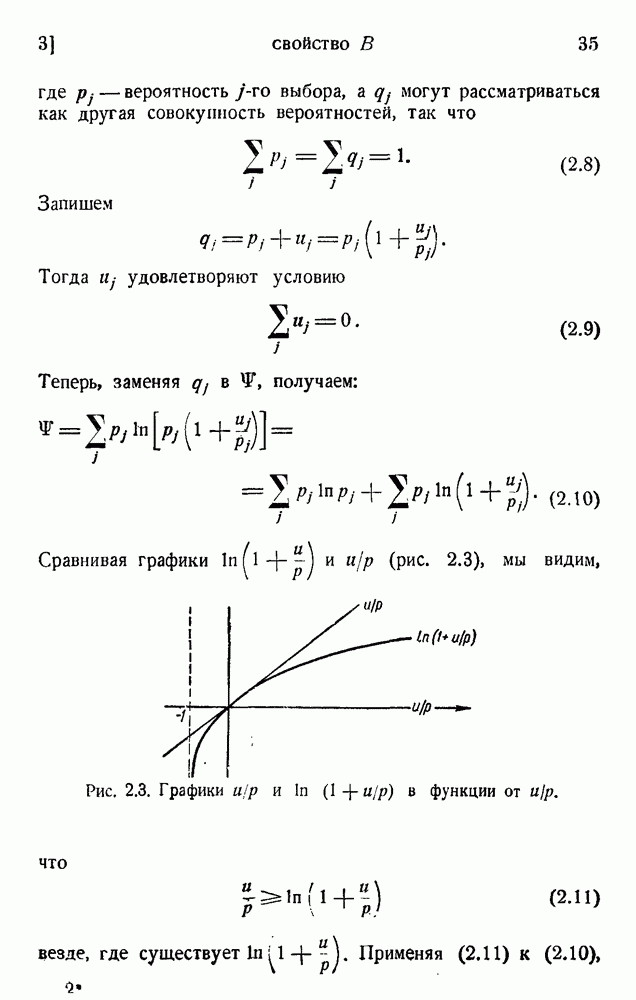
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
- 2. Корреляция в языке
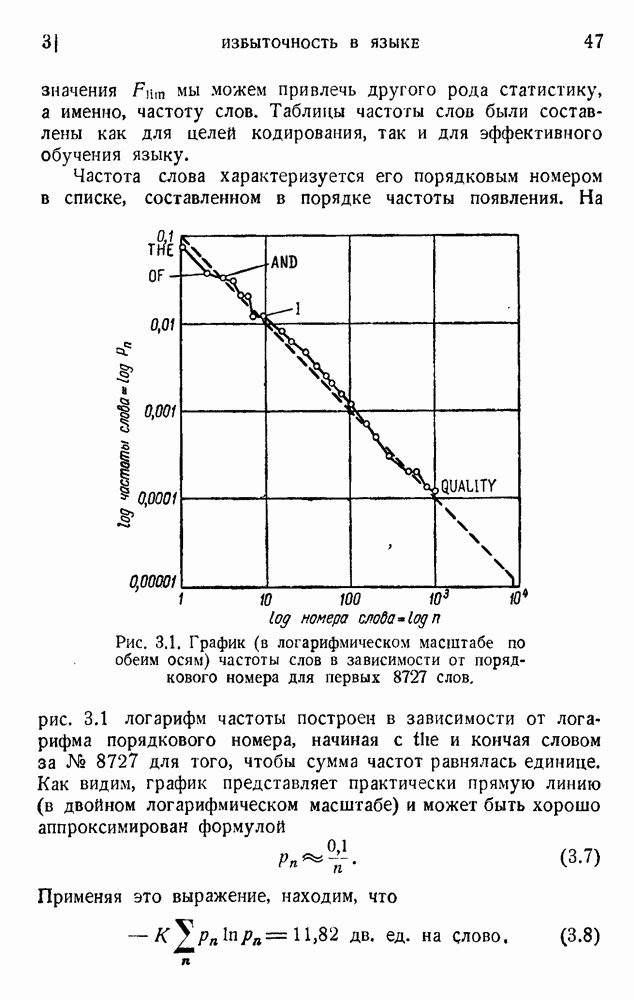
- 3. Избыточность в языке
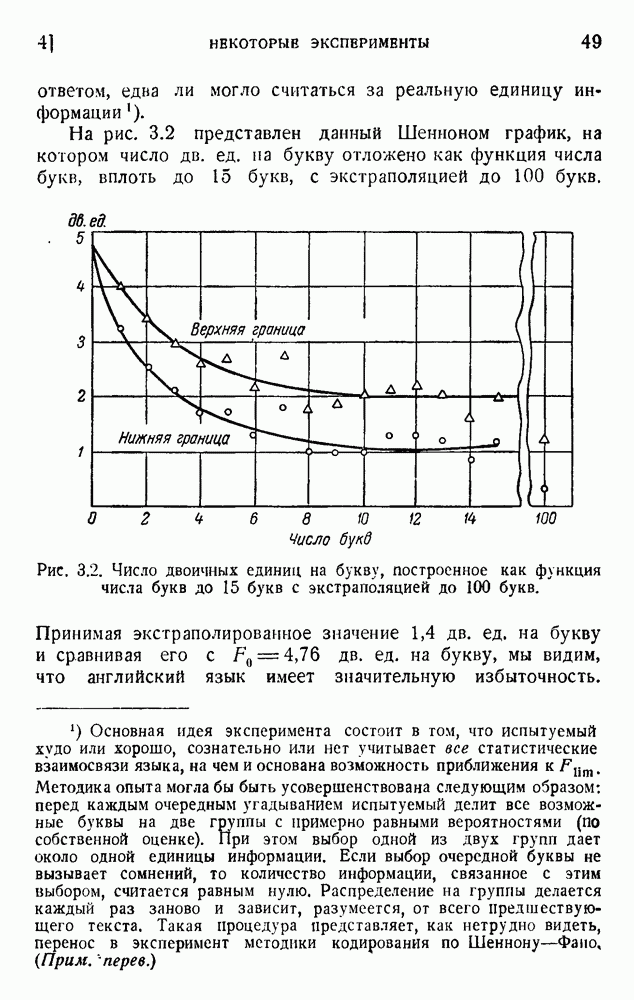
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
- 10. Проблемы статистики слов
- 11. Решение проблемы согласования
- Приложение
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
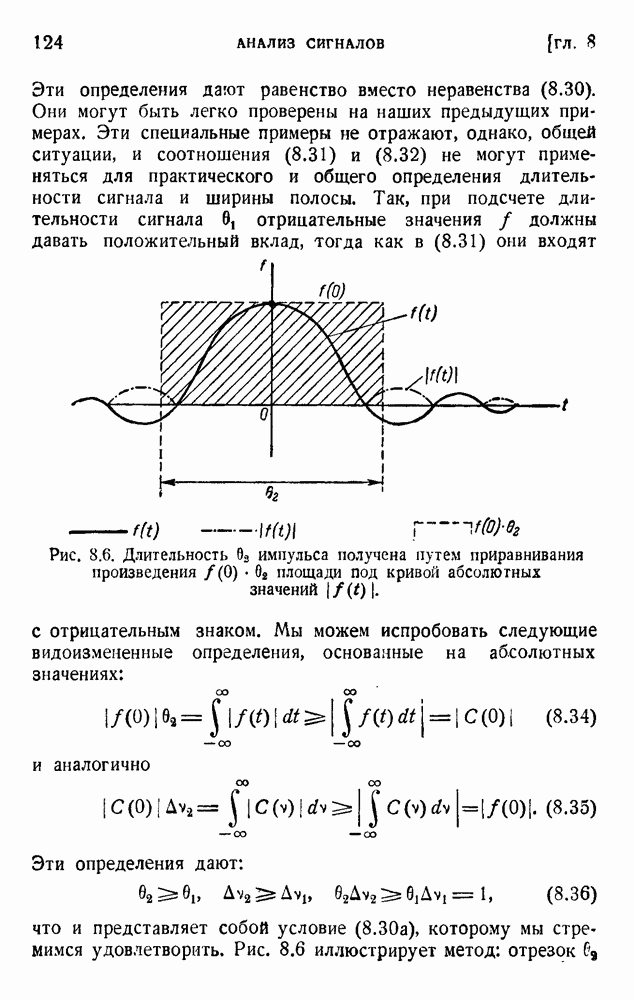
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
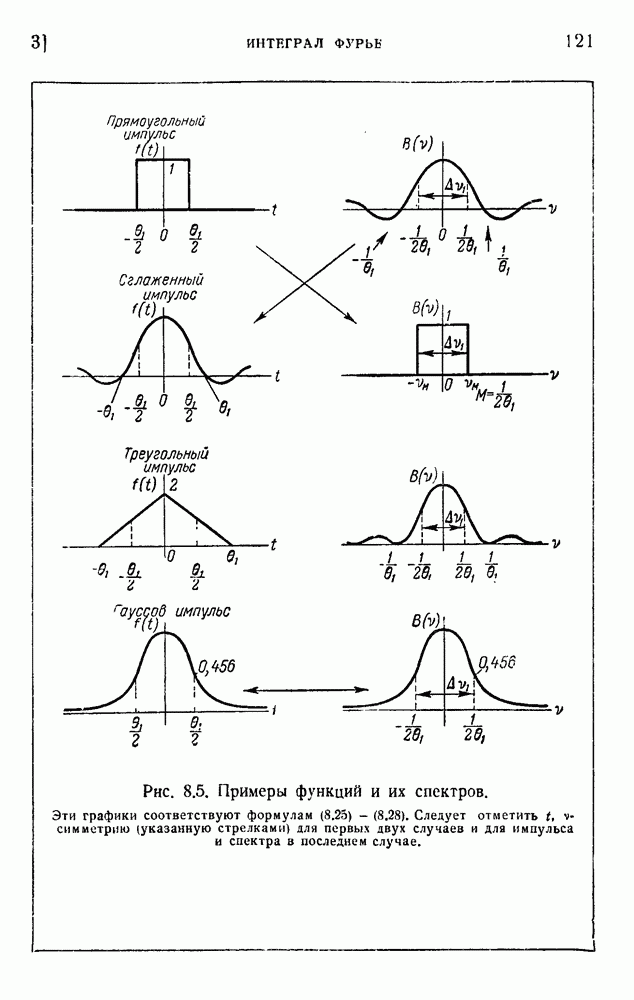
- 1. Ряд Фурье
- 2. Явление Гиббса и сходимость рядов Фурье
- 3. Интеграл Фурье
- 4. Роль конечной ширины полосы частот
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
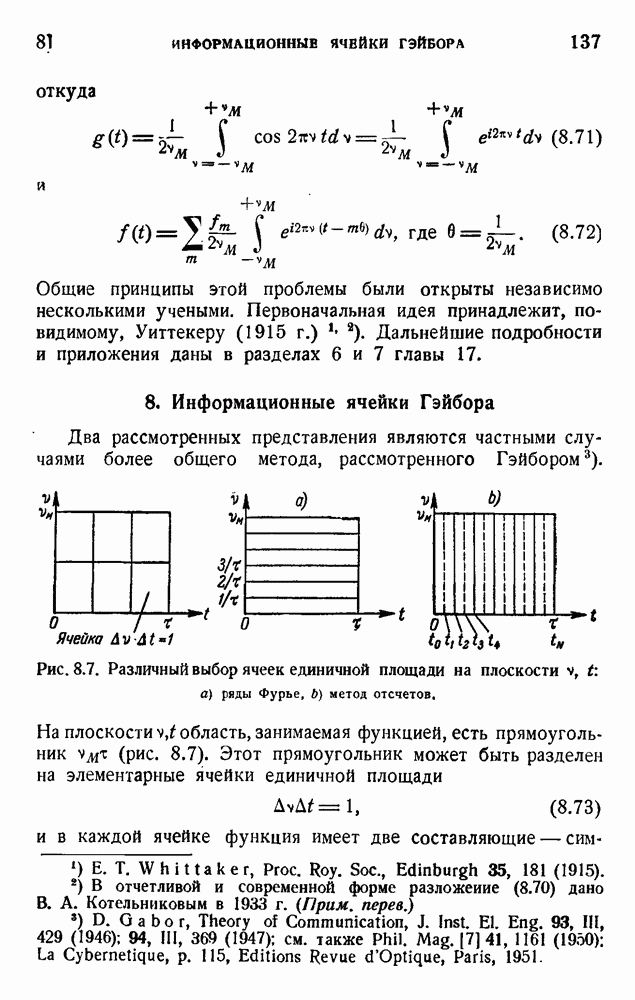
- 7. Метод отсчетов Шеннона
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
- 10. Линейные преобразования и фильтры
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
- 1. Тепловое движение
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
- 5. Тепловое движение в электрической цепи
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
- 5. Тепловое движение в выпрямителе
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
- 5. Негэнтропия, требуемая при наблюдении
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
- 4. Пределы евклидовой геометрии
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
- 6. Проблемы семантической информации