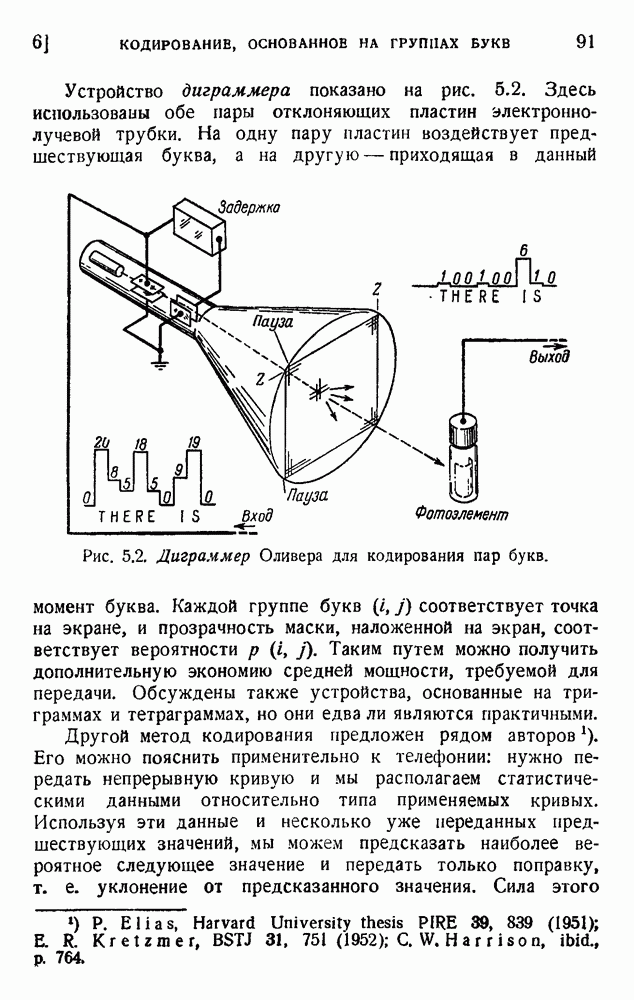
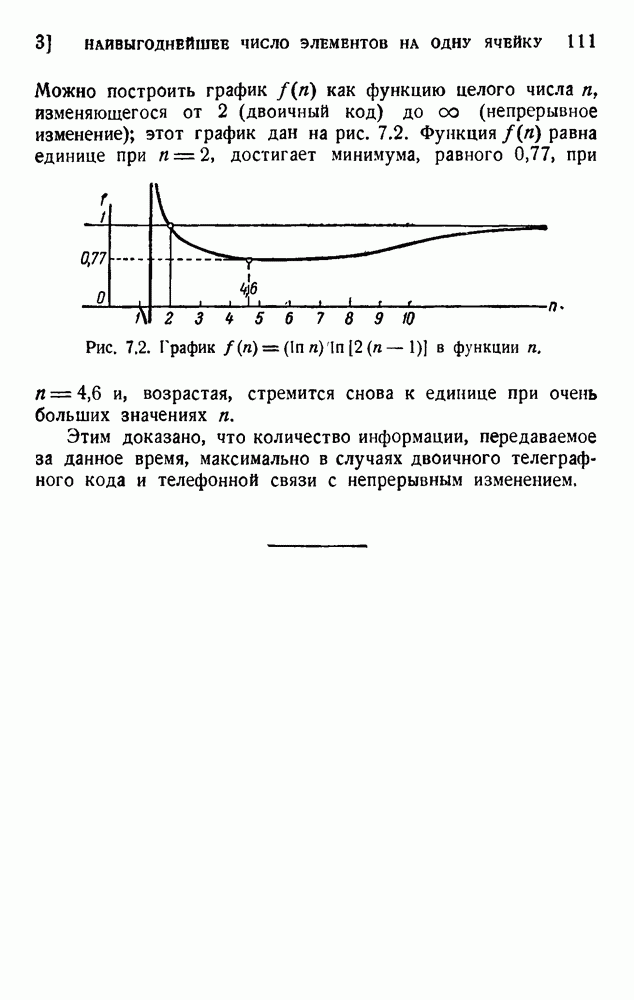
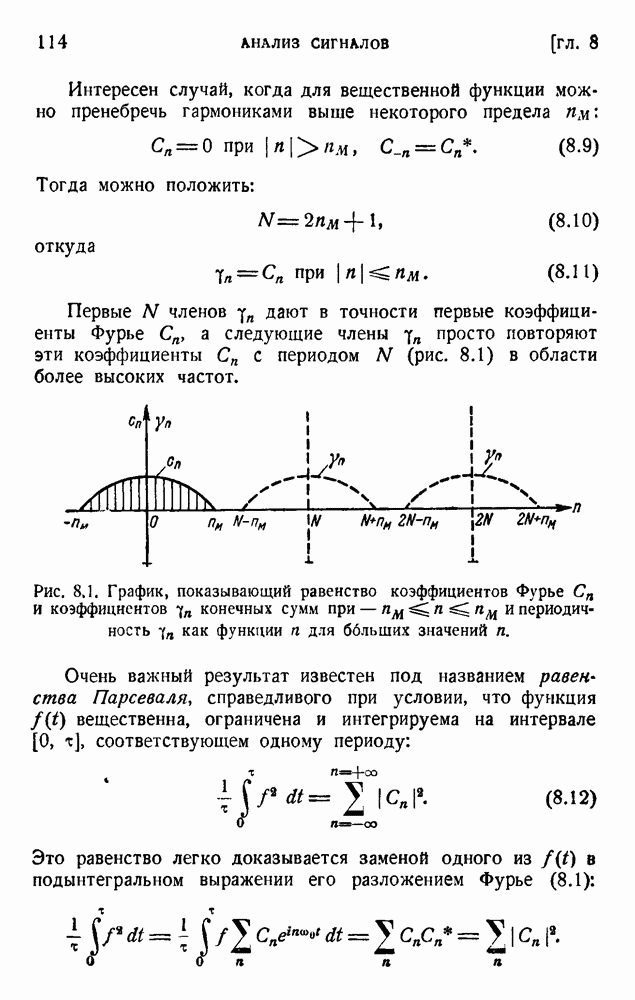
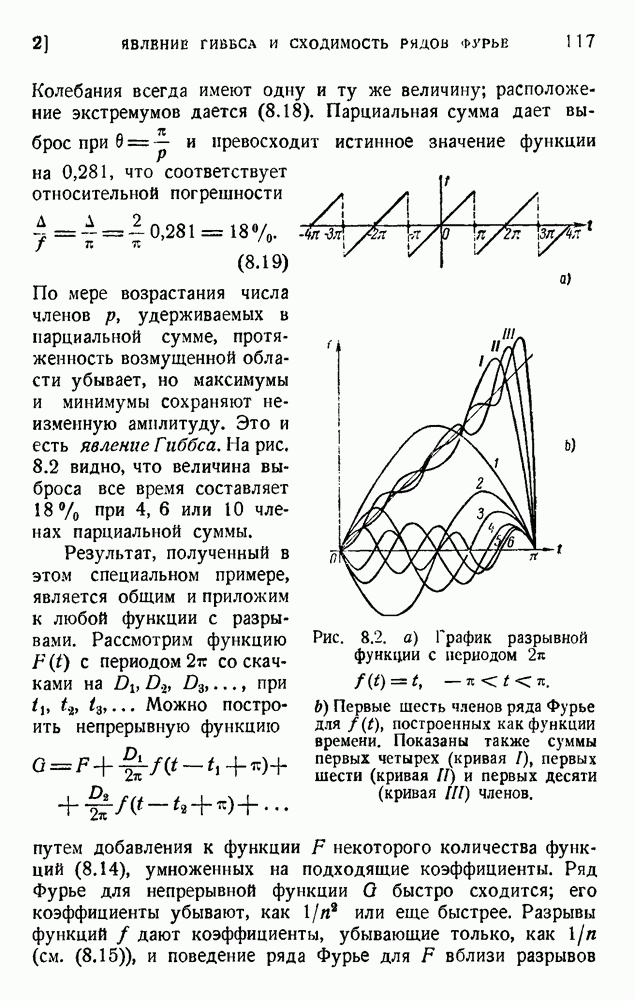
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
1. Вычислительные машины
Мы рассмотрим теперь вычислительные машины и их действие на информацию. Часто говорят, что вычислительная машина производит новую информацию. Это в действительности не так. Машины могут обрабатывать информацию: они берут сырой материал и выдают законченный продукт, но общее количество информации не возрастает. При идеальных обстоятельствах информация может оставаться постоянной на протяжении вычисления, но в обычных условиях имеются некоторые потери, и конечная информация меньше начальной.
Рассмотрим вопрос более внимательно. Процесс распадается на две стадии: программирование и собственно вычисление. Программирование выполняется учеными, которые намерены использовать машину. Они обсуждают задачу, выбирают математические законы, которые должны быть применены, приготавливают программу арифметических операций, которые должны быть выполнены в определенной последовательности. Все эти операции записываются в таком виде, чтобы машина могла их прочитать: на перфоленте, на магнитной ленте и т. п. Эта часть работы требует от ученых мышления и знания. Это может быть названо информацией в общем смысле, но это является типичным случаем, когда наши определения информации неприложимы. Мы неоднократно подчеркивали, что наше статистическое определение информации не включает какого-либо человеческого рассуждения и что мы не можем, по крайней мере в настоящее время, обсуждать проблему мышления.
Когда программа работы приготовлена в виде перфоленты, мы можем сосчитать число двоичных единиц на ней и найти
количество информации в этой окончательной программе. Едва ли это имело бы большое значение.
Следующий шаг состоит в рассмотрении машины с ее специальной программой и в изучении того, как она в действительности работает. Мы вводим определенные цифровые данные на вход. Машина обрабатывает эти данные, следуя заданной программе, вычисляет окончательные данные и выдает их на выход. Если машина не делает ошибок в вычислениях, то она действует в точности как кодирующая машина. Она использует информацию, содержащуюся во входных данных, и переводит ее в выходные данные, которые в лучшем случае могут содержать всю входную информацию, но не более.
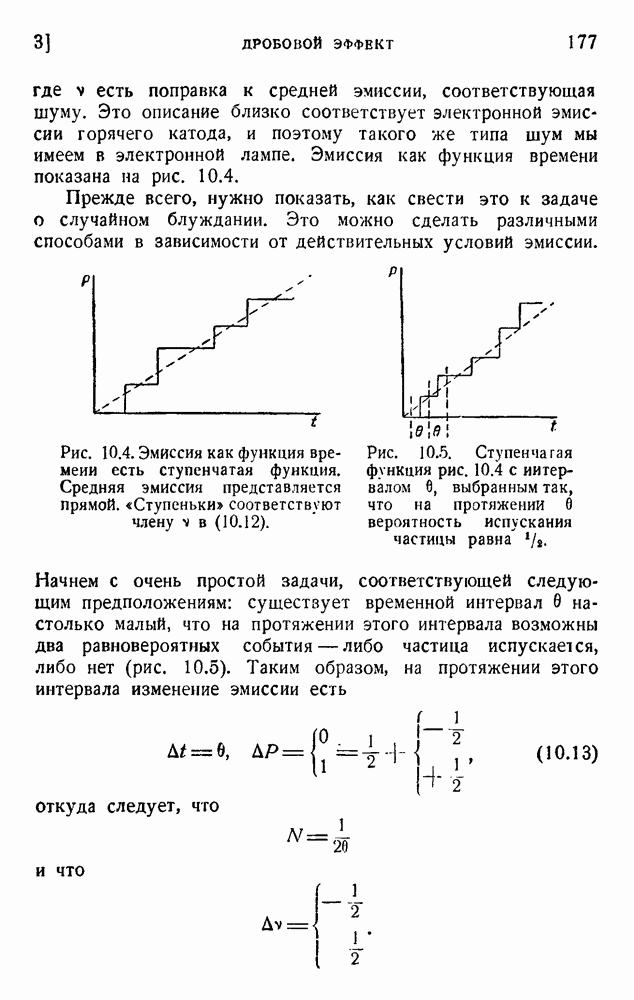
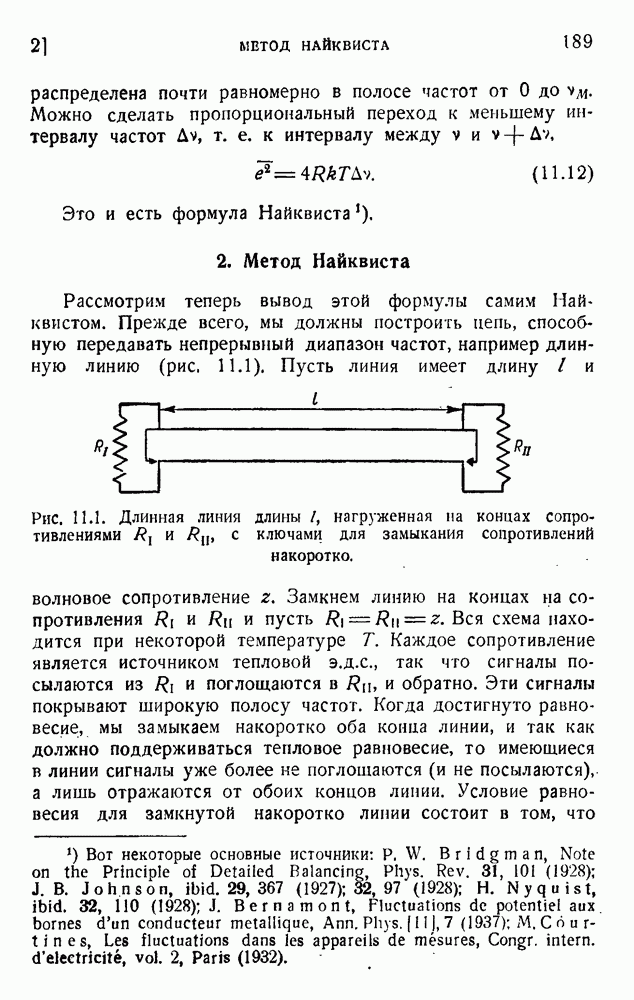
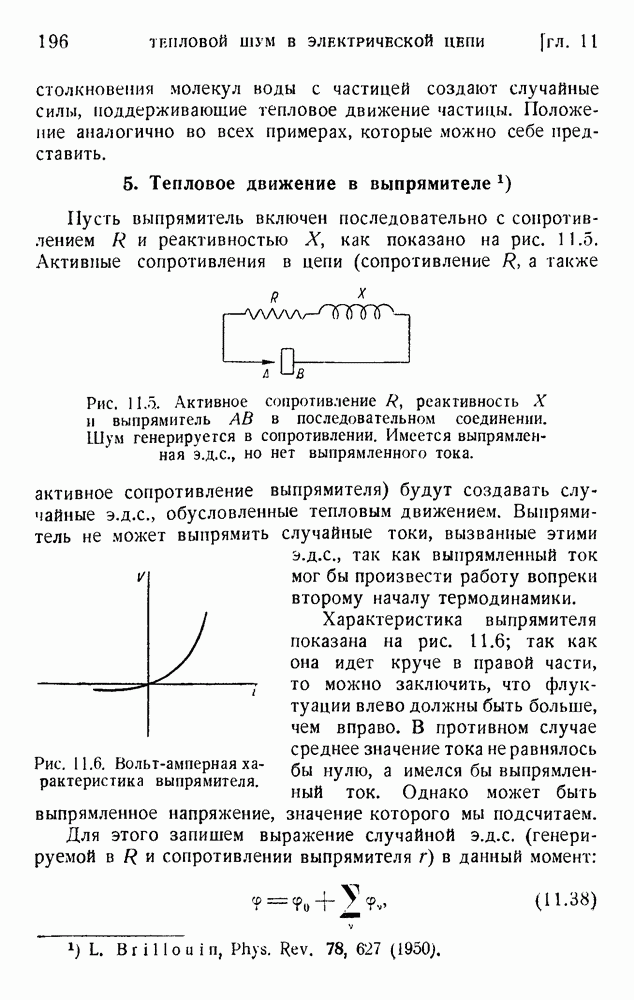
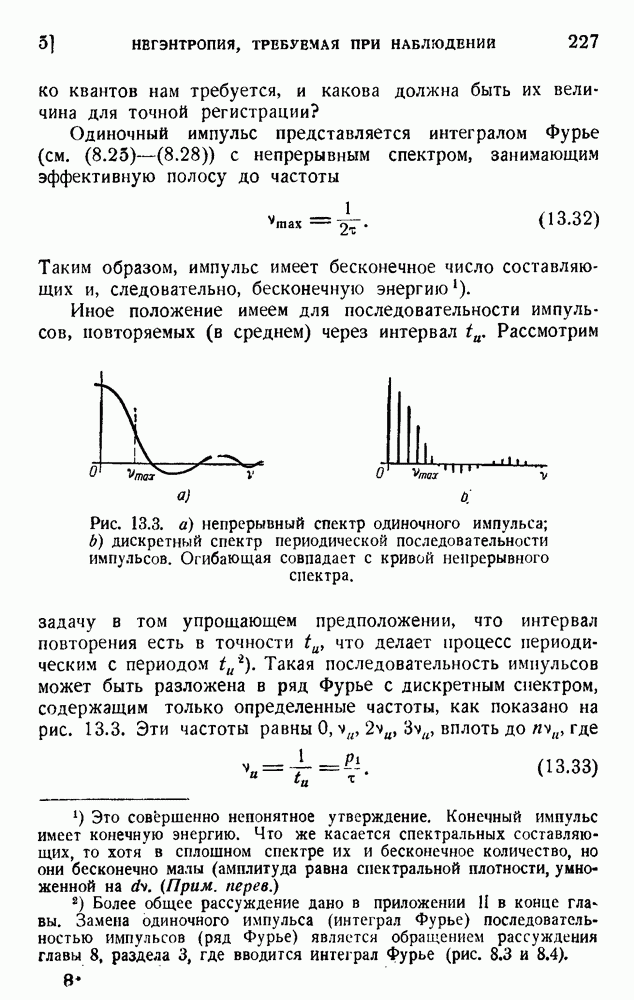
Машину можно сравнить с каналом передачи, включая кодирование и декодирование. При идеальных условиях сообщение передается правильно, и информационное содержание остается постоянным. Ошибки и приближения при вычислении ведут к потере информации. Работу машины лучше всего сравнить с работой переводчика: переводчику даны словарь и правила грамматики, что позволяет ему перевести на английский язык статью, первоначально написанную по-японски. Словарь и грамматика соответствуют программе работы. Японская статья — это входные данные, а английский перевод — выходные данные. Общая информация, имевшаяся на входе, может быть (в лучшем случае) обнаружена на выходе.
Сходным образом машине, вычисляющей, например, таблицы стрельбы, дана программа, учитывающая законы движения снаряда и атмосферные условия. Входные данные представлены начальными положением и скоростью. Выходные данные — точка попадания и конечная скорость. Входные данные логически содержат решение, но мы не в состоянии непосредственно прочесть его. Это есть кодированное сообщение, требующее декодирования, и это, в сущности, означает то же, что и перевод. Если действие машины совершенно, то она должна быть обратима: если дано попадание, то она может вычислять в обратном порядке и найти начальные условия. Аналогично переводчик может сделать перевод обратно на японский язык и получить оригинал, или его эквивалент. Идеальные условия работы соответствуют обратимости, а следовательно, сохранению информации.
Обратимость в целом может быть получена путем последовательных шагов, которые могут включать и необратимые
операции, как-то: запись данных в запоминающем устройстве с последующим прочтением их. Каждая из этих операций имеет определенную негэнтропийную цену (см. разделы 3 и 4 главы 18). Работа машины по определенной программе действительно обойдется в некоторое количество негэнтропии (энергия деградирует). Это имеет значение с технической точки зрения, но не изменяет наших заключений, и можно себе представить, что эта цена работы будет снижена в будущих лучших машинах.
Процитируем здесь очень интересное рассуждение, написанное более ста лет назад Эдгаром По. Этот автор рассматривает различные автоматы, и, в частности, вычислительную машину Бэббеджа. Нижеследующая цитата очень точно выражает нашу теперешнюю точку зрения:
«Но если эти машины остроумны, то что же мы должны думать о вычислительной машине Бэббеджа? Что мы должны думать о машине из дерева и металла, которая может не только вычислять астрономические и навигационные таблицы любой заданной протяженности, но и сделать точность своих действий математически достоверной благодаря своей способности исправлять свои возможные ошибки? Что мы должны думать о машине, которая может не только выполнять все это, но и печатать свои сложные результаты, когда они получены, без малейшего вмешательства интеллекта человека? Будет, возможно, сказано в ответ, что машина, какую мы описали, всецело выше, в сравнении с игроком в шахматы Мельцеля. Никоим образом — она всецело ниже его, если мы допустим (чего никогда не следует допускать), что игрок в шахматы есть чистая машина и выполняет свои действия без всякого непосредственного воздействия человека. Арифметические и алгебраические вычисления по своей природе фиксированы и определены. Если имеются определенные данные, то определенные результаты последуют необходимо и неизбежно. Эти результаты ничем не определяются и ничем не обусловливаются, кроме как исходными данными. И подлежащий решению вопрос продвигается к своему окончательному определению последовательными непогрешимыми шагами, не подверженными никаким изменениям. Если так, мы можем без труда представить себе возможность построения такого механизма, который после запуска его в соответствии с данными подлежащего решению вопроса продолжает свои
движения регулярно, последовательно и неуклонно в направлении требуемого решения, так как эти движения, хотя бы и сложные, никогда нельзя представить себе иначе, как конечными и определенными».
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
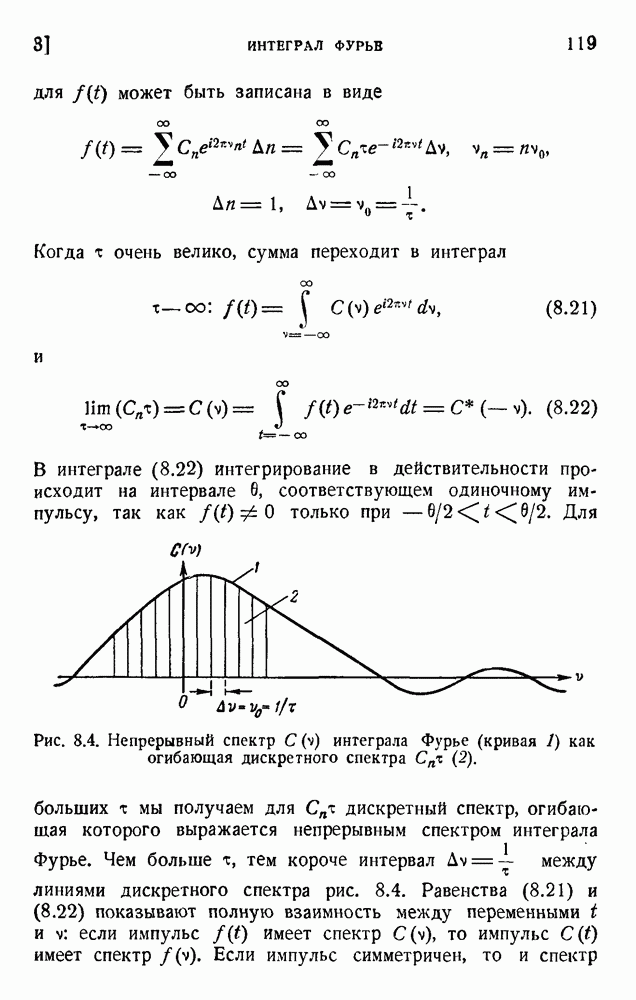
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
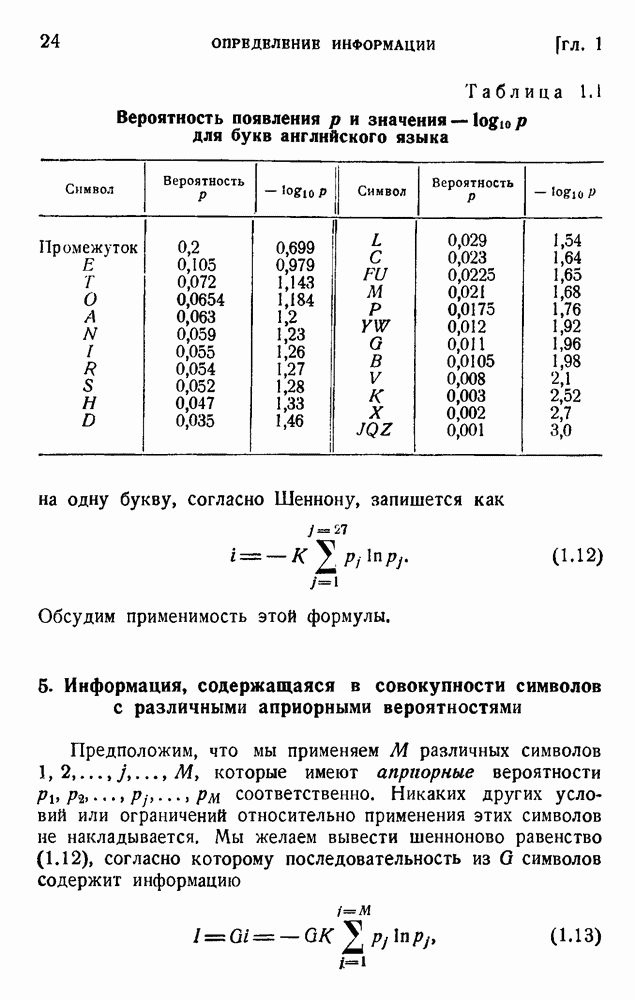
- 4. Информация и алфавит
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
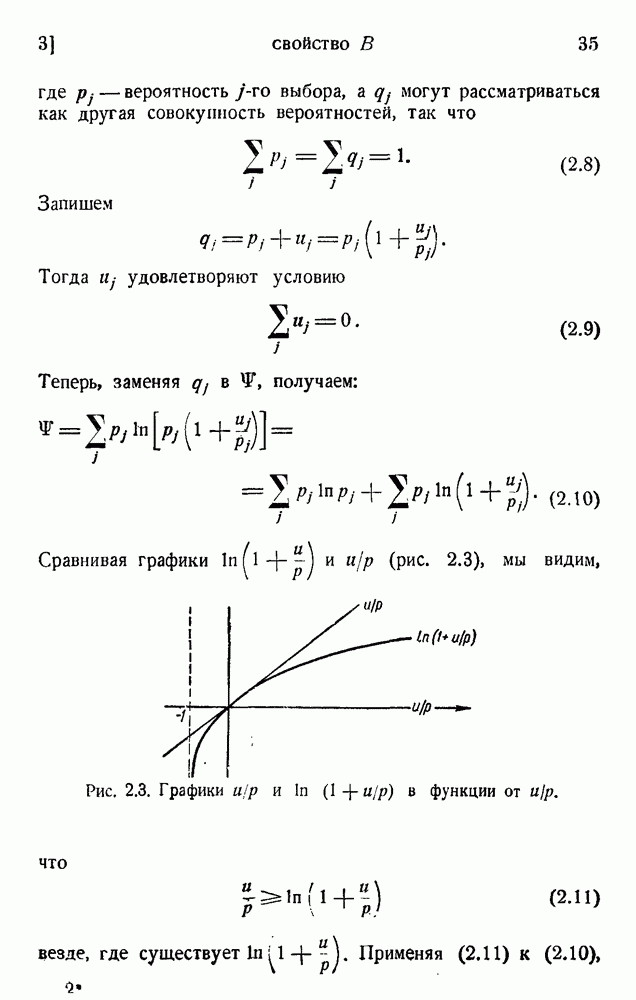
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
- 2. Корреляция в языке
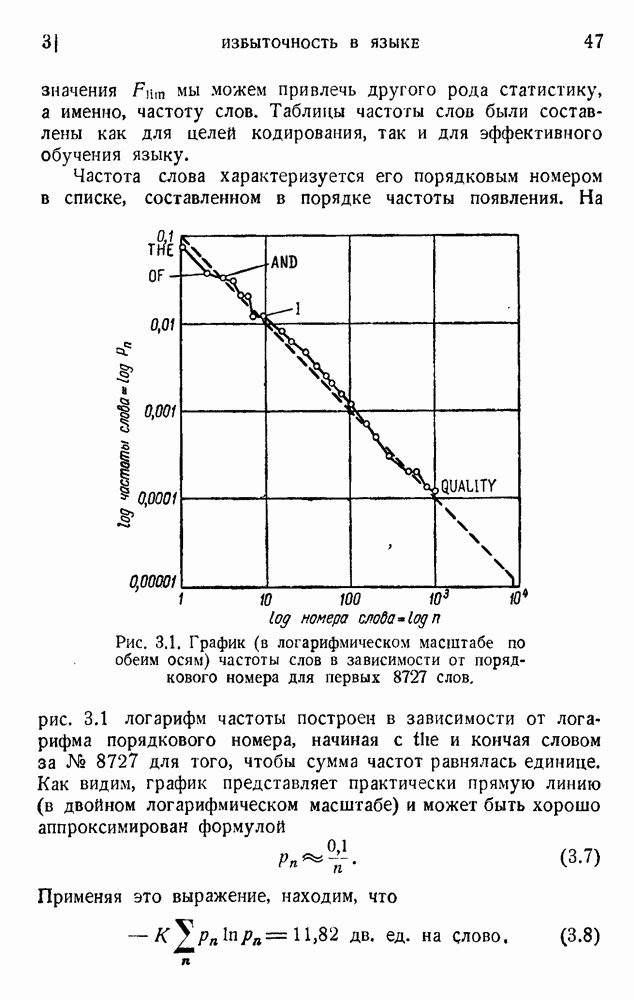
- 3. Избыточность в языке
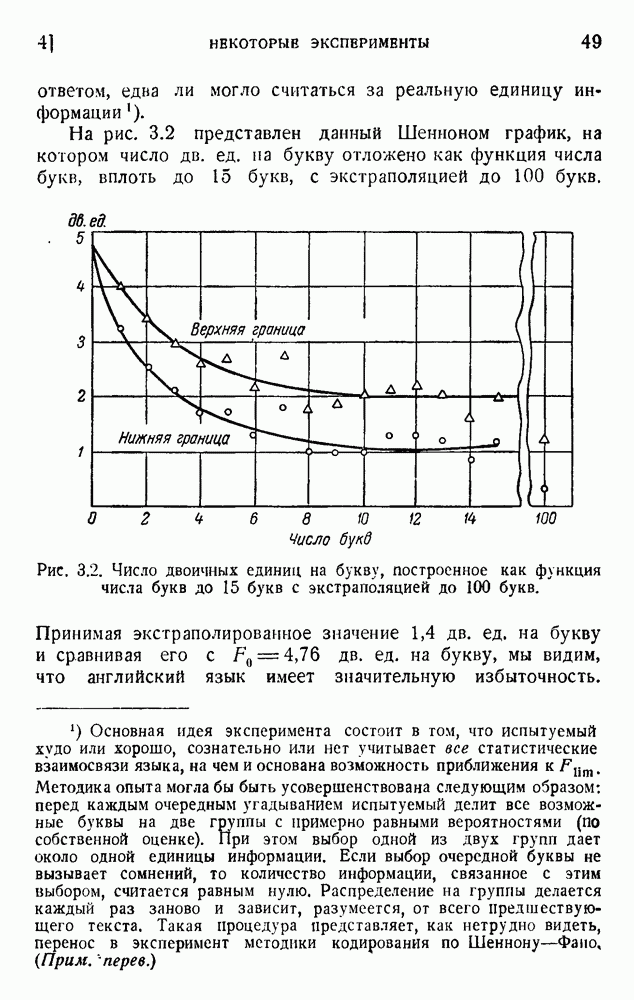
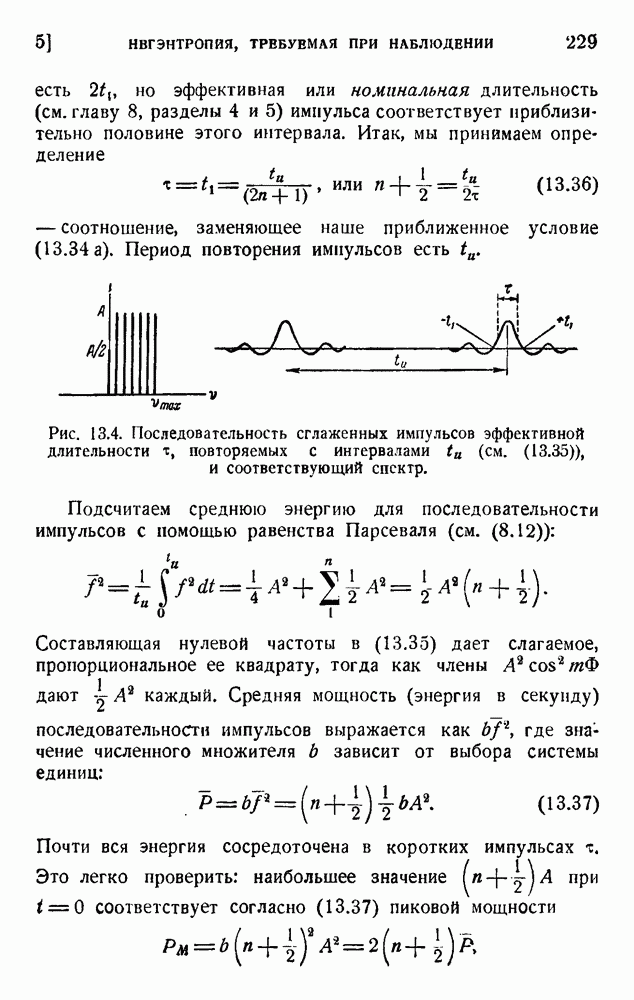
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
- 10. Проблемы статистики слов
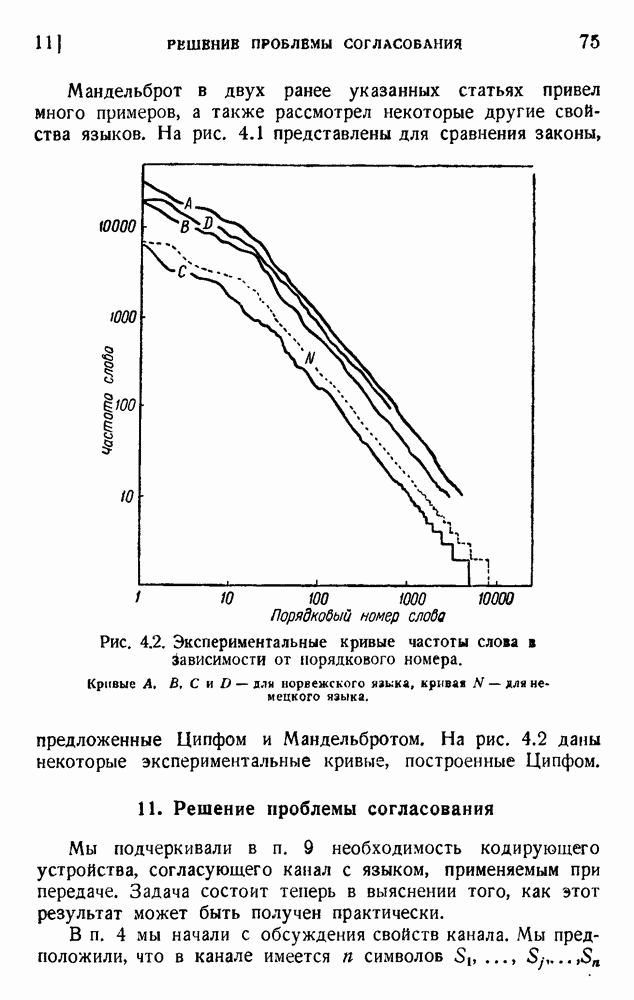
- 11. Решение проблемы согласования
- Приложение
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
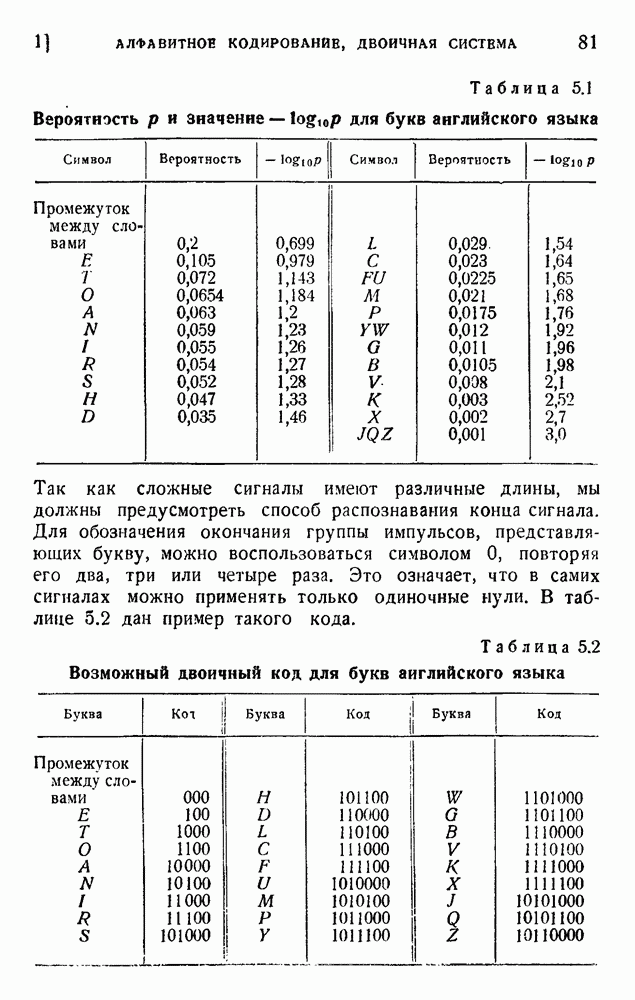
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
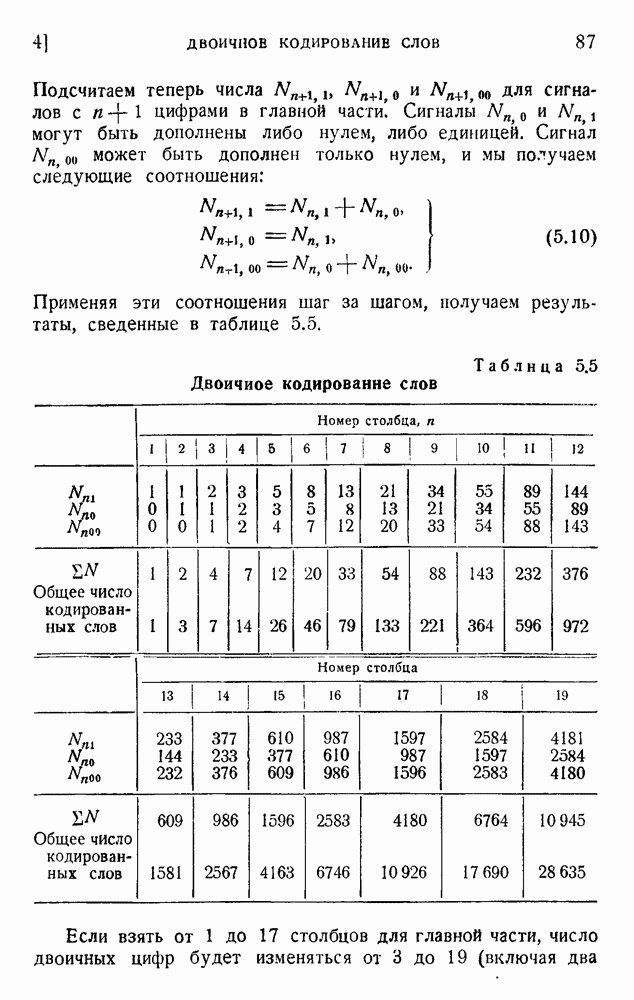
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
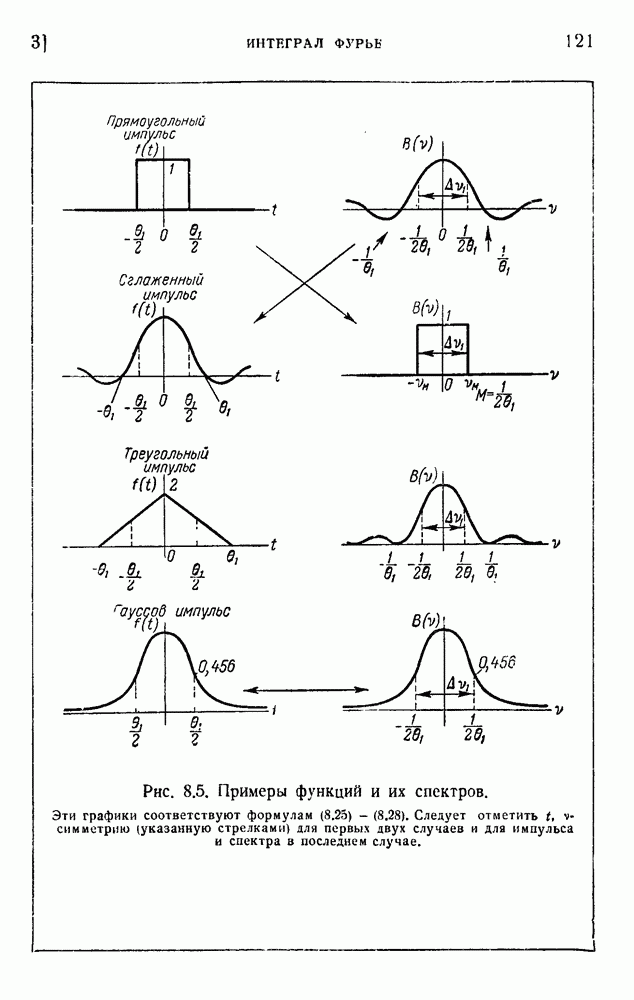
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
- 1. Ряд Фурье
- 2. Явление Гиббса и сходимость рядов Фурье
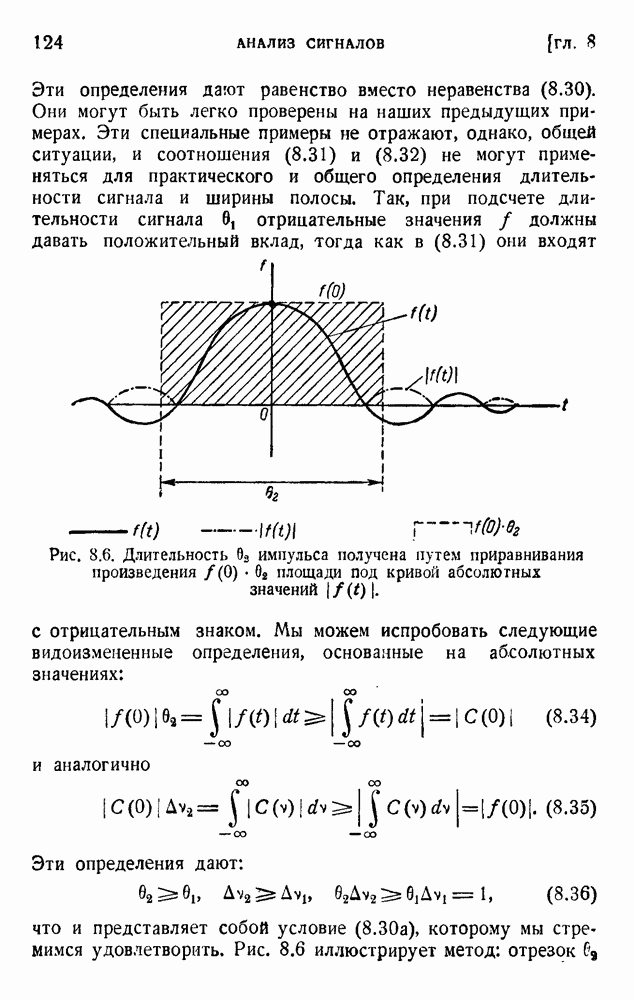
- 3. Интеграл Фурье
- 4. Роль конечной ширины полосы частот
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
- 7. Метод отсчетов Шеннона
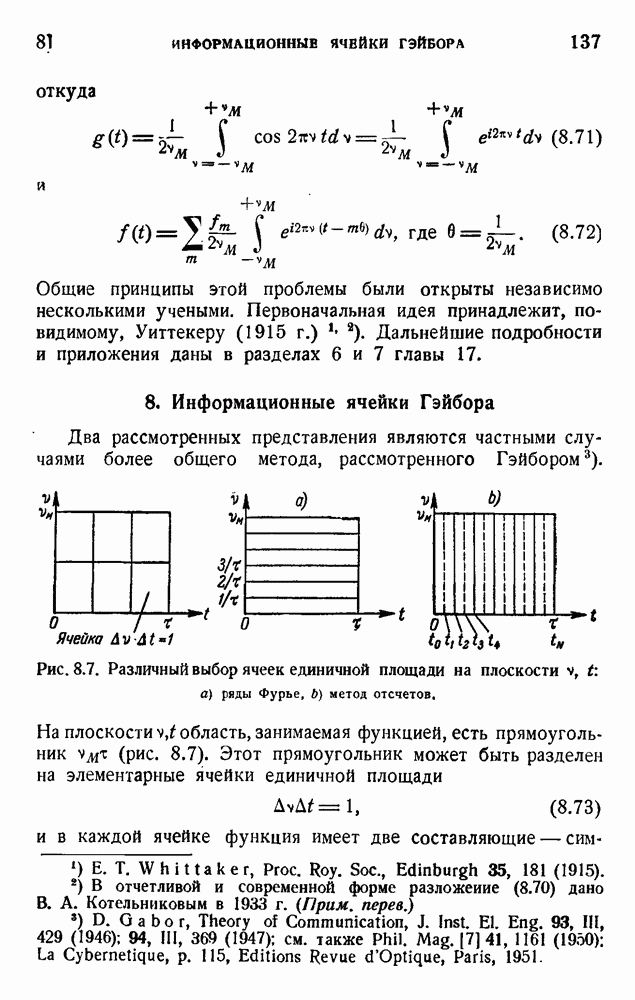
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
- 10. Линейные преобразования и фильтры
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
- 1. Тепловое движение
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
- 5. Тепловое движение в электрической цепи
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
- 5. Тепловое движение в выпрямителе
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
- 5. Негэнтропия, требуемая при наблюдении
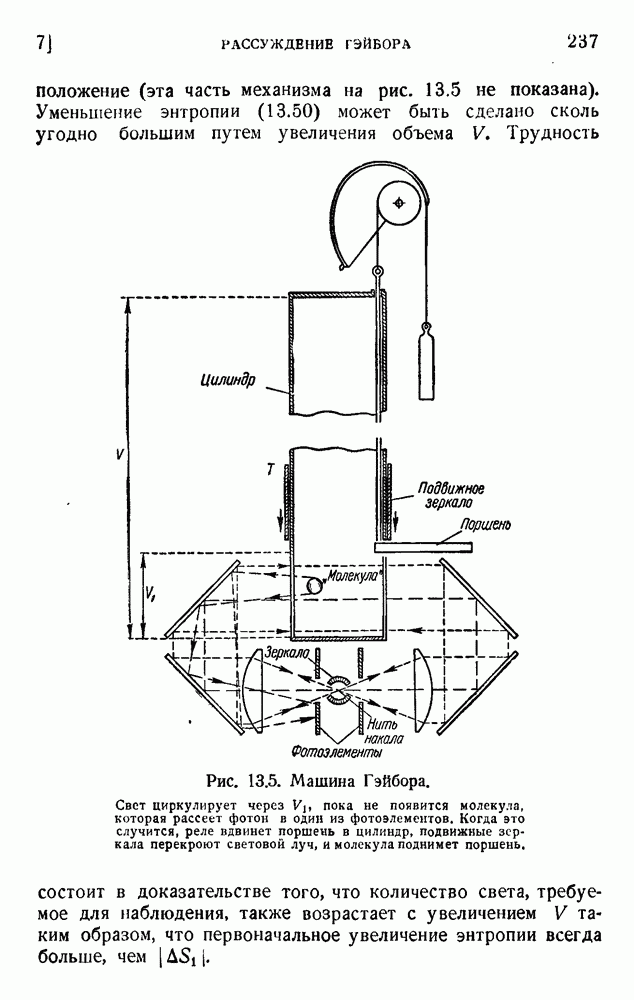
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
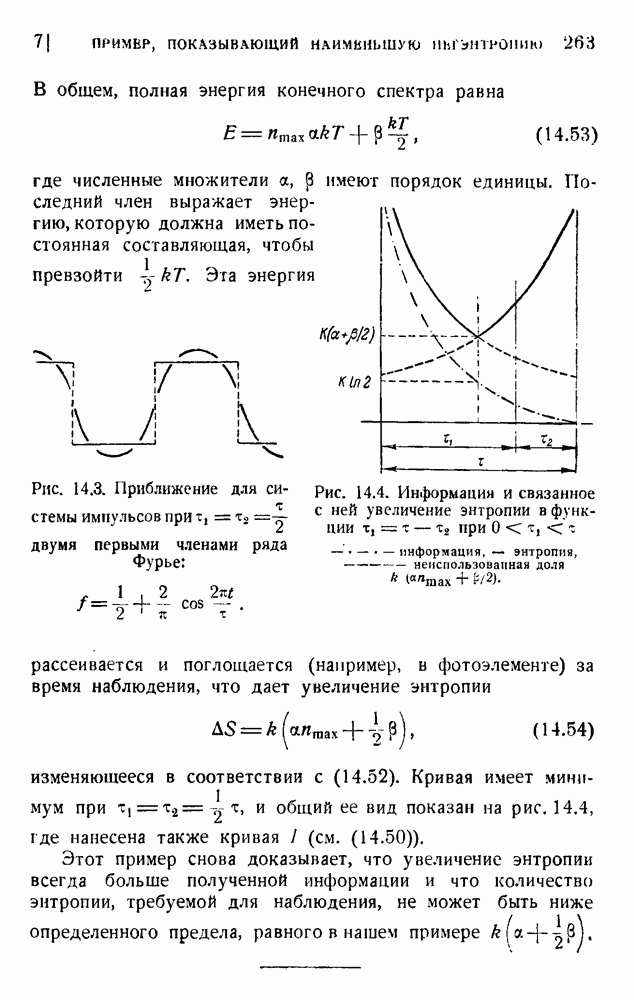
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
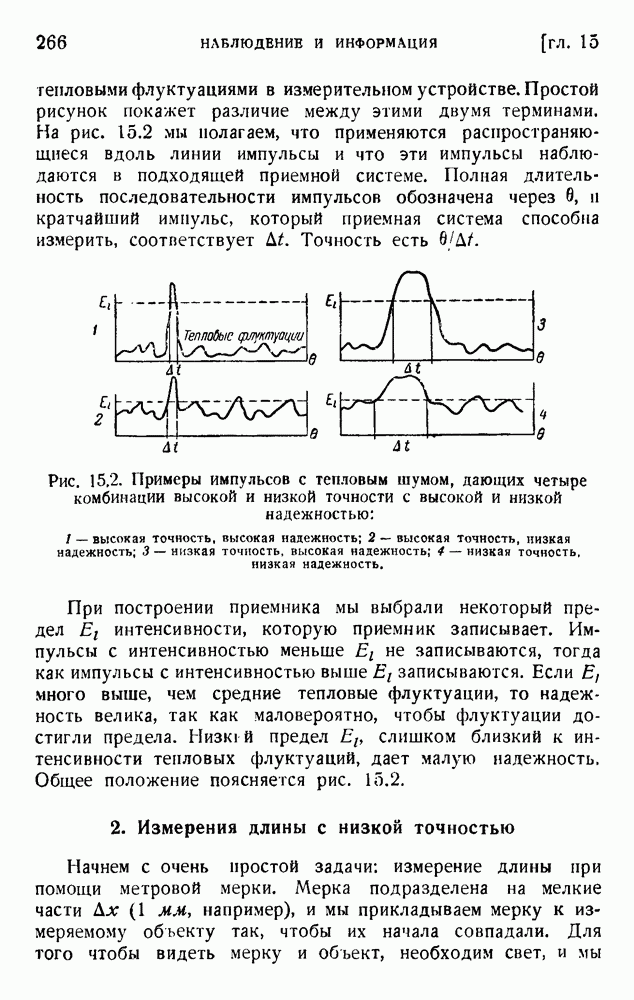
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
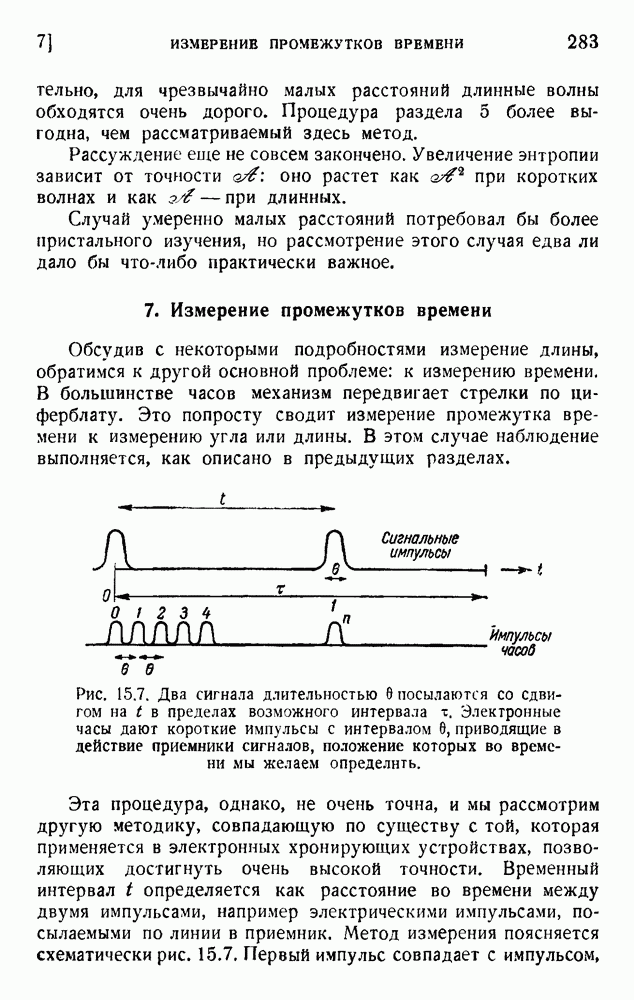
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
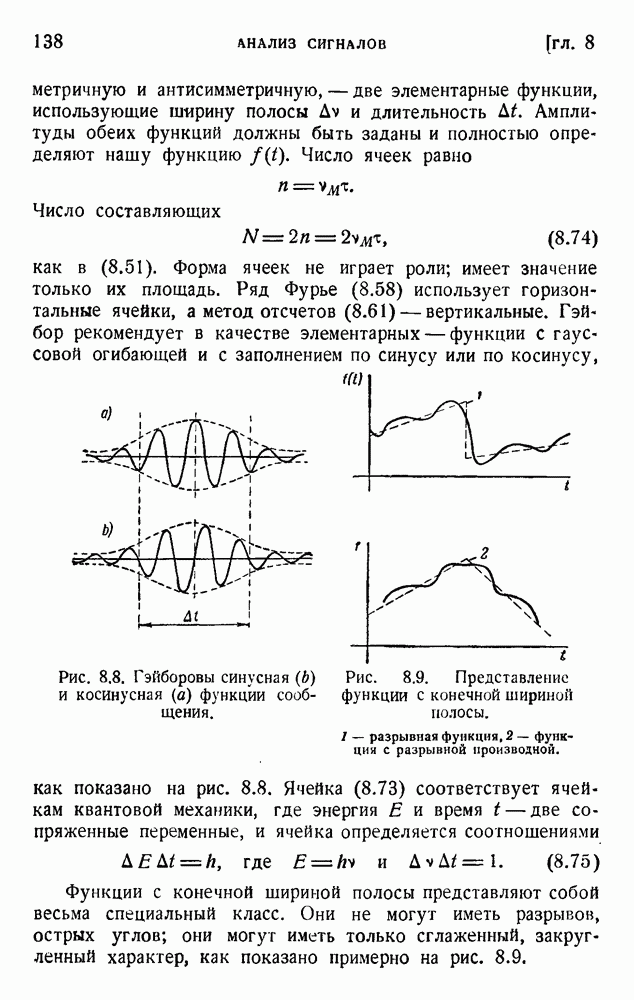
- 4. Пределы евклидовой геометрии
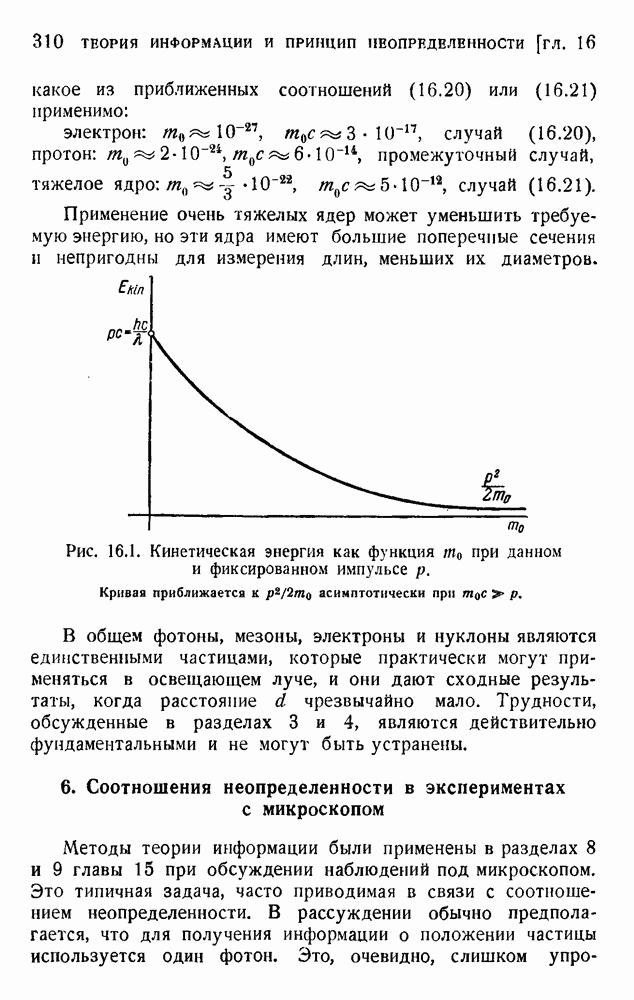
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
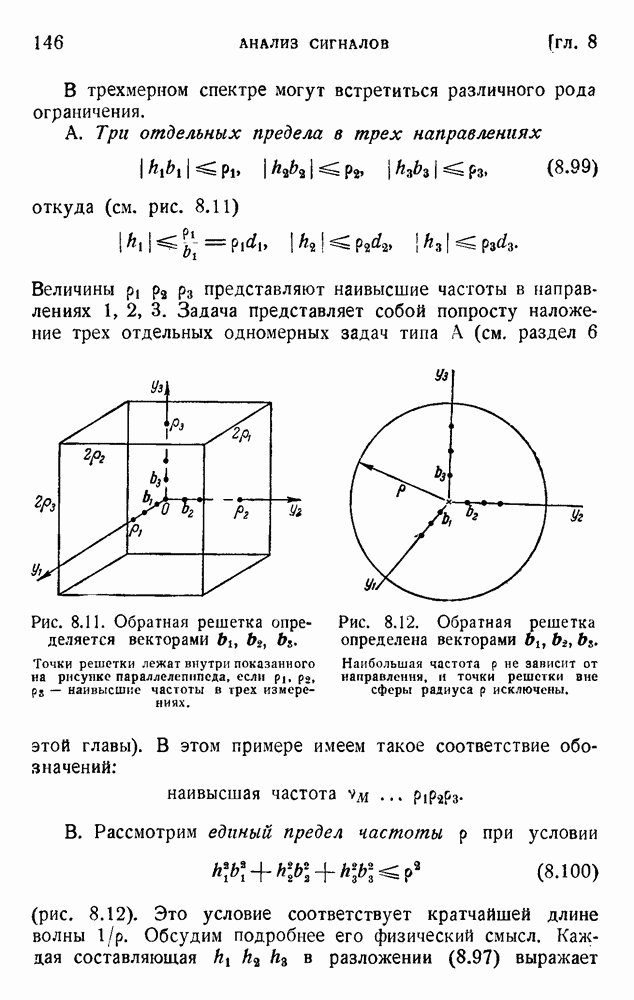
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
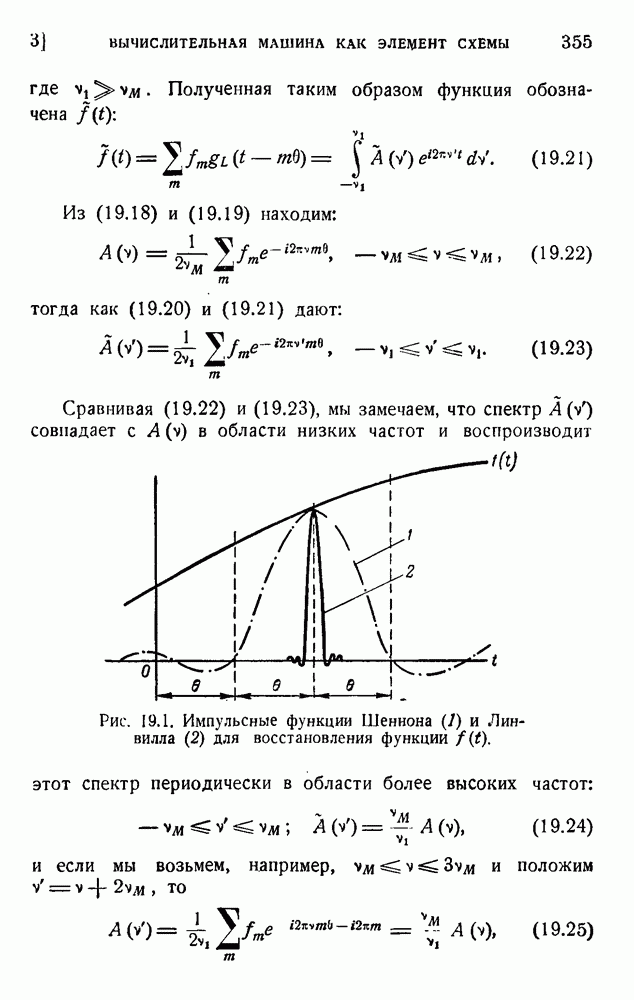
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
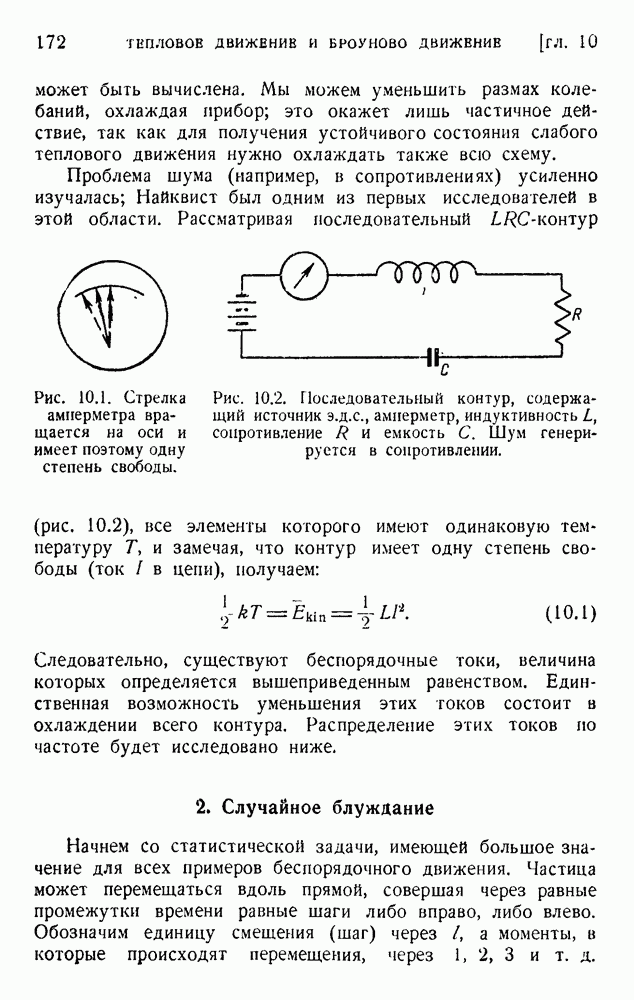
- 6. Проблемы семантической информации