| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6. Задача Силарда: полностью информированная тепловая машина
Силард опубликовал в 1929 г. очень примечательную работу, посвященную проблеме демона Максвелла, и впервые обнаружил связь между информацией и энтропией. Мы исследуем некоторые интересные вопросы, поставленные Силардом, и обсудим недавнюю работу Гэйбора, посвященную этой же проблеме.
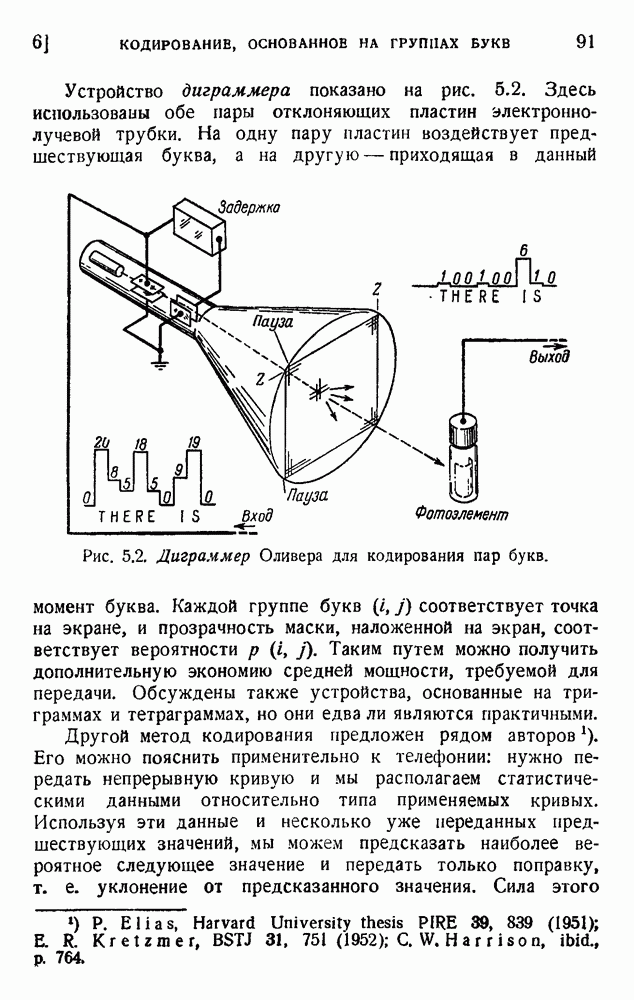
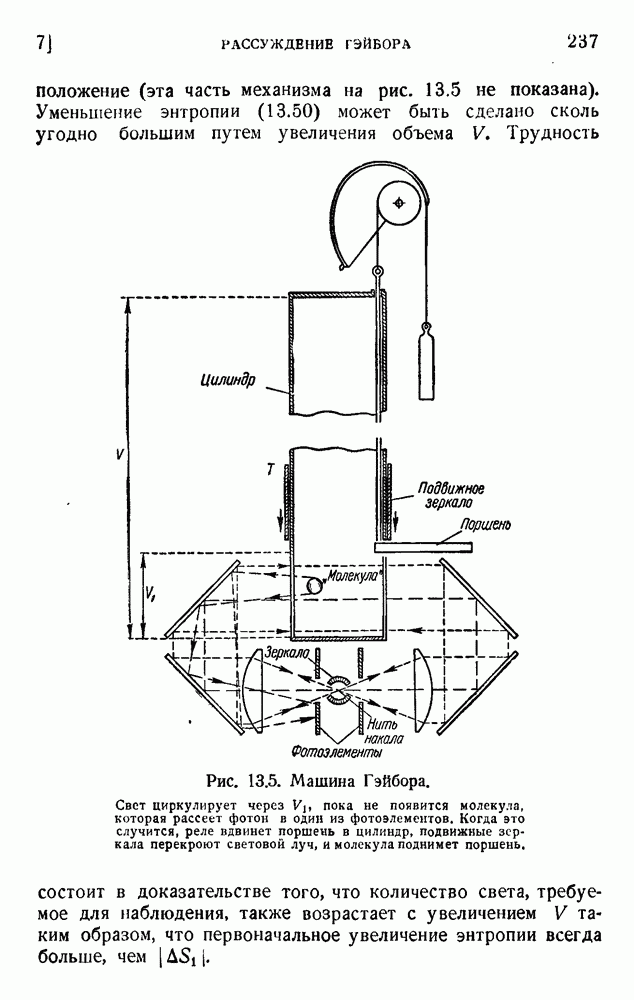
Силард рассматривает следующий случай: замкнутый цилиндр объема V может быть разделен на две части V, и путем вдвигания определенным образом расположенной заслонки. Цилиндр содержит только одну молекулу. В тот момент, когда наблюдатель вдвигает заслонку, он может так или иначе знать, находится молекула в V] или в Положим, что молекула находится в  . Тогда заслонка передвигается, как поршень, вдоль цилиндра и объем V, медленно расширяется до исходной величины V, причем вся система поддерживается термостатом при постоянной температуре Т. Молекула может удариться о поршень много раз на протяжении этой медленной операции, и результатом
. Тогда заслонка передвигается, как поршень, вдоль цилиндра и объем V, медленно расширяется до исходной величины V, причем вся система поддерживается термостатом при постоянной температуре Т. Молекула может удариться о поршень много раз на протяжении этой медленной операции, и результатом
этих соударений является среднее давление, сходное с давлением идеального газа. При этот совершается некоторая работа. Затем заслонка удаляется вбок, возвращается в исходное положение, и операция может быть повторена. Эта система дает механическую работу. Она использует только температуру, но требует информации о положении молекулы, и мы должны выяснить, как связана эта информация с изменениями энтропии. Наше точное определение информации и результаты, полученные в предыдущих примерах, позволяют нам упростить и уточнить рассуждения.
В схеме Силарда этапы следуют в таком порядке:
A. Заслонка вдвигается в некотором положении.
B. Выясняется, где находится молекула — в  или в
или в  .
.
C. В соответствии с этим поршень (заслонка) движется вверх или вниз.
Первый этап А не требует обсуждения. Что касается В, то мы должны придумать экспериментальное устройство для определения местонахождения молекулы. Мы можем использовать луч света  проходящий через
проходящий через  и другой луч
и другой луч  проходящий через
проходящий через  . Два фотоэлемента
. Два фотоэлемента  могут воспринимать рассеянный свет из К, и соответственно. Включим сперва луч
могут воспринимать рассеянный свет из К, и соответственно. Включим сперва луч  Если С, получает рассеянный свет, это означает, что молекула находится в
Если С, получает рассеянный свет, это означает, что молекула находится в  Если
Если  не обнаруживает света, то еще ничего не известно, так как молекула может не находиться в
не обнаруживает света, то еще ничего не известно, так как молекула может не находиться в  молекула может не рассеять свет, рассеянный световой квант может не попасть в
молекула может не рассеять свет, рассеянный световой квант может не попасть в  . Затем мы повторим опыт рассеяния со вторым лучом
. Затем мы повторим опыт рассеяния со вторым лучом  в
в  . В конце концов квант
. В конце концов квант  рассеивается либо от
рассеивается либо от  либо от и мы определяем местоположение молекулы. Поглощение кванта
либо от и мы определяем местоположение молекулы. Поглощение кванта  в одном из фотоэлементов соответствует увеличению энтропии на
в одном из фотоэлементов соответствует увеличению энтропии на
 (13.45)
(13.45)
в соответствии с предыдущим рассуждением (см. (13.7)). Более подробное исследование (см. (14.17)) несколько понижает предел и дает:

Подсчитаем теперь полученную информацию. Вероятность  застать молекулу в
застать молекулу в  равна, очевидно,
равна, очевидно,  а вероятность
а вероятность
того, что молекула находится в  равна
равна  :
:

Рассмотрим эти два случая порознь. С помощью формул (1.5) и (1.6) можно подсчитать:

и средняя информация на одну операцию равна

что соответствует формуле Шеннона (см. (2.1)). Каждая отдельная операция может дать информацию больше или меньше увеличения энтропии  , потребовавшегося для получения этой информации, но средняя информация (13.46а) меньше, чем среднее увеличение энтропии на одну операцию:
, потребовавшегося для получения этой информации, но средняя информация (13.46а) меньше, чем среднее увеличение энтропии на одну операцию:

Знак равенства получается при равенстве объемов  и V:
и V:

что соответствует наибольшей средней информации. Мы можем иметь флуктуации информации, полученной при отдельных операциях. Однако в длинной серии испытаний средняя информация меньше, чем уплаченная за нее цена, выраженная через негэнтропию  . Обобщенный принпип Карно (глава 13) удовлетворяется в среднем с положительными и отрицательными флуктуациями
. Обобщенный принпип Карно (глава 13) удовлетворяется в среднем с положительными и отрицательными флуктуациями

Рассмотрим теперь изменение энтропии газа и последний этап С действия машины, Энтропия идеального газа равна
(см. (12.12)):

Когда заслонка вдвигается, мы получаем некоторое уменьшение энтропии:

Вероятности, соответствующие этим двум возможностям, равны  и
и  . Заметим, что уменьшение энтропии
. Заметим, что уменьшение энтропии  или
или  всегда в точности равно получаемой в данном случае информации
всегда в точности равно получаемой в данном случае информации  или
или  , так как (13.46) и (13.48) совпадают, за исключением знака. Средняя энтропия газа убывает за одну операцию на
, так как (13.46) и (13.48) совпадают, за исключением знака. Средняя энтропия газа убывает за одну операцию на

Когда мы двигаем поршень и увеличиваем объем до его первоначальной величины V, мы восстанавливаем исходное значение энтропии. Совершенная работа W равна теплу Q, полученному из резервуара тепла (в предположении медленного обратимого процесса); применяя закон Бойля к одной молекуле, для случая 1 (молекула находится в  ) имеем:
) имеем:

Увеличение энтропии на протяжении процесса расширения составляет:

аналогично обстоит дело, когда молекула находится в  .
.
Последняя операция подтверждает справедливость равенств (13.48) и показывает, каким образом получается первоначальное уменьшение энтропии. В общем, за полный цикл
действия получается (см. (13.47)) возрастание энтропии на  .
.
Таким образом, мы показали на этом примере, что информация соответствует негэнтропии (см. (13.47) и (13.49)), но мы должны были учитывать флуктуации, так как предполагалось, что заслонка вначале вдвигается без предварительного знания местонахождения молекулы.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- ВВЕДЕНИЕ
- ГЛАВА 1. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИИ
- 1. Определение информации
- 2. Системы единиц
- 3. Обобщение и примеры
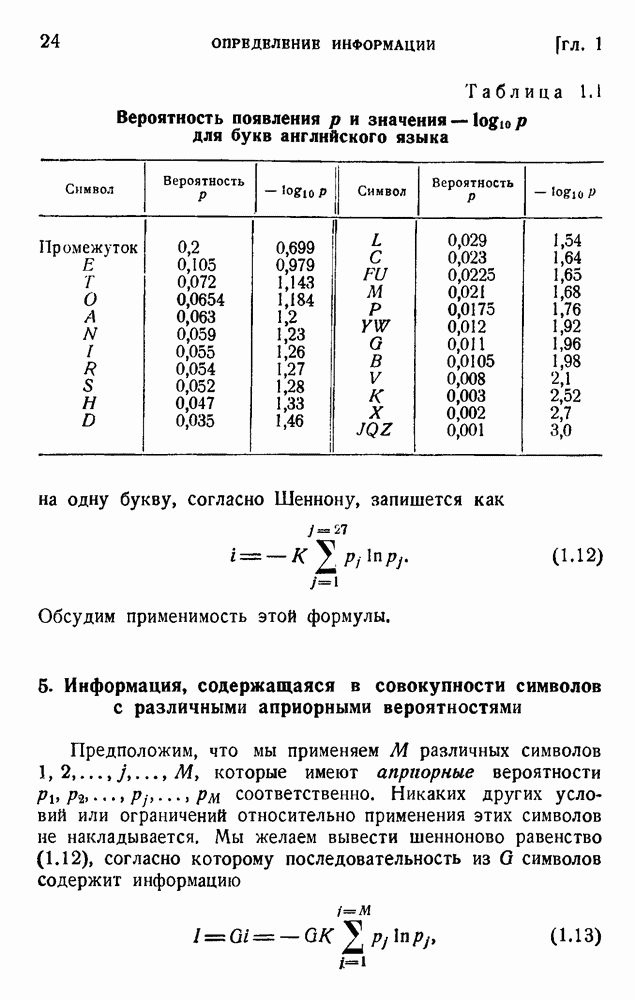
- 4. Информация и алфавит
- 5. Информация, содержащаяся в совокупности символов с различными априорными вероятностями
- 6. Общие замечания
- ГЛАВА 2. ПРИМЕНЕНИЕ ОПРЕДЕЛЕНИЙ И ОБЩЕЕ ОБСУЖДЕНИЕ
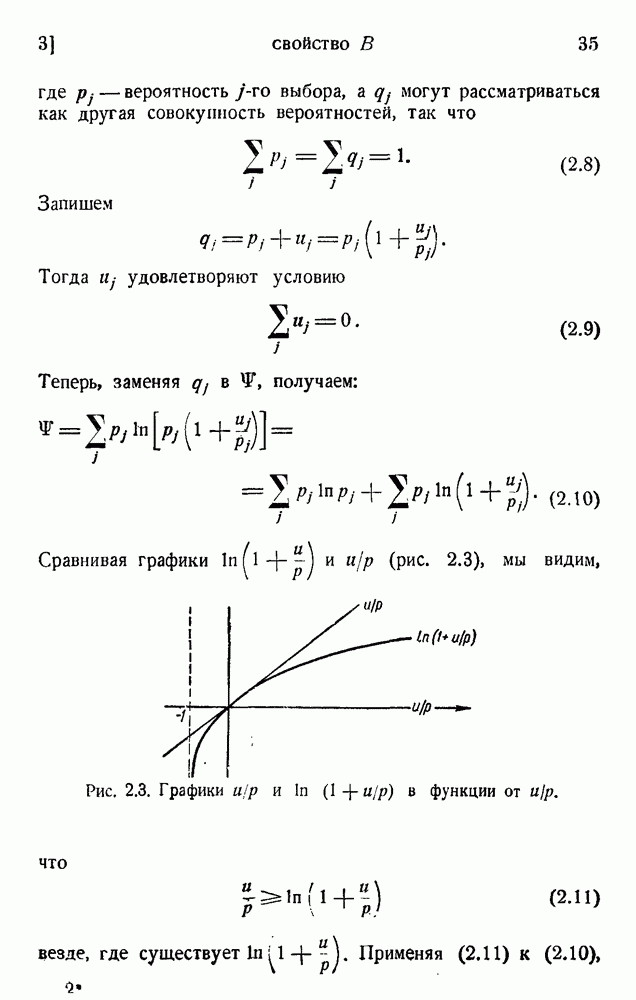
- 3. Свойство В
- 4. Свойство С
- 5. Зависимые события
- 6. Условная информация
- ГЛАВА 3. ИЗБЫТОЧНОСТЬ В ЯЗЫКЕ
- 1. Корреляция и зависимые события
- 2. Корреляция в языке
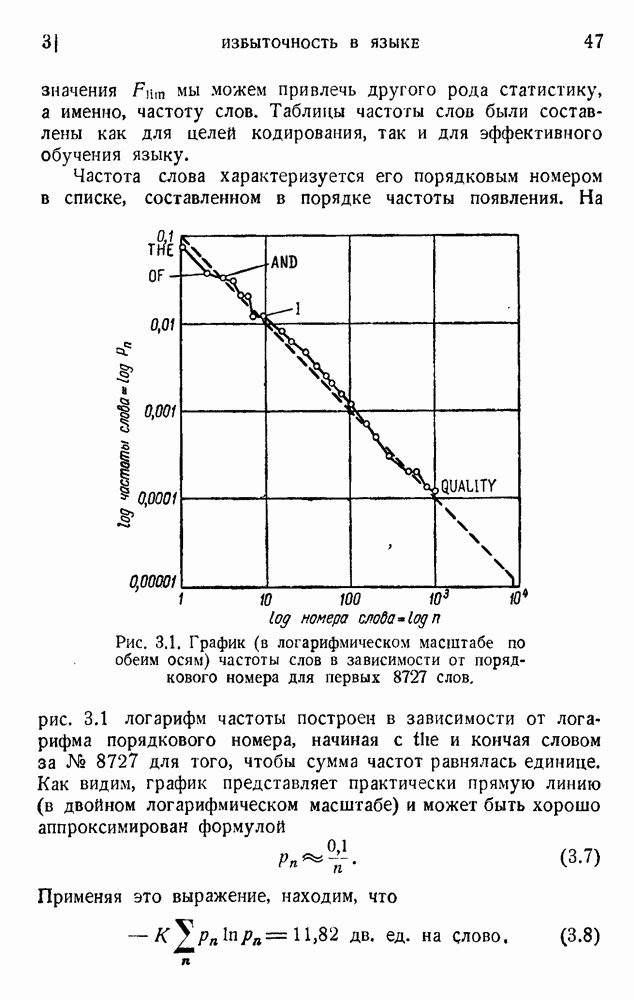
- 3. Избыточность в языке
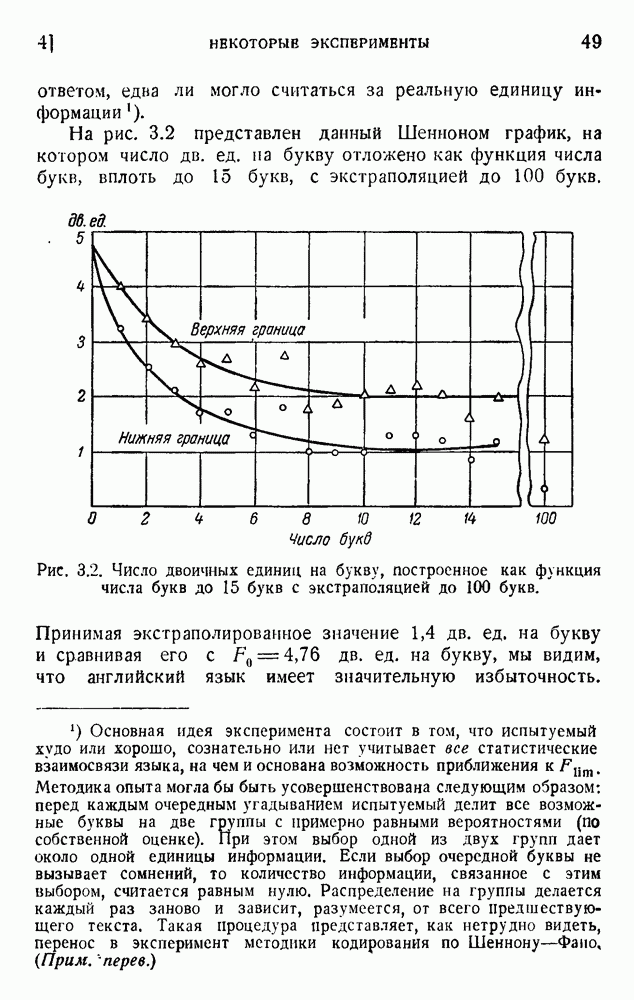
- 4. Некоторые эксперименты
- 5. Кодирующие устройства
- ГЛАВА 4. ПРИНЦИПЫ КОДИРОВАНИЯ; ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- 2. Определение канала и его пропускной способности
- 3. Символы, слова и сообщения при кодировании последовательностей
- 4. Обсуждение
- 5. Примеры
- 6. Вычисление пропускной способности канала
- 7. Согласование кода с каналом
- 8. Общая задача: символы различной длины
- 9. Проблема согласования
- 10. Проблемы статистики слов
- 11. Решение проблемы согласования
- Приложение
- ГЛАВА 5. ПРОБЛЕМЫ КОДИРОВАНИЯ
- 1. Алфавитное кодирование, двоичная система
- 2. Алфавитное кодирование, троичная система
- 3. Алфавит и числа
- 4. Двоичное кодирование слов
- 5. Алфавитное кодирование слов
- 6. Кодирование, основанное на группах букв и на корреляции
- ГЛАВА 6. КОДЫ, ОБНАРУЖИВАЮЩИЕ И ИСПРАВЛЯЮЩИЕ ОШИБКИ
- 1. Коды, обнаруживающие ошибки
- 2. Коды, исправляющие одиночную ошибку
- 3. Коды, исправляющие одиночную ошибку и обнаруживающие двойную
- 4. Эффективность исправляющих кодов
- 5. Пропускная способность двоичного канала с шумом
- ГЛАВА 7. ПРИЛОЖЕНИЯ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ПРОБЛЕМАМ
- 1. Задача о расположении с применением смешанной ячейки
- 2. Расположение с перекрестными ссылками
- 3. Наивыгоднейшее число элементов на одну элементарную ячейку
- ГЛАВА 8. АНАЛИЗ СИГНАЛОВ: МЕТОД ФУРЬЕ И ПРОЦЕДУРЫ ОТСЧЕТОВ
- 1. Ряд Фурье
- 2. Явление Гиббса и сходимость рядов Фурье
- 3. Интеграл Фурье
- 4. Роль конечной ширины полосы частот
- 5. Соотношение неопределенности для времени и частоты
- 6. Степени свободы сообщения
- 7. Метод отсчетов Шеннона
- 8. Информационные ячейки Гэйбора
- 9. Автокорреляция и спектр; формула Винера — Хинчина
- 10. Линейные преобразования и фильтры
- 11. Анализ Фурье и метод отсчетов в трех измерениях
- 12. Исследование кристаллов рентгеновыми лучами
- Приложение. Неравенство Шварца
- ГЛАВА 9. ОСНОВЫ ТЕРМОДИНАМИКИ
- 2. Два начала термодинамики; энтропия и негэнтропия
- 3. Невозможность вечного движения; тепловые машины
- 4. Статистическое толкование энтропии
- 5. Примеры статистических рассуждений
- 6. Флуктуации энергии; формула Гиббса
- 7. Квантованный осциллятор
- 8. Флуктуации
- ГЛАВА 10. ТЕПЛОВОЕ ДВИЖЕНИЕ И БРОУНОВО ДВИЖЕНИЕ
- 1. Тепловое движение
- 2. Случайное блуждание
- 3. Дробовой эффект
- 4. Броуново движение
- 5. Тепловое движение в электрической цепи
- ГЛАВА II. ТЕПЛОВОЙ ШУМ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ; ФОРМУЛА НАЙКВИСТА
- 1. Модель со случайными импульсами
- 2. Метод Найквиста
- 3. Обсуждение и приложения
- 4. Обобщения формулы Найквиста
- 5. Тепловое движение в выпрямителе
- ГЛАВА 12. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Связь между информацией и энтропией
- 2. Негэнтропийный принцип информации; обобщение принципа Карно
- 3. Несколько типичных физических примеров
- 4. Несколько общих замечаний
- ГЛАВА 13. ДЕМОН МАКСВЕЛЛА И НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ
- 1. Демон Максвелла; исторический обзор
- 2. Изгнание демона
- 3. Обсуждение
- 4. Действие демона как преобразование информации в негэнтропию
- 5. Негэнтропия, требуемая при наблюдении
- 6. Задача Силарда: полностью информированная тепловая машина
- 7. Рассуждение Гэйбора
- Приложение I
- Приложение II
- ГЛАВА 14. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ОБЩЕЙ ФИЗИКЕ
- 1. Проблема измерения в физике
- 2. Наблюдения над осциллятором
- 4. Эксперименты, требующие многих одновременных наблюдений при низких частотах
- 5. Проблемы, требующие высокой надежности
- 6. Более подробное обсуждение экспериментов с высокими частотами
- 7. Пример, показывающий наименьшую негэнтропию, необходимую для наблюдения
- ГЛАВА 15. НАБЛЮДЕНИЕ И ИНФОРМАЦИЯ
- 1. Экспериментальные ошибки и информация
- 2. Измерения длины с низкой точностью
- 3. Измерения длины с высокой точностью
- 4. Эффективность наблюдения
- 5. Измерение расстояния с помощью интерферометра
- 6. Другая схема для измерения расстояния
- 7. Измерение промежутков времени
- 8. Наблюдения под микроскопом
- 9. Рассуждение о фокусе в волноводе
- 10. Примеры и обсуждение
- 11. Заключение
- ГЛАВА 16. ТЕОРИЯ ИНФОРМАЦИИ, ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ И ФИЗИЧЕСКИЕ ПРЕДЕЛЫ НАБЛЮДАЕМОСТИ
- 2. Наблюдение есть необратимый процесс
- 3. Общие ограничения точности физических измерений
- 4. Пределы евклидовой геометрии
- 5. Возможность использования тяжелых частиц вместо фотонов
- 6. Соотношения неопределенности в экспериментах с микроскопом
- 7. Измерение импульса
- 8. Неопределенность в измерении поля
- ГЛАВА 17. НЕГЭНТРОПИЙНЫЙ ПРИНЦИП ИНФОРМАЦИИ В ПРИМЕНЕНИИ К СВЯЗИ
- 1. Анализ сигналов с конечной шириной полосы
- 2. Сигналы и тепловой шум: представление в многомерном пространстве
- 3. Пропускная способность канала с шумом
- 4. Обсуждение формулы Таллера — Шеннона
- 5. Практический пример
- 6. Негэнтропийный принцип в применении к каналу с шумом
- 7. Видоизмененная формула Гэйбора и роль биений
- ГЛАВА 18. ПИСЬМО, ПЕЧАТЬ И ЧТЕНИЕ
- 1. Передача информации; живая информация
- 2. Проблема чтения и письма
- 3. Мертвая информация и как ее оживить
- 4. Письмо и печать
- 5. Обсуждение специального примера
- 6. Новая информация и избыточность
- ГЛАВА 19. ПРОБЛЕМА ВЫЧИСЛЕНИЯ
- 2. Вычислительная машина как математический элемент
- 3. Вычислительная машина как элемент схемы; отсчитывание и восстановление
- 4. Вычисление по отсчетам в момент t
- 5. Коэффициент передачи вычислительной машины
- 6. Схемы, содержащие вычислительную машину; проблема устойчивости
- 7. Обсуждение устойчивости программы
- 8. Несколько примеров
- ГЛАВА 20. ИНФОРМАЦИЯ, ОРГАНИЗАЦИЯ И ДРУГИЕ ПРОБЛЕМЫ
- 1. Информация и организация
- 2. Информация, содержащаяся в физическом законе
- 3. Информация, содержащаяся в числовой таблице
- 4. Общие замечания
- 5. Примеры проблем, выходящих за рамки данной теории
- 6. Проблемы семантической информации