| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.1.7. Описание «благоприятных» оценочных ситуаций; доверительные области
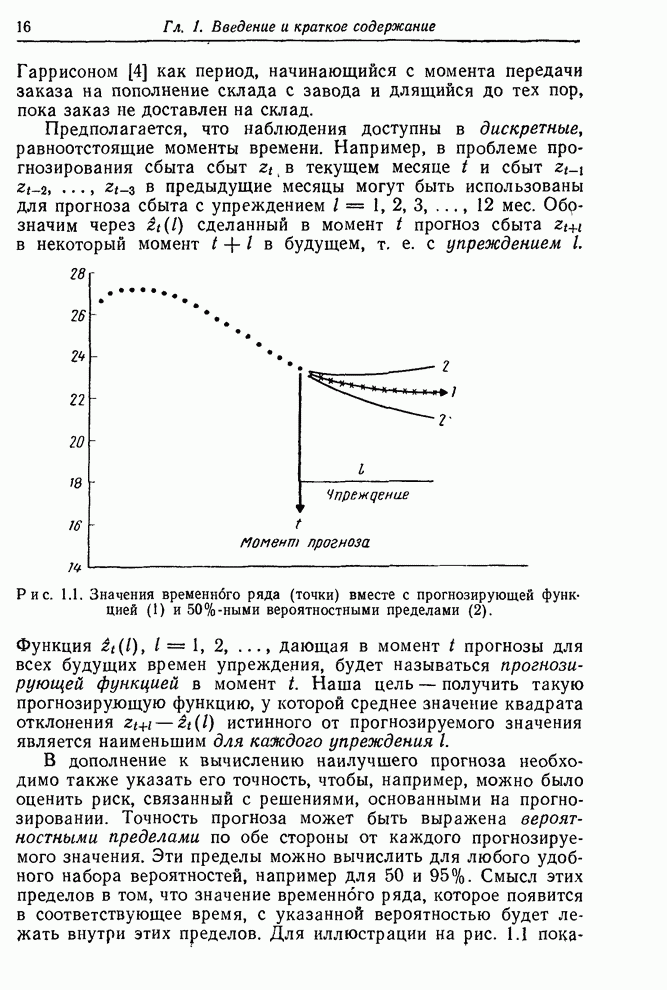
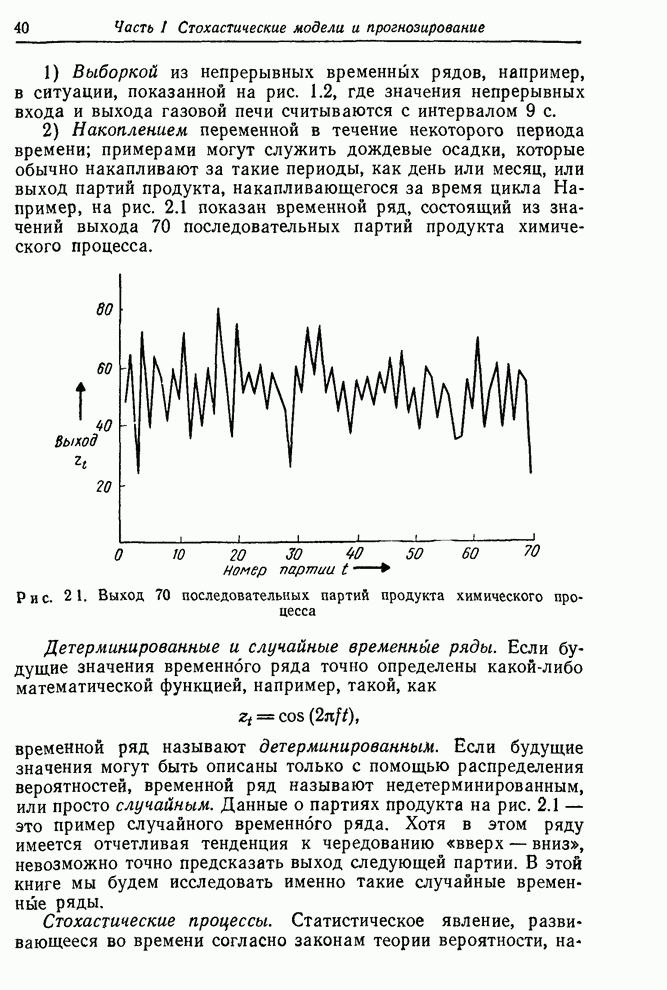
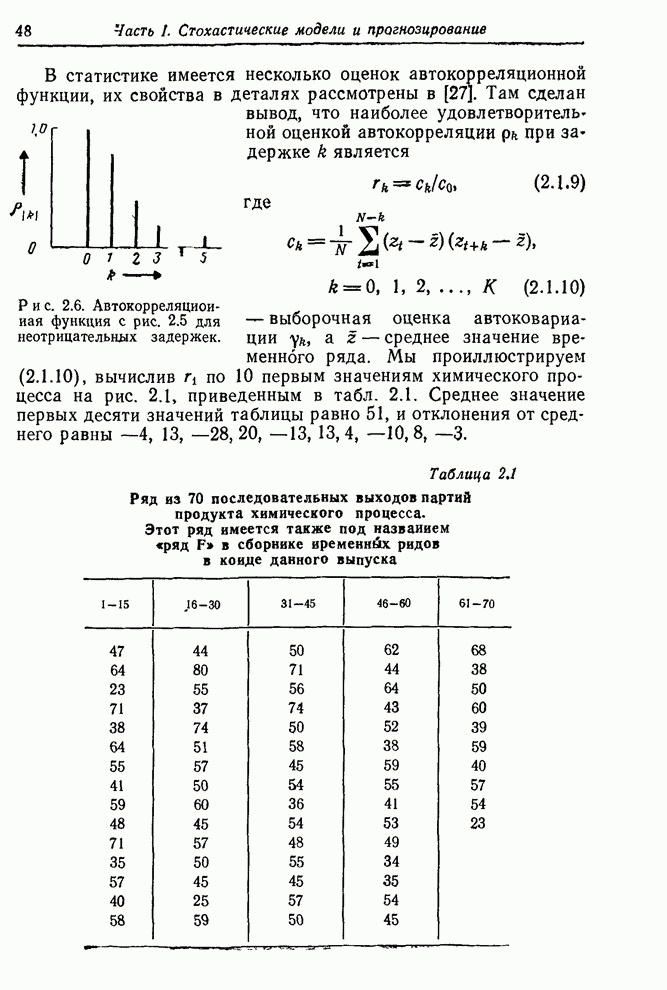
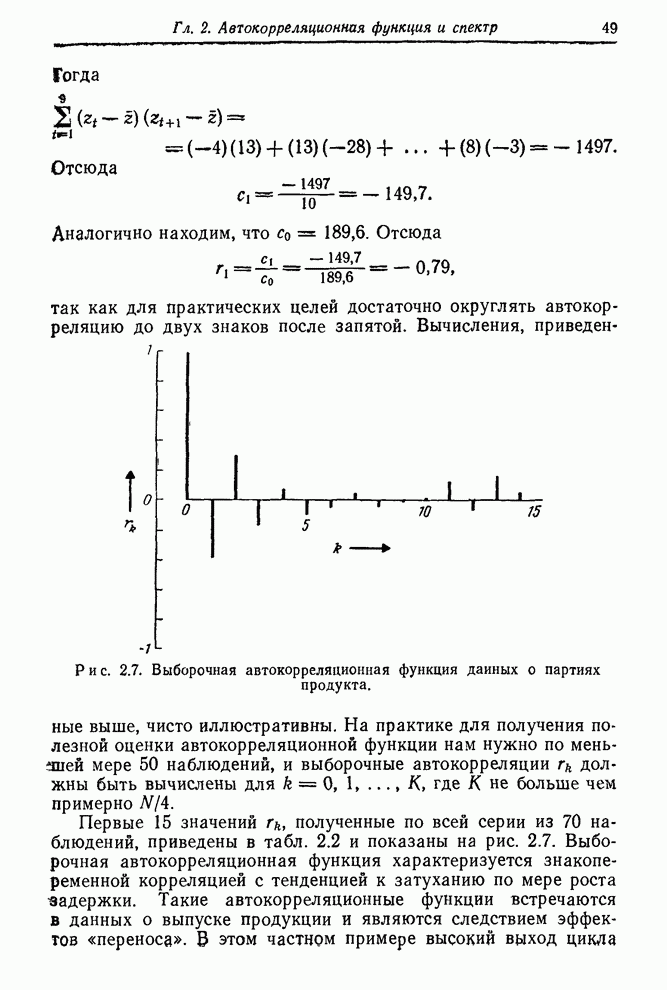
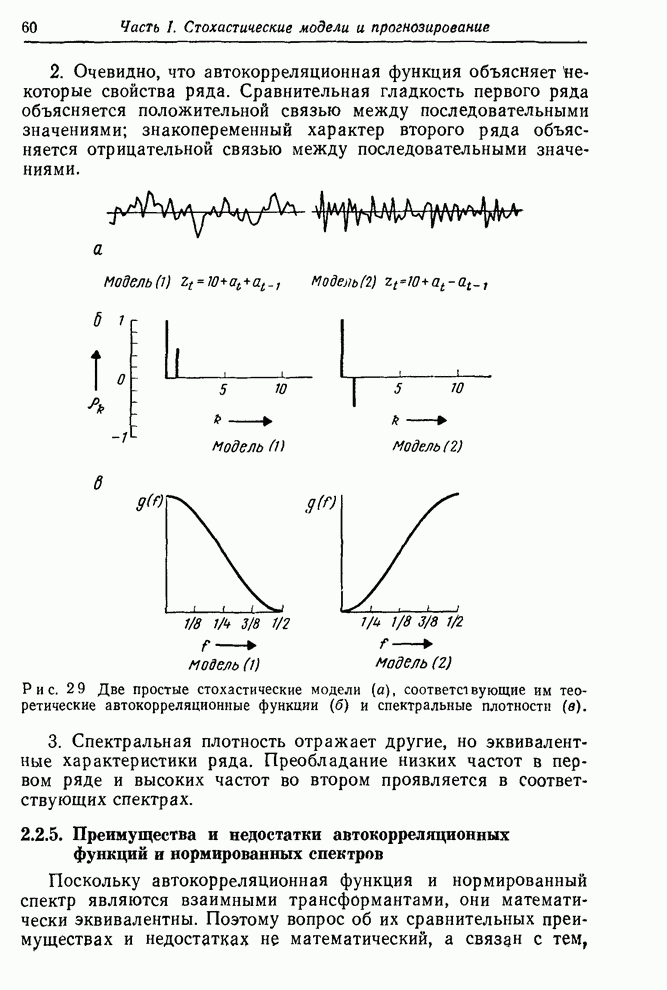
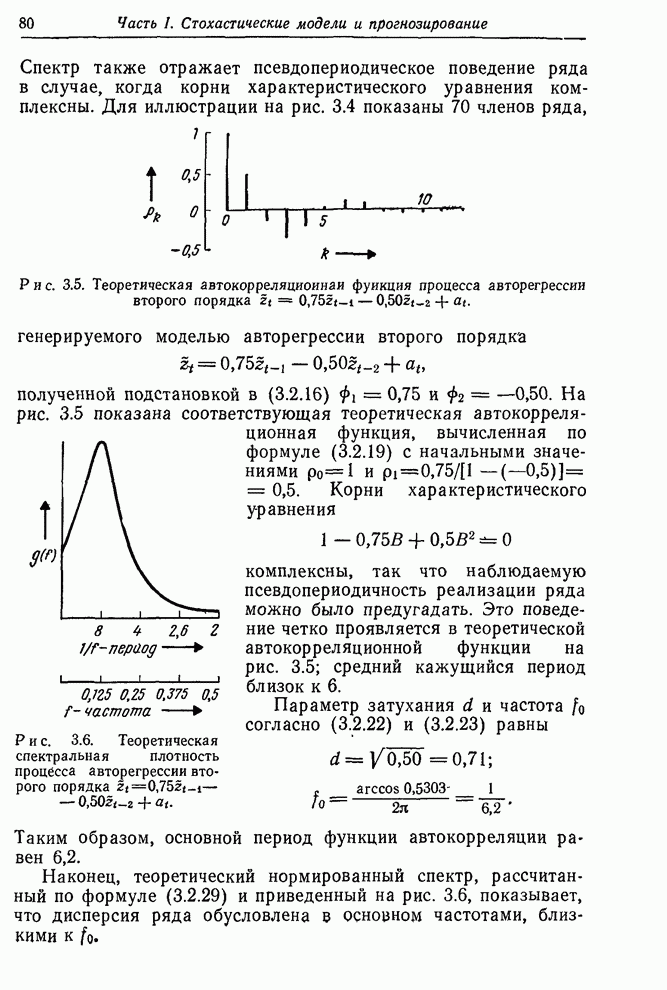
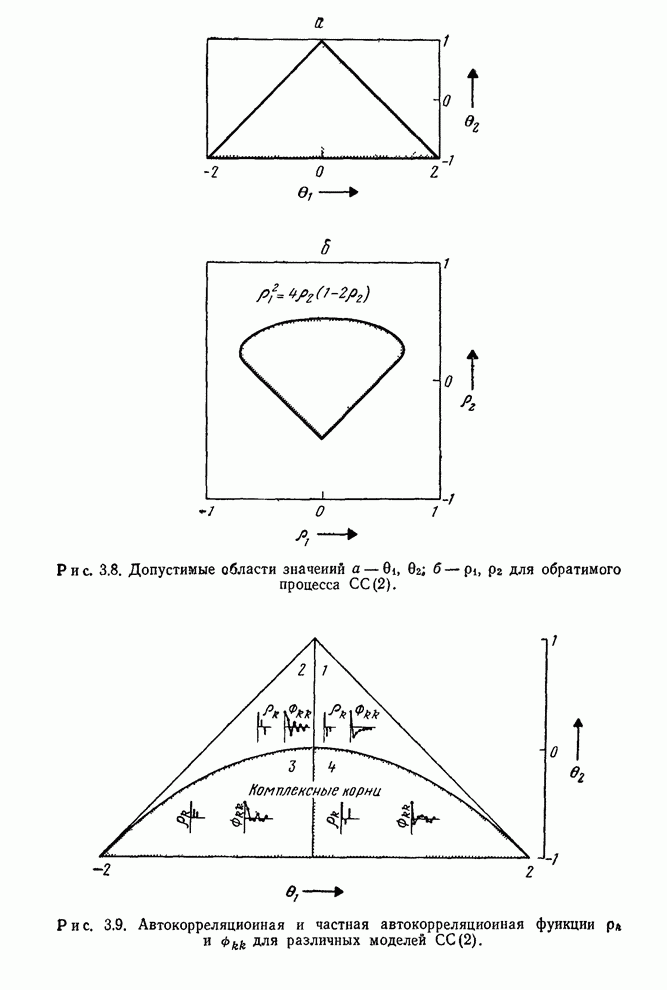
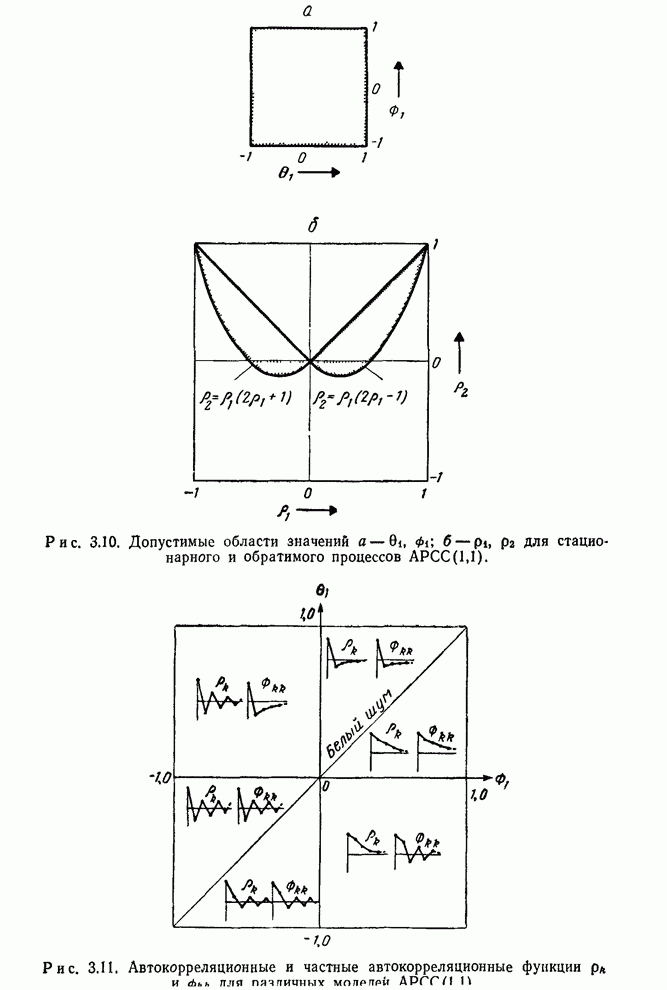
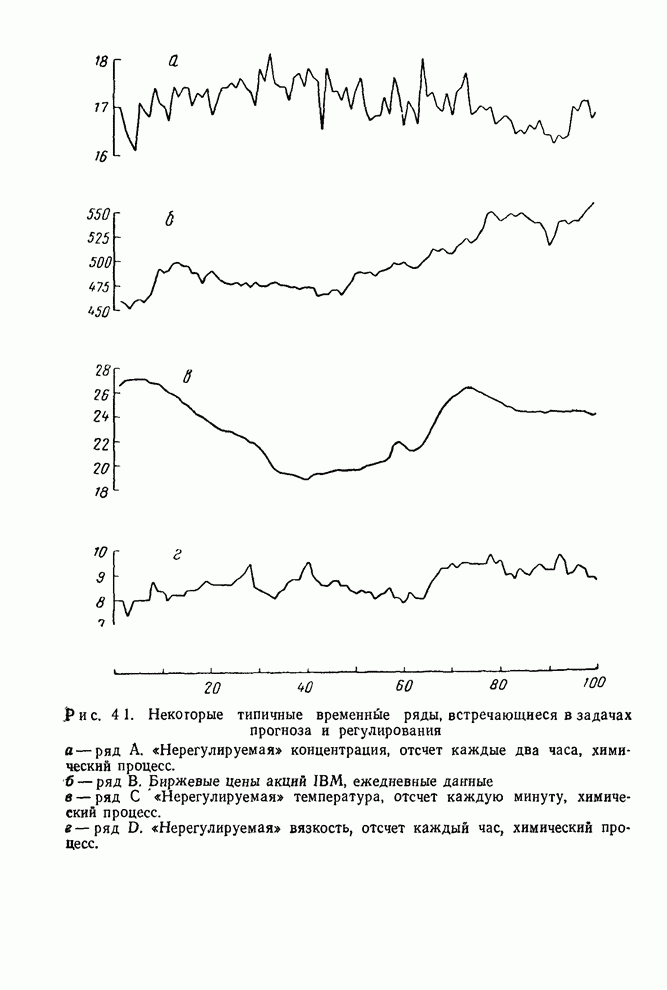
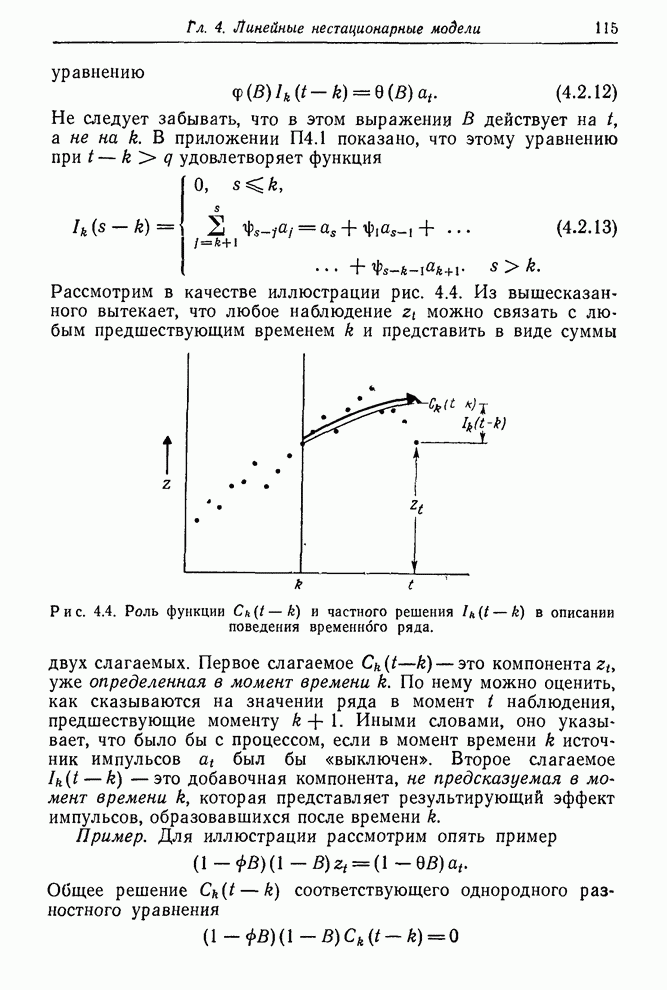
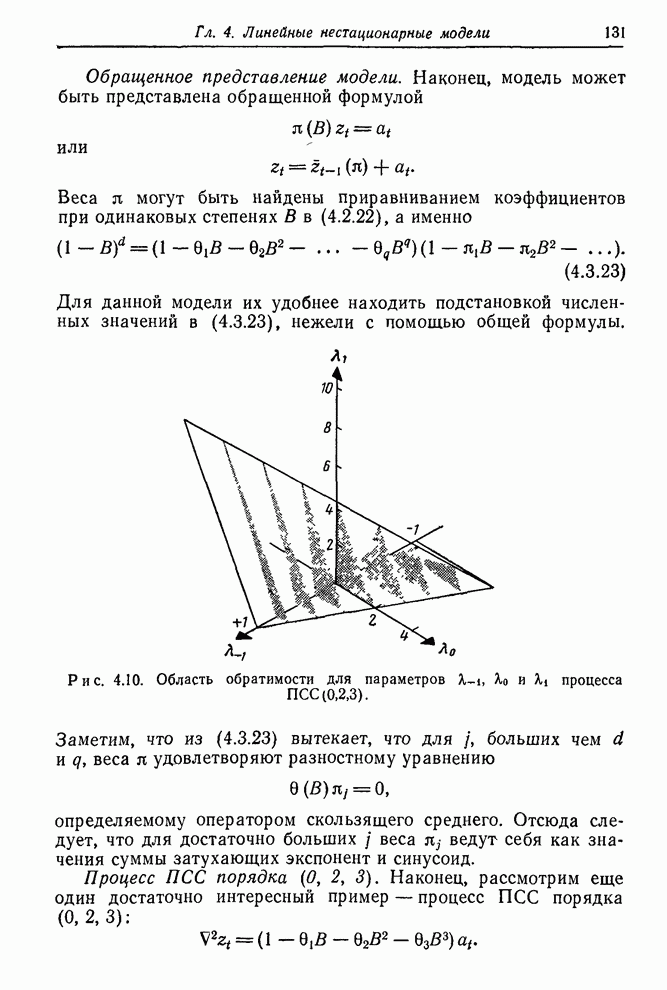
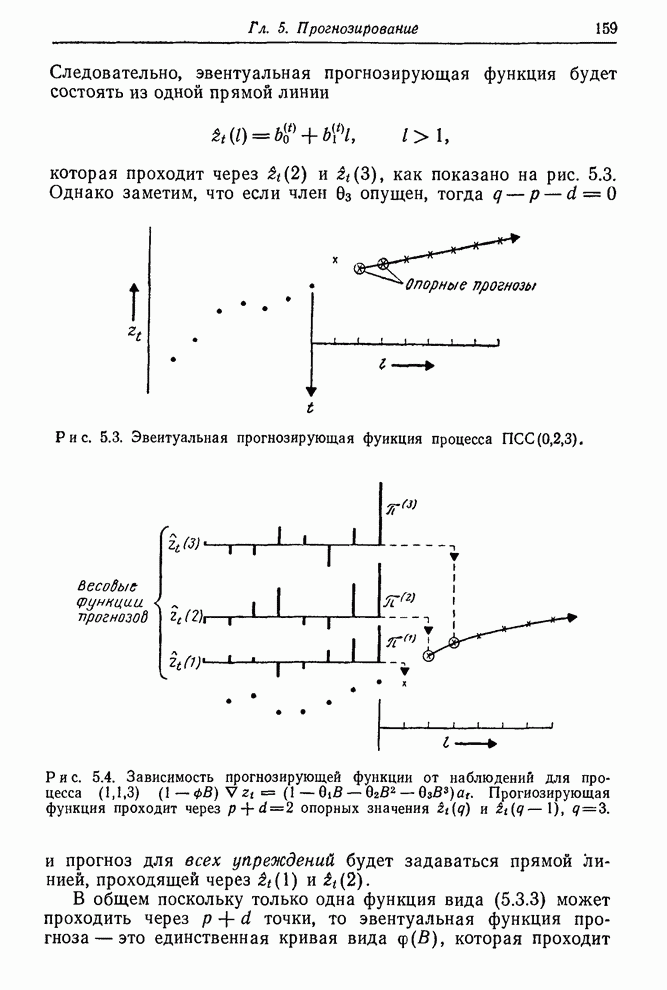
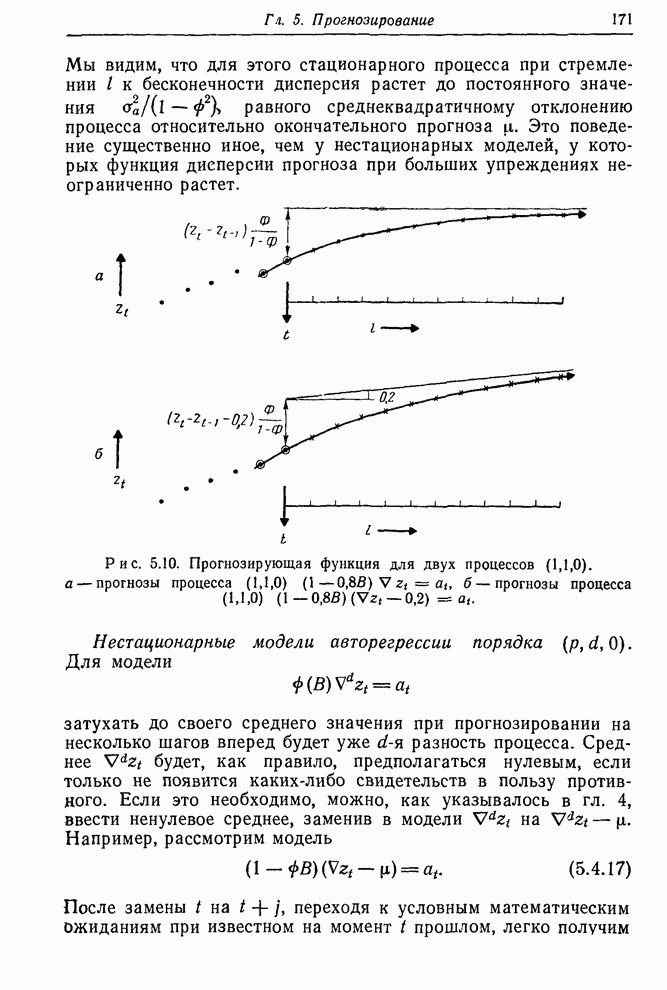
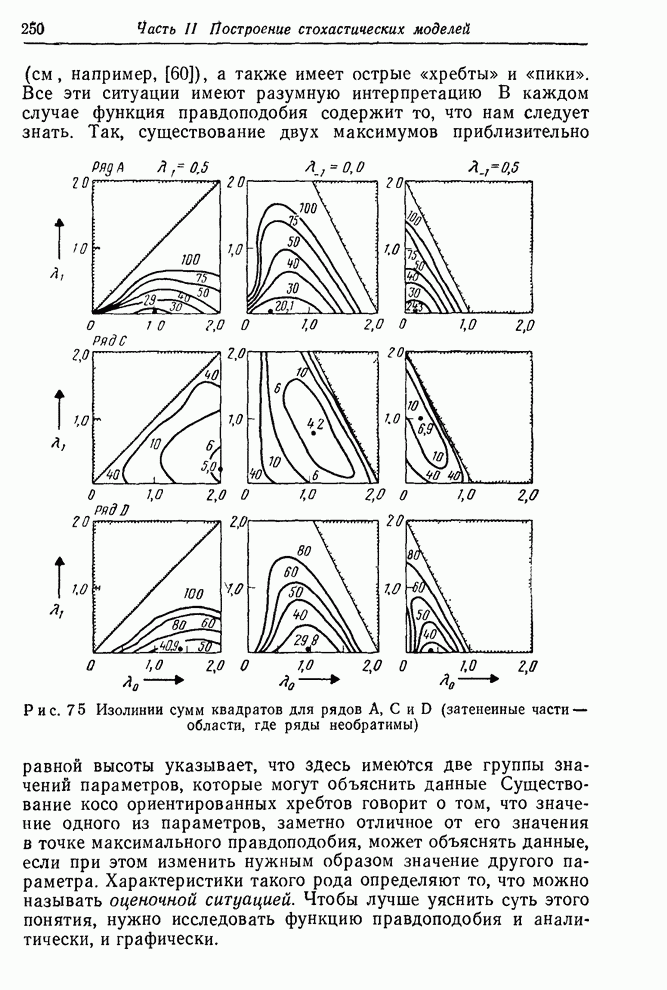
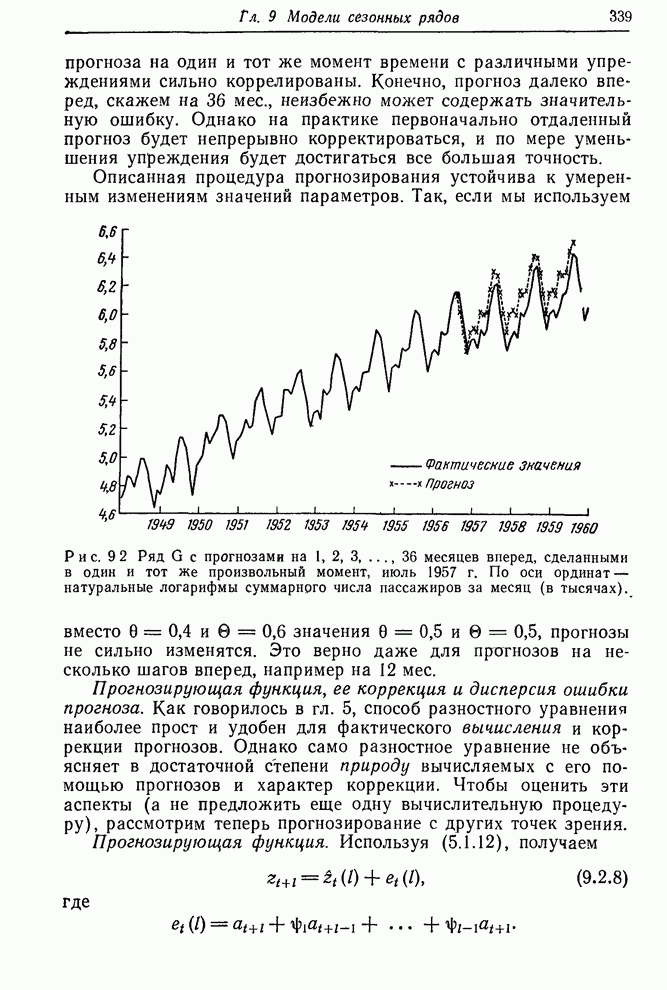
Функция правдоподобия строится, конечно, не только для того, чтобы показать максимальные значения правдоподобия. Эта функция в целом содержит весь объем информации, приходящей с данными. В некоторых проблемах возникает ситуация, когда функция правдоподобия имеет два и более максимума (см, например, [60]), а также имеет острые «хребты» и «пики». Все эти ситуации имеют разумную интерпретацию. В каждом случае функция правдоподобия содержит то, что нам следует знать. Так, существование двух максимумов приблизительно равной высоты указывает, что здесь имеются две группы значений параметров, которые могут объяснить данные. Существование косо ориентированных хребтов говорит о том, что значение одного из параметров, заметно отличное от его значения в точке максимального правдоподобия, может объяснять данные, если при этом изменить нужным образом значение другого параметра. Характеристики такого рода определяют то, что можно называть оценочной ситуацией. Чтобы лучше уяснить суть этого понятия, нужно исследовать функцию правдоподобия и аналитически, и графически.

Рисунок 7.5.
Изолинии сумм квадратов для рядов ![]() и
и ![]() (затененные части — области, где ряды
необратимы)
(затененные части — области, где ряды
необратимы)
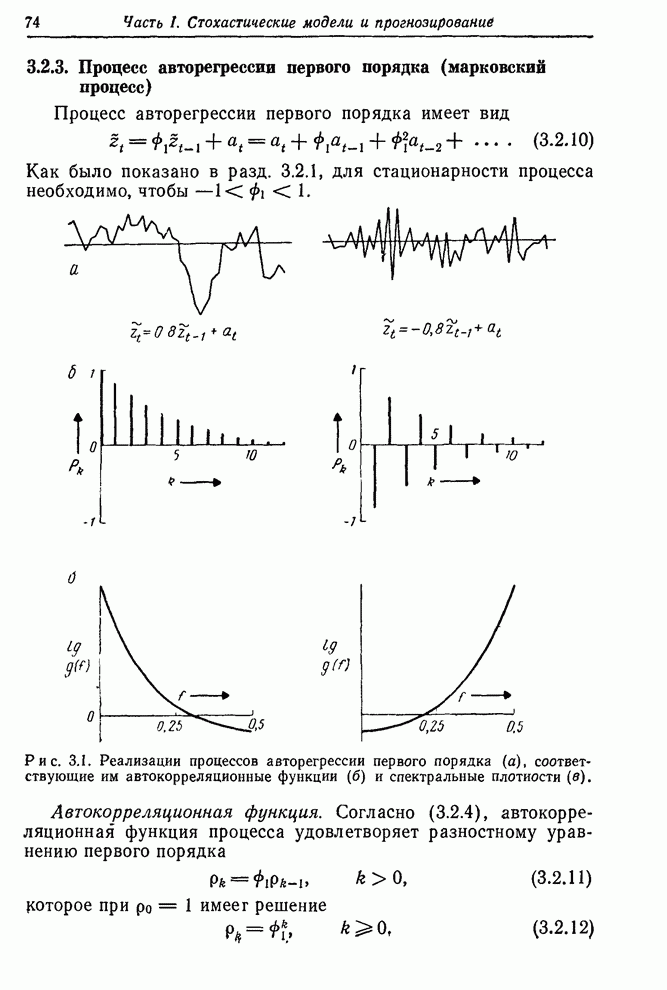
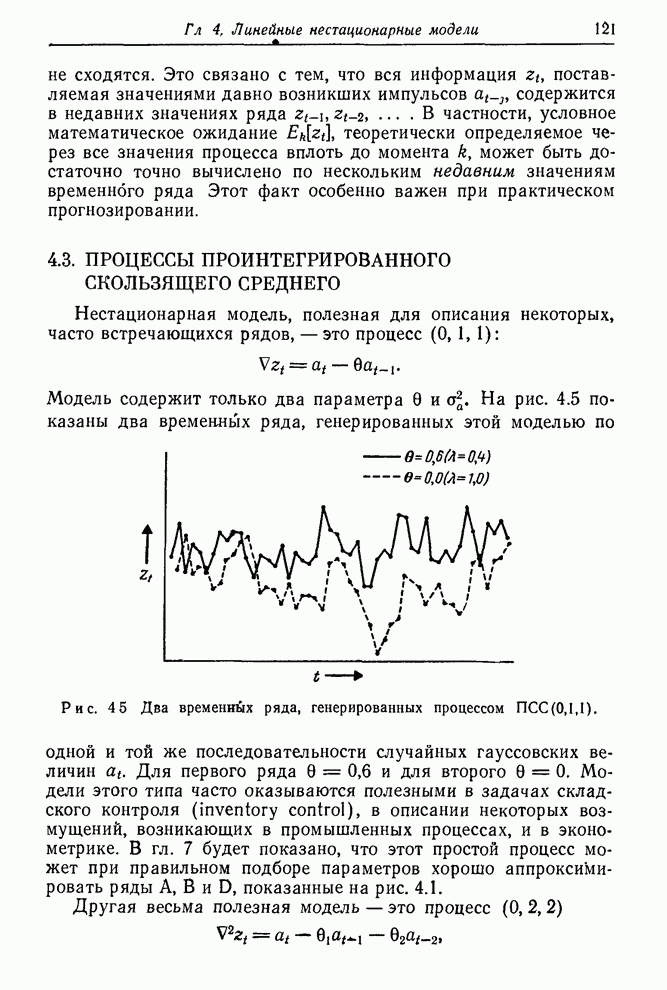
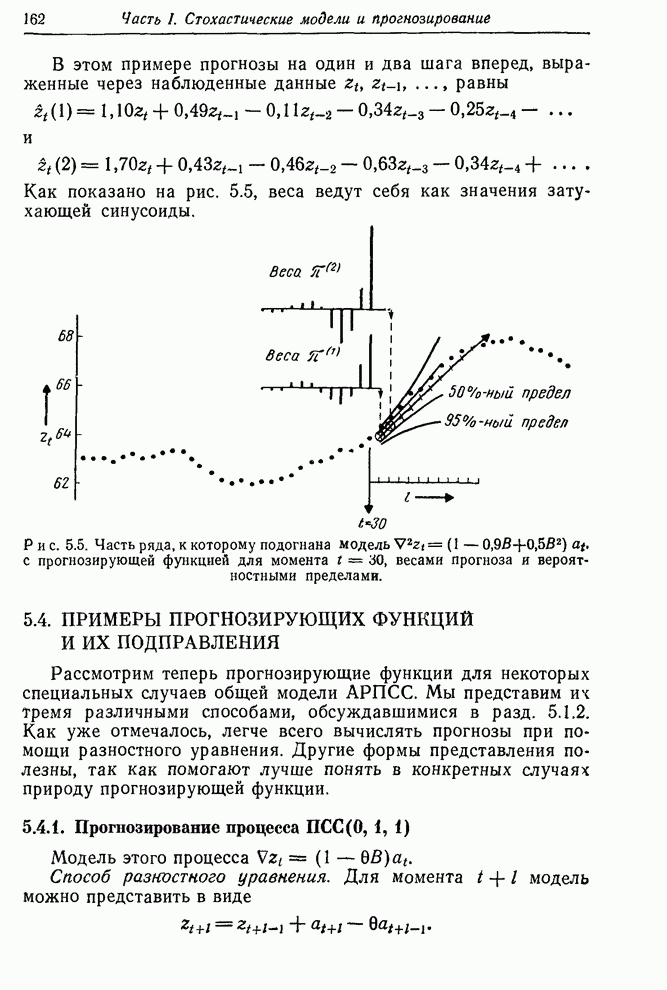
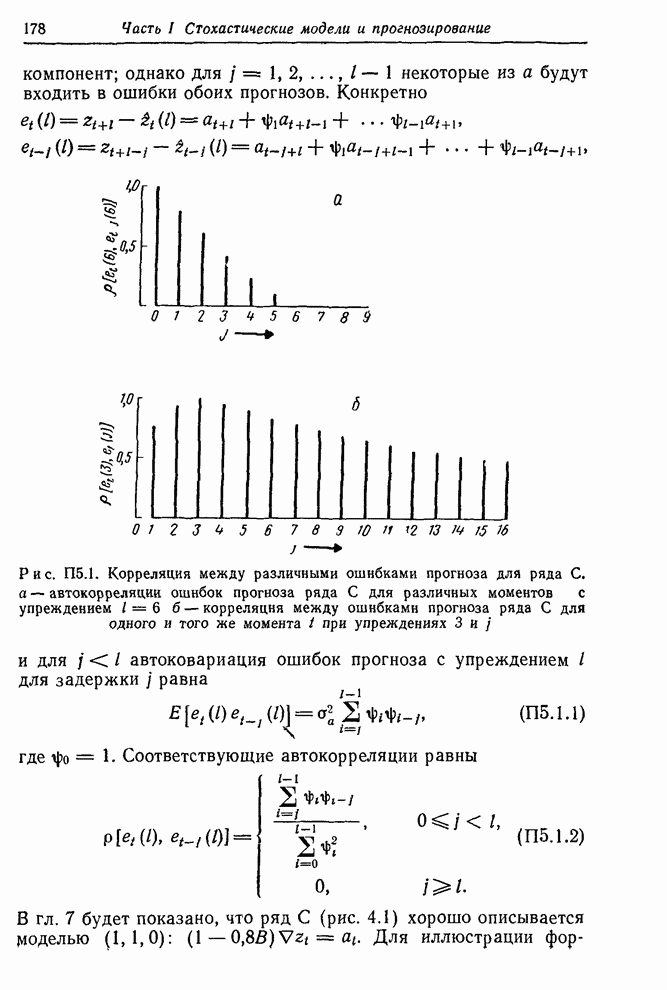
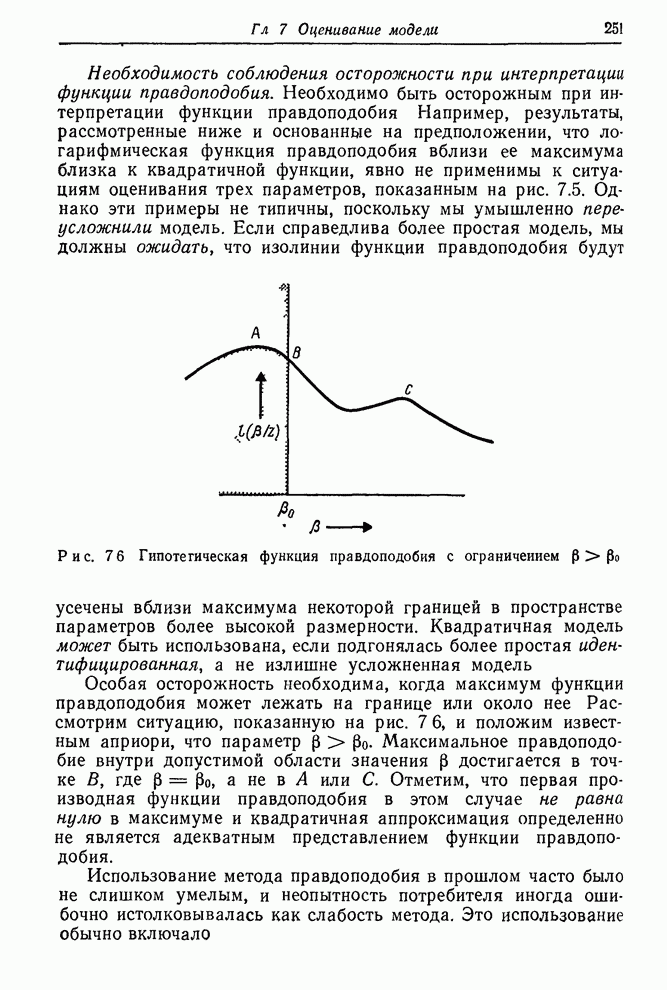
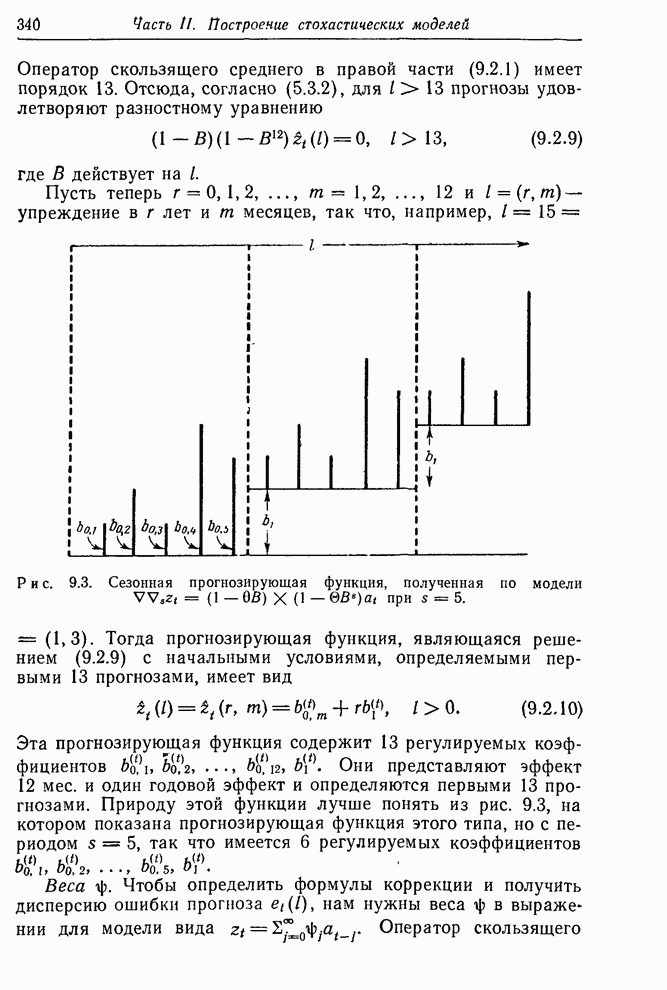
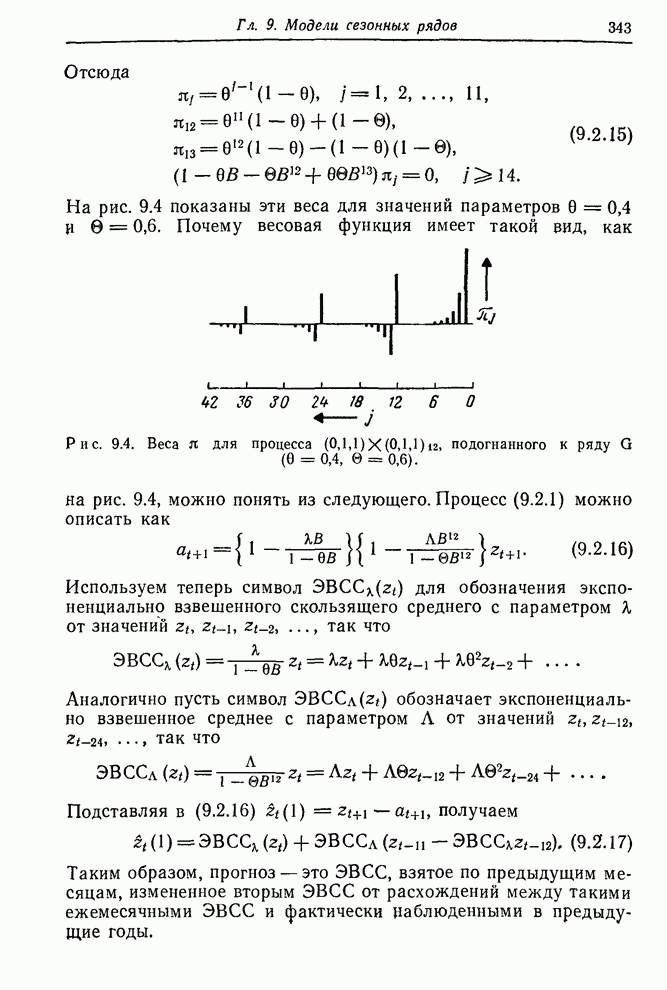
Необходимость соблюдения осторожности при интерпретации функции правдоподобия. Необходимо быть осторожным при интерпретации функции правдоподобия. Например, результаты, рассмотренные ниже и основанные на предположении, что логарифмическая функция правдоподобия вблизи ее максимума близка к квадратичной функции, явно не применимы к ситуациям оценивания трех параметров, показанным на рис. 7.5. Однако эти примеры не типичны, поскольку мы умышленно переусложнили модель. Если справедлива более простая модель, мы должны ожидать, что изолинии функции правдоподобия будут усечены вблизи максимума некоторой границей в пространстве параметров более высокой размерности. Квадратичная модель может быть использована, если подгонялась более простая идентифицированная, а не излишне усложненная модель усечены вблизи максимума некоторой границей в пространстве параметров более высокой размерности. Квадратичная модель может быть использована, если подгонялась более простая идентифицированная, а не излишне усложненная модель.

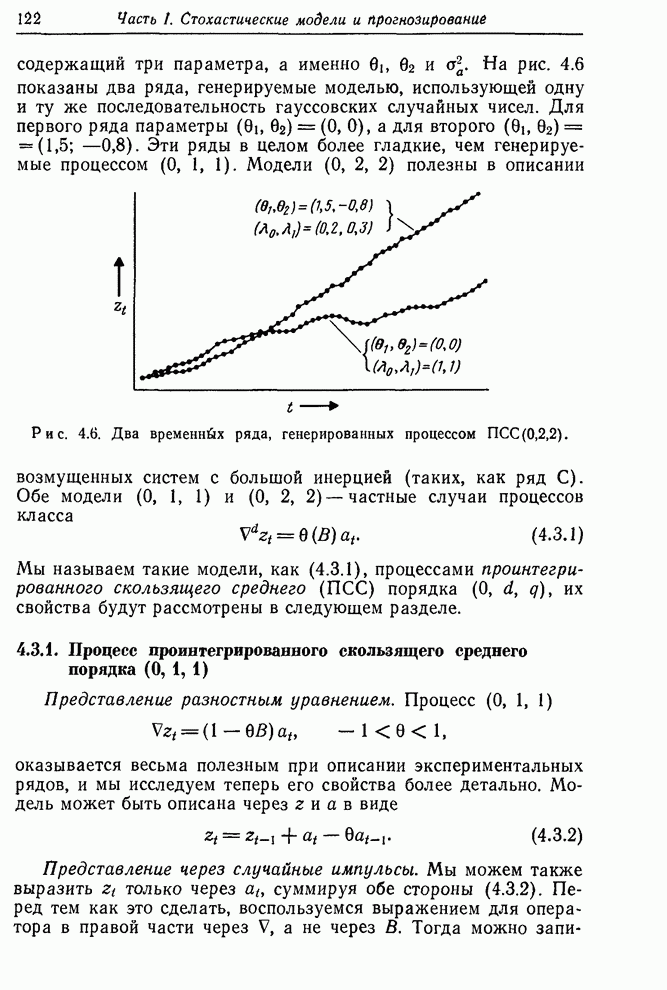
Рисунок 7.6.
Гипотетическая функция правдоподобия с ограничением ![]()
Особая
осторожность необходима, когда максимум функции правдоподобия может лежать на
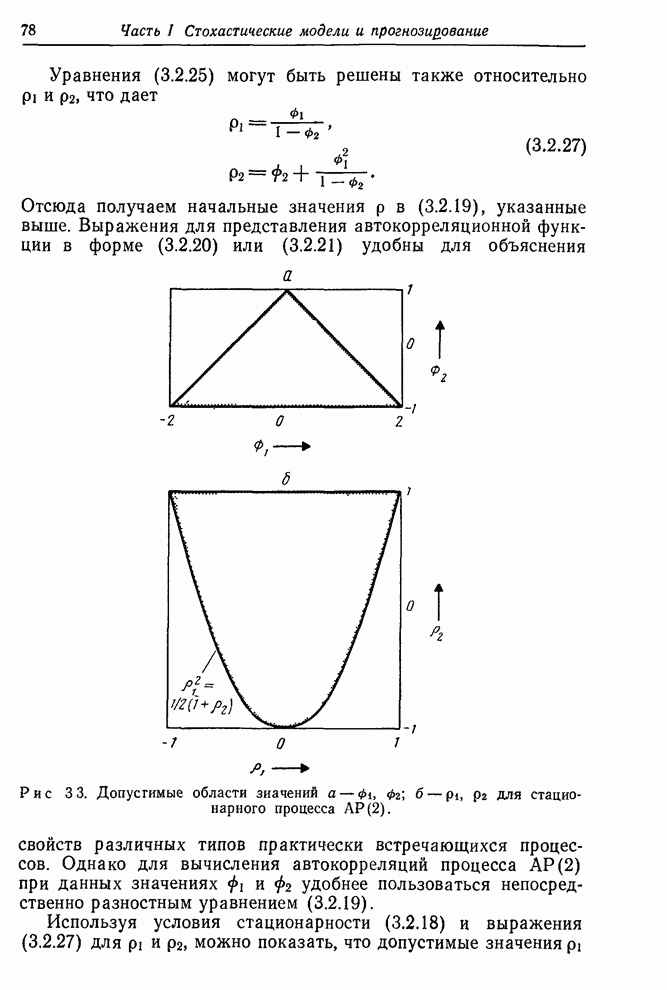
границе или около нее. Рассмотрим ситуацию, показанную на рис. 7.6, и положим
известным априори, что параметр ![]() . Максимальное правдоподобие внутри
допустимой области значения
. Максимальное правдоподобие внутри
допустимой области значения ![]() достигается в точке
достигается в точке ![]() , где
, где ![]() , а не в
, а не в ![]() или
или ![]() . Отметим, что
первая производная функции правдоподобия в этом случае не равна нулю в
максимуме и квадратичная аппроксимация определенно не является адекватным представлением
функции правдоподобия.
. Отметим, что
первая производная функции правдоподобия в этом случае не равна нулю в
максимуме и квадратичная аппроксимация определенно не является адекватным представлением
функции правдоподобия.
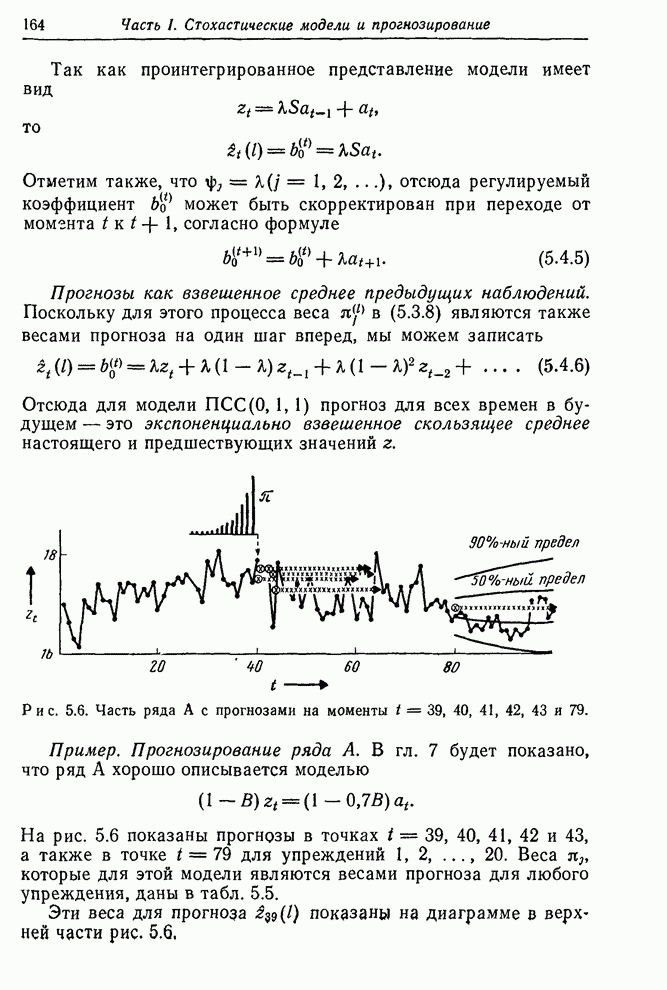
Использование метода правдоподобия в прошлом часто было не слишком умелым, и неопытность потребителя иногда ошибочно истолковывалась как слабость метода. Это использование обычно включало
1) дифференцирование логарифмической функции правдоподобия и приравнивание первых производных нулю для получения оценок максимального правдоподобия (МП);
2) получение приближенных дисперсий и ковариаций этих оценок по вторым производным логарифмической функции правдоподобия или их математическим ожиданиям.
Формальное применение этих приемов может привести к бессмысленным результатам. Это, во-первых, связано с тем элементарным фактом, что приравнивание производных нулю может не приводить нас к максимуму, и, во-вторых, с тем, что информация, содержащаяся в функции правдоподобия, выражается полностью оценками МП и вторыми производными этой функции, только если в интересующей нас области применимо квадратичное приближение. Узнать, выполняется ли это условие для новой задачи оценивания, можно обычно только путем тщательного аналитического и графического исследования.
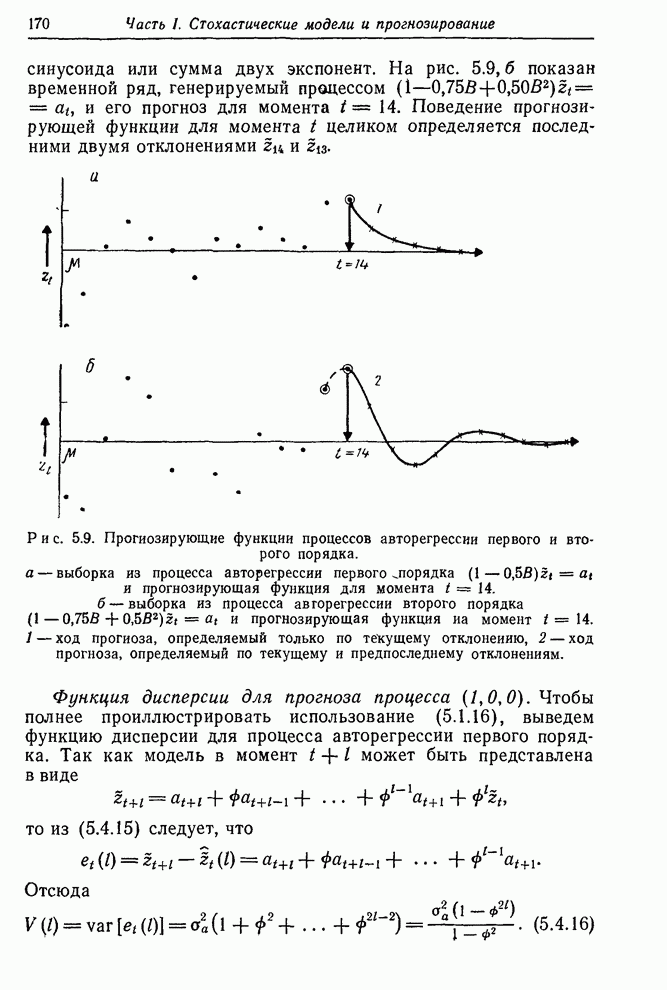
Когда исследуется некоторый новый класс задач оценивания (например, возникающих при оценивании параметров модели АРСС), следует широко пользоваться графическими представлениями функции правдоподобия. После того как поведение данного класса моделей достаточно хорошо понято и представления о ситуации указывают на допустимость такого подхода, мы можем действовать более прямыми методами, к рассмотрению которых мы переходим. Эти результаты подробно описаны в приложениях П7.4 и П7.5. Мы начнем с рассмотрения выражений для дисперсий и ковариаций оценок максимального правдоподобия, пригодных в случае, когда логарифмическая функция правдоподобия приближенно квадратичная и размер выборки сравнительно велик.
В
последующем изложении удобно ввести вектор ![]() элементов которого — параметры
авторегрессии и скользящего среднего
элементов которого — параметры
авторегрессии и скользящего среднего ![]() и
и ![]() . Тогда полный набор
. Тогда полный набор ![]() параметров
процесса АРСС может быть представлен как
параметров
процесса АРСС может быть представлен как ![]() , или как
, или как ![]() , или просто как
, или просто как ![]() .
.
Дисперсии
и ковариаций оценок МП. Для правильно параметризованной модели АРСС часто
оказывается, что в пределах значимой области пространства параметров логарифмическая
функция правдоподобия будет примерно квадратичной формой от компонент ![]() (т.е.
(т.е. ![]() и
и ![]() ), так что
), так что
 , (7.1.18)
, (7.1.18)
где в рассматриваемом приближении производные
 (7.1.19)
(7.1.19)
постоянны.
При
больших ![]() влиянием
члена
влиянием
члена ![]() или,
что то же самое,
или,
что то же самое, ![]() в
(7.1.5) в большинстве случаев можно пренебречь. Отсюда, если
в
(7.1.5) в большинстве случаев можно пренебречь. Отсюда, если ![]() близко к
квадратичной форме, и
близко к
квадратичной форме, и ![]() также будет близко к ней. Иначе
говоря,
также будет близко к ней. Иначе
говоря, ![]() будет
близко к квадратичной форме от
будет
близко к квадратичной форме от ![]() , если условные математические ожидания
, если условные математические ожидания
![]() в (7.1.6)
локально близки к линейным функциям компонент вектора
в (7.1.6)
локально близки к линейным функциям компонент вектора ![]() .
.
Для средних и больших выборок при условии, что допустимо локальное квадратичное приближение (7.1.18), можно получить полезные приближенные выражения для дисперсий и ковариаций оценок и для доверительных интервалов.
Информационная
матрица для параметров ![]() . Матрица
. Матрица ![]() размером
размером ![]() названа в [56, 87] информационной
матрицей для параметров
названа в [56, 87] информационной
матрицей для параметров ![]() ; здесь математическое ожидание взято
по распределению
; здесь математическое ожидание взято
по распределению ![]() .
Для данного значения
.
Для данного значения ![]() матрица ковариаций
матрица ковариаций ![]() МП-оценок
МП-оценок ![]() при больших
размерах выборки является обратной к информационной матрице
при больших
размерах выборки является обратной к информационной матрице
![]() . (7.1.20)
. (7.1.20)
Например, если ![]() , матрица ковариаций
для большой выборки имеет вид
, матрица ковариаций
для большой выборки имеет вид
 .
.
Далее, используя (7.1.5), получаем
 ,
(7.1.21)
,
(7.1.21)
где
 .
.
Кроме того, если
для больших выборок мы аппроксимируем математические ожидания величин ![]() или
или ![]() фактически
наблюдаемыми значениями, то, используя (7.1.20), получим
фактически
наблюдаемыми значениями, то, используя (7.1.20), получим
![]() . (7.1.22)
. (7.1.22)
Отсюда для ![]()
 .
.
Если ![]() была бы точно
квадратичной функцией
была бы точно
квадратичной функцией ![]() в рассматриваемой области пространства
параметров, то все производные
в рассматриваемой области пространства
параметров, то все производные ![]() были бы постоянны во всей этой области.
На практике
были бы постоянны во всей этой области.
На практике ![]() ,
будут несколько варьировать, и мы будем предполагать, что эти производные
определяются в точке
,
будут несколько варьировать, и мы будем предполагать, что эти производные
определяются в точке ![]() либо вблизи нее. В приложениях П7.4 и
П7.5 показано, что оценка
либо вблизи нее. В приложениях П7.4 и
П7.5 показано, что оценка ![]() имеет вид
имеет вид
![]() (7.1.23)
(7.1.23)
и что для
больших выборок ![]() и
и
![]() не
коррелированы. Наконец, элементы (7.1.22) можно оценить, пользуясь тем, что
не
коррелированы. Наконец, элементы (7.1.22) можно оценить, пользуясь тем, что
![]() , (7.1.24)
, (7.1.24)
где матрица ![]() равна
равна
![]() .
.
Выражение
(7.1.24) при ![]() определяет
дисперсию
определяет
дисперсию ![]() .
.
Приближенные
доверительные области для параметров. Эти результаты позволяют, в
частности, получить приближенные значения дисперсии наших оценок. Извлекая
корень из дисперсий, мы найдем стандартные отклонения, которые обычно называют стандартными
ошибками оценок. Стандартную ошибку оценки ![]() мы будем обозначать
мы будем обозначать ![]() . Когда нужно рассматривать
несколько параметров одновременно, необходимо иметь способ суждения о совместной
точности оценок. Один из способов осуществления такого подхода — определение доверительной
области. Можно показать (см., например, [61]), что
. Когда нужно рассматривать
несколько параметров одновременно, необходимо иметь способ суждения о совместной
точности оценок. Один из способов осуществления такого подхода — определение доверительной
области. Можно показать (см., например, [61]), что ![]() -я доверительная область
имеет следующее свойство: если делать повторные выборки размера
-я доверительная область
имеет следующее свойство: если делать повторные выборки размера ![]() из той же популяции
и строить доверительную область для каждой такой выборки, то
из той же популяции
и строить доверительную область для каждой такой выборки, то ![]() -я часть этих
областей будет включать точку с истинным значением параметра.
-я часть этих
областей будет включать точку с истинным значением параметра.
Если
для данного ![]() —
приближенно квадратичная функция
—
приближенно квадратичная функция ![]() вблизи
вблизи ![]() , то, пользуясь (7.1.20) (см. также
приложение П7.1), можно получить приближенную
, то, пользуясь (7.1.20) (см. также
приложение П7.1), можно получить приближенную ![]() -ю доверительную область в виде
-ю доверительную область в виде
![]() , (7.1.25)
, (7.1.25)
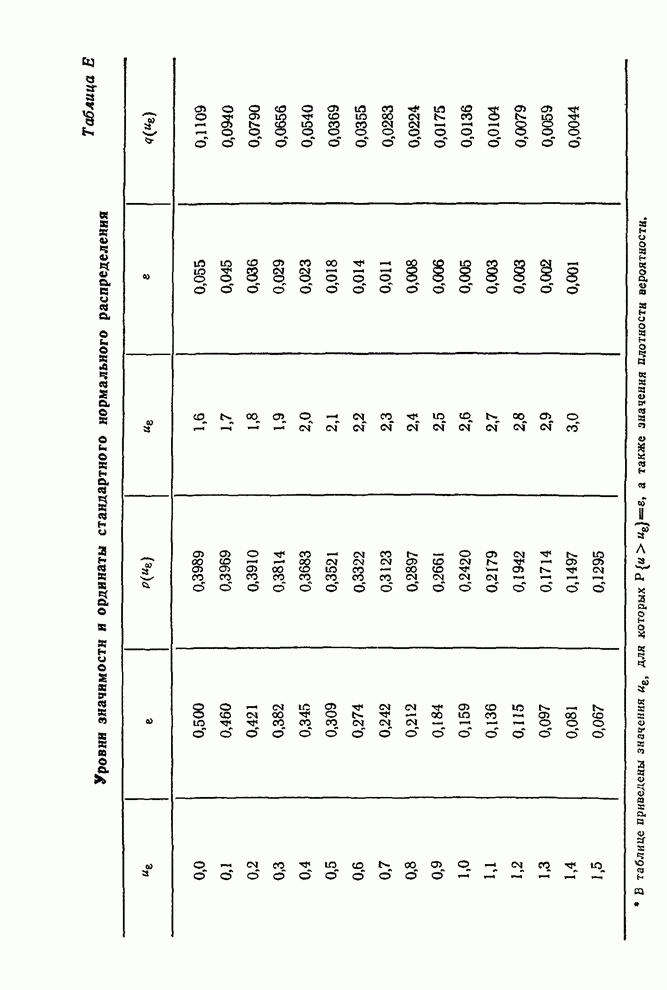
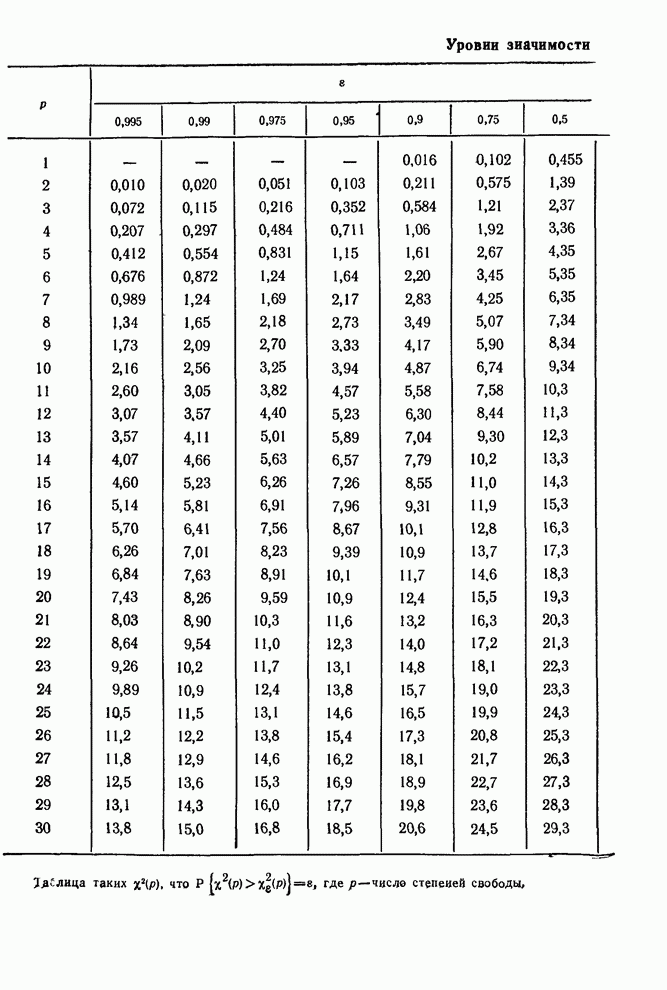
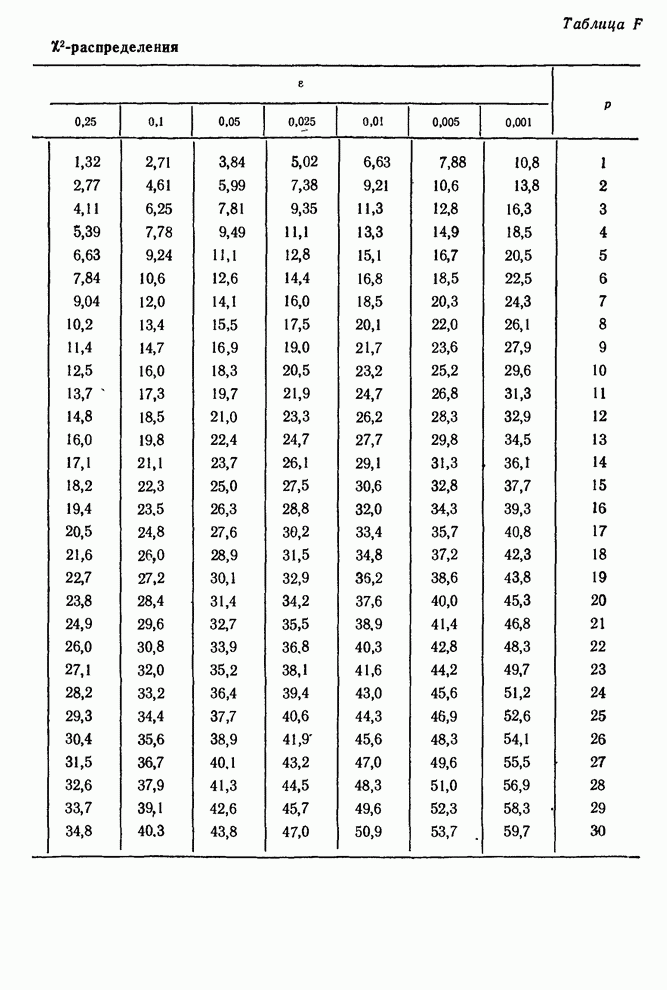
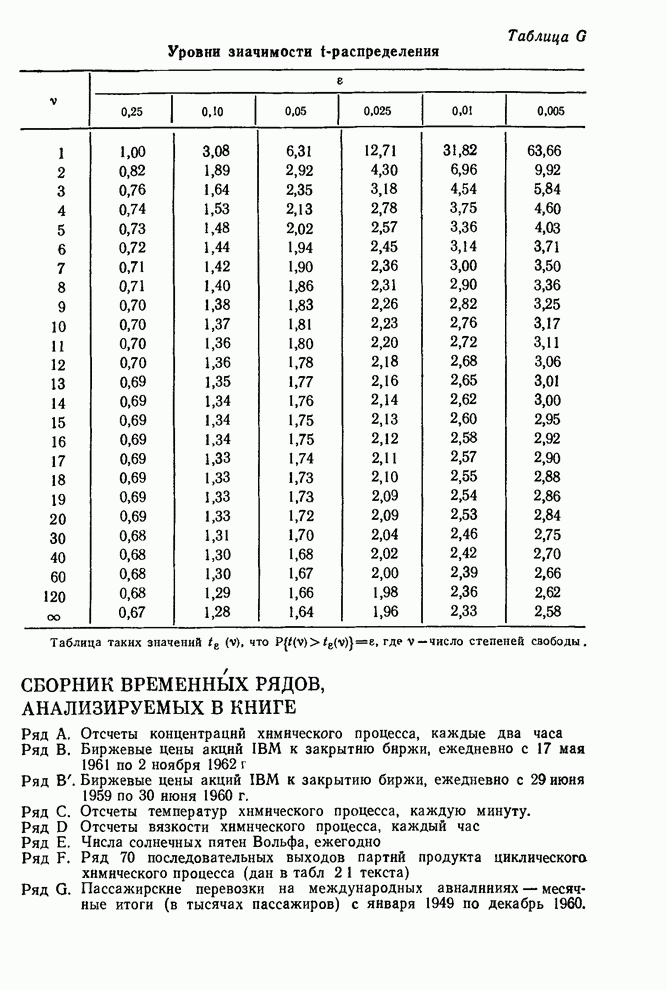
где ![]() — это квантиль
уровня
— это квантиль
уровня ![]() распределения
распределения
![]() с
с ![]() степенями свободы.
Можно получить и другое приближенное выражение для доверительной области, если
воспользоваться (7.1.22) и подставить туда оценку (7.1.23) вместо
степенями свободы.
Можно получить и другое приближенное выражение для доверительной области, если
воспользоваться (7.1.22) и подставить туда оценку (7.1.23) вместо ![]() :
:
![]() . (7.1.26)
. (7.1.26)
Однако если
поверхность ![]() квадратичная,
то
квадратичная,
то
 . (7.1.27)
. (7.1.27)
Тогда, пользуясь
(7.1.23) и (7.1.26), находим, что приближенная ![]() -я доверительная область ограничена
изолинией суммы квадратов, для которой
-я доверительная область ограничена
изолинией суммы квадратов, для которой
 (7.1.28)
(7.1.28)
Примеры вычисления приближенных доверительных интервалов и областей.
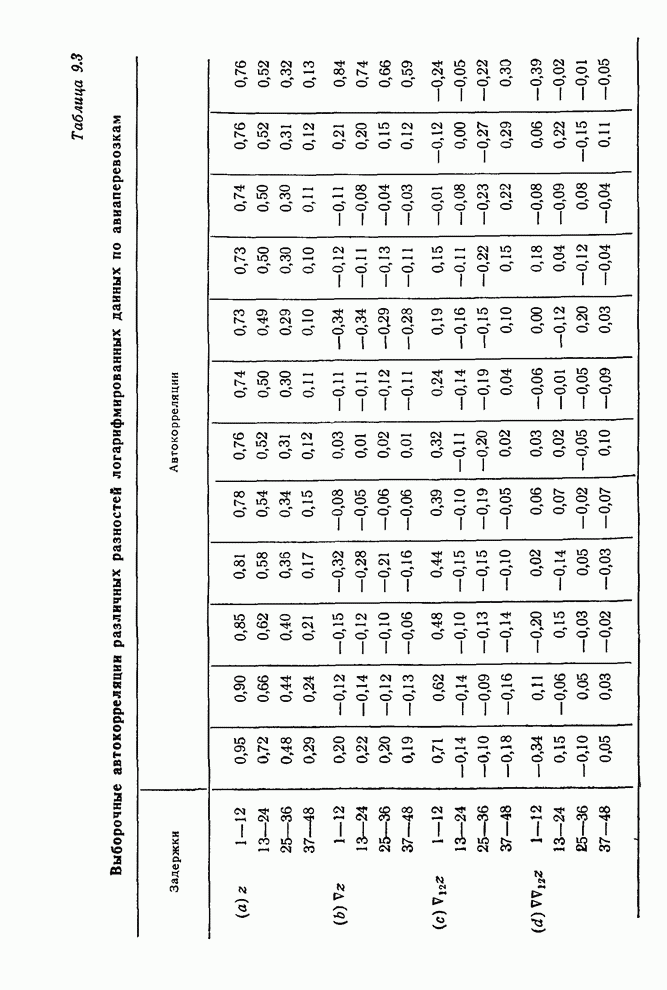
1) Ряд ![]() . Значения
. Значения ![]() и ее разностей для
ряда
и ее разностей для
ряда ![]() приведены
в табл. 7.8. Вторая разность
приведены
в табл. 7.8. Вторая разность ![]() не постоянна, и поэтому
не постоянна, и поэтому ![]() не является строго
квадратичной функцией. Однако на интервале от
не является строго
квадратичной функцией. Однако на интервале от ![]() до
до ![]()
![]() изменяется незначительно, так что можно
считать (7.1.28) достаточно хорошим приближением. Так как минимальное значение
изменяется незначительно, так что можно
считать (7.1.28) достаточно хорошим приближением. Так как минимальное значение ![]() , то критическое
значение
, то критическое
значение ![]() ,
определяющее приближенно 95%-ный доверительный интервал, равно
,
определяющее приближенно 95%-ный доверительный интервал, равно
![]() .
.
Таблица 7.8. ![]() и ее первые и
вторые разности для различных значений
и ее первые и
вторые разности для различных значений ![]() , ряд
, ряд ![]()
|
|
|
|
|
|
1,5 1,4 1,3 1,2 1,1 1,0 0,9 0,8 0,7 0,6 0,5 |
23929 21595 20222 19483 19220 19363 19896 20851 22315 24471 27694 |
2 334 1373 739 263 -143 -533 -955 -1464 -2156 -3223 |
961 634 476 406 390 422 509 692 1067 |
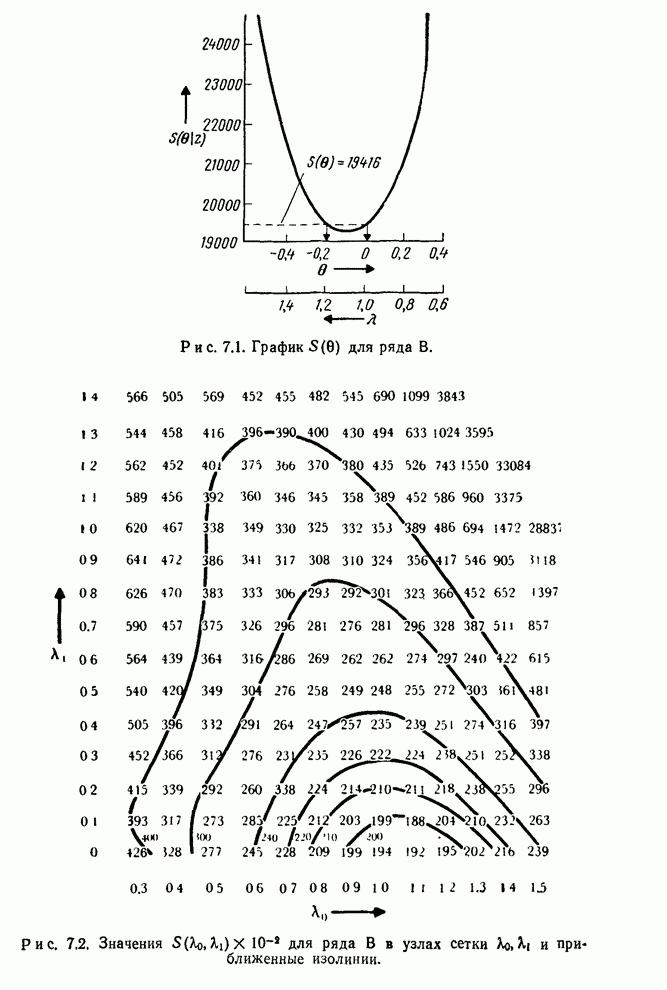
Считывая
значение ![]() ,
соответствующее
,
соответствующее ![]() на
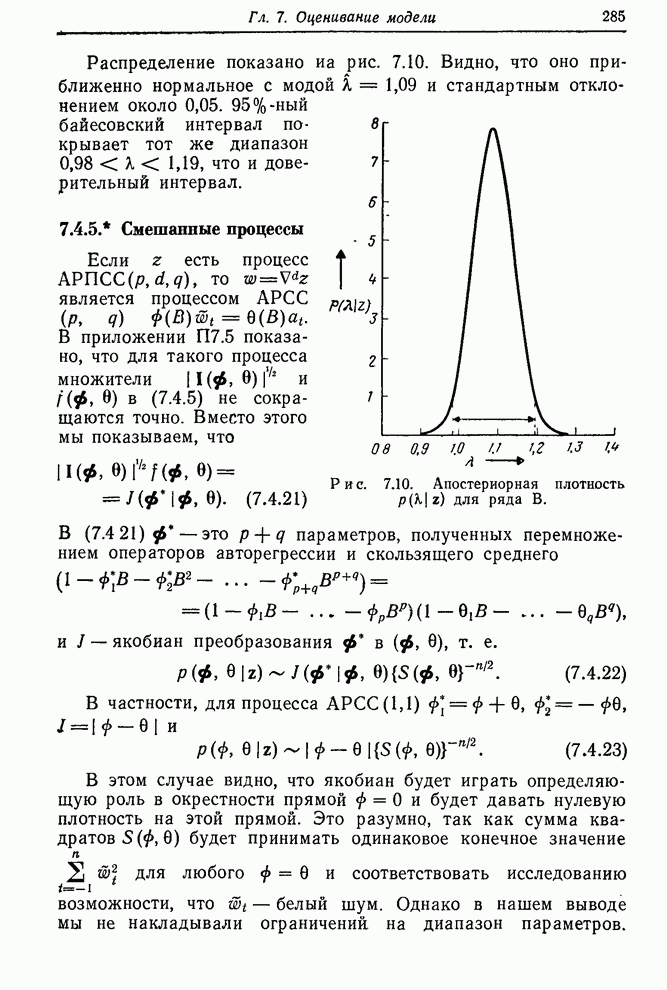
рис. 7.1, получаем приближенный доверительный интервал
на
рис. 7.1, получаем приближенный доверительный интервал ![]() .
.
Можно
поступить и по-другому, используя (7.1.26). Пользуясь второй разностью из табл.
7.8 при ![]() ,
чтобы оценить производную, получаем
,
чтобы оценить производную, получаем
 .
.
Пользуясь
(7.1.23), находим, что ![]() . Отсюда 95%-ный доверительный интервал,
согласно (7.1.26), будет
. Отсюда 95%-ный доверительный интервал,
согласно (7.1.26), будет
 ,
,
т. е.
![]() .
.
Отсюда интервал
равен ![]() ,
что хорошо согласуется с предыдущими вычислениями.
,
что хорошо согласуется с предыдущими вычислениями.
В
этом примере, где имеется только один параметр ![]() , использование (7.1.25) и (7.1.26)
эквивалентно использованию интервала
, использование (7.1.25) и (7.1.26)
эквивалентно использованию интервала
![]() ,
,
где ![]() — квантиль уровня
— квантиль уровня ![]() стандартного
нормального распределения. Приближенная стандартная ошибка
стандартного
нормального распределения. Приближенная стандартная ошибка ![]() находится из (7.1.24). В
этом примере
находится из (7.1.24). В
этом примере
![]() ,
,
и приближенная
стандартная ошибка ![]() равна
равна
![]() .
.
Отсюда приближенный доверительный интервал равен, как и ранее,
![]() .
.
Наконец, в разд. 7.2 мы покажем, что для больших выборок процесса СС(1) можно оценить (7.1.20) аналитически, что дает
![]() .
.
В рассматриваемом
примере, заменяя ![]() на
на
![]() , находим
, находим
![]() ,
,
что хорошо
согласуется с предыдущими оценками, дает ту же стандартную ошибку ![]() и тот же
доверительный интервал.
и тот же
доверительный интервал.

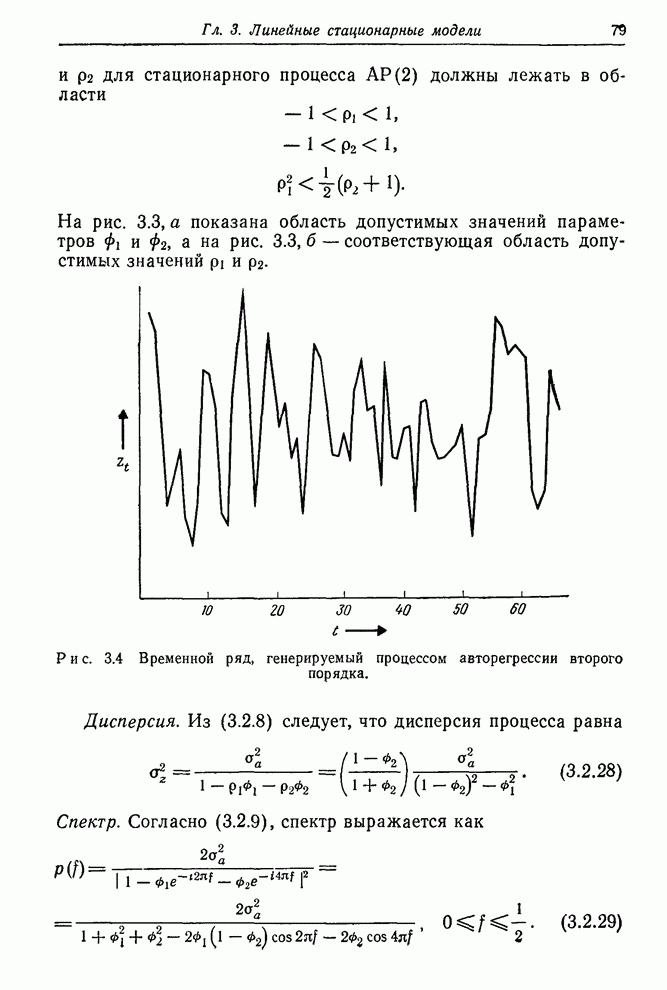
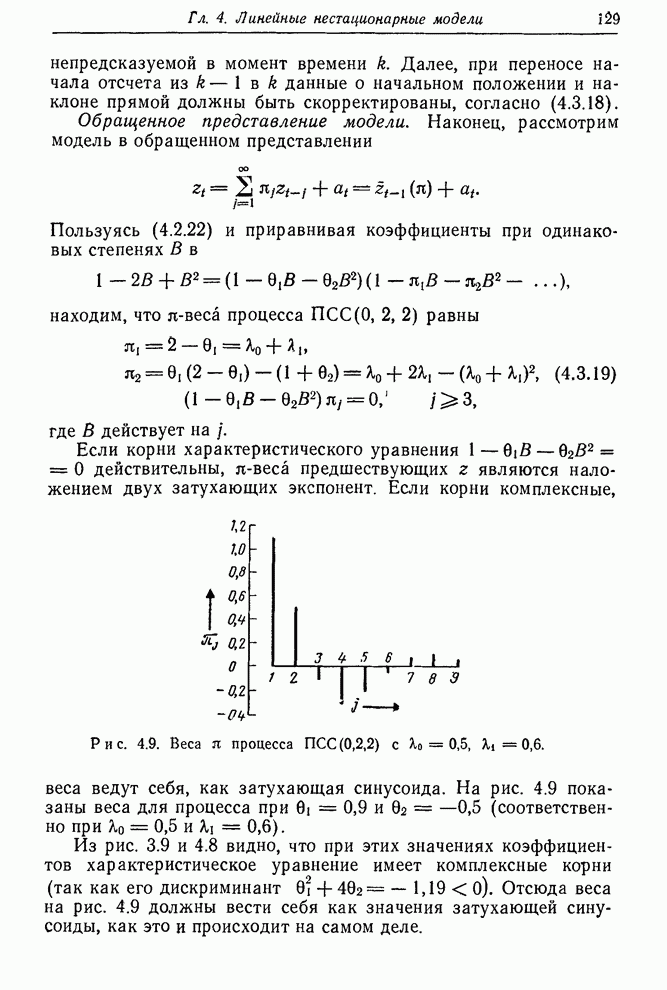
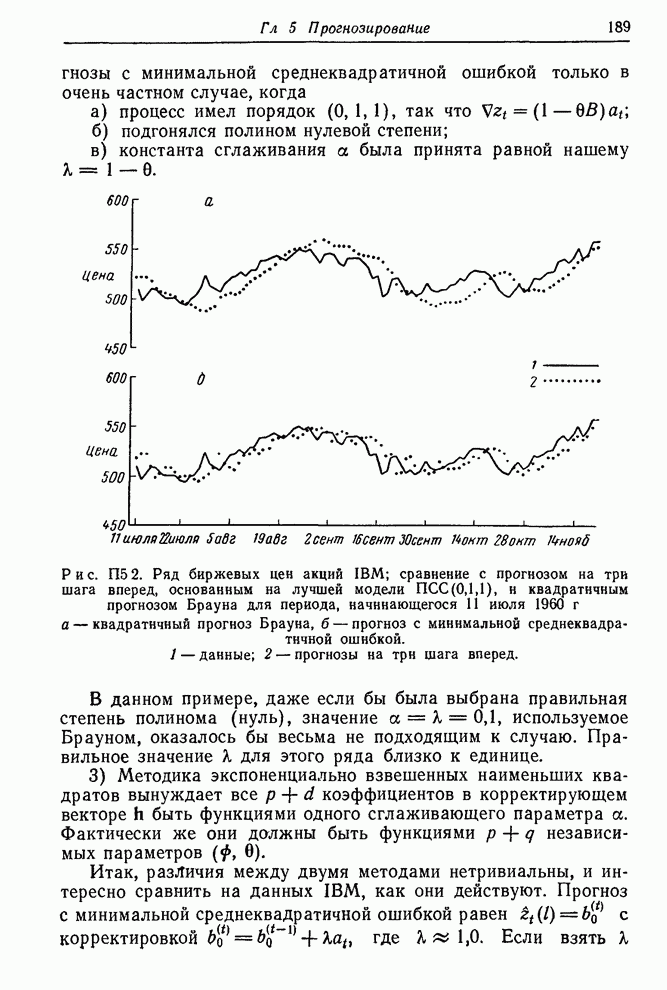
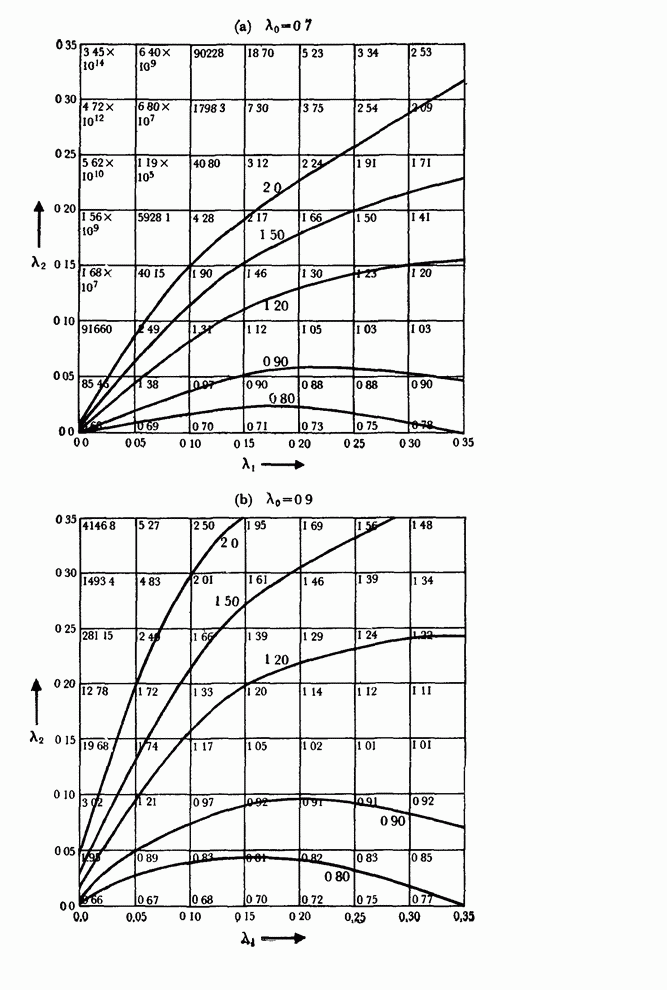
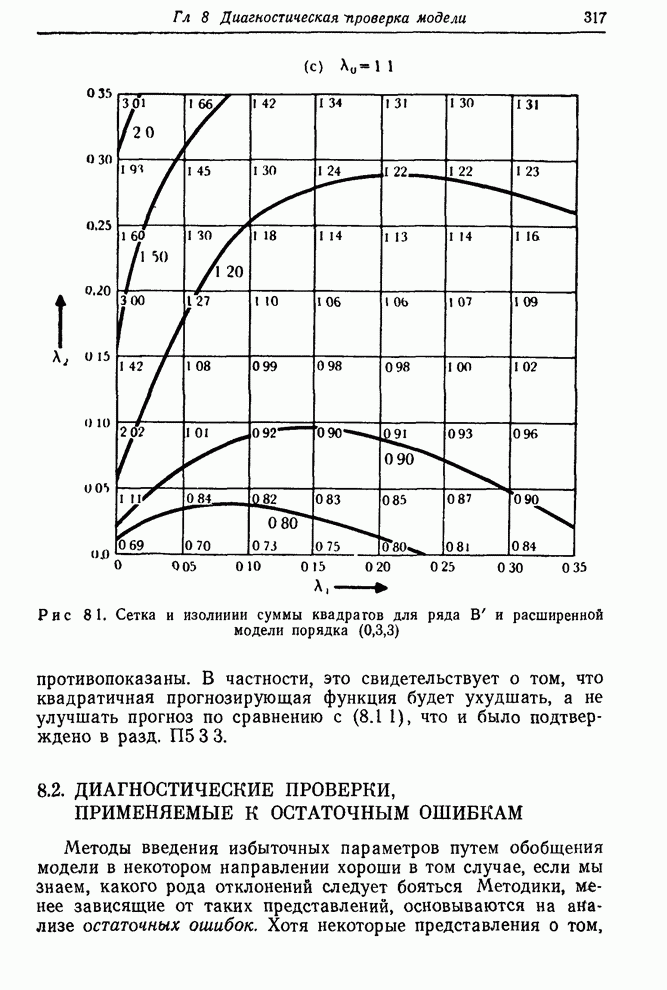
Рис. 7.7. Изолинии
суммы квадратов для ряда ![]() в предположении модели порядка
в предположении модели порядка ![]() ; в центре
заштрихована 95%-ная доверительная область.
; в центре
заштрихована 95%-ная доверительная область.
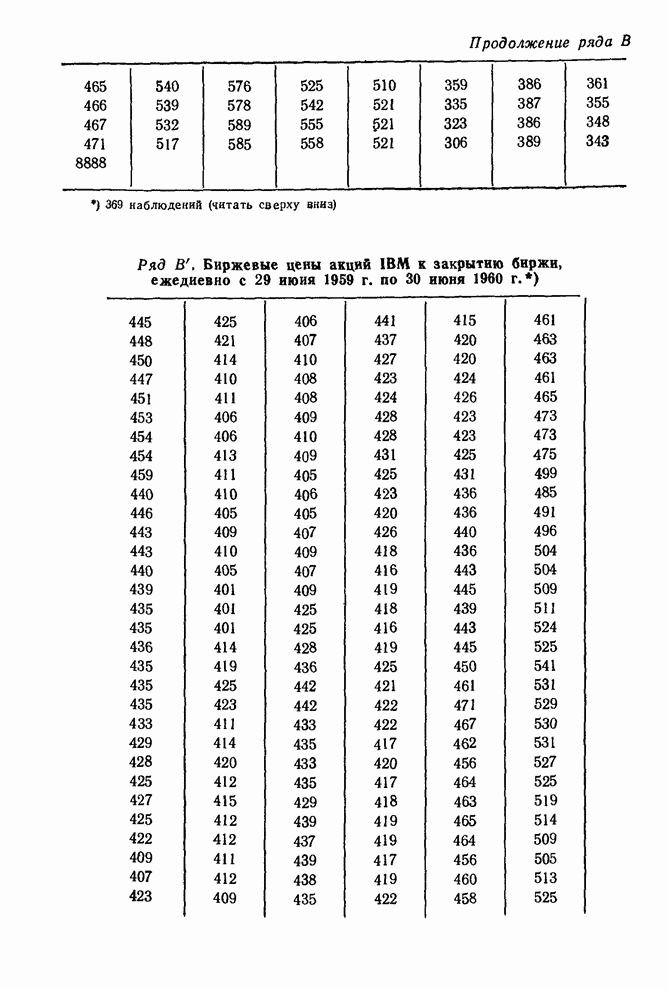
2)
Ряд ![]() . При
идентификации ряда
. При
идентификации ряда ![]() в качестве одной из опробованных моделей
использовался процесс
в качестве одной из опробованных моделей
использовался процесс ![]() . Для иллюстрации использования формулы
(7.1.28) в случае, когда число параметров больше 1, на рис. 7.7 заштрихована
95%-ная доверительная область значения параметров
. Для иллюстрации использования формулы
(7.1.28) в случае, когда число параметров больше 1, на рис. 7.7 заштрихована
95%-ная доверительная область значения параметров ![]() и
и ![]() . В этом примере
. В этом примере ![]() , так что 95%-ная
доверительная область ограничена изолинией
, так что 95%-ная
доверительная область ограничена изолинией
![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- Предисловие
- План книги
- Глава 1. Введение и краткое содержание
- 1.1. Три важные практические проблемы
- 1.1.1. Прогнозирование временных рядов
- 1.1.2. Оценивание передаточных функций
- 1.1.3. Проектирование дискретных регулирующих систем
- 1.2. Стохастические и детерминированные динамические математические модели
- 1.2.1. Стационарные нестационарные стохастические модели для прогнозирования и регулирования
- 1.2.2. Модели передаточных функций
- 1.2.3. Модели дискретных систем регулирования
- 1.3. Основные понятия в построении моделей
- 1.3.1. Экономия
- 1.3.2. Интерактивные этапы в выборе модели
- Часть 1. Стохастические модели и основанное на них прогнозирование
- Глава 2. Автокорреляционная функция и спектр
- 2.1. Автокорреляционные свойства стационарных моделей
- 2.1.1. Временные ряды и стохастические процессы
- 2.1.2. Стационарные стохастические процессы
- 2.1.3. Положительная определённость и автоковариационная матрица
- 2.1.4. Автоковариационные и автокорреляционные функции
- 2.1.5. Оценивание автоковариационной и автокорреляционной функций
- 2.1.6. Стандартные ошибки оценок автокорреляций
- 2.2. Спектральные свойства стационарных моделей
- 2.2.1. Периодограмма
- 2.2.2. Дисперсионный анализ
- 2.2.3. Спектральная плотность и нормированный спектр
- 2.2.4. Простые примеры автокорреляционных функций и нормированных спектров
- 2.2.5. Преимущества и недостатки автокорреляционных функций и нормированных спектров
- Приложение П2.1. Связь между выборочным спектром и оценкой автоковариационной функции
- Глава 3. Линейные стационарные модели
- 3.1. Общий линейный процесс
- 3.1.1. Две эквивалентные формы линейного процесса
- 3.1.2. Производящая функция автоковариаций линейного процесса
- 3.1.3. Условия стационарности и обратимости линейного процесса
- 3.1.4. Процессы авторегрессии и скользящего среднего
- 3.2. Процессы авторегрессии
- 3.2.1. Условия стационарности для процессов авторегрессии
- 3.2.2. Автокорреляционная функция и спектр процессов авторегрессии
- 3.2.3. Процесс авторегрессии первого порядка (марковский процесс)
- 3.2.4. Процесс авторегрессии второго порядка
- 3.2.5. Частная автокорреляционная функция
- 3.2.6. Оценивание частной автокорреляционной функции
- 3.2.7. Стандартные ошибки частной автокорреляции
- 3.3. Процессы скользящего среднего
- 3.3.1. Условия обратимости для процессов скользящего среднего
- 3.3.2. Автокорреляционная функция и спектр процесса скользящего среднего
- 3.3.3. Процесс скользящего среднего первого порядка
- 3.3.4. Процесс скользящего среднего второго порядка
- 3.3.5. Взаимность процессов авторегрессии и скользящего среднего
- 3.4. Смешанные процессы авторегрессии — скользящего среднего
- 3.4.1. Свойства стационарности и обратимости
- 3.4.2. Автокорреляционная функция и спектр смешанных процессов
- 3.4.3. Процесс авторегрессии первого порядка — скользящего среднего первого порядка
- 3.3.4. Резюме
- Приложение П3.1. Автоковариации.
- Приложение П3.2. Рекурентный метод вычисления оценок параметров авторегрессии
- Глава 4. Линейные нестационарные модели
- 4.1. Процессы авторегрессии — проинтегрированного скользящего среднего
- 4.1.1. Нестационарность процесса авторегрессии первого порядка
- 4.1.2. Общая модель для нестационарного процесса, проявляющего однородность
- 4.1.3. Общий вид процесса авторегрессии – проинтегрированного скользящего среднего
- 4.2. Три формы представления модели авторегрессии – проинтегрированного скользящего среднего
- 4.2.1. Представление модели в виде разности уравнения
- 4.2.2. Представление модели, использующее случайные импульсы
- 4.2.3. Обращенное представление модели
- 4.3. Процессы проинтегрированного скользящего среднего
- 4.3.1. Процесс проинтегрированного скользящего среднего порядка (0,1,1)
- 4.3.2. Процесс проинтегрированного скользящего среднего порядка (0.2.2)
- 4.3.3. Общий процесс проинтегрированного скользящего среднего порядка (0, d, q)
- Приложение П4.1. Линейные разностные уравнения
- Приложение П4.2. Процесс ПСС(0,1,1) с детерминированным дрейфом нуля
- Приложение П4.3. Свойства конечного оператора ссумирования
- Приложение П4.4. Процессы АРПСС с добавленным шумом
- Глава 5. Прогнозирование
- 5.1. Прогнозы с минимальной среднеквадратичной ошибкой и их свойства
- 5.1.1. Вывод формулы для прогнозов с минимальной среднеквадратичной ошибкой
- 5.1.2. Три основных представления прогноза
- 5.2. Вычисление и подправление прогноза
- 5.2.1. Удобная схема для вычисления прогнозов
- 5.2.2. Вычисление весов
- 5.2.3. Использование весов при подправлении прогнозов
- 5.2.4. Вычисление вероятностных пределов прогнозов при произвольном упреждении
- 5.3. Прогнозирующая функция и веса прогноза
- 5.3.1. Эвентуальная прогнозирующая функция, определенная оператором авторегрессии
- 5.3.2. Роль оператора скользящего среднего в определении начальных величин
- 5.3.3. Веса прогноза для упреждения l
- 5.4. Примеры прогнозирующих функций и их подправления
- 5.4.1. Прогнозирование процесса ПСС(0, 1, 1)
- 5.4.2. Прогнозирование процесса ПСС(0, 2, 2)
- 5.4.3. Прогнозирование общего процесса ПСС(0, d, q)
- 5.4.4. Прогнозирование процессов авторегрессии
- 5.4.5. Прогнозирование процесса (1, 0, 1)
- 5.4.6. Прогнозирование процесса (1,1,1)
- 5.5. Резюме
- Приложение П5.1. Корреляция между ошибками прогноза
- Приложение П5.2. Веса прогноза для произвольного упреждения
- Приложение П5.3. Прогнозирование при помощи общего проинтегрированного представления
- Часть II. Построение стохастических моделей
- Глава 6. Идентификация моделей
- 6.1. Цели идентификации
- 6.1.1. Этапы процедуры идентификации
- 6.2. Методика идентификации
- 6.2.1. Использование при идентификаций автокорреляционной и частной автокорреляционной функций
- 6.2.2. Стандартные ошибки выборочных автокорреляций и частных автокорреляций
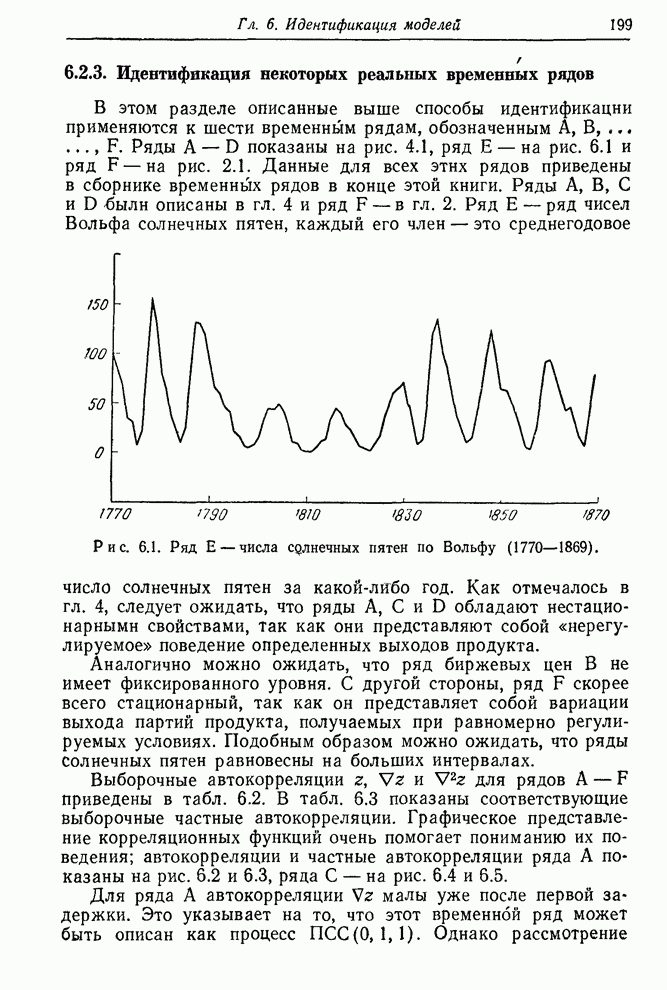
- 6.2.3. Идентификация некоторых реальных временных рядов
- 6.3. Начальные оценки параметров
- 6.3.1. Единственность оценок, получаемых по автоковариационной функции
- 6.3.2. Начальные оценки для процессов скользящего среднего
- 6.3.3. Начальные оценки для процессов авторегрессии
- 6.3.4. Начальные оценки для смешанных процессов авторегрессии — скользящего среднего
- 6.3.5. Выбор между стационарными и нестационарными моделями в спорных случаях
- 6.3.6. Начальные оценки остаточной дисперсии
- 6.3.7. Приближенная стандартная ошибка для
- 6.4. Многозначность моделей
- 6.4.1. Многозначность моделей авторегрессии — скользящего среднего
- 6.4.2. Многозначные решения при оценке параметров скользящего среднего методом моментов
- 6.4.3. Использование возвратного процесса для определения начальных значений
- Приложение П6.1. Среднее значение выборочной автокорреляционной функции нестационарного процесса
- Приложение П6.2. Общий метод получения начальных оценок параметров смешанного процесса авторегрессии – скользящего среднего
- Приложение П6.3. Прямой и возратный процессы ПСС порядка (0, 1, 1)
- Глава 7. Оценивание модели
- 7.1. Исследование функций правдоподобия и суммы квадратов
- 7.1.1. Функция правдоподобия
- 7.1.2. Условное правдоподобие для процесса АРПСС
- 7.1.3. Выбор начальных значений для вычисления условного правдоподобия
- 7.1.4. Безусловное правдоподобие; сумма квадратов; оценки наименьших квадратов
- 7.1.5. Общий способ вычисления безусловной суммы квадратов
- 7.1.6. Графическое исследование суммы квадратов
- 7.1.7. Описание «благоприятных» оценочных ситуаций; доверительные области
- 7.2. Нелинейное оценивание
- 7.2.2. Численный метод нахождения производных
- 7.2.3. Прямой метод нахождения производных
- 7.2.4. Общий алгоритм наименьших квадратов для условной модели
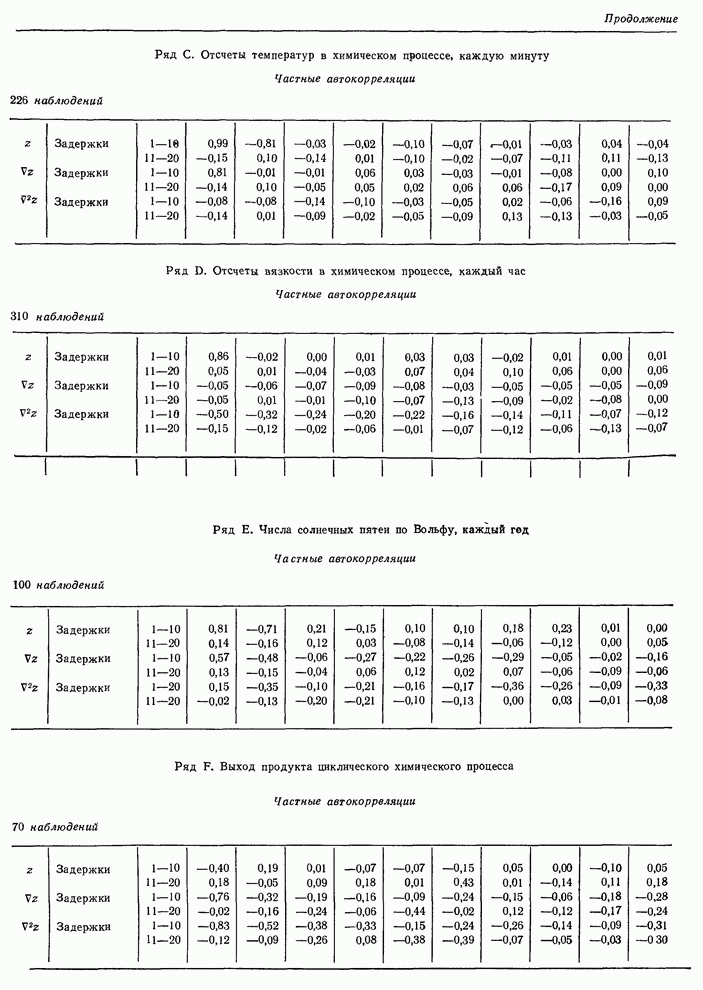
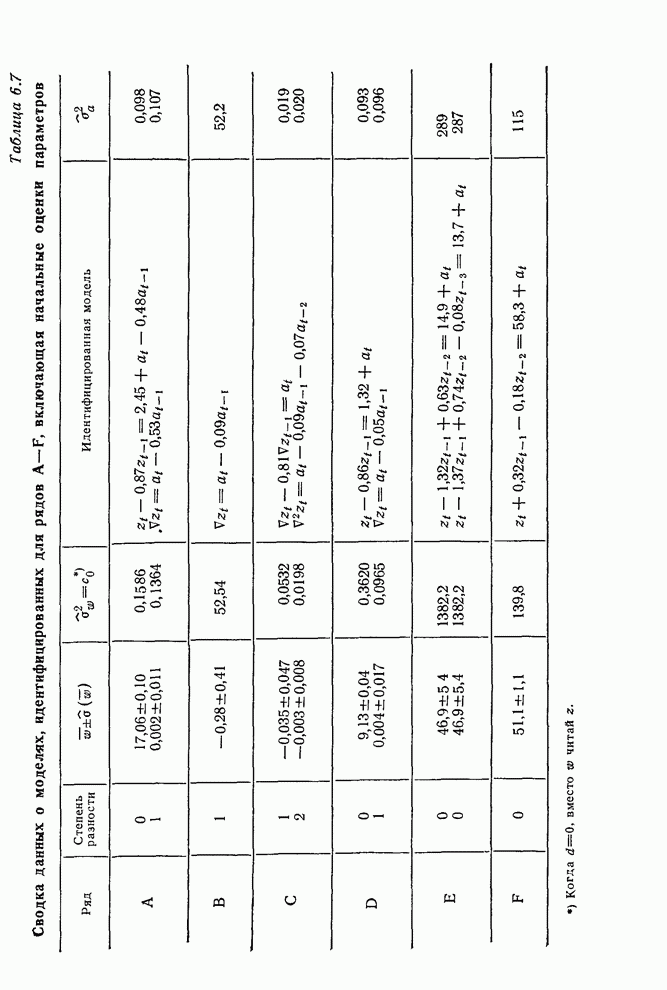
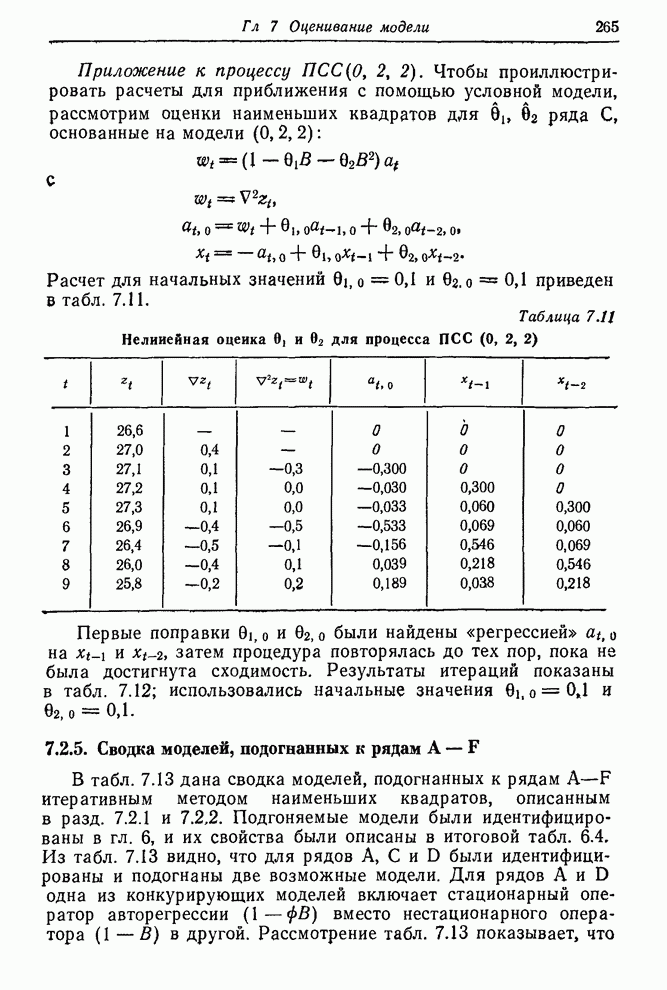
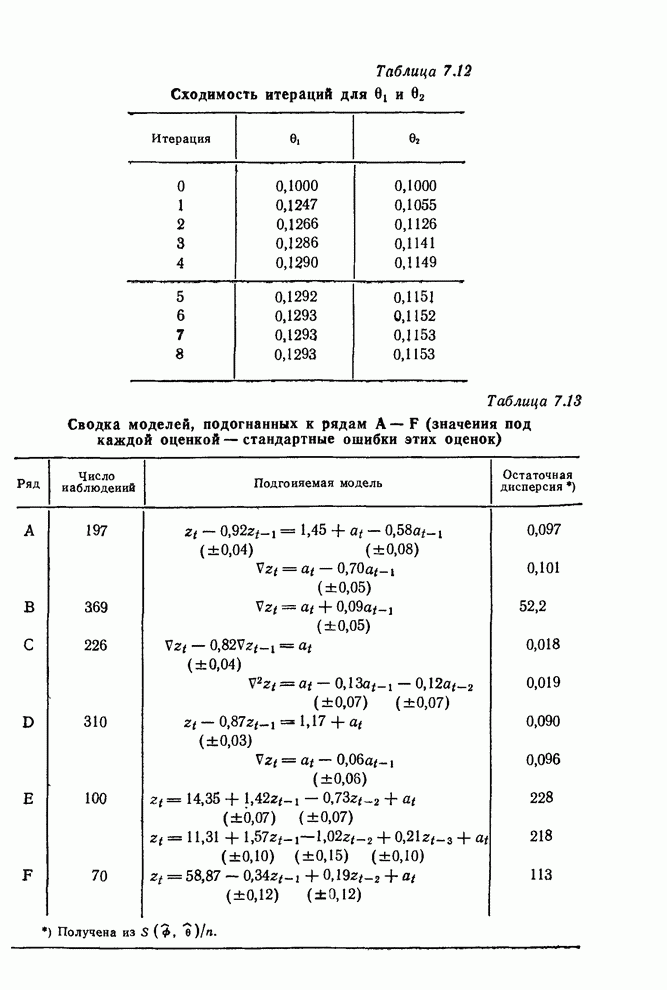
- 7.2.5. Сводка моделей, подогнанных к рядам A-F
- 7.2.6. Информационные матрицы при больших выборках и оценки ковариаций
- 7.3. Результаты оценивания для некоторых частных моделей
- 7.З.2. Процессы скользящего среднего
- 7.3.3. Смешанные процессы
- 7.3.4. Разделение линейных и нелинейных компонент при оценивании
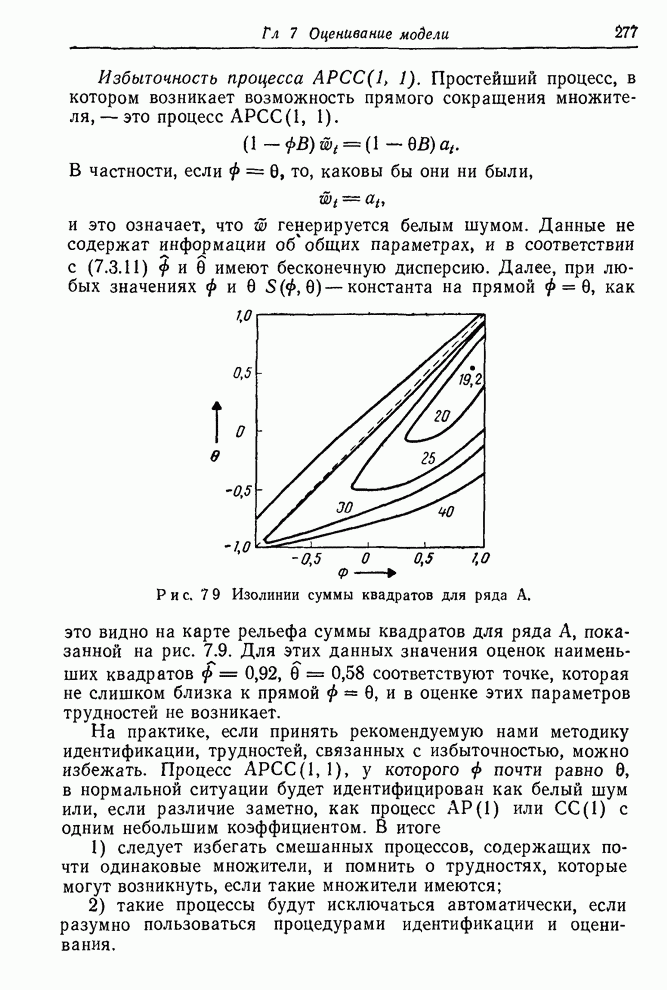
- 7.3.5. Избыточность параметров
- 7.4. Оценивание при помощи теоремы Байеса
- 7.4.2. Байесовское оценивание параметров
- 7.4.3. Процессы авторегрессии
- 7.4.4. Процессы скользящего среднего
- 7.4.5. Смешанные процессы
- Приложение П7.1. Обзор теории нормального распределения
- Приложение П7.2. Обзор линейной теории наименьших квадратов
- Приложение П7.3. Примеры влияния ошибок оценивания параметров на вероятностные пределы прогнозов
- Приложение П7.4. Точная функция правдоподобия для процесса скользящего среднего
- Приложение П7.5. Точная функция правдоподобия для процесса авторегрессии
- Глава 8. Диагностическая проверка модели
- 8.1. Проверка стохастических моделей
- 8.1.2. Введение избыточных параметров
- 8.2.1. Проверка при помощи автокорреляций
- 8.2.2. Совокупный критерий согласия
- 8.2.3. Неадекватность модели, возникающая из-за изменения значений параметров
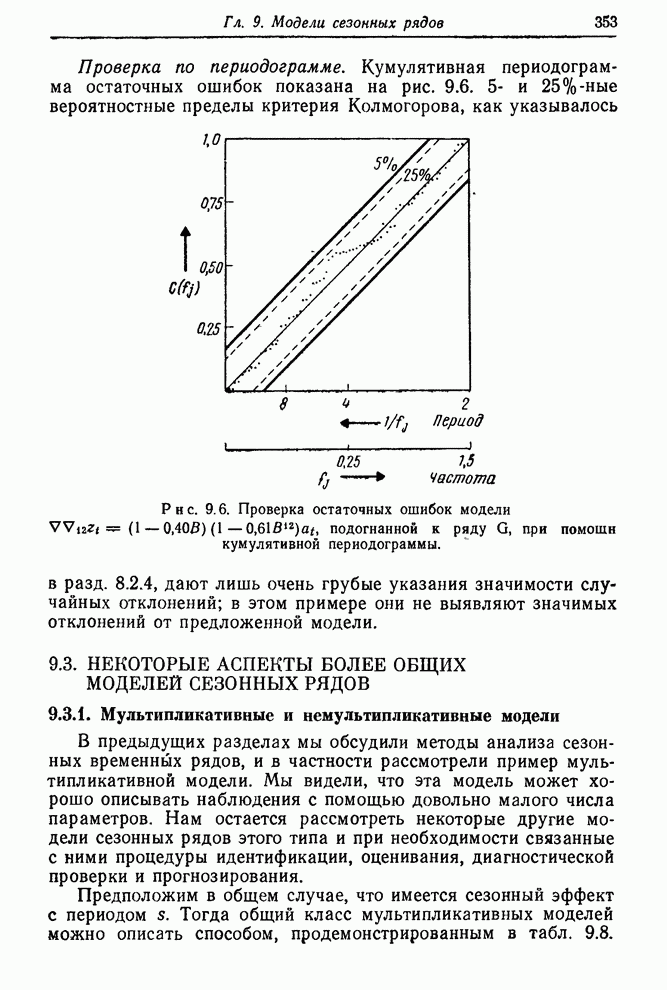
- 8.2.4. Проверка при помощи кумулятивной периодограммы
- 8.3. Использование остаточных ошибок для изменения модели
- 8.3.1. Природа корреляций остаточных ошибок при использовании неверной модели
- 8.3.2. Использование остаточных ошибок для изменения модели
- Глава 9. Модели сезонных рядов
- 9.1. Экономические модели сезонных временных рядов
- 9.1.1. Сопоставление подгонки и прогнозирования
- 9.1.2. Сезонные модели, включающие подстраивающиеся синусоиды и косинусоиды
- 9.1.3. Общая мультипликативная модель сезонного ряда
- 9.2. Представление данных об авиаперевозках мультипликативной моделью
- 9.2.1. Мультипликативная модель
- 9.2.2. Прогнозирование
- 9.2.3. Идентификация
- 9.2.4. Оценивание
- 9.2.5. Диагностическая проверка
- 9.3. Некоторые аспекты более общих моделей сезонных рядов
- 9.3.1. Мультипликативные и немультипликативные модели
- 9.3.2. Идентификация
- 9.3.3. Оценивание
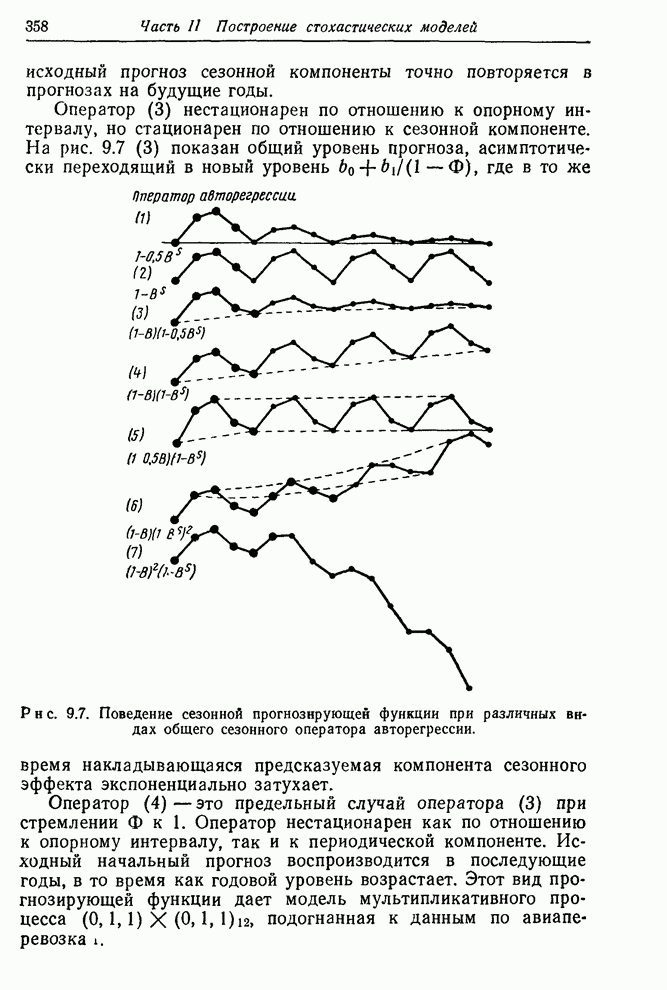
- 9.3.4. Эвентуальные прогнозирующие функции для различных моделей сезонных рядов
- Вспомогательные материалы
- Программа 1 Идентификация стохастической модели
- Программа 2 Предварительное оценивание стохастической модели
- Программа 3. Оценивание стохастической модели
- Алгоритм марквардта для нелинейного метода наименьших квадратов
- Программа 4. Прогнозирование с помощью стохастической модели
- Сборник таблиц и диаграмм