| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
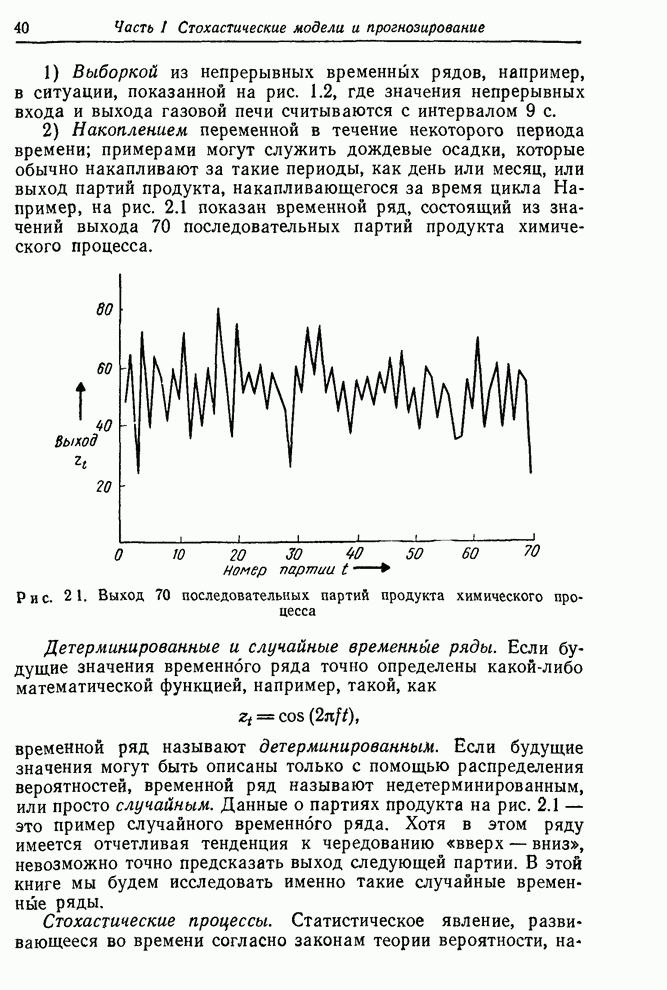
Приложение П5.3. Прогнозирование при помощи общего проинтегрированного представления
П5.3.1. Общий метод получения проинтегрированного представления
Подчеркнем еще раз, что для практического
вычисления прогнозов использование разностного уравнения — наиболее простой
путь. Нижеследующее общее рассмотрение проинтегрированного представления нужно,
чтобы совершенствовать уже полученные прогнозы. В этом рассмотрении вместо
того, чтобы получить явное выражение для функции прогноза, как мы делали в
примерах из разд. 5.4, будет удобнее выписать общее выражение для эвентуальной
прогнозирующей функции, включающее ![]() подстраиваемых
коэффициентов. Мы затем покажем, как нужно изменять эвентуальную прогнозирующую
функцию, чтобы получать первые
подстраиваемых
коэффициентов. Мы затем покажем, как нужно изменять эвентуальную прогнозирующую
функцию, чтобы получать первые ![]() прогнозов при
прогнозов при ![]() В завершение будет показано, как корректировать
подстраиваемые коэффициенты при переходе от момента
В завершение будет показано, как корректировать
подстраиваемые коэффициенты при переходе от момента ![]() к моменту
к моменту ![]() .
.
Поскольку очевидно,
что ![]() для
для
![]() то,
используя рассуждения об условных математических ожиданиях в разд. 5.1.2, легко
прийти к разностному уравнению для прогнозов
то,
используя рассуждения об условных математических ожиданиях в разд. 5.1.2, легко
прийти к разностному уравнению для прогнозов
 (П5.3.1)
(П5.3.1)
Эвентуальная прогнозирующая функция — это решение последнего уравнения и может быть представлена как
 (П5.3.2)
(П5.3.2)
Когда ![]() эвентуальная прогнозирующая функция дает
прогнозы
эвентуальная прогнозирующая функция дает
прогнозы ![]() ...
для всех упреждений
...
для всех упреждений ![]()
Как пример такой модели с ![]() рассмотрим
рассмотрим
![]()
так что ![]() и
и ![]() Тогда
Тогда
![]()
где ![]() действует теперь на
действует теперь на ![]() , а не на
, а не на ![]() . Решение этого
разностного уравнения дает функцию прогноза
. Решение этого
разностного уравнения дает функцию прогноза

Если ![]() то для упреждения
то для упреждения ![]() прогнозирующая функция будет
иметь дополнительные члены, содержащие
прогнозирующая функция будет
иметь дополнительные члены, содержащие ![]() . Отсюда
. Отсюда
 (П5.3.3)
(П5.3.3)
где ![]() и
и ![]() можно выразить явно, подставив (П5.3.3)
в (П5.3.1). Например, рассмотрим стохастическую модель
можно выразить явно, подставив (П5.3.3)
в (П5.3.1). Например, рассмотрим стохастическую модель
![]()
в которой ![]() и
и ![]() Пользуясь рекуррентным
соотношением (5.2.3), получаем
Пользуясь рекуррентным
соотношением (5.2.3), получаем ![]() Далее, из (П5.3.3) следует
Далее, из (П5.3.3) следует
 (П5.2.3)
(П5.2.3)
Кроме того, (П5.3.1) дает
![]()
![]()
так что из (П5.3.4) имеем
![]()
и, следовательно, ![]() Аналогично из (П5.3.1)
Аналогично из (П5.3.1)
![]()
и отсюда, пользуясь (П5.3.4), имеем
![]()
что приводит к
![]()
Следовательно, прогнозирующая функция будет

П5.3.2. Коррекция общего проинтегрированного представления
Коррекцию формул для коэффициентов можно
осуществить, используя тождество (5.2.5) с ![]() замененным на
замененным на ![]()
![]()
Тогда для ![]()
 (П5.3.5)
(П5.3.5)
Решив ![]() таких уравнений для разных
таких уравнений для разных ![]() , получим требуемую
формулу для коррекции в виде
, получим требуемую
формулу для коррекции в виде

Заметим, что коррекция каждого коэффициента функции
прогноза зависит только от ошибки прогноза на один шаг ![]() В качестве примера рассмотрим
опять стохастическую модель
В качестве примера рассмотрим
опять стохастическую модель
![]()
В разд. П5.3.1 было показано, что прогнозирующая функция для этого примера равна
![]()
Удобно использовать тождество коррекции (П5.3.5) для
частных значений ![]() Пользуясь
рекуррентным соотношением (5.2.3), получаем веса
Пользуясь
рекуррентным соотношением (5.2.3), получаем веса ![]() для этих значений:
для этих значений: ![]()
![]()
![]() Отсюда, используя (П5.3.5),
получаем матричное уравнение
Отсюда, используя (П5.3.5),
получаем матричное уравнение

Первые три уравнения легко решить
относительно![]() а четвертое и пятое — относительно
а четвертое и пятое — относительно ![]() Окончательное решение будет
Окончательное решение будет

что дает требуемую формулу коррекции для каждого из 5
коэффициентов ![]()
П5.3.3. Сравнение с методом взвешенных наименьших квадратов Брауна
Хотя проинтегрированное представление приводит к усложнению вычисления прогнозов, оно позволяет нам сравнить рассмотренный здесь прогноз с наименьшей среднеквадратичной ошибкой с другим достаточно известным типом прогноза. Запишем

Тогда, пользуясь (П5.3.5) для ![]() получим для
получим для ![]()
![]()
что дает
![]()
или
![]() (П5.3.6)
(П5.3.6)
Это выражение имеет ту же алгебраическую форму, что и корректирующая функция, предлагаемая в
методике «взвешенных наименьших квадратов» Брауна [2, 50]. Для сравнения, если
мы обозначим ошибку прогноза, даваемую этим методом, ![]() , то формулу коррекции Брауна можно записать в виде
, то формулу коррекции Брауна можно записать в виде
![]() (П5.3.7)
(П5.3.7)
где ![]() — вектор настраиваемых коэффициентов.
Та же матрица
— вектор настраиваемых коэффициентов.
Та же матрица ![]() появляется
в (П5.3.6) и (П5.3.7). Это неизбежно, так как первый множитель просто учитывает
изменения в коэффициентах, возникающие при переходе к новому начальному
моменту, и должен появиться в любой формуле такого типа. Рассмотрим, например,
функцию прогноза в виде прямой линии
появляется
в (П5.3.6) и (П5.3.7). Это неизбежно, так как первый множитель просто учитывает
изменения в коэффициентах, возникающие при переходе к новому начальному
моменту, и должен появиться в любой формуле такого типа. Рассмотрим, например,
функцию прогноза в виде прямой линии
![]()
где ![]() — ордината в момент
— ордината в момент ![]() начала прогноза Можно также
записать
начала прогноза Можно также
записать
![]()
где ![]() — теперь ордината в момент
— теперь ордината в момент ![]() . Очевидно, если мы корректируем прогноз в момент
. Очевидно, если мы корректируем прогноз в момент ![]() коэффициент
коэффициент ![]() должен быть
соответствующим образом подправлен, даже если бы функция прогноза осталась
неизменной.
должен быть
соответствующим образом подправлен, даже если бы функция прогноза осталась
неизменной.
В общем матрица ![]() не изменяет прогнозирующую
функцию, а просто перемещает ее. Истинная корректировка производится вектором
коэффициентов
не изменяет прогнозирующую
функцию, а просто перемещает ее. Истинная корректировка производится вектором
коэффициентов ![]() или
или
![]() . Далее мы
увидим, что коэффициенты
. Далее мы
увидим, что коэффициенты ![]() , дающие прогнозы с минимальной
среднеквадратичной ошибкой, и коэффициенты
, дающие прогнозы с минимальной
среднеквадратичной ошибкой, и коэффициенты ![]() Брауна в общем полностью отличны друг
от друга.
Брауна в общем полностью отличны друг
от друга.
Метод прогнозирования Брауна
1) Прогнозирующая функция выбирается из общего класса линейных комбинаций и произведений полиномов, экспонент, синусов и косинусов.
2) Выбранная прогнозирующая функция подгоняется к прошлым значениям при помощи методики «взвешенных наименьших квадратов». В этой методике коэффициенты оцениваются и корректируются так, что минимизируется сумма
 (П5.3.8)
(П5.3.8)
взвешенных квадратов расхождения прошлых
значений ряда и значений, даваемых для соответствующих времен в прошлом
прогнозирующей функцией. Весовая функция ![]() выбирается произвольно, так чтобы она
спадала по степенному закону
выбирается произвольно, так чтобы она
спадала по степенному закону ![]() где константа
где константа ![]() , обычно называемая константой сглаживания, выбирается равной опять-таки произвольному значению
в диапазоне 0,1—0,3.
, обычно называемая константой сглаживания, выбирается равной опять-таки произвольному значению
в диапазоне 0,1—0,3.
Различие между прогнозами с минимальной среднеквадратичной ошибкой и прогнозами Брауна.
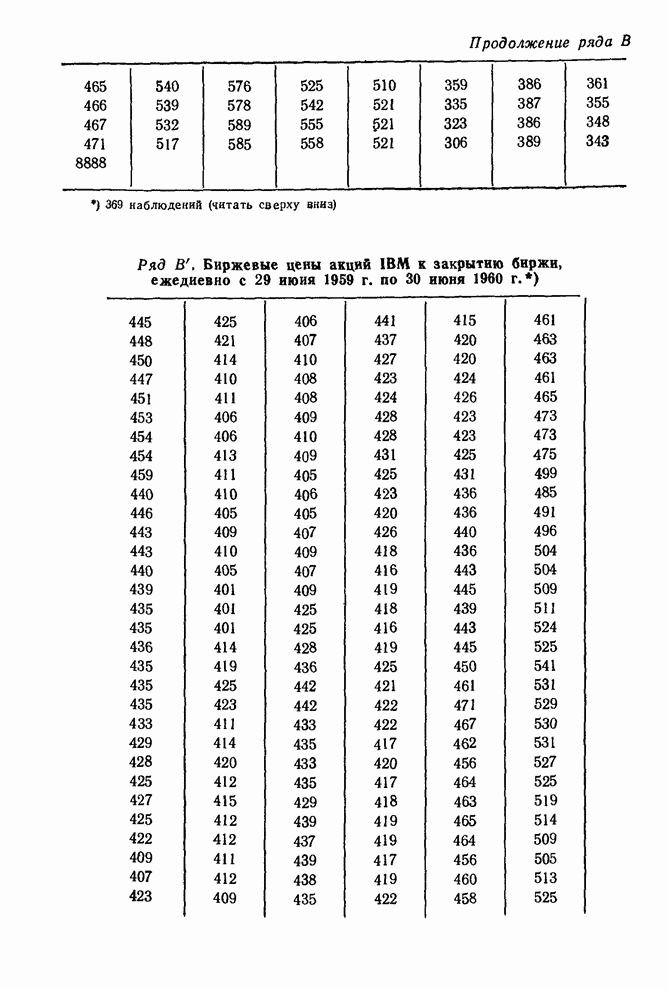
Чтобы проиллюстрировать эти замечания, рассмотрим прогнозирование цен акций IВМ, обсуждавшееся Брауном [2, стр. 141]. В этом исследовании он использовал квадратичную модель, которая в обозначениях этой книги может быть представлена как
![]()
Он применил к этой модели свой метод «взвешенных наименьших квадратов», чтобы предсказать биржевые цены на три дня вперед. Результаты, полученные его методом, показаны для участка ряда IВМ на рис. П5.2, где они сравниваются с прогнозами с минимальной среднеквадратичной ошибкой.
Метод «взвешенных наименьших квадратов» можно подвергнуть критике на следующих основаниях:
1) Вид прогнозирующей функции должен определяться
оператором авторегрессии ![]() стохастической модели, а не выбираться
произвольно. В частности, его нельзя уверенно выбрать в результате визуального
просмотра ряда. Рассмотрим, например, биржевые цены акций IBM
на рис. П5.2. Видно, что квадратичная функция может быть использована для подгонок коротких участков этого ряда к уже имеющимся
значениям. Если бы такая подгонка имела отношение к прогнозированию, мы могли
бы заключить, как и сделал Браун, что прогнозирующая функция должна быть
полиномом второй степени.
стохастической модели, а не выбираться
произвольно. В частности, его нельзя уверенно выбрать в результате визуального
просмотра ряда. Рассмотрим, например, биржевые цены акций IBM
на рис. П5.2. Видно, что квадратичная функция может быть использована для подгонок коротких участков этого ряда к уже имеющимся
значениям. Если бы такая подгонка имела отношение к прогнозированию, мы могли
бы заключить, как и сделал Браун, что прогнозирующая функция должна быть
полиномом второй степени.
Наиболее общий линейный процесс, для
которого квадратичная функция давала бы прогнозы с наименьшей среднеквадратичной
ошибкой при любом упреждении ![]() определяется моделью
(0,3,3)
определяется моделью
(0,3,3)
![]()
которая на основании тех же рассуждений, что и в разд. 4.3.3, может быть представлена в виде
![]()
Однако в гл. 7 будет показано, что если
правильно подогнать эту модель, оценки ее параметров, полученные методом
наименьших квадратов, окажутся равными ![]() и
и ![]() Отсюда
Отсюда ![]() с
с ![]() , близкими к нулю, будет подходящей
стохастической моделью, и соответствующий прогнозирующий полином будет
, близкими к нулю, будет подходящей
стохастической моделью, и соответствующий прогнозирующий полином будет ![]() , т.е. нулевой, а не второй степени по
, т.е. нулевой, а не второй степени по ![]() .
.
2) Выбор весовой функции ![]() , в (П5.3.8) должен также определяться
стохастической моделью, а не быть произвольным. Метод «взвешенных наименьших
квадратов» будет давать прогнозы с минимальной среднеквадратичной ошибкой
только в очень частном случае, когда
, в (П5.3.8) должен также определяться
стохастической моделью, а не быть произвольным. Метод «взвешенных наименьших
квадратов» будет давать прогнозы с минимальной среднеквадратичной ошибкой
только в очень частном случае, когда
а) процесс имел порядок (0,1,1), так что![]()
б) подгонялся полином нулевой степени;
в) константа сглаживания ![]() была принята равной
нашему
была принята равной
нашему ![]() .
.

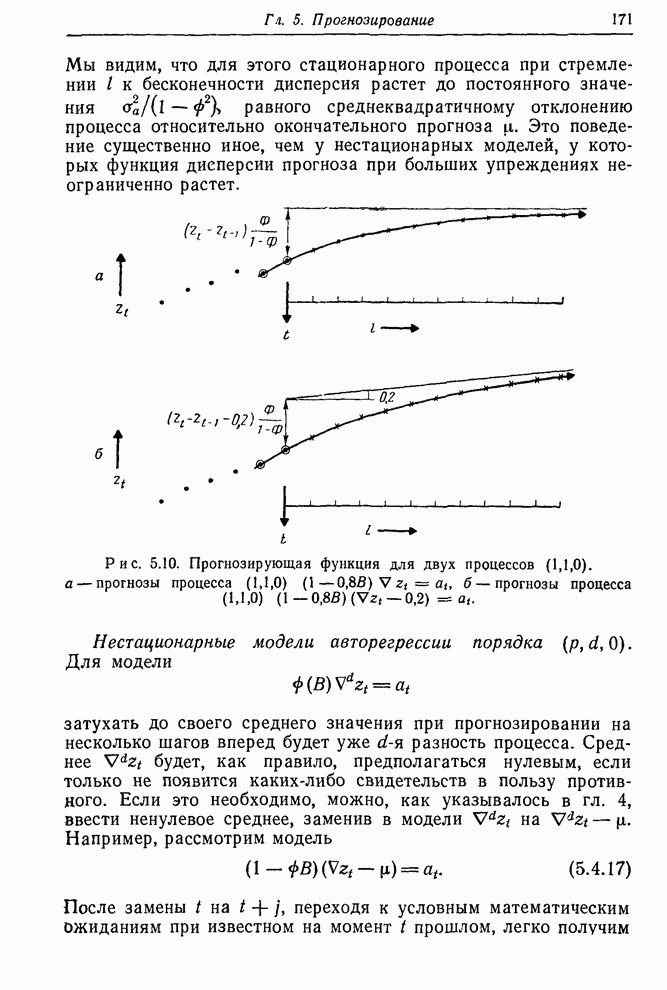
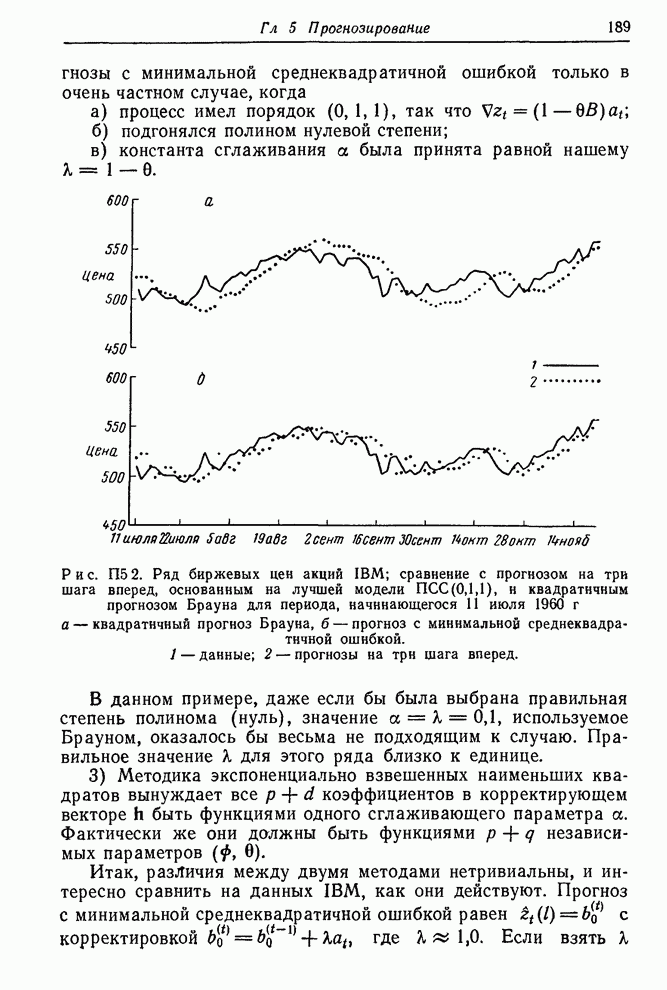
Рис. П5 2. Ряд биржевых цен акций IВМ; сравнение с прогнозом на три шага вперед, основанным на лучшей модели ПСС (0,1,1), к квадратичным
прогнозом Брауна для периода, начинающегося 11 июля 1960 г.: а — квадратичный прогноз Брауна, б — прогноз с минимальной среднеквадратичной ошибкой.
1 — данные; 2 — прогнозы на три шага вперед.
В данном примере, даже если бы была
выбрана правильная степень полинома (нуль), значение ![]() , используемое Брауном,
оказалось бы весьма не подходящим к случаю. Правильное значение
, используемое Брауном,
оказалось бы весьма не подходящим к случаю. Правильное значение ![]() для этого ряда
близко к единице.
для этого ряда
близко к единице.
3) Методика экспоненциально взвешенных
наименьших квадратов вынуждает все ![]() коэффициентов в корректирующем векторе
коэффициентов в корректирующем векторе ![]() быть функциями
одного сглаживающего параметра
быть функциями
одного сглаживающего параметра ![]() . Фактически же они должны быть
функциями
. Фактически же они должны быть
функциями ![]() независимых
параметров
независимых
параметров ![]() .
.
Итак, различия между двумя методами
нетривиальны, и интересно сравнить на данных IBM, как они
действуют. Прогноз с минимальной среднеквадратичной ошибкой равен ![]() с корректировкой
с корректировкой ![]() где
где ![]() . Если взять
. Если взять ![]() точно
равным единице, это эквивалентно использованию
точно
равным единице, это эквивалентно использованию
![]() ,
,
т. е. лучший прогноз цен акций для всех будущих
моментов времени есть текущая цена. Идея, что биржевые цены ведут себя так,
конечно, не нова и восходит к Бейгельеру [51]. При ![]() , что свидетельствует, что
, что свидетельствует, что ![]() —
случайное блуждание.
—
случайное блуждание.
Для сопоставления прогноза с минимальной
среднеквадратичной ошибкой (СКО) с квадратичными прогнозами Брауна было
проведено прямое сравнение на базе ряда цен акций IBM за период с
11 июля 1960 г. по 10 февраля 1961 г. (150 наблюдений). Для этого участка ряда
прогноз с минимальной СКО был получен для модели ![]() , или
, или ![]() . На рис.
П5.2 показаны прогнозы с минимальной СКО для упреждения 3 и соответствующие
значения квадратичного прогноза Брауна. Видно, что прогнозы с минимальной СКО,
которые, по существу, эквивалентны использованию сегодняшней цены для
предсказания цены на 3 дня вперед, значительно лучше, чем полученные с помощью
существенно более сложной методики Брауна.
. На рис.
П5.2 показаны прогнозы с минимальной СКО для упреждения 3 и соответствующие
значения квадратичного прогноза Брауна. Видно, что прогнозы с минимальной СКО,
которые, по существу, эквивалентны использованию сегодняшней цены для
предсказания цены на 3 дня вперед, значительно лучше, чем полученные с помощью
существенно более сложной методики Брауна.
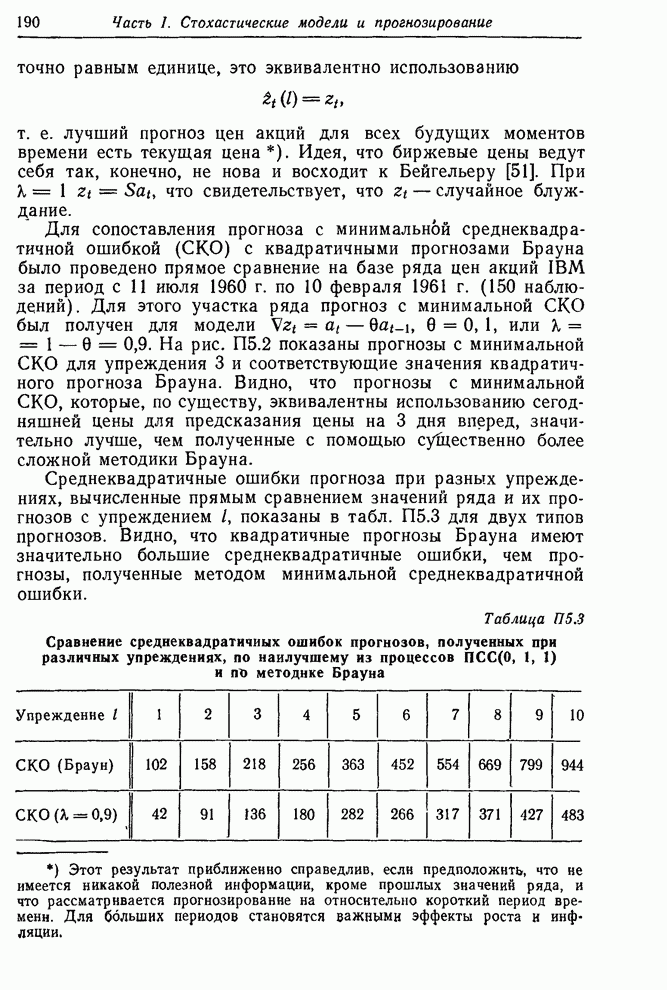
Среднеквадратичные ошибки прогноза при разных
упреждениях, вычисленные прямым сравнением значений ряда и их прогнозов с
упреждением ![]() ,
показаны в табл. П5.3 для двух типов прогнозов. Видно, что квадратичные
прогнозы Брауна имеют значительно большие среднеквадратичные ошибки, чем
прогнозы, полученные методом минимальной среднеквадратичной ошибки.
,
показаны в табл. П5.3 для двух типов прогнозов. Видно, что квадратичные
прогнозы Брауна имеют значительно большие среднеквадратичные ошибки, чем
прогнозы, полученные методом минимальной среднеквадратичной ошибки.
Таблица П5.3. Сравнение среднеквадратичных ошибок прогнозов, полученных при различных упреждениях, по наилучшему из процессов ПСС(0,1,1) и по методике Брауна
|
Упреждение
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
СКО (Браун) |
102 |
158 |
218 |
256 |
363 |
452 |
554 |
669 |
799 |
944 |
|
СКО
|
42 |
91 |
136 |
180 |
282 |
266 |
317 |
371 |
427 |
483 |
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- Предисловие
- План книги
- Глава 1. Введение и краткое содержание
- 1.1. Три важные практические проблемы
- 1.1.1. Прогнозирование временных рядов
- 1.1.2. Оценивание передаточных функций
- 1.1.3. Проектирование дискретных регулирующих систем
- 1.2. Стохастические и детерминированные динамические математические модели
- 1.2.1. Стационарные нестационарные стохастические модели для прогнозирования и регулирования
- 1.2.2. Модели передаточных функций
- 1.2.3. Модели дискретных систем регулирования
- 1.3. Основные понятия в построении моделей
- 1.3.1. Экономия
- 1.3.2. Интерактивные этапы в выборе модели
- Часть 1. Стохастические модели и основанное на них прогнозирование
- Глава 2. Автокорреляционная функция и спектр
- 2.1. Автокорреляционные свойства стационарных моделей
- 2.1.1. Временные ряды и стохастические процессы
- 2.1.2. Стационарные стохастические процессы
- 2.1.3. Положительная определённость и автоковариационная матрица
- 2.1.4. Автоковариационные и автокорреляционные функции
- 2.1.5. Оценивание автоковариационной и автокорреляционной функций
- 2.1.6. Стандартные ошибки оценок автокорреляций
- 2.2. Спектральные свойства стационарных моделей
- 2.2.1. Периодограмма
- 2.2.2. Дисперсионный анализ
- 2.2.3. Спектральная плотность и нормированный спектр
- 2.2.4. Простые примеры автокорреляционных функций и нормированных спектров
- 2.2.5. Преимущества и недостатки автокорреляционных функций и нормированных спектров
- Приложение П2.1. Связь между выборочным спектром и оценкой автоковариационной функции
- Глава 3. Линейные стационарные модели
- 3.1. Общий линейный процесс
- 3.1.1. Две эквивалентные формы линейного процесса
- 3.1.2. Производящая функция автоковариаций линейного процесса
- 3.1.3. Условия стационарности и обратимости линейного процесса
- 3.1.4. Процессы авторегрессии и скользящего среднего
- 3.2. Процессы авторегрессии
- 3.2.1. Условия стационарности для процессов авторегрессии
- 3.2.2. Автокорреляционная функция и спектр процессов авторегрессии
- 3.2.3. Процесс авторегрессии первого порядка (марковский процесс)
- 3.2.4. Процесс авторегрессии второго порядка
- 3.2.5. Частная автокорреляционная функция
- 3.2.6. Оценивание частной автокорреляционной функции
- 3.2.7. Стандартные ошибки частной автокорреляции
- 3.3. Процессы скользящего среднего
- 3.3.1. Условия обратимости для процессов скользящего среднего
- 3.3.2. Автокорреляционная функция и спектр процесса скользящего среднего
- 3.3.3. Процесс скользящего среднего первого порядка
- 3.3.4. Процесс скользящего среднего второго порядка
- 3.3.5. Взаимность процессов авторегрессии и скользящего среднего
- 3.4. Смешанные процессы авторегрессии — скользящего среднего
- 3.4.1. Свойства стационарности и обратимости
- 3.4.2. Автокорреляционная функция и спектр смешанных процессов
- 3.4.3. Процесс авторегрессии первого порядка — скользящего среднего первого порядка
- 3.3.4. Резюме
- Приложение П3.1. Автоковариации.
- Приложение П3.2. Рекурентный метод вычисления оценок параметров авторегрессии
- Глава 4. Линейные нестационарные модели
- 4.1. Процессы авторегрессии — проинтегрированного скользящего среднего
- 4.1.1. Нестационарность процесса авторегрессии первого порядка
- 4.1.2. Общая модель для нестационарного процесса, проявляющего однородность
- 4.1.3. Общий вид процесса авторегрессии – проинтегрированного скользящего среднего
- 4.2. Три формы представления модели авторегрессии – проинтегрированного скользящего среднего
- 4.2.1. Представление модели в виде разности уравнения
- 4.2.2. Представление модели, использующее случайные импульсы
- 4.2.3. Обращенное представление модели
- 4.3. Процессы проинтегрированного скользящего среднего
- 4.3.1. Процесс проинтегрированного скользящего среднего порядка (0,1,1)
- 4.3.2. Процесс проинтегрированного скользящего среднего порядка (0.2.2)
- 4.3.3. Общий процесс проинтегрированного скользящего среднего порядка (0, d, q)
- Приложение П4.1. Линейные разностные уравнения
- Приложение П4.2. Процесс ПСС(0,1,1) с детерминированным дрейфом нуля
- Приложение П4.3. Свойства конечного оператора ссумирования
- Приложение П4.4. Процессы АРПСС с добавленным шумом
- Глава 5. Прогнозирование
- 5.1. Прогнозы с минимальной среднеквадратичной ошибкой и их свойства
- 5.1.1. Вывод формулы для прогнозов с минимальной среднеквадратичной ошибкой
- 5.1.2. Три основных представления прогноза
- 5.2. Вычисление и подправление прогноза
- 5.2.1. Удобная схема для вычисления прогнозов
- 5.2.2. Вычисление весов
- 5.2.3. Использование весов при подправлении прогнозов
- 5.2.4. Вычисление вероятностных пределов прогнозов при произвольном упреждении
- 5.3. Прогнозирующая функция и веса прогноза
- 5.3.1. Эвентуальная прогнозирующая функция, определенная оператором авторегрессии
- 5.3.2. Роль оператора скользящего среднего в определении начальных величин
- 5.3.3. Веса прогноза для упреждения l
- 5.4. Примеры прогнозирующих функций и их подправления
- 5.4.1. Прогнозирование процесса ПСС(0, 1, 1)
- 5.4.2. Прогнозирование процесса ПСС(0, 2, 2)
- 5.4.3. Прогнозирование общего процесса ПСС(0, d, q)
- 5.4.4. Прогнозирование процессов авторегрессии
- 5.4.5. Прогнозирование процесса (1, 0, 1)
- 5.4.6. Прогнозирование процесса (1,1,1)
- 5.5. Резюме
- Приложение П5.1. Корреляция между ошибками прогноза
- Приложение П5.2. Веса прогноза для произвольного упреждения
- Приложение П5.3. Прогнозирование при помощи общего проинтегрированного представления
- Часть II. Построение стохастических моделей
- Глава 6. Идентификация моделей
- 6.1. Цели идентификации
- 6.1.1. Этапы процедуры идентификации
- 6.2. Методика идентификации
- 6.2.1. Использование при идентификаций автокорреляционной и частной автокорреляционной функций
- 6.2.2. Стандартные ошибки выборочных автокорреляций и частных автокорреляций
- 6.2.3. Идентификация некоторых реальных временных рядов
- 6.3. Начальные оценки параметров
- 6.3.1. Единственность оценок, получаемых по автоковариационной функции
- 6.3.2. Начальные оценки для процессов скользящего среднего
- 6.3.3. Начальные оценки для процессов авторегрессии
- 6.3.4. Начальные оценки для смешанных процессов авторегрессии — скользящего среднего
- 6.3.5. Выбор между стационарными и нестационарными моделями в спорных случаях
- 6.3.6. Начальные оценки остаточной дисперсии
- 6.3.7. Приближенная стандартная ошибка для
- 6.4. Многозначность моделей
- 6.4.1. Многозначность моделей авторегрессии — скользящего среднего
- 6.4.2. Многозначные решения при оценке параметров скользящего среднего методом моментов
- 6.4.3. Использование возвратного процесса для определения начальных значений
- Приложение П6.1. Среднее значение выборочной автокорреляционной функции нестационарного процесса
- Приложение П6.2. Общий метод получения начальных оценок параметров смешанного процесса авторегрессии – скользящего среднего
- Приложение П6.3. Прямой и возратный процессы ПСС порядка (0, 1, 1)
- Глава 7. Оценивание модели
- 7.1. Исследование функций правдоподобия и суммы квадратов
- 7.1.1. Функция правдоподобия
- 7.1.2. Условное правдоподобие для процесса АРПСС
- 7.1.3. Выбор начальных значений для вычисления условного правдоподобия
- 7.1.4. Безусловное правдоподобие; сумма квадратов; оценки наименьших квадратов
- 7.1.5. Общий способ вычисления безусловной суммы квадратов
- 7.1.6. Графическое исследование суммы квадратов
- 7.1.7. Описание «благоприятных» оценочных ситуаций; доверительные области
- 7.2. Нелинейное оценивание
- 7.2.2. Численный метод нахождения производных
- 7.2.3. Прямой метод нахождения производных
- 7.2.4. Общий алгоритм наименьших квадратов для условной модели
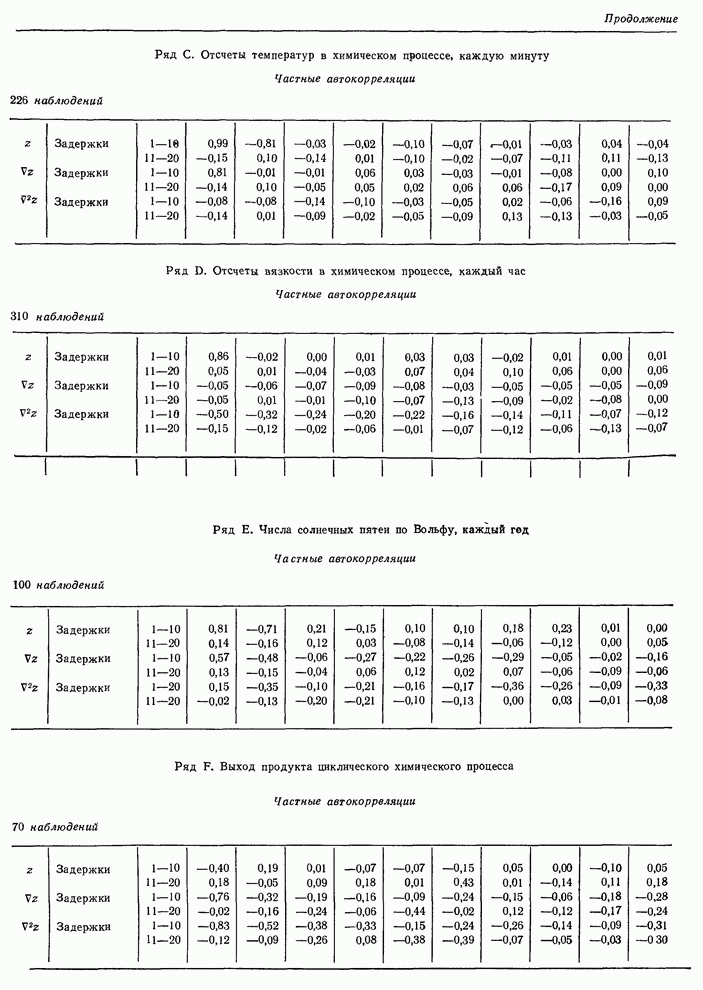
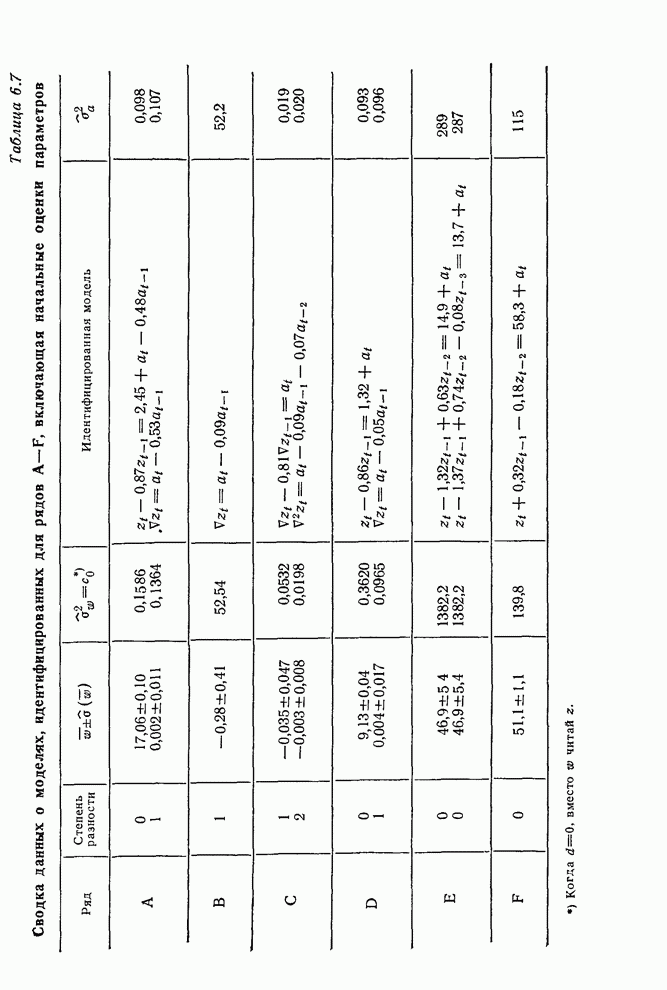
- 7.2.5. Сводка моделей, подогнанных к рядам A-F
- 7.2.6. Информационные матрицы при больших выборках и оценки ковариаций
- 7.3. Результаты оценивания для некоторых частных моделей
- 7.З.2. Процессы скользящего среднего
- 7.3.3. Смешанные процессы
- 7.3.4. Разделение линейных и нелинейных компонент при оценивании
- 7.3.5. Избыточность параметров
- 7.4. Оценивание при помощи теоремы Байеса
- 7.4.2. Байесовское оценивание параметров
- 7.4.3. Процессы авторегрессии
- 7.4.4. Процессы скользящего среднего
- 7.4.5. Смешанные процессы
- Приложение П7.1. Обзор теории нормального распределения
- Приложение П7.2. Обзор линейной теории наименьших квадратов
- Приложение П7.3. Примеры влияния ошибок оценивания параметров на вероятностные пределы прогнозов
- Приложение П7.4. Точная функция правдоподобия для процесса скользящего среднего
- Приложение П7.5. Точная функция правдоподобия для процесса авторегрессии
- Глава 8. Диагностическая проверка модели
- 8.1. Проверка стохастических моделей
- 8.1.2. Введение избыточных параметров
- 8.2.1. Проверка при помощи автокорреляций
- 8.2.2. Совокупный критерий согласия
- 8.2.3. Неадекватность модели, возникающая из-за изменения значений параметров
- 8.2.4. Проверка при помощи кумулятивной периодограммы
- 8.3. Использование остаточных ошибок для изменения модели
- 8.3.1. Природа корреляций остаточных ошибок при использовании неверной модели
- 8.3.2. Использование остаточных ошибок для изменения модели
- Глава 9. Модели сезонных рядов
- 9.1. Экономические модели сезонных временных рядов
- 9.1.1. Сопоставление подгонки и прогнозирования
- 9.1.2. Сезонные модели, включающие подстраивающиеся синусоиды и косинусоиды
- 9.1.3. Общая мультипликативная модель сезонного ряда
- 9.2. Представление данных об авиаперевозках мультипликативной моделью
- 9.2.1. Мультипликативная модель
- 9.2.2. Прогнозирование
- 9.2.3. Идентификация
- 9.2.4. Оценивание
- 9.2.5. Диагностическая проверка
- 9.3. Некоторые аспекты более общих моделей сезонных рядов
- 9.3.1. Мультипликативные и немультипликативные модели
- 9.3.2. Идентификация
- 9.3.3. Оценивание
- 9.3.4. Эвентуальные прогнозирующие функции для различных моделей сезонных рядов
- Вспомогательные материалы
- Программа 1 Идентификация стохастической модели
- Программа 2 Предварительное оценивание стохастической модели
- Программа 3. Оценивание стохастической модели
- Алгоритм марквардта для нелинейного метода наименьших квадратов
- Программа 4. Прогнозирование с помощью стохастической модели
- Сборник таблиц и диаграмм