| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение П7.5. Точная функция правдоподобия для процесса авторегрессии
Положим, что
данный ряд ![]() генерируется
стационарной моделью авторегрессии
генерируется
стационарной моделью авторегрессии ![]() -го порядка
-го порядка
![]() ,
,
причем временно предполагается, что ![]() имеют среднее
значение
имеют среднее
значение ![]() ,
но, как и прежде, допускается обобщение на случай
,
но, как и прежде, допускается обобщение на случай ![]() . Предполагая, что
. Предполагая, что ![]() , а следовательно, и
, а следовательно, и ![]() подчиняются
нормальному закону, получаем функцию совместной плотности вероятности:
подчиняются
нормальному закону, получаем функцию совместной плотности вероятности:
 ; (П7.5.1)
; (П7.5.1)
из-за обратимости общего процесса
матрица ![]() размером
размером
![]() симметрична
относительно обеих главных диагоналей. Можно сказать, что такая матрица дважды симметрична.
Имеем
симметрична
относительно обеих главных диагоналей. Можно сказать, что такая матрица дважды симметрична.
Имеем
![]() ,
,
где ![]() . Первый множитель в правой части можно
получить, используя распределение
. Первый множитель в правой части можно
получить, используя распределение
 . (П7.5.2)
. (П7.5.2)
Для фиксированных ![]() и
и ![]() связаны преобразованием
связаны преобразованием

с единичным якобианом. Отсюда имеем
 .
.
Кроме того,
 .
.
Тогда
 , (П7.5.3)
, (П7.5.3)
где
 . (П7.5.4)
. (П7.5.4)
Кроме того,
 , (П7.5.5)
, (П7.5.5)
где ![]() - теоретические автоковариации
процесса, а
- теоретические автоковариации
процесса, а ![]() .
.
Пусть ![]() , так что
, так что
 .
.
Тогда
 .
.
и элементы ![]() можно найти, пользуясь
соображением о двойной симметричности как
можно найти, пользуясь
соображением о двойной симметричности как ![]() , так и
, так и ![]() . Так, например
. Так, например
 ,
,
и после приравнивания элементов двух матриц имеем
![]() .
.
Продолжая действовать таким же образом, для процессов порядка 1 и 2 находим

Например, для ![]()
 ,
,
что совпадает с результатом (П7.4.15).
Эта процедура должна привести к матрицам ![]() , элементы которых — квадратичные функции
, элементы которых — квадратичные функции
![]() .
.
Из (П7.5.4)
очевидно, что ![]() -
квадратичная форма не только от
-
квадратичная форма не только от ![]() , но и от параметров
, но и от параметров ![]() . Если представить
. Если представить ![]() в виде
в виде ![]() , становится
очевидным, что для некоторой матрицы
, становится
очевидным, что для некоторой матрицы ![]() размером
размером ![]() , элементы которой -
квадратичные функции, справедливо равенство
, элементы которой -
квадратичные функции, справедливо равенство
![]() .
.
Запишем теперь
 . (П7.5.6)
. (П7.5.6)
Рассмотрение (П7.5.4) показывает, что
элементы ![]() —
симметричные суммы квадратов и произведения членов с задержками, определяемые
как
—
симметричные суммы квадратов и произведения членов с задержками, определяемые
как
![]() , (П7.5.7)
, (П7.5.7)
где сумма ![]() содержит
содержит ![]() слагаемых.
слагаемых.
Наконец, мы можем записать точное выражение для плотности вероятности и, следовательно, для функции правдоподобия:
 , (П7.5.8)
, (П7.5.8)
где
 , (П7.5.9)
, (П7.5.9)
и логарифмическая функция правдоподобия равна
 . (П7.5.10)
. (П7.5.10)
Оценки
максимального правдоподобия. Дифференцируя по ![]() и каждому из
и каждому из ![]() в (П7.5.10),
получаем
в (П7.5.10),
получаем
 , (П7.5.11)
, (П7.5.11)
![]() , (П7.5.12)
, (П7.5.12)
где
 .
.
Отсюда можно получить оценки максимального правдоподобия - для этого надо приравнять все производные нулю и решить получающиеся уравнения.
Из (П7.5.11) сразу получаем
![]() . (П7.5.13)
. (П7.5.13)
Оценки ![]() . При решении
уравнения (П7.5.12) возникают трудности, так как в общем случае величины
. При решении
уравнения (П7.5.12) возникают трудности, так как в общем случае величины ![]() — сложные функции
— сложные функции ![]() . Рассмотрим кратко
три возможных приближенных способа решения.
. Рассмотрим кратко
три возможных приближенных способа решения.
1) Оценки наименьших квадратов.
В то время как
математическое ожидание ![]() пропорционально
пропорционально ![]() , значение
, значение ![]() от
от ![]() не зависит; для
средних и больших выборок в (П7.5.8) доминирует член, содержащий
не зависит; для
средних и больших выборок в (П7.5.8) доминирует член, содержащий ![]() , а член с
, а член с ![]() сравнительно мал.
сравнительно мал.
Если мы пренебрежем влиянием этого члена, то
 , (П7.5.14)
, (П7.5.14)
и оценки ![]() параметров
параметров ![]() , полученные путем
максимизации (П7.5.14), совпадают с оценками наименьших квадратов, полученными
минимизацией
, полученные путем
максимизации (П7.5.14), совпадают с оценками наименьших квадратов, полученными
минимизацией ![]() .
Так, из (П7.5.9) следует, что
.
Так, из (П7.5.9) следует, что ![]() , где
, где ![]() - матрица симметричных сумм квадратов
и произведений размером
- матрица симметричных сумм квадратов
и произведений размером ![]() , определенная в (П7.5.7).
Дифференцируя, находим значения, дающие минимум сумм
, определенная в (П7.5.7).
Дифференцируя, находим значения, дающие минимум сумм
 (П7.5.15)
(П7.5.15)
которые в очевидных матричных обозначениях можно записать как
![]() ,
,
так что
![]() .
.
Эти оценки наименьших квадратов максимизируют апостериорную плотность вероятности (7.4.15).
2) Приближенные оценки максимального правдоподобия.
Вспомним полученный ранее результат (3.2.3), который можно записать в виде
![]() . (П7.5.16)
. (П7.5.16)
Беря математические ожидания от обеих
частей (П7.5.12) и пользуясь тем, что ![]() , получаем
, получаем
![]() . (П7.5.17)
. (П7.5.17)
Умножив (П7.5.16) на ![]() и вычтя результат из
(П7.5.17), получим
и вычтя результат из
(П7.5.17), получим
![]() .
.
Далее, используя ![]() как оценку
как оценку ![]() получаем
естественную оценку
получаем
естественную оценку ![]() :
:
![]() .
.
Подставляя эту оценку в (П7.5.12), находим
 , (П7.5.18)
, (П7.5.18)
что ведет к системе линейных уравнений в
форме (П7.5.15), в которых вместо ![]() стоит
стоит
![]() .
.
3) Оценки Юла-Уокера.
Наконец, если ![]() не мало, мы можем
приближенно заменить симметричные суммы квадратов и произведений в (П7.5.15)
соответствующими оценками автоковариаций, умноженными на
не мало, мы можем
приближенно заменить симметричные суммы квадратов и произведений в (П7.5.15)
соответствующими оценками автоковариаций, умноженными на ![]() . Например,
. Например, ![]() , где
, где ![]() , нужно заменить на
, нужно заменить на  . Разделив все
члены полученных уравнений на
. Разделив все
члены полученных уравнений на ![]() , получим следующие соотношения,
содержащие выборочные оценки автокорреляций
, получим следующие соотношения,
содержащие выборочные оценки автокорреляций ![]() :
:

Это хорошо известные уравнения Юла—Уокера.
В матричных
обозначениях (7.3.1) их можно записать как ![]() , и отсюда
, и отсюда
![]() , (П7.5.19)
, (П7.5.19)
что соответствует уравнению (3.2.7), в
котором ![]() заменено
на
заменено
на ![]() , а
, а ![]() на
на ![]() .
.
Чтобы
продемонстрировать различия трех оценок, рассмотрим случай ![]() . Тогда
. Тогда ![]() , и в соответствии с
(П7.5.12) точная оценка максимального правдоподобия для
, и в соответствии с
(П7.5.12) точная оценка максимального правдоподобия для ![]() будет решением уравнения
будет решением уравнения
 .
.
Приближение (1) полностью игнорирует
слагаемое ![]() что
дает
что
дает
 .
.
Приближение (2) соответствует
подстановке вместо ![]() его выборочной оценки
его выборочной оценки  , что приводит к
, что приводит к
 .
.
Приближение (3) заменяет числитель и знаменатель этой дроби стандартными выборочными оценками автоковариаций (2.1.10), что дает
 .
.
Обычно, как и в этом примере, для не слишком малых выборок различия между оценками, получаемыми путем разных приближений, малы. Как правило, мы пользуемся оценками наименьших квадратов из приближения (1). Эти оценки можно, конечно, вычислить и прямо по (П7.5.15). Однако, предполагая возможность расчетов на ЭВМ, вряд ли стоит рассматривать отдельно процессы авторегрессии; мы нашли, что более просто, даже в случае подгонки процессов авторегрессии, пользоваться общим итеративным алгоритмом, описанным в разд. 7.2.1, позволяющим находить оценки наименьших квадратов для любого процесса АРСС.
Оценки ![]() . Пользуясь
приближением (3), а также (П7.5.9) и (П7.5.13), находим
. Пользуясь
приближением (3), а также (П7.5.9) и (П7.5.13), находим
 .
.
Выполнив умножение в правой части и
учтя, что ![]() ,
найдем
,
найдем
![]() . (П7.5.20а)
. (П7.5.20а)
Легко показать, что ![]() можно аналогичным образом
выразить через теоретические корреляции
можно аналогичным образом
выразить через теоретические корреляции
![]() , (П7.5.20б)
, (П7.5.20б)
что согласуется с результатом (3.2.8).
Сходные выражения для ![]() можно получить при помощи приближений
(1) и (2).
можно получить при помощи приближений
(1) и (2).
Информационная матрица. Дифференцируя (П7.5.11) и (П7.5.18) второй раз, получим
 , (П7.5.21а)
, (П7.5.21а)
 , (П7.5.21б)
, (П7.5.21б)
 . (П7.5.21в)
. (П7.5.21в)
Далее, так как
 ,
,
отсюда следует, что для средних и больших выборок

и
![]() ,
,
где
 .
.
Далее, пользуясь (П7.5.21в), получим
 . (П7.5.22)
. (П7.5.22)
Отсюда
 .
.
Дисперсии и ковариации выборочных оценок параметров авторегрессии. При условиях, подробно рассмотренных в [87], матрица, обратная информационной, является асимптотической матрицей ковариации оценок максимального правдоподобия (МП). Более того, если логарифмическая функция правдоподобия приближенно квадратична и ее максимум не близок к границе, даже для выборки средних размеров элементы этой матрицы хорошо аппроксимируют дисперсии и ковариации оценок. Пользуясь (П7.5.22) и (П7.5.20б), находим
 (П7.5.23)
(П7.5.23)
В частности, для процессов авторегрессии первого и второго порядков
 (П7.5.24)
(П7.5.24)
Оценки дисперсий и ковариаций можно
получить, заменив в (П7.5.24) параметры их выборочными оценками. Например,
подставив ![]() вместо
вместо
![]() и
и ![]() вместо
вместо ![]() в (П7.5.23),
получим
в (П7.5.23),
получим
![]() . (П7.5.25)
. (П7.5.25)
Распространение результатов для
авторегрессий на более общие процессы. Имеется интересное соотношение, позволяющее
нам распространить результаты оценивания для моделей авторегрессии на более
общие модели. Пусть наблюдения генерируются моделью АРСС ![]()
![]() , (П7.5.26)
, (П7.5.26)
где ![]() . Модель можно представить в виде
. Модель можно представить в виде
 . (П7.5.27)
. (П7.5.27)
Пусть ![]() - значения параметров скользящего
среднего, несколько отличающиеся от
- значения параметров скользящего
среднего, несколько отличающиеся от ![]() , и положим, что делается
преобразование
, и положим, что делается
преобразование
 . (П7.5.28)
. (П7.5.28)
Заменив
неизвестные предварительные значения нулями, мы можем использовать это
выражение для генерирования соответствующего ряда ![]() для каждого временного ряда
для каждого временного ряда ![]() из
из ![]() наблюдений,
порождаемого моделью (П7.5.27). Обозначим это преобразование через
наблюдений,
порождаемого моделью (П7.5.27). Обозначим это преобразование через ![]() , так что
, так что ![]() , и так как
, и так как ![]() - треугольная матрица с
диагональными элементами, равными
- треугольная матрица с
диагональными элементами, равными ![]() . Примем
. Примем ![]() . Тогда функция правдоподобия для
параметров
. Тогда функция правдоподобия для
параметров ![]() ,
т. е. для параметров
,
т. е. для параметров ![]() , будет
, будет
![]() .
.
Такой выбор параметров показывает, что ![]() генерируются
моделью АРСС
генерируются
моделью АРСС ![]()
 ,
,
и, следовательно, ![]() генерируются моделью
генерируются моделью
 ,
,
или с хорошей степенью приближения при
малых ![]() моделью
моделью
![]()
 .
.
Соответствующая функция правдоподобия имеет вид
![]() .
.
Для средних и больших выборок
приближения на концах ряда не будут оказывать существенного влияния; функция
правдоподобия мала для больших ![]() , так что существенны только малые
отклонения. Отсюда следует, что
, так что существенны только малые
отклонения. Отсюда следует, что
![]() . (П7.5.29)
. (П7.5.29)
Немедленно получаем следующие результаты.
1)
Положим,
что информационная матрица для параметров ![]() , связанная с моделью АРСС
, связанная с моделью АРСС ![]()
 ,
,
есть ![]() . Положим, что информационная матрица
для параметров
. Положим, что информационная матрица
для параметров ![]() чистой
модели
чистой
модели ![]()

равна
 ,
,
где матрица разбита на части после ![]() строки и столбца.
Тогда для средних и больших выборок
строки и столбца.
Тогда для средних и больших выборок
 . (П7.5.30)
. (П7.5.30)
2) На
рассмотренном уровне приближения отсюда следует, что определители
информационных матриц для процессов АРСС ![]() и
и ![]() идентичны.
идентичны.
3) Так как для
средних и больших выборок матрица, обратная информационной, является хорошим
приближением к ковариационной матрице параметров ![]() , получаем
, получаем
![]() . (П7.5.31)
. (П7.5.31)
4) Запишем теперь
 .
.
Тогда, пользуясь (П7.5.22), находим
![]() . (П7.5.32)
. (П7.5.32)
Кроме того,
![]() , (П7.5.33)
, (П7.5.33)
где
 (П7.5.34)
(П7.5.34)
— якобиан преобразования.
Процессы скользящего среднего; дисперсии и ковариаций оценок МП. Легко показать, что для больших выборок ковариационная матрица оценок МП чистого процесса скользящего среднего точно такая же, как для чистого процесса авторегрессии того же порядка. Тогда, согласно (П7.5.24), для процессов скользящего среднего первого и второго порядков имеем
 .
.
Смешанные
процессы авторегрессии — скользящего среднего; дисперсии и ковариаций
оценок МП.
Для
того чтобы проиллюстрировать, как используется (П7.5.31), рассмотрим процесс
АРСС ![]()
![]() ,
,
который мы сопоставим с процессом ![]()
![]() . (П7.5.35)
. (П7.5.35)
Матрица ковариаций для ![]() и
и ![]() в модели авторегрессии
(П7.5.35), согласно (7.2.22), имеет вид
в модели авторегрессии
(П7.5.35), согласно (7.2.22), имеет вид
 .
.
Отсюда соответствующие дисперсии и
ковариации для процесса АРСС ![]() равны
равны
 .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- Предисловие
- План книги
- Глава 1. Введение и краткое содержание
- 1.1. Три важные практические проблемы
- 1.1.1. Прогнозирование временных рядов
- 1.1.2. Оценивание передаточных функций
- 1.1.3. Проектирование дискретных регулирующих систем
- 1.2. Стохастические и детерминированные динамические математические модели
- 1.2.1. Стационарные нестационарные стохастические модели для прогнозирования и регулирования
- 1.2.2. Модели передаточных функций
- 1.2.3. Модели дискретных систем регулирования
- 1.3. Основные понятия в построении моделей
- 1.3.1. Экономия
- 1.3.2. Интерактивные этапы в выборе модели
- Часть 1. Стохастические модели и основанное на них прогнозирование
- Глава 2. Автокорреляционная функция и спектр
- 2.1. Автокорреляционные свойства стационарных моделей
- 2.1.1. Временные ряды и стохастические процессы
- 2.1.2. Стационарные стохастические процессы
- 2.1.3. Положительная определённость и автоковариационная матрица
- 2.1.4. Автоковариационные и автокорреляционные функции
- 2.1.5. Оценивание автоковариационной и автокорреляционной функций
- 2.1.6. Стандартные ошибки оценок автокорреляций
- 2.2. Спектральные свойства стационарных моделей
- 2.2.1. Периодограмма
- 2.2.2. Дисперсионный анализ
- 2.2.3. Спектральная плотность и нормированный спектр
- 2.2.4. Простые примеры автокорреляционных функций и нормированных спектров
- 2.2.5. Преимущества и недостатки автокорреляционных функций и нормированных спектров
- Приложение П2.1. Связь между выборочным спектром и оценкой автоковариационной функции
- Глава 3. Линейные стационарные модели
- 3.1. Общий линейный процесс
- 3.1.1. Две эквивалентные формы линейного процесса
- 3.1.2. Производящая функция автоковариаций линейного процесса
- 3.1.3. Условия стационарности и обратимости линейного процесса
- 3.1.4. Процессы авторегрессии и скользящего среднего
- 3.2. Процессы авторегрессии
- 3.2.1. Условия стационарности для процессов авторегрессии
- 3.2.2. Автокорреляционная функция и спектр процессов авторегрессии
- 3.2.3. Процесс авторегрессии первого порядка (марковский процесс)
- 3.2.4. Процесс авторегрессии второго порядка
- 3.2.5. Частная автокорреляционная функция
- 3.2.6. Оценивание частной автокорреляционной функции
- 3.2.7. Стандартные ошибки частной автокорреляции
- 3.3. Процессы скользящего среднего
- 3.3.1. Условия обратимости для процессов скользящего среднего
- 3.3.2. Автокорреляционная функция и спектр процесса скользящего среднего
- 3.3.3. Процесс скользящего среднего первого порядка
- 3.3.4. Процесс скользящего среднего второго порядка
- 3.3.5. Взаимность процессов авторегрессии и скользящего среднего
- 3.4. Смешанные процессы авторегрессии — скользящего среднего
- 3.4.1. Свойства стационарности и обратимости
- 3.4.2. Автокорреляционная функция и спектр смешанных процессов
- 3.4.3. Процесс авторегрессии первого порядка — скользящего среднего первого порядка
- 3.3.4. Резюме
- Приложение П3.1. Автоковариации.
- Приложение П3.2. Рекурентный метод вычисления оценок параметров авторегрессии
- Глава 4. Линейные нестационарные модели
- 4.1. Процессы авторегрессии — проинтегрированного скользящего среднего
- 4.1.1. Нестационарность процесса авторегрессии первого порядка
- 4.1.2. Общая модель для нестационарного процесса, проявляющего однородность
- 4.1.3. Общий вид процесса авторегрессии – проинтегрированного скользящего среднего
- 4.2. Три формы представления модели авторегрессии – проинтегрированного скользящего среднего
- 4.2.1. Представление модели в виде разности уравнения
- 4.2.2. Представление модели, использующее случайные импульсы
- 4.2.3. Обращенное представление модели
- 4.3. Процессы проинтегрированного скользящего среднего
- 4.3.1. Процесс проинтегрированного скользящего среднего порядка (0,1,1)
- 4.3.2. Процесс проинтегрированного скользящего среднего порядка (0.2.2)
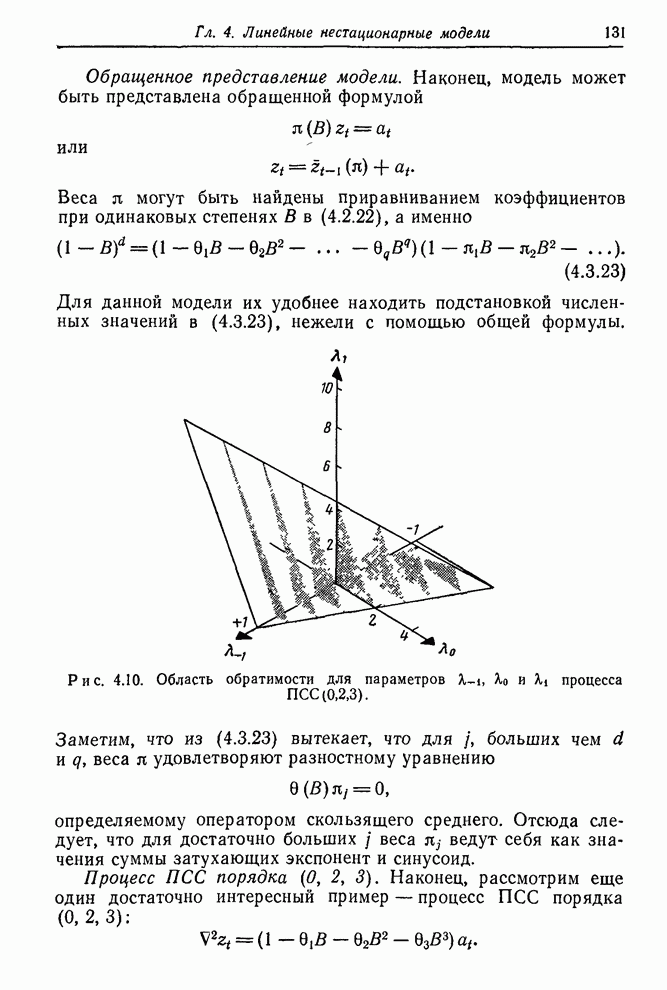
- 4.3.3. Общий процесс проинтегрированного скользящего среднего порядка (0, d, q)
- Приложение П4.1. Линейные разностные уравнения
- Приложение П4.2. Процесс ПСС(0,1,1) с детерминированным дрейфом нуля
- Приложение П4.3. Свойства конечного оператора ссумирования
- Приложение П4.4. Процессы АРПСС с добавленным шумом
- Глава 5. Прогнозирование
- 5.1. Прогнозы с минимальной среднеквадратичной ошибкой и их свойства
- 5.1.1. Вывод формулы для прогнозов с минимальной среднеквадратичной ошибкой
- 5.1.2. Три основных представления прогноза
- 5.2. Вычисление и подправление прогноза
- 5.2.1. Удобная схема для вычисления прогнозов
- 5.2.2. Вычисление весов
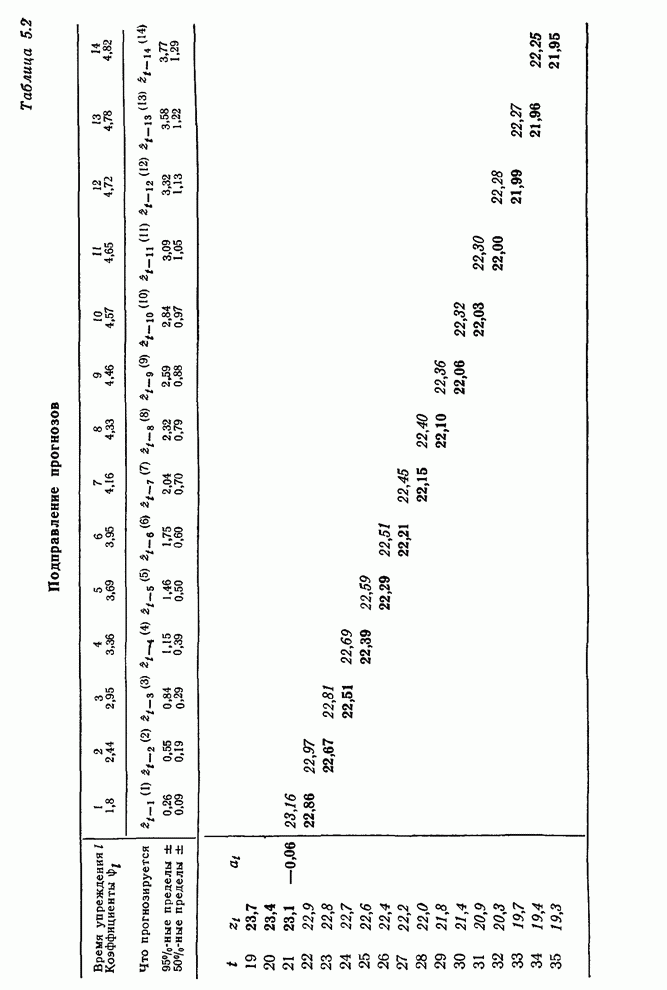
- 5.2.3. Использование весов при подправлении прогнозов
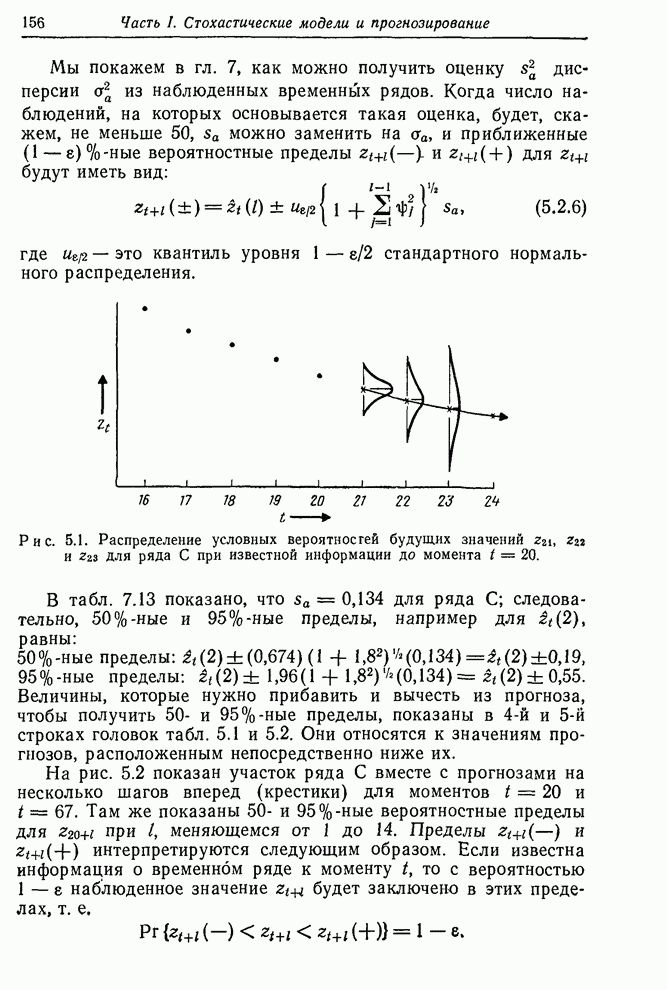
- 5.2.4. Вычисление вероятностных пределов прогнозов при произвольном упреждении
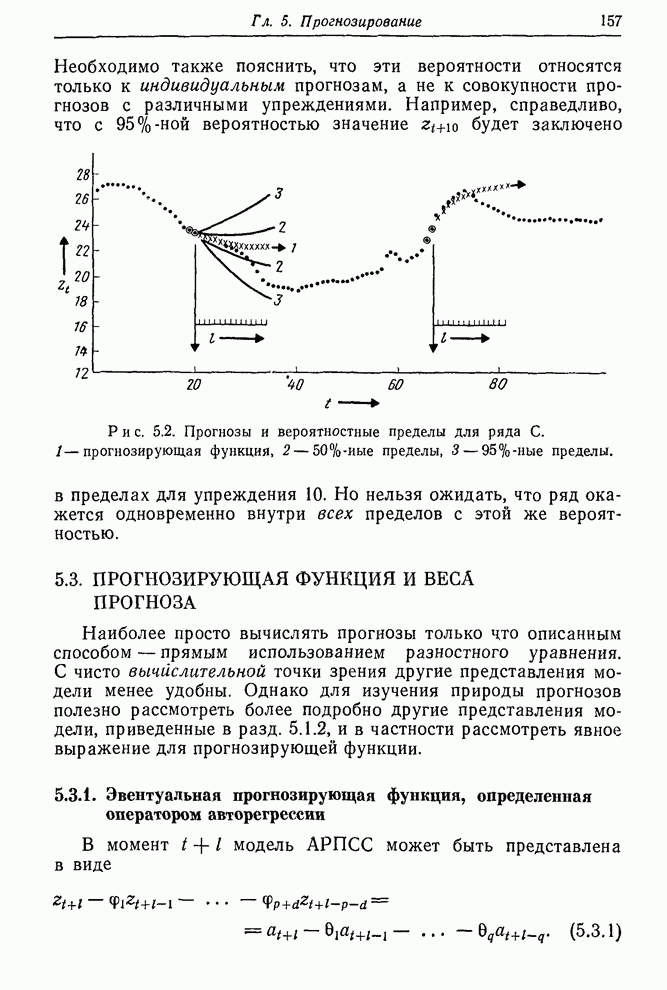
- 5.3. Прогнозирующая функция и веса прогноза
- 5.3.1. Эвентуальная прогнозирующая функция, определенная оператором авторегрессии
- 5.3.2. Роль оператора скользящего среднего в определении начальных величин
- 5.3.3. Веса прогноза для упреждения l
- 5.4. Примеры прогнозирующих функций и их подправления
- 5.4.1. Прогнозирование процесса ПСС(0, 1, 1)
- 5.4.2. Прогнозирование процесса ПСС(0, 2, 2)
- 5.4.3. Прогнозирование общего процесса ПСС(0, d, q)
- 5.4.4. Прогнозирование процессов авторегрессии
- 5.4.5. Прогнозирование процесса (1, 0, 1)
- 5.4.6. Прогнозирование процесса (1,1,1)
- 5.5. Резюме
- Приложение П5.1. Корреляция между ошибками прогноза
- Приложение П5.2. Веса прогноза для произвольного упреждения
- Приложение П5.3. Прогнозирование при помощи общего проинтегрированного представления
- Часть II. Построение стохастических моделей
- Глава 6. Идентификация моделей
- 6.1. Цели идентификации
- 6.1.1. Этапы процедуры идентификации
- 6.2. Методика идентификации
- 6.2.1. Использование при идентификаций автокорреляционной и частной автокорреляционной функций
- 6.2.2. Стандартные ошибки выборочных автокорреляций и частных автокорреляций
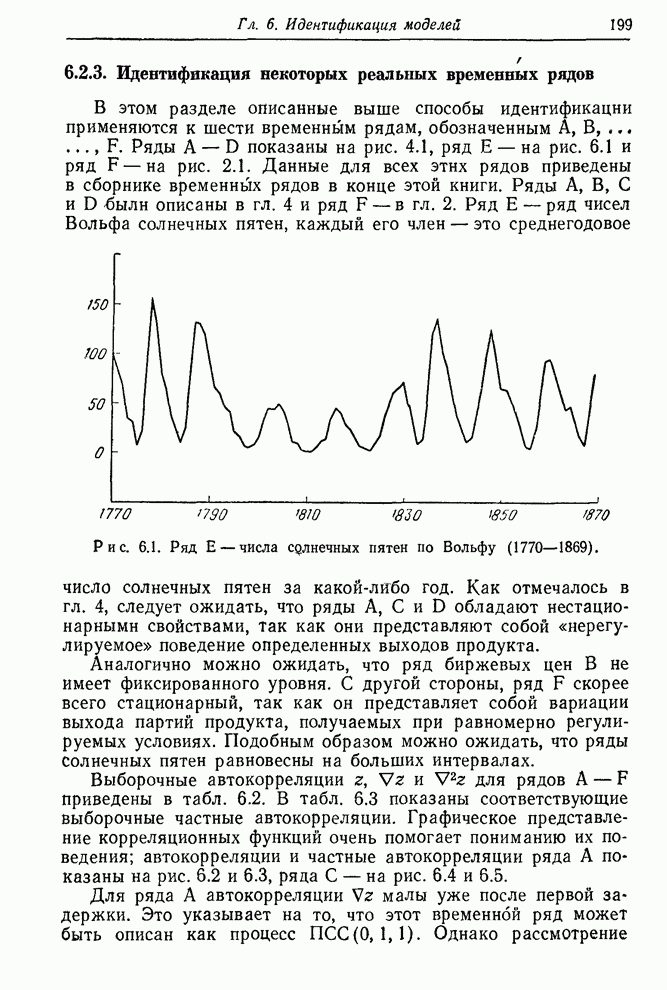
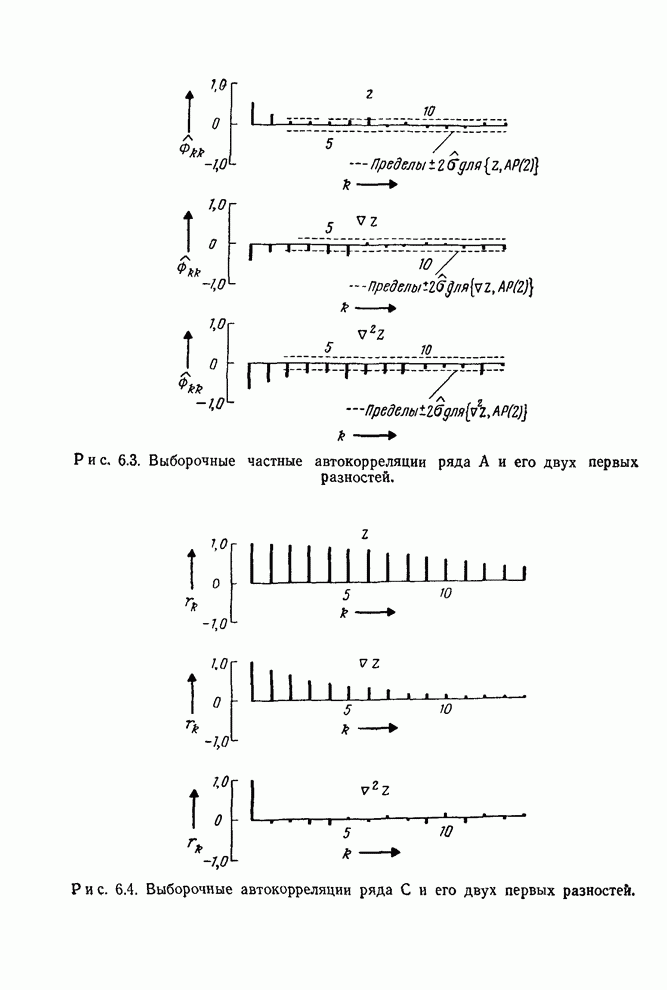
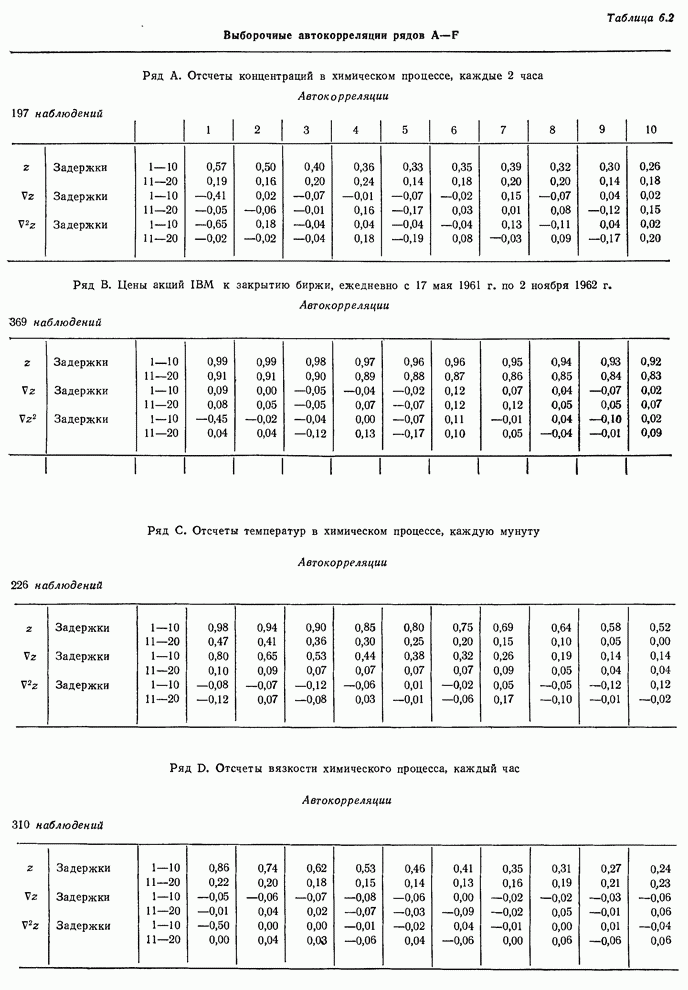
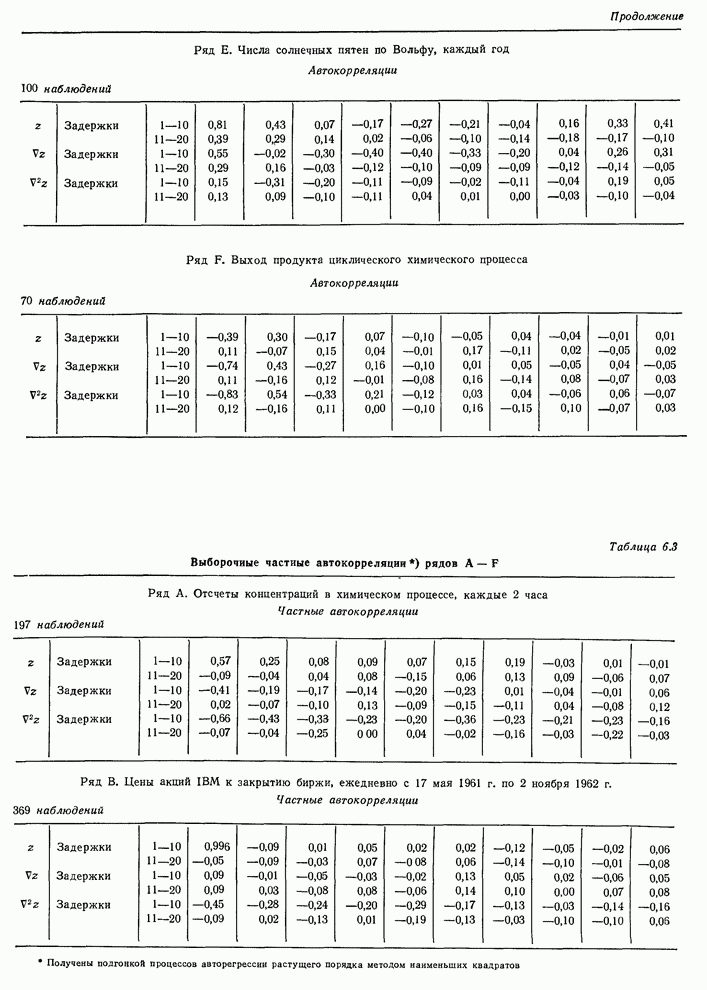
- 6.2.3. Идентификация некоторых реальных временных рядов
- 6.3. Начальные оценки параметров
- 6.3.1. Единственность оценок, получаемых по автоковариационной функции
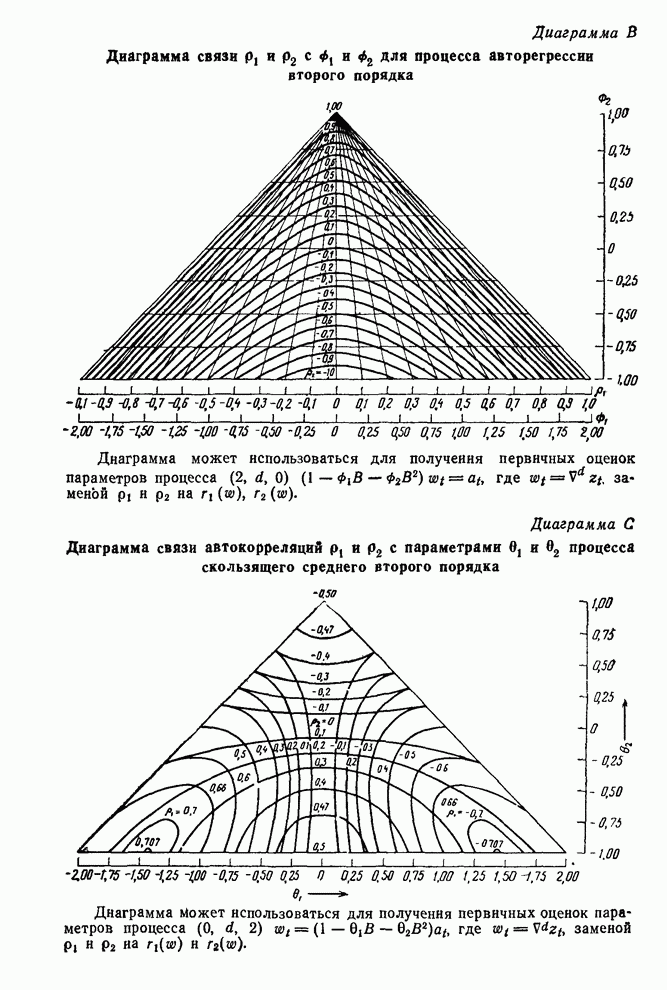
- 6.3.2. Начальные оценки для процессов скользящего среднего
- 6.3.3. Начальные оценки для процессов авторегрессии
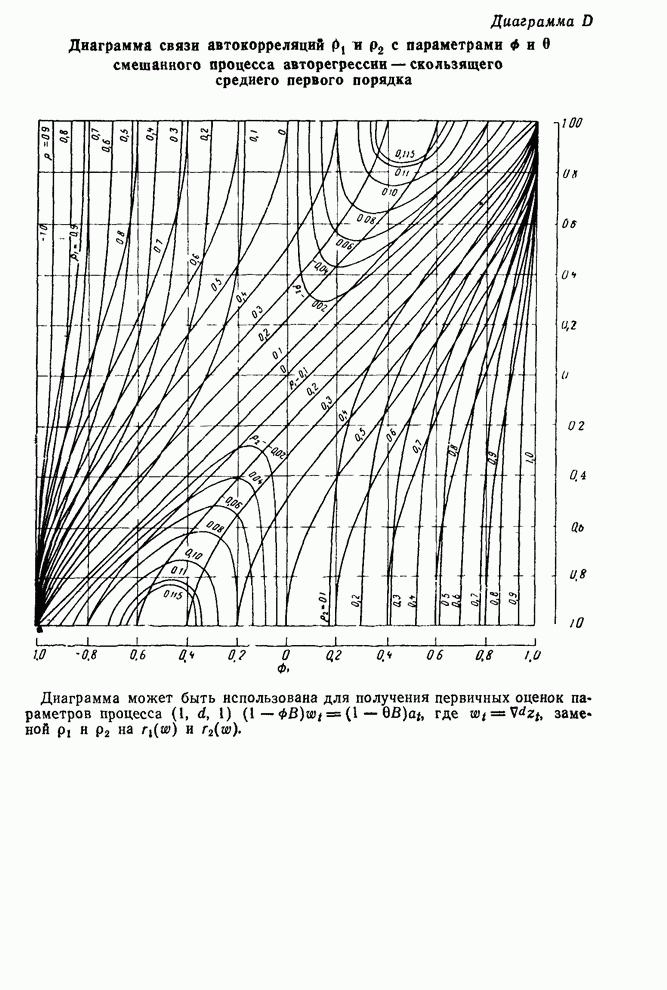
- 6.3.4. Начальные оценки для смешанных процессов авторегрессии — скользящего среднего
- 6.3.5. Выбор между стационарными и нестационарными моделями в спорных случаях
- 6.3.6. Начальные оценки остаточной дисперсии
- 6.3.7. Приближенная стандартная ошибка для
- 6.4. Многозначность моделей
- 6.4.1. Многозначность моделей авторегрессии — скользящего среднего
- 6.4.2. Многозначные решения при оценке параметров скользящего среднего методом моментов
- 6.4.3. Использование возвратного процесса для определения начальных значений
- Приложение П6.1. Среднее значение выборочной автокорреляционной функции нестационарного процесса
- Приложение П6.2. Общий метод получения начальных оценок параметров смешанного процесса авторегрессии – скользящего среднего
- Приложение П6.3. Прямой и возратный процессы ПСС порядка (0, 1, 1)
- Глава 7. Оценивание модели
- 7.1. Исследование функций правдоподобия и суммы квадратов
- 7.1.1. Функция правдоподобия
- 7.1.2. Условное правдоподобие для процесса АРПСС
- 7.1.3. Выбор начальных значений для вычисления условного правдоподобия
- 7.1.4. Безусловное правдоподобие; сумма квадратов; оценки наименьших квадратов
- 7.1.5. Общий способ вычисления безусловной суммы квадратов
- 7.1.6. Графическое исследование суммы квадратов
- 7.1.7. Описание «благоприятных» оценочных ситуаций; доверительные области
- 7.2. Нелинейное оценивание
- 7.2.2. Численный метод нахождения производных
- 7.2.3. Прямой метод нахождения производных
- 7.2.4. Общий алгоритм наименьших квадратов для условной модели
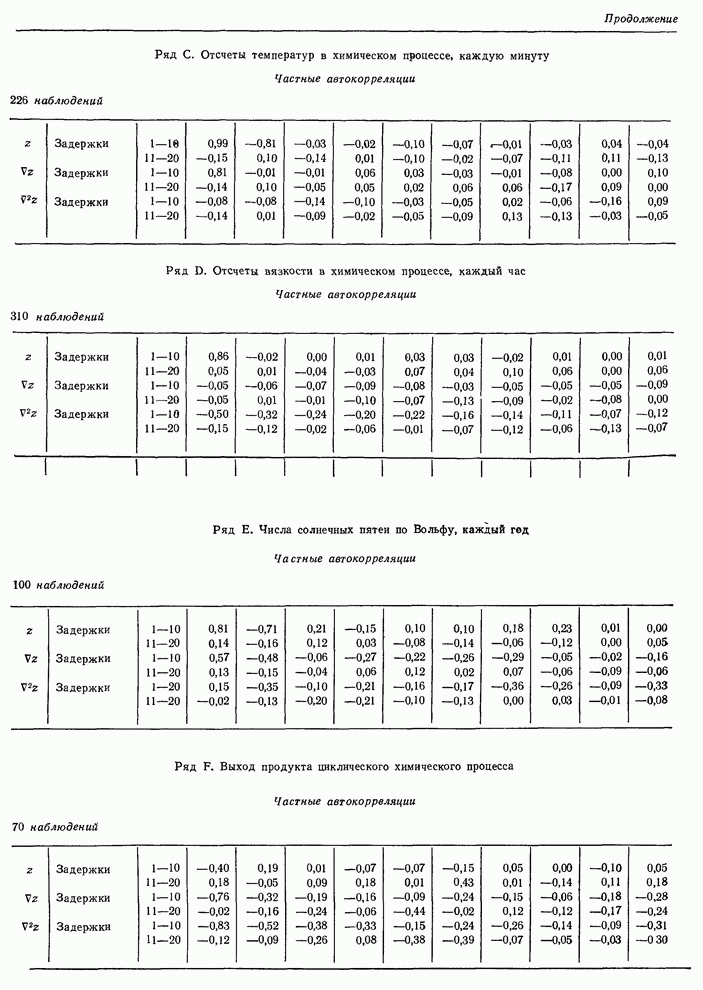
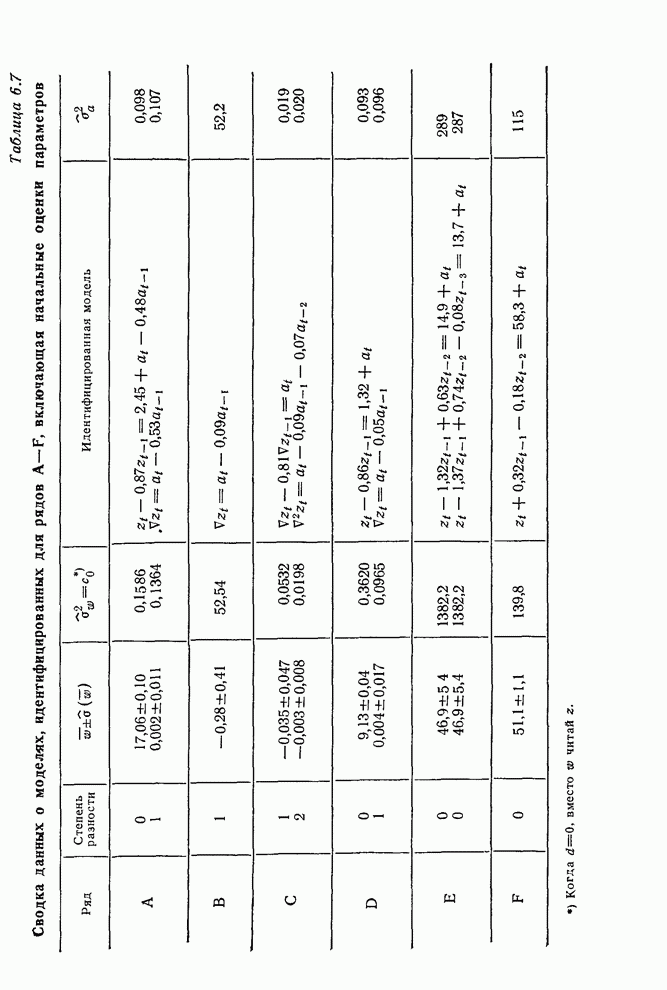
- 7.2.5. Сводка моделей, подогнанных к рядам A-F
- 7.2.6. Информационные матрицы при больших выборках и оценки ковариаций
- 7.3. Результаты оценивания для некоторых частных моделей
- 7.З.2. Процессы скользящего среднего
- 7.3.3. Смешанные процессы
- 7.3.4. Разделение линейных и нелинейных компонент при оценивании
- 7.3.5. Избыточность параметров
- 7.4. Оценивание при помощи теоремы Байеса
- 7.4.2. Байесовское оценивание параметров
- 7.4.3. Процессы авторегрессии
- 7.4.4. Процессы скользящего среднего
- 7.4.5. Смешанные процессы
- Приложение П7.1. Обзор теории нормального распределения
- Приложение П7.2. Обзор линейной теории наименьших квадратов
- Приложение П7.3. Примеры влияния ошибок оценивания параметров на вероятностные пределы прогнозов
- Приложение П7.4. Точная функция правдоподобия для процесса скользящего среднего
- Приложение П7.5. Точная функция правдоподобия для процесса авторегрессии
- Глава 8. Диагностическая проверка модели
- 8.1. Проверка стохастических моделей
- 8.1.2. Введение избыточных параметров
- 8.2.1. Проверка при помощи автокорреляций
- 8.2.2. Совокупный критерий согласия
- 8.2.3. Неадекватность модели, возникающая из-за изменения значений параметров
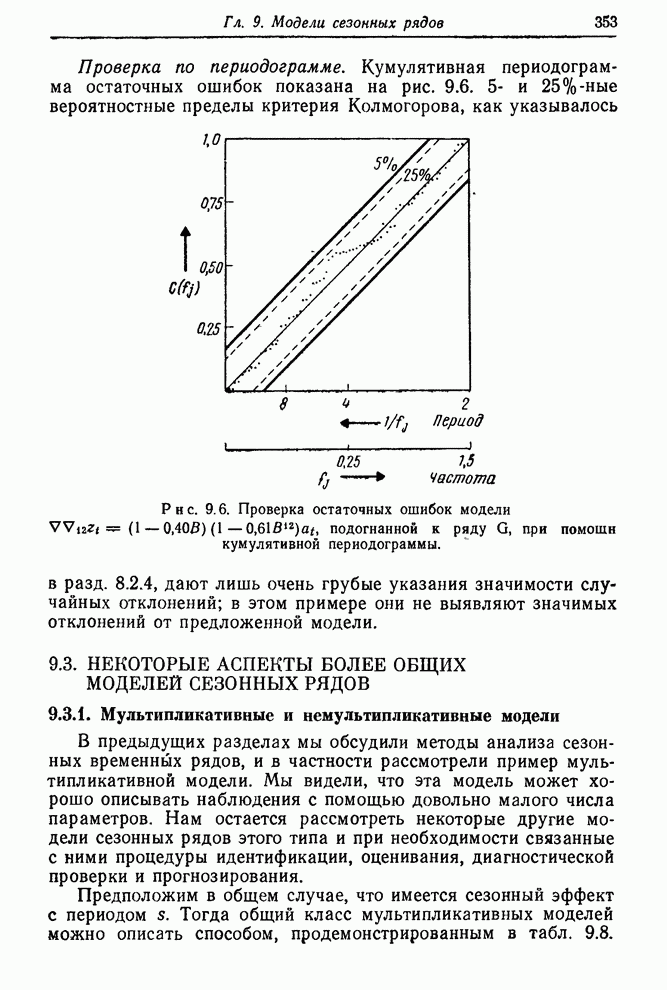
- 8.2.4. Проверка при помощи кумулятивной периодограммы
- 8.3. Использование остаточных ошибок для изменения модели
- 8.3.1. Природа корреляций остаточных ошибок при использовании неверной модели
- 8.3.2. Использование остаточных ошибок для изменения модели
- Глава 9. Модели сезонных рядов
- 9.1. Экономические модели сезонных временных рядов
- 9.1.1. Сопоставление подгонки и прогнозирования
- 9.1.2. Сезонные модели, включающие подстраивающиеся синусоиды и косинусоиды
- 9.1.3. Общая мультипликативная модель сезонного ряда
- 9.2. Представление данных об авиаперевозках мультипликативной моделью
- 9.2.1. Мультипликативная модель
- 9.2.2. Прогнозирование
- 9.2.3. Идентификация
- 9.2.4. Оценивание
- 9.2.5. Диагностическая проверка
- 9.3. Некоторые аспекты более общих моделей сезонных рядов
- 9.3.1. Мультипликативные и немультипликативные модели
- 9.3.2. Идентификация
- 9.3.3. Оценивание
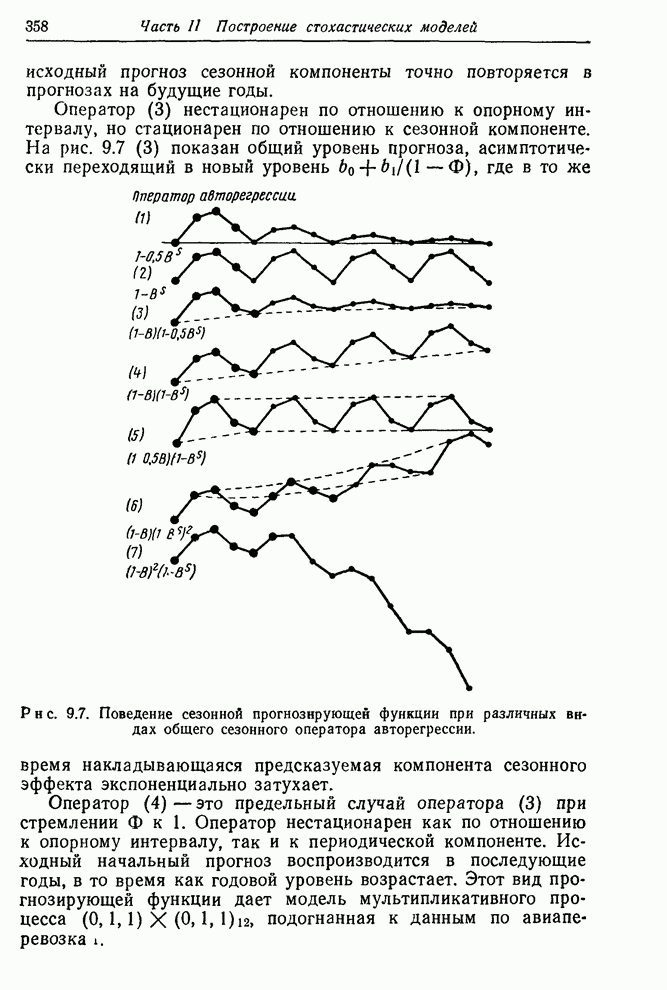
- 9.3.4. Эвентуальные прогнозирующие функции для различных моделей сезонных рядов
- Вспомогательные материалы
- Программа 1 Идентификация стохастической модели
- Программа 2 Предварительное оценивание стохастической модели
- Программа 3. Оценивание стохастической модели
- Алгоритм марквардта для нелинейного метода наименьших квадратов
- Программа 4. Прогнозирование с помощью стохастической модели
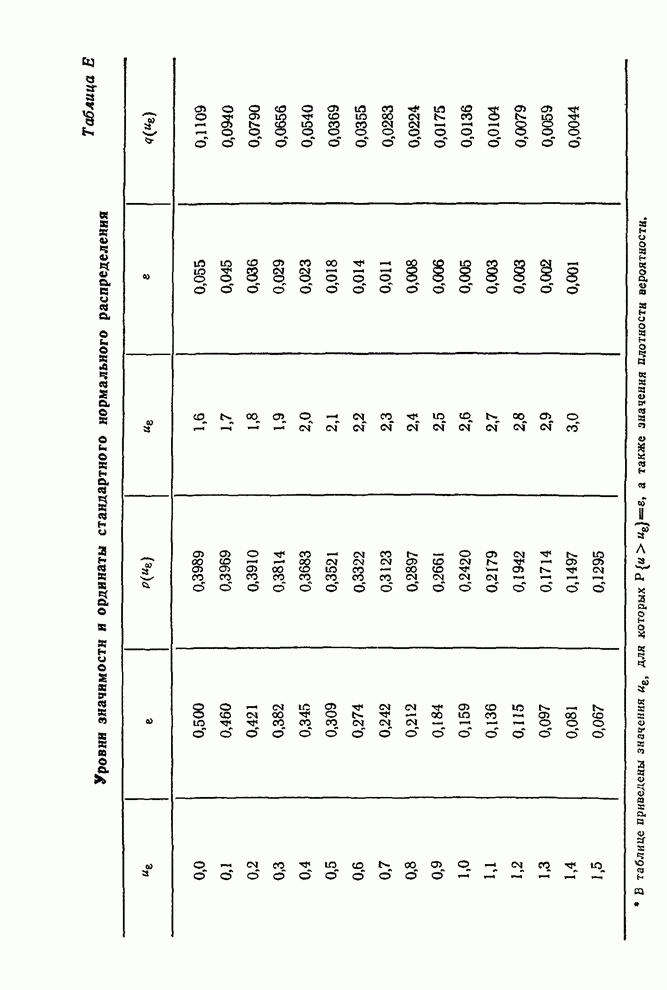
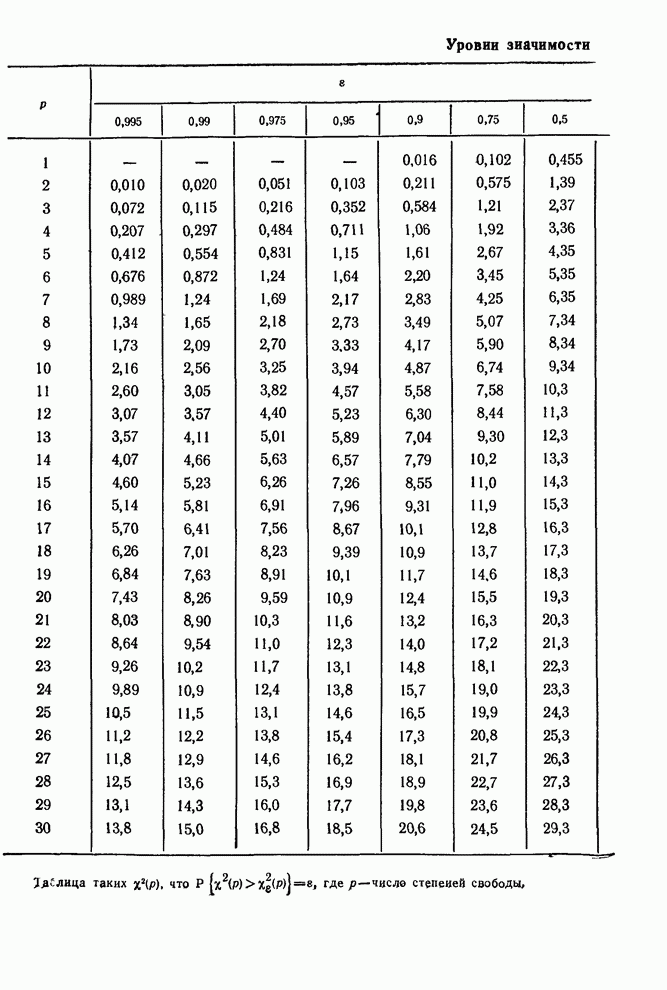
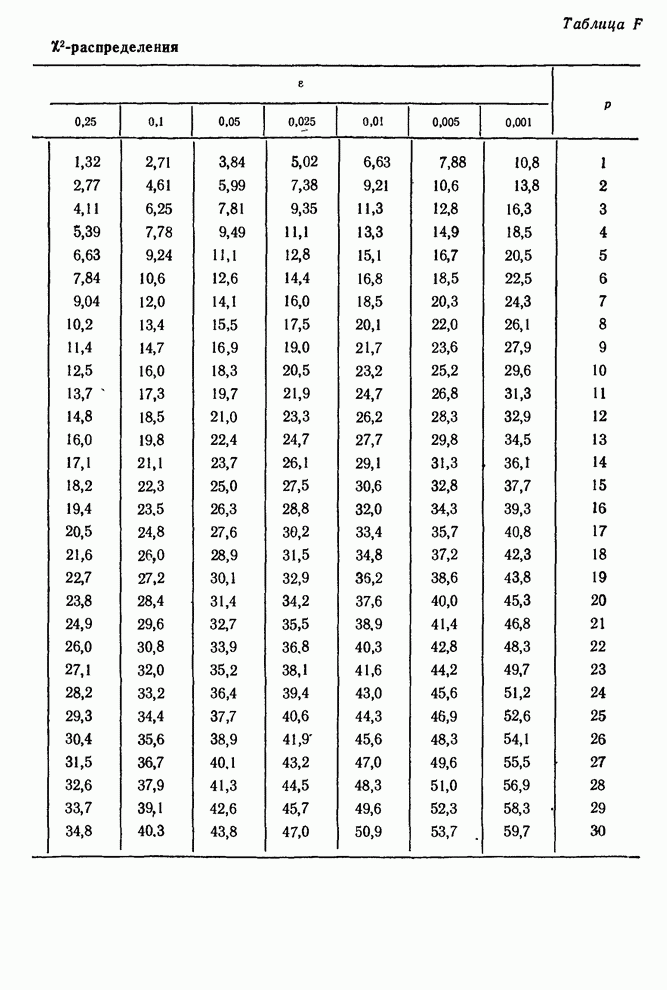
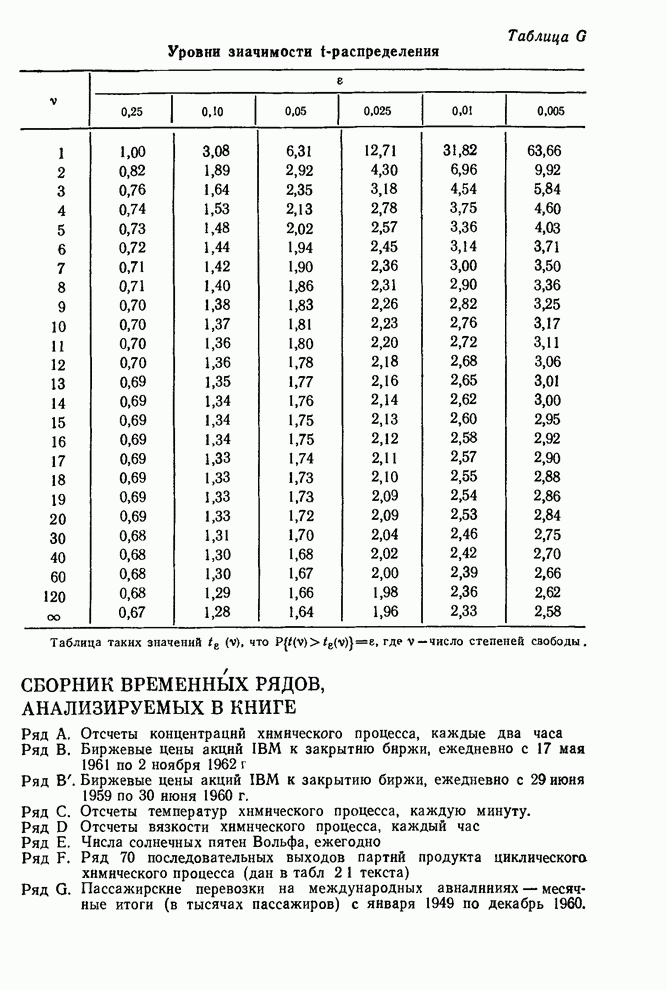
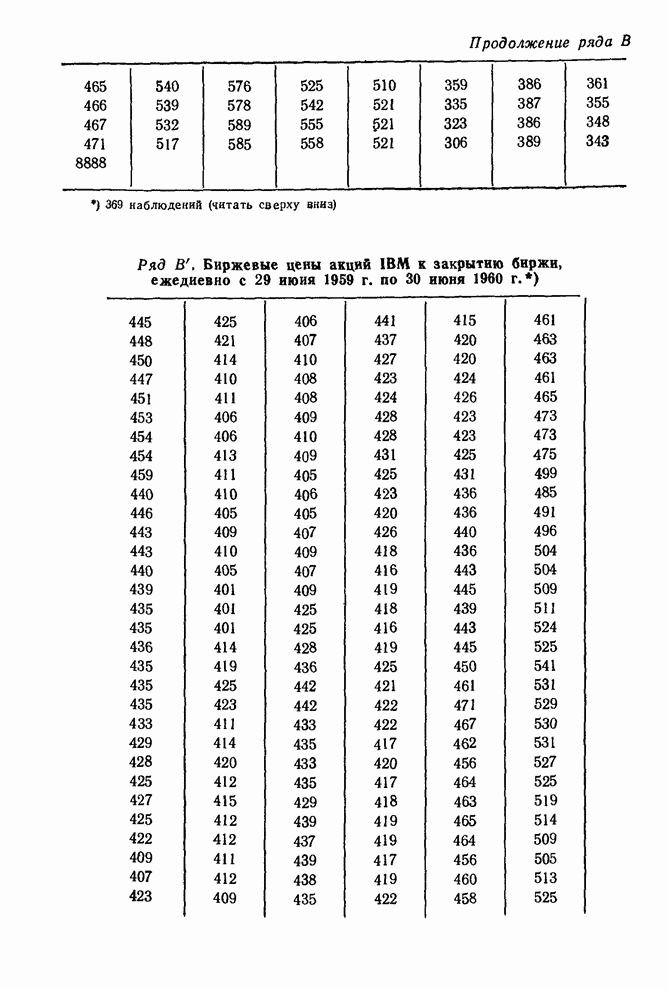
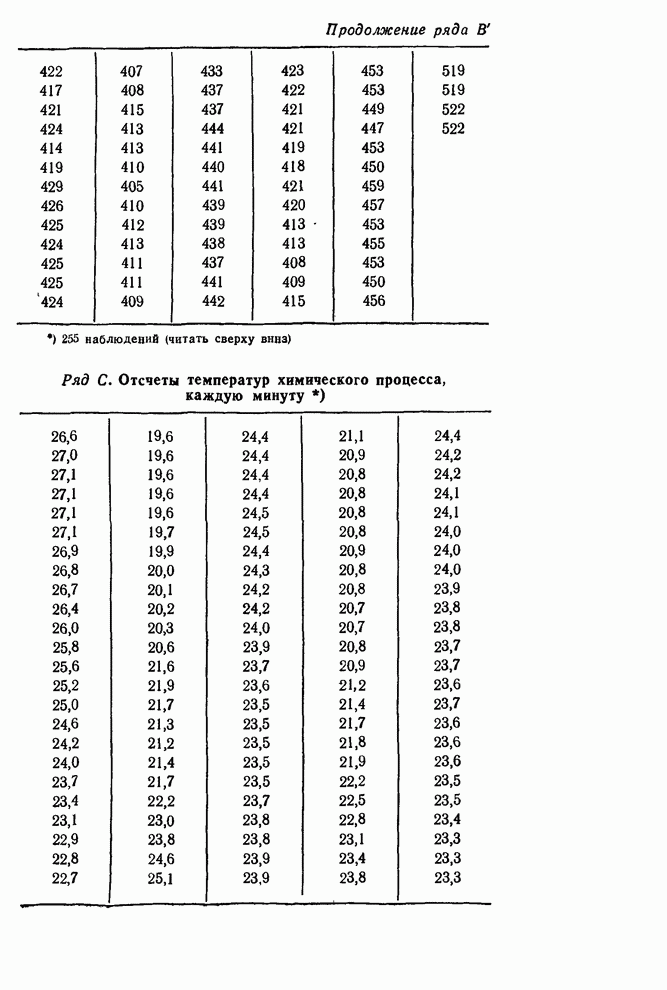
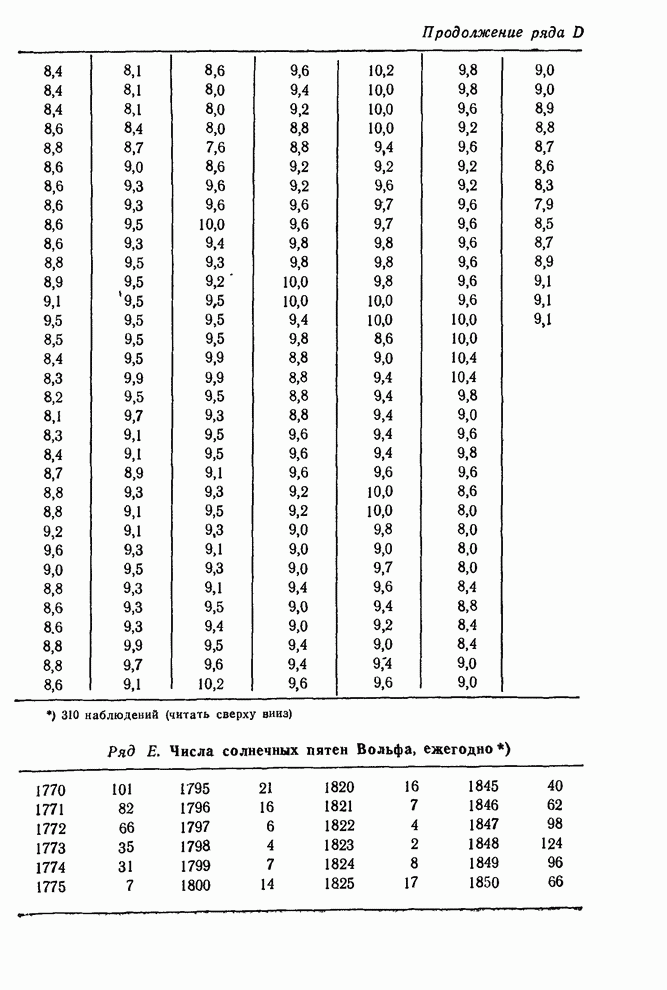
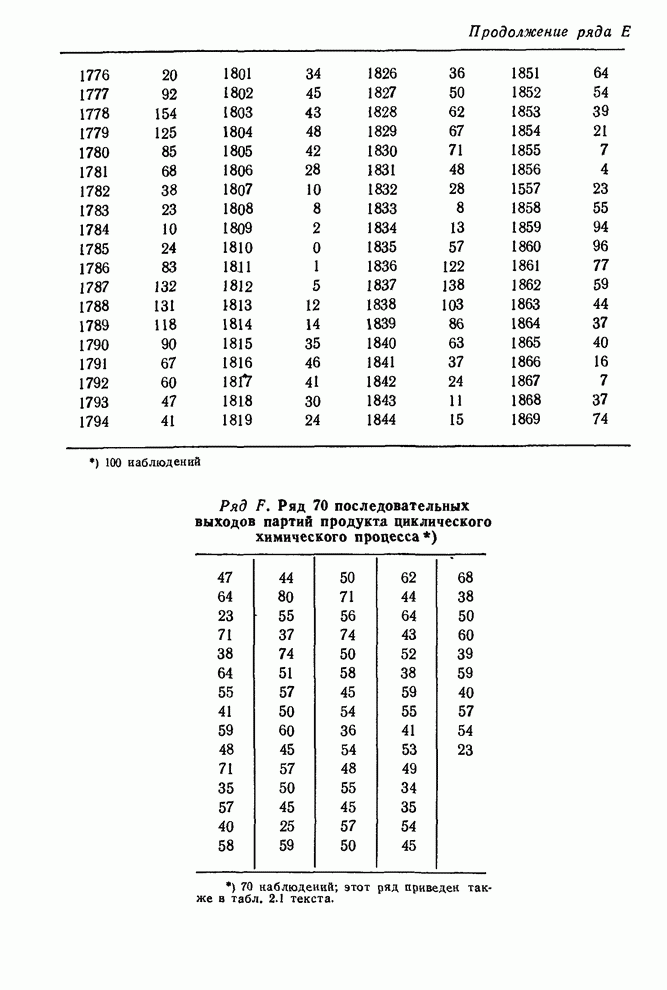
- Сборник таблиц и диаграмм