| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
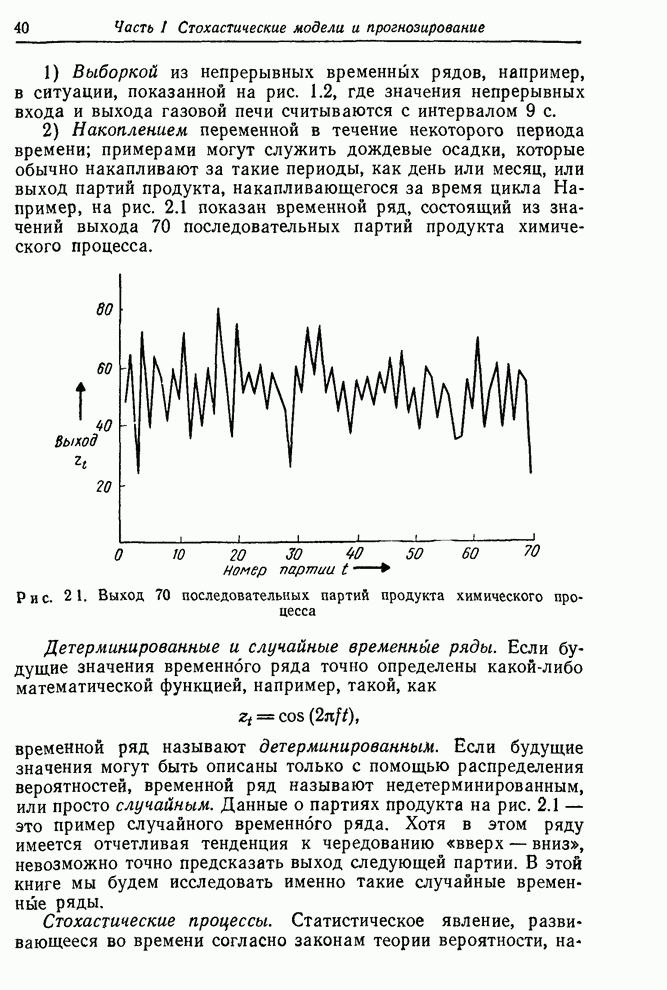
9.1.3. Общая мультипликативная модель сезонного ряда
Упрощающий
оператор ![]() . Фундаментальным
фактом, относящимся к сезонным временным рядам, является сходство наблюдений,
разделенных интервалом
. Фундаментальным
фактом, относящимся к сезонным временным рядам, является сходство наблюдений,
разделенных интервалом ![]() . Следовательно, можно ожидать, что
операция
. Следовательно, можно ожидать, что
операция ![]() будет
играть особо важную роль в анализе сезонных рядов; далее, так как в ряде
будет
играть особо важную роль в анализе сезонных рядов; далее, так как в ряде ![]() можно ожидать
нестационарности, может оказаться полезным упрощающий оператор
можно ожидать
нестационарности, может оказаться полезным упрощающий оператор ![]() . Устойчивый
нестационарный оператор
. Устойчивый
нестационарный оператор ![]() имеет
имеет ![]() нулей
нулей ![]() равномерно распределенных на единичной
окружности. Далее, эвентуальная прогнозирующая функция удовлетворяет уравнению
равномерно распределенных на единичной
окружности. Далее, эвентуальная прогнозирующая функция удовлетворяет уравнению ![]() и поэтому может
(но не обязана) быть представлена в виде набора синусоид и косинусоид
и поэтому может
(но не обязана) быть представлена в виде набора синусоид и косинусоид
 ,
,
где ![]() — подстраивающиеся коэффициенты и
— подстраивающиеся коэффициенты и ![]() для четных
для четных ![]() для нечетных
для нечетных ![]() .
.
Мультипликативная
модель.
Когда
мы имеем дело с рядом, проявляющим сезонные особенности с известным периодом ![]() , полезно
представить данные в виде таблицы, состоящей из
, полезно
представить данные в виде таблицы, состоящей из ![]() столбцов, как, например, табл. 9.1,
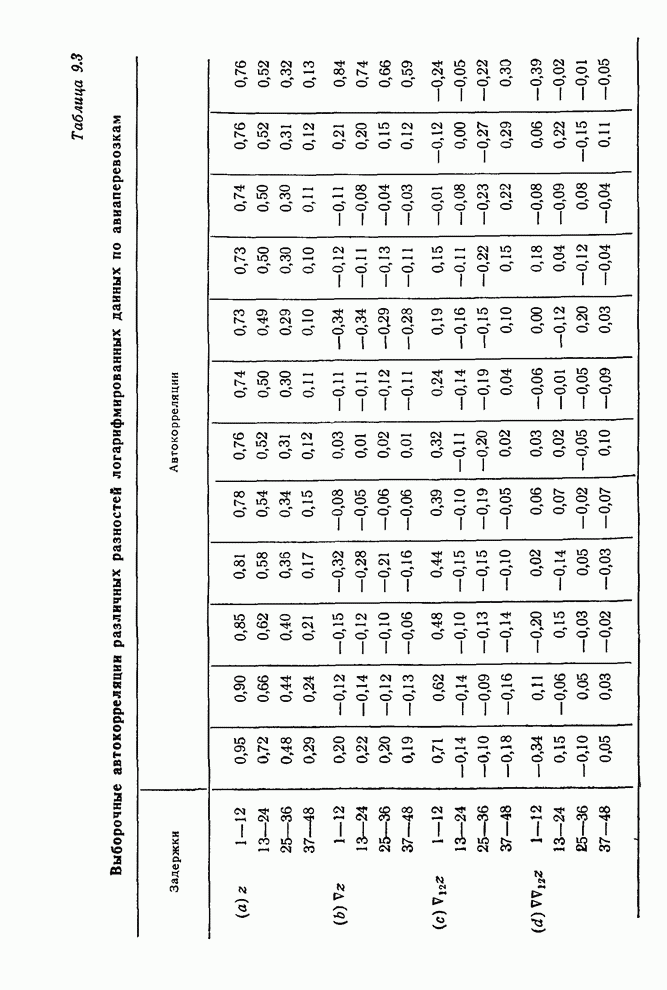
содержащая логарифмы данных об авиаперевозках. (Перед анализом данных о
распродажах и других временных рядах этого типа часто переходят к логарифмам,
поскольку сопоставимыми при разных объемах распродажи могут быть процентные флуктуации.)
столбцов, как, например, табл. 9.1,
содержащая логарифмы данных об авиаперевозках. (Перед анализом данных о
распродажах и других временных рядах этого типа часто переходят к логарифмам,
поскольку сопоставимыми при разных объемах распродажи могут быть процентные флуктуации.)
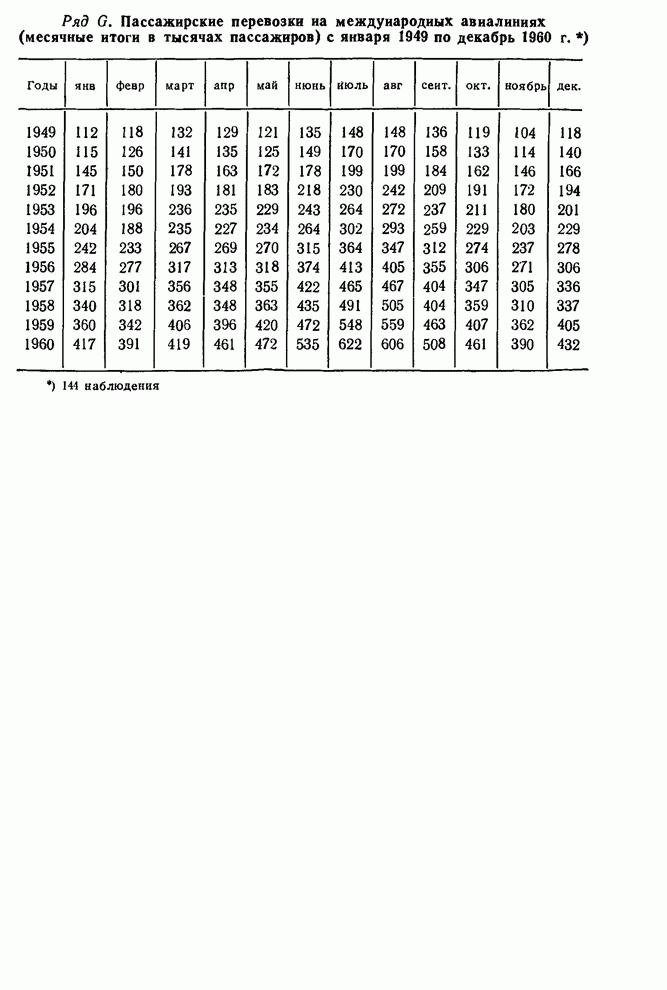
Таблица 9.1. Натуральные
логарифмы месячных количеств (в тыс.) пассажирских перевозок на международных
авиалиниях (ряд ![]() )
)
|
Годы |
Янв |
Февр |
Март |
Апр |
Май |
Июнь |
Июль |
Авг |
Сент |
Окт |
Нояб |
Дек |
|
1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960 |
4,718 4,745 4,977 5,142 5,278 5,318 5,489 5,649 5,753 5,829 5,886 6,033 |
4,771 4,836 5,011 5,193 5,278 5,236 5,451 5,624 5,707 5,762 5,835 5,969 |
4,883 4,949 5,182 5,263 5,464 5,460 5,587 5,759 5,875 5,892 6,006 6,038 |
4,860 4,905 5,094 5,199 5,460 5,425 5,595 5,746 5,852 5,852 5,981 6,133 |
4,796 4,828 5,147 5,209 5,434 5,455 5,598 5,762 5,872 5,894 6,040 6,157 |
4,905 5,004 5,182 5,384 5,493 5,576 5,753 5,924 6,045 6,075 6,157 6,282 |
4,997 5,136 5,293 5,438 5,576 5,710 5,897 6,023 6,146 6,196 6,306 6,433 |
4,997 5,136 5,293 5,489 5,606 5,680 5,849 6,004 6,146 6,225 6,326 6,407 |
4,913 5,063 5,215 5,342 5,468 5,557 5,743 5,872 6,001 6,001 6,138 6,230 |
4,779 4,890 5,088 5,252 5,352 5,434 5,613 5,724 5,849 5,883 6,009 6,133 |
4,644 4,763 4,984 5,147 5,193 5,313 5,468 5,602 5,720 5,737 5,892 5,966 |
4,771 4,942 5,112 5,268 5,303 5,434 5,628 5,724 5,817 5,820 6,004 6,068 |
Структура табл. 9.1 подчеркивает, что в периодических данных важен не один, а два временных интервала. В этом примере эти интервалы соответствуют месяцу и году. Конкретнее, мы ожидаем, что существуют определенные соотношения между
а) наблюдениями за последовательные месяцы данного года,
б) наблюдениями того же месяца в последовательные годы.
Ситуация несколько сходна с встречаемой при изучении таблиц с двумя входами в дисперсионном анализе, где можно ожидать сходства между наблюдениями в одной и той же строке или в одном и том же столбце.
Если рассмотреть
с этой точки зрения табл. 9.1, то сезонный эффект должен проявиться в ней так:
наблюдения за какой-либо месяц (скажем, апрель) некоторого года должны быть связаны
с наблюдениями за тот же месяц предыдущего года. Пусть ![]() -е наблюдение
-е наблюдение ![]() относится к апрелю.
Тогда мы можем связать это наблюдение с наблюдением в предыдущем апреле моделью
вида
относится к апрелю.
Тогда мы можем связать это наблюдение с наблюдением в предыдущем апреле моделью
вида
![]() , (9.1.4)
, (9.1.4)
где ![]() и
и ![]() - полиномы
- полиномы ![]() степеней
степеней ![]() и
и ![]() соответственно,
удовлетворяющие условиям стационарности и обратимости. Подобным образом модель
соответственно,
удовлетворяющие условиям стационарности и обратимости. Подобным образом модель
![]() (9.1.5)
(9.1.5)
может быть использована для связи
наблюдений за март этого и предшествующего года и т. д. для любого из 12 мес.
Кроме того, обычно оказывается разумным предположение, что параметры ![]() и
и ![]() , содержащиеся в
этих ежемесячных моделях, примерно одинаковы для всех месяцев.
, содержащиеся в
этих ежемесячных моделях, примерно одинаковы для всех месяцев.
Ошибки ![]() этих моделей не
обязательно должны быть некоррелированы. Например, количество авиапассажиров в
апреле 1960 г., будучи связанным с количеством пассажиров в апреле предыдущего
года, связано также с количеством пассажиров в марте, феврале, январе 1960 г. и
т. д. Поэтому можно ожидать, что
этих моделей не
обязательно должны быть некоррелированы. Например, количество авиапассажиров в
апреле 1960 г., будучи связанным с количеством пассажиров в апреле предыдущего
года, связано также с количеством пассажиров в марте, феврале, январе 1960 г. и
т. д. Поэтому можно ожидать, что ![]() в (9.1.4) связано с
в (9.1.4) связано с ![]() в (9.1.5), с
в (9.1.5), с ![]() и т. д.
Следовательно, чтобы учесть эти связи, мы вводим вторую модель
и т. д.
Следовательно, чтобы учесть эти связи, мы вводим вторую модель
![]() , (9.1.6)
, (9.1.6)
где ![]() - белый шум, а
- белый шум, а ![]() и
и ![]() - полиномы
- полиномы ![]() степеней
степеней ![]() и
и ![]() соответственно,
удовлетворяющие условиям стационарности и обратимости;
соответственно,
удовлетворяющие условиям стационарности и обратимости; ![]() .
.
Подставляя (9.1.6) в (9.1.4), получаем окончательную общую мультипликативную модель
![]() , (9.1.7)
, (9.1.7)
где в этом частном примере ![]() . Индексы
. Индексы ![]() в (9.1.7) были
введены, чтобы напомнить читателю о порядках различных операторов. Говорят, что
результирующий мультипликативный процесс имеет порядок
в (9.1.7) были
введены, чтобы напомнить читателю о порядках различных операторов. Говорят, что
результирующий мультипликативный процесс имеет порядок ![]() . Аналогичные рассуждения
можно использовать для получения моделей с тремя и более периодическими
компонентами, учитывающими многообразие сезонных явлений.
. Аналогичные рассуждения
можно использовать для получения моделей с тремя и более периодическими
компонентами, учитывающими многообразие сезонных явлений.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к русскому изданию
- Предисловие
- План книги
- Глава 1. Введение и краткое содержание
- 1.1. Три важные практические проблемы
- 1.1.1. Прогнозирование временных рядов
- 1.1.2. Оценивание передаточных функций
- 1.1.3. Проектирование дискретных регулирующих систем
- 1.2. Стохастические и детерминированные динамические математические модели
- 1.2.1. Стационарные нестационарные стохастические модели для прогнозирования и регулирования
- 1.2.2. Модели передаточных функций
- 1.2.3. Модели дискретных систем регулирования
- 1.3. Основные понятия в построении моделей
- 1.3.1. Экономия
- 1.3.2. Интерактивные этапы в выборе модели
- Часть 1. Стохастические модели и основанное на них прогнозирование
- Глава 2. Автокорреляционная функция и спектр
- 2.1. Автокорреляционные свойства стационарных моделей
- 2.1.1. Временные ряды и стохастические процессы
- 2.1.2. Стационарные стохастические процессы
- 2.1.3. Положительная определённость и автоковариационная матрица
- 2.1.4. Автоковариационные и автокорреляционные функции
- 2.1.5. Оценивание автоковариационной и автокорреляционной функций
- 2.1.6. Стандартные ошибки оценок автокорреляций
- 2.2. Спектральные свойства стационарных моделей
- 2.2.1. Периодограмма
- 2.2.2. Дисперсионный анализ
- 2.2.3. Спектральная плотность и нормированный спектр
- 2.2.4. Простые примеры автокорреляционных функций и нормированных спектров
- 2.2.5. Преимущества и недостатки автокорреляционных функций и нормированных спектров
- Приложение П2.1. Связь между выборочным спектром и оценкой автоковариационной функции
- Глава 3. Линейные стационарные модели
- 3.1. Общий линейный процесс
- 3.1.1. Две эквивалентные формы линейного процесса
- 3.1.2. Производящая функция автоковариаций линейного процесса
- 3.1.3. Условия стационарности и обратимости линейного процесса
- 3.1.4. Процессы авторегрессии и скользящего среднего
- 3.2. Процессы авторегрессии
- 3.2.1. Условия стационарности для процессов авторегрессии
- 3.2.2. Автокорреляционная функция и спектр процессов авторегрессии
- 3.2.3. Процесс авторегрессии первого порядка (марковский процесс)
- 3.2.4. Процесс авторегрессии второго порядка
- 3.2.5. Частная автокорреляционная функция
- 3.2.6. Оценивание частной автокорреляционной функции
- 3.2.7. Стандартные ошибки частной автокорреляции
- 3.3. Процессы скользящего среднего
- 3.3.1. Условия обратимости для процессов скользящего среднего
- 3.3.2. Автокорреляционная функция и спектр процесса скользящего среднего
- 3.3.3. Процесс скользящего среднего первого порядка
- 3.3.4. Процесс скользящего среднего второго порядка
- 3.3.5. Взаимность процессов авторегрессии и скользящего среднего
- 3.4. Смешанные процессы авторегрессии — скользящего среднего
- 3.4.1. Свойства стационарности и обратимости
- 3.4.2. Автокорреляционная функция и спектр смешанных процессов
- 3.4.3. Процесс авторегрессии первого порядка — скользящего среднего первого порядка
- 3.3.4. Резюме
- Приложение П3.1. Автоковариации.
- Приложение П3.2. Рекурентный метод вычисления оценок параметров авторегрессии
- Глава 4. Линейные нестационарные модели
- 4.1. Процессы авторегрессии — проинтегрированного скользящего среднего
- 4.1.1. Нестационарность процесса авторегрессии первого порядка
- 4.1.2. Общая модель для нестационарного процесса, проявляющего однородность
- 4.1.3. Общий вид процесса авторегрессии – проинтегрированного скользящего среднего
- 4.2. Три формы представления модели авторегрессии – проинтегрированного скользящего среднего
- 4.2.1. Представление модели в виде разности уравнения
- 4.2.2. Представление модели, использующее случайные импульсы
- 4.2.3. Обращенное представление модели
- 4.3. Процессы проинтегрированного скользящего среднего
- 4.3.1. Процесс проинтегрированного скользящего среднего порядка (0,1,1)
- 4.3.2. Процесс проинтегрированного скользящего среднего порядка (0.2.2)
- 4.3.3. Общий процесс проинтегрированного скользящего среднего порядка (0, d, q)
- Приложение П4.1. Линейные разностные уравнения
- Приложение П4.2. Процесс ПСС(0,1,1) с детерминированным дрейфом нуля
- Приложение П4.3. Свойства конечного оператора ссумирования
- Приложение П4.4. Процессы АРПСС с добавленным шумом
- Глава 5. Прогнозирование
- 5.1. Прогнозы с минимальной среднеквадратичной ошибкой и их свойства
- 5.1.1. Вывод формулы для прогнозов с минимальной среднеквадратичной ошибкой
- 5.1.2. Три основных представления прогноза
- 5.2. Вычисление и подправление прогноза
- 5.2.1. Удобная схема для вычисления прогнозов
- 5.2.2. Вычисление весов
- 5.2.3. Использование весов при подправлении прогнозов
- 5.2.4. Вычисление вероятностных пределов прогнозов при произвольном упреждении
- 5.3. Прогнозирующая функция и веса прогноза
- 5.3.1. Эвентуальная прогнозирующая функция, определенная оператором авторегрессии
- 5.3.2. Роль оператора скользящего среднего в определении начальных величин
- 5.3.3. Веса прогноза для упреждения l
- 5.4. Примеры прогнозирующих функций и их подправления
- 5.4.1. Прогнозирование процесса ПСС(0, 1, 1)
- 5.4.2. Прогнозирование процесса ПСС(0, 2, 2)
- 5.4.3. Прогнозирование общего процесса ПСС(0, d, q)
- 5.4.4. Прогнозирование процессов авторегрессии
- 5.4.5. Прогнозирование процесса (1, 0, 1)
- 5.4.6. Прогнозирование процесса (1,1,1)
- 5.5. Резюме
- Приложение П5.1. Корреляция между ошибками прогноза
- Приложение П5.2. Веса прогноза для произвольного упреждения
- Приложение П5.3. Прогнозирование при помощи общего проинтегрированного представления
- Часть II. Построение стохастических моделей
- Глава 6. Идентификация моделей
- 6.1. Цели идентификации
- 6.1.1. Этапы процедуры идентификации
- 6.2. Методика идентификации
- 6.2.1. Использование при идентификаций автокорреляционной и частной автокорреляционной функций
- 6.2.2. Стандартные ошибки выборочных автокорреляций и частных автокорреляций
- 6.2.3. Идентификация некоторых реальных временных рядов
- 6.3. Начальные оценки параметров
- 6.3.1. Единственность оценок, получаемых по автоковариационной функции
- 6.3.2. Начальные оценки для процессов скользящего среднего
- 6.3.3. Начальные оценки для процессов авторегрессии
- 6.3.4. Начальные оценки для смешанных процессов авторегрессии — скользящего среднего
- 6.3.5. Выбор между стационарными и нестационарными моделями в спорных случаях
- 6.3.6. Начальные оценки остаточной дисперсии
- 6.3.7. Приближенная стандартная ошибка для
- 6.4. Многозначность моделей
- 6.4.1. Многозначность моделей авторегрессии — скользящего среднего
- 6.4.2. Многозначные решения при оценке параметров скользящего среднего методом моментов
- 6.4.3. Использование возвратного процесса для определения начальных значений
- Приложение П6.1. Среднее значение выборочной автокорреляционной функции нестационарного процесса
- Приложение П6.2. Общий метод получения начальных оценок параметров смешанного процесса авторегрессии – скользящего среднего
- Приложение П6.3. Прямой и возратный процессы ПСС порядка (0, 1, 1)
- Глава 7. Оценивание модели
- 7.1. Исследование функций правдоподобия и суммы квадратов
- 7.1.1. Функция правдоподобия
- 7.1.2. Условное правдоподобие для процесса АРПСС
- 7.1.3. Выбор начальных значений для вычисления условного правдоподобия
- 7.1.4. Безусловное правдоподобие; сумма квадратов; оценки наименьших квадратов
- 7.1.5. Общий способ вычисления безусловной суммы квадратов
- 7.1.6. Графическое исследование суммы квадратов
- 7.1.7. Описание «благоприятных» оценочных ситуаций; доверительные области
- 7.2. Нелинейное оценивание
- 7.2.2. Численный метод нахождения производных
- 7.2.3. Прямой метод нахождения производных
- 7.2.4. Общий алгоритм наименьших квадратов для условной модели
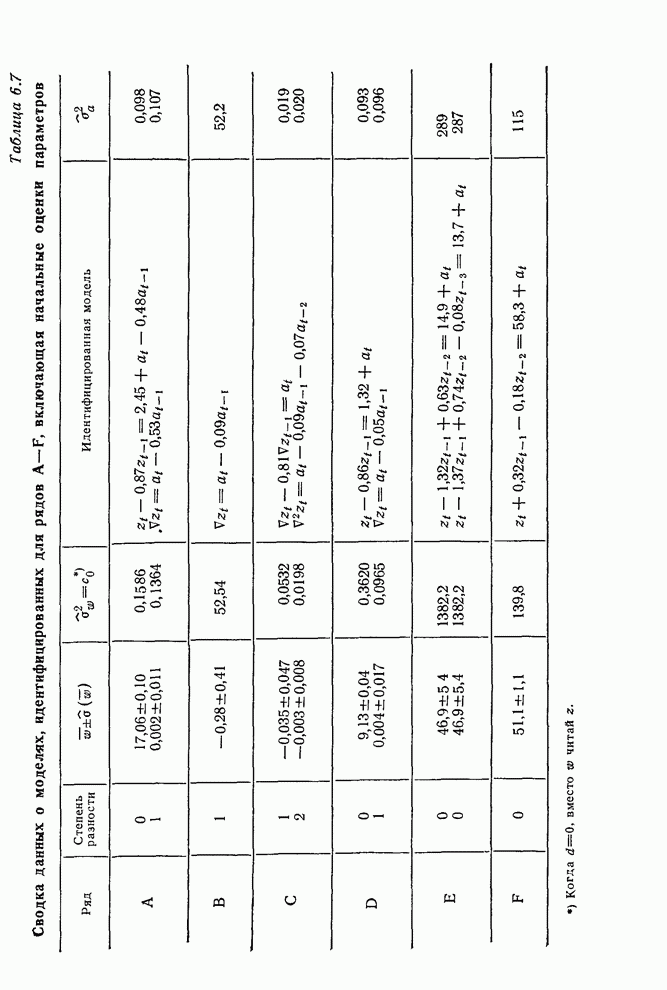
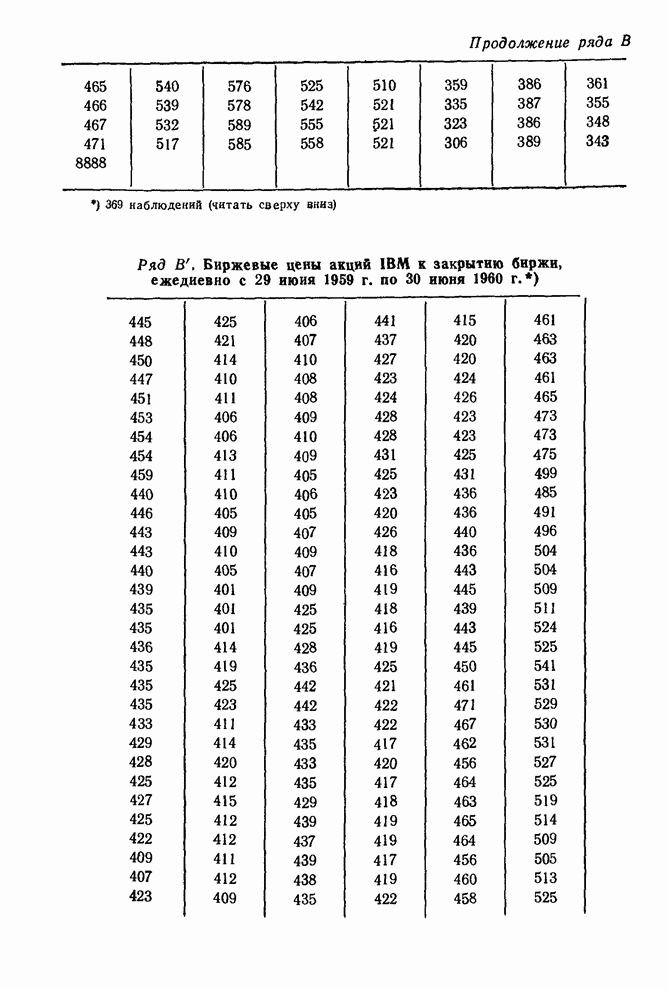
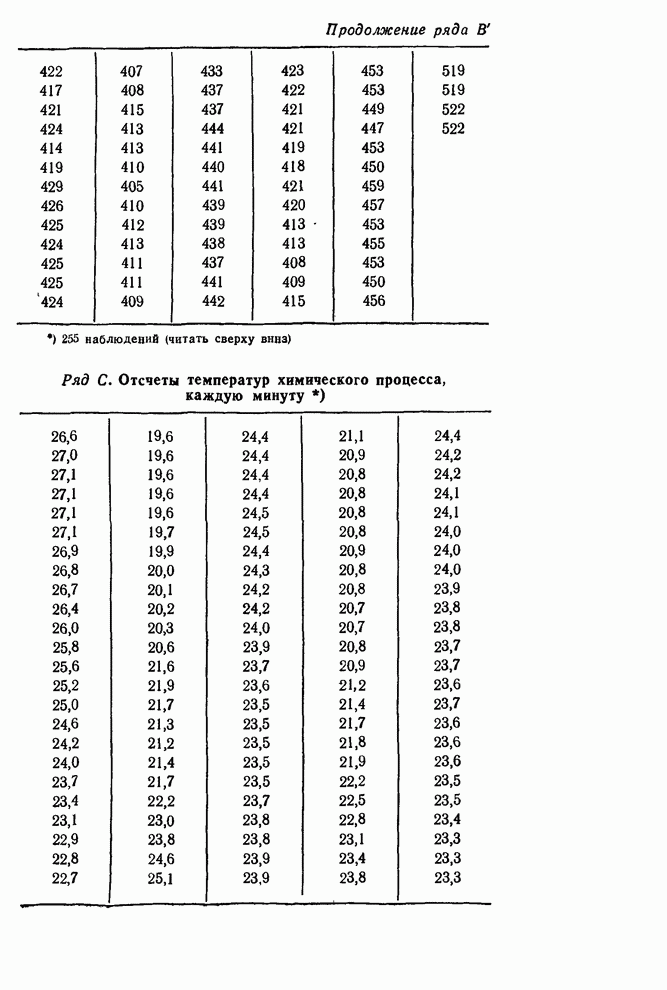
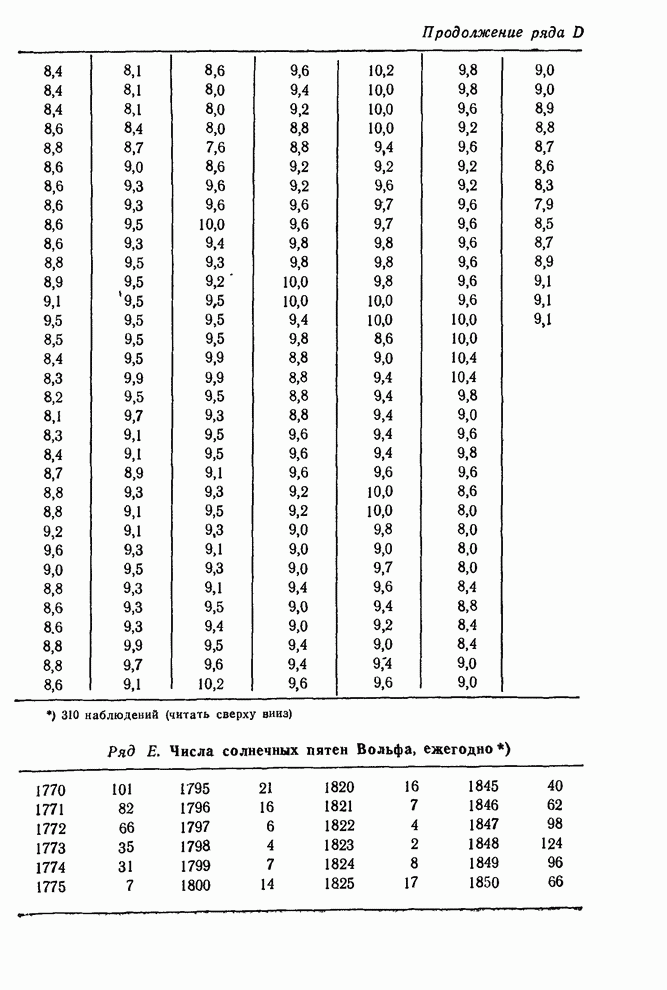
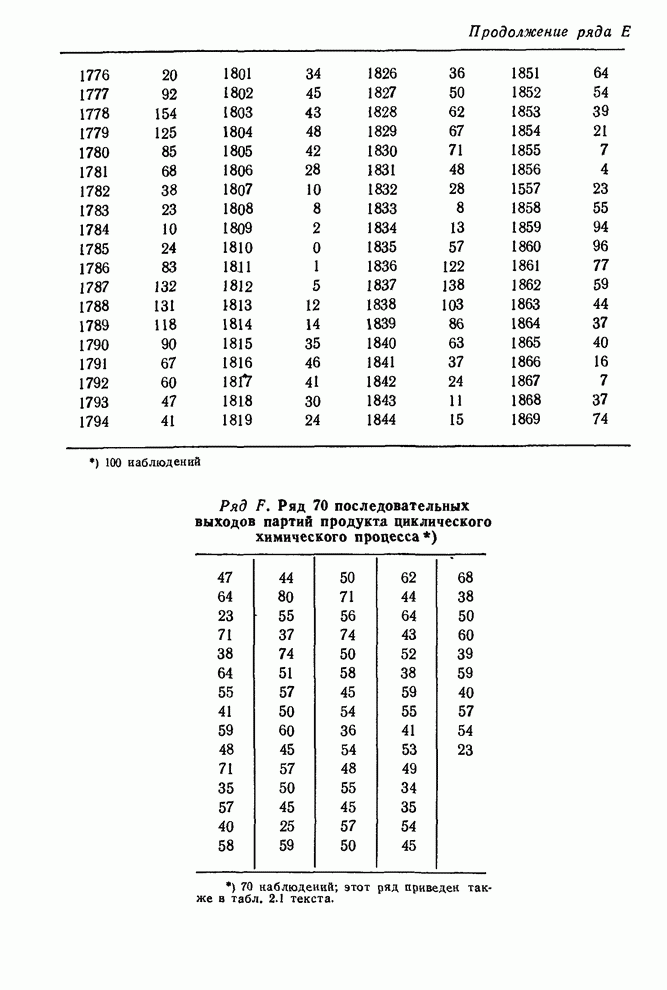
- 7.2.5. Сводка моделей, подогнанных к рядам A-F
- 7.2.6. Информационные матрицы при больших выборках и оценки ковариаций
- 7.3. Результаты оценивания для некоторых частных моделей
- 7.З.2. Процессы скользящего среднего
- 7.3.3. Смешанные процессы
- 7.3.4. Разделение линейных и нелинейных компонент при оценивании
- 7.3.5. Избыточность параметров
- 7.4. Оценивание при помощи теоремы Байеса
- 7.4.2. Байесовское оценивание параметров
- 7.4.3. Процессы авторегрессии
- 7.4.4. Процессы скользящего среднего
- 7.4.5. Смешанные процессы
- Приложение П7.1. Обзор теории нормального распределения
- Приложение П7.2. Обзор линейной теории наименьших квадратов
- Приложение П7.3. Примеры влияния ошибок оценивания параметров на вероятностные пределы прогнозов
- Приложение П7.4. Точная функция правдоподобия для процесса скользящего среднего
- Приложение П7.5. Точная функция правдоподобия для процесса авторегрессии
- Глава 8. Диагностическая проверка модели
- 8.1. Проверка стохастических моделей
- 8.1.2. Введение избыточных параметров
- 8.2.1. Проверка при помощи автокорреляций
- 8.2.2. Совокупный критерий согласия
- 8.2.3. Неадекватность модели, возникающая из-за изменения значений параметров
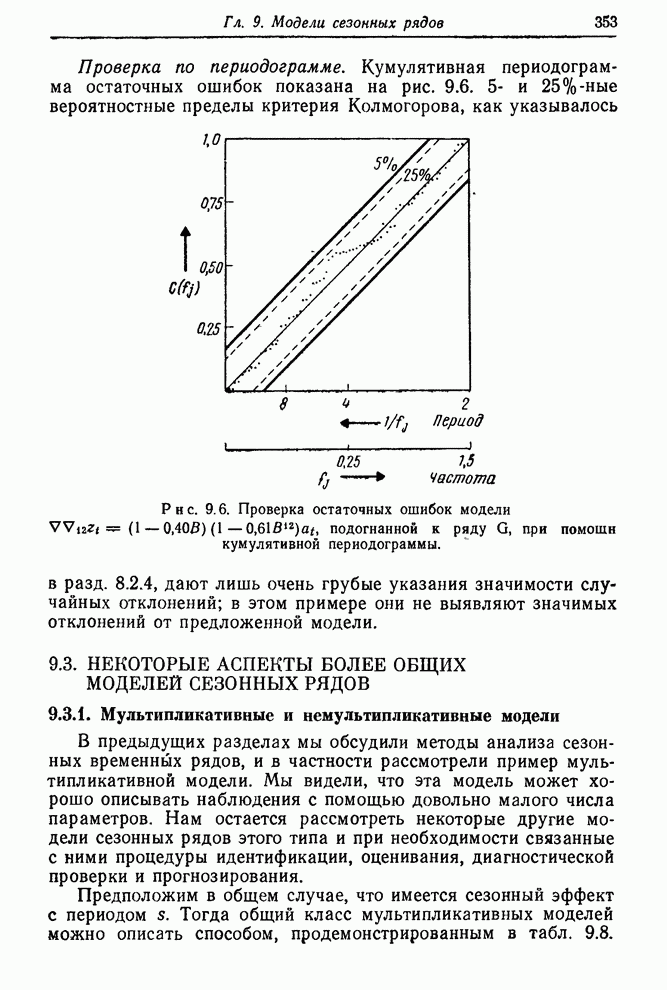
- 8.2.4. Проверка при помощи кумулятивной периодограммы
- 8.3. Использование остаточных ошибок для изменения модели
- 8.3.1. Природа корреляций остаточных ошибок при использовании неверной модели
- 8.3.2. Использование остаточных ошибок для изменения модели
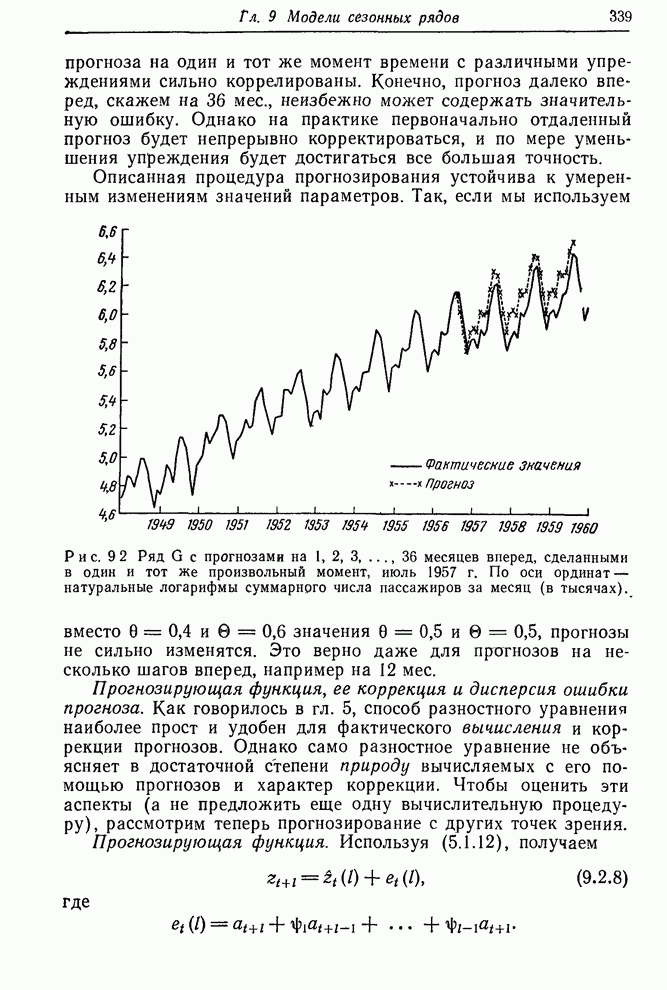
- Глава 9. Модели сезонных рядов
- 9.1. Экономические модели сезонных временных рядов
- 9.1.1. Сопоставление подгонки и прогнозирования
- 9.1.2. Сезонные модели, включающие подстраивающиеся синусоиды и косинусоиды
- 9.1.3. Общая мультипликативная модель сезонного ряда
- 9.2. Представление данных об авиаперевозках мультипликативной моделью
- 9.2.1. Мультипликативная модель
- 9.2.2. Прогнозирование
- 9.2.3. Идентификация
- 9.2.4. Оценивание
- 9.2.5. Диагностическая проверка
- 9.3. Некоторые аспекты более общих моделей сезонных рядов
- 9.3.1. Мультипликативные и немультипликативные модели
- 9.3.2. Идентификация
- 9.3.3. Оценивание
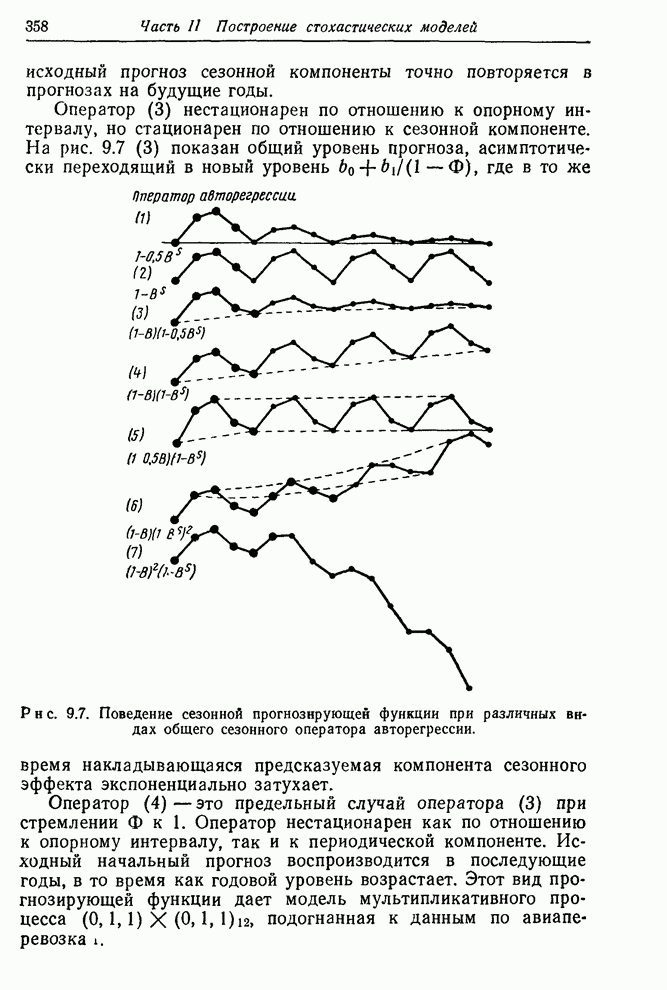
- 9.3.4. Эвентуальные прогнозирующие функции для различных моделей сезонных рядов
- Вспомогательные материалы
- Программа 1 Идентификация стохастической модели
- Программа 2 Предварительное оценивание стохастической модели
- Программа 3. Оценивание стохастической модели
- Алгоритм марквардта для нелинейного метода наименьших квадратов
- Программа 4. Прогнозирование с помощью стохастической модели
- Сборник таблиц и диаграмм