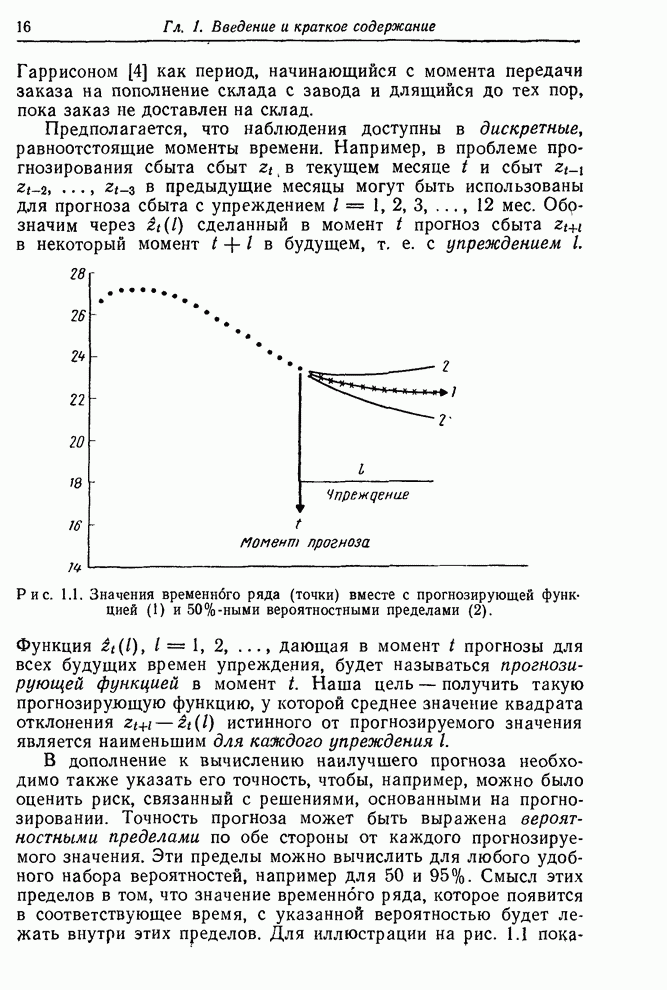
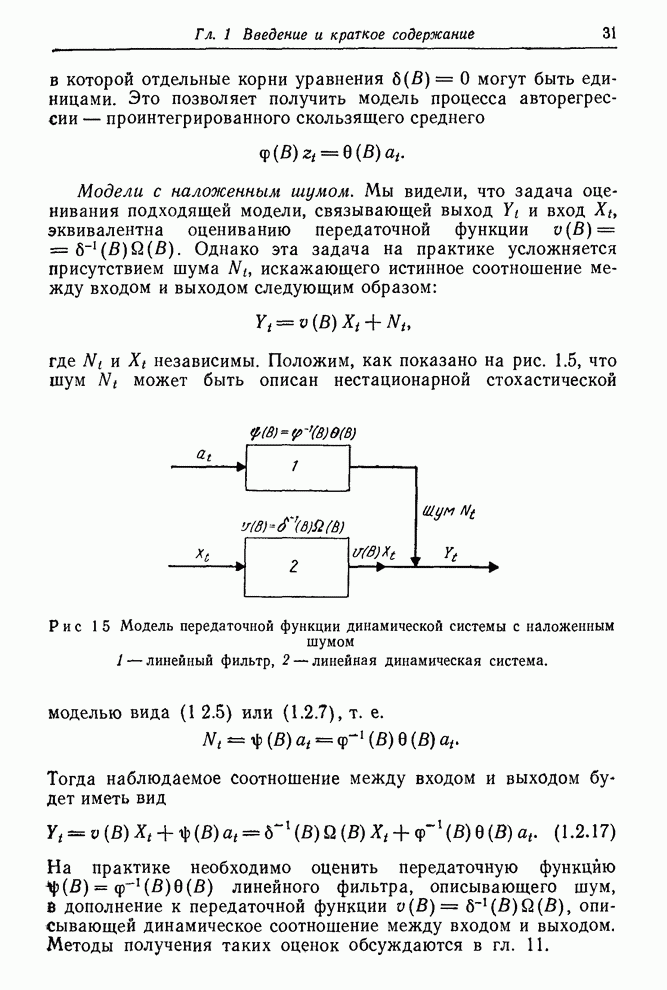
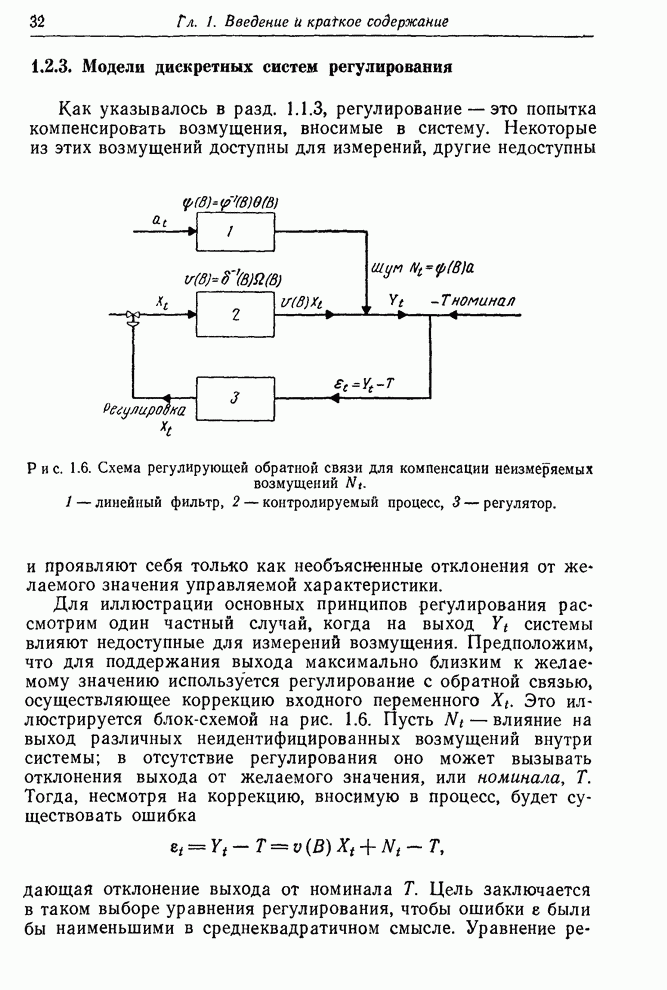
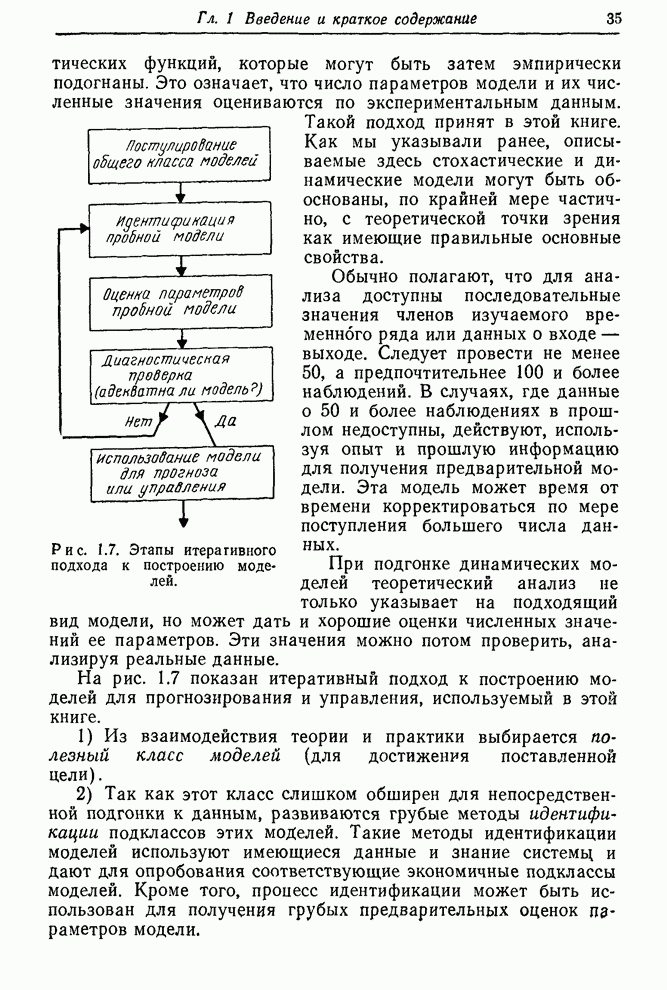
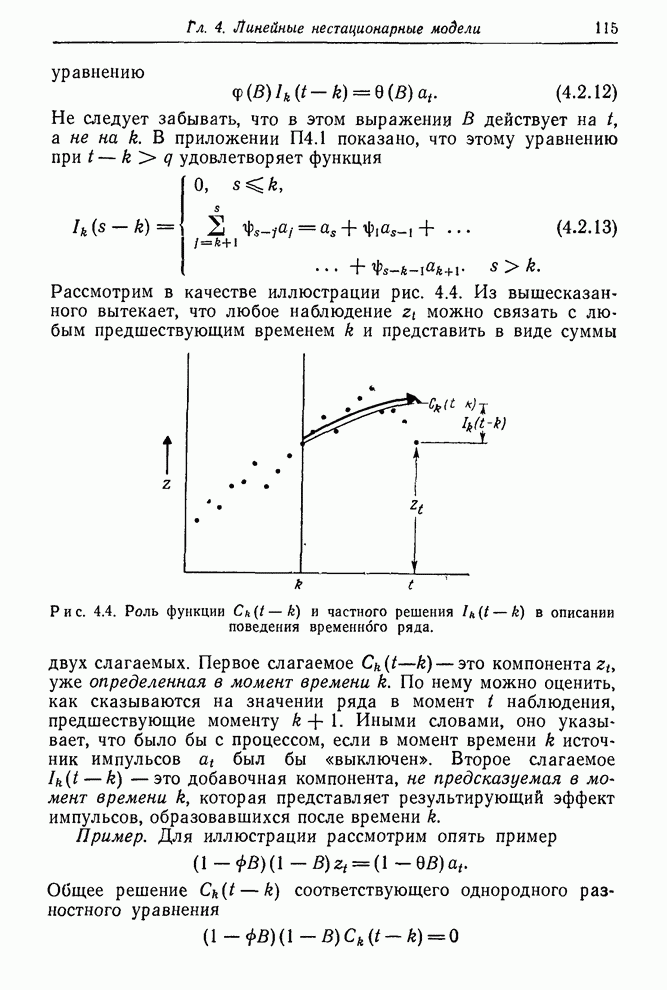
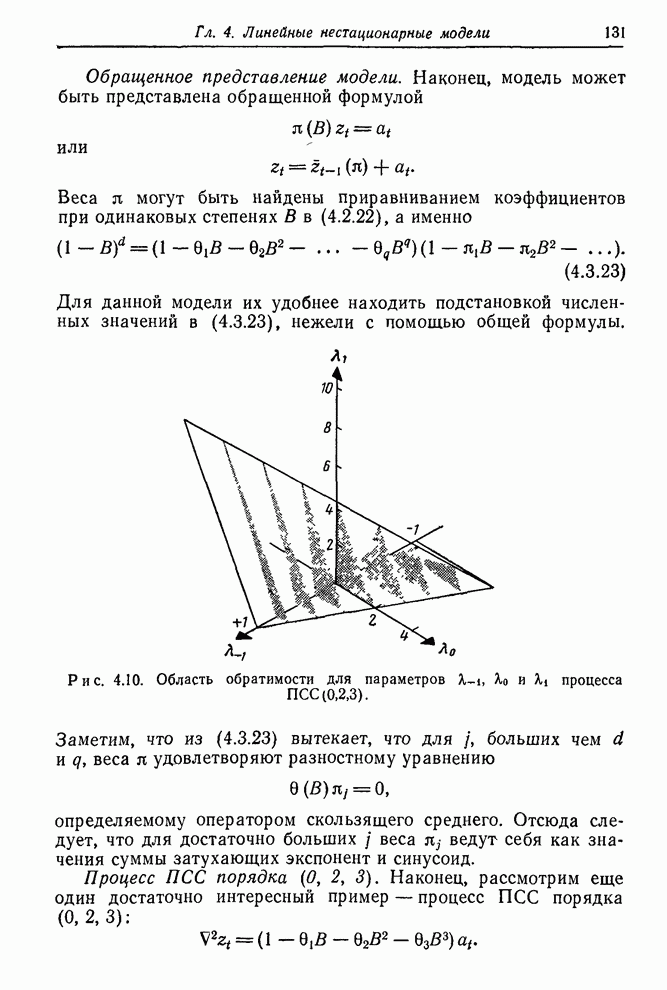
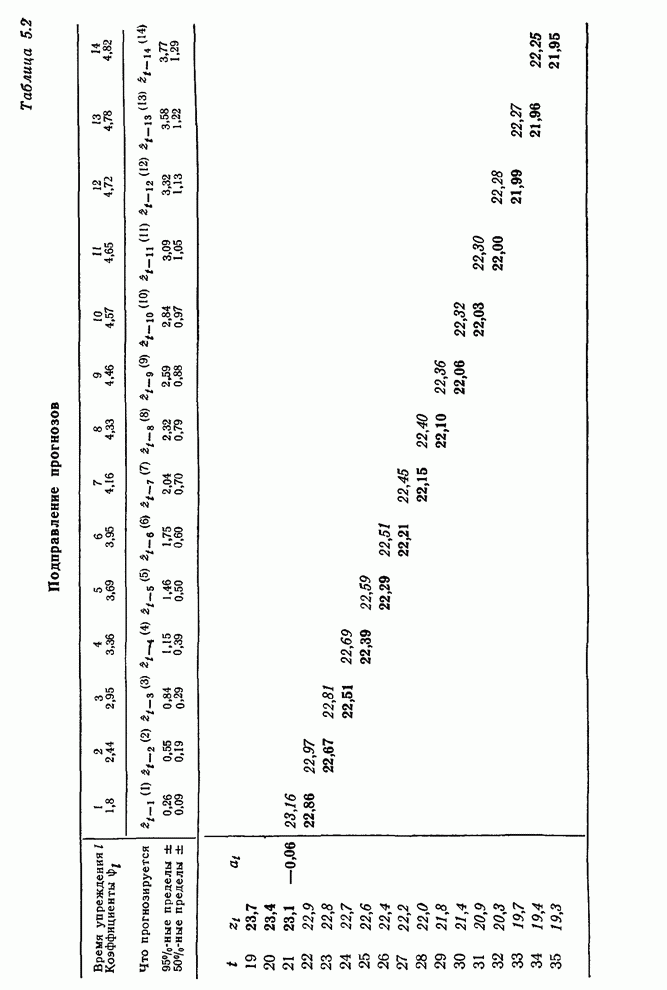
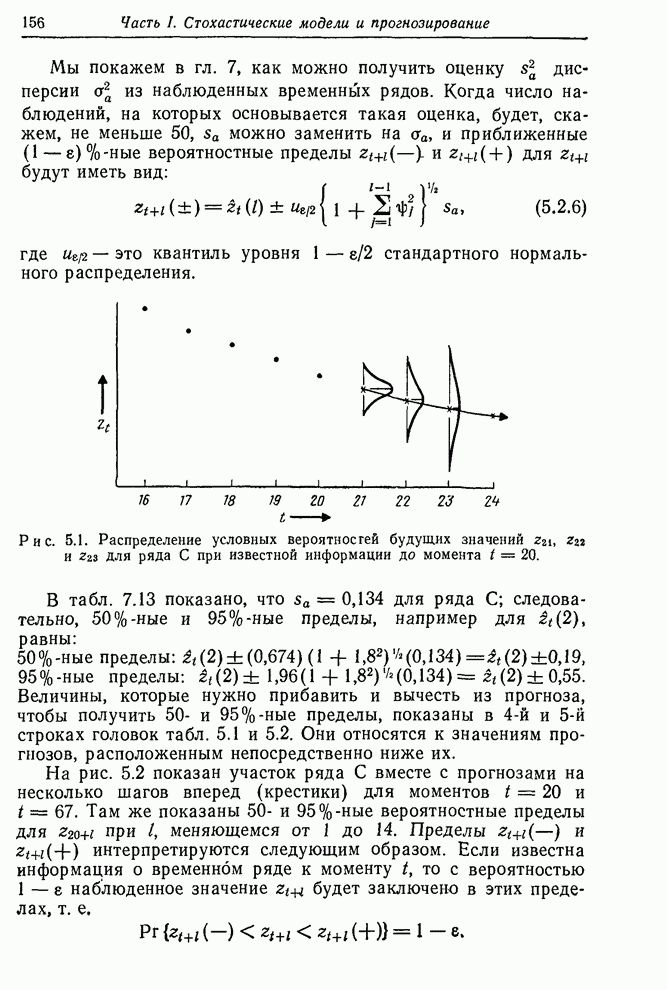
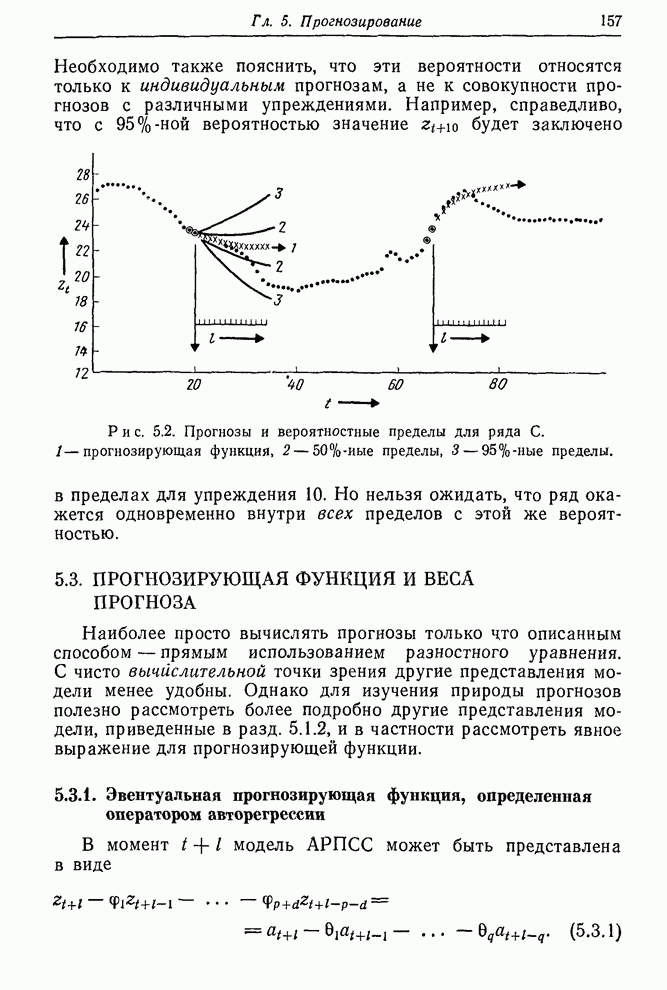
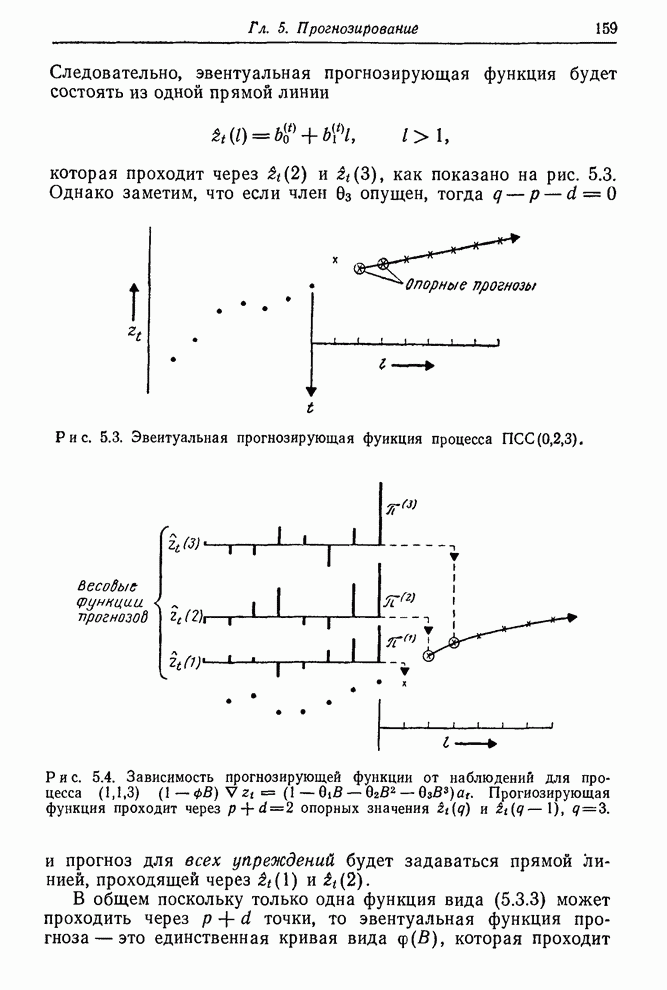
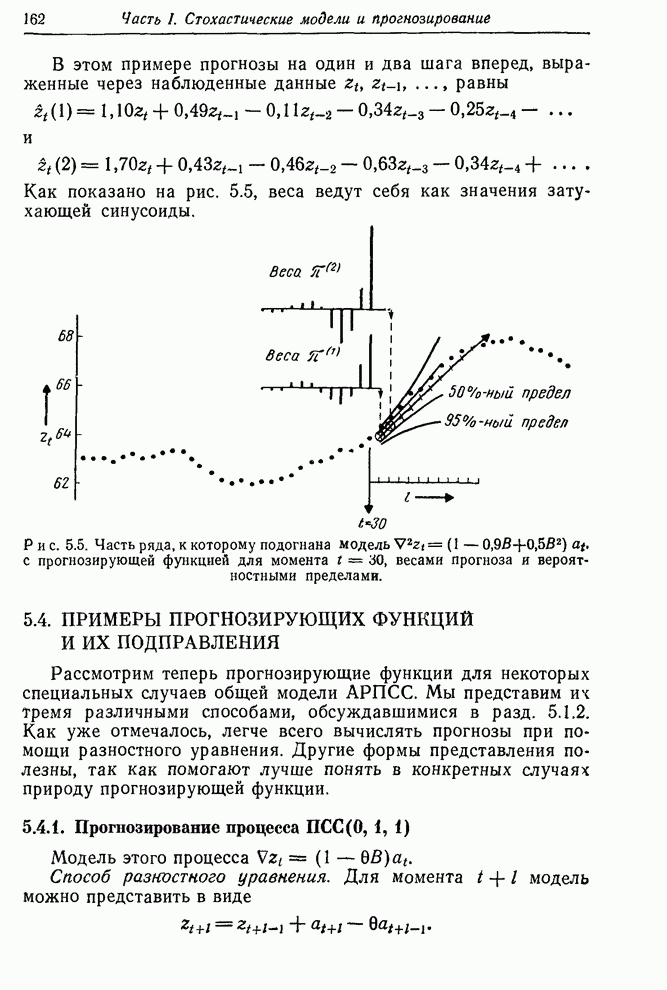
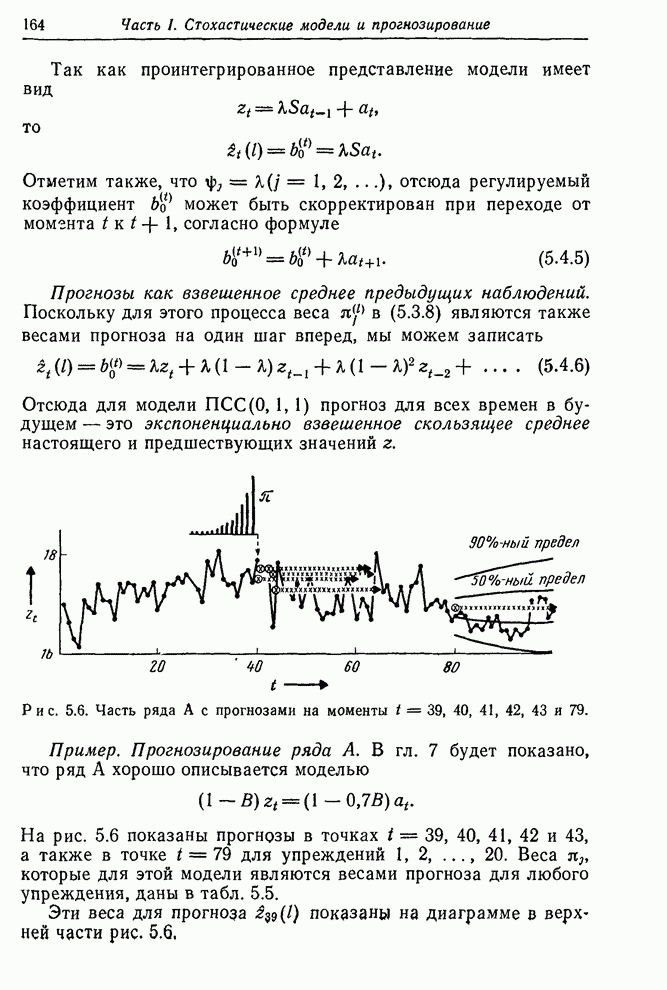
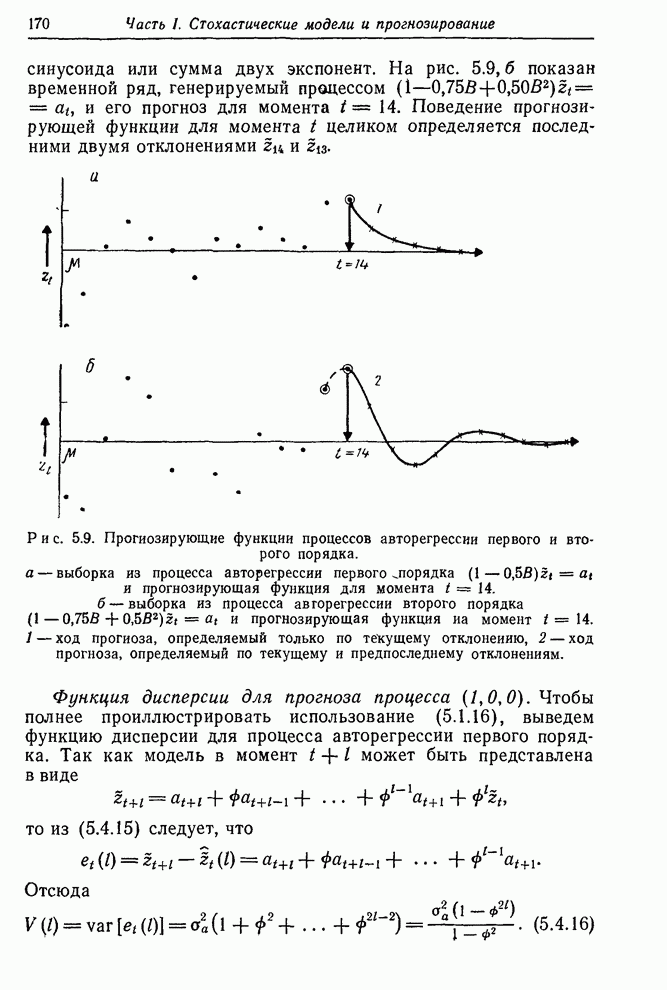
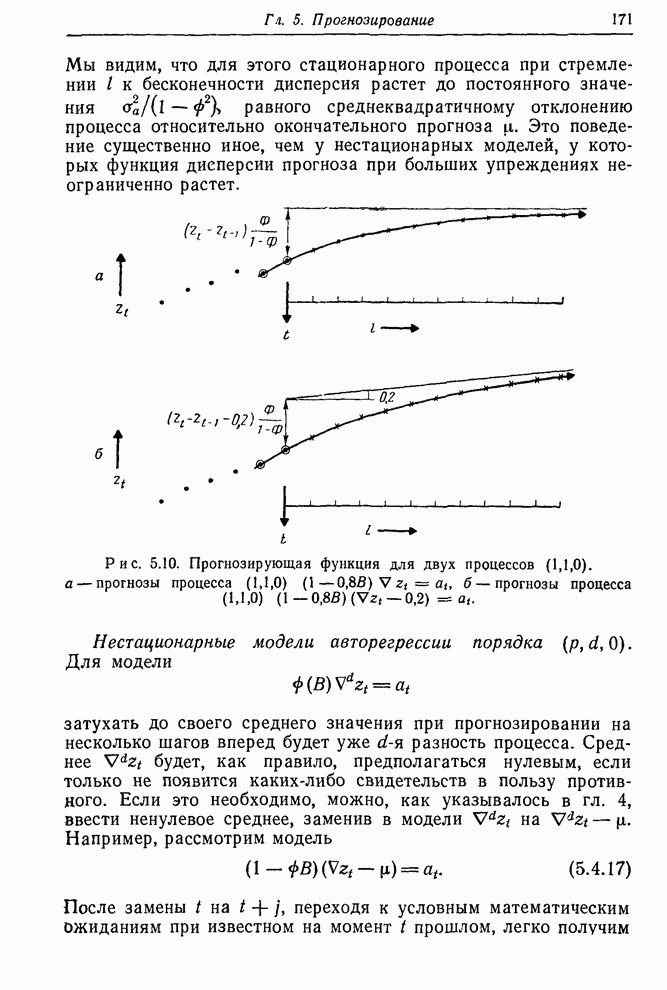
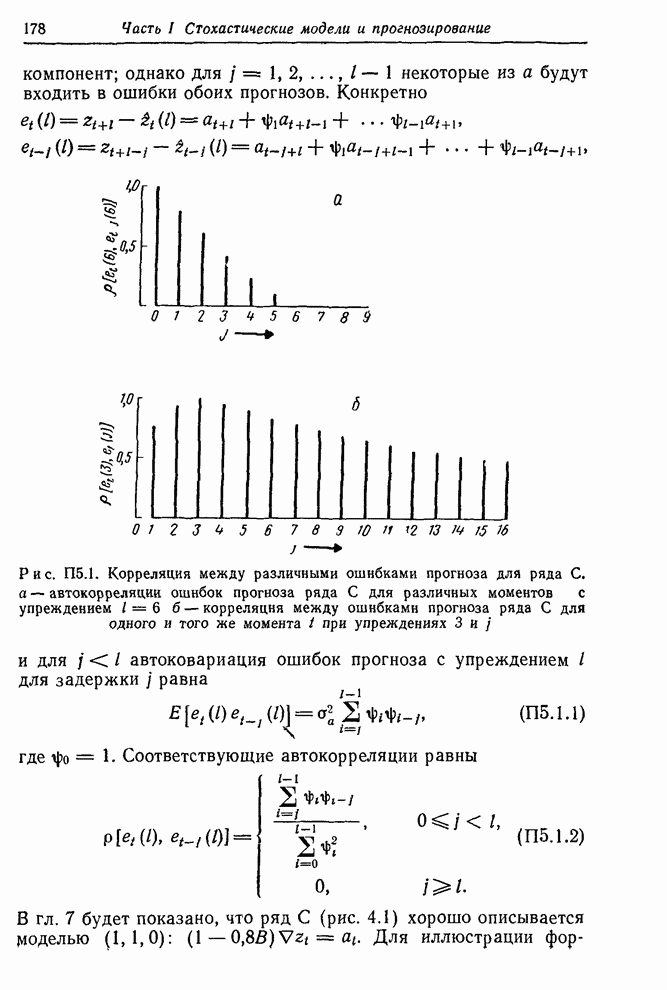
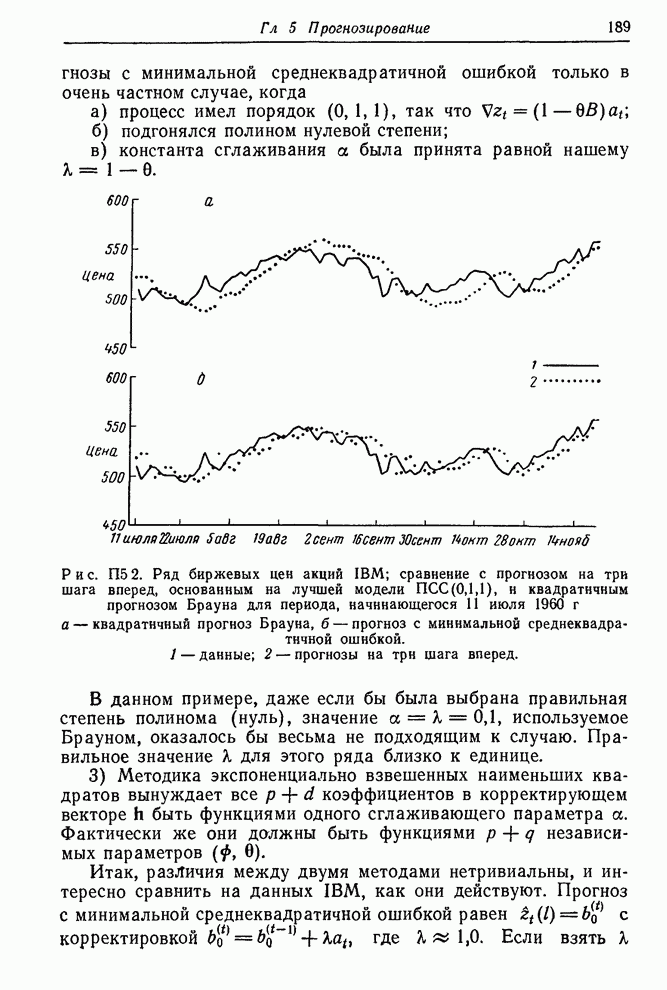
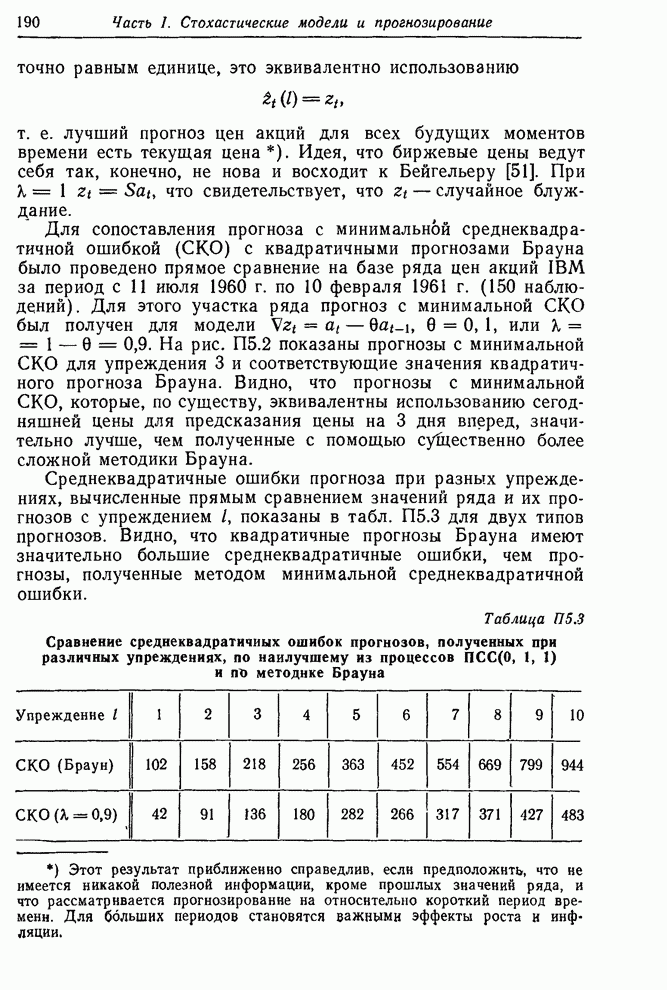
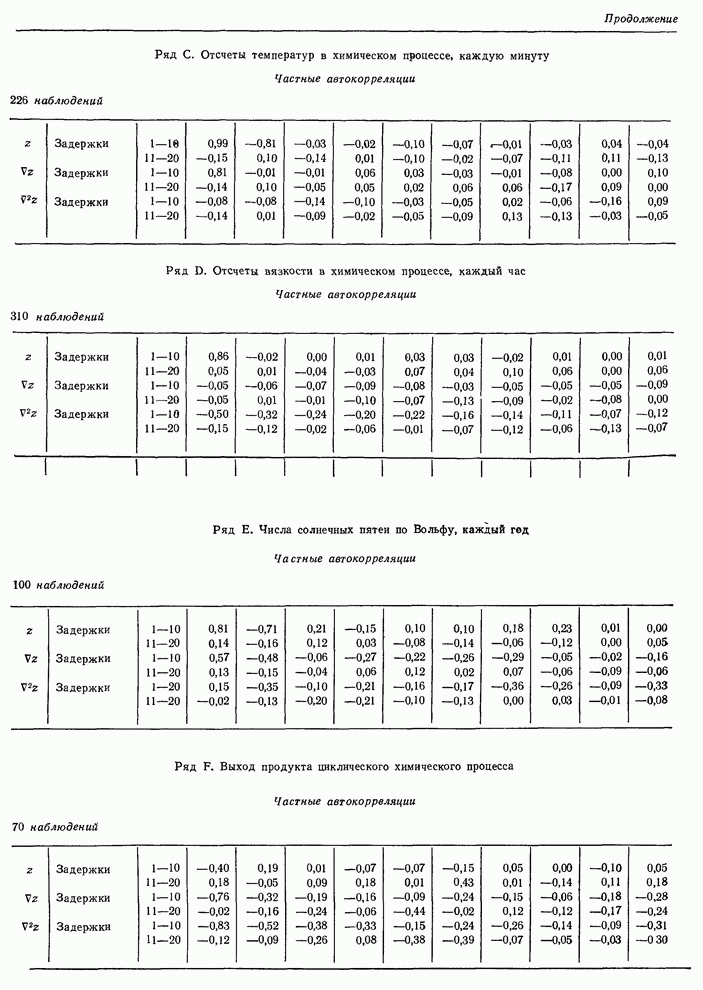
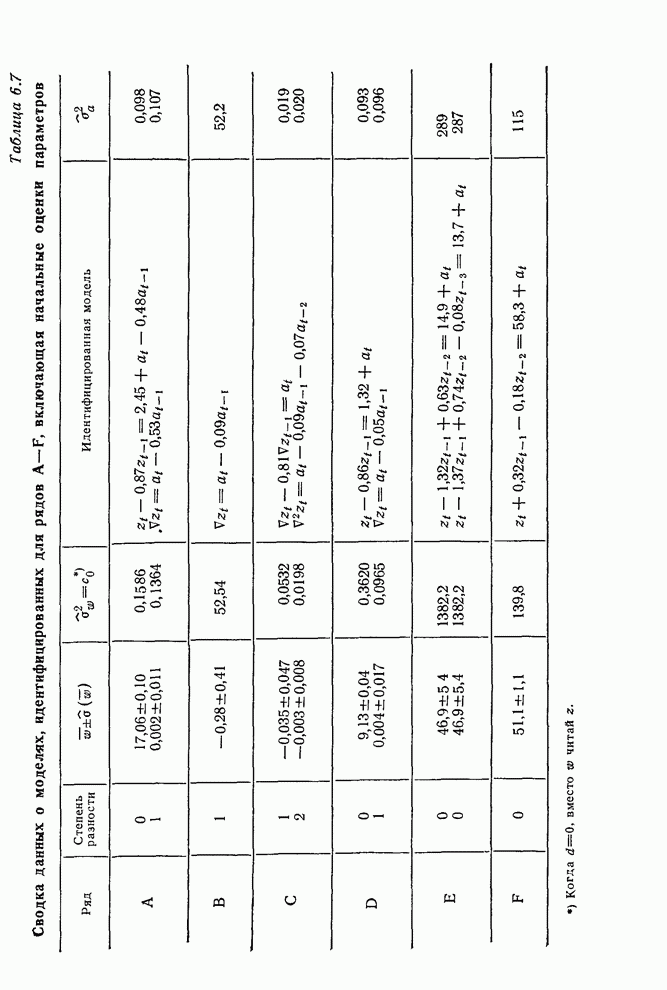
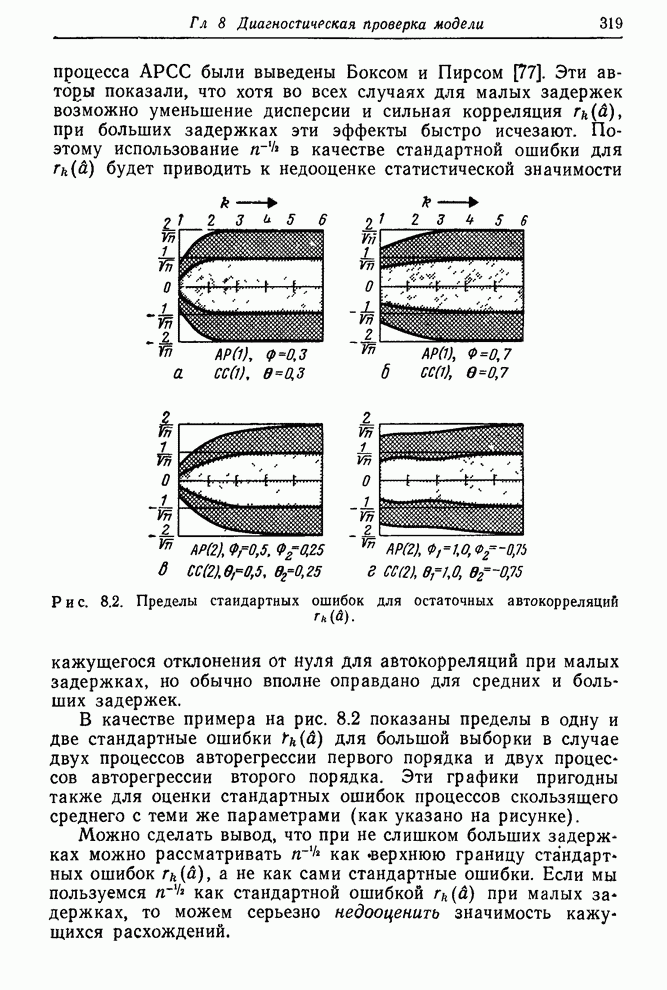
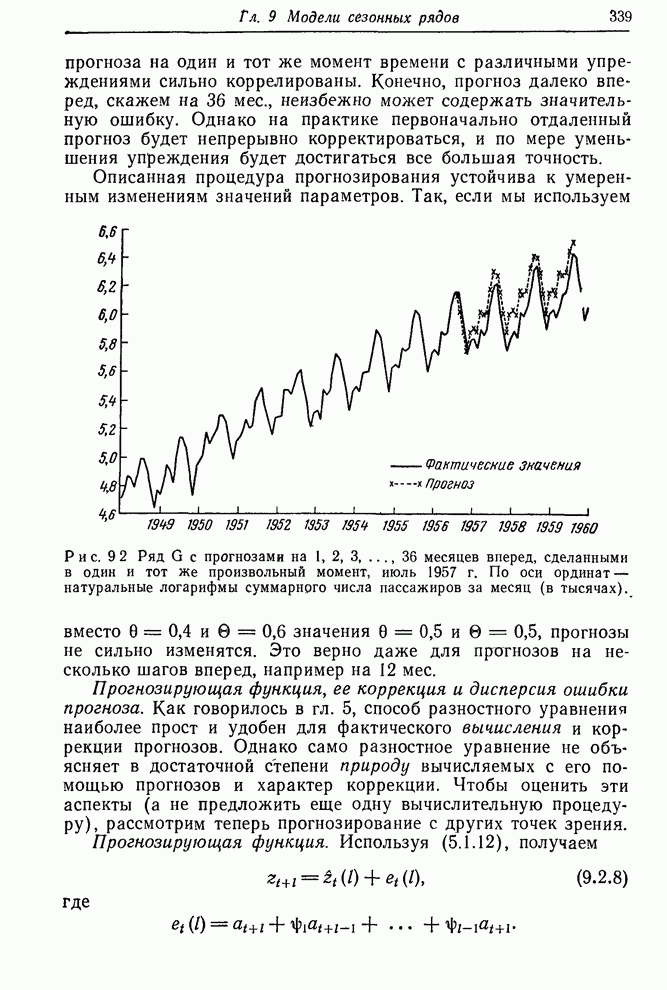
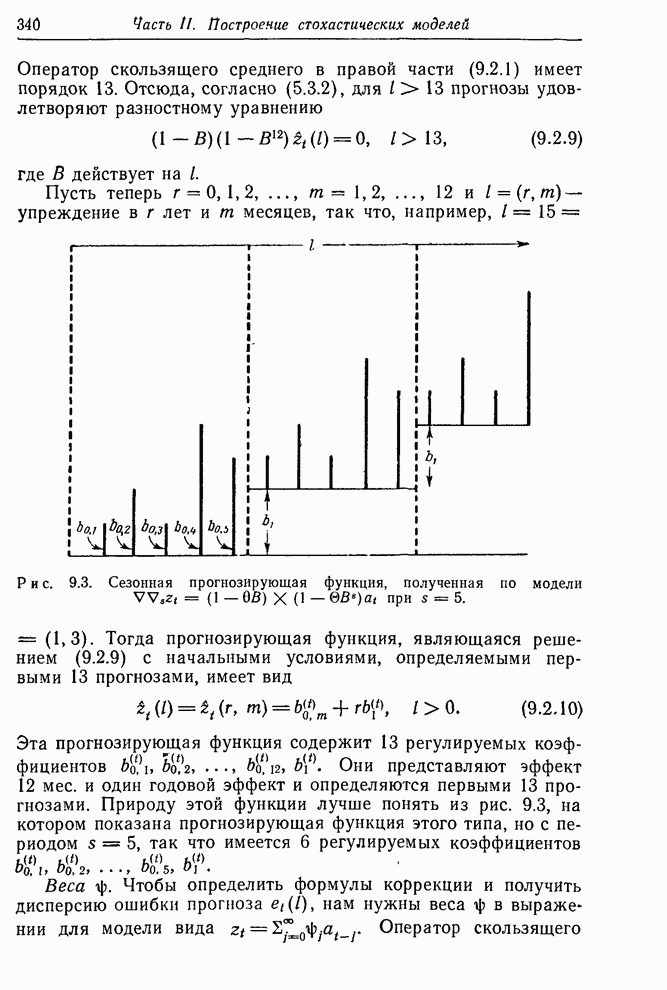
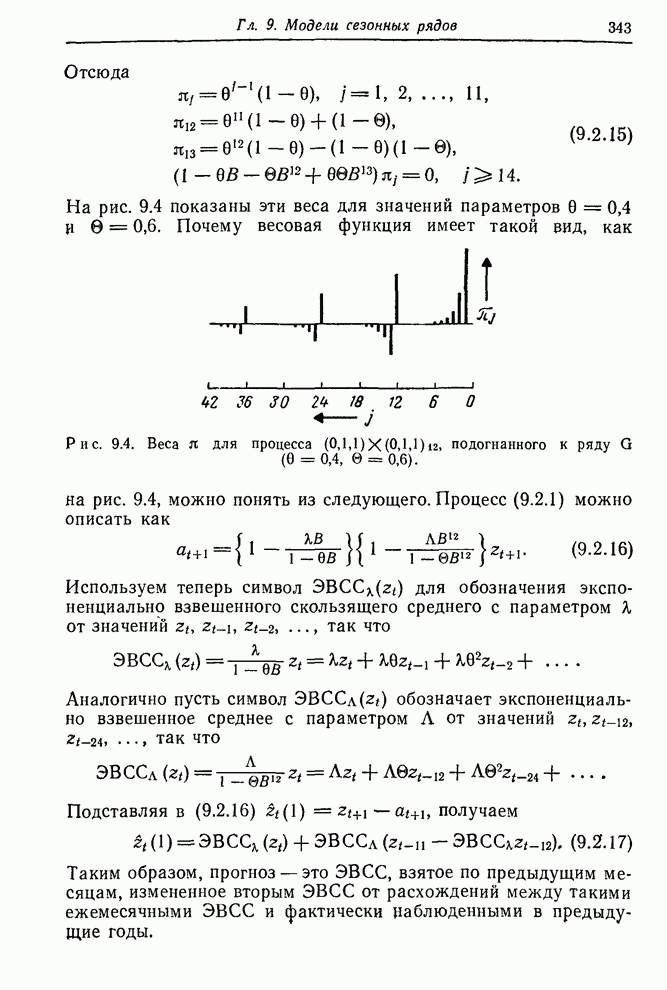
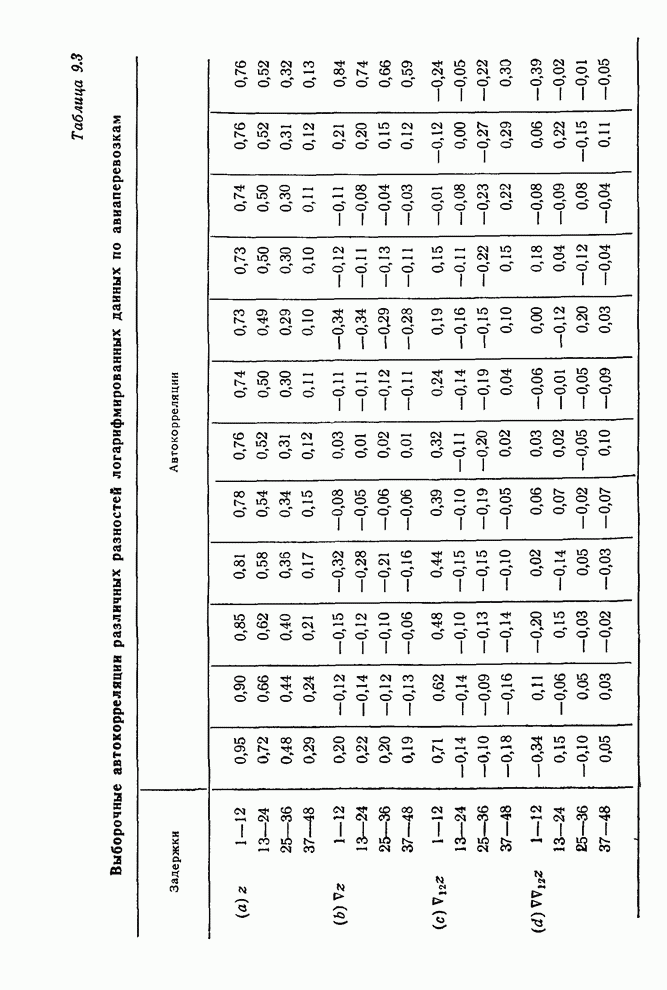
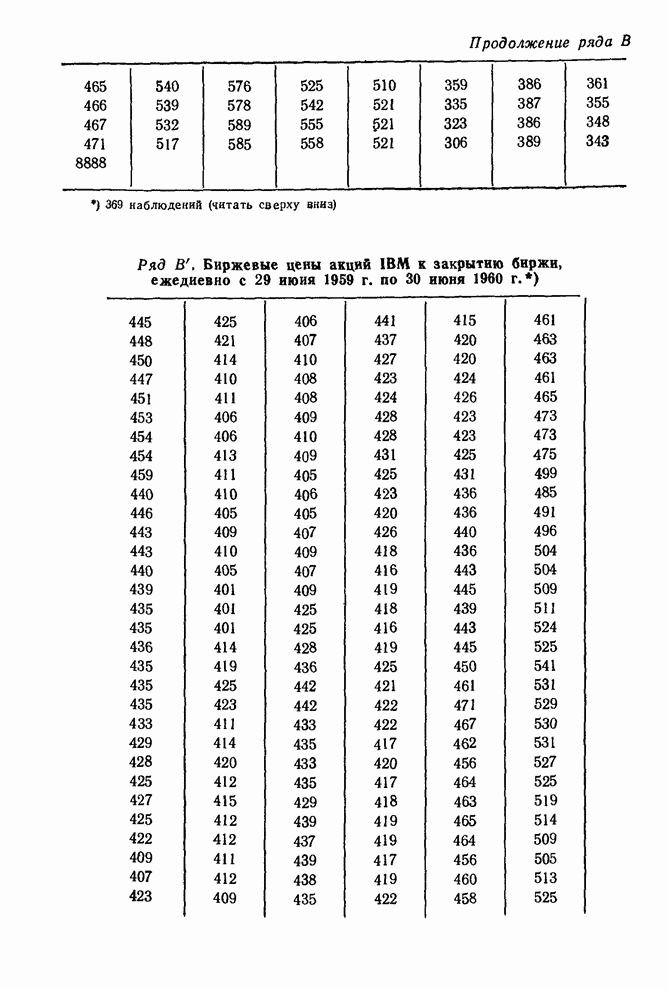
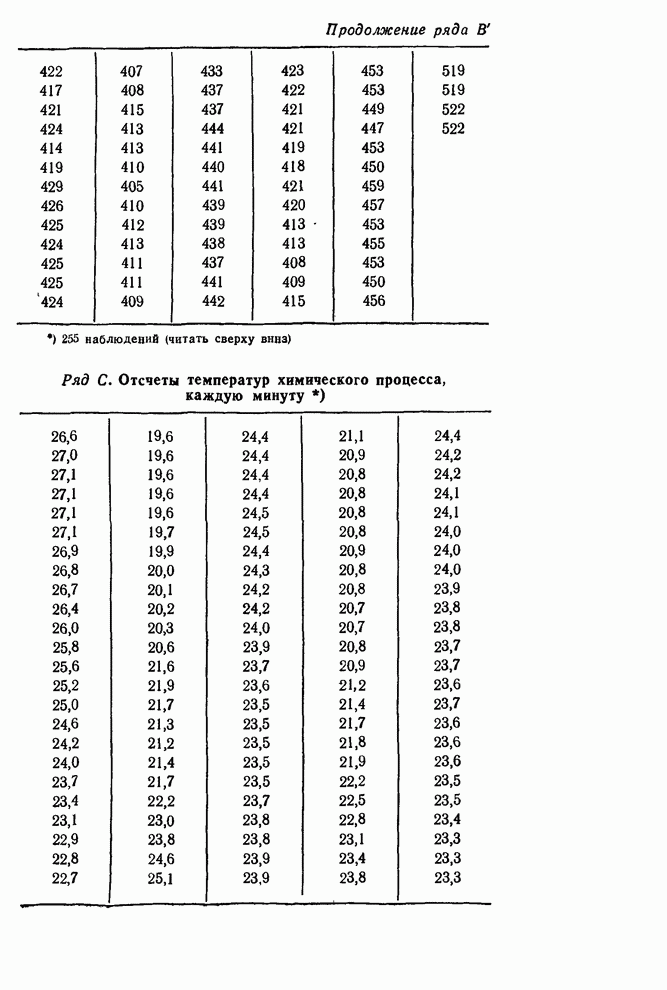
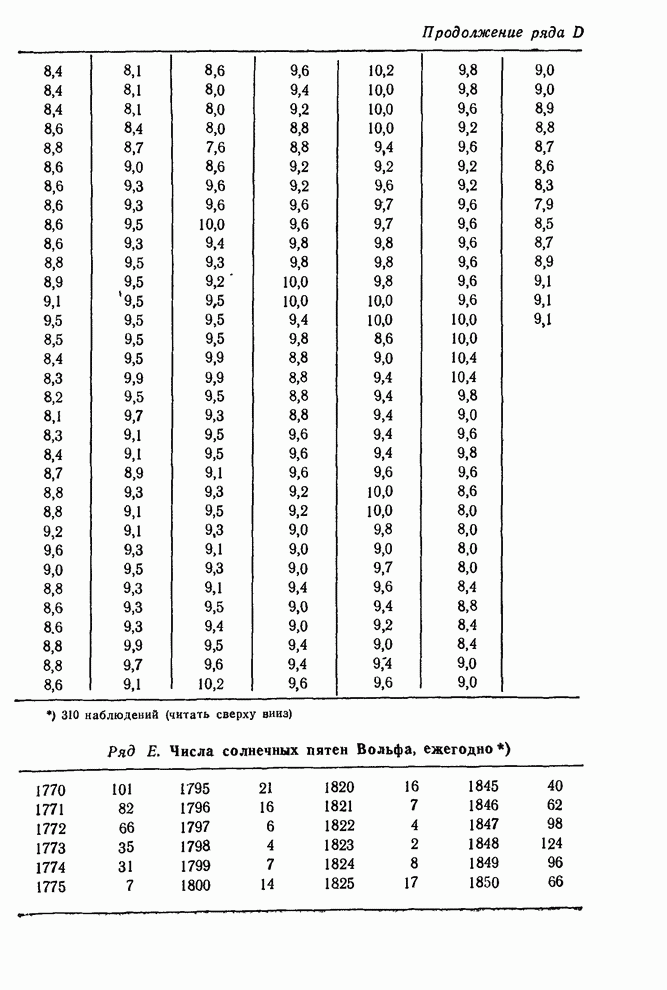
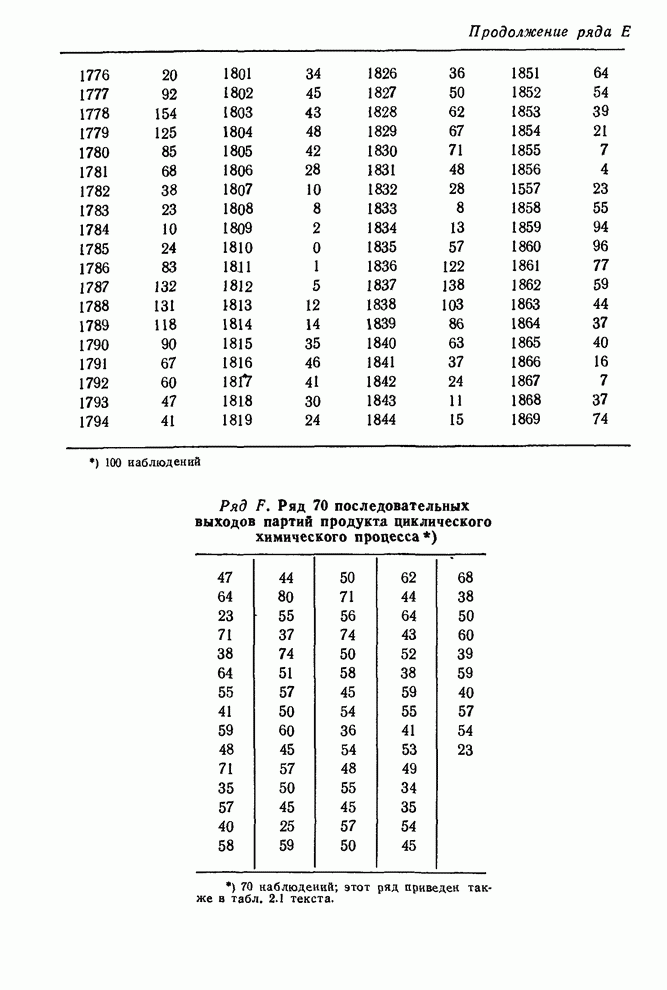
| << Предыдущий параграф | Следующий параграф >> |
Пред.
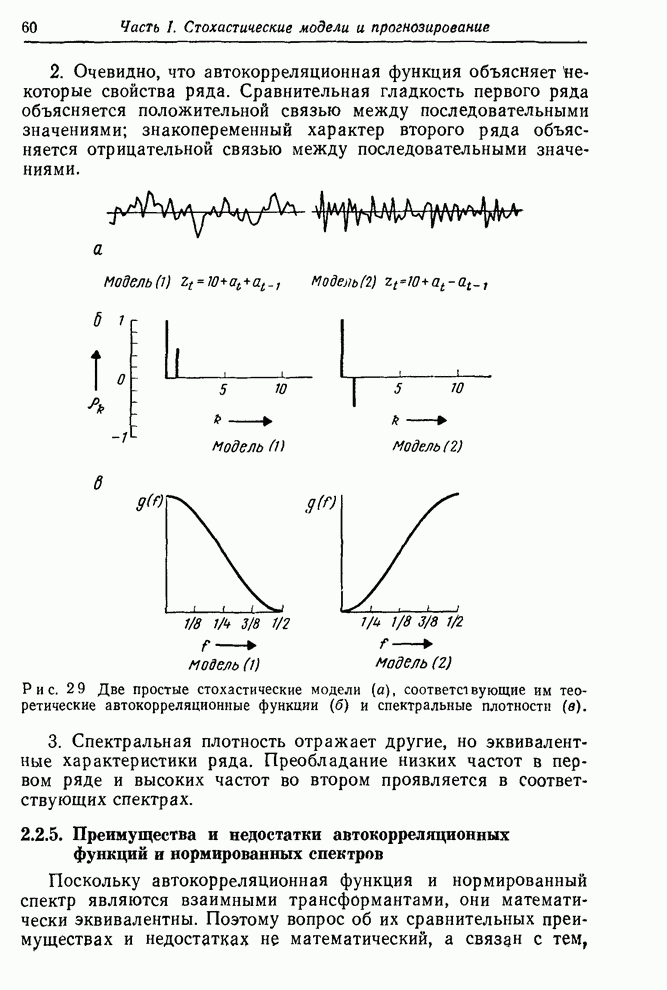
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
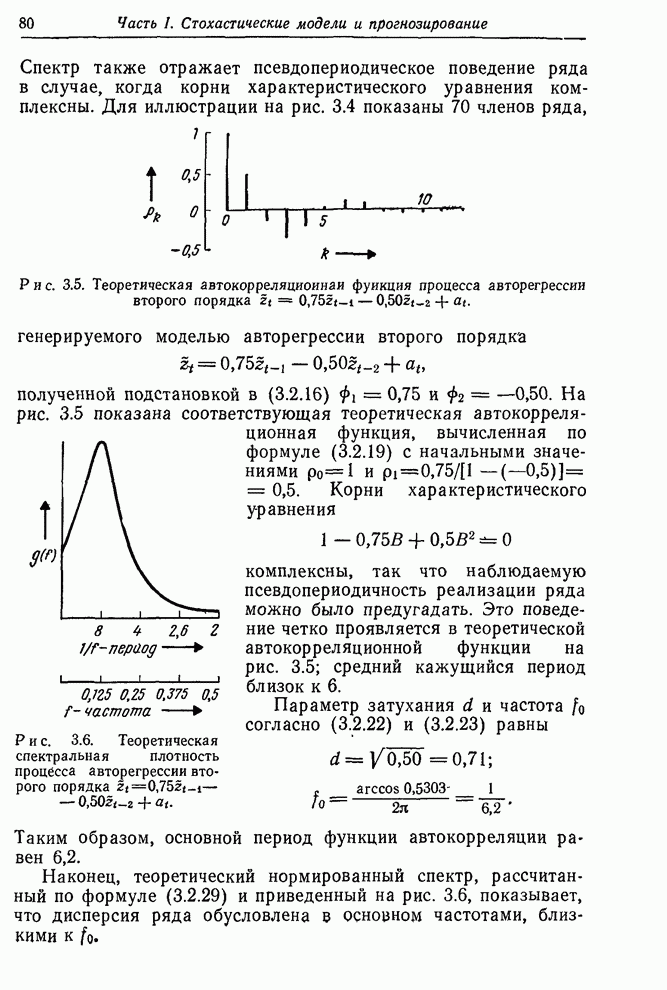
7.2.2. Численный метод нахождения производных
Как
будет показано позднее, производные ![]() могут быть получены непосредственно. Однако
для машинных расчетов оказался весьма эффективным общий нелинейный метод
наименьших квадратов, в котором производные оцениваются численно. Это делается
поочередным возмущением одного из параметров. Затем для данной модели
вычисляются рекуррентным образом значения
могут быть получены непосредственно. Однако
для машинных расчетов оказался весьма эффективным общий нелинейный метод
наименьших квадратов, в котором производные оцениваются численно. Это делается
поочередным возмущением одного из параметров. Затем для данной модели
вычисляются рекуррентным образом значения ![]() для
для ![]() ; при этом используется необходимое
число значений «прогнозов назад». Затем вычисления повторяются для
; при этом используется необходимое
число значений «прогнозов назад». Затем вычисления повторяются для ![]() , затем для
, затем для ![]() и т. д. Величина, обратная
по знаку требуемой производной, находится затем достаточно точно по формуле
и т. д. Величина, обратная
по знаку требуемой производной, находится затем достаточно точно по формуле
![]() . (7.2.2)
. (7.2.2)
Описанный
численный метод получения производных универсален и требует только наличия
программы для вычисления ![]() . Общие стандартные программы
нахождения нелинейных оценок, нуждающиеся только в дополнительной подпрограмме
для вычисления
. Общие стандартные программы
нахождения нелинейных оценок, нуждающиеся только в дополнительной подпрограмме
для вычисления ![]() ,
сейчас уже широко распространены [62]. В некоторых вариантах программы
,
сейчас уже широко распространены [62]. В некоторых вариантах программы ![]() необходимо указать
заранее; в других программа сама выполняет необходимые итерации для выбора
подходящего
необходимо указать
заранее; в других программа сама выполняет необходимые итерации для выбора
подходящего ![]() .
Некоторые программы включают специальные логические схемы, позволяющие избежать
проскоков области минимума и ускорить сходимость [63].
.
Некоторые программы включают специальные логические схемы, позволяющие избежать
проскоков области минимума и ускорить сходимость [63].
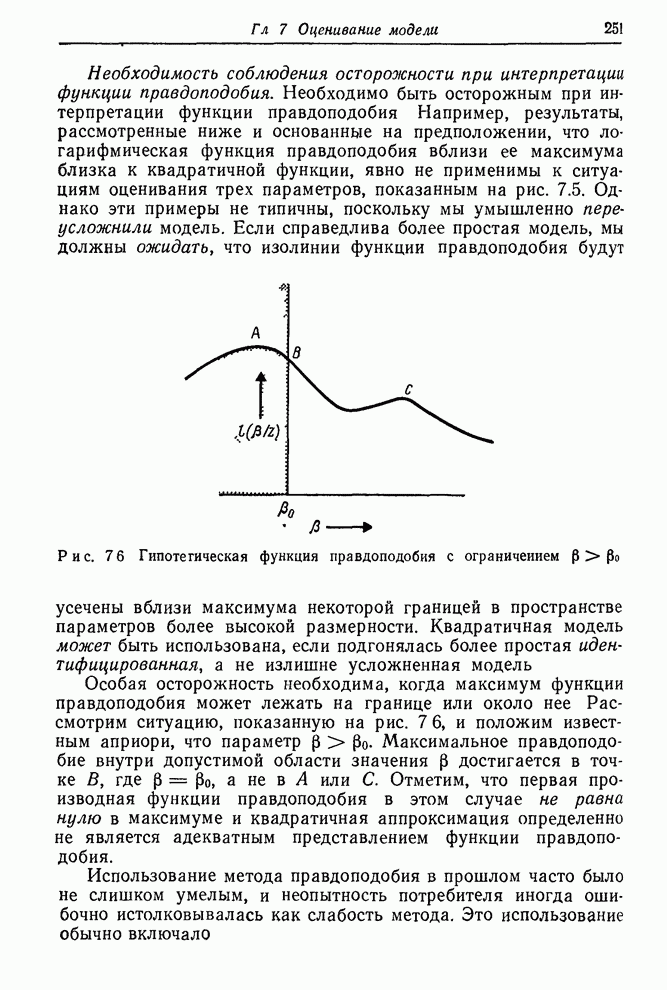
При
условии, что решение наименьших квадратов не лежит вблизи границы или на
границе области, значения ![]() из последней итерации можно использовать
для вычисления приближенных дисперсий, ковариаций и доверительных интервалов.
Конкретнее,
из последней итерации можно использовать
для вычисления приближенных дисперсий, ковариаций и доверительных интервалов.
Конкретнее, ![]() аппроксимирует
матрицу ковариаций
аппроксимирует
матрицу ковариаций ![]() , а
, а ![]() оценивается по
оценивается по ![]() .
.
Применение
к процессу (0, 1, 1). В качестве элементарного примера рассмотрим подгонку
к ряду ![]() процесса
процесса
![]()
![]()
с ![]() . Начало вычислений
для пробного значения
. Начало вычислений
для пробного значения ![]() показано в табл. 7.9. Значения
прогноза назад для
показано в табл. 7.9. Значения
прогноза назад для ![]() были получены приравниванием
были получены приравниванием ![]() и применением
возвратной рекуррентной формулы
и применением
возвратной рекуррентной формулы ![]() . Большая точность могла бы быть
достигнута применением этой рекуррентной формулы к более далеким значениям
ряда. Значения
. Большая точность могла бы быть
достигнута применением этой рекуррентной формулы к более далеким значениям
ряда. Значения ![]() ,
найденные последовательно из уравнения
,
найденные последовательно из уравнения ![]() для
для ![]() и
и ![]() , приведены в четвертом и пятом столбцах
вместе со значениями отрицательных производных
, приведены в четвертом и пятом столбцах
вместе со значениями отрицательных производных ![]() найденных по формуле (7.2.2). Для получения
первой поправки для
найденных по формуле (7.2.2). Для получения
первой поправки для ![]() вычислим
вычислим
 .
.
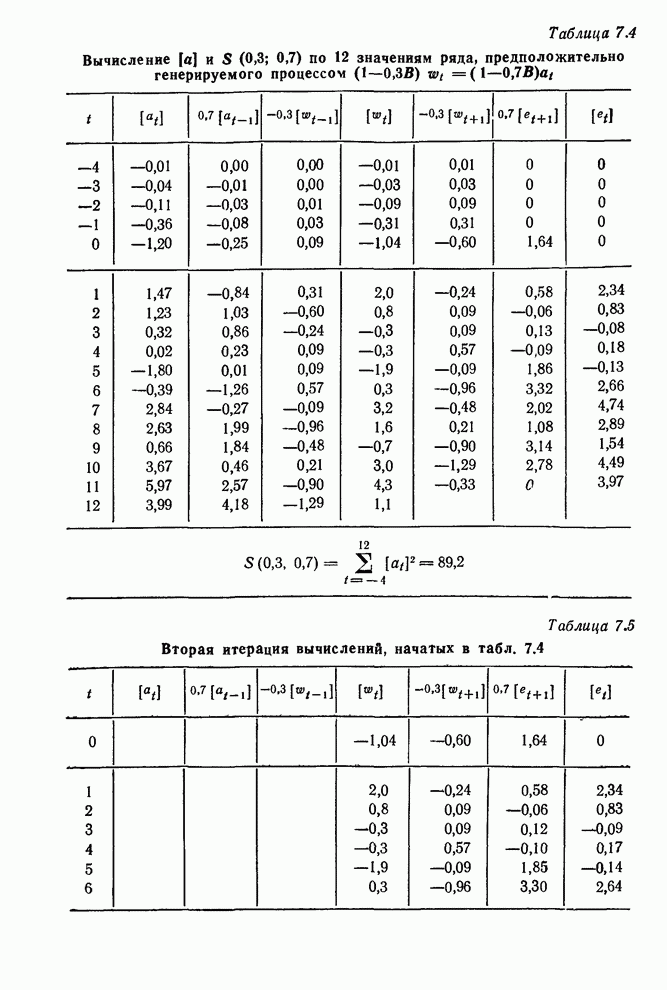
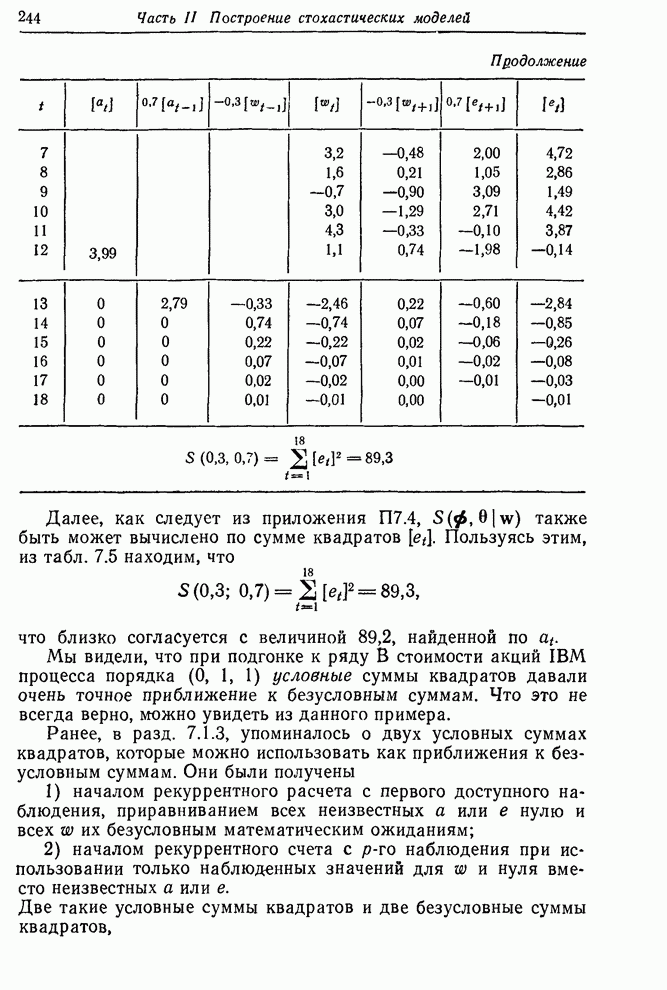
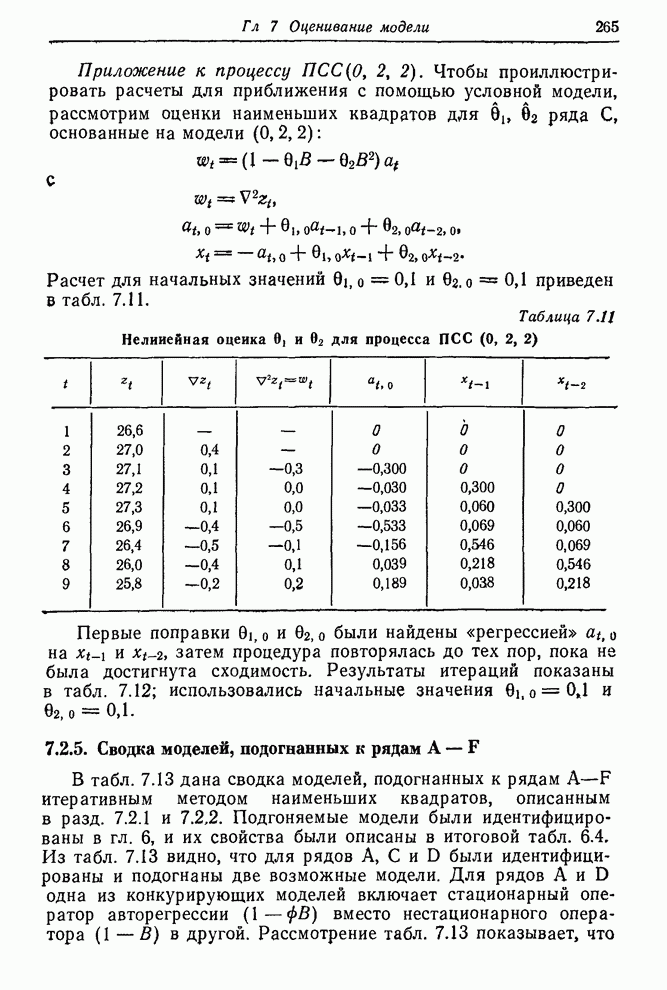
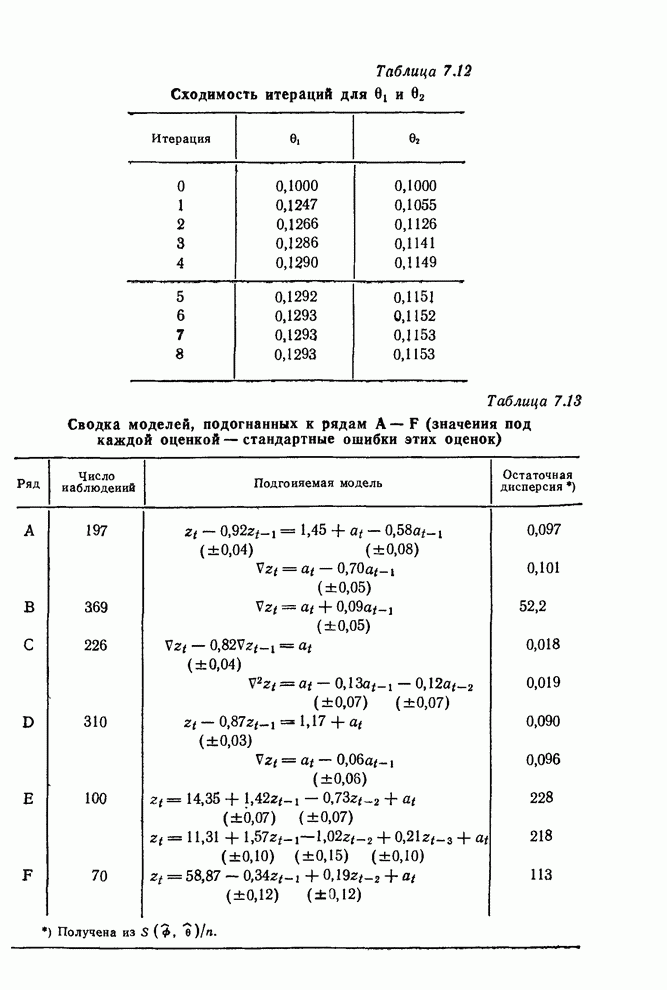
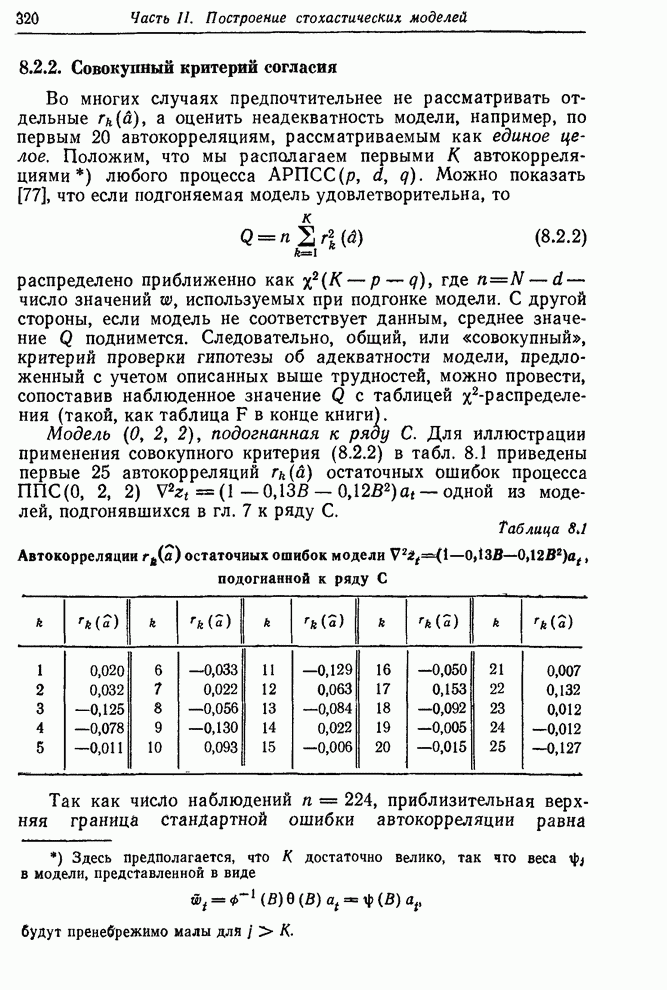
В этом примере, используя весь ряд длиной в 197 наблюдений, мы получили сходящийся результат после четырех итераций. Расчет шел следующим образом:
|
Итерация |
|
|
0 1 2 3 4 5 |
0,50 0,63 0,68 0,69 0,70 0,70 |
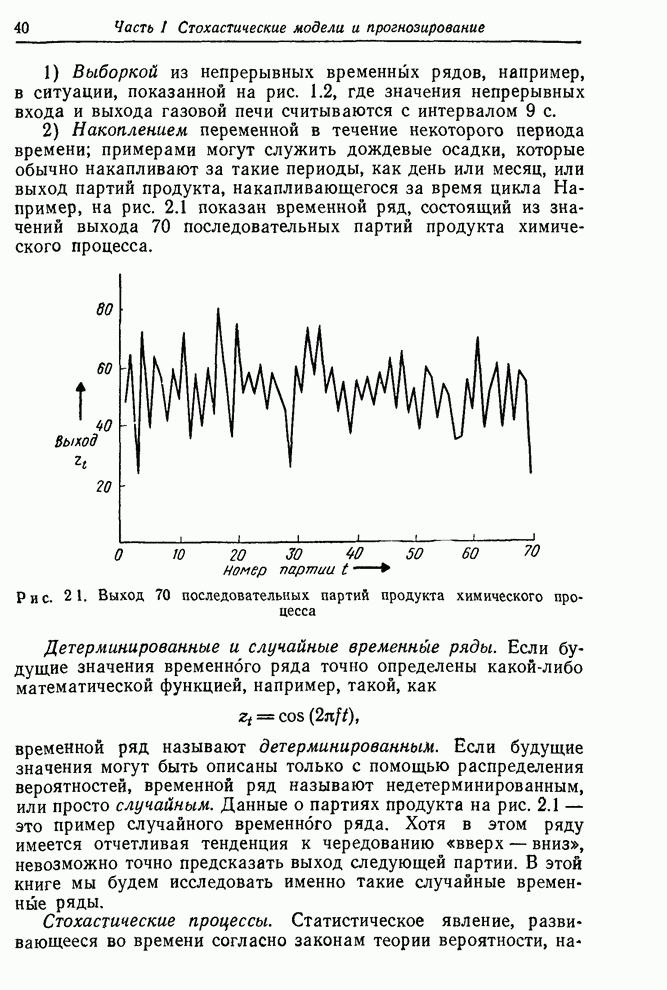
Таблица 7.9. Пример
расчета производных по данным ряда ![]()
|
|
|
|
|
|
|
|
0 1 2 3 4 5 6 7 8 9 10 |
17,0 16,6 16,3 16,1 17,1 16,9 16,8 17,4 17,1 17,0 16,7 |
-0,40 -0,30 -0,20 1,00 -0,20 -0,10 0,60 -0,30 -0,10 -0,30 |
0,2453 -0,2773 -0,4387 -0,4193 0,7903 0,1952 -0,0024 0,5988 -0,0006 -0,1003 -0,3502 |
0,2496 -0,2727 -0,4391 -0,4239 0,7838 0,1997 0,0019 0,6010 0,0065 -0,0967 -0,3493 |
-0,43 -0,46 0,04 0,46 0,65 -0,45 -0,43 -0,22 -0,71 -0,36 -0,09 |
В
общем значения ![]() и
и
![]() ,
минимизирующие
,
минимизирующие ![]() ,
могут быть найдены этим методом с любой необходимой степенью точности. Этот
метод особенно удобен потому, что нам не нужно специально программировать
расчет производных; не требуется никаких дополнительных процедур, кроме как для
вычисления
,
могут быть найдены этим методом с любой необходимой степенью точности. Этот
метод особенно удобен потому, что нам не нужно специально программировать
расчет производных; не требуется никаких дополнительных процедур, кроме как для
вычисления ![]() .
.
Программа
3, описанная в сборнике машинных программ в конце этой книги, позволяет
численно оценивать производные и включает возможность прогнозирования назад.
Она позволяет найти оценки наименьших квадратов для параметров любого ![]() процесса.
процесса.
Теперь мы покажем также, что производные можно получить и непосредственно, но для этого нужны дополнительные рекуррентные расчеты.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к русскому изданию
- Предисловие
- План книги
- Глава 1. Введение и краткое содержание
- 1.1. Три важные практические проблемы
- 1.1.1. Прогнозирование временных рядов
- 1.1.2. Оценивание передаточных функций
- 1.1.3. Проектирование дискретных регулирующих систем
- 1.2. Стохастические и детерминированные динамические математические модели
- 1.2.1. Стационарные нестационарные стохастические модели для прогнозирования и регулирования
- 1.2.2. Модели передаточных функций
- 1.2.3. Модели дискретных систем регулирования
- 1.3. Основные понятия в построении моделей
- 1.3.1. Экономия
- 1.3.2. Интерактивные этапы в выборе модели
- Часть 1. Стохастические модели и основанное на них прогнозирование
- Глава 2. Автокорреляционная функция и спектр
- 2.1. Автокорреляционные свойства стационарных моделей
- 2.1.1. Временные ряды и стохастические процессы
- 2.1.2. Стационарные стохастические процессы
- 2.1.3. Положительная определённость и автоковариационная матрица
- 2.1.4. Автоковариационные и автокорреляционные функции
- 2.1.5. Оценивание автоковариационной и автокорреляционной функций
- 2.1.6. Стандартные ошибки оценок автокорреляций
- 2.2. Спектральные свойства стационарных моделей
- 2.2.1. Периодограмма
- 2.2.2. Дисперсионный анализ
- 2.2.3. Спектральная плотность и нормированный спектр
- 2.2.4. Простые примеры автокорреляционных функций и нормированных спектров
- 2.2.5. Преимущества и недостатки автокорреляционных функций и нормированных спектров
- Приложение П2.1. Связь между выборочным спектром и оценкой автоковариационной функции
- Глава 3. Линейные стационарные модели
- 3.1. Общий линейный процесс
- 3.1.1. Две эквивалентные формы линейного процесса
- 3.1.2. Производящая функция автоковариаций линейного процесса
- 3.1.3. Условия стационарности и обратимости линейного процесса
- 3.1.4. Процессы авторегрессии и скользящего среднего
- 3.2. Процессы авторегрессии
- 3.2.1. Условия стационарности для процессов авторегрессии
- 3.2.2. Автокорреляционная функция и спектр процессов авторегрессии
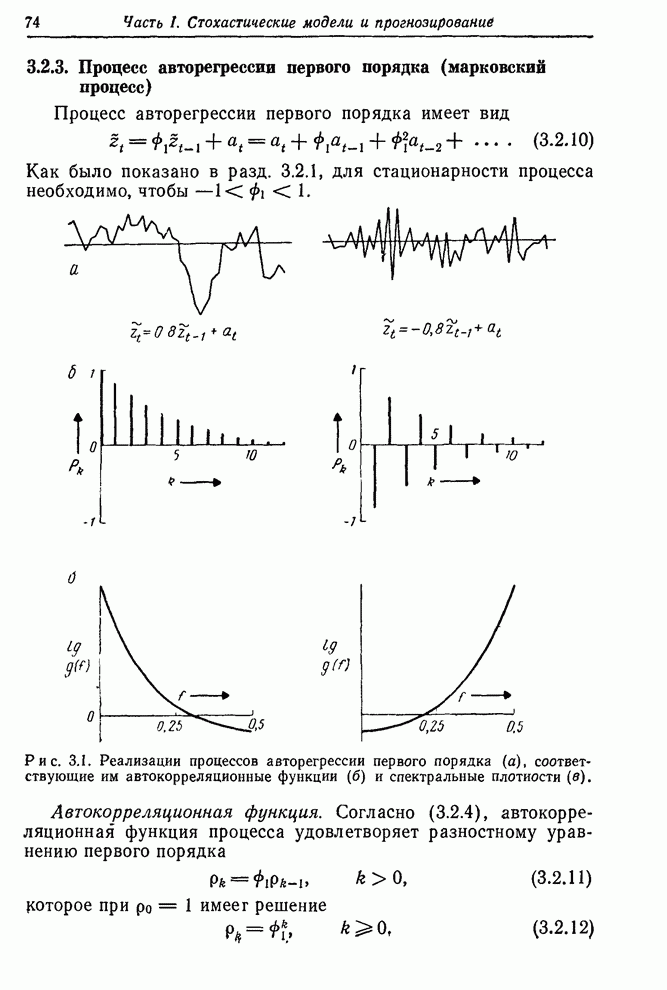
- 3.2.3. Процесс авторегрессии первого порядка (марковский процесс)
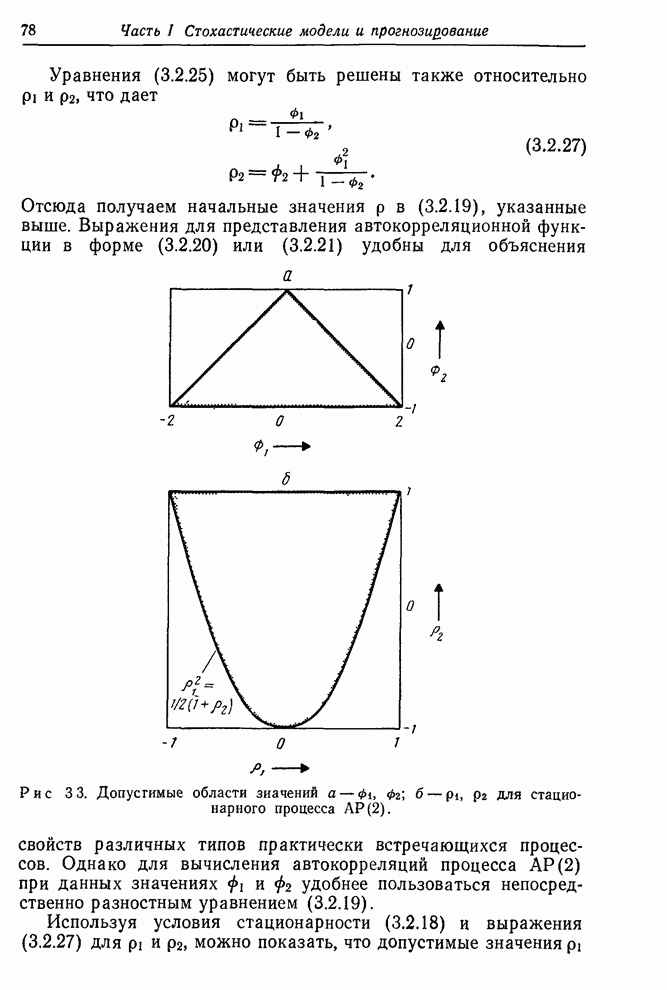
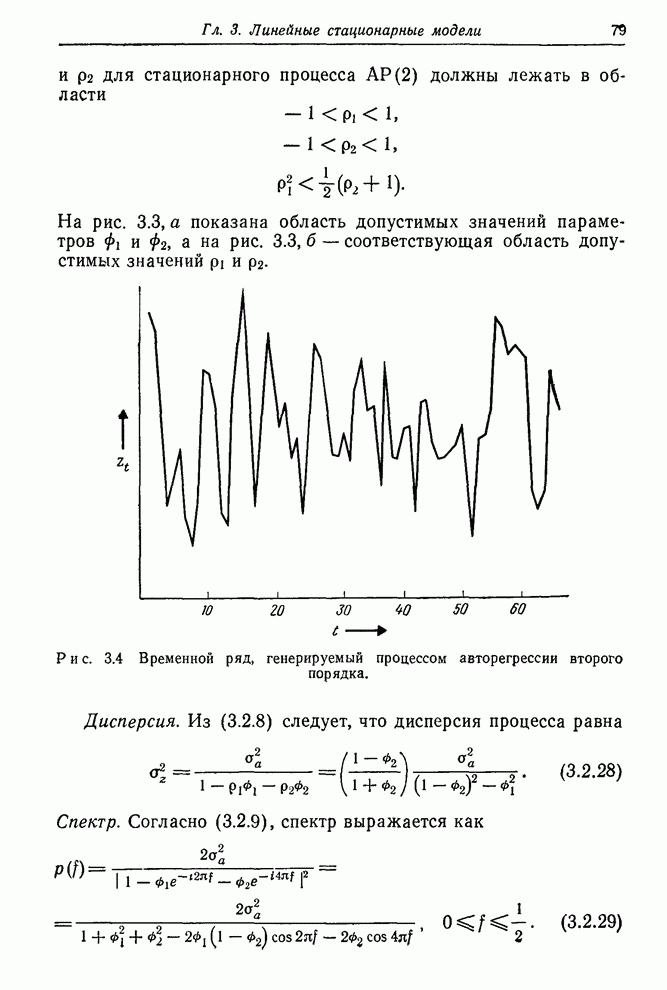
- 3.2.4. Процесс авторегрессии второго порядка
- 3.2.5. Частная автокорреляционная функция
- 3.2.6. Оценивание частной автокорреляционной функции
- 3.2.7. Стандартные ошибки частной автокорреляции
- 3.3. Процессы скользящего среднего
- 3.3.1. Условия обратимости для процессов скользящего среднего
- 3.3.2. Автокорреляционная функция и спектр процесса скользящего среднего
- 3.3.3. Процесс скользящего среднего первого порядка
- 3.3.4. Процесс скользящего среднего второго порядка
- 3.3.5. Взаимность процессов авторегрессии и скользящего среднего
- 3.4. Смешанные процессы авторегрессии — скользящего среднего
- 3.4.1. Свойства стационарности и обратимости
- 3.4.2. Автокорреляционная функция и спектр смешанных процессов
- 3.4.3. Процесс авторегрессии первого порядка — скользящего среднего первого порядка
- 3.3.4. Резюме
- Приложение П3.1. Автоковариации.
- Приложение П3.2. Рекурентный метод вычисления оценок параметров авторегрессии
- Глава 4. Линейные нестационарные модели
- 4.1. Процессы авторегрессии — проинтегрированного скользящего среднего
- 4.1.1. Нестационарность процесса авторегрессии первого порядка
- 4.1.2. Общая модель для нестационарного процесса, проявляющего однородность
- 4.1.3. Общий вид процесса авторегрессии – проинтегрированного скользящего среднего
- 4.2. Три формы представления модели авторегрессии – проинтегрированного скользящего среднего
- 4.2.1. Представление модели в виде разности уравнения
- 4.2.2. Представление модели, использующее случайные импульсы
- 4.2.3. Обращенное представление модели
- 4.3. Процессы проинтегрированного скользящего среднего
- 4.3.1. Процесс проинтегрированного скользящего среднего порядка (0,1,1)
- 4.3.2. Процесс проинтегрированного скользящего среднего порядка (0.2.2)
- 4.3.3. Общий процесс проинтегрированного скользящего среднего порядка (0, d, q)
- Приложение П4.1. Линейные разностные уравнения
- Приложение П4.2. Процесс ПСС(0,1,1) с детерминированным дрейфом нуля
- Приложение П4.3. Свойства конечного оператора ссумирования
- Приложение П4.4. Процессы АРПСС с добавленным шумом
- Глава 5. Прогнозирование
- 5.1. Прогнозы с минимальной среднеквадратичной ошибкой и их свойства
- 5.1.1. Вывод формулы для прогнозов с минимальной среднеквадратичной ошибкой
- 5.1.2. Три основных представления прогноза
- 5.2. Вычисление и подправление прогноза
- 5.2.1. Удобная схема для вычисления прогнозов
- 5.2.2. Вычисление весов
- 5.2.3. Использование весов при подправлении прогнозов
- 5.2.4. Вычисление вероятностных пределов прогнозов при произвольном упреждении
- 5.3. Прогнозирующая функция и веса прогноза
- 5.3.1. Эвентуальная прогнозирующая функция, определенная оператором авторегрессии
- 5.3.2. Роль оператора скользящего среднего в определении начальных величин
- 5.3.3. Веса прогноза для упреждения l
- 5.4. Примеры прогнозирующих функций и их подправления
- 5.4.1. Прогнозирование процесса ПСС(0, 1, 1)
- 5.4.2. Прогнозирование процесса ПСС(0, 2, 2)
- 5.4.3. Прогнозирование общего процесса ПСС(0, d, q)
- 5.4.4. Прогнозирование процессов авторегрессии
- 5.4.5. Прогнозирование процесса (1, 0, 1)
- 5.4.6. Прогнозирование процесса (1,1,1)
- 5.5. Резюме
- Приложение П5.1. Корреляция между ошибками прогноза
- Приложение П5.2. Веса прогноза для произвольного упреждения
- Приложение П5.3. Прогнозирование при помощи общего проинтегрированного представления
- Часть II. Построение стохастических моделей
- Глава 6. Идентификация моделей
- 6.1. Цели идентификации
- 6.1.1. Этапы процедуры идентификации
- 6.2. Методика идентификации
- 6.2.1. Использование при идентификаций автокорреляционной и частной автокорреляционной функций
- 6.2.2. Стандартные ошибки выборочных автокорреляций и частных автокорреляций
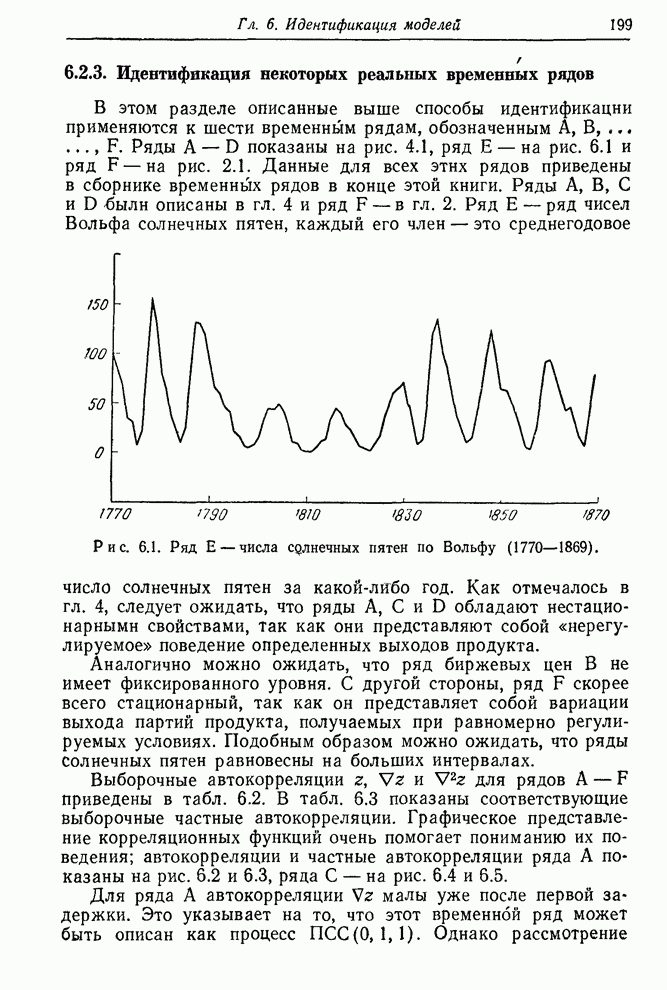
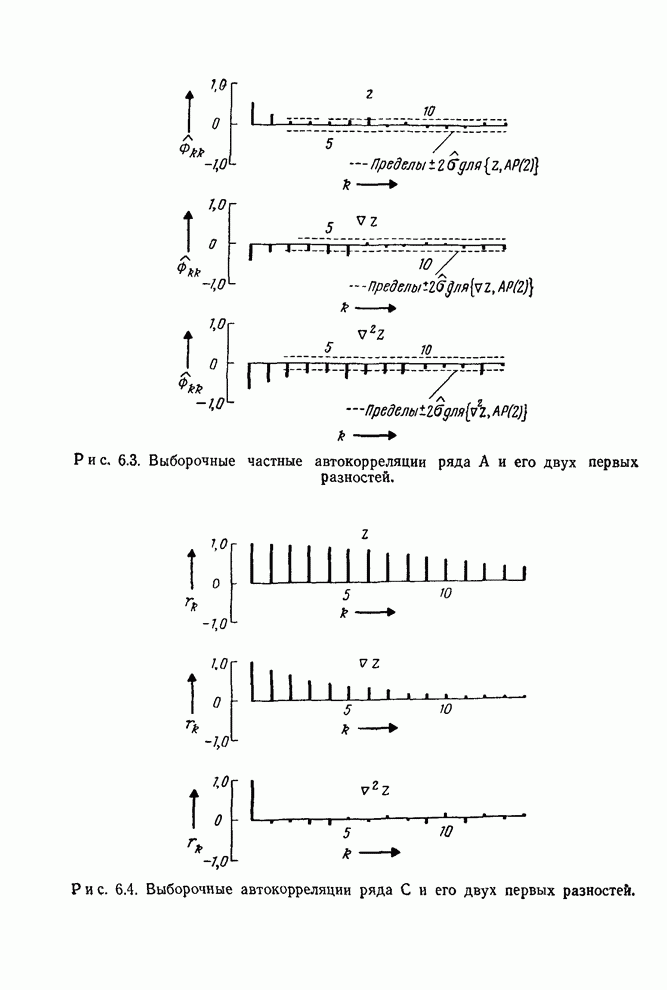
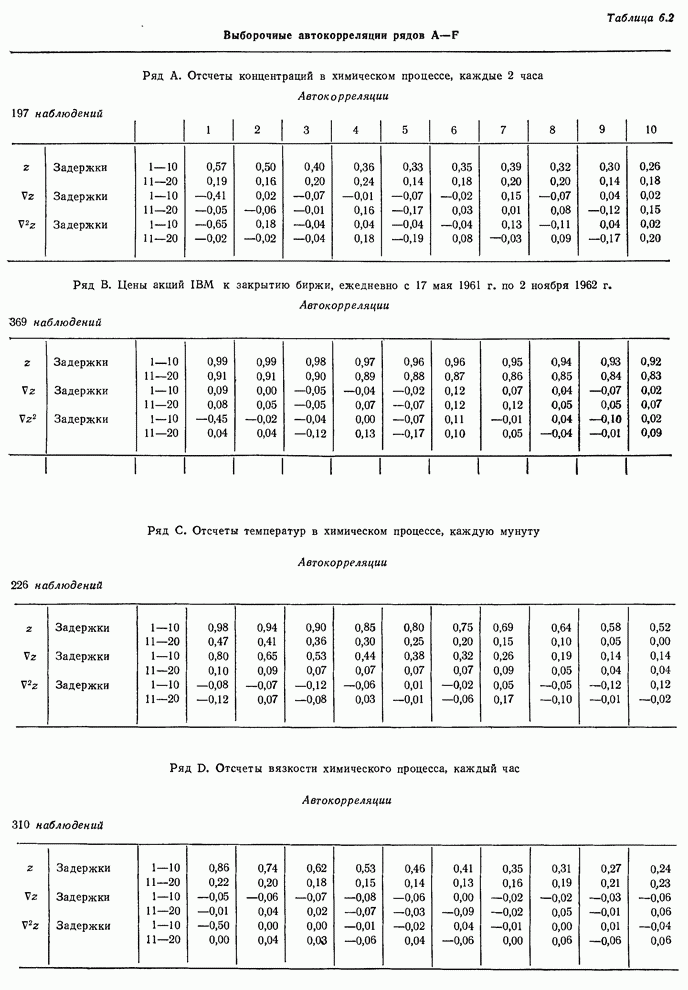
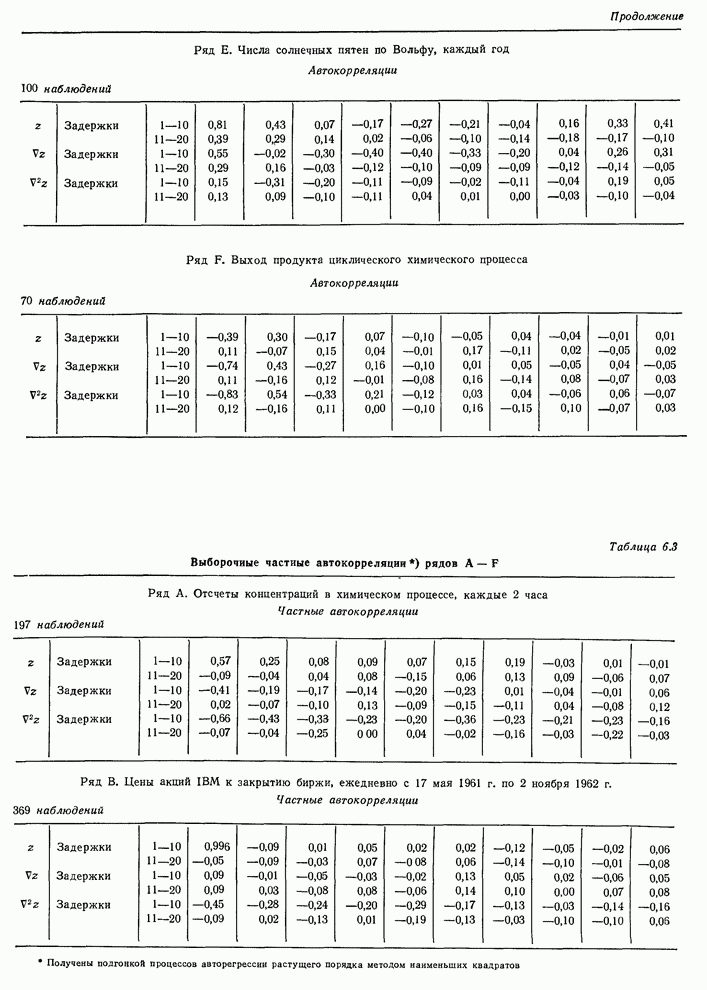
- 6.2.3. Идентификация некоторых реальных временных рядов
- 6.3. Начальные оценки параметров
- 6.3.1. Единственность оценок, получаемых по автоковариационной функции
- 6.3.2. Начальные оценки для процессов скользящего среднего
- 6.3.3. Начальные оценки для процессов авторегрессии
- 6.3.4. Начальные оценки для смешанных процессов авторегрессии — скользящего среднего
- 6.3.5. Выбор между стационарными и нестационарными моделями в спорных случаях
- 6.3.6. Начальные оценки остаточной дисперсии
- 6.3.7. Приближенная стандартная ошибка для
- 6.4. Многозначность моделей
- 6.4.1. Многозначность моделей авторегрессии — скользящего среднего
- 6.4.2. Многозначные решения при оценке параметров скользящего среднего методом моментов
- 6.4.3. Использование возвратного процесса для определения начальных значений
- Приложение П6.1. Среднее значение выборочной автокорреляционной функции нестационарного процесса
- Приложение П6.2. Общий метод получения начальных оценок параметров смешанного процесса авторегрессии – скользящего среднего
- Приложение П6.3. Прямой и возратный процессы ПСС порядка (0, 1, 1)
- Глава 7. Оценивание модели
- 7.1. Исследование функций правдоподобия и суммы квадратов
- 7.1.1. Функция правдоподобия
- 7.1.2. Условное правдоподобие для процесса АРПСС
- 7.1.3. Выбор начальных значений для вычисления условного правдоподобия
- 7.1.4. Безусловное правдоподобие; сумма квадратов; оценки наименьших квадратов
- 7.1.5. Общий способ вычисления безусловной суммы квадратов
- 7.1.6. Графическое исследование суммы квадратов
- 7.1.7. Описание «благоприятных» оценочных ситуаций; доверительные области
- 7.2. Нелинейное оценивание
- 7.2.2. Численный метод нахождения производных
- 7.2.3. Прямой метод нахождения производных
- 7.2.4. Общий алгоритм наименьших квадратов для условной модели
- 7.2.5. Сводка моделей, подогнанных к рядам A-F
- 7.2.6. Информационные матрицы при больших выборках и оценки ковариаций
- 7.3. Результаты оценивания для некоторых частных моделей
- 7.З.2. Процессы скользящего среднего
- 7.3.3. Смешанные процессы
- 7.3.4. Разделение линейных и нелинейных компонент при оценивании
- 7.3.5. Избыточность параметров
- 7.4. Оценивание при помощи теоремы Байеса
- 7.4.2. Байесовское оценивание параметров
- 7.4.3. Процессы авторегрессии
- 7.4.4. Процессы скользящего среднего
- 7.4.5. Смешанные процессы
- Приложение П7.1. Обзор теории нормального распределения
- Приложение П7.2. Обзор линейной теории наименьших квадратов
- Приложение П7.3. Примеры влияния ошибок оценивания параметров на вероятностные пределы прогнозов
- Приложение П7.4. Точная функция правдоподобия для процесса скользящего среднего
- Приложение П7.5. Точная функция правдоподобия для процесса авторегрессии
- Глава 8. Диагностическая проверка модели
- 8.1. Проверка стохастических моделей
- 8.1.2. Введение избыточных параметров
- 8.2.1. Проверка при помощи автокорреляций
- 8.2.2. Совокупный критерий согласия
- 8.2.3. Неадекватность модели, возникающая из-за изменения значений параметров
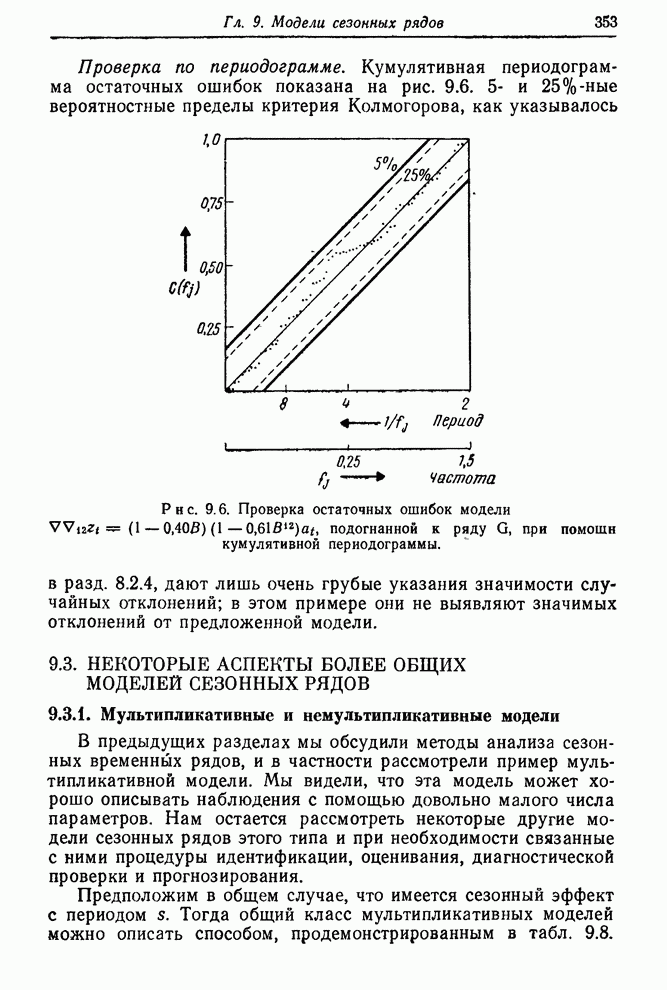
- 8.2.4. Проверка при помощи кумулятивной периодограммы
- 8.3. Использование остаточных ошибок для изменения модели
- 8.3.1. Природа корреляций остаточных ошибок при использовании неверной модели
- 8.3.2. Использование остаточных ошибок для изменения модели
- Глава 9. Модели сезонных рядов
- 9.1. Экономические модели сезонных временных рядов
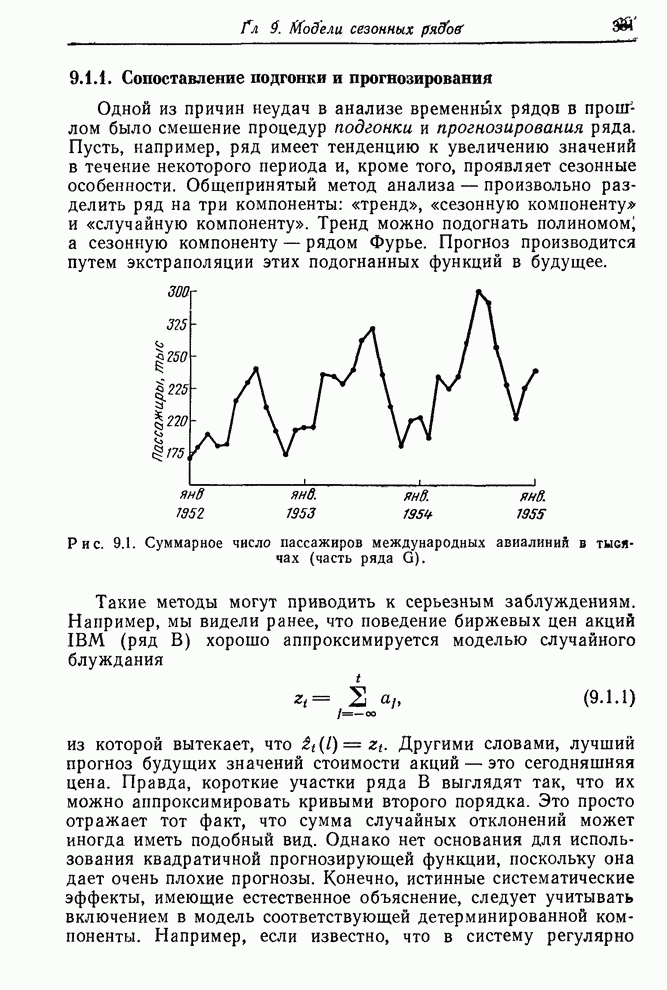
- 9.1.1. Сопоставление подгонки и прогнозирования
- 9.1.2. Сезонные модели, включающие подстраивающиеся синусоиды и косинусоиды
- 9.1.3. Общая мультипликативная модель сезонного ряда
- 9.2. Представление данных об авиаперевозках мультипликативной моделью
- 9.2.1. Мультипликативная модель
- 9.2.2. Прогнозирование
- 9.2.3. Идентификация
- 9.2.4. Оценивание
- 9.2.5. Диагностическая проверка
- 9.3. Некоторые аспекты более общих моделей сезонных рядов
- 9.3.1. Мультипликативные и немультипликативные модели
- 9.3.2. Идентификация
- 9.3.3. Оценивание
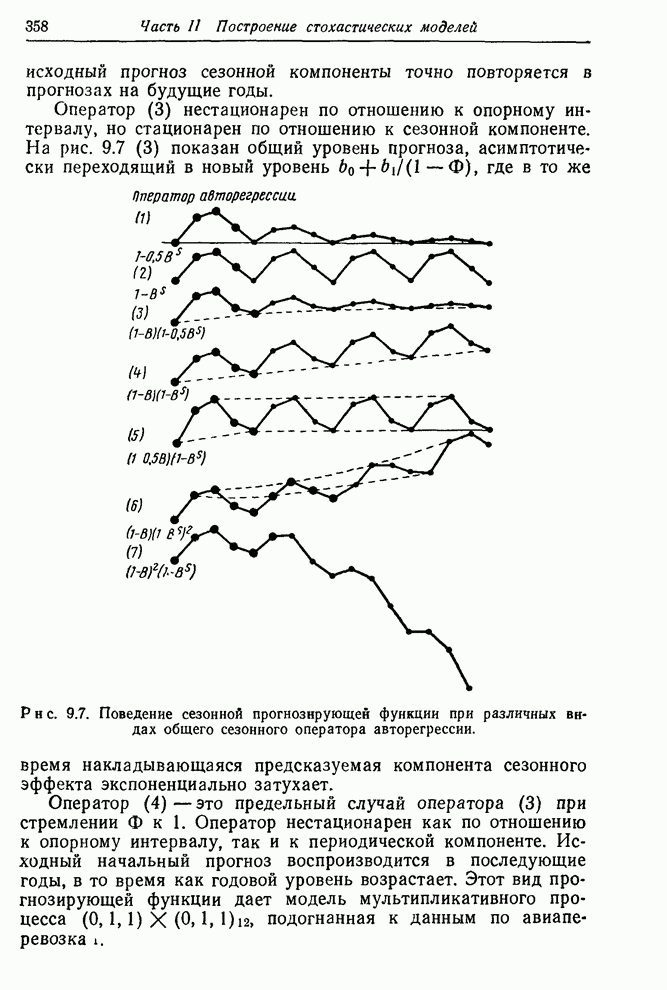
- 9.3.4. Эвентуальные прогнозирующие функции для различных моделей сезонных рядов
- Вспомогательные материалы
- Программа 1 Идентификация стохастической модели
- Программа 2 Предварительное оценивание стохастической модели
- Программа 3. Оценивание стохастической модели
- Алгоритм марквардта для нелинейного метода наименьших квадратов
- Программа 4. Прогнозирование с помощью стохастической модели
- Сборник таблиц и диаграмм