| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.1.3. Проектирование дискретных регулирующих систем
В прошлом слово «control» (контроль, регулирование, управление) для статистиков означало обычно методику контроля качества, разработанную Шьюхартом [8] в США и Дадингом и Дженнетом [9] в Великобритании.
Недавно повысился интерес к применению принципов последовательного анализа для контроля качества, что привело к введению диаграмм кумулятивных сумм [10-12] и диаграмм геометрического скользящего среднего [13].
Слово «control» имеет другое значения для инженера по регулированию, Он подразумевает под ним контуры прямых и обратных регулирующих связей, вопросы динамики и устойчивости системы и конкретные устройства для выполнения регулирующих действий. Эти регулирующие устройства являются автоматическими в том смысле, что информация о процессе поступает к ним автоматически и информация на регулирование входов процесса автоматически выбирается из них.
В этой книге мы описываем статистический подход к прогнозированию временных рядов и к разработке регулирующих систем прямой и обратной связей, развитый в предшествующих статьях [14-20]. Обсуждаемые методы регулирования ближе к используемым инженерам по регулированию, чем к стандартным операциям по контролю качества, развитым статистикам. Это не означает, что мы считаем традиционные диаграммы контроля качества ненужными; просто они выполняют функции, которые мы не рассматриваем в этой работе. Важная функция стандартных диаграмм контроля качества – обеспечить способ непрерывного просмотра для обнаружения возможных причин отклонения. Удобное изображение данных о продукции позволяет лицам, управляющим процессом, быстро обнаружить изменения. Зная ответ на вопрос: «Когда произошли изменения этого типа?», мы можем спросить: «Почему они произошли?». Это означает непрерывно действующий стимул к улучшению процесса, часто ведущий к его переосмыслению.
Напротив, регулирующие схемы, обсуждаемые в этой книге, предназначены для периодических, оптимальных регулировок управляющего переменного, влияние которого на некоторые характеристики качества уже известно. Это позволяет уменьшить отклонение этой характеристики от некоторой желаемой величины.
Причина, по которой необходимо регулирование, заключается в неизбежном присутствии в процессе возмущения или шума. Когда мы можем измерять эти возмущения, возникает возможность провести необходимые компенсирующие изменения некоторых других переменных. Такой способ называется регулированием с прямой связью. Вместо этого или в дополнение к этому мы можем использовать отклонения от желаемого значения, или «сигнал ошибок» выходной характеристики, для вычисления компенсирующих значений. Такой способ называется регулированием с обратной связью. В отличие от первого способа этот вид коррекции может быть использован даже тогда, когда источник возмущения не известен достаточно точно или величина возмущения не измерена. В общем плане может оказаться целесообразным использование регулировок, как с прямой, так и с обратной связью; первая может быть использована для компенсации измеряемых возмущений, а вторая – для компенсации неизмеряемых.
Принятый здесь подход к регулированию заключается в выборе для описания возмущений соответствующего временного ряда, или стохатической модели, и для описания инерциальных характеристик системы – проходящей модели передаточной функции.
Тогда появляется возможность ввести уравнение регулирования. Это уравнение позволяет рассчитать необходимые действия в любой момент времени по заданным настоящему и предыдущему состоянию системы. Под «оптимальным» действием понимается такое, которое приводит к минимальной среднеквадратичной ошибке на выходе.
Выполнение регулирующего действия, указываемого уравнением регулирования, может быть достигнуто различными путями в зависимости от уровня технологии. В этой книге мы не будем указывать, какие средства должны быть использованы в конкретных ситуациях. Однако стоит упомянуть, что на одном полюсе мы имеем регулирование, осуществляемое с применением ЭВМ; действие, указываемое уравнением регулирования, вычисляется на ЭВМ. Оно автоматически реализуется соответствующими датчиками, например, открывающими и закрывающими клапаны, регулирующие переменные процесса: температуру, давление, скорость потока. На промежуточном уровне существуют автоматические регуляторы, использующие для выполнения регулирующих действий различные пневматические и электрические устройства. На другом полюсе действие, предписываемое уравнением регулирования, определяется по соответствующей диаграмме или номограмме. Оператор периодически берет один или несколько отчётов, наблюдений или определений, справляется по номограмме, какое действие необходимо предпринять, и затем вручную вводит необходимые изменения в процесс.
Даже в современной промышленности часто встречаются ситуации, где используется ручное регулирование, которое может быть улучшено. В главе 12 кратко рассматривается подготовка диаграмм и номограмм, по которым в простых случаях можно определить оптимальные регулирующие действия. Например, верхняя диаграмма на рис. 1.3 показывает ряд изменений вязкости полимера, выполняемых с часовым интервалом в течение 42 ч. Вязкость должна поддерживаться вблизи значения 90 единиц. После каждого измерения вязкости оператор процесса использует номограмму, показанную в середине рисунка, для вычисления необходимой оптимальной регулировке управляемой переменной (подачи газа). На нижней диаграмме рис. 1.3 показана регулировка, сделанная в соответствии с номограммой.
На практике точная природа стохастических моделей и моделей передаточных функций, пригодных для любой конкретной ситуации и необходимых для разработки схем оптимального регулирования, обычно неизвестна. Далее, неизвестны соответствующие численные значения параметров этих моделей. Поэтому, как это почти всегда бывает при построении моделей, нам приходится использовать интерактивный метод.
Любые доступные записи и дополнительная информация могут использоваться для разработок пробной регулирующей схемы, которая должна управлять процессом в течение некоторого периода. Данные рис. 1.3 были получены при реализации такой схемы. В гл. 12 показано, как по данным такой регулирующей схемы, состоящим из отклонений от требуемого значения характеристики качества и соответствующих регулировок, может быть проведён статистический анализ. В результате можно изменить модель и оценки параметров, что приведет к улучшению регулирующей схемы.
Хотя наши приложения часто имели отношения к ручным схемам регулирования, обсуждаемые методы могут быть с успешно использованы в процессах, управляемых вычислительной машиной, как описано, например, Офтоном [21]. При этом удаётся следить одновременно за большим числом регулируемых переменных, используя для каждой свой управляющий алгоритм. При помощи ЭВМ может быть также обеспечено взаимодействие

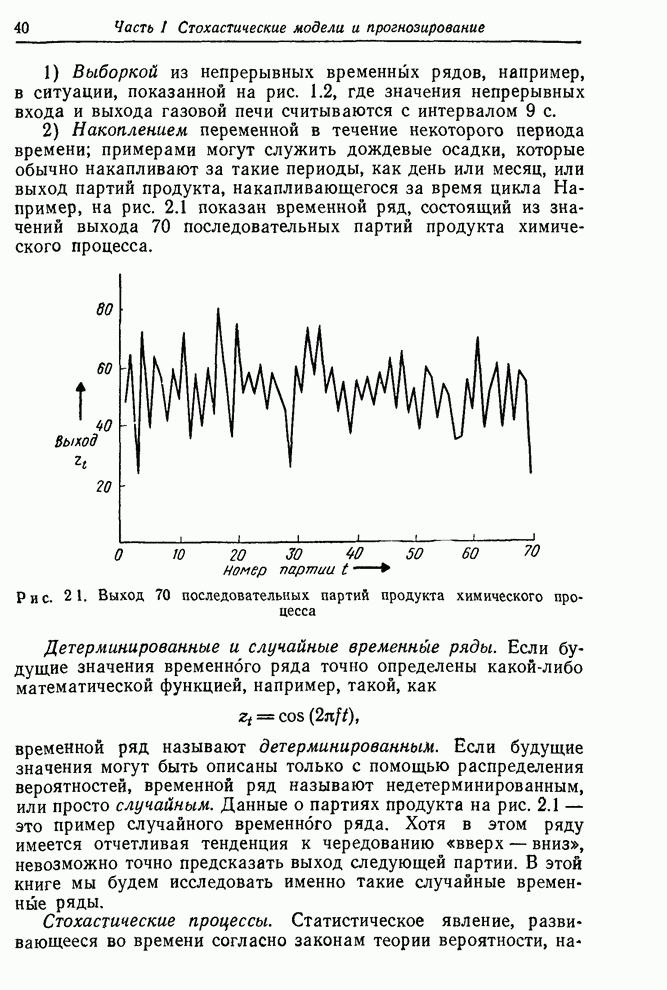
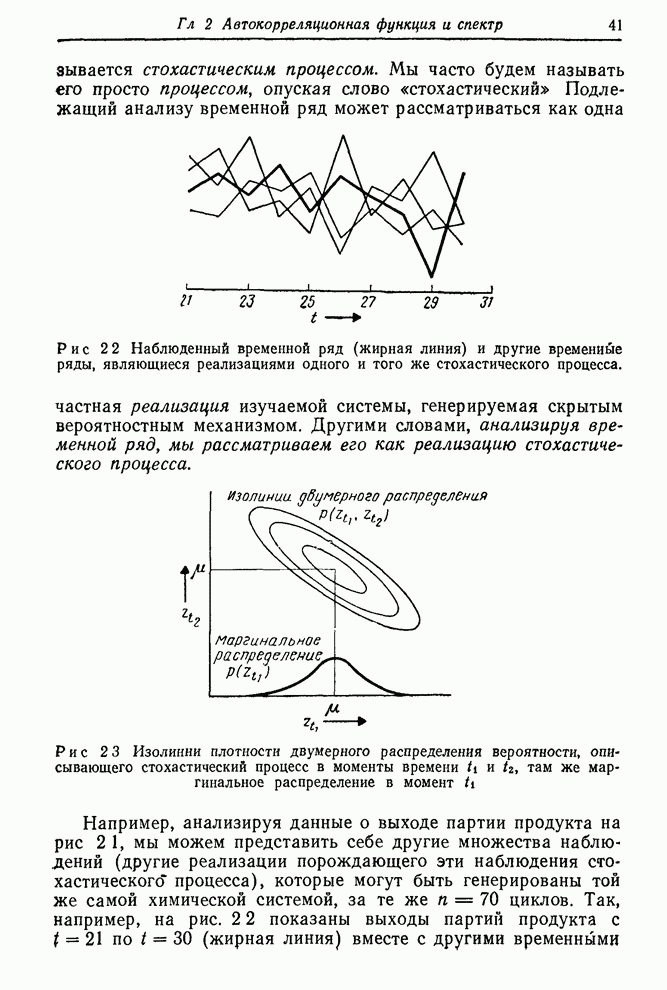
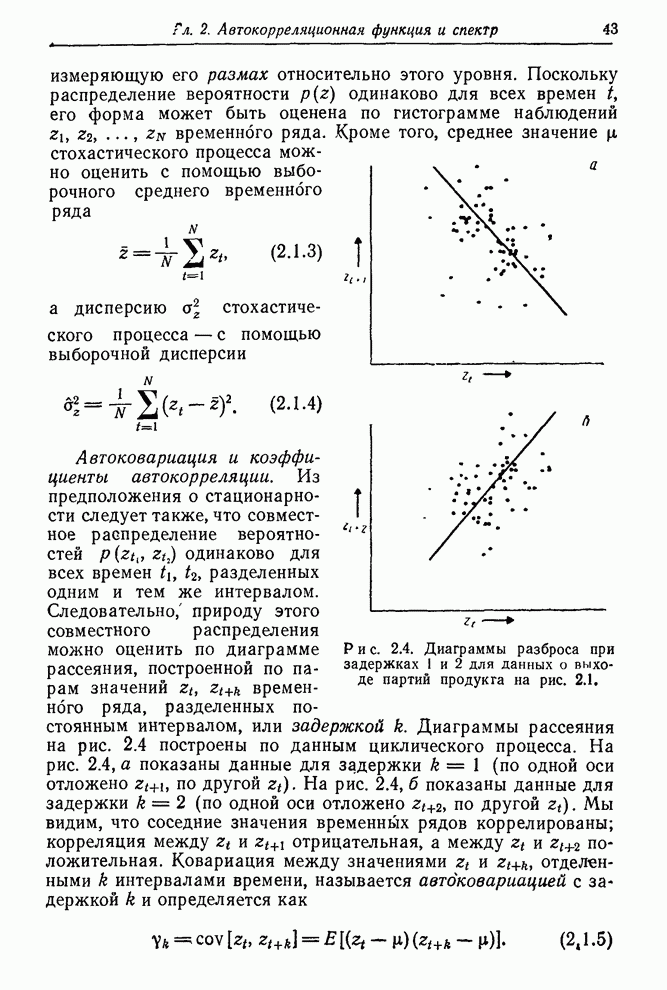
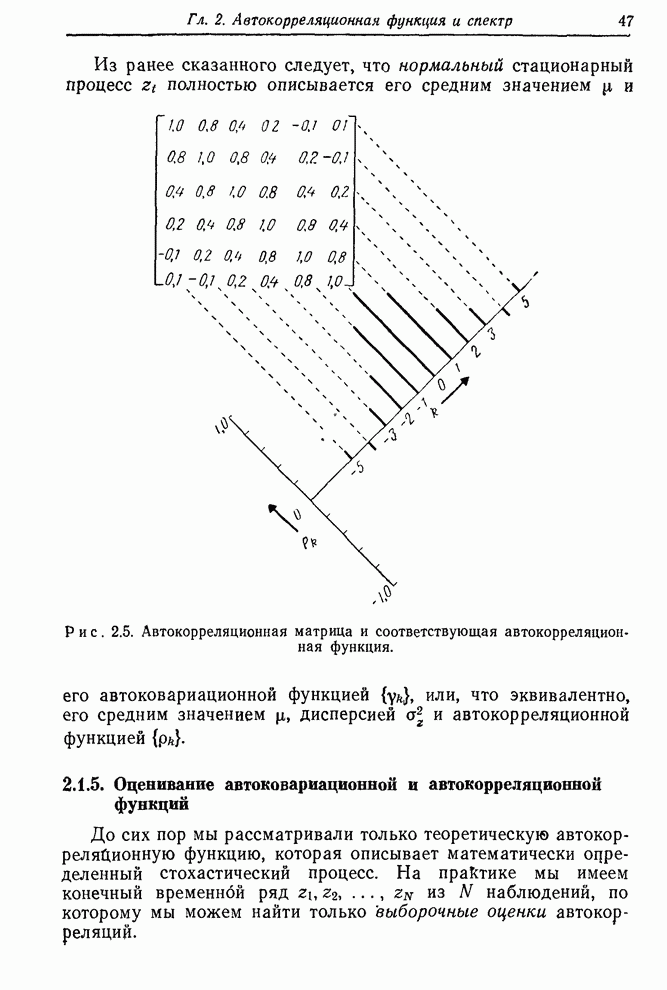
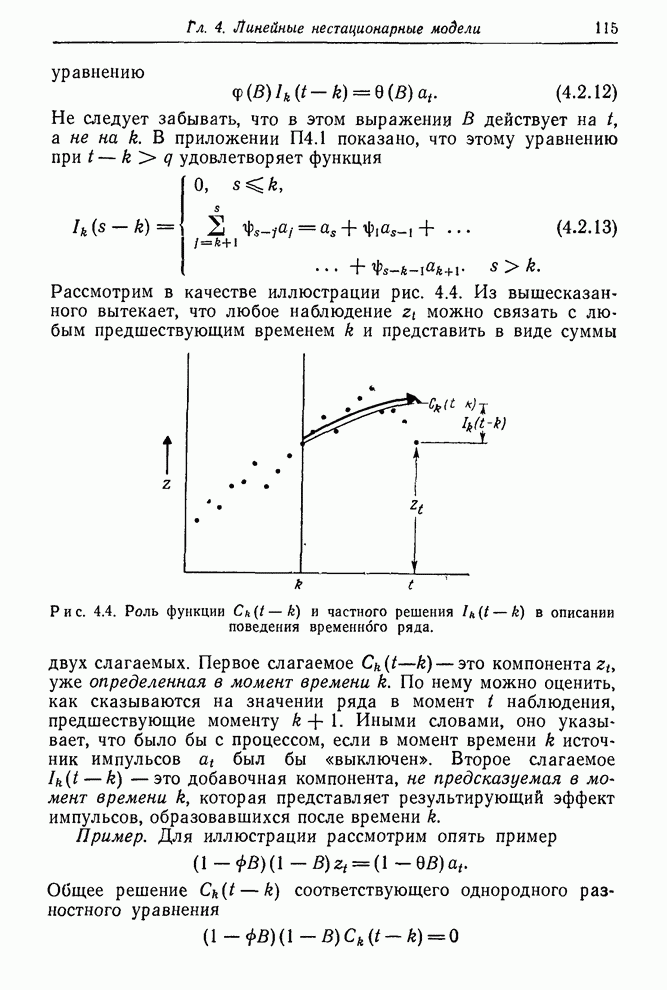
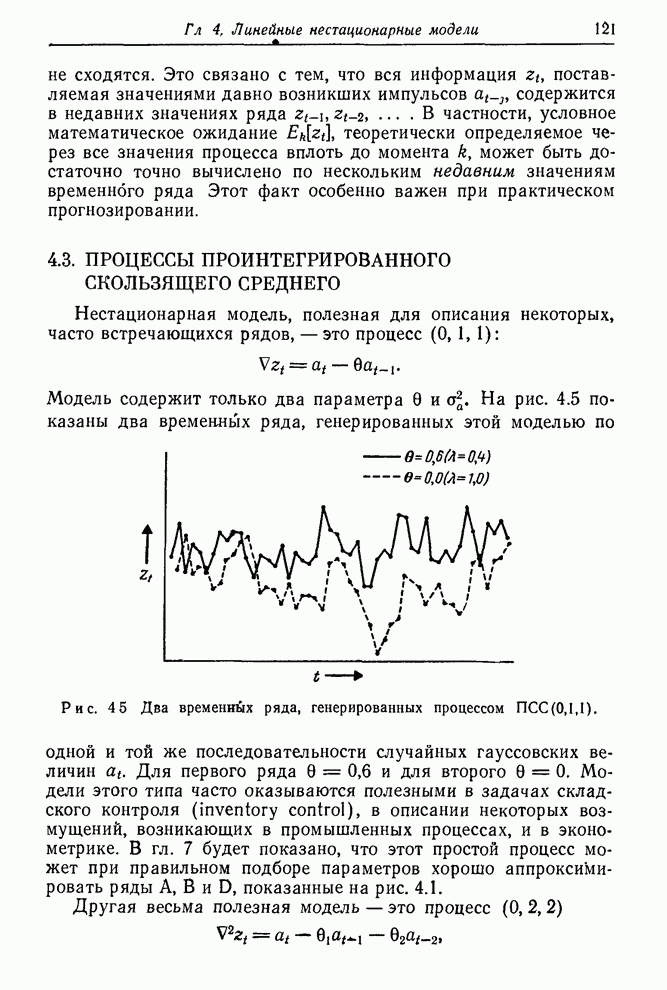
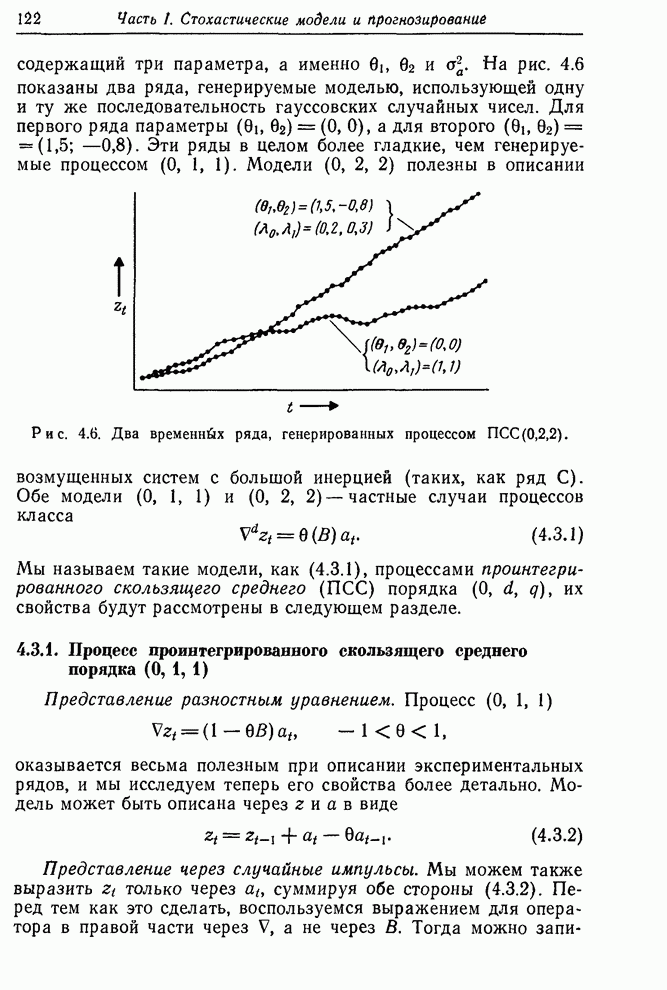
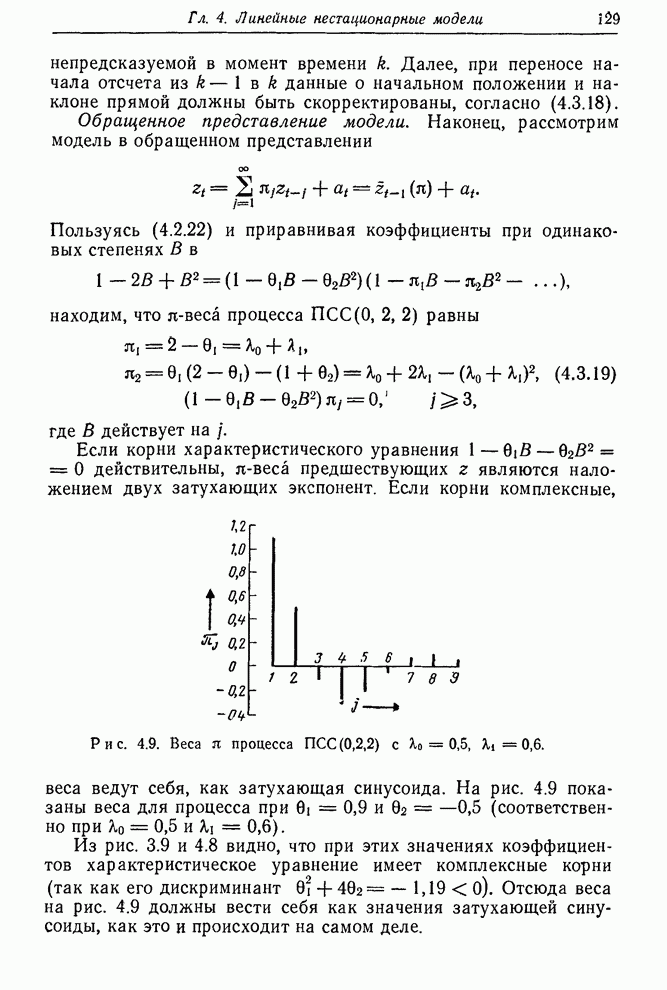
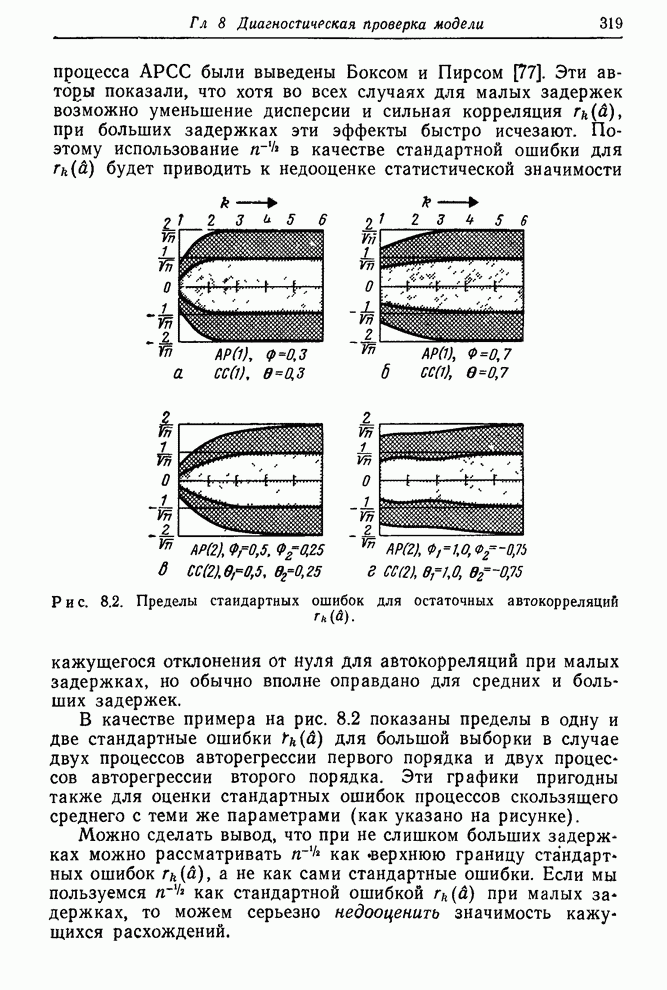
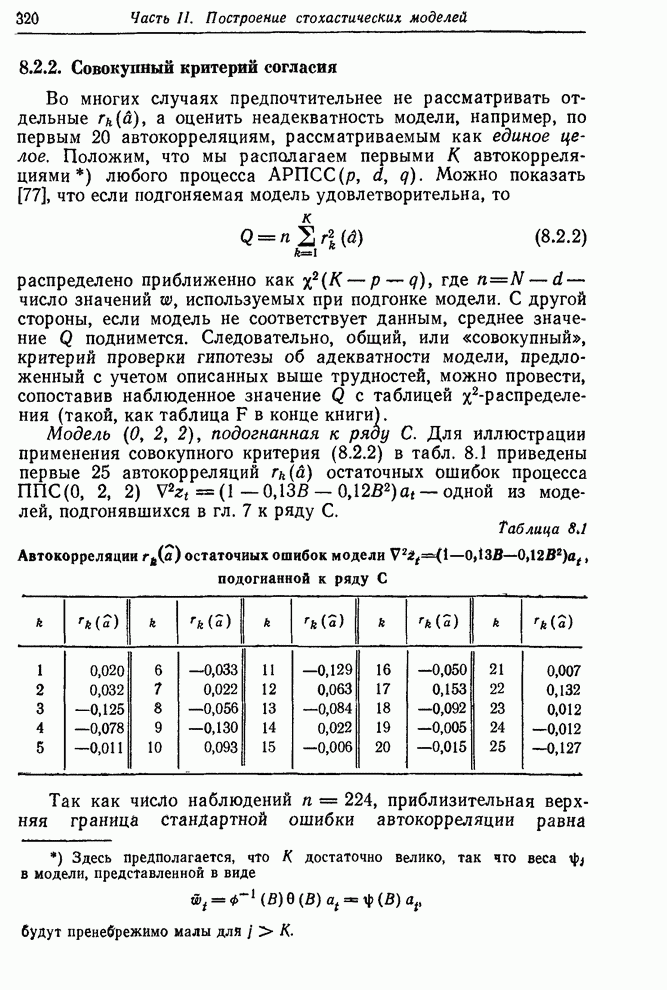
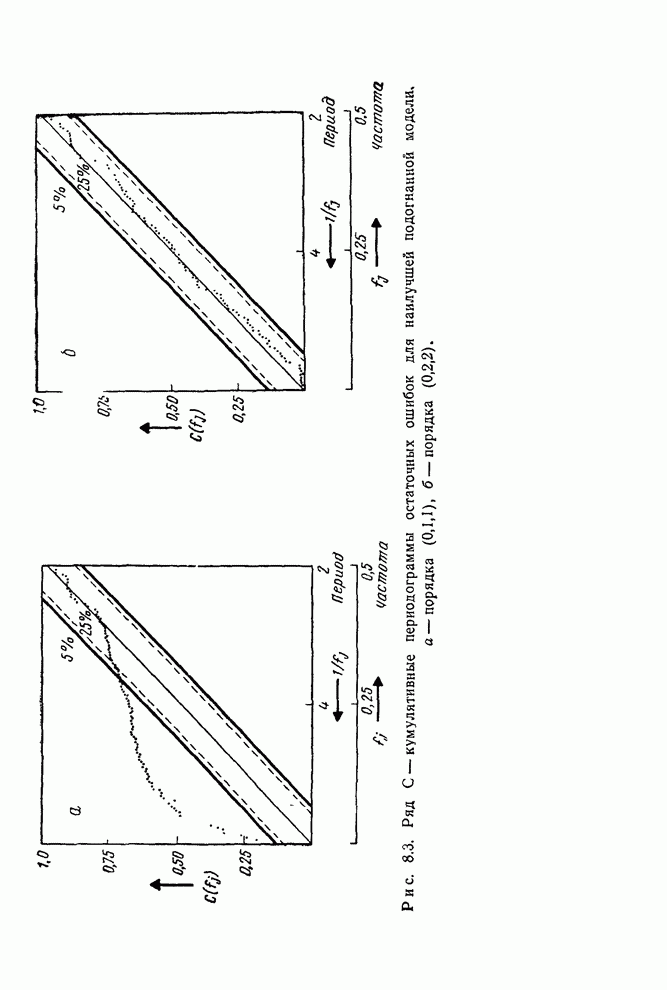
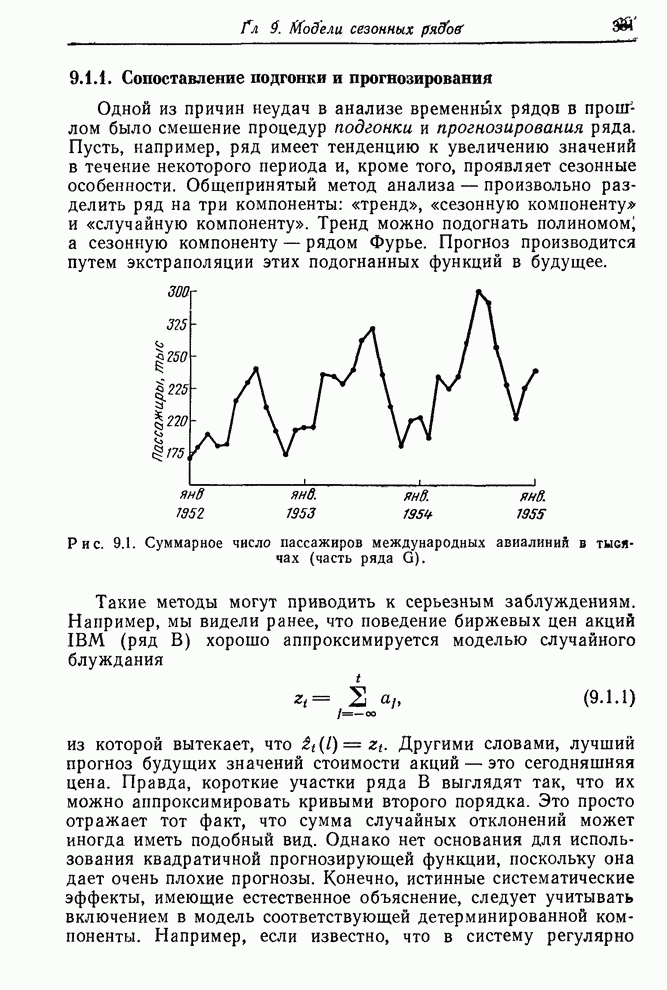
Рис. 1.3. Контроль вязкости. Запись наблюденной вязкости и регулировка подачи газа согласно номограмме.
между несколькими контурами управления. Многие современные схемы прямого цифрового управления (ПЦУ), использующие ЭВМ, основаны на замене стандартных одно-, двух- и трёхступенчатых регуляторов соответствующими численными алгоритмами. Подход, который мы опишем здесь, может привести к более общим управляющим алгоритмам, чем те, которые применялись до сих пор, и более гибкому использованию цифровой вычислительной машины.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к русскому изданию
- Предисловие
- План книги
- Глава 1. Введение и краткое содержание
- 1.1. Три важные практические проблемы
- 1.1.1. Прогнозирование временных рядов
- 1.1.2. Оценивание передаточных функций
- 1.1.3. Проектирование дискретных регулирующих систем
- 1.2. Стохастические и детерминированные динамические математические модели
- 1.2.1. Стационарные нестационарные стохастические модели для прогнозирования и регулирования
- 1.2.2. Модели передаточных функций
- 1.2.3. Модели дискретных систем регулирования
- 1.3. Основные понятия в построении моделей
- 1.3.1. Экономия
- 1.3.2. Интерактивные этапы в выборе модели
- Часть 1. Стохастические модели и основанное на них прогнозирование
- Глава 2. Автокорреляционная функция и спектр
- 2.1. Автокорреляционные свойства стационарных моделей
- 2.1.1. Временные ряды и стохастические процессы
- 2.1.2. Стационарные стохастические процессы
- 2.1.3. Положительная определённость и автоковариационная матрица
- 2.1.4. Автоковариационные и автокорреляционные функции
- 2.1.5. Оценивание автоковариационной и автокорреляционной функций
- 2.1.6. Стандартные ошибки оценок автокорреляций
- 2.2. Спектральные свойства стационарных моделей
- 2.2.1. Периодограмма
- 2.2.2. Дисперсионный анализ
- 2.2.3. Спектральная плотность и нормированный спектр
- 2.2.4. Простые примеры автокорреляционных функций и нормированных спектров
- 2.2.5. Преимущества и недостатки автокорреляционных функций и нормированных спектров
- Приложение П2.1. Связь между выборочным спектром и оценкой автоковариационной функции
- Глава 3. Линейные стационарные модели
- 3.1. Общий линейный процесс
- 3.1.1. Две эквивалентные формы линейного процесса
- 3.1.2. Производящая функция автоковариаций линейного процесса
- 3.1.3. Условия стационарности и обратимости линейного процесса
- 3.1.4. Процессы авторегрессии и скользящего среднего
- 3.2. Процессы авторегрессии
- 3.2.1. Условия стационарности для процессов авторегрессии
- 3.2.2. Автокорреляционная функция и спектр процессов авторегрессии
- 3.2.3. Процесс авторегрессии первого порядка (марковский процесс)
- 3.2.4. Процесс авторегрессии второго порядка
- 3.2.5. Частная автокорреляционная функция
- 3.2.6. Оценивание частной автокорреляционной функции
- 3.2.7. Стандартные ошибки частной автокорреляции
- 3.3. Процессы скользящего среднего
- 3.3.1. Условия обратимости для процессов скользящего среднего
- 3.3.2. Автокорреляционная функция и спектр процесса скользящего среднего
- 3.3.3. Процесс скользящего среднего первого порядка
- 3.3.4. Процесс скользящего среднего второго порядка
- 3.3.5. Взаимность процессов авторегрессии и скользящего среднего
- 3.4. Смешанные процессы авторегрессии — скользящего среднего
- 3.4.1. Свойства стационарности и обратимости
- 3.4.2. Автокорреляционная функция и спектр смешанных процессов
- 3.4.3. Процесс авторегрессии первого порядка — скользящего среднего первого порядка
- 3.3.4. Резюме
- Приложение П3.1. Автоковариации.
- Приложение П3.2. Рекурентный метод вычисления оценок параметров авторегрессии
- Глава 4. Линейные нестационарные модели
- 4.1. Процессы авторегрессии — проинтегрированного скользящего среднего
- 4.1.1. Нестационарность процесса авторегрессии первого порядка
- 4.1.2. Общая модель для нестационарного процесса, проявляющего однородность
- 4.1.3. Общий вид процесса авторегрессии – проинтегрированного скользящего среднего
- 4.2. Три формы представления модели авторегрессии – проинтегрированного скользящего среднего
- 4.2.1. Представление модели в виде разности уравнения
- 4.2.2. Представление модели, использующее случайные импульсы
- 4.2.3. Обращенное представление модели
- 4.3. Процессы проинтегрированного скользящего среднего
- 4.3.1. Процесс проинтегрированного скользящего среднего порядка (0,1,1)
- 4.3.2. Процесс проинтегрированного скользящего среднего порядка (0.2.2)
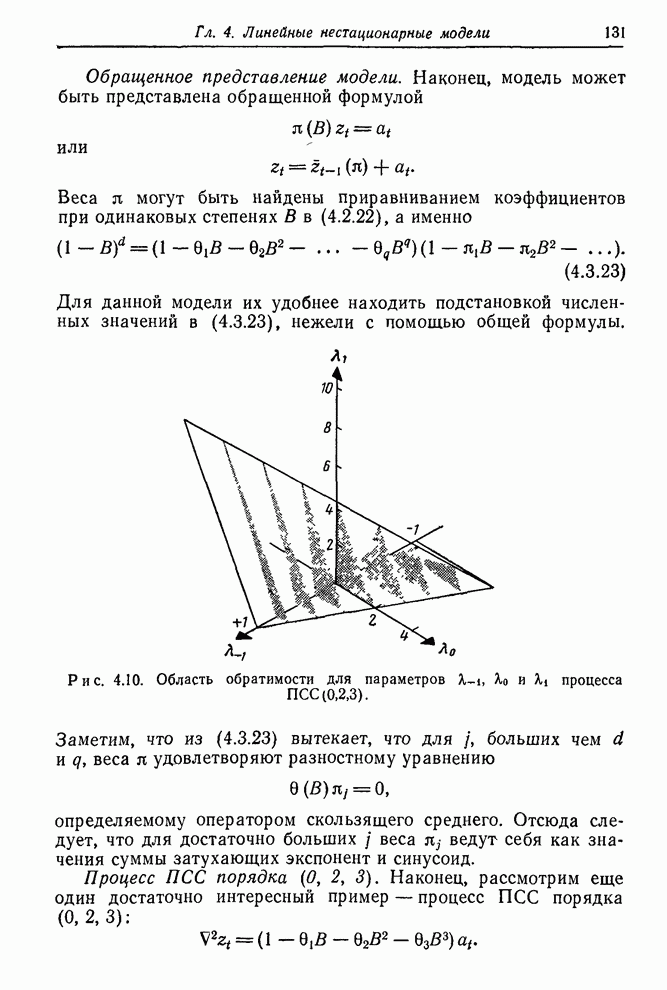
- 4.3.3. Общий процесс проинтегрированного скользящего среднего порядка (0, d, q)
- Приложение П4.1. Линейные разностные уравнения
- Приложение П4.2. Процесс ПСС(0,1,1) с детерминированным дрейфом нуля
- Приложение П4.3. Свойства конечного оператора ссумирования
- Приложение П4.4. Процессы АРПСС с добавленным шумом
- Глава 5. Прогнозирование
- 5.1. Прогнозы с минимальной среднеквадратичной ошибкой и их свойства
- 5.1.1. Вывод формулы для прогнозов с минимальной среднеквадратичной ошибкой
- 5.1.2. Три основных представления прогноза
- 5.2. Вычисление и подправление прогноза
- 5.2.1. Удобная схема для вычисления прогнозов
- 5.2.2. Вычисление весов
- 5.2.3. Использование весов при подправлении прогнозов
- 5.2.4. Вычисление вероятностных пределов прогнозов при произвольном упреждении
- 5.3. Прогнозирующая функция и веса прогноза
- 5.3.1. Эвентуальная прогнозирующая функция, определенная оператором авторегрессии
- 5.3.2. Роль оператора скользящего среднего в определении начальных величин
- 5.3.3. Веса прогноза для упреждения l
- 5.4. Примеры прогнозирующих функций и их подправления
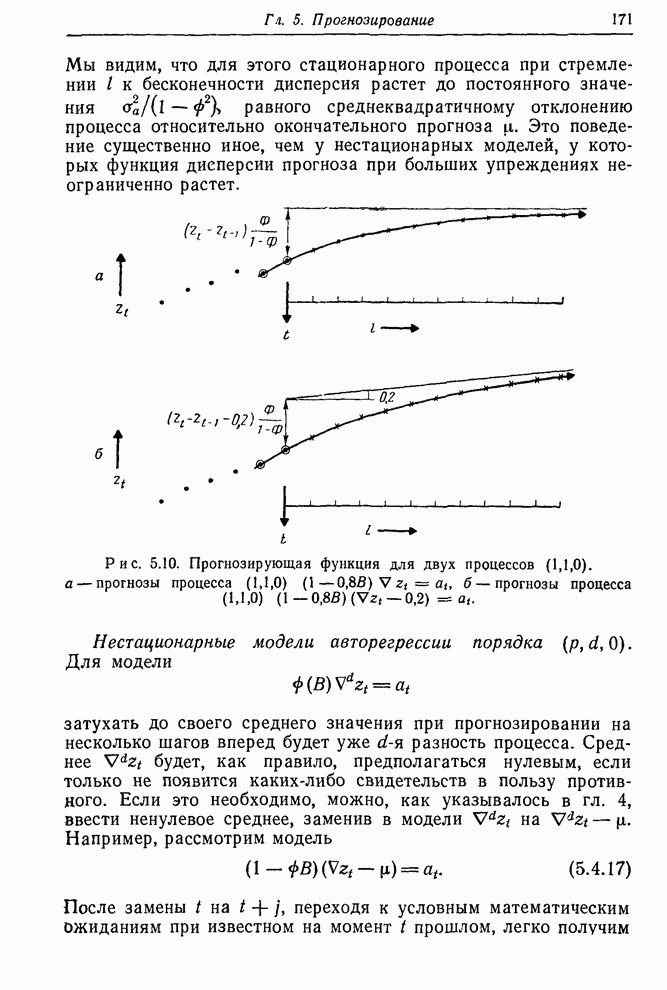
- 5.4.1. Прогнозирование процесса ПСС(0, 1, 1)
- 5.4.2. Прогнозирование процесса ПСС(0, 2, 2)
- 5.4.3. Прогнозирование общего процесса ПСС(0, d, q)
- 5.4.4. Прогнозирование процессов авторегрессии
- 5.4.5. Прогнозирование процесса (1, 0, 1)
- 5.4.6. Прогнозирование процесса (1,1,1)
- 5.5. Резюме
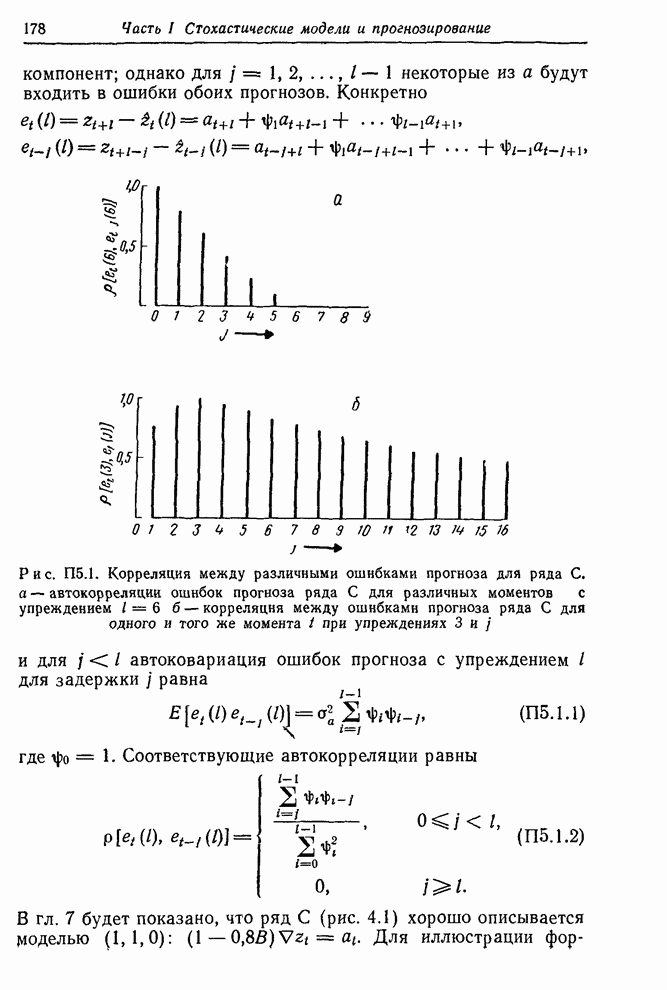
- Приложение П5.1. Корреляция между ошибками прогноза
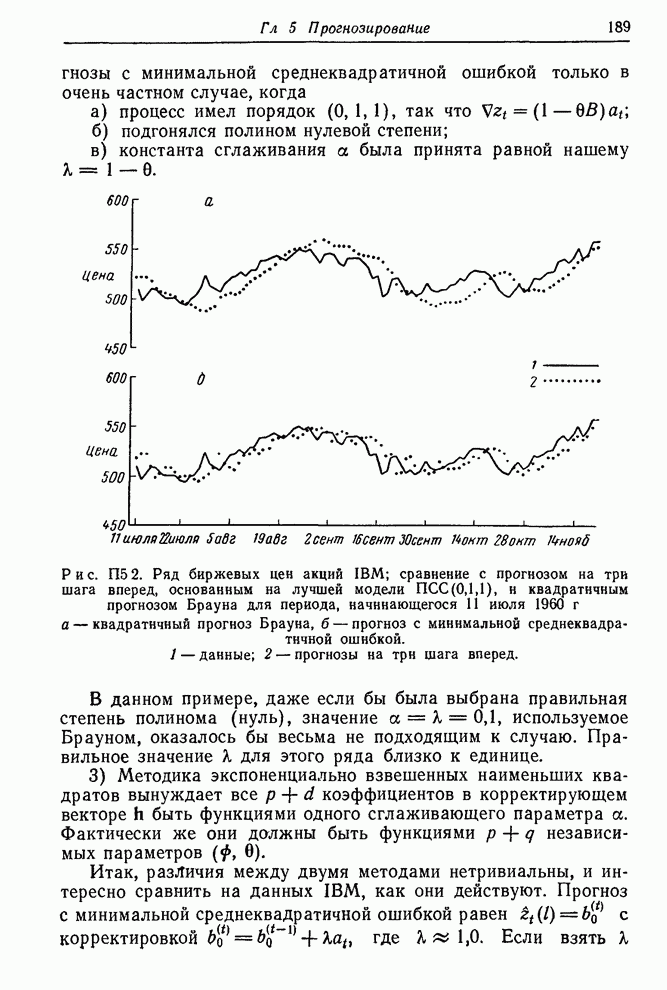
- Приложение П5.2. Веса прогноза для произвольного упреждения
- Приложение П5.3. Прогнозирование при помощи общего проинтегрированного представления
- Часть II. Построение стохастических моделей
- Глава 6. Идентификация моделей
- 6.1. Цели идентификации
- 6.1.1. Этапы процедуры идентификации
- 6.2. Методика идентификации
- 6.2.1. Использование при идентификаций автокорреляционной и частной автокорреляционной функций
- 6.2.2. Стандартные ошибки выборочных автокорреляций и частных автокорреляций
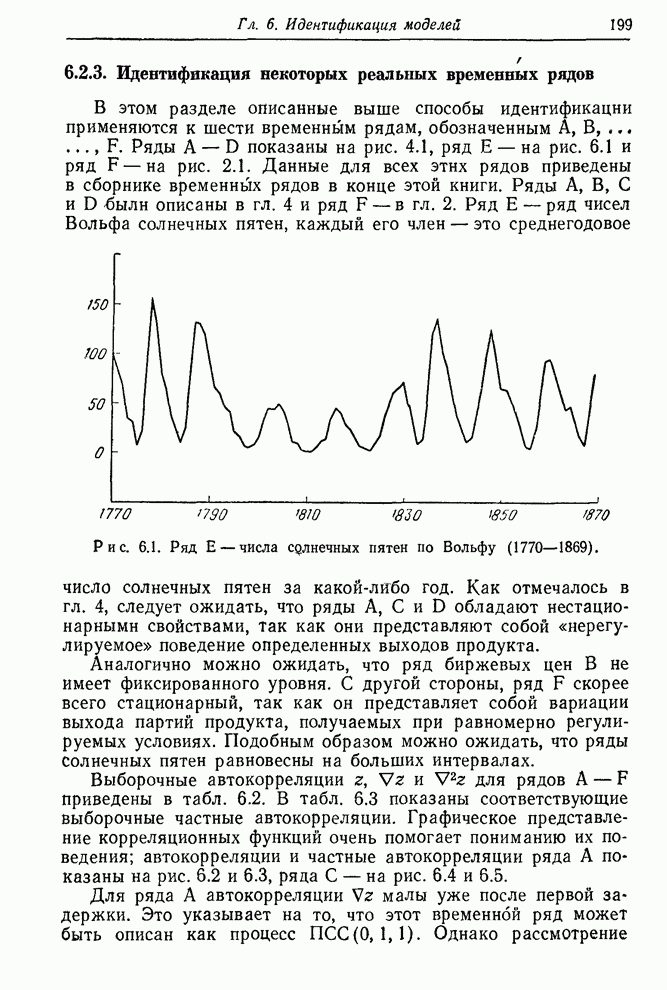
- 6.2.3. Идентификация некоторых реальных временных рядов
- 6.3. Начальные оценки параметров
- 6.3.1. Единственность оценок, получаемых по автоковариационной функции
- 6.3.2. Начальные оценки для процессов скользящего среднего
- 6.3.3. Начальные оценки для процессов авторегрессии
- 6.3.4. Начальные оценки для смешанных процессов авторегрессии — скользящего среднего
- 6.3.5. Выбор между стационарными и нестационарными моделями в спорных случаях
- 6.3.6. Начальные оценки остаточной дисперсии
- 6.3.7. Приближенная стандартная ошибка для
- 6.4. Многозначность моделей
- 6.4.1. Многозначность моделей авторегрессии — скользящего среднего
- 6.4.2. Многозначные решения при оценке параметров скользящего среднего методом моментов
- 6.4.3. Использование возвратного процесса для определения начальных значений
- Приложение П6.1. Среднее значение выборочной автокорреляционной функции нестационарного процесса
- Приложение П6.2. Общий метод получения начальных оценок параметров смешанного процесса авторегрессии – скользящего среднего
- Приложение П6.3. Прямой и возратный процессы ПСС порядка (0, 1, 1)
- Глава 7. Оценивание модели
- 7.1. Исследование функций правдоподобия и суммы квадратов
- 7.1.1. Функция правдоподобия
- 7.1.2. Условное правдоподобие для процесса АРПСС
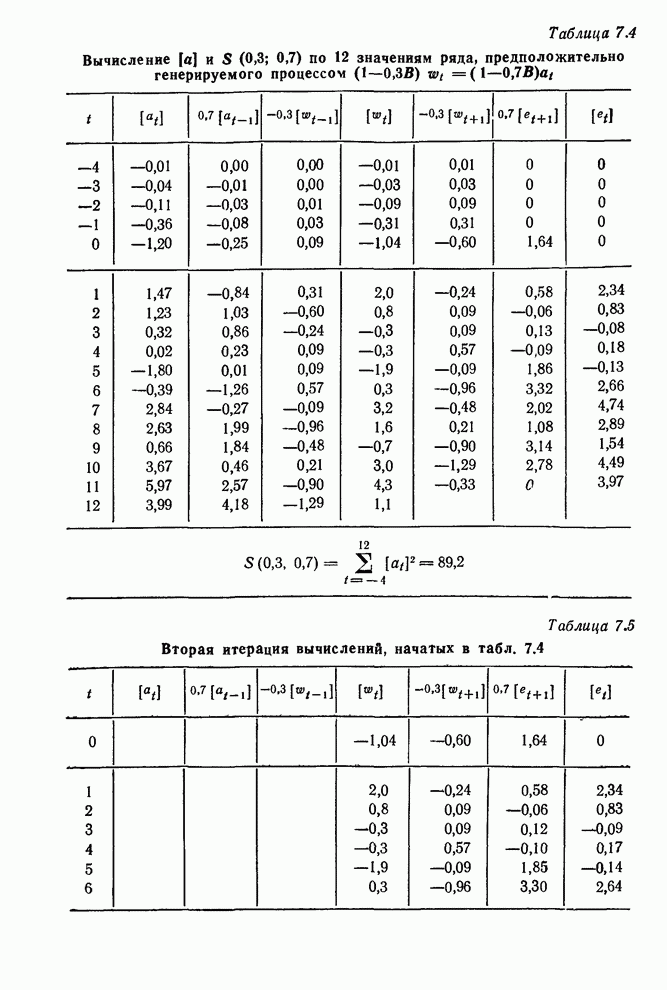
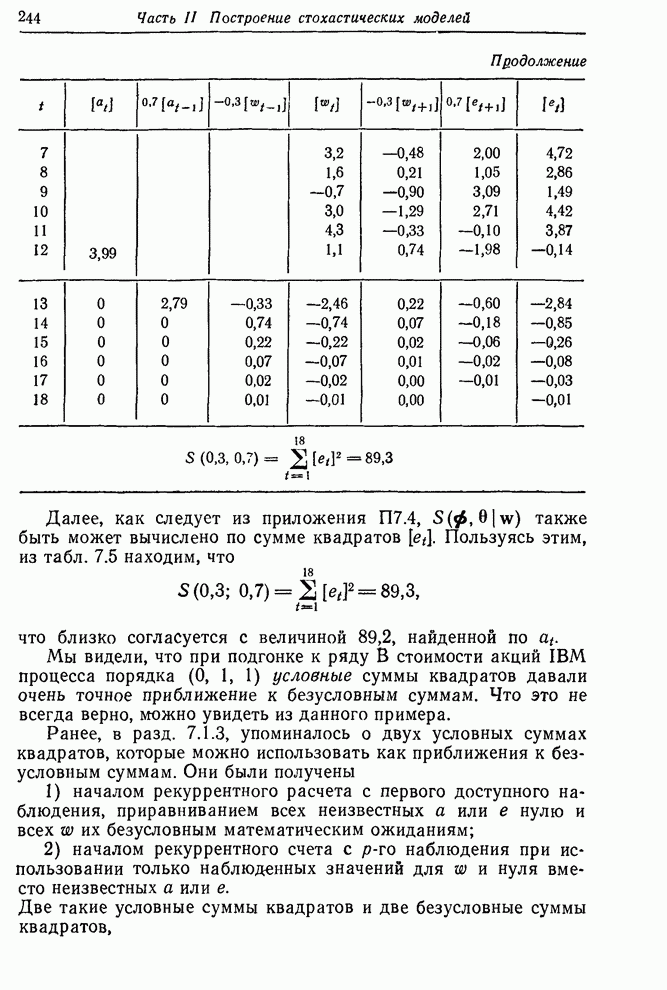
- 7.1.3. Выбор начальных значений для вычисления условного правдоподобия
- 7.1.4. Безусловное правдоподобие; сумма квадратов; оценки наименьших квадратов
- 7.1.5. Общий способ вычисления безусловной суммы квадратов
- 7.1.6. Графическое исследование суммы квадратов
- 7.1.7. Описание «благоприятных» оценочных ситуаций; доверительные области
- 7.2. Нелинейное оценивание
- 7.2.2. Численный метод нахождения производных
- 7.2.3. Прямой метод нахождения производных
- 7.2.4. Общий алгоритм наименьших квадратов для условной модели
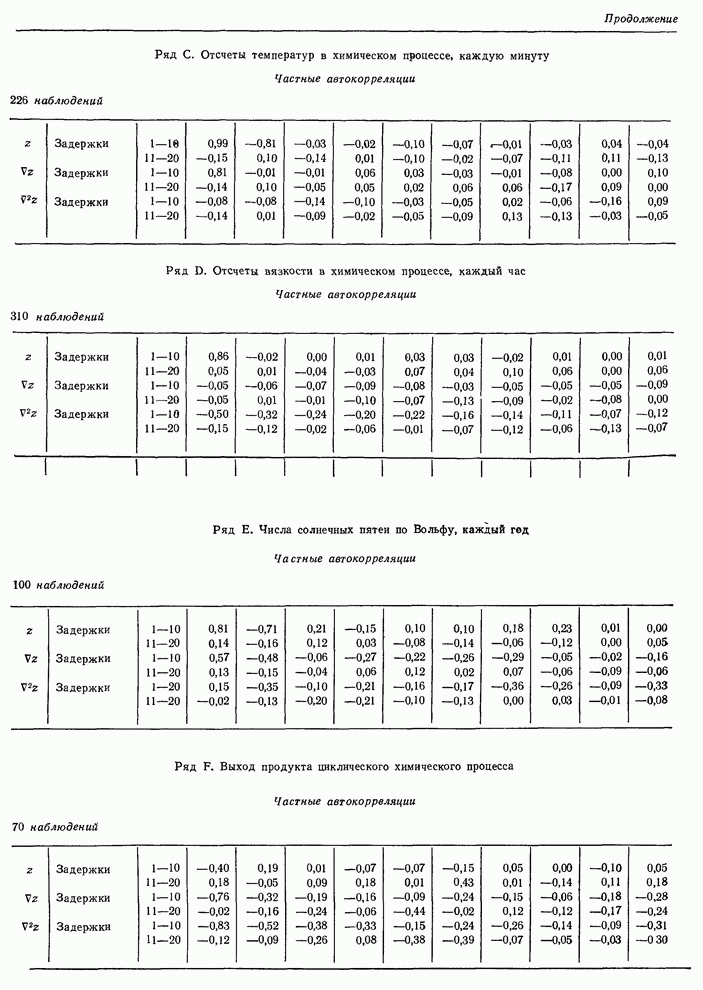
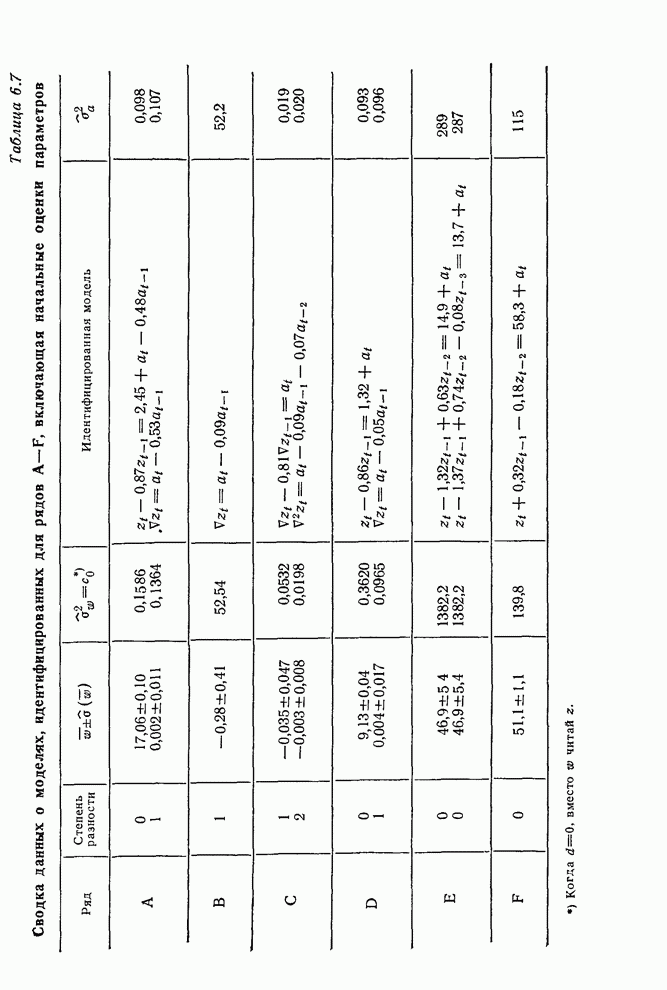
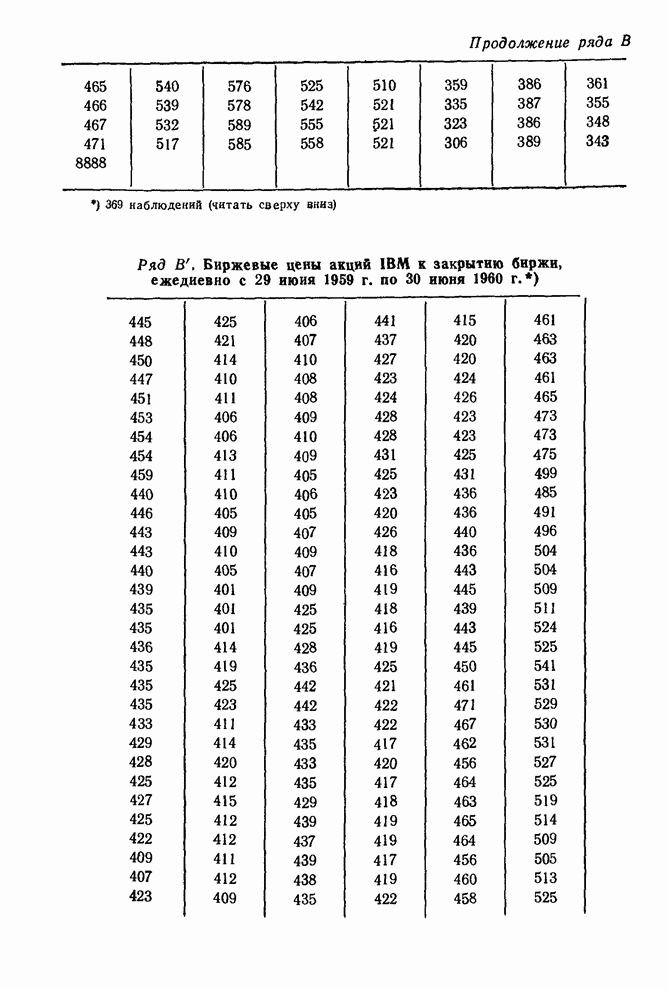
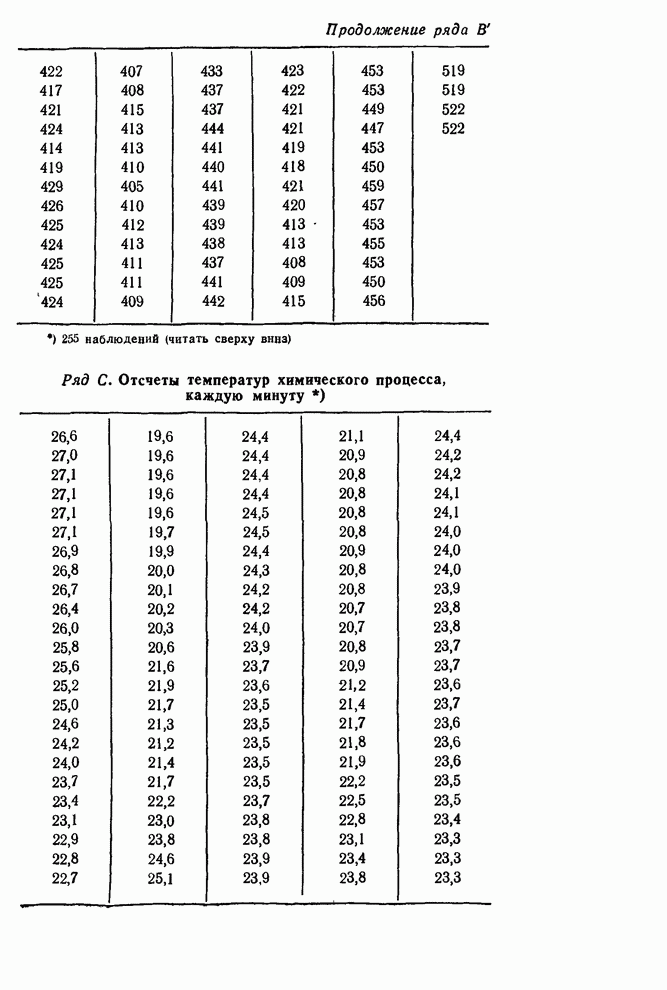
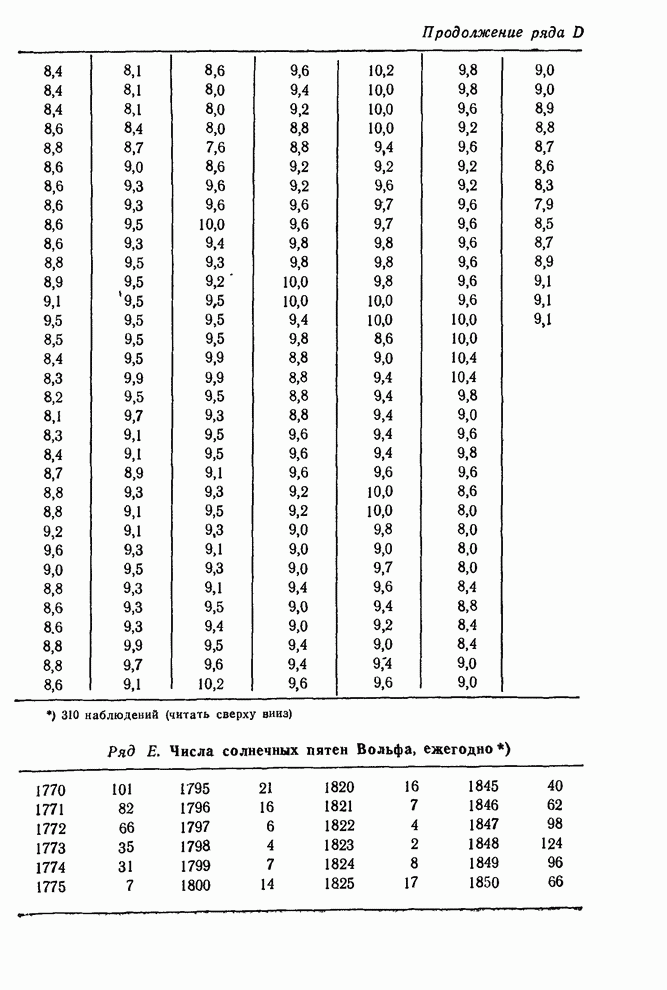
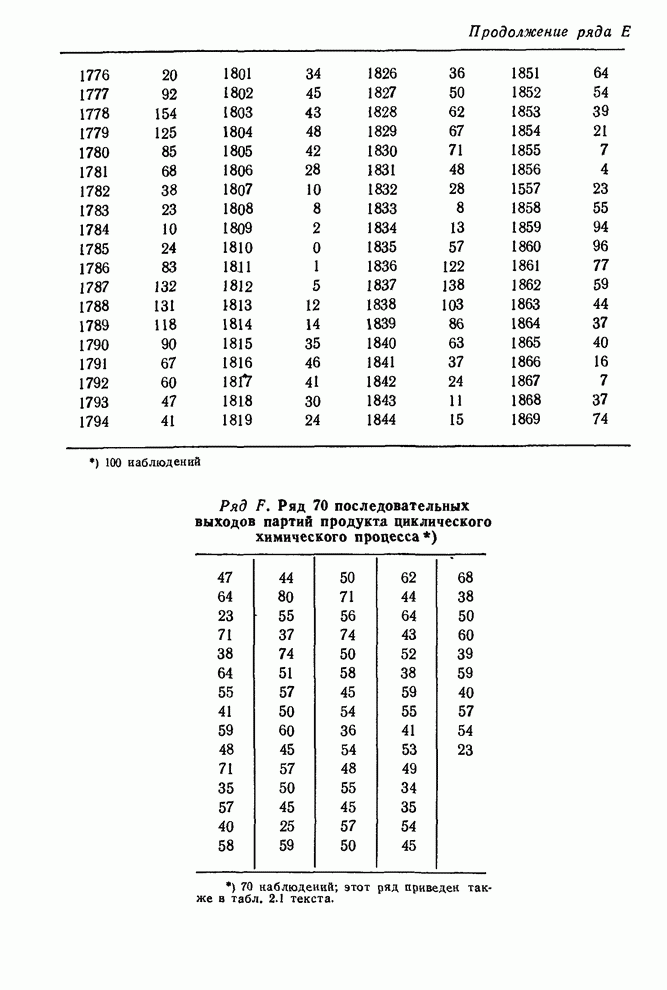
- 7.2.5. Сводка моделей, подогнанных к рядам A-F
- 7.2.6. Информационные матрицы при больших выборках и оценки ковариаций
- 7.3. Результаты оценивания для некоторых частных моделей
- 7.З.2. Процессы скользящего среднего
- 7.3.3. Смешанные процессы
- 7.3.4. Разделение линейных и нелинейных компонент при оценивании
- 7.3.5. Избыточность параметров
- 7.4. Оценивание при помощи теоремы Байеса
- 7.4.2. Байесовское оценивание параметров
- 7.4.3. Процессы авторегрессии
- 7.4.4. Процессы скользящего среднего
- 7.4.5. Смешанные процессы
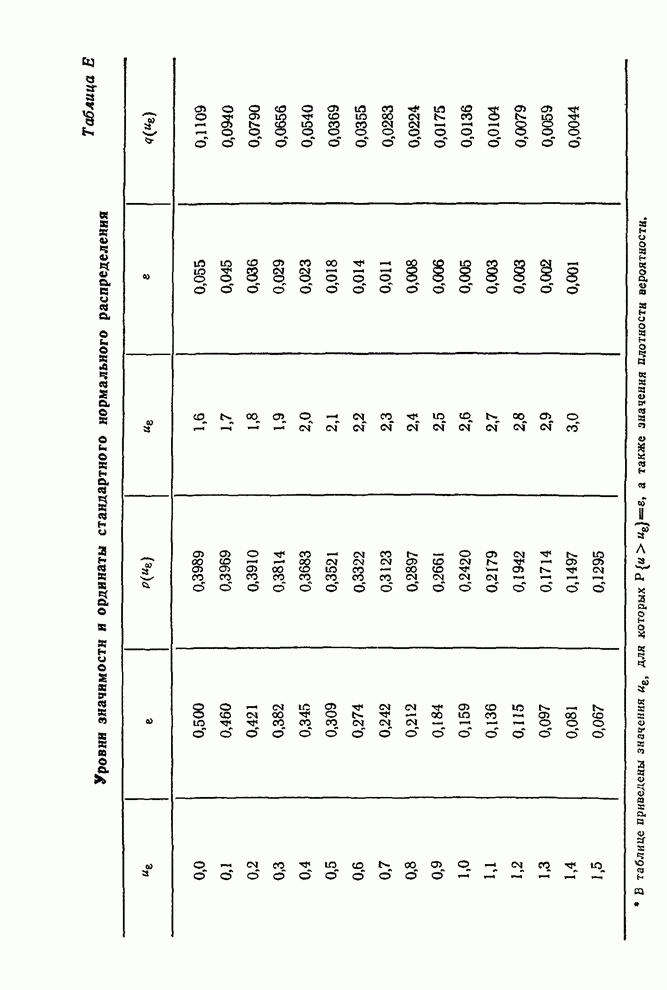
- Приложение П7.1. Обзор теории нормального распределения
- Приложение П7.2. Обзор линейной теории наименьших квадратов
- Приложение П7.3. Примеры влияния ошибок оценивания параметров на вероятностные пределы прогнозов
- Приложение П7.4. Точная функция правдоподобия для процесса скользящего среднего
- Приложение П7.5. Точная функция правдоподобия для процесса авторегрессии
- Глава 8. Диагностическая проверка модели
- 8.1. Проверка стохастических моделей
- 8.1.2. Введение избыточных параметров
- 8.2.1. Проверка при помощи автокорреляций
- 8.2.2. Совокупный критерий согласия
- 8.2.3. Неадекватность модели, возникающая из-за изменения значений параметров
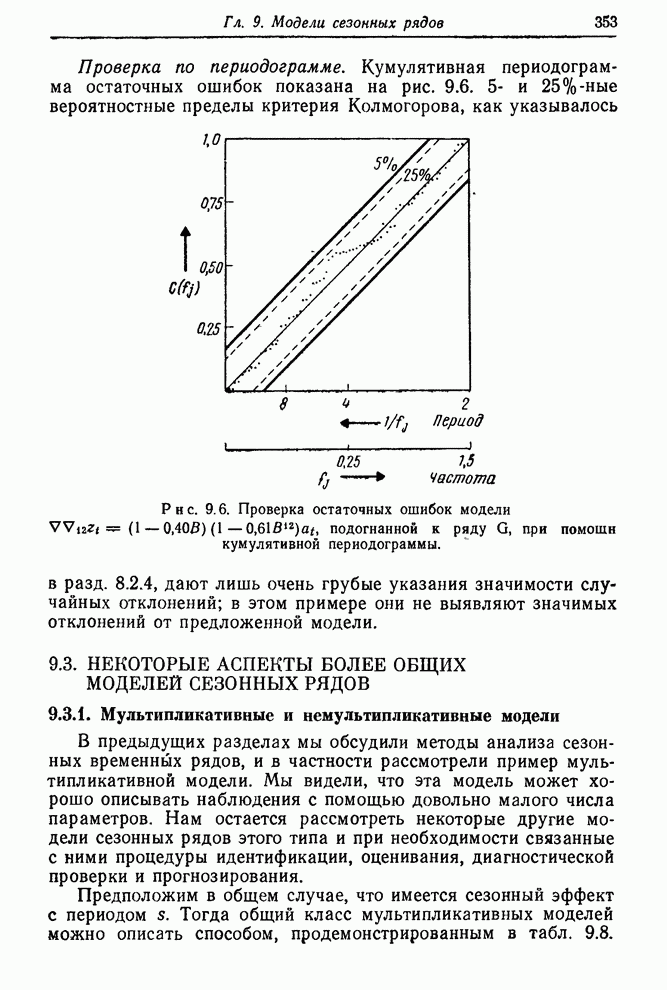
- 8.2.4. Проверка при помощи кумулятивной периодограммы
- 8.3. Использование остаточных ошибок для изменения модели
- 8.3.1. Природа корреляций остаточных ошибок при использовании неверной модели
- 8.3.2. Использование остаточных ошибок для изменения модели
- Глава 9. Модели сезонных рядов
- 9.1. Экономические модели сезонных временных рядов
- 9.1.1. Сопоставление подгонки и прогнозирования
- 9.1.2. Сезонные модели, включающие подстраивающиеся синусоиды и косинусоиды
- 9.1.3. Общая мультипликативная модель сезонного ряда
- 9.2. Представление данных об авиаперевозках мультипликативной моделью
- 9.2.1. Мультипликативная модель
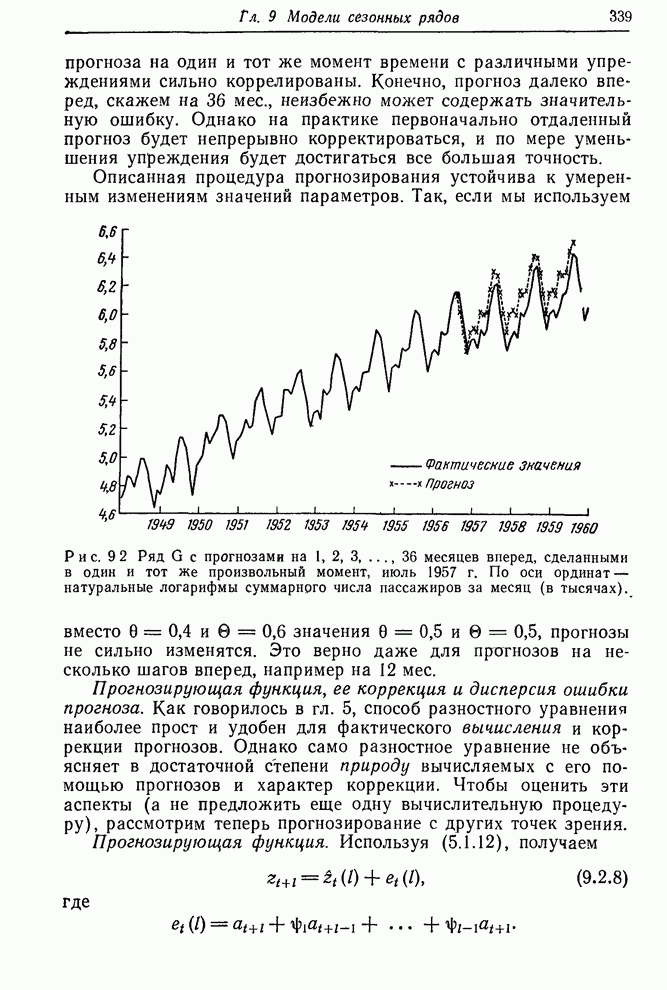
- 9.2.2. Прогнозирование
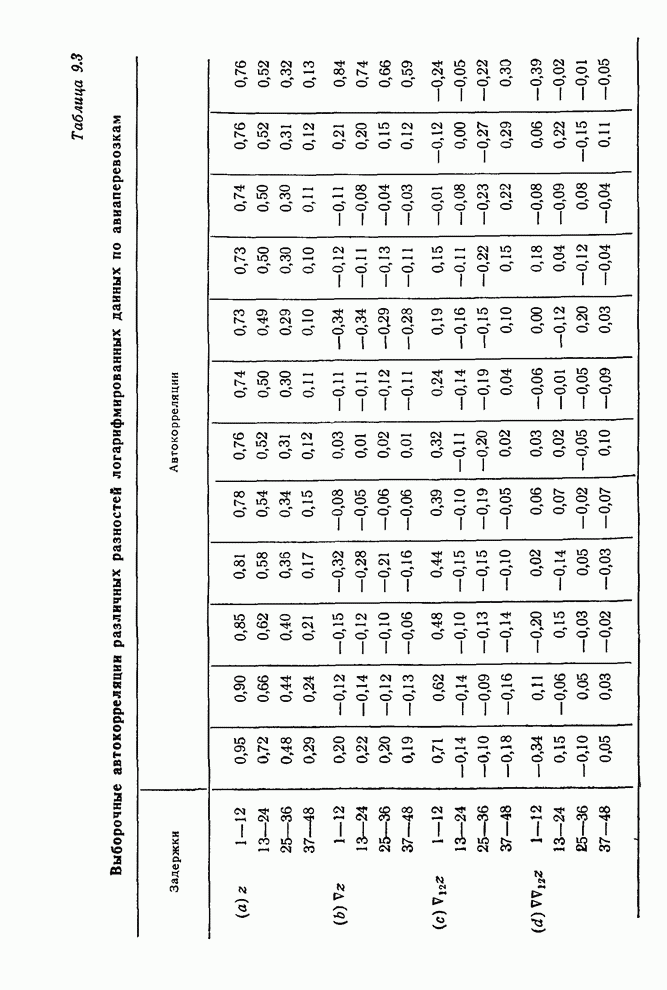
- 9.2.3. Идентификация
- 9.2.4. Оценивание
- 9.2.5. Диагностическая проверка
- 9.3. Некоторые аспекты более общих моделей сезонных рядов
- 9.3.1. Мультипликативные и немультипликативные модели
- 9.3.2. Идентификация
- 9.3.3. Оценивание
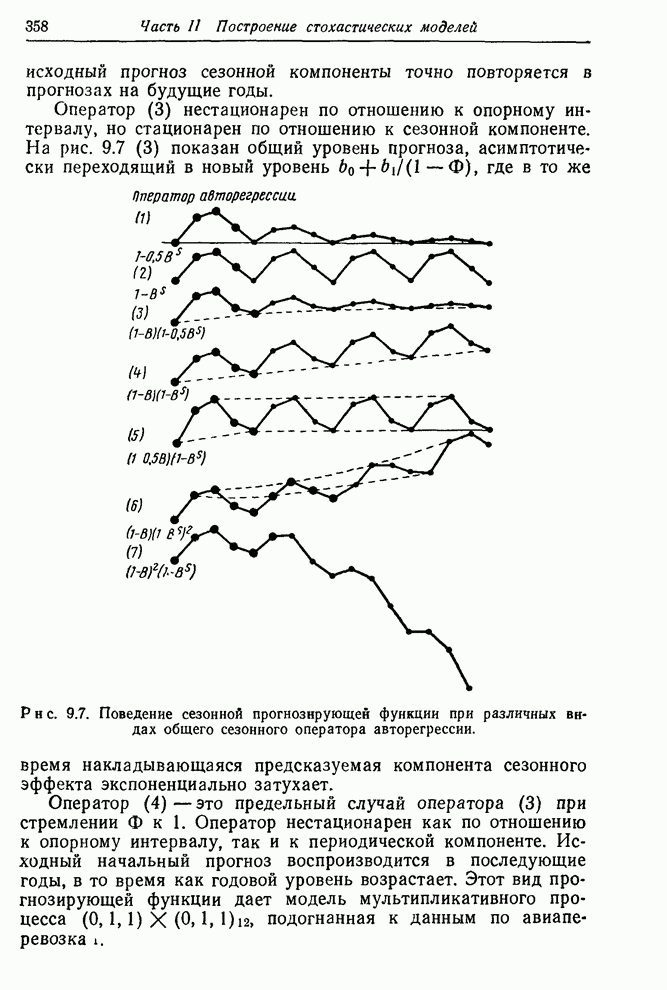
- 9.3.4. Эвентуальные прогнозирующие функции для различных моделей сезонных рядов
- Вспомогательные материалы
- Программа 1 Идентификация стохастической модели
- Программа 2 Предварительное оценивание стохастической модели
- Программа 3. Оценивание стохастической модели
- Алгоритм марквардта для нелинейного метода наименьших квадратов
- Программа 4. Прогнозирование с помощью стохастической модели
- Сборник таблиц и диаграмм