| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
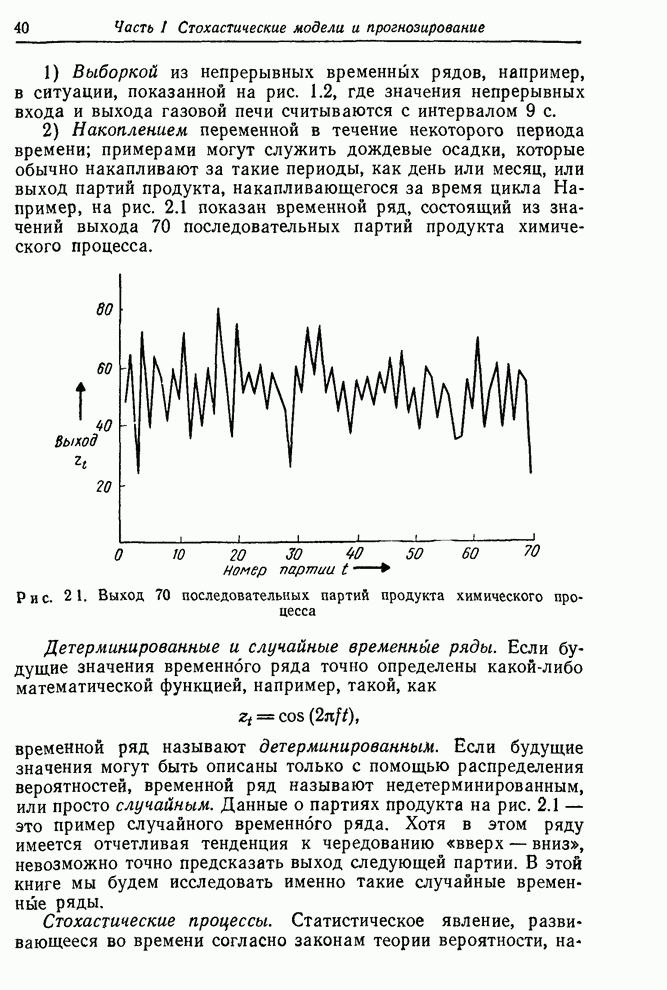
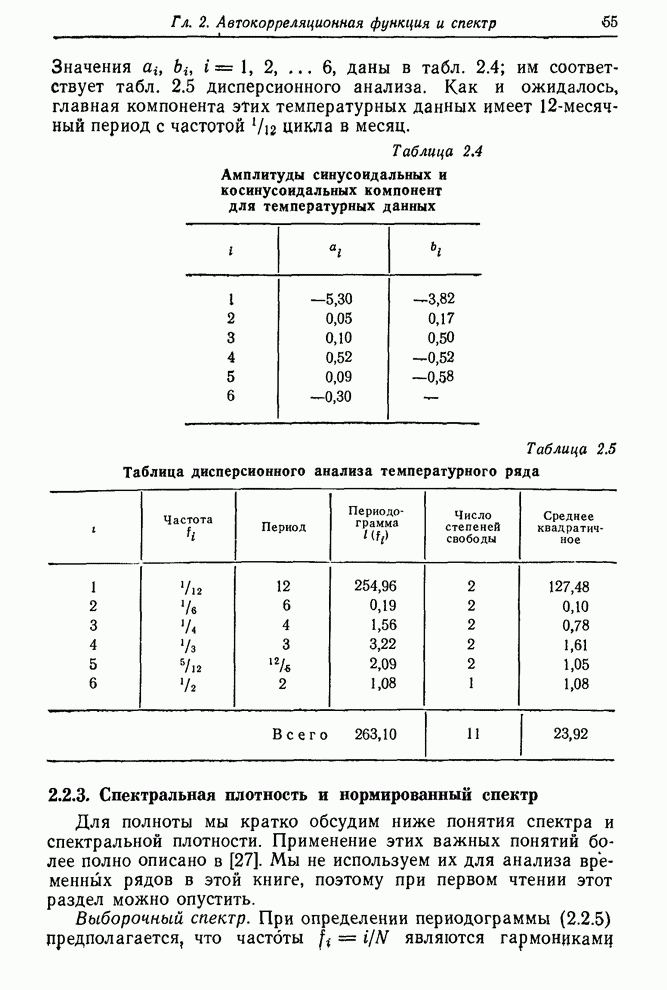
6.2.3. Идентификация некоторых реальных временных рядов
В этом разделе описанные выше способы идентификации
применяются к шести временным рядам, обозначенным ![]() . Ряды
. Ряды ![]() показаны на рис. 4.1, ряд Е
— на рис. 6.1 и ряд
показаны на рис. 4.1, ряд Е
— на рис. 6.1 и ряд ![]() — на рис. 2.1. Данные для всех этих
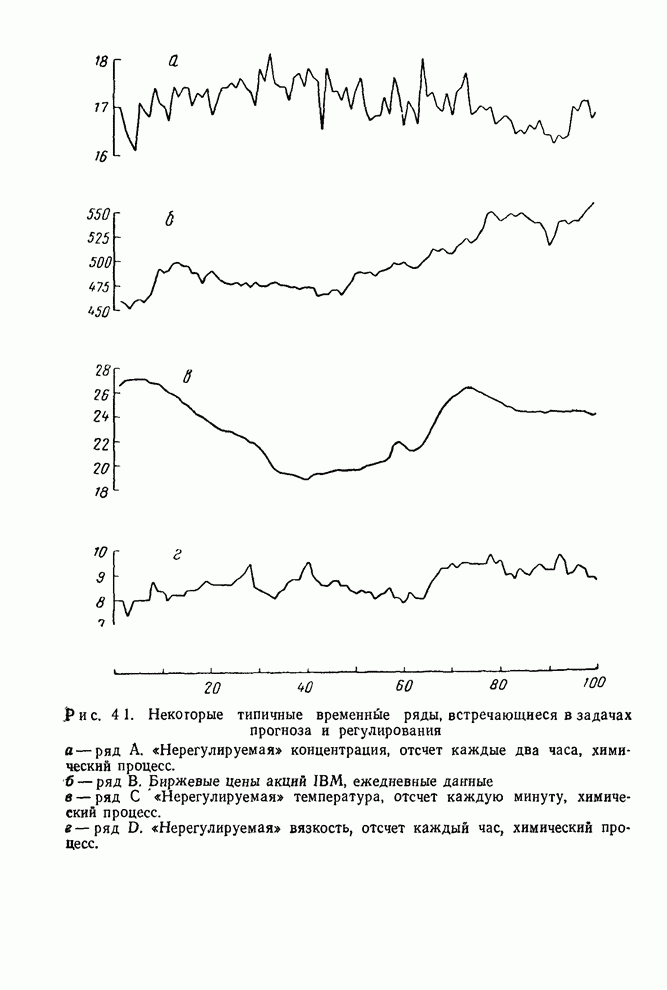
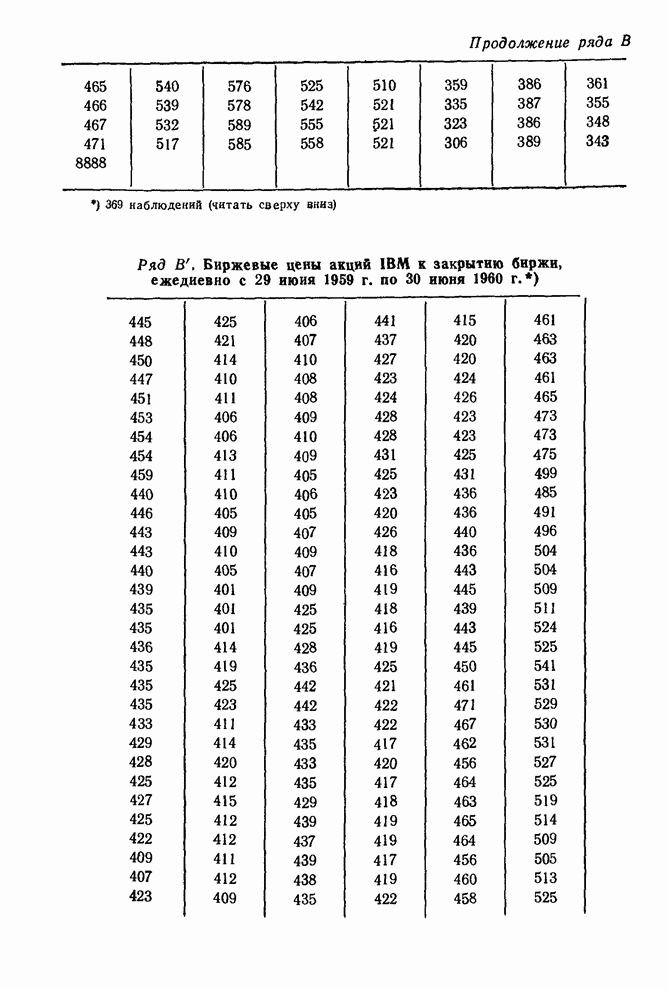
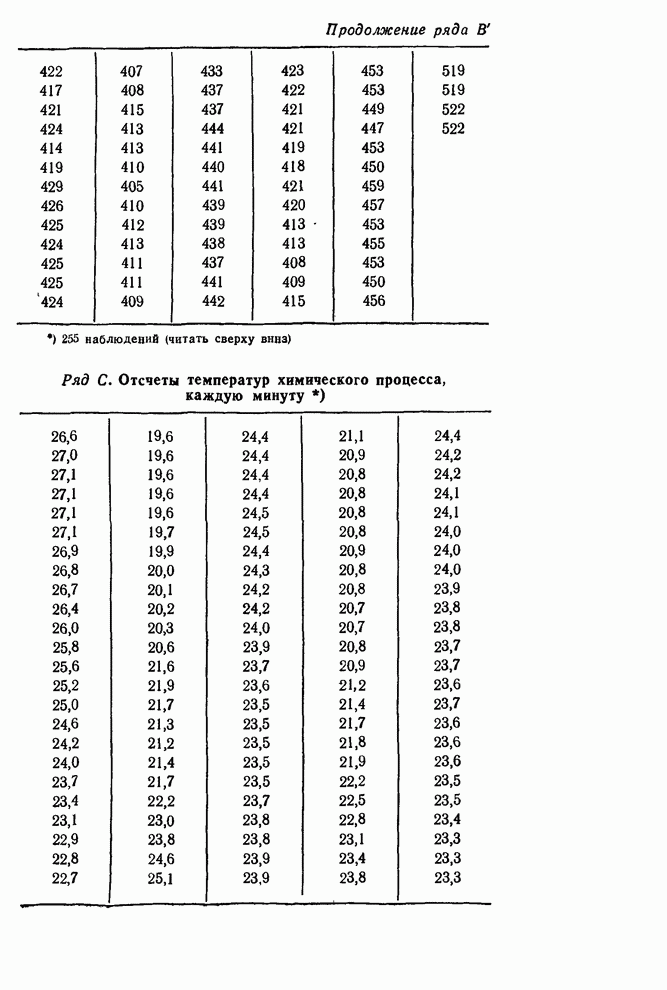
рядов приведены в сборнике временных рядов в конце этой книги. Ряды А, В, С
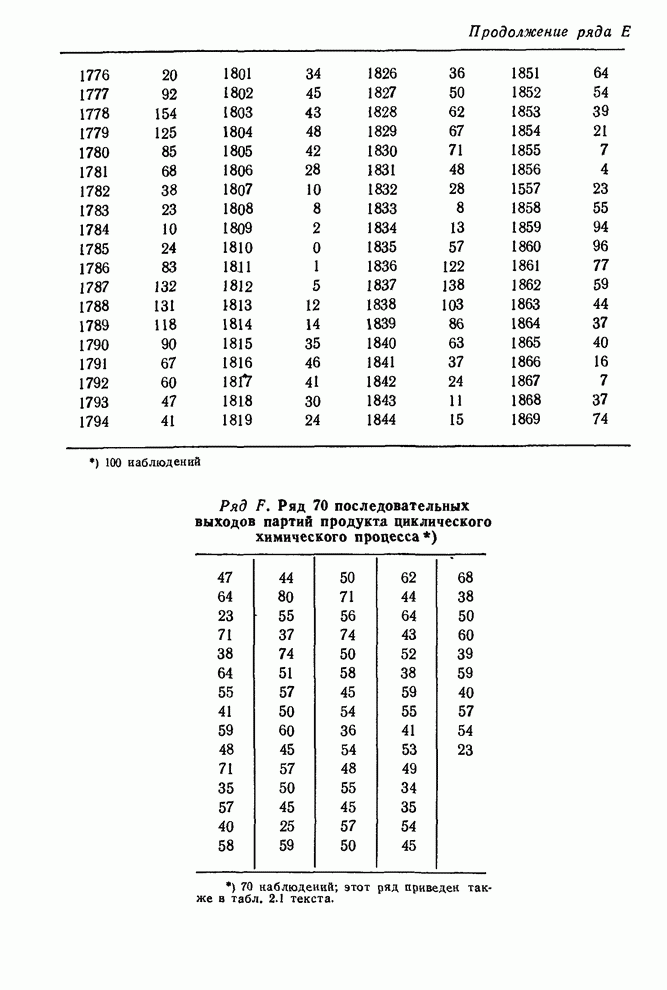
и D были описаны в гл. 4 и ряд F
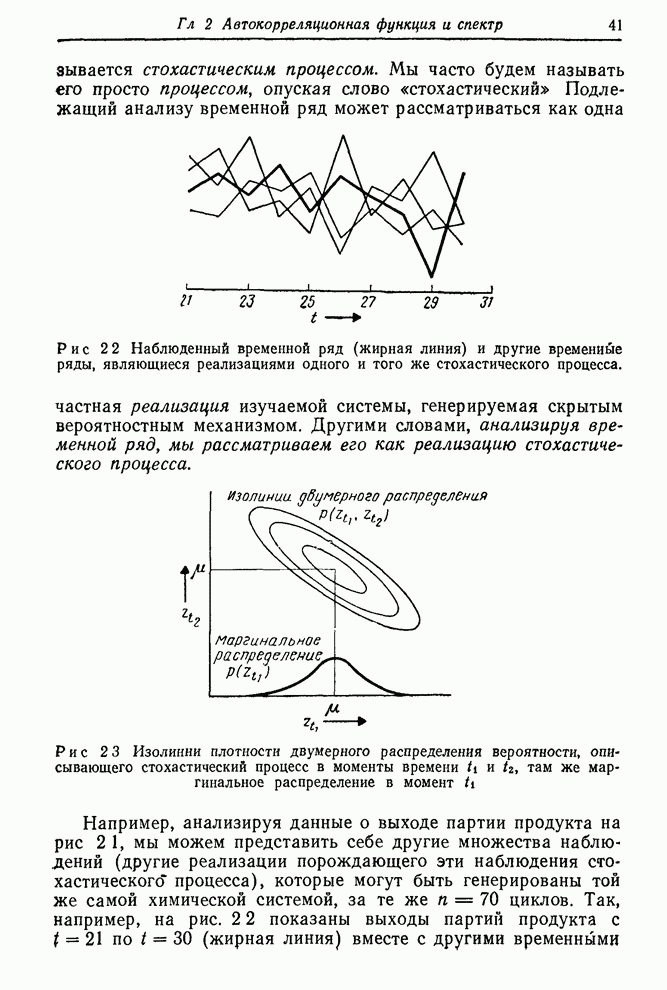
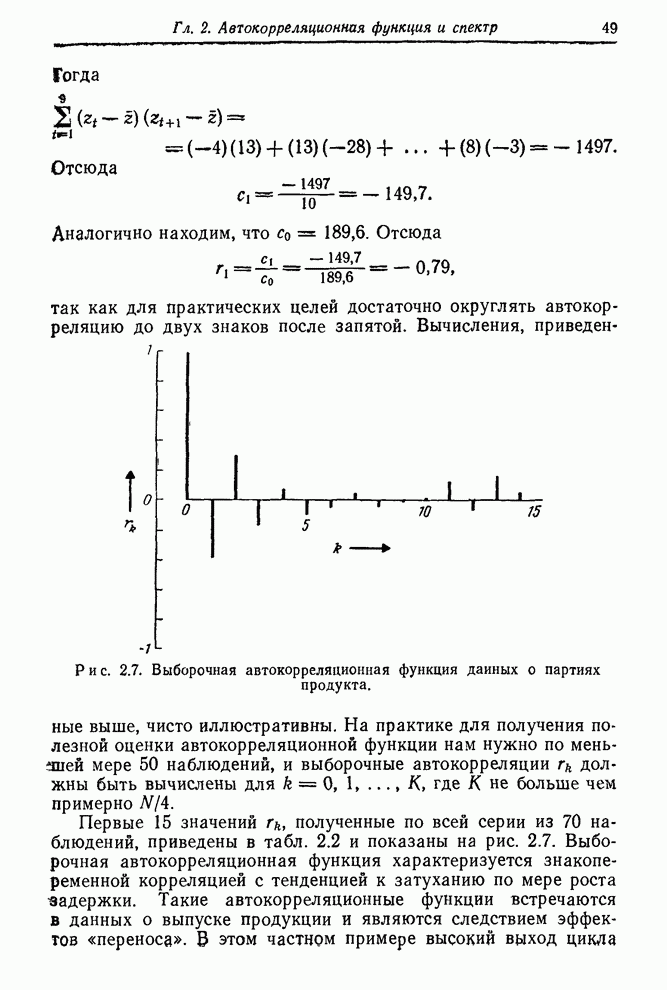
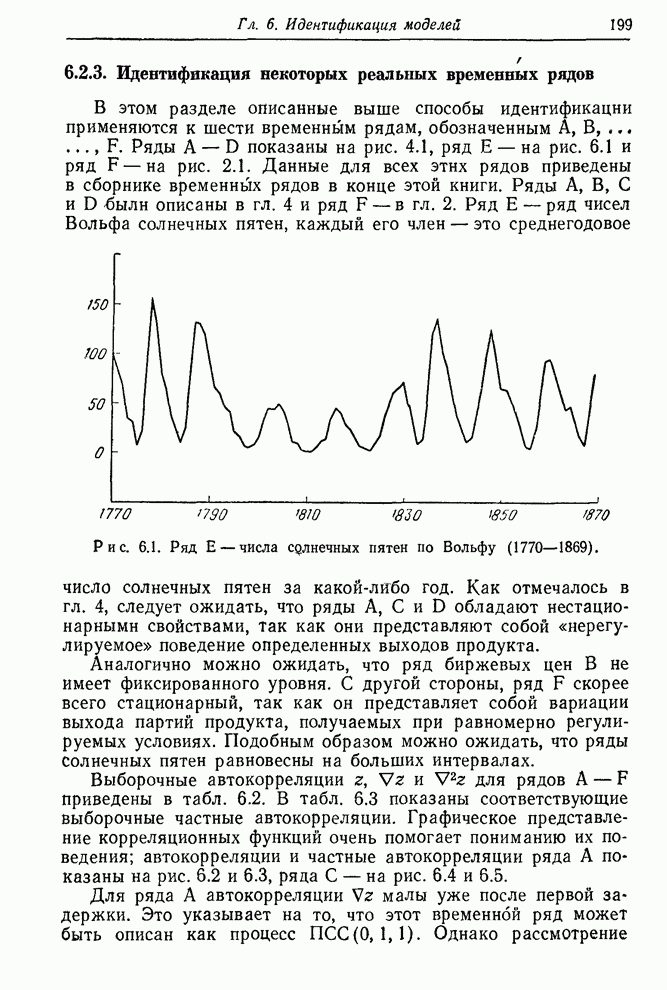
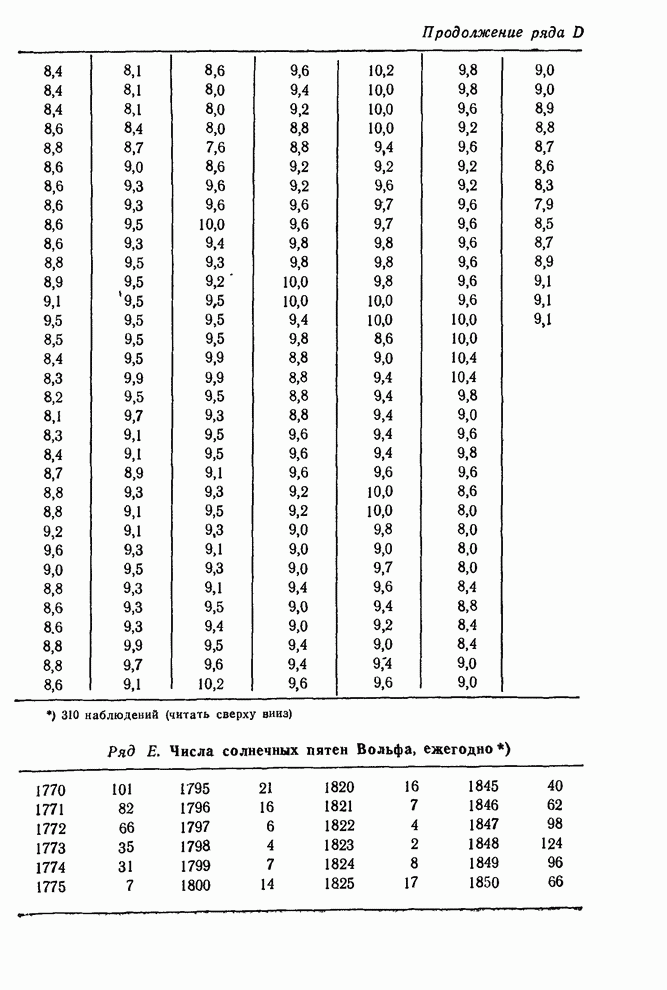
— в гл. 2. Ряд Е — ряд чисел Вольфа солнечных пятен, каждый его член —
это среднегодовое число солнечных пятен за какой-либо год. Как отмечалось в гл.
4, следует ожидать, что ряды А, С и D обладают
нестационарными свойствами, так как они представляют собой «нерегулируемое»
поведение определенных выходов продукта.
— на рис. 2.1. Данные для всех этих
рядов приведены в сборнике временных рядов в конце этой книги. Ряды А, В, С
и D были описаны в гл. 4 и ряд F
— в гл. 2. Ряд Е — ряд чисел Вольфа солнечных пятен, каждый его член —
это среднегодовое число солнечных пятен за какой-либо год. Как отмечалось в гл.
4, следует ожидать, что ряды А, С и D обладают
нестационарными свойствами, так как они представляют собой «нерегулируемое»
поведение определенных выходов продукта.

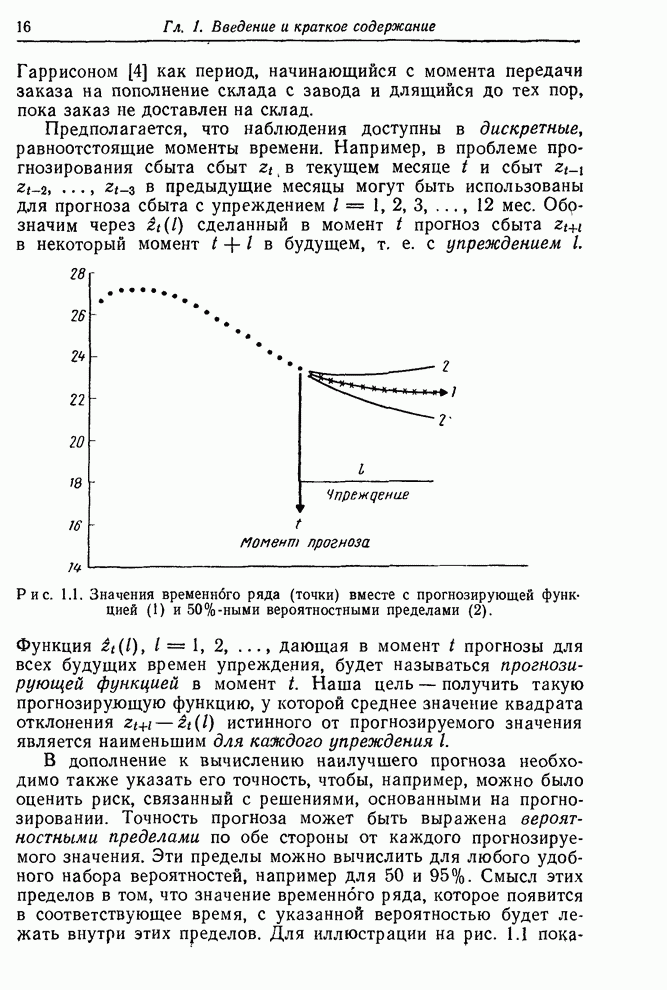
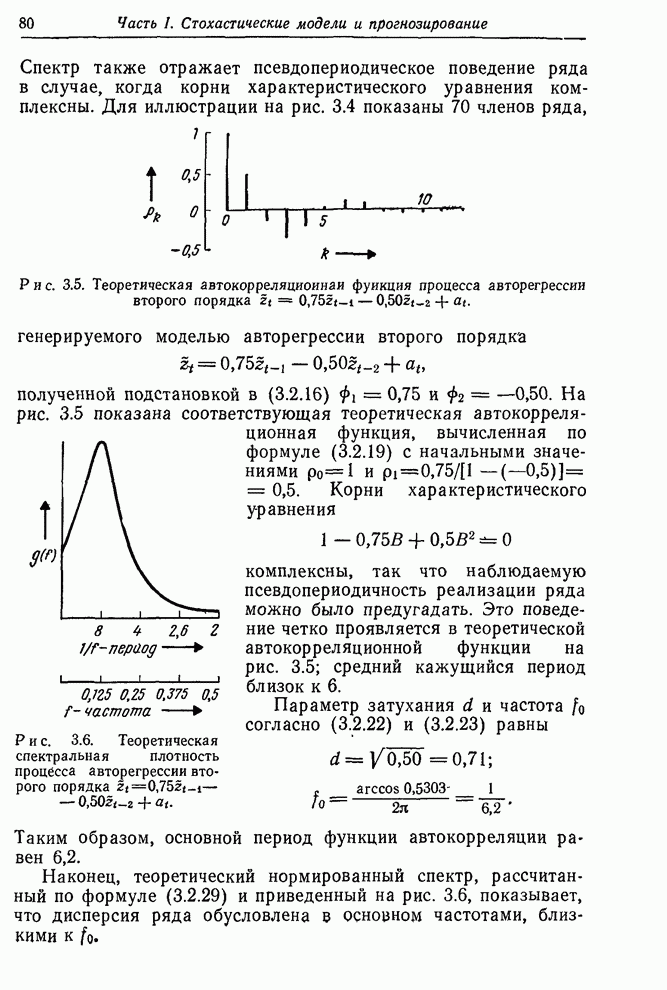
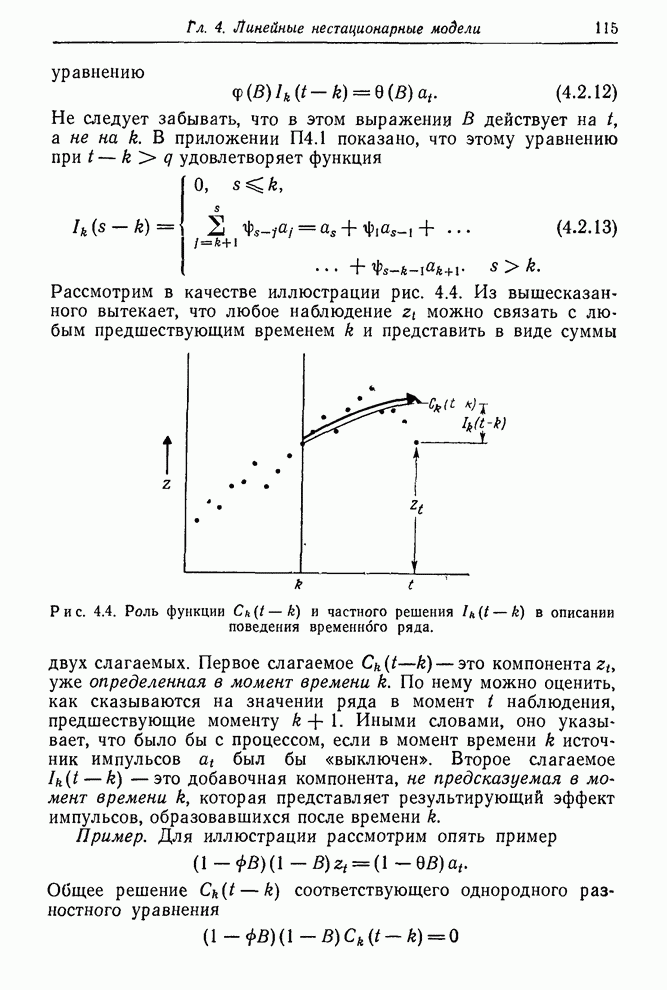
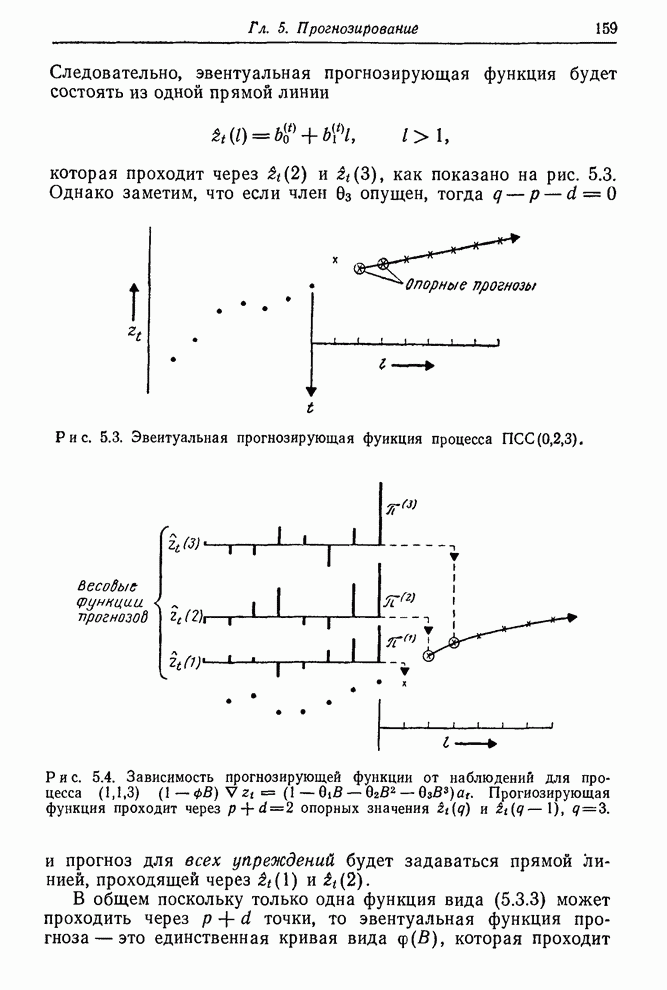
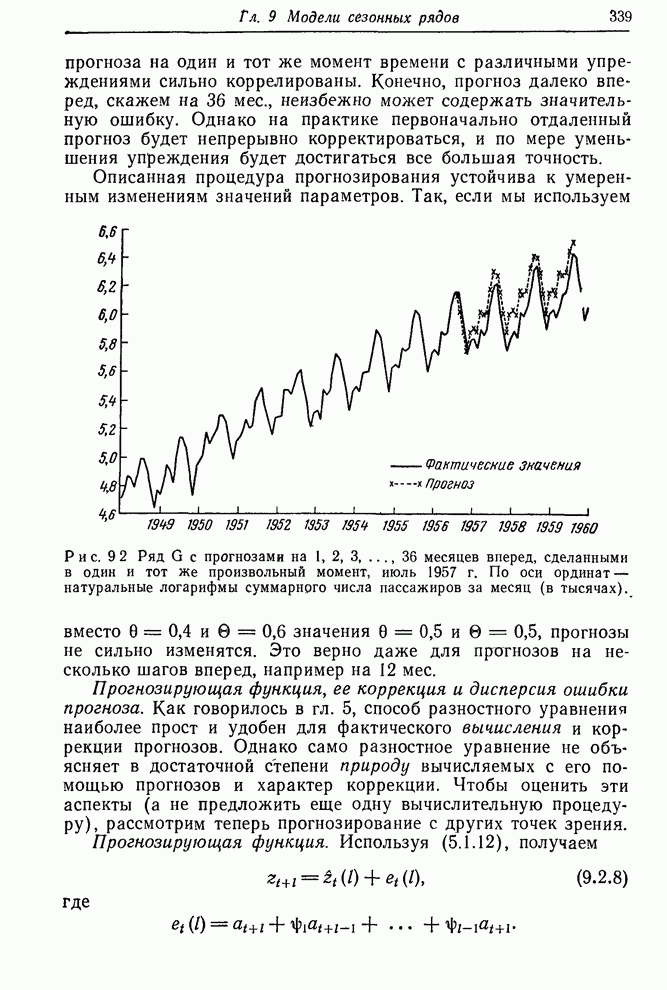
Рис. 6.1. Ряд Е — числа солнечных пятен по Вольфу (1770—1869).
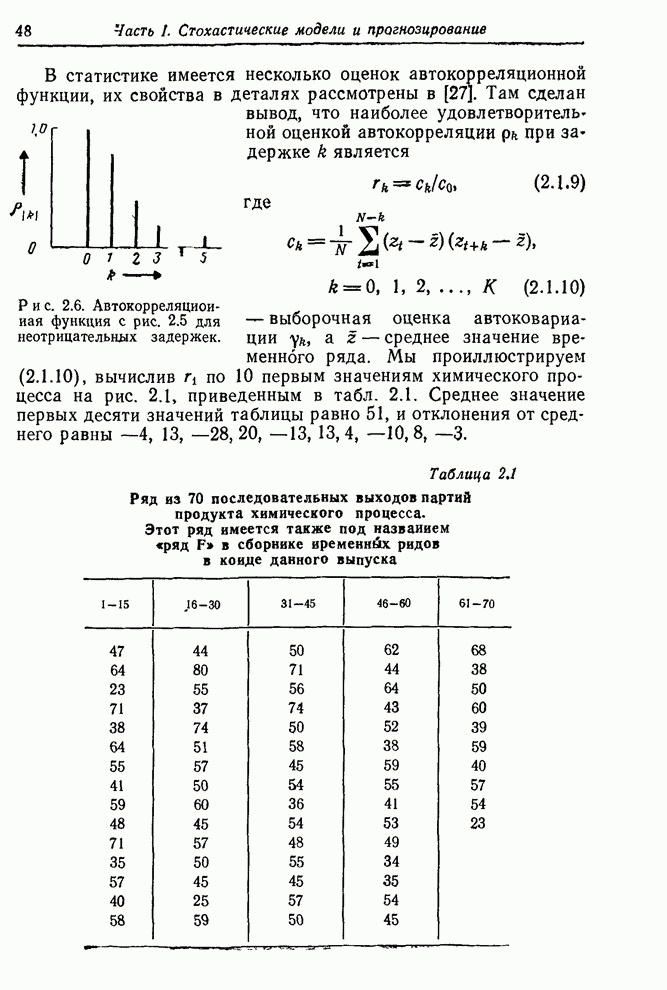
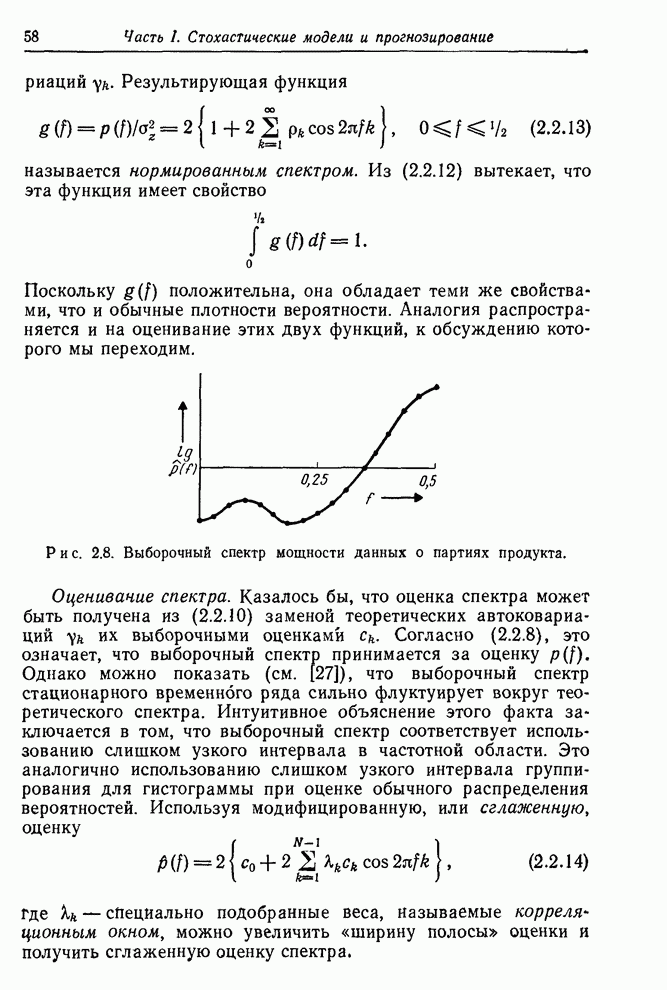
Аналогично можно ожидать, что ряд биржевых цен В не имеет фиксированного уровня. С другой стороны, ряд F скорее всего стационарный, так как он представляет собой вариации выхода партий продукта, получаемых при равномерно регулируемых условиях. Подобным образом можно ожидать, что ряды солнечных пятен равновесны на больших интервалах.
Выборочные автокорреляции ![]() ,
, ![]() и
и ![]() для рядов А — F
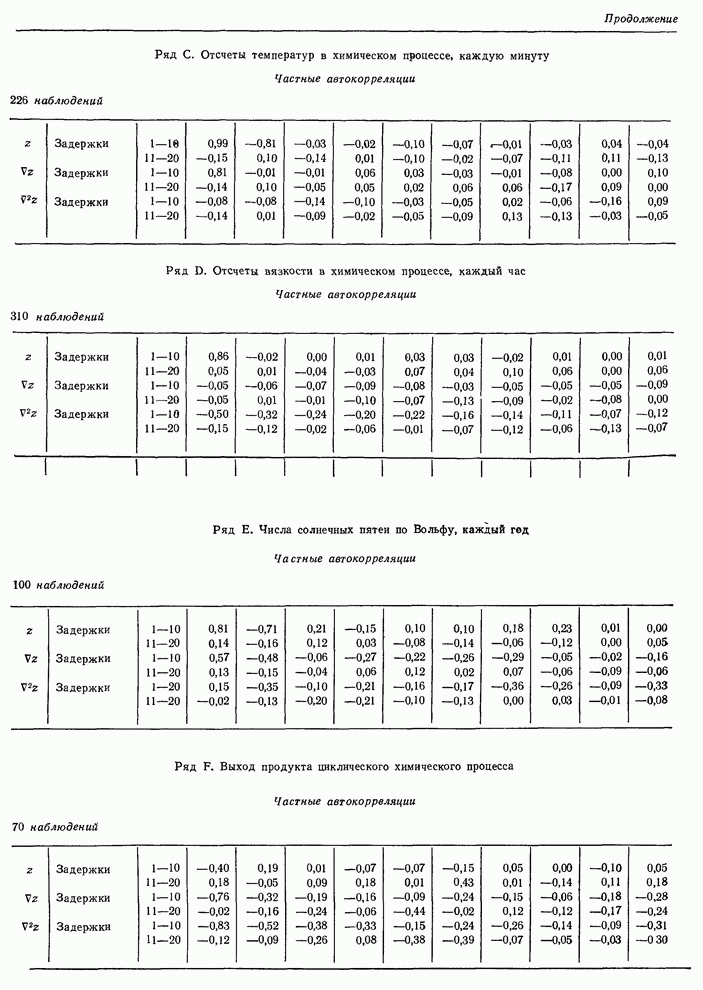
приведены в табл. 6.2. В табл. 6.3 показаны соответствующие выборочные частные
автокорреляции. Графическое представление корреляционных функций очень помогает
пониманию их поведения; автокорреляции и частные автокорреляции ряда А
показаны на рис. 6.2 и 6.3, ряда С — на рис. 6.4 и 6.5.
для рядов А — F
приведены в табл. 6.2. В табл. 6.3 показаны соответствующие выборочные частные
автокорреляции. Графическое представление корреляционных функций очень помогает
пониманию их поведения; автокорреляции и частные автокорреляции ряда А
показаны на рис. 6.2 и 6.3, ряда С — на рис. 6.4 и 6.5.
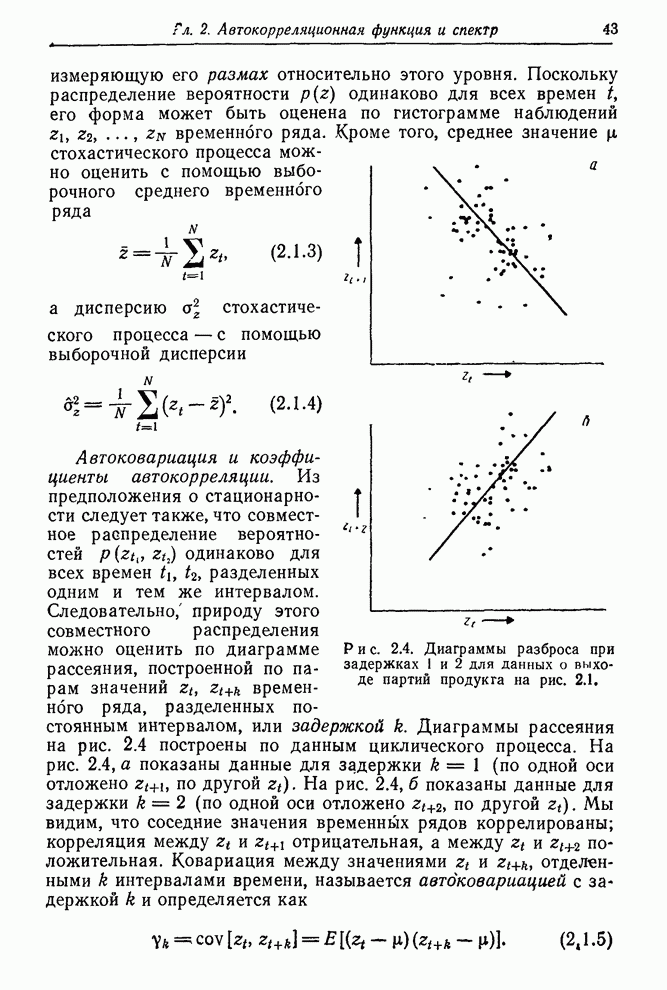
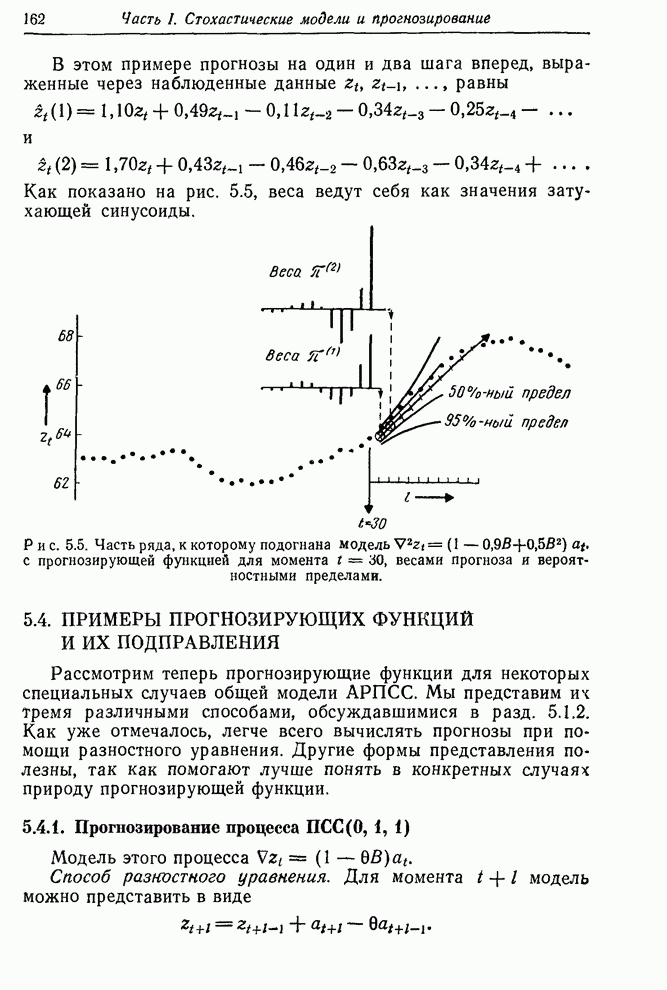
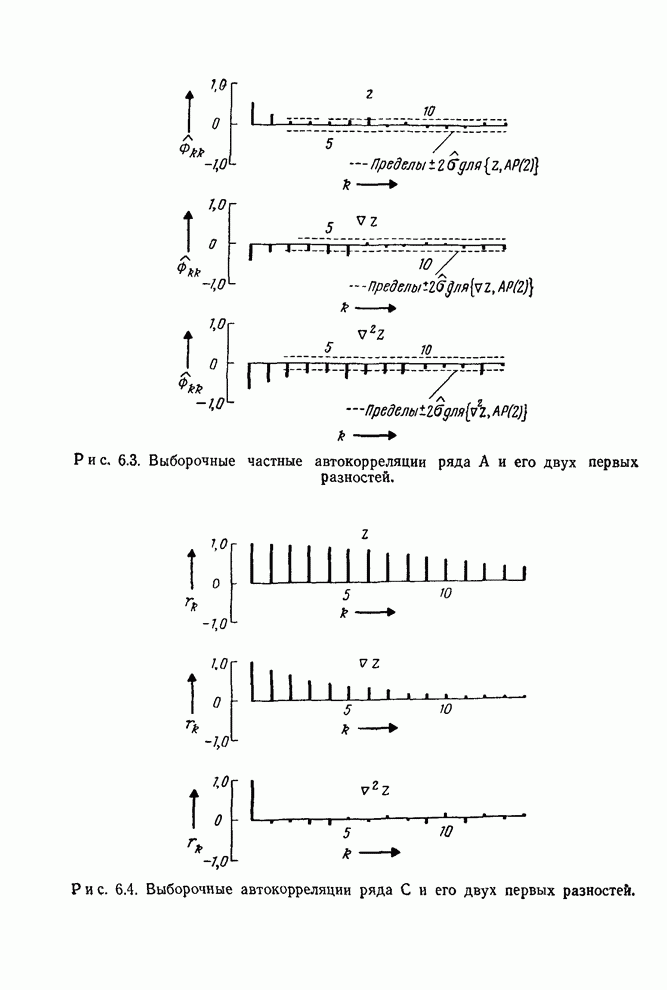
Для ряда А автокорреляции ![]() малы уже после первой
задержки. Это указывает на то, что этот временной ряд может быть описан как
процесс ПСС(0,1,1). Однако рассмотрение автокорреляционной функции
малы уже после первой
задержки. Это указывает на то, что этот временной ряд может быть описан как
процесс ПСС(0,1,1). Однако рассмотрение автокорреляционной функции ![]() показывает, что при
задержке больше 1 корреляции спадают довольно
монотонно. Следовательно, имеется и другая возможность — что ряд описывается
смешанным процессом АРСС(1,0,1). Частная автокорреляционная функция
показывает, что при
задержке больше 1 корреляции спадают довольно
монотонно. Следовательно, имеется и другая возможность — что ряд описывается
смешанным процессом АРСС(1,0,1). Частная автокорреляционная функция ![]() ведет себя
соответствующим этому предположению образом. Позднее мы увидим, что оба
предположения приводят по существу к одной и той же модели.
ведет себя
соответствующим этому предположению образом. Позднее мы увидим, что оба
предположения приводят по существу к одной и той же модели.

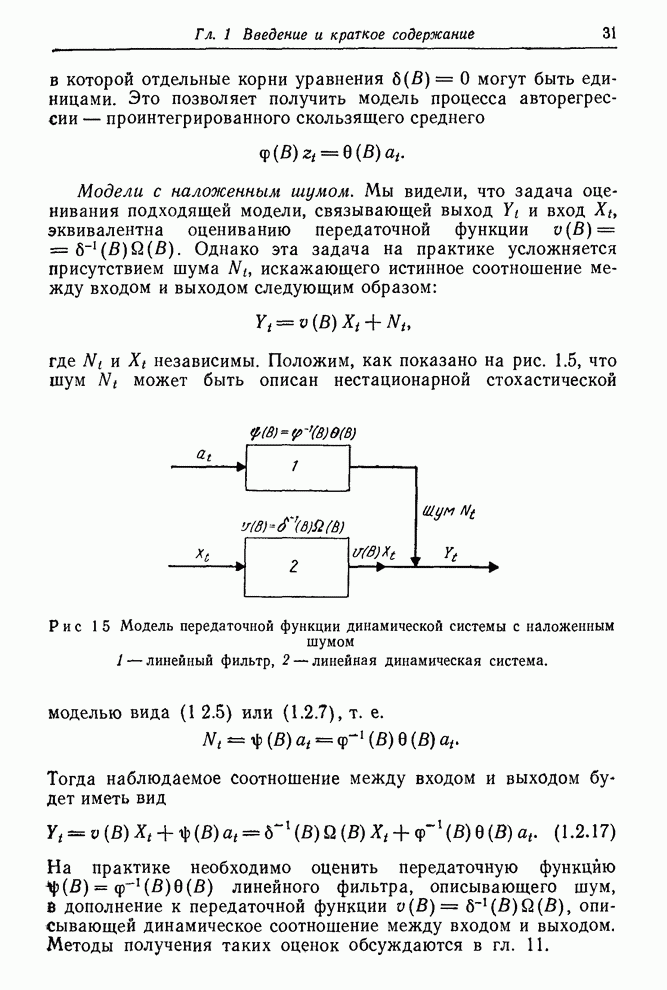
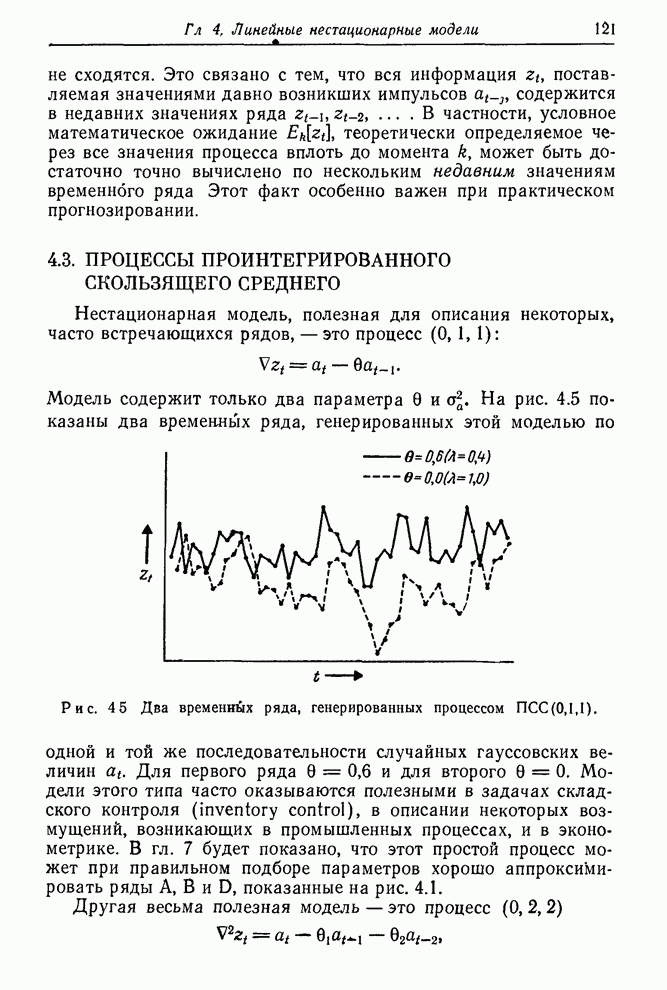
Рис. 6.2. Выборочные автокорреляции различных разностей ряда А.
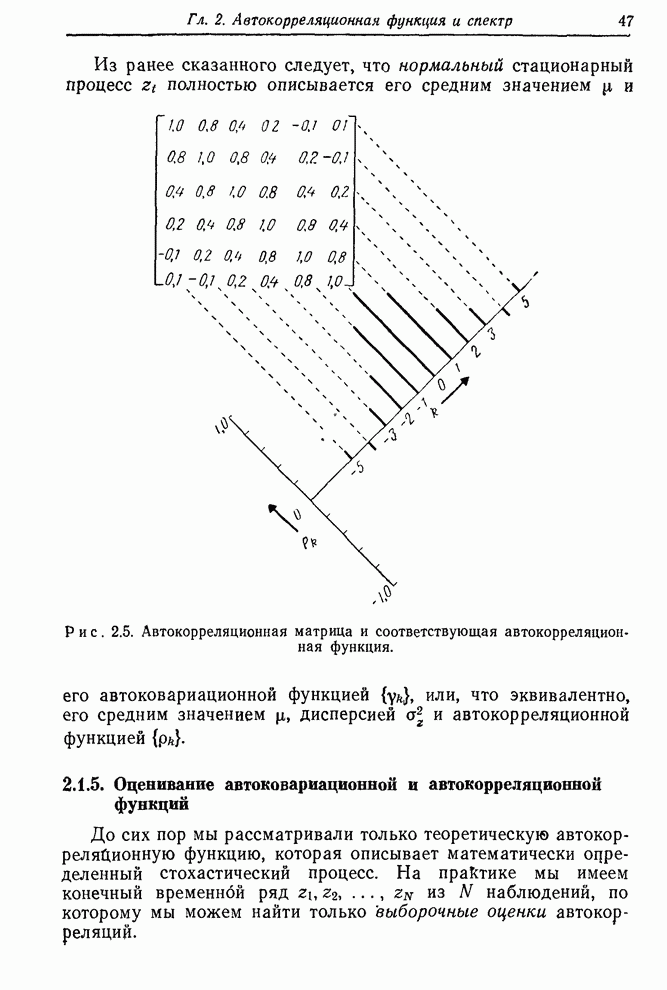
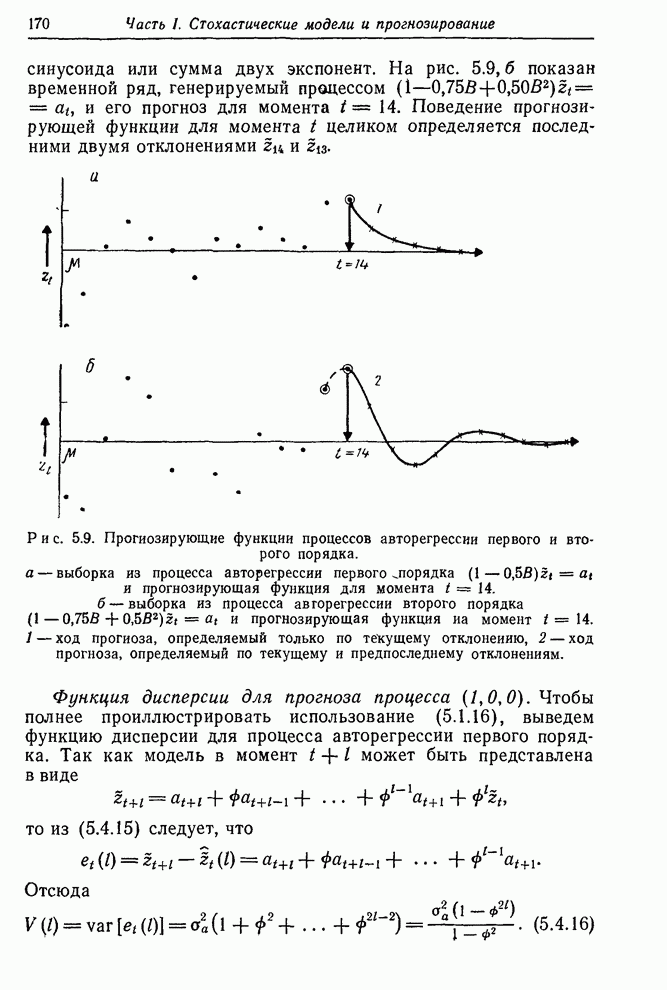
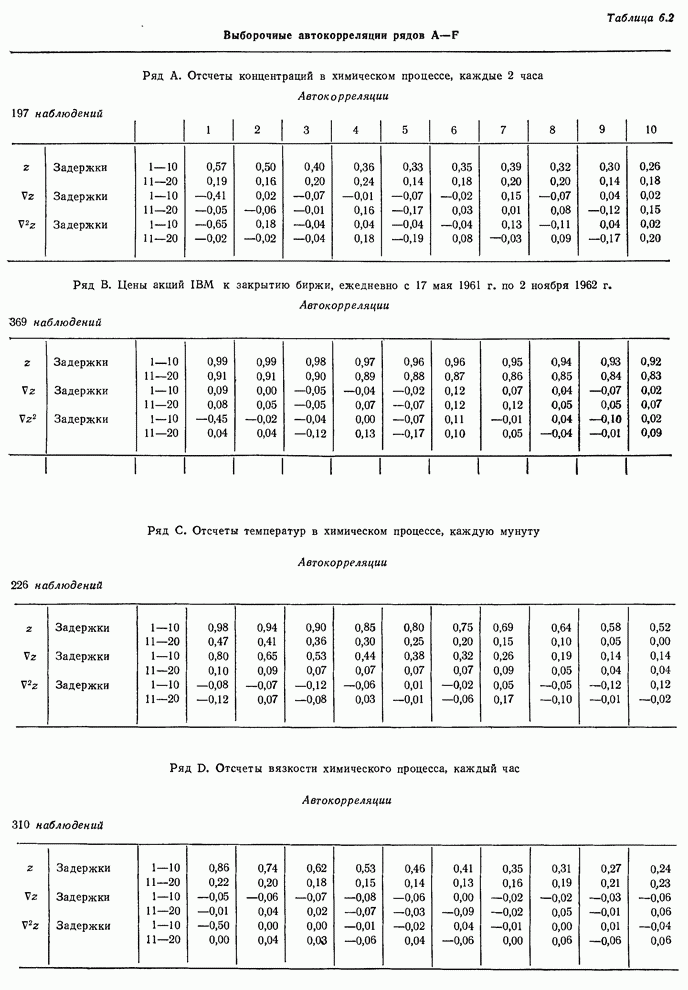
Автокорреляции ряда С, показанные на рис. 6.4,
свидетельствуют о необходимости по меньшей мере одного взятия разностей.
Приближенно экспоненциальный спад корреляций первой разности указывает, что
процесс имеет порядок (1,1,0) с параметром авторегрессии ![]() С другой стороны, из малости
автокорреляций
С другой стороны, из малости
автокорреляций ![]() вытекает,
что приемлем и процесс ПСС (0,2,0). К тем же выводам приводит рассмотрение
частной автокорреляционной функции. Для отсчетов
вытекает,
что приемлем и процесс ПСС (0,2,0). К тем же выводам приводит рассмотрение
частной автокорреляционной функции. Для отсчетов ![]() приходим к обобщенному оператору
авторегрессии второй степени; для
приходим к обобщенному оператору
авторегрессии второй степени; для ![]() — к оператору авторегрессии первого
порядка, действующему на
— к оператору авторегрессии первого
порядка, действующему на ![]() с
с![]() ; для
; для ![]() — к некоррелированному шуму.
Отсюда следуют две возможности:
— к некоррелированному шуму.
Отсюда следуют две возможности:
![]()
![]()
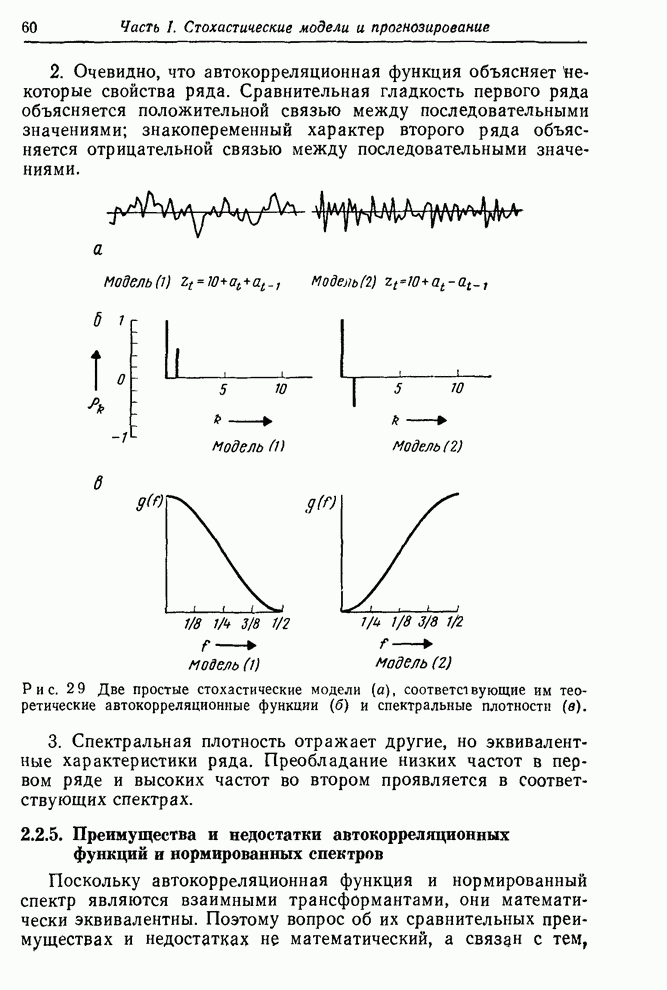
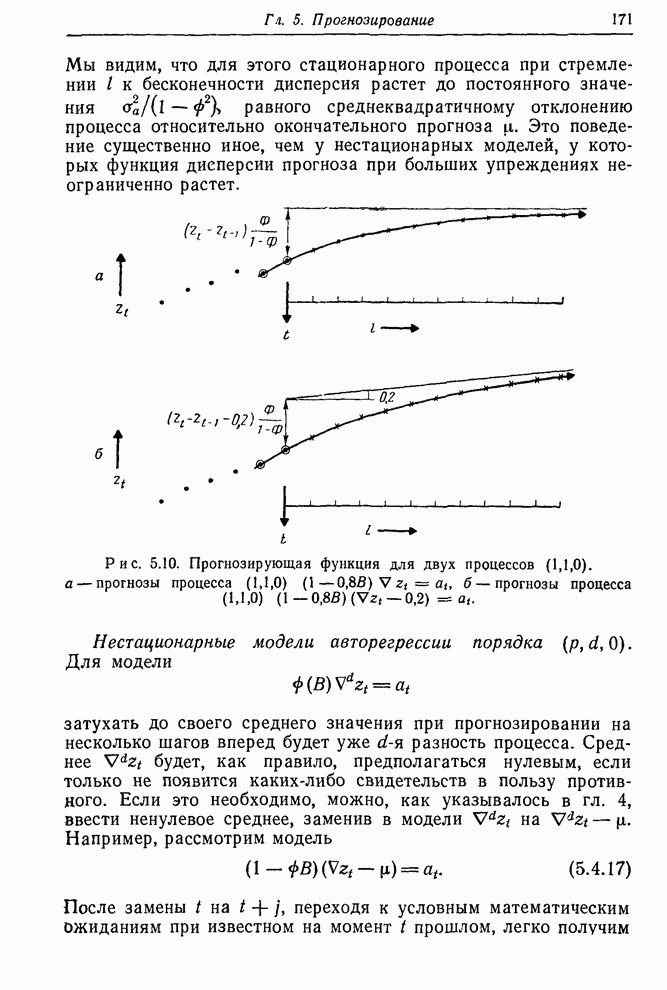
Вторая модель очень похожа на первую, отличаясь только выбором 0,8 вместо 1 для одного из коэффициентов авторегрессии.
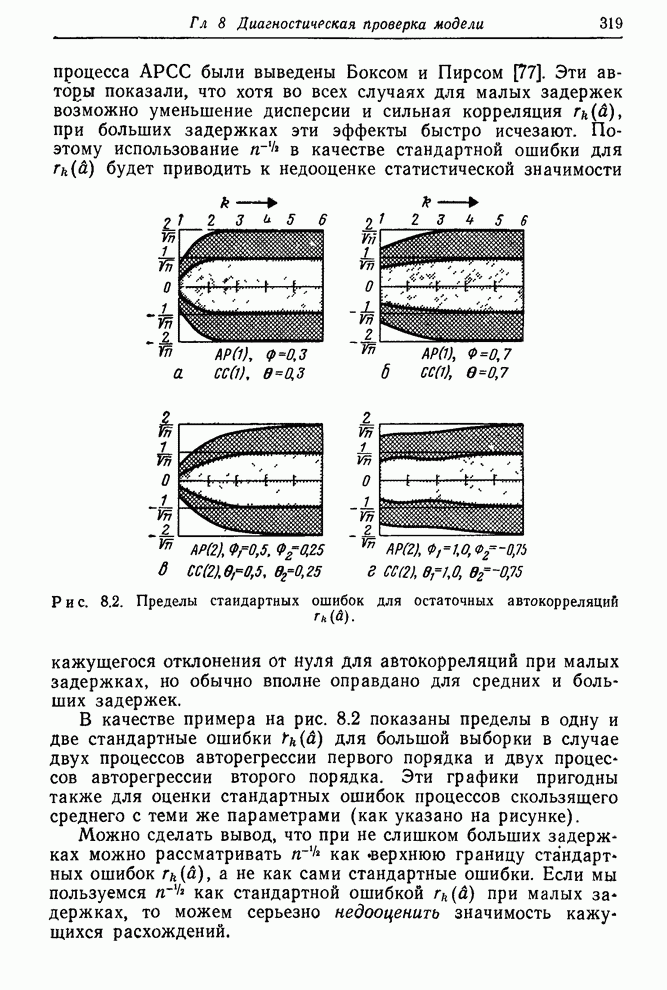
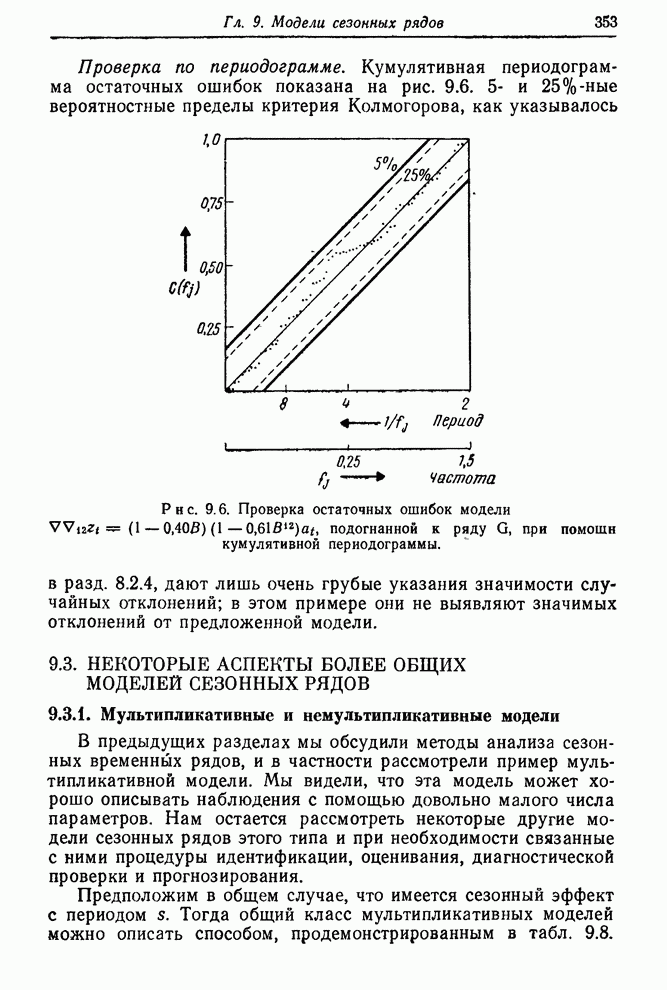
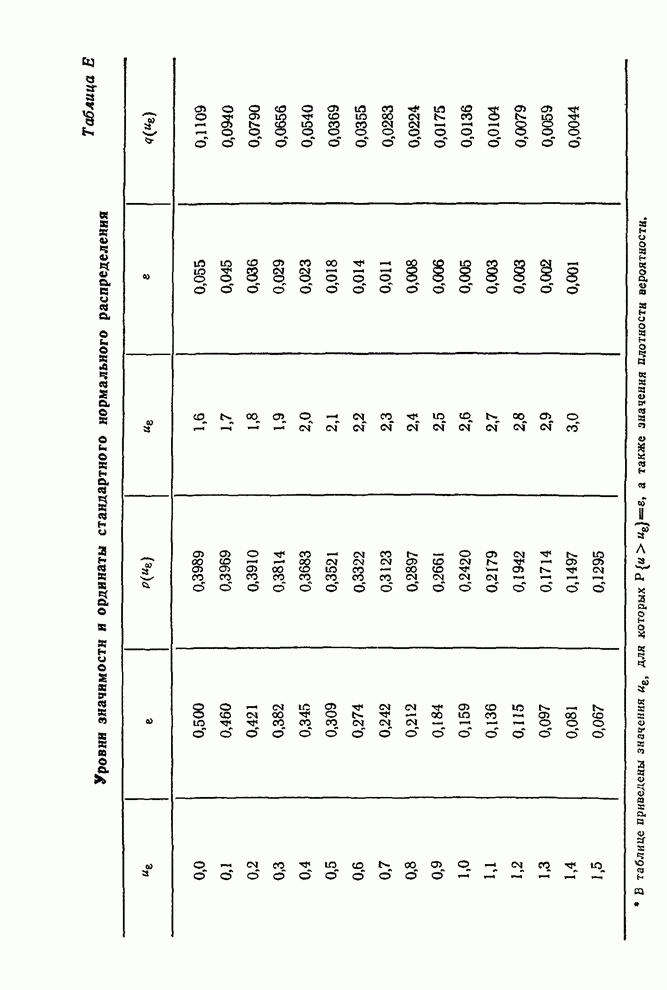
При оценке свойств выборочных корреляционных функций весьма
полезно проводить «контрольные» линии, параллельные оси абсцисс на уровнях ![]() или
или ![]() . Их должно
сопровождать указание имеющейся гипотезы. Так, на рис. 6.5 надпись «пределы
. Их должно
сопровождать указание имеющейся гипотезы. Так, на рис. 6.5 надпись «пределы ![]() для
для![]() » на предельных линиях показывает, что
использованное значение
» на предельных линиях показывает, что
использованное значение ![]() приблизительно верно при гипотезе, что
процесс — авторегрессия второго порядка. Пробная идентификация каждого из рядов
приблизительно верно при гипотезе, что
процесс — авторегрессия второго порядка. Пробная идентификация каждого из рядов
![]() дана в
табл. 6.4.
дана в
табл. 6.4.

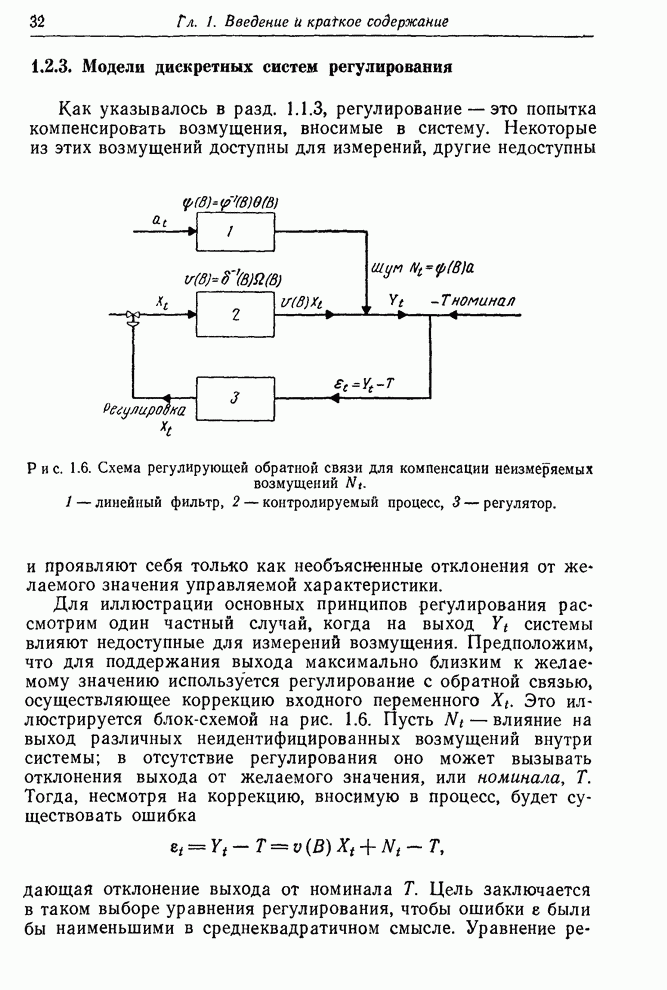
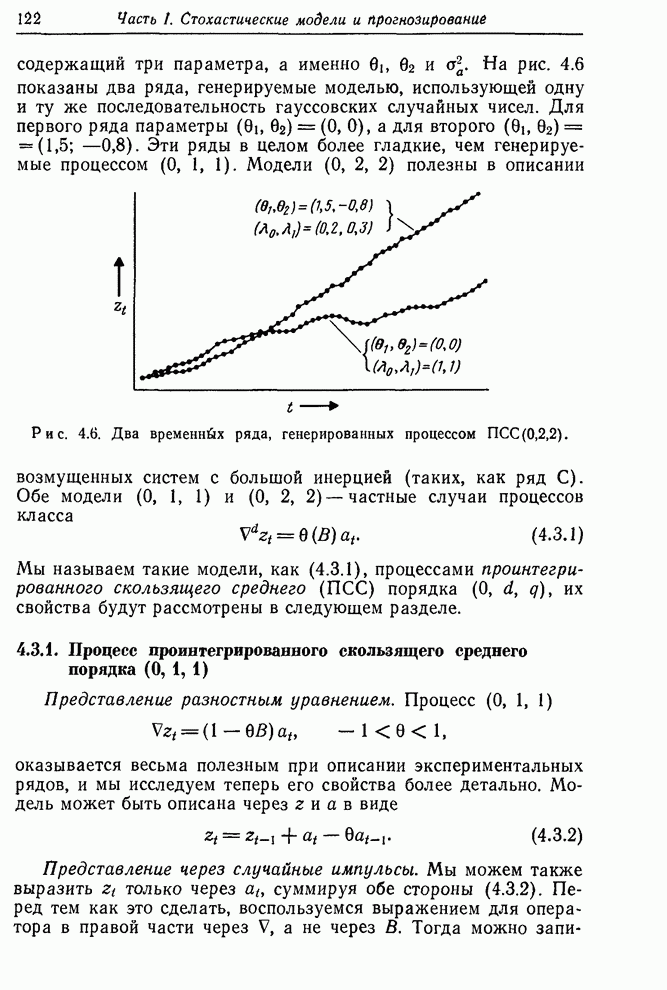
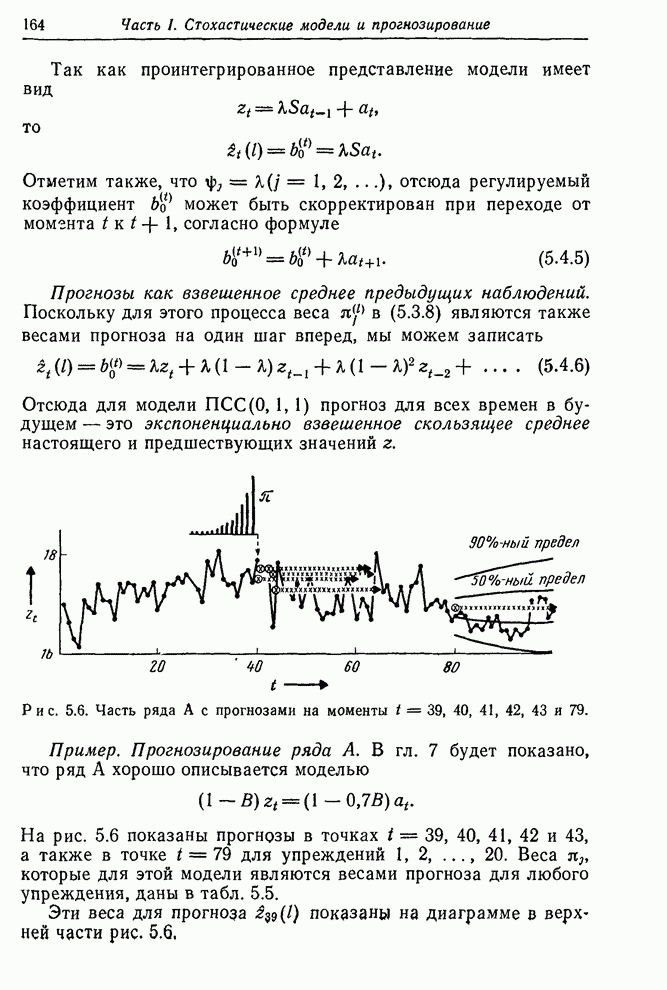
Рис. 6.3. Выборочные частные автокорреляции ряда А и его двух первых разностей

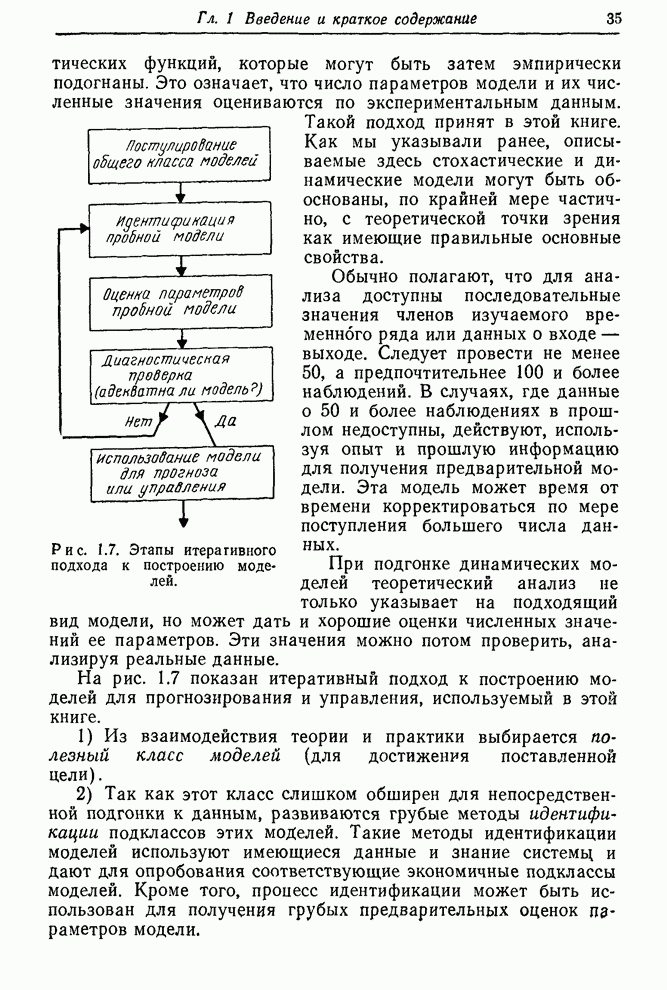
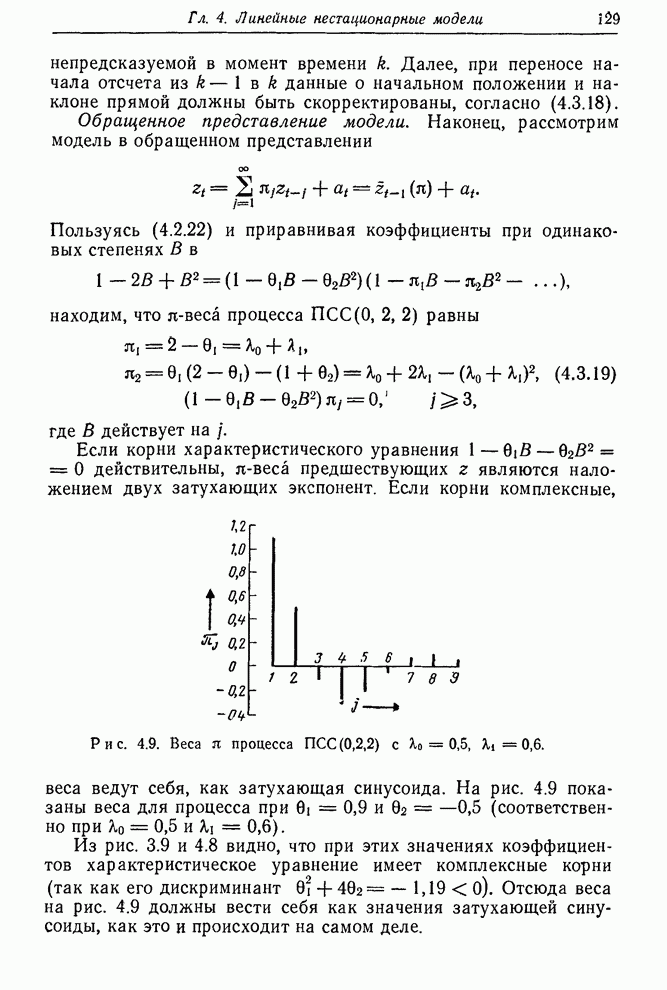
Рис. 6.4. Выборочные автокорреляции ряда С и его двух первых разностей
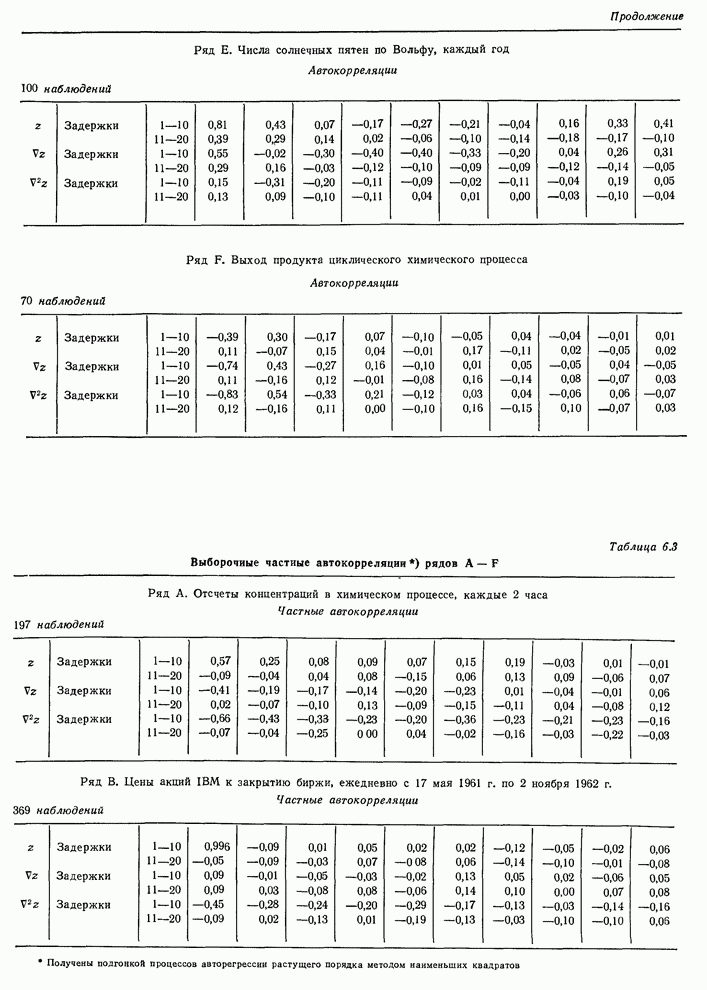
Ряд А. Отсчеты концентраций в химическом процессе, каждые 2 часа. Автокорреляции, 197 наблюдений
|
|
Задержки |
1—10 |
0,86 |
0,74 |
0,62 |
0,53 |
0,46 |
0,41 |
0,35 |
0,31 |
0,27 |
0,24 |
|
|
|
11—20 |
0,22 |
0,20 |
0,18 |
0,15 |
0,14 |
0,13 |
0,16 |
0,19 |
0,21 |
0,23 |
|
|
Задержки |
1—10 |
—0,05 |
—0,06 |
—0,07 |
—0,08 |
—0,06 |
0,00 |
—0,02 |
—0,02 |
—0,03 |
—0,06 |
|
|
|
11—20 |
—0,01 |
0,04 |
0,02 |
—0,07 |
—0,03 |
—0,09 |
—0,02 |
0,05 |
—0,01 |
0,06 |
|
|
Задержки |
1—10 |
—0,50 |
0,00 |
0,00 |
—0,01 |
—0,02 |
0,04 |
—0,01 |
0,00 |
0,01 |
—0,04 |
|
|
|
11—20 |
0,00 |
0,04 |
0,03 |
—0,06 |
0,04 |
—0,06 |
0,00 |
0,06 |
—0,06 |
0,06 |
Ряд В. Цены акций IBM к закрытию биржи, ежедневно с 17 мая 1961 г. по 2 ноября 1962 г. Автокорреляции, 369 наблюдений
|
|
Задержки |
1—10 |
0,98 |
0,94 |
0,90 |
0,85 |
0,80 |
0,75 |
0,69 |
0,64 |
0,58 |
0,52 |
|
|
|
11—20 |
0,47 |
0,41 |
0,36 |
0,30 |
0,25 |
0,20 |
0,15 |
0,10 |
0,05 |
0,00 |
|
|
Задержки |
1—10 |
0,80 |
0,65 |
0,53 |
0,44 |
0,38 |
0,32 |
0,26 |
0,19 |
0,14 |
0,14 |
|
|
|
11—20 |
0,10 |
0,09 |
0,07 |
0,07 |
0,07 |
0,07 |
0,09 |
0,05 |
0,04 |
0,04 |
|
|
Задержки |
1—10 |
—0,08 |
—0,07 |
—0,12 |
—0,06 |
0,01 |
—0,02 |
0,05 |
—0,05 |
—0,12 |
0,12 |
|
|
|
11—20 |
—0,12 |
0,07 |
—0,08 |
0,03 |
—0,01 |
—0,06 |
0,17 |
—0,10 |
—0,01 |
—0,02 |
Ряд С. Отсчеты температур в химическом процессе, каждую минуту. Автокорреляции, 226 наблюдений
|
|
Задержки |
1—10 |
0,99 |
0,99 |
0,98 |
0,97 |
0,96 |
0,96 |
0,95 |
0,94 |
0,93 |
0,92 |
|
|
|
11—20 |
0,91 |
0,91 |
0,90 |
0,89 |
0,88 |
0,87 |
0,86 |
0,85 |
0,84 |
0,83 |
|
|
Задержки |
1—10 |
0,09 |
0,00 |
-0,05 |
—0,04 |
—0,02 |
0,12 |
0,07 |
0,04 |
—0,07 |
0,02 |
|
|
|
11—20 |
0,08 |
0,05 |
—0,05 |
0,07 |
—0,07 |
0,12 |
0,12 |
0,05 |
0,05 |
0,07 |
|
|
Задержки |
1 — 10 |
—0,45 |
—0,02 |
—0,04 |
0,00 |
—0,07 |
0,11 |
—0,01 |
0,04 |
—0,10 |
0,02 |
|
|
|
11—20 |
0,04 |
0,04 |
—0,12 |
0,13 |
—0,17 |
0,10 |
0,05 |
—0,04 |
—0,01 |
0,09 |
Ряд D. Отсчеты вязкости химического процесса, каждый час. Автокорреляции, 310 наблюдений
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
Задержки |
1—10 |
0,57 |
0,50 |
0,40 |
0,36 |
0,33 |
0,35 |
0,39 |
0,32 |
0,30 |
0,26 |
|
|
|
11—20 |
0,19 |
0,16 |
0,20 |
0,24 |
0,14 |
0,18 |
0,20 |
0,20 |
0,14 |
0,18 |
|
|
Задержки |
1—10 |
—0,41 |
0,02 |
—0,07 |
—0,01 |
—0,07 |
—0,02 |
0,15 |
—0,07 |
0,04 |
0,02 |
|
|
|
11—20 |
—0,05 |
—0,06 |
—0,01 |
0,16 |
—0,17 |
0,03 |
0,01 |
0,08 |
—0,12 |
0,15 |
|
|
Задержки |
1-10 |
—0,65 |
0,18 |
—0,04 |
0,04 |
—0,04 |
—0,04 |
0,13 |
—0,11 |
0,04 |
0,02 |
|
|
|
11—20 |
—0,02 |
—0,02 |
—0,04 |
0,18 |
—0,19 |
0,08 |
—0,03 |
0,09 |
—0,17 |
0,20 |
Ряд Е. Числа солнечных пятен по Вольфу, каждый год. Автокорреляции, 100 наблюдений
|
|
Задержки |
1—10 |
0,996 |
—0,09 |
0,01 |
0,05 |
0,02 |
0,02 |
—0,12 |
—0,05 |
—0,02 |
0,06 |
|
|
|
11—20 |
—0,05 |
—0,09 |
—0,03 |
0,07 |
—0 08 |
0,06 |
—0,14 |
—0,10 |
—0,01 |
—0,08 |
|
|
Задержки |
1—10 |
0,09 |
—0,01 |
—0,05 |
—0,03 |
—0,02 |
0,13 |
0,05 |
0,02 |
—0,06 |
0,05 |
|
|
|
11—20 |
0,09 |
0,03 |
—0,08 |
0,08 |
—0,06 |
0,14 |
0,10 |
0,00 |
0,07 |
0,08 |
|
|
Задержки |
1—10 |
—0,45 |
—0,28 |
—0,24 |
—0,20 |
—0,29 |
—0,17 |
—0,13 |
—0,03 |
—0,14 |
—0,16 |
|
|
|
11—20 |
—0,09 |
0,02 |
—0,13 |
0,01 |
—0,19 |
—0,13 |
—0,03 |
—0,10 |
—0,10 |
0,06 |
Ряд F. Выход продукта циклического химического процесса. Автокорреляции, 70 наблюдений
|
|
Задержки |
1-10 |
0,57 |
0,25 |
0,08 |
0,09 |
0,07 |
0,15 |
0,19 |
—0,03 |
0,01 |
—0,01 |
|
|
|
11—20 |
—0,09 |
—0,04 |
0,04 |
0,08 |
—0,15 |
0,06 |
0,13 |
0,09 |
—0,06 |
0,07 |
|
|
Задержки |
1-10 |
—0,41 |
—0,19 |
—0,17 |
—0,14 |
—0,20 |
—0,23 |
0,01 |
—0,04 |
—0,01 |
0,06 |
|
|
|
11—20 |
0,02 |
—0,07 |
—0,10 |
0,13 |
—0,09 |
—0,15 |
-0,11 |
0,04 |
—0,08 |
0,12 |
|
|
Задержки |
1—10 |
—0,66 |
—0,43 |
—0,33 |
—0,23 |
—0,20 |
—0,36 |
—0,23 |
—0,21 |
—0,23 |
—0,16 |
|
|
|
11—20 |
—0,07 |
—0,04 |
—0,25 |
0 00 |
0,04 |
—0,02 |
—0,16 |
—0,03 |
—0,22 |
—0,03 |
Таблица 6.3. Выборочные частные автокорреляции рядов А— F.
Ряд А. Отсчеты концентраций в химическом процессе, каждые 2 часа. Частные автокоррекции, 197 наблюдений.
|
|
Задержки |
1—10 |
—0,39 |
0,30 |
—0,17 |
0,07 |
-0,10 |
—0,05 |
0,04 |
—0,04 |
—0,01 |
0,01 |
|
|
|
11—20 |
0,11 |
—0,07 |
0,15 |
0,04 |
—0,01 |
0,17 |
—0,11 |
0,02 |
—0,05 |
0,02 |
|
|
Задержки |
1—10 |
—0,74 |
0,43 |
—0,27 |
0,16 |
—0,10 |
0,01 |
0,05 |
—0,05 |
0,04 |
—0,05 |
|
|
|
11—20 |
0,11 |
—0,16 |
0,12 |
—0,01 |
—0,08 |
0,16 |
—0,14 |
0,08 |
—0,07 |
0,03 |
|
|
Задержки |
1—10 |
—0,83 |
0,54 |
—0,33 |
0,21 |
—0,12 |
0,03 |
0,04 |
—0,06 |
0,06 |
—0,07 |
|
|
|
11—20 |
0,12 |
—0,16 |
0,11 |
0,00 |
—0,10 |
0,16 |
—0,15 |
0,10 |
—0,07 |
0,03 |
Ряд В. Цены акций 1ВМ к закрытию биржи, ежедневно с 17 мая 1961 г. по 2 ноября 1962 г. Частные автокорреляции, 369 наблюдений.
|
|
Задержки |
1—10 |
0,81 |
0,43 |
0,07 |
—0,17 |
—0,27 |
—0,21 |
—0,04 |
0,16 |
0,33 |
0,41 |
|
|
|
11—20 |
0,39 |
0,^9 |
0,14 |
0,02 |
—0,06 |
—0,10 |
—0,14 |
—0,18 |
—0,17 |
—0,10 |
|
|
Задержки |
1—10 |
0,55 |
—0,02 |
—0,30 |
—0,40 |
—0,40 |
—0,33 |
—0,20 |
0,04 |
0,26 |
0,31 |
|
|
|
11—20 |
0,29 |
0,16 |
—0,03 |
—0,12 |
—0,10 |
—0,09 |
—0,09 |
—0,12 |
—0,14 |
—0,05 |
|
|
Задержки |
1—10 |
0,15 |
—0,31 |
—0,20 |
—0,11 |
—0,09 |
—0,02 |
—0,11 |
—0,04 |
0,19 |
0,05 |
|
|
|
11—20 |
0,13 |
0,09 |
—0,10 |
—0,11 |
0,04 |
0,01 |
0,00 |
—0,03 |
—0,10 |
—0,04 |
Ряд С. Отсчеты температур в химическом процессе, каждую минуту. Частные автокорреляции, 226 наблюдений.
|
|
Задержки |
1—10 |
—0,40 |
0,19 |
0,01 |
—0,07 |
—0,07 |
—0,15 |
0,05 |
0,00 |
—0,10 |
0,05 |
|
|
|
11—20 |
0,18 |
—0,05 |
0,09 |
0,18 |
0,01 |
0,43 |
0,01 |
—0,14 |
0,11 |
0,18 |
|
|
Задержки |
1—10 |
—0,76 |
—0,32 |
—0,19 |
—0,16 |
—0,09 |
—0,24 |
—0,15 |
—0,06 |
—0,18 |
—0,28 |
|
|
|
11—20 |
—0,02 |
—0,16 |
—0,24 |
—0,06 |
—0,44 |
—0,02 |
0,12 |
—0,12 |
—0,17 |
—0,24 |
|
|
Задержки |
1 — 10 |
—0,83 |
—0,52 |
—0,38 |
—0,33 |
—0,15 |
—0,24 |
—0,26 |
—0,14 |
—0,09 |
—0,31 |
|
|
|
11—20 |
—0,12 |
—0,09 |
—0,26 |
0,08 |
—0,38 |
-0,39 |
—0,07 |
—0,05 |
—0,03 |
—0 30 |
Ряд D. Отсчеты вязкости в химическом процессе, каждый час. Частные автокорреляции, 310 наблюдений.
|
|
Задержки |
1 — 10 |
0,81 |
—0,71 |
0,21 |
—0,15 |
0,10 |
0,10 |
0,18 |
0,23 |
0,01 |
0,00 |
|
|
|
11—20 |
0,14 |
—0,16 |
0,12 |
0,03 |
—0,08 |
—0,14 |
—0,06 |
—0,12 |
0,00 |
0,05 |
|
|
Задержки |
1 — 10 |
0,57 |
—0,48 |
—0,06 |
—0,27 |
—0,22 |
—0,26 |
—0,29 |
—0,05 |
—0,02 |
—0,16 |
|
|
|
11—20 |
0,13 |
—0,15 |
—0,04 |
0,06 |
0,12 |
0,02 |
0,07 |
—0,06 |
—0,09 |
—0,06 |
|
|
Задержки |
1—20 |
0,15 |
—0,35 |
—0,10 |
—0,21 |
—0,16 |
—0,17 |
—0,36 |
—0,26 |
—0,09 |
—0,33 |
|
|
|
11—20 |
—0,02 |
—0,13 |
—0,20 |
—0,21 |
—0,10 |
—0,13 |
0,00 |
0,03 |
—0,01 |
—0,08 |
Ряд Е. Числа солнечных пятен по Вольфу, каждый год. Частные автокорреляции, 100 наблюдений
|
|
Задержки |
1 — 10 |
0,86 |
—0,02 |
0,00 |
0,01 |
0,03 |
0,03 |
—0,02 |
0,01 |
0,00 |
0,01 |
|
|
|
11—20 |
0,05 |
0,01 |
—0,04 |
—0,03 |
0,07 |
0,04 |
0,10 |
0,06 |
0,00 |
0,06 |
|
|
Задержки |
1—10 |
—0,05 |
—0,06 |
—0,07 |
—0,09 |
—0,08 |
—0,03 |
—0,05 |
—0,05 |
—0,05 |
—0,09 |
|
|
|
11—20 |
—0,05 |
0,01 |
—0,01 |
—0,10 |
—0,07 |
—0,13 |
—0,09 |
—0,02 |
—0,08 |
0,00 |
|
|
Задержки |
1 — 10 |
—0,50 |
—0,32 |
—0,24 |
—0,20 |
—0,22 |
—0,16 |
—0,14 |
—0,11 |
—0,07 |
—0,12 |
|
|
|
11—20 |
—0,15 |
—0,12 |
—0,02 |
—0,06 |
—0,01 |
-0,07 |
—0,12 |
—0,06 |
—0,13 |
—0,07 |
Ряд F. Выход продукта циклического химического процесса. Частные автокорреляции, 70 наблюдений.
|
|
Задержки |
1—10 |
0,99 |
—0,81 |
—0,03 |
—0,02 |
—0,10 |
—0,07 |
—0,01 |
—0,03 |
0,04 |
—0,04 |
|
|
|
11—20 |
—0,15 |
0,10 |
—0,14 |
0,01 |
—0,10 |
—0,02 |
—0,07 |
—0,11 |
0,11 |
—0,13 |
|
|
Задержки |
1-10 |
0,81 |
—0,01 |
—0,01 |
0,06 |
0,03 |
—0,03 |
—0,01 |
—0,08 |
0,00 |
0,10 |
|
|
|
11—20 |
—0,14 |
0,10 |
—0,05 |
0,05 |
0,02 |
0,06 |
0,06 |
—0,17 |
0,09 |
0,00 |
|
|
Задержки |
1—10 |
—0,08 |
—0,08 |
—0,14 |
-0,10 |
—0,03 |
—0,05 |
0,02 |
—0,06 |
—0,16 |
0,09 |
|
|
|
11—20 |
—0,14 |
0,01 |
—0,09 |
—0,02 |
—0,05 |
—0,09 |
0,13 |
—0,13 |
—0,03 |
—0,05 |

Рис. 6.5. Выборочные частные автокорреляции ряда С и его двух первых разностей.
Таблица 6.4.
Пробная идентификация моделей рядов ![]()
|
Ряд |
Степень разности |
Кажущаяся природа разность ряда |
Идентификация для |
|
A |
|
Смешанный АР первого порядка и СС первого порядка СС первого порядка |
(1, 0, 1)
(0, 1, 1) |
|
B |
1 |
СС первого порядка |
(0, 1, 1) |
|
C |
|
АР первого порядка Некоррелированный шум |
(1, 1, 0) (0, 2, 2) |
|
D |
|
АР первого порядка Некоррелированный шум |
(1, 0, 0) (0, 1, 1) |
|
E |
|
АР второго порядка АР третьего порядка |
(2, 0, 0) (3, 0, 0) |
|
F |
0 |
АР второго порядка |
(2, 0, 0) |
Нужно остановиться на трех других вопросах, связанных с процедурой такой идентификации.
1) Простое взятие разностей, которым мы пользуемся, не дает стационарности в рядах, содержащих сезонные компоненты. В гл. 9 мы обсудим подходящие модификации исследования таких рядов.
2) Как обсуждалось в гл. 4, ненулевое значение ![]() в (6.1.1) указывает
на существование систематического полиномиального тренда степени
в (6.1.1) указывает
на существование систематического полиномиального тренда степени ![]() . Для нестационарных
моделей в табл. 6.4 значение
. Для нестационарных
моделей в табл. 6.4 значение ![]() вполне приемлемо для описания поведения
ряда. Однако иногда могут существовать реальные физические явления, требующие
введения ненулевого
вполне приемлемо для описания поведения
ряда. Однако иногда могут существовать реальные физические явления, требующие
введения ненулевого ![]() . В других случаях может быть неясно,
необходим ли такой член. Некоторые основанные на наблюденных данных указания о
необходимости включения
. В других случаях может быть неясно,
необходим ли такой член. Некоторые основанные на наблюденных данных указания о
необходимости включения ![]() в модель можно получить на этапе
идентификации, сравнивая среднее значение
в модель можно получить на этапе
идентификации, сравнивая среднее значение ![]() ряда
ряда![]() с его приближенной стандартной ошибкой,
найденной по формуле
с его приближенной стандартной ошибкой,
найденной по формуле ![]() .
.
3) В разд. 3.4.2 отмечалось, что для любого процесса
АРСС ![]() с
с ![]() вся положительная
половина автокорреляционной функции будет суперпозицией затухающих
синусоид и экспонент. Это, конечно, не мешает нам пробно идентифицировать
вся положительная
половина автокорреляционной функции будет суперпозицией затухающих
синусоид и экспонент. Это, конечно, не мешает нам пробно идентифицировать ![]() , так как а) частная
автокорреляционная функция примет
, так как а) частная
автокорреляционная функция примет ![]() «аномальных» значений, прежде чем
начнет вести себя как частная автокорреляция процесса СС
«аномальных» значений, прежде чем
начнет вести себя как частная автокорреляция процесса СС![]() ; б)
; б) ![]() должно быть таким, что
автокорреляционная функция могла бы, согласно общему правилу, принимать в
качестве начальных значений величины от
должно быть таким, что
автокорреляционная функция могла бы, согласно общему правилу, принимать в
качестве начальных значений величины от ![]() до
до ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие к русскому изданию
- Предисловие
- План книги
- Глава 1. Введение и краткое содержание
- 1.1. Три важные практические проблемы
- 1.1.1. Прогнозирование временных рядов
- 1.1.2. Оценивание передаточных функций
- 1.1.3. Проектирование дискретных регулирующих систем
- 1.2. Стохастические и детерминированные динамические математические модели
- 1.2.1. Стационарные нестационарные стохастические модели для прогнозирования и регулирования
- 1.2.2. Модели передаточных функций
- 1.2.3. Модели дискретных систем регулирования
- 1.3. Основные понятия в построении моделей
- 1.3.1. Экономия
- 1.3.2. Интерактивные этапы в выборе модели
- Часть 1. Стохастические модели и основанное на них прогнозирование
- Глава 2. Автокорреляционная функция и спектр
- 2.1. Автокорреляционные свойства стационарных моделей
- 2.1.1. Временные ряды и стохастические процессы
- 2.1.2. Стационарные стохастические процессы
- 2.1.3. Положительная определённость и автоковариационная матрица
- 2.1.4. Автоковариационные и автокорреляционные функции
- 2.1.5. Оценивание автоковариационной и автокорреляционной функций
- 2.1.6. Стандартные ошибки оценок автокорреляций
- 2.2. Спектральные свойства стационарных моделей
- 2.2.1. Периодограмма
- 2.2.2. Дисперсионный анализ
- 2.2.3. Спектральная плотность и нормированный спектр
- 2.2.4. Простые примеры автокорреляционных функций и нормированных спектров
- 2.2.5. Преимущества и недостатки автокорреляционных функций и нормированных спектров
- Приложение П2.1. Связь между выборочным спектром и оценкой автоковариационной функции
- Глава 3. Линейные стационарные модели
- 3.1. Общий линейный процесс
- 3.1.1. Две эквивалентные формы линейного процесса
- 3.1.2. Производящая функция автоковариаций линейного процесса
- 3.1.3. Условия стационарности и обратимости линейного процесса
- 3.1.4. Процессы авторегрессии и скользящего среднего
- 3.2. Процессы авторегрессии
- 3.2.1. Условия стационарности для процессов авторегрессии
- 3.2.2. Автокорреляционная функция и спектр процессов авторегрессии
- 3.2.3. Процесс авторегрессии первого порядка (марковский процесс)
- 3.2.4. Процесс авторегрессии второго порядка
- 3.2.5. Частная автокорреляционная функция
- 3.2.6. Оценивание частной автокорреляционной функции
- 3.2.7. Стандартные ошибки частной автокорреляции
- 3.3. Процессы скользящего среднего
- 3.3.1. Условия обратимости для процессов скользящего среднего
- 3.3.2. Автокорреляционная функция и спектр процесса скользящего среднего
- 3.3.3. Процесс скользящего среднего первого порядка
- 3.3.4. Процесс скользящего среднего второго порядка
- 3.3.5. Взаимность процессов авторегрессии и скользящего среднего
- 3.4. Смешанные процессы авторегрессии — скользящего среднего
- 3.4.1. Свойства стационарности и обратимости
- 3.4.2. Автокорреляционная функция и спектр смешанных процессов
- 3.4.3. Процесс авторегрессии первого порядка — скользящего среднего первого порядка
- 3.3.4. Резюме
- Приложение П3.1. Автоковариации.
- Приложение П3.2. Рекурентный метод вычисления оценок параметров авторегрессии
- Глава 4. Линейные нестационарные модели
- 4.1. Процессы авторегрессии — проинтегрированного скользящего среднего
- 4.1.1. Нестационарность процесса авторегрессии первого порядка
- 4.1.2. Общая модель для нестационарного процесса, проявляющего однородность
- 4.1.3. Общий вид процесса авторегрессии – проинтегрированного скользящего среднего
- 4.2. Три формы представления модели авторегрессии – проинтегрированного скользящего среднего
- 4.2.1. Представление модели в виде разности уравнения
- 4.2.2. Представление модели, использующее случайные импульсы
- 4.2.3. Обращенное представление модели
- 4.3. Процессы проинтегрированного скользящего среднего
- 4.3.1. Процесс проинтегрированного скользящего среднего порядка (0,1,1)
- 4.3.2. Процесс проинтегрированного скользящего среднего порядка (0.2.2)
- 4.3.3. Общий процесс проинтегрированного скользящего среднего порядка (0, d, q)
- Приложение П4.1. Линейные разностные уравнения
- Приложение П4.2. Процесс ПСС(0,1,1) с детерминированным дрейфом нуля
- Приложение П4.3. Свойства конечного оператора ссумирования
- Приложение П4.4. Процессы АРПСС с добавленным шумом
- Глава 5. Прогнозирование
- 5.1. Прогнозы с минимальной среднеквадратичной ошибкой и их свойства
- 5.1.1. Вывод формулы для прогнозов с минимальной среднеквадратичной ошибкой
- 5.1.2. Три основных представления прогноза
- 5.2. Вычисление и подправление прогноза
- 5.2.1. Удобная схема для вычисления прогнозов
- 5.2.2. Вычисление весов
- 5.2.3. Использование весов при подправлении прогнозов
- 5.2.4. Вычисление вероятностных пределов прогнозов при произвольном упреждении
- 5.3. Прогнозирующая функция и веса прогноза
- 5.3.1. Эвентуальная прогнозирующая функция, определенная оператором авторегрессии
- 5.3.2. Роль оператора скользящего среднего в определении начальных величин
- 5.3.3. Веса прогноза для упреждения l
- 5.4. Примеры прогнозирующих функций и их подправления
- 5.4.1. Прогнозирование процесса ПСС(0, 1, 1)
- 5.4.2. Прогнозирование процесса ПСС(0, 2, 2)
- 5.4.3. Прогнозирование общего процесса ПСС(0, d, q)
- 5.4.4. Прогнозирование процессов авторегрессии
- 5.4.5. Прогнозирование процесса (1, 0, 1)
- 5.4.6. Прогнозирование процесса (1,1,1)
- 5.5. Резюме
- Приложение П5.1. Корреляция между ошибками прогноза
- Приложение П5.2. Веса прогноза для произвольного упреждения
- Приложение П5.3. Прогнозирование при помощи общего проинтегрированного представления
- Часть II. Построение стохастических моделей
- Глава 6. Идентификация моделей
- 6.1. Цели идентификации
- 6.1.1. Этапы процедуры идентификации
- 6.2. Методика идентификации
- 6.2.1. Использование при идентификаций автокорреляционной и частной автокорреляционной функций
- 6.2.2. Стандартные ошибки выборочных автокорреляций и частных автокорреляций
- 6.2.3. Идентификация некоторых реальных временных рядов
- 6.3. Начальные оценки параметров
- 6.3.1. Единственность оценок, получаемых по автоковариационной функции
- 6.3.2. Начальные оценки для процессов скользящего среднего
- 6.3.3. Начальные оценки для процессов авторегрессии
- 6.3.4. Начальные оценки для смешанных процессов авторегрессии — скользящего среднего
- 6.3.5. Выбор между стационарными и нестационарными моделями в спорных случаях
- 6.3.6. Начальные оценки остаточной дисперсии
- 6.3.7. Приближенная стандартная ошибка для
- 6.4. Многозначность моделей
- 6.4.1. Многозначность моделей авторегрессии — скользящего среднего
- 6.4.2. Многозначные решения при оценке параметров скользящего среднего методом моментов
- 6.4.3. Использование возвратного процесса для определения начальных значений
- Приложение П6.1. Среднее значение выборочной автокорреляционной функции нестационарного процесса
- Приложение П6.2. Общий метод получения начальных оценок параметров смешанного процесса авторегрессии – скользящего среднего
- Приложение П6.3. Прямой и возратный процессы ПСС порядка (0, 1, 1)
- Глава 7. Оценивание модели
- 7.1. Исследование функций правдоподобия и суммы квадратов
- 7.1.1. Функция правдоподобия
- 7.1.2. Условное правдоподобие для процесса АРПСС
- 7.1.3. Выбор начальных значений для вычисления условного правдоподобия
- 7.1.4. Безусловное правдоподобие; сумма квадратов; оценки наименьших квадратов
- 7.1.5. Общий способ вычисления безусловной суммы квадратов
- 7.1.6. Графическое исследование суммы квадратов
- 7.1.7. Описание «благоприятных» оценочных ситуаций; доверительные области
- 7.2. Нелинейное оценивание
- 7.2.2. Численный метод нахождения производных
- 7.2.3. Прямой метод нахождения производных
- 7.2.4. Общий алгоритм наименьших квадратов для условной модели
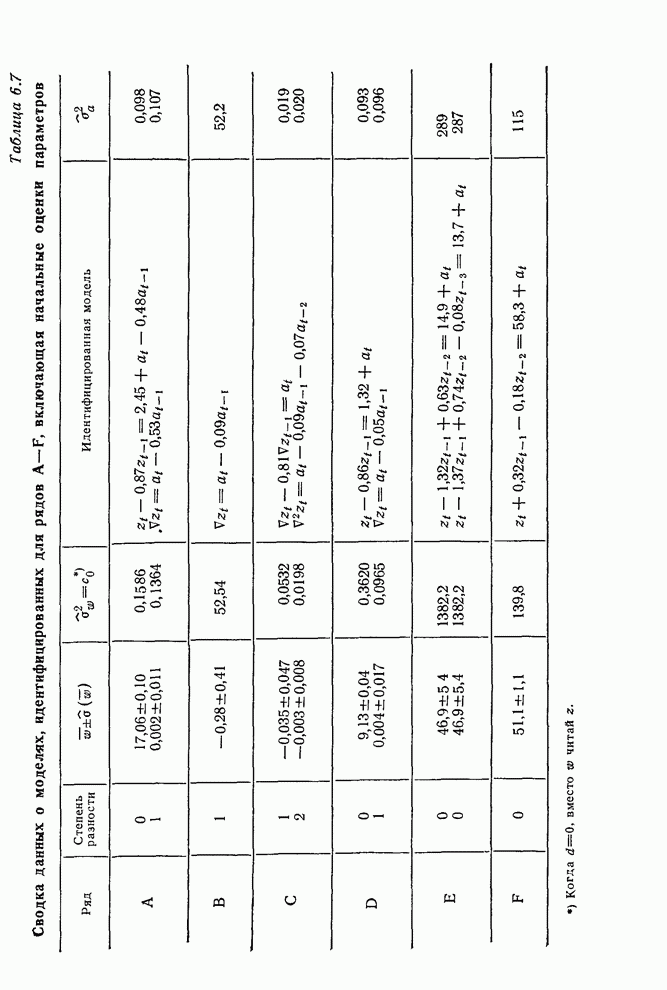
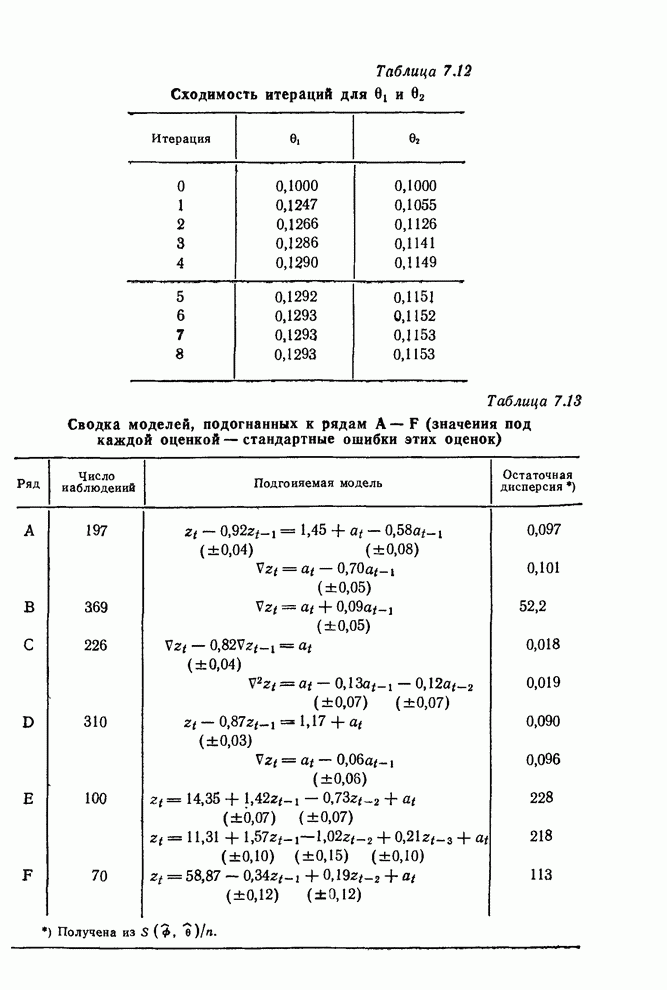
- 7.2.5. Сводка моделей, подогнанных к рядам A-F
- 7.2.6. Информационные матрицы при больших выборках и оценки ковариаций
- 7.3. Результаты оценивания для некоторых частных моделей
- 7.З.2. Процессы скользящего среднего
- 7.3.3. Смешанные процессы
- 7.3.4. Разделение линейных и нелинейных компонент при оценивании
- 7.3.5. Избыточность параметров
- 7.4. Оценивание при помощи теоремы Байеса
- 7.4.2. Байесовское оценивание параметров
- 7.4.3. Процессы авторегрессии
- 7.4.4. Процессы скользящего среднего
- 7.4.5. Смешанные процессы
- Приложение П7.1. Обзор теории нормального распределения
- Приложение П7.2. Обзор линейной теории наименьших квадратов
- Приложение П7.3. Примеры влияния ошибок оценивания параметров на вероятностные пределы прогнозов
- Приложение П7.4. Точная функция правдоподобия для процесса скользящего среднего
- Приложение П7.5. Точная функция правдоподобия для процесса авторегрессии
- Глава 8. Диагностическая проверка модели
- 8.1. Проверка стохастических моделей
- 8.1.2. Введение избыточных параметров
- 8.2.1. Проверка при помощи автокорреляций
- 8.2.2. Совокупный критерий согласия
- 8.2.3. Неадекватность модели, возникающая из-за изменения значений параметров
- 8.2.4. Проверка при помощи кумулятивной периодограммы
- 8.3. Использование остаточных ошибок для изменения модели
- 8.3.1. Природа корреляций остаточных ошибок при использовании неверной модели
- 8.3.2. Использование остаточных ошибок для изменения модели
- Глава 9. Модели сезонных рядов
- 9.1. Экономические модели сезонных временных рядов
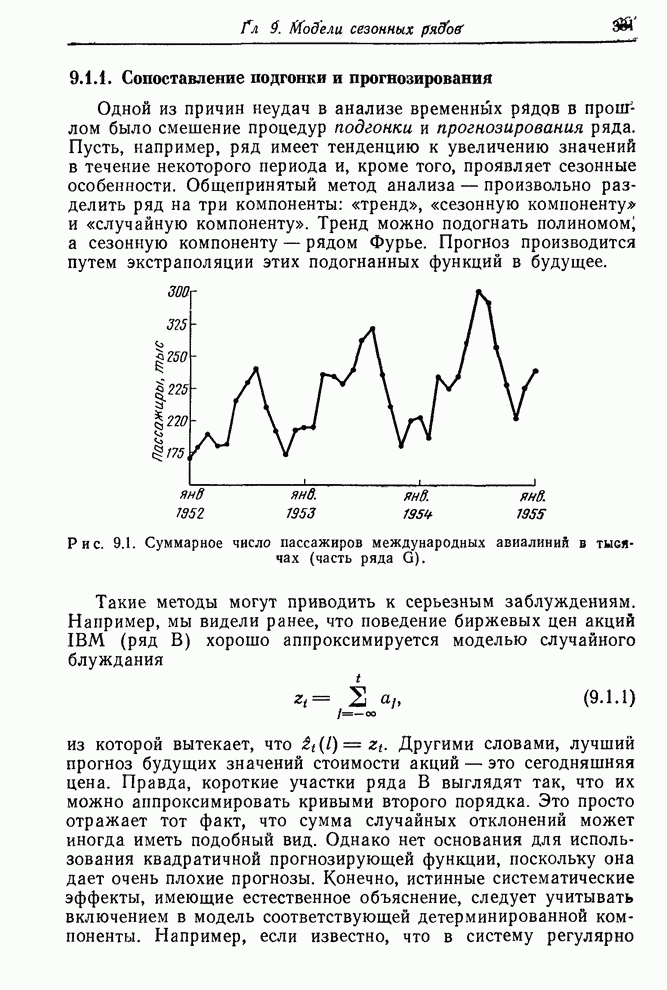
- 9.1.1. Сопоставление подгонки и прогнозирования
- 9.1.2. Сезонные модели, включающие подстраивающиеся синусоиды и косинусоиды
- 9.1.3. Общая мультипликативная модель сезонного ряда
- 9.2. Представление данных об авиаперевозках мультипликативной моделью
- 9.2.1. Мультипликативная модель
- 9.2.2. Прогнозирование
- 9.2.3. Идентификация
- 9.2.4. Оценивание
- 9.2.5. Диагностическая проверка
- 9.3. Некоторые аспекты более общих моделей сезонных рядов
- 9.3.1. Мультипликативные и немультипликативные модели
- 9.3.2. Идентификация
- 9.3.3. Оценивание
- 9.3.4. Эвентуальные прогнозирующие функции для различных моделей сезонных рядов
- Вспомогательные материалы
- Программа 1 Идентификация стохастической модели
- Программа 2 Предварительное оценивание стохастической модели
- Программа 3. Оценивание стохастической модели
- Алгоритм марквардта для нелинейного метода наименьших квадратов
- Программа 4. Прогнозирование с помощью стохастической модели
- Сборник таблиц и диаграмм