| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
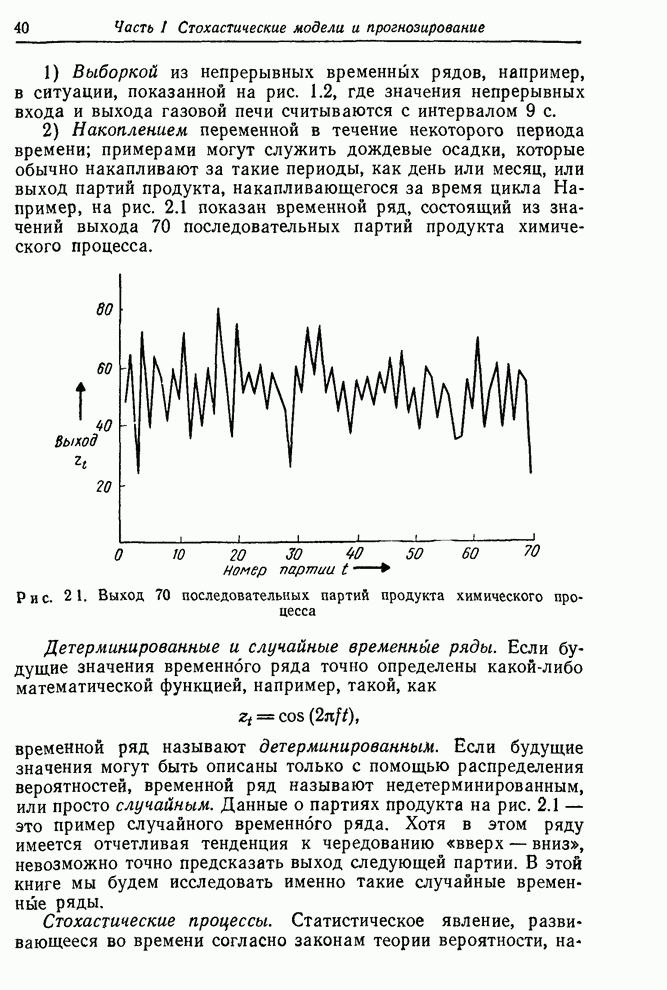
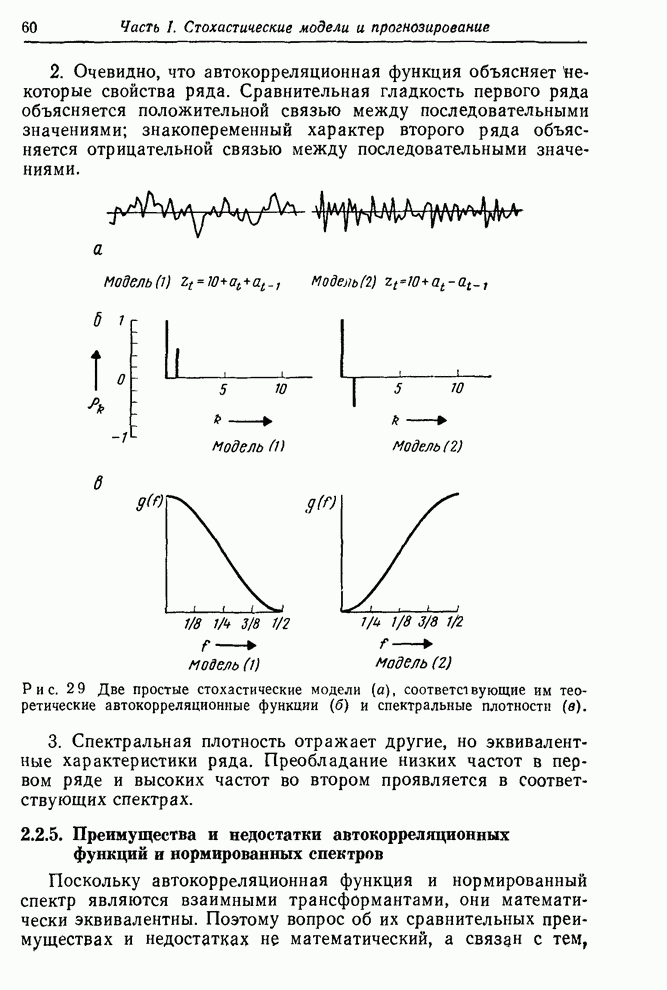
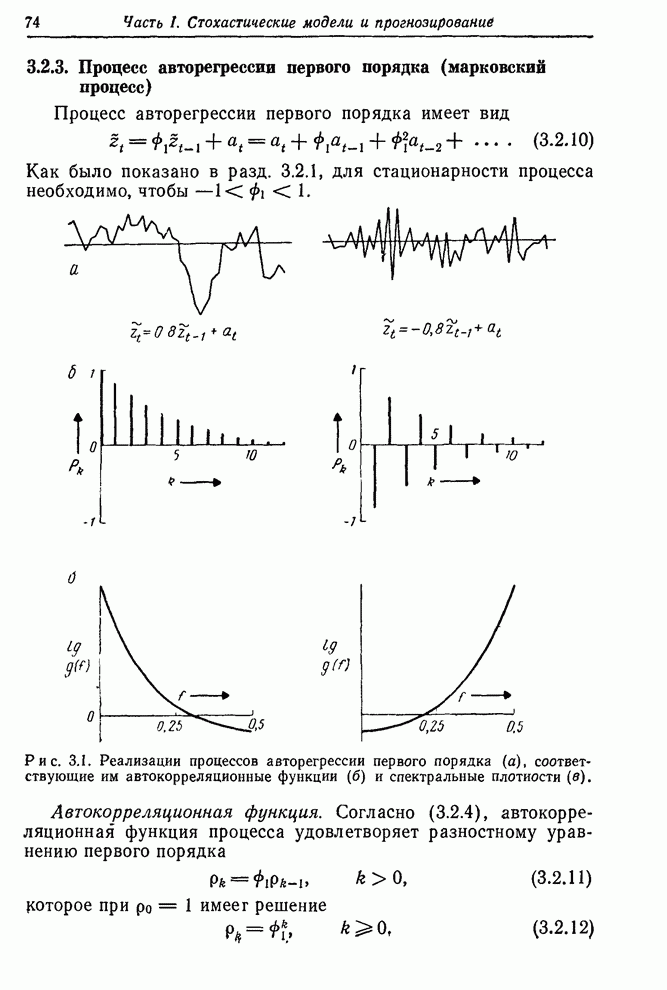
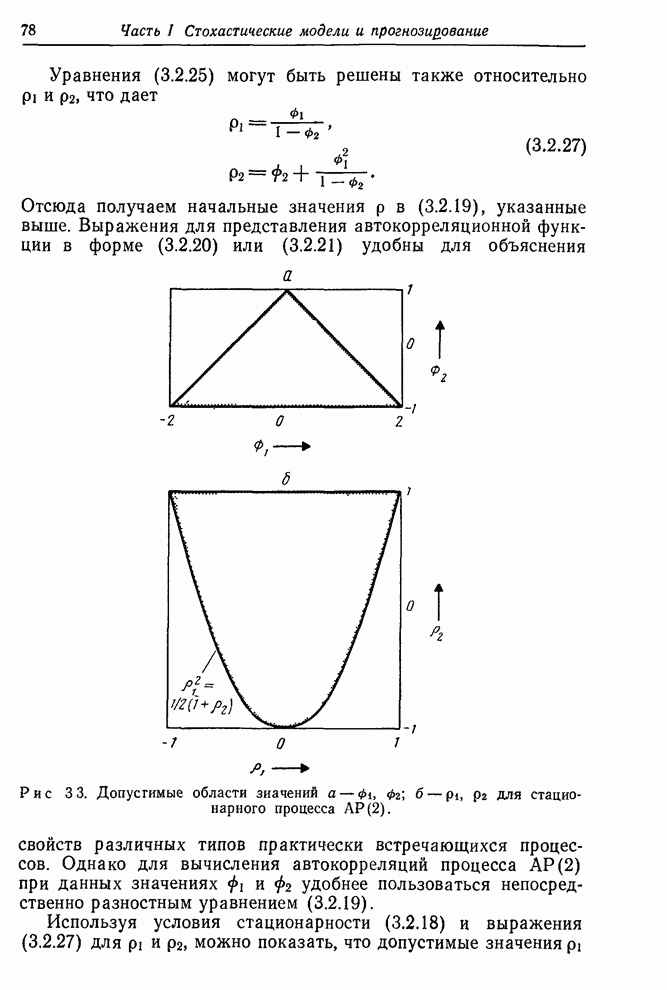
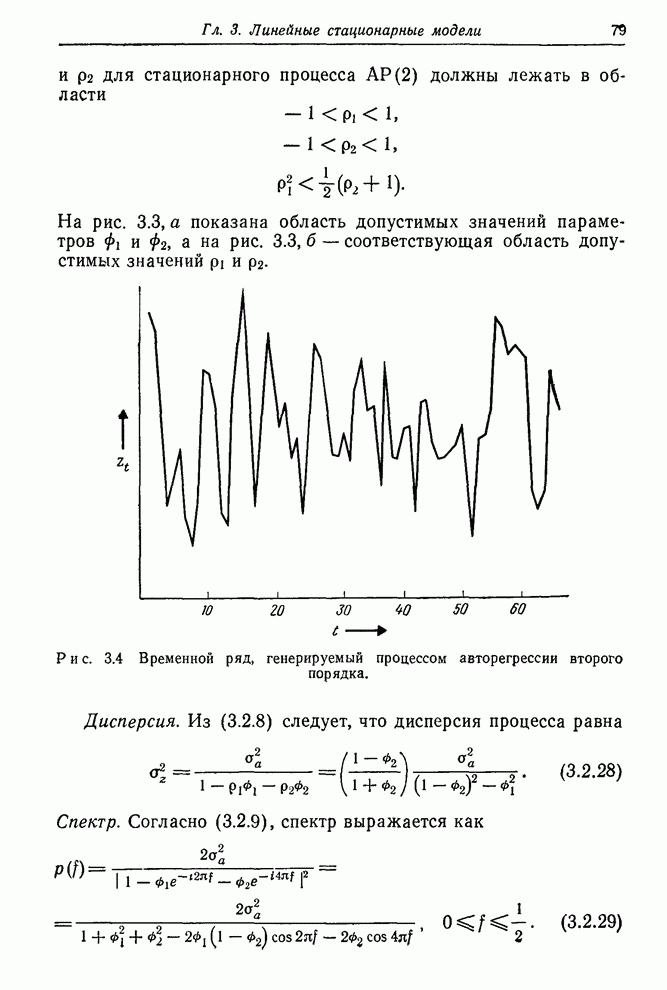
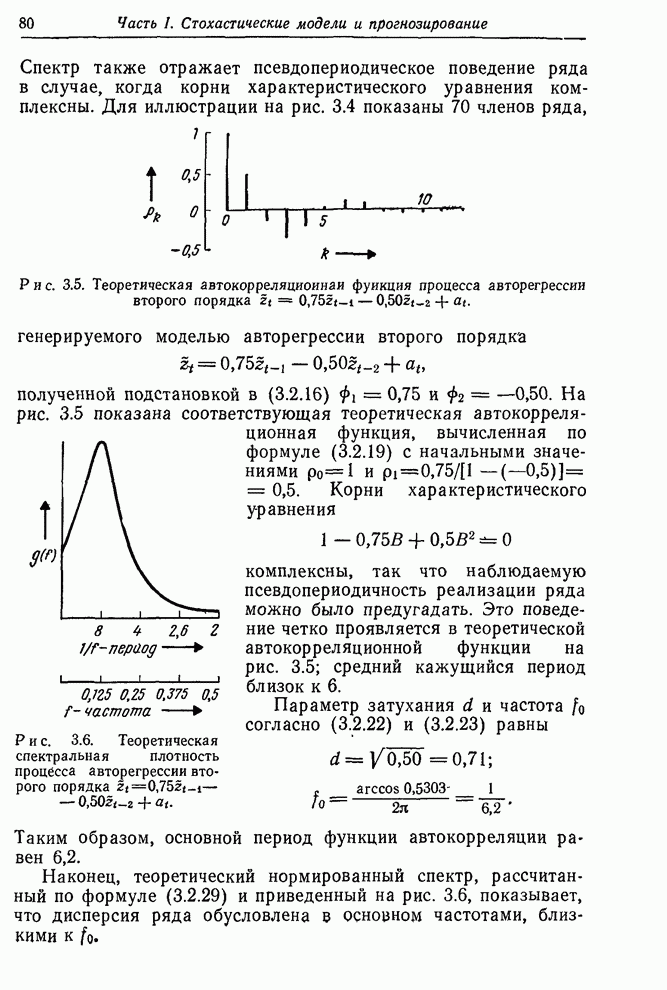
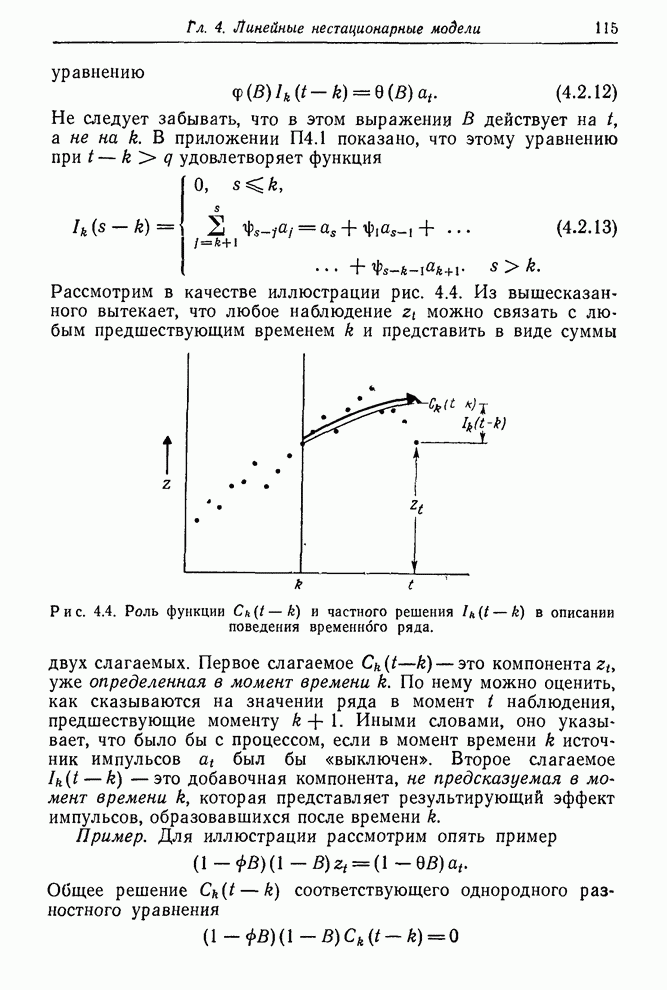
3.4.3 Процесс авторегрессии первого порядка - скользящего среднего первого порядка
Важный для практики смешанный процесс авторегрессии первого порядка – скользящего среднего первого порядка АРСС(1,1) описывается формулой
![]() (3.4.6)
(3.4.6)
или, что равносильно,
![]() .
.
Выведем некоторые важнейшие свойство этого процесса.
Условия
стационарности и обратимости. Прежде всего, заметим, что процесс
стационарен, если ![]() ,
и обратим, если
,
и обратим, если ![]() .
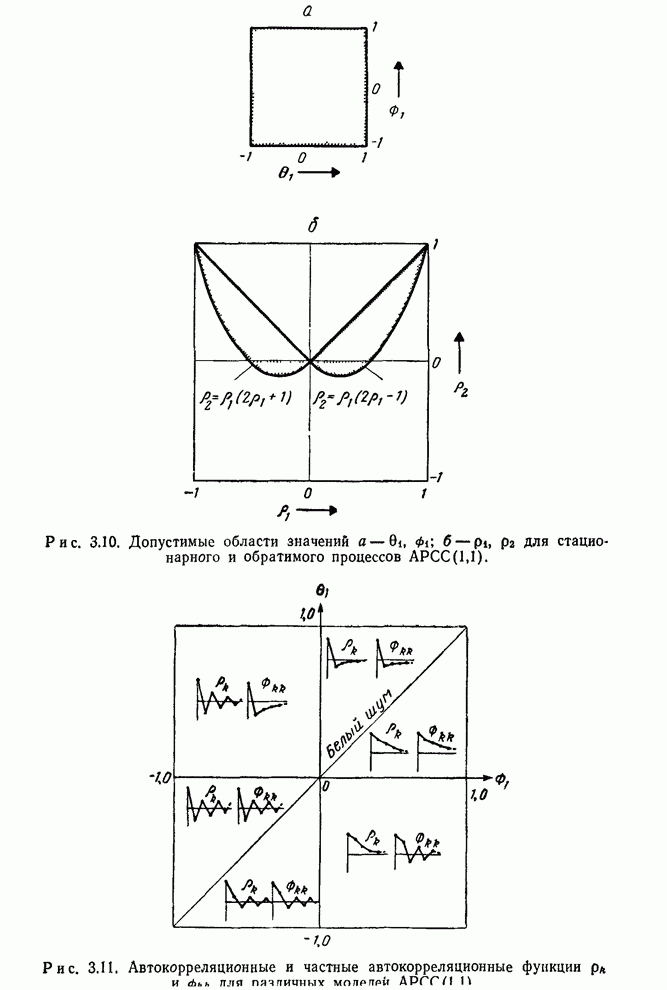
Обусловленная этим область допустимых значений параметров показана на рис.
3.10, а.
.
Обусловленная этим область допустимых значений параметров показана на рис.
3.10, а.
Автокорреляционная функция. Из (3.4.2) и (3.4.4) мы получаем

Умножив все члены (3.4.6) на ![]() и переходя к
математическим ожиданиям, получим
и переходя к
математическим ожиданиям, получим
![]() .
.
Отсюда автоковариационная функция процесса равна
 (3.4.7)
(3.4.7)
Отсюда следует, что автокорреляционная
функция экспоненциально убывает от начального значения ![]() , зависящего от
, зависящего от ![]() и
и ![]() . Как показано на
рис. 3.11, это затухание монотонное, если
. Как показано на
рис. 3.11, это затухание монотонное, если ![]() положительно, и
колебательное, если
положительно, и
колебательное, если ![]() отрицательно. Далее, знак
отрицательно. Далее, знак ![]() определяется знаком
определяется знаком ![]() и указывает,
происходит ли затухание в области положительных или отрицательных значений.
и указывает,
происходит ли затухание в области положительных или отрицательных значений.
Пользуясь (3.4.7), можно выразить две первые автокорреляции через параметры процесса, а именно
 (3.4.8)
(3.4.8)
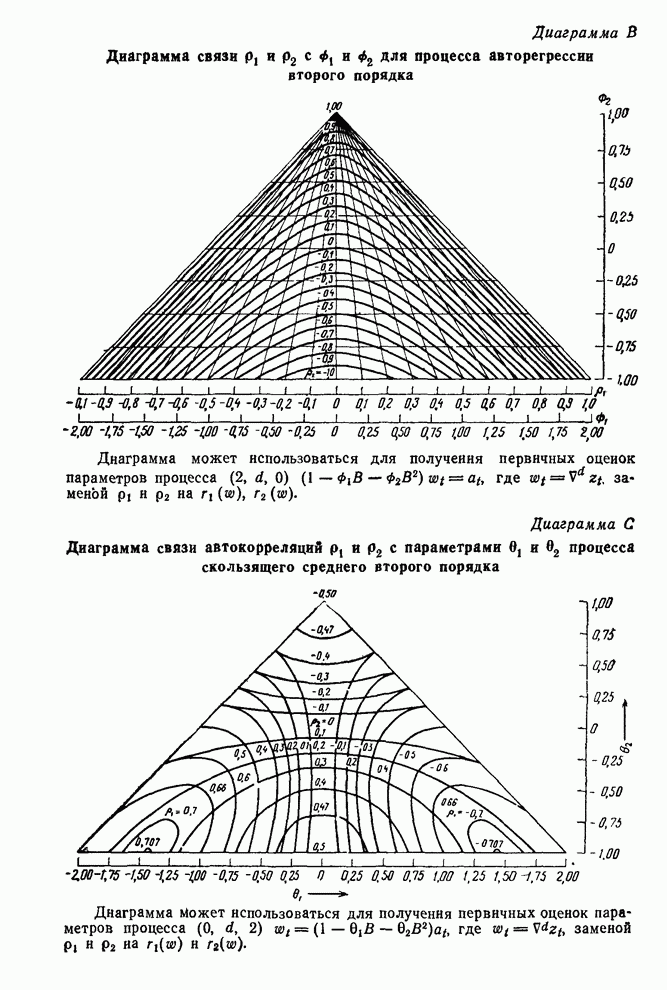
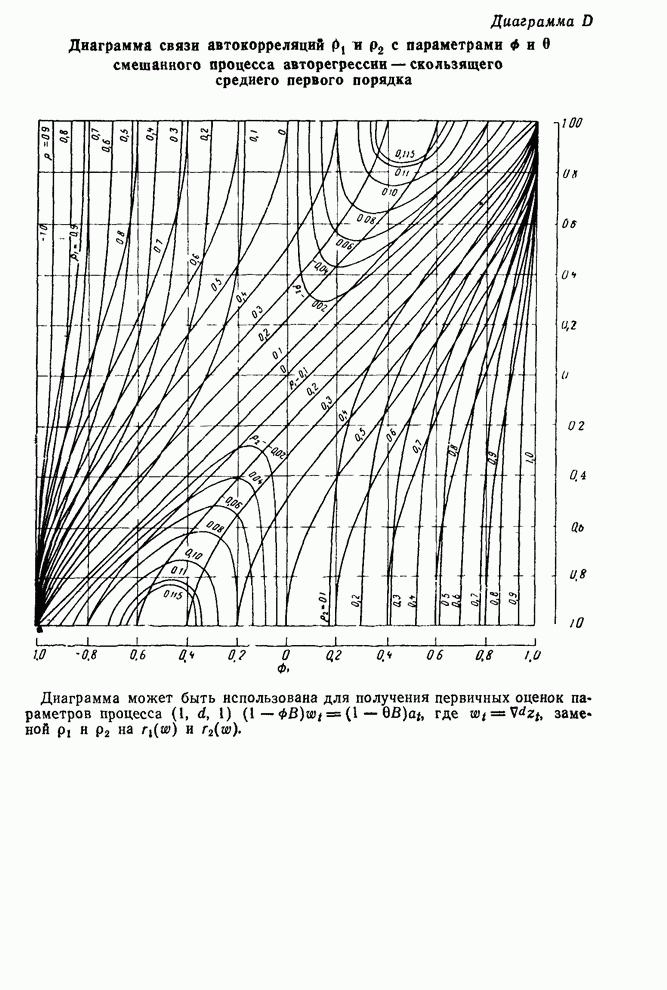
Диаграмма D в конце книги
построена так, что позволяет находить решения уравнений (3.4.8) для ![]() и
и ![]() по заданным
по заданным ![]() и
и ![]() . Использую оценки
. Использую оценки ![]() и
и ![]() вместо
вместо ![]() и
и ![]() можно получить,
таким образом, исходные выборочные оценки параметров
можно получить,
таким образом, исходные выборочные оценки параметров ![]() и
и![]() .
.
Из (3.4.8) и
условий стационарности и обратимости вытекает, что ![]() и
и ![]() должны лежать в области
должны лежать в области
 (3.4.9)
(3.4.9)

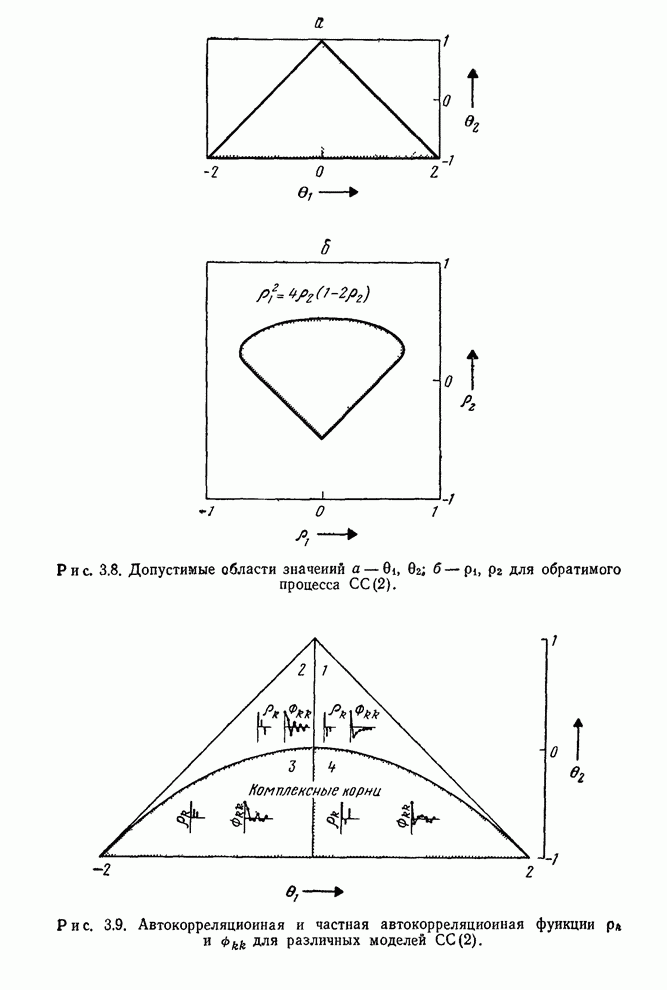
Рис. 3.10. Допустимые области значений
а-![]() ,
,![]() ;б-
;б-![]() для стационарного и
обратимого процессов АРСС(1,1).
для стационарного и
обратимого процессов АРСС(1,1).

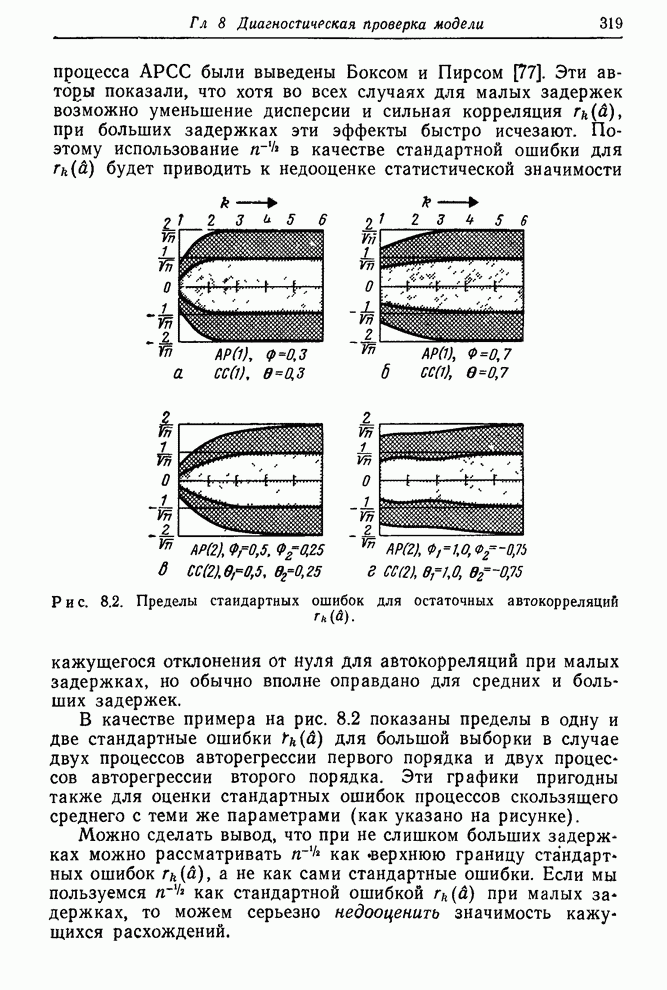
Рис. 3.11. Автокорреляционные и частные
автокорреляционные функции ![]() или
или ![]() для различных моделей АРСС(1,1).
для различных моделей АРСС(1,1).
Область
допустимых значений ![]() и
и ![]() на рис. 3.10,б, она ограничивает
диапазон допустимых комбинаций
на рис. 3.10,б, она ограничивает
диапазон допустимых комбинаций ![]() и
и ![]() для стационарного обратимого процесса
АРСС(1,1).
для стационарного обратимого процесса
АРСС(1,1).
Частная автокорреляционная
функция. Частная
автокорреляционная функция смешанного процесса АРСС(1,1), описываемого (3 4 6),
состоит только из одного начального значения ![]() . Поэтому она ведет себя подобно функции
частной автокорреляции чистого процесса СС(1), и в ней преобладает затухающий
экспоненциальный член. Как показано на рис. 3.11, при положительном
. Поэтому она ведет себя подобно функции
частной автокорреляции чистого процесса СС(1), и в ней преобладает затухающий
экспоненциальный член. Как показано на рис. 3.11, при положительном ![]() она монотонно
затухает от значения
она монотонно
затухает от значения ![]() , знак которого совпадает со знаком
, знак которого совпадает со знаком ![]() . При отрицательном
. При отрицательном ![]() в ней преобладает
экспоненциально затухающий осциллирующий член, амплитуда которого убывает от
значения
в ней преобладает
экспоненциально затухающий осциллирующий член, амплитуда которого убывает от
значения ![]() .
Знак
.
Знак ![]() определяется
знаком
определяется
знаком ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие к русскому изданию
- Предисловие
- План книги
- Глава 1. Введение и краткое содержание
- 1.1. Три важные практические проблемы
- 1.1.1. Прогнозирование временных рядов
- 1.1.2. Оценивание передаточных функций
- 1.1.3. Проектирование дискретных регулирующих систем
- 1.2. Стохастические и детерминированные динамические математические модели
- 1.2.1. Стационарные нестационарные стохастические модели для прогнозирования и регулирования
- 1.2.2. Модели передаточных функций
- 1.2.3. Модели дискретных систем регулирования
- 1.3. Основные понятия в построении моделей
- 1.3.1. Экономия
- 1.3.2. Интерактивные этапы в выборе модели
- Часть 1. Стохастические модели и основанное на них прогнозирование
- Глава 2. Автокорреляционная функция и спектр
- 2.1. Автокорреляционные свойства стационарных моделей
- 2.1.1. Временные ряды и стохастические процессы
- 2.1.2. Стационарные стохастические процессы
- 2.1.3. Положительная определённость и автоковариационная матрица
- 2.1.4. Автоковариационные и автокорреляционные функции
- 2.1.5. Оценивание автоковариационной и автокорреляционной функций
- 2.1.6. Стандартные ошибки оценок автокорреляций
- 2.2. Спектральные свойства стационарных моделей
- 2.2.1. Периодограмма
- 2.2.2. Дисперсионный анализ
- 2.2.3. Спектральная плотность и нормированный спектр
- 2.2.4. Простые примеры автокорреляционных функций и нормированных спектров
- 2.2.5. Преимущества и недостатки автокорреляционных функций и нормированных спектров
- Приложение П2.1. Связь между выборочным спектром и оценкой автоковариационной функции
- Глава 3. Линейные стационарные модели
- 3.1. Общий линейный процесс
- 3.1.1. Две эквивалентные формы линейного процесса
- 3.1.2. Производящая функция автоковариаций линейного процесса
- 3.1.3. Условия стационарности и обратимости линейного процесса
- 3.1.4. Процессы авторегрессии и скользящего среднего
- 3.2. Процессы авторегрессии
- 3.2.1. Условия стационарности для процессов авторегрессии
- 3.2.2. Автокорреляционная функция и спектр процессов авторегрессии
- 3.2.3. Процесс авторегрессии первого порядка (марковский процесс)
- 3.2.4. Процесс авторегрессии второго порядка
- 3.2.5. Частная автокорреляционная функция
- 3.2.6. Оценивание частной автокорреляционной функции
- 3.2.7. Стандартные ошибки частной автокорреляции
- 3.3. Процессы скользящего среднего
- 3.3.1. Условия обратимости для процессов скользящего среднего
- 3.3.2. Автокорреляционная функция и спектр процесса скользящего среднего
- 3.3.3. Процесс скользящего среднего первого порядка
- 3.3.4. Процесс скользящего среднего второго порядка
- 3.3.5. Взаимность процессов авторегрессии и скользящего среднего
- 3.4. Смешанные процессы авторегрессии — скользящего среднего
- 3.4.1. Свойства стационарности и обратимости
- 3.4.2. Автокорреляционная функция и спектр смешанных процессов
- 3.4.3. Процесс авторегрессии первого порядка — скользящего среднего первого порядка
- 3.3.4. Резюме
- Приложение П3.1. Автоковариации.
- Приложение П3.2. Рекурентный метод вычисления оценок параметров авторегрессии
- Глава 4. Линейные нестационарные модели
- 4.1. Процессы авторегрессии — проинтегрированного скользящего среднего
- 4.1.1. Нестационарность процесса авторегрессии первого порядка
- 4.1.2. Общая модель для нестационарного процесса, проявляющего однородность
- 4.1.3. Общий вид процесса авторегрессии – проинтегрированного скользящего среднего
- 4.2. Три формы представления модели авторегрессии – проинтегрированного скользящего среднего
- 4.2.1. Представление модели в виде разности уравнения
- 4.2.2. Представление модели, использующее случайные импульсы
- 4.2.3. Обращенное представление модели
- 4.3. Процессы проинтегрированного скользящего среднего
- 4.3.1. Процесс проинтегрированного скользящего среднего порядка (0,1,1)
- 4.3.2. Процесс проинтегрированного скользящего среднего порядка (0.2.2)
- 4.3.3. Общий процесс проинтегрированного скользящего среднего порядка (0, d, q)
- Приложение П4.1. Линейные разностные уравнения
- Приложение П4.2. Процесс ПСС(0,1,1) с детерминированным дрейфом нуля
- Приложение П4.3. Свойства конечного оператора ссумирования
- Приложение П4.4. Процессы АРПСС с добавленным шумом
- Глава 5. Прогнозирование
- 5.1. Прогнозы с минимальной среднеквадратичной ошибкой и их свойства
- 5.1.1. Вывод формулы для прогнозов с минимальной среднеквадратичной ошибкой
- 5.1.2. Три основных представления прогноза
- 5.2. Вычисление и подправление прогноза
- 5.2.1. Удобная схема для вычисления прогнозов
- 5.2.2. Вычисление весов
- 5.2.3. Использование весов при подправлении прогнозов
- 5.2.4. Вычисление вероятностных пределов прогнозов при произвольном упреждении
- 5.3. Прогнозирующая функция и веса прогноза
- 5.3.1. Эвентуальная прогнозирующая функция, определенная оператором авторегрессии
- 5.3.2. Роль оператора скользящего среднего в определении начальных величин
- 5.3.3. Веса прогноза для упреждения l
- 5.4. Примеры прогнозирующих функций и их подправления
- 5.4.1. Прогнозирование процесса ПСС(0, 1, 1)
- 5.4.2. Прогнозирование процесса ПСС(0, 2, 2)
- 5.4.3. Прогнозирование общего процесса ПСС(0, d, q)
- 5.4.4. Прогнозирование процессов авторегрессии
- 5.4.5. Прогнозирование процесса (1, 0, 1)
- 5.4.6. Прогнозирование процесса (1,1,1)
- 5.5. Резюме
- Приложение П5.1. Корреляция между ошибками прогноза
- Приложение П5.2. Веса прогноза для произвольного упреждения
- Приложение П5.3. Прогнозирование при помощи общего проинтегрированного представления
- Часть II. Построение стохастических моделей
- Глава 6. Идентификация моделей
- 6.1. Цели идентификации
- 6.1.1. Этапы процедуры идентификации
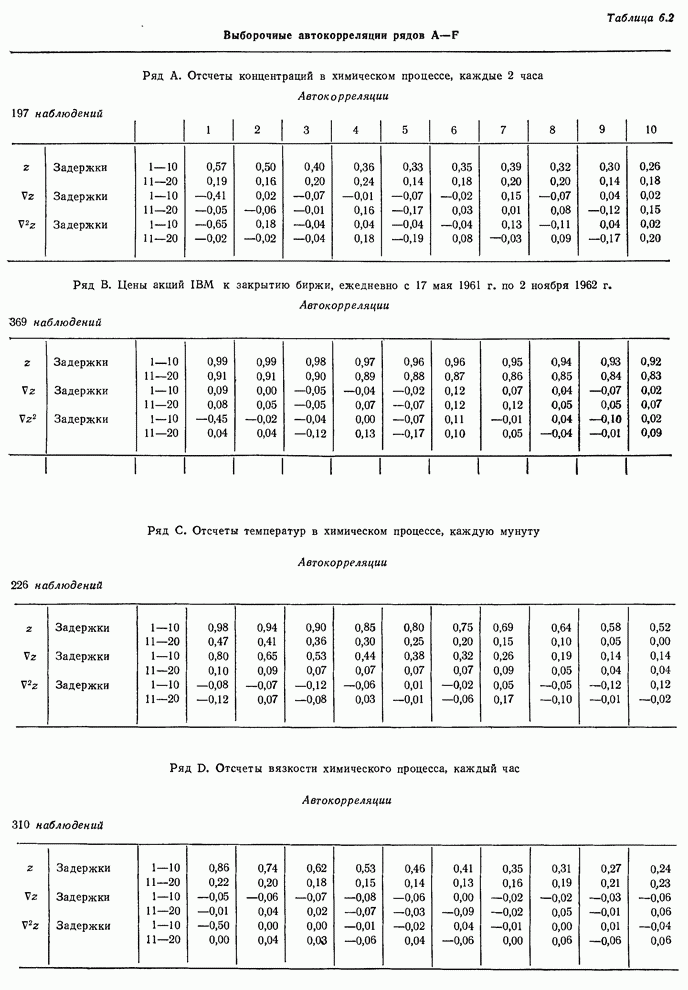
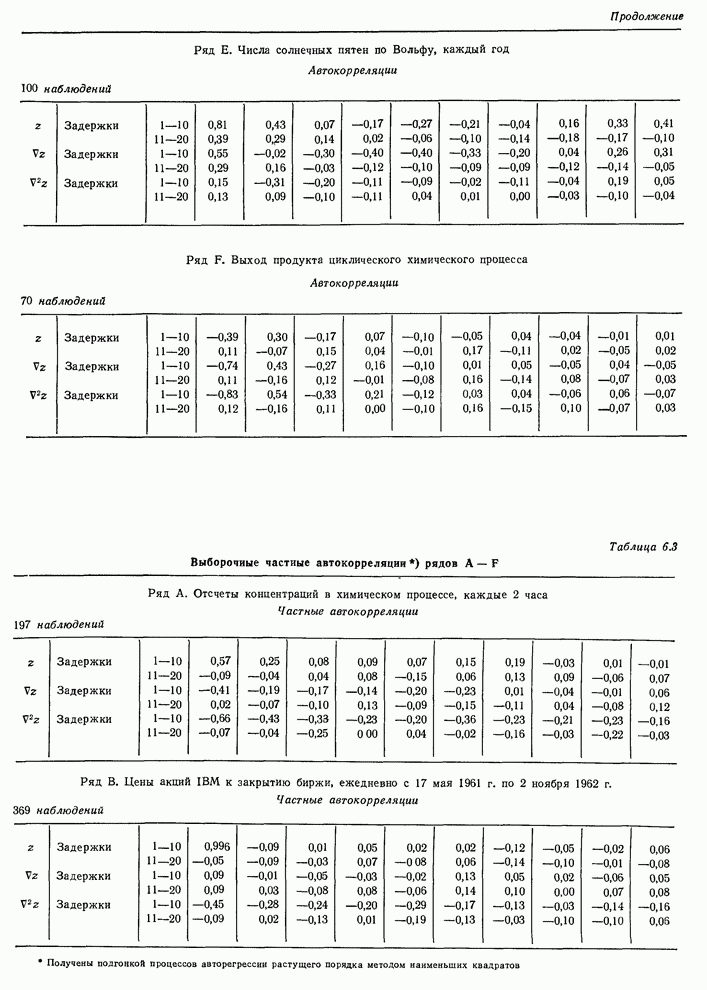
- 6.2. Методика идентификации
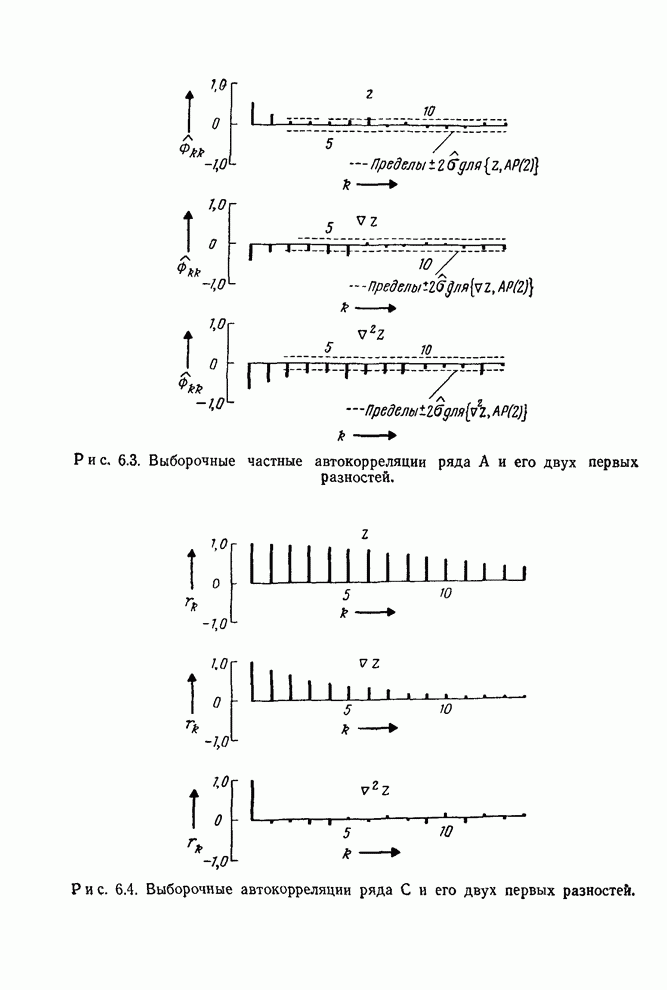
- 6.2.1. Использование при идентификаций автокорреляционной и частной автокорреляционной функций
- 6.2.2. Стандартные ошибки выборочных автокорреляций и частных автокорреляций
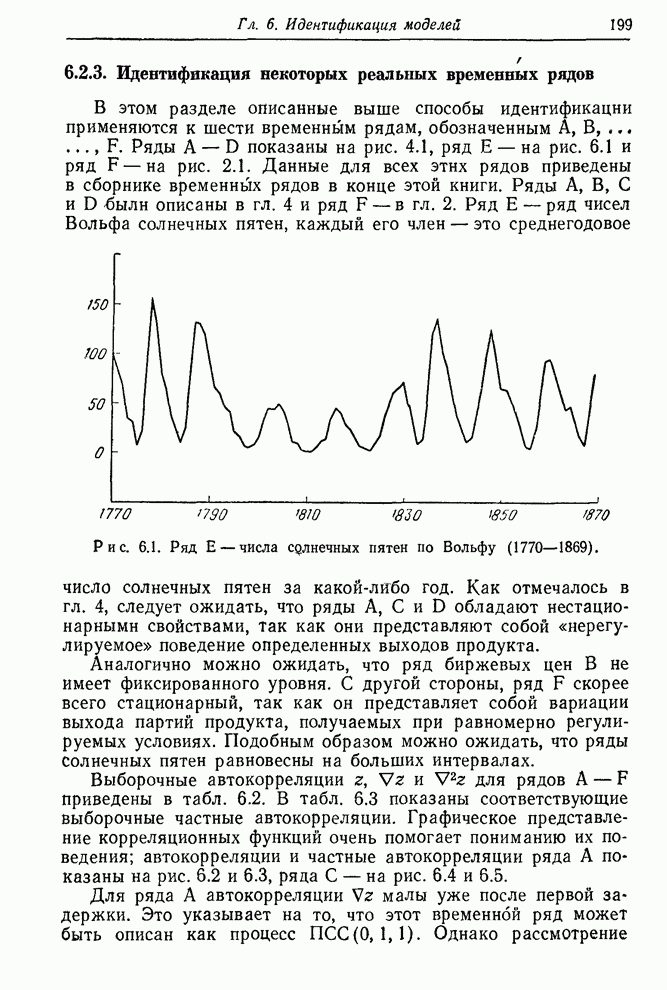
- 6.2.3. Идентификация некоторых реальных временных рядов
- 6.3. Начальные оценки параметров
- 6.3.1. Единственность оценок, получаемых по автоковариационной функции
- 6.3.2. Начальные оценки для процессов скользящего среднего
- 6.3.3. Начальные оценки для процессов авторегрессии
- 6.3.4. Начальные оценки для смешанных процессов авторегрессии — скользящего среднего
- 6.3.5. Выбор между стационарными и нестационарными моделями в спорных случаях
- 6.3.6. Начальные оценки остаточной дисперсии
- 6.3.7. Приближенная стандартная ошибка для
- 6.4. Многозначность моделей
- 6.4.1. Многозначность моделей авторегрессии — скользящего среднего
- 6.4.2. Многозначные решения при оценке параметров скользящего среднего методом моментов
- 6.4.3. Использование возвратного процесса для определения начальных значений
- Приложение П6.1. Среднее значение выборочной автокорреляционной функции нестационарного процесса
- Приложение П6.2. Общий метод получения начальных оценок параметров смешанного процесса авторегрессии – скользящего среднего
- Приложение П6.3. Прямой и возратный процессы ПСС порядка (0, 1, 1)
- Глава 7. Оценивание модели
- 7.1. Исследование функций правдоподобия и суммы квадратов
- 7.1.1. Функция правдоподобия
- 7.1.2. Условное правдоподобие для процесса АРПСС
- 7.1.3. Выбор начальных значений для вычисления условного правдоподобия
- 7.1.4. Безусловное правдоподобие; сумма квадратов; оценки наименьших квадратов
- 7.1.5. Общий способ вычисления безусловной суммы квадратов
- 7.1.6. Графическое исследование суммы квадратов
- 7.1.7. Описание «благоприятных» оценочных ситуаций; доверительные области
- 7.2. Нелинейное оценивание
- 7.2.2. Численный метод нахождения производных
- 7.2.3. Прямой метод нахождения производных
- 7.2.4. Общий алгоритм наименьших квадратов для условной модели
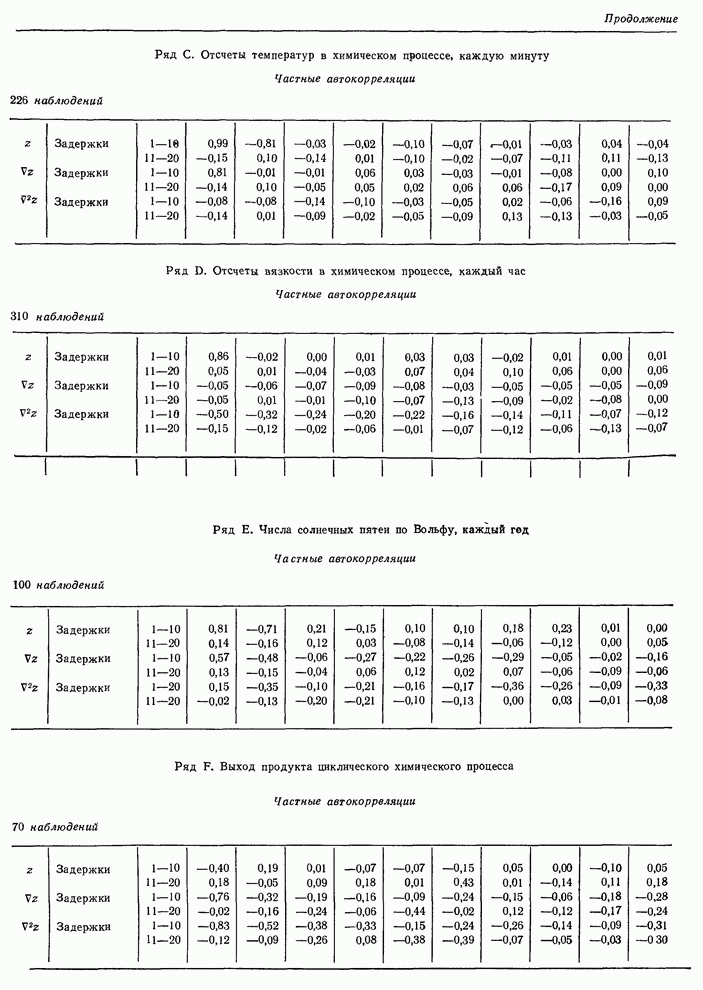
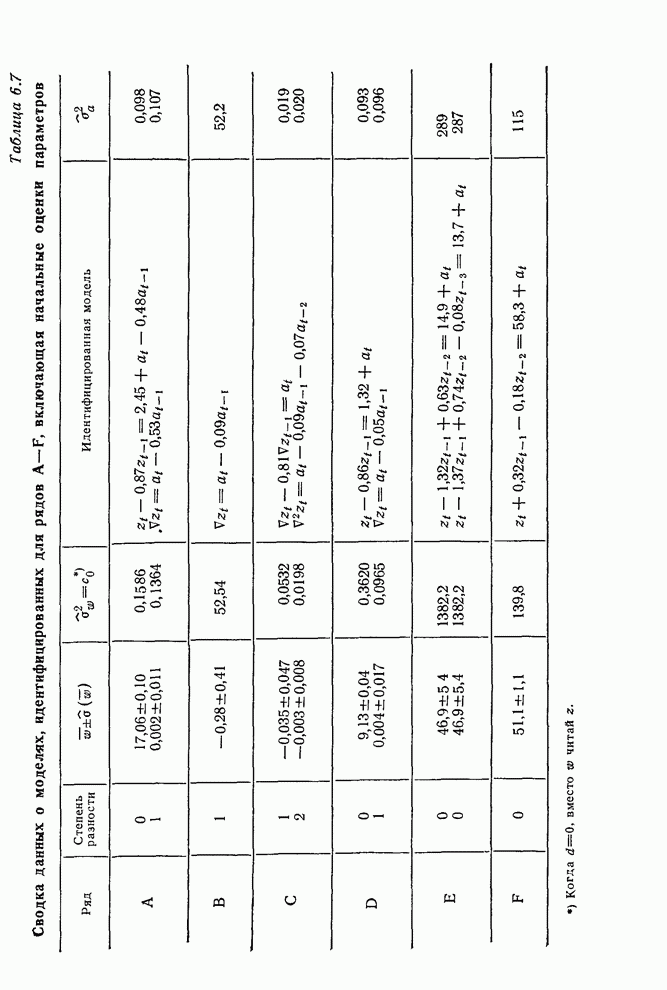
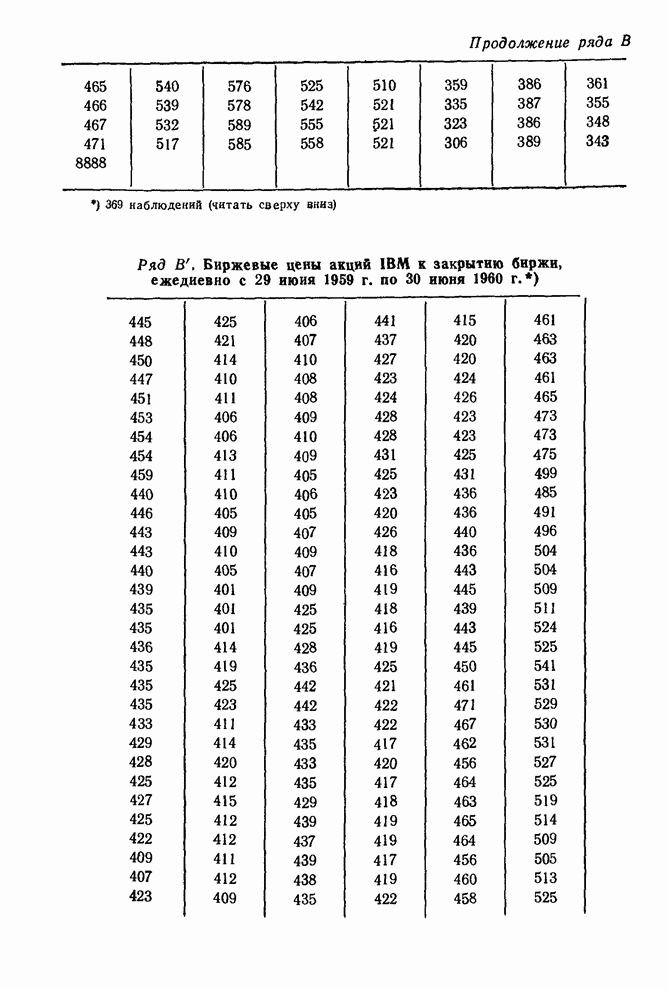
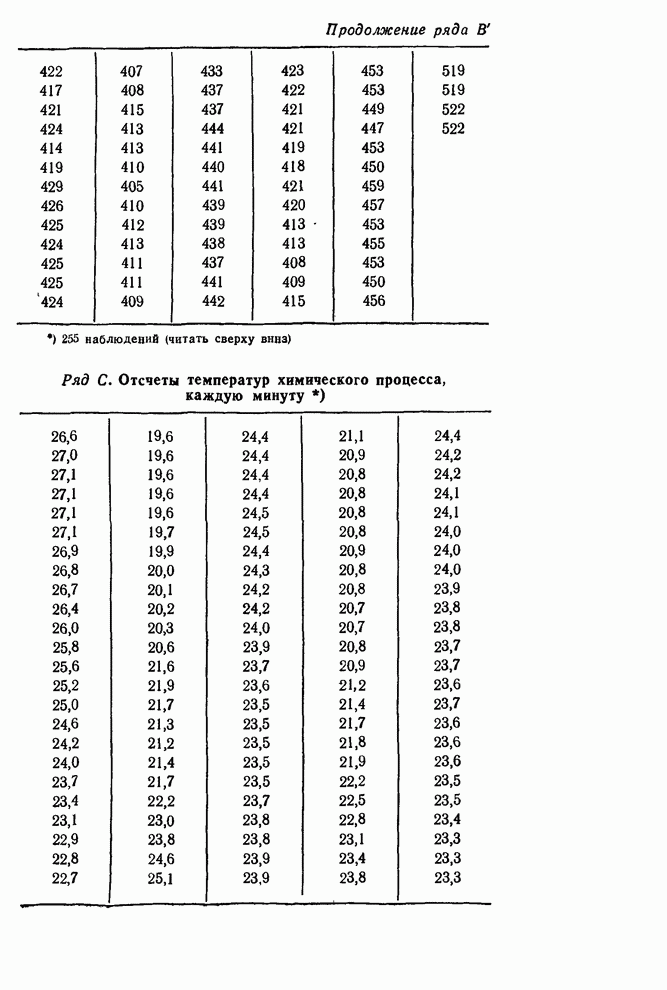
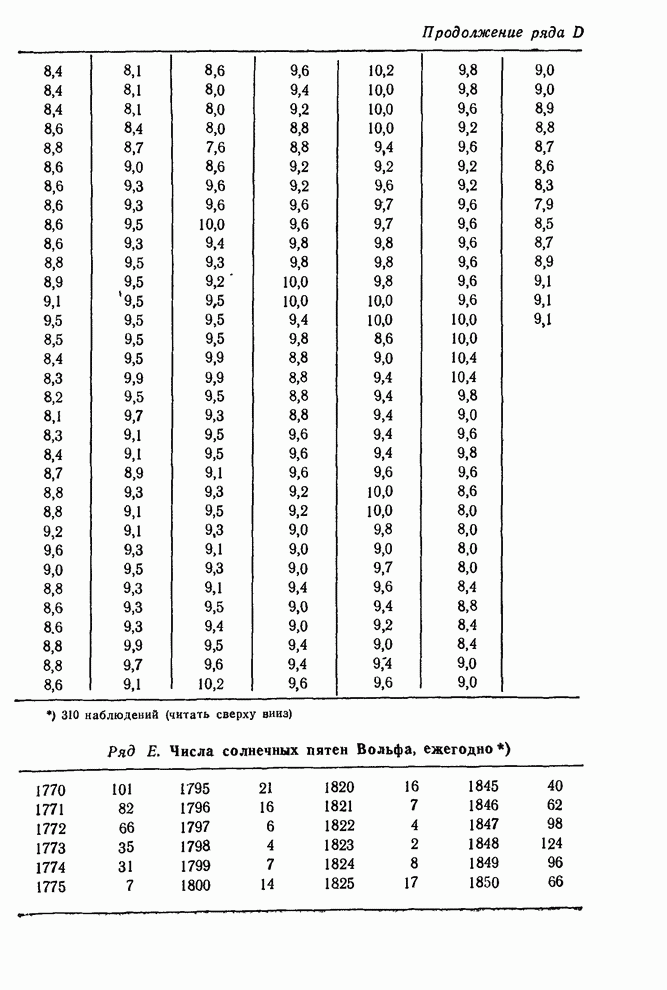
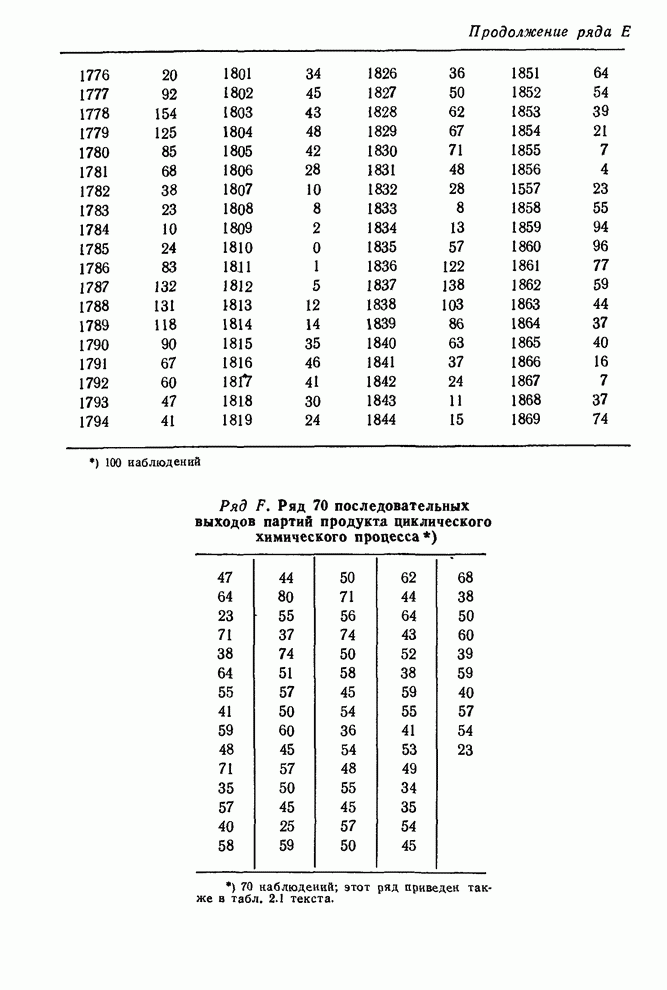
- 7.2.5. Сводка моделей, подогнанных к рядам A-F
- 7.2.6. Информационные матрицы при больших выборках и оценки ковариаций
- 7.3. Результаты оценивания для некоторых частных моделей
- 7.З.2. Процессы скользящего среднего
- 7.3.3. Смешанные процессы
- 7.3.4. Разделение линейных и нелинейных компонент при оценивании
- 7.3.5. Избыточность параметров
- 7.4. Оценивание при помощи теоремы Байеса
- 7.4.2. Байесовское оценивание параметров
- 7.4.3. Процессы авторегрессии
- 7.4.4. Процессы скользящего среднего
- 7.4.5. Смешанные процессы
- Приложение П7.1. Обзор теории нормального распределения
- Приложение П7.2. Обзор линейной теории наименьших квадратов
- Приложение П7.3. Примеры влияния ошибок оценивания параметров на вероятностные пределы прогнозов
- Приложение П7.4. Точная функция правдоподобия для процесса скользящего среднего
- Приложение П7.5. Точная функция правдоподобия для процесса авторегрессии
- Глава 8. Диагностическая проверка модели
- 8.1. Проверка стохастических моделей
- 8.1.2. Введение избыточных параметров
- 8.2.1. Проверка при помощи автокорреляций
- 8.2.2. Совокупный критерий согласия
- 8.2.3. Неадекватность модели, возникающая из-за изменения значений параметров
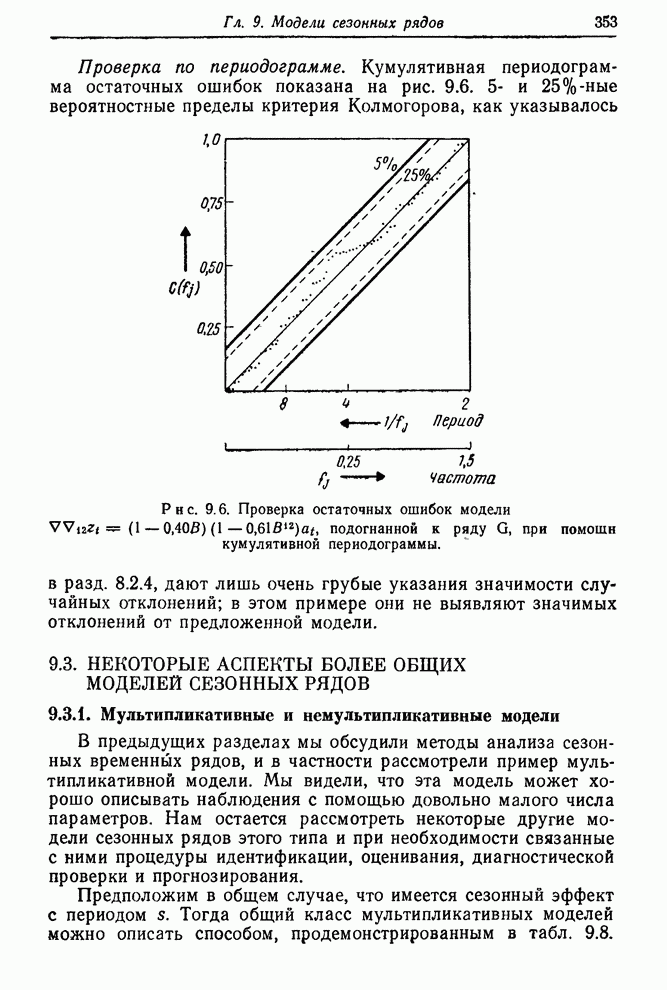
- 8.2.4. Проверка при помощи кумулятивной периодограммы
- 8.3. Использование остаточных ошибок для изменения модели
- 8.3.1. Природа корреляций остаточных ошибок при использовании неверной модели
- 8.3.2. Использование остаточных ошибок для изменения модели
- Глава 9. Модели сезонных рядов
- 9.1. Экономические модели сезонных временных рядов
- 9.1.1. Сопоставление подгонки и прогнозирования
- 9.1.2. Сезонные модели, включающие подстраивающиеся синусоиды и косинусоиды
- 9.1.3. Общая мультипликативная модель сезонного ряда
- 9.2. Представление данных об авиаперевозках мультипликативной моделью
- 9.2.1. Мультипликативная модель
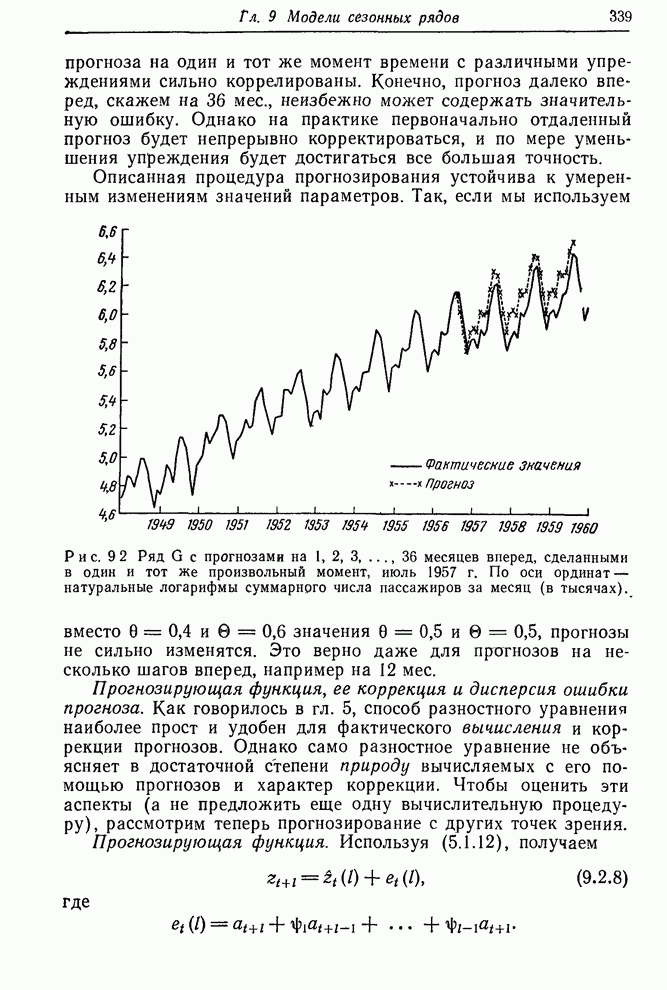
- 9.2.2. Прогнозирование
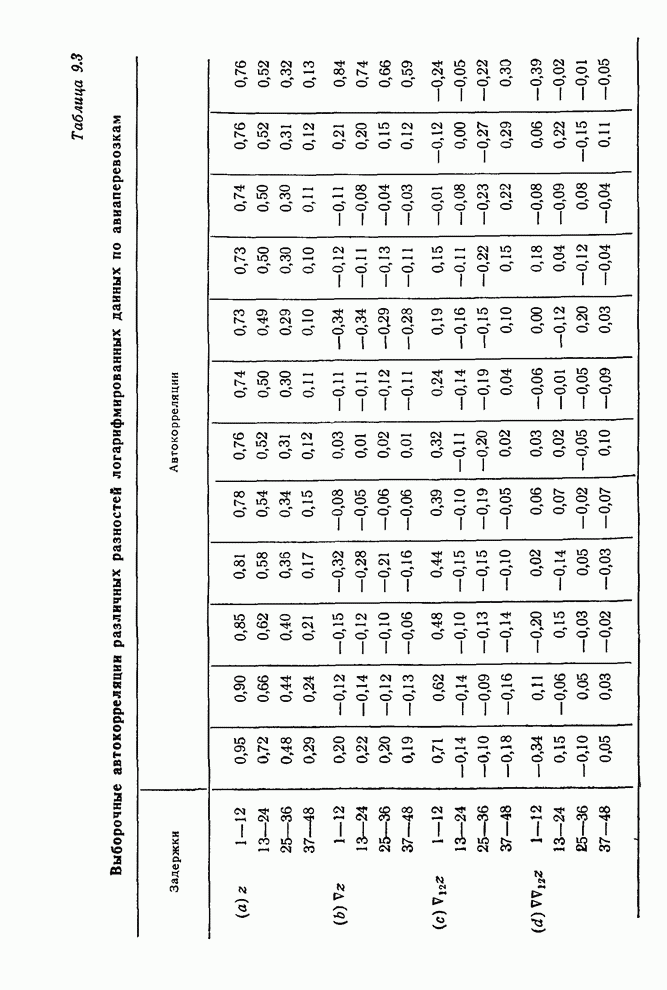
- 9.2.3. Идентификация
- 9.2.4. Оценивание
- 9.2.5. Диагностическая проверка
- 9.3. Некоторые аспекты более общих моделей сезонных рядов
- 9.3.1. Мультипликативные и немультипликативные модели
- 9.3.2. Идентификация
- 9.3.3. Оценивание
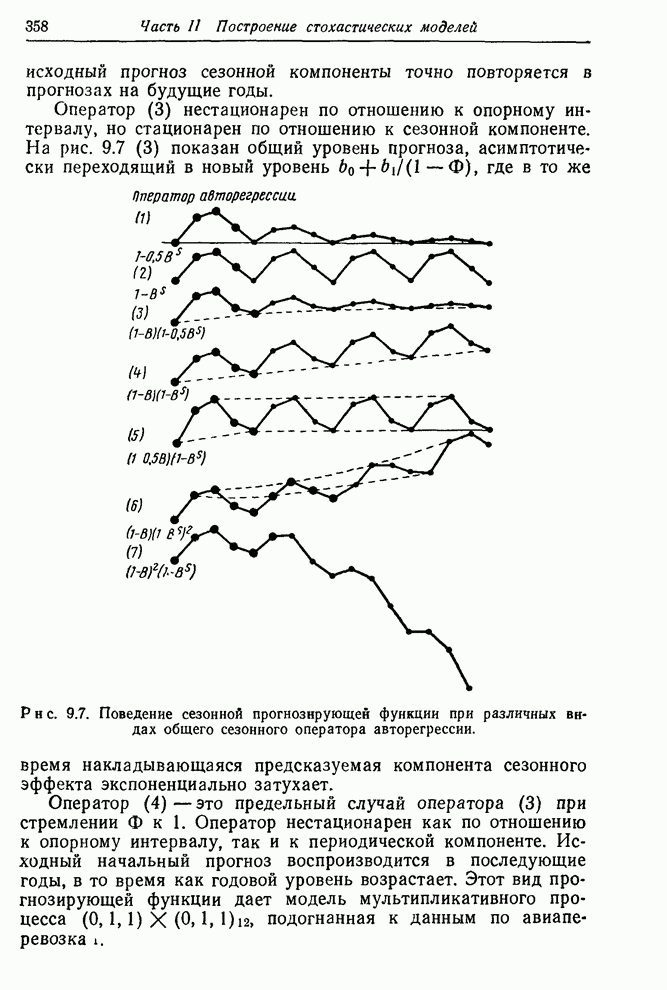
- 9.3.4. Эвентуальные прогнозирующие функции для различных моделей сезонных рядов
- Вспомогательные материалы
- Программа 1 Идентификация стохастической модели
- Программа 2 Предварительное оценивание стохастической модели
- Программа 3. Оценивание стохастической модели
- Алгоритм марквардта для нелинейного метода наименьших квадратов
- Программа 4. Прогнозирование с помощью стохастической модели
- Сборник таблиц и диаграмм