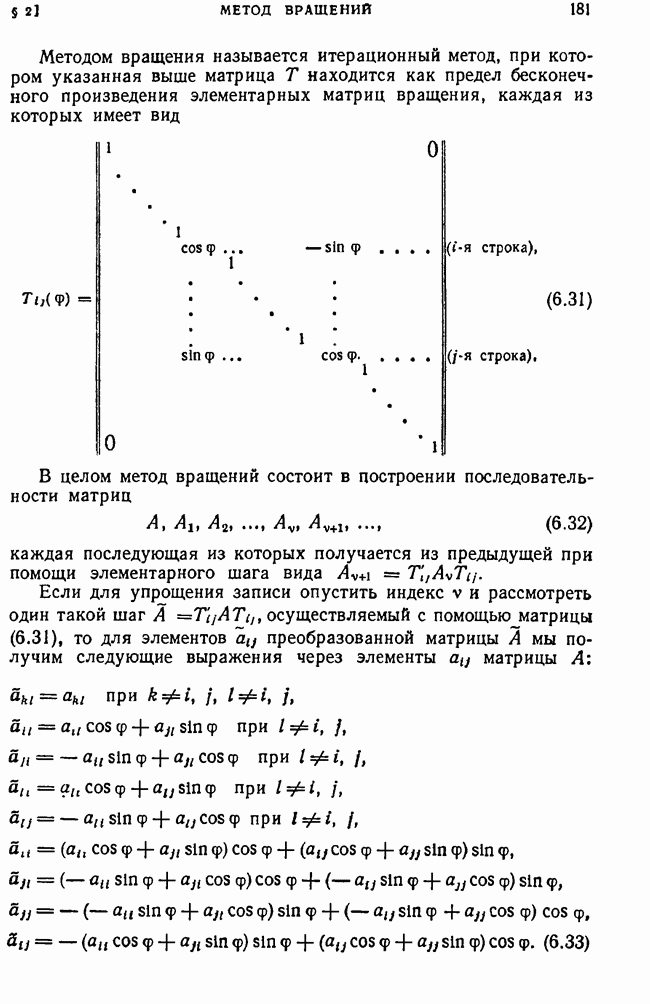
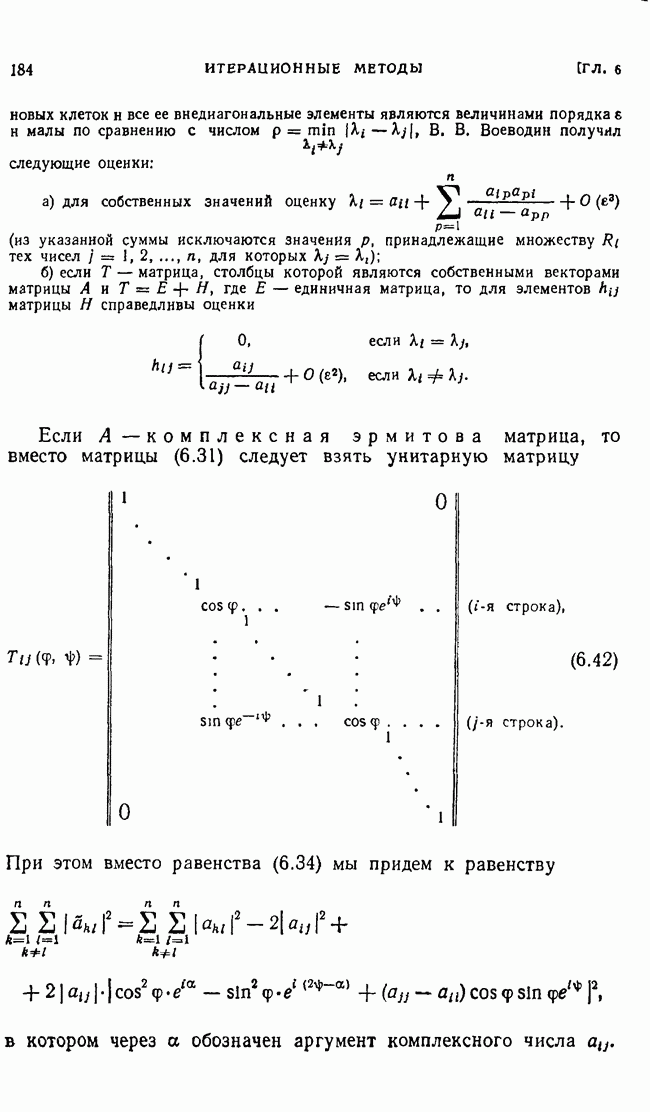
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Метрический тензор псевдоевклидова пространства
1. Понятие псевдоевклидова пространства и метрического тензора псевдоевклидова пространства.
Рассмотрим n-мерное линейное пространство в котором задана невырожденная, симметричная билинейная форма
в котором задана невырожденная, симметричная билинейная форма  полярная знакопеременной квадратичной форме.
полярная знакопеременной квадратичной форме.
Будем называть скалярным произведением  векторов х и у значение
векторов х и у значение  билинейной формы. Наименование
билинейной формы. Наименование
«скалярное произведение» условно, поскольку в рассматриваемом случае не выполняется четвертая аксиома скалярного произведения. Именно, в случае, когда билинейная форма  полярна знакопеременной квадратичной форме, выражение
полярна знакопеременной квадратичной форме, выражение  в зависимости от выбора может иметь как положительное, так и отрицательное значение и обращаться в нуль для ненулевых векторов х. Все же мы будем пользоваться термином «скалярное произведение», так как это общепринято.
в зависимости от выбора может иметь как положительное, так и отрицательное значение и обращаться в нуль для ненулевых векторов х. Все же мы будем пользоваться термином «скалярное произведение», так как это общепринято.
Сформулируем определение псевдоевклидова пространства.
Определение. Псевдоевклидовым пространством называется n-мерное линейное пространство  в котором задано скалярное произведение посредством невырожденной симметричной билинейной формы
в котором задано скалярное произведение посредством невырожденной симметричной билинейной формы  полярной знакопеременной квадратичной форме.
полярной знакопеременной квадратичной форме.
Число  называется размерностью псевдоевклидова пространства.
называется размерностью псевдоевклидова пространства.
Выделим в линейном пространстве  базис
базис  и обозначим через
и обозначим через  матрицу билинейной формы
матрицу билинейной формы  в этом базисе (напомним, что
в этом базисе (напомним, что  ) Если
) Если  — контравариантные координаты векторов х и у, то
— контравариантные координаты векторов х и у, то

В полной аналогии с рассуждениями  § 2 этой главы доказывается, что
§ 2 этой главы доказывается, что  представляют собой координаты тензора С типа (2,0). Этот тензор мы будем в дальнейшем называть метрическим тензором псевдоевклидова пространства.
представляют собой координаты тензора С типа (2,0). Этот тензор мы будем в дальнейшем называть метрическим тензором псевдоевклидова пространства.
Так как скалярное произведение  равно
равно  то, согласно (8.67), имеем
то, согласно (8.67), имеем 
Известно, что матрицу  билинейной формы
билинейной формы  можно привести к диагональному виду. При этом в силу невырожденности формы
можно привести к диагональному виду. При этом в силу невырожденности формы  координаты
координаты  метрического тензора после приведения к диагональному виду будут равны нулю при
метрического тензора после приведения к диагональному виду будут равны нулю при  и единице или минус единице при
и единице или минус единице при  Число
Число  положительных и число
положительных и число  отрицательных диагональных элементов не зависит от способа приведения к диагональному виду, причем, в силу невырожденности формы
отрицательных диагональных элементов не зависит от способа приведения к диагональному виду, причем, в силу невырожденности формы 
Приведенные рассуждения поясняют обозначение  для
для  -мерного псевдоевклидова пространства.
-мерного псевдоевклидова пространства.
Естественно поставить вопрос об измерении длин векторов в псевдоевклидовом пространстве.
В евклидовом пространстве с метрическим тензором  квадрат длины вектора
квадрат длины вектора  координатами
координатами  считается равным
считается равным  Если определить квадрат длины
Если определить квадрат длины  вектора х с помощью соотношения
вектора х с помощью соотношения

то, очевидно (поскольку форма  знакопеременная), можно указать ненулевые векторы с положительным квадратом длины, с отрицательным квадратом длины и с нулевым квадратом длины. Поэтому, чтобы получить в качестве меры длины векторов лишь действительные числа, обычно за длину вектора принимают
знакопеременная), можно указать ненулевые векторы с положительным квадратом длины, с отрицательным квадратом длины и с нулевым квадратом длины. Поэтому, чтобы получить в качестве меры длины векторов лишь действительные числа, обычно за длину вектора принимают

В дальнейшем мы будем использовать следующую терминологию, заимствованную из специальной теории относительности: мы будем называть ненулевой вектор х времениподобным, если для этого вектора  пространственноподобны
пространственноподобны  если а
если а  и изотропным, если
и изотропным, если 
Справедливо следующее утверждение:
Множество концов всех времениподобных (пространственноподобных, изотропных) векторов, начала которых совпадают с произвольной фиксированной точкой М псевдоевклидова пространства, образует конус.
Для определенности докажем утверждение, рассматривая времениподобные векторы. Очевидно, достаточно доказать, что если х — времениподобный вектор, то при любом вещественном  вектор
вектор  также времен и подобен.
также времен и подобен.
Так как координаты вектора  равны
равны  то, согласно (8.68),
то, согласно (8.68),  . Отсюда и из (8.69) следует, что вектор
. Отсюда и из (8.69) следует, что вектор  будет времениподобным.
будет времениподобным.
Для случая времениподобных векторов утверждение доказано. Рассуждая аналогично, убедимся в справедливости утверждения для случая пространственноподобных и изотропных векторов.
Конус времениподобных векторов обозначается часто символом Т (от англ. time — время), а конус пространственноподобных векторов — символом 5 (от англ.  — пространство).
— пространство).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- 1. Понятие матрицы.
- 2. Основные операции над матрицами и их свойства.
- 3. Блочные матрицы.
- § 2. Определители
- 2. Выражение определителя непосредственно через его элементы.
- 3. Теорема Лапласа.
- 4. Свойства определителей.
- 5. Примеры вычисления определителей.
- 6. Определитель суммы и произведения матриц.
- 7. Понятие обратной матрицы.
- § 3. Теорема о базисном миноре матрицы
- 1. Понятие линейной зависимости строк.
- 2. Теорема о базисном мнноре.
- 3. Необходимое и достаточное условие равенства нулю определителя.
- ГЛАВА 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- § 1. Понятие линейного пространства
- 2. Некоторые свойства произвольных линейных пространств.
- § 2. Базис и размерность линейного пространства
- 1. Понятие линейной зависимости элементов линейного пространства.
- 2. Базис и координаты.
- 3. Размерность линейного пространства.
- 4. Понятие изоморфизма линейных пространств.
- § 3. Подпространства линейных пространств
- 1. Понятие подпространства и линейной оболочки.
- 2. Новое определение ранга матрицы.
- 3. Сумма и пересечение подпространств.
- 4. Разложение линейного пространства в прямую сумму подпространств.
- § 4. Преобразование координат при преобразовании базиса n-мерного линейного пространства
- 2. Связь между преобразованием базисов и преобразованием соответствующих координат.
- ГЛАВА 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Условие совместности линейной системы
- 2. Нетривиальная совместность однородной системы.
- 3. Условие совместности общей линейной системы.
- § 2. Отыскание решений линейной системы
- 2. Отыскание всех решений общей линейной системы.
- 3. Свойства совокупности решений однородной системы.
- 4. Заключительные замечания о решении линейных систем.
- ГЛАВА 4. ЕВКЛИДОВЫ ПРОСТРАНСТВА
- § 1. Вещественное евклидово пространство и его простейшие свойства
- 2. Простейшие свойства произвольного евклидова пространства.
- § 2. Ортонормированный базис конечномерного евклидова пространства
- 2. Свойства ортонормированного базиса.
- 3. Разложение n-мерного евклидова пространства на прямую сумму подпространства и его ортогонального дополнения.
- 4. Изоморфизм n-мерных евклидовых пространств.
- § 3. Комплексное евклидово пространство
- 2. Неравенство Коши — Буняковского. Понятие нормы.
- 3. Ортонормированный базис и его свойства.
- § 4. Метод регуляризации для отыскания нормального решения линейной системы
- ГЛАВА 5. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- § 1. Понятие линейного оператора. Основные свойства
- 2. Действия над линейными операторами. Пространство линейных операторов.
- 3. Свойства множества L(V, V) линейных операторов.
- § 2. Матричная запись линейных операторов
- 2. Преобразование матрицы линейного оператора при переходе к новому базису.
- 3. Характеристический многочлен линейного оператора.
- § 3. Собственные значения и собственные векторы линейных операторов
- § 4. Линейные и полуторалинейные формы в евклидовом пространстве
- 2. Полуторалинейные формы в евклидовом пространстве. Специальное представление таких форм.
- § 5. Линейные самосопряженные операторы в евклидовом пространстве
- 2. Самосопряженные операторы. Основные свойства.
- 3. Норма линейного оператора.
- 4. Дальнейшие свойства самосопряженных операторов.
- 5. Спектральное разложение самосопряженных операторов. Теорема Гамильтона—Кэли.
- 6. Положительные операторы. Корни m-й степени из оператора.
- § 6. Приведение квадратичной формы к сумме квадратов
- § 7. Унитарные и нормальные операторы
- § 8. Канонический вид линейных операторов
- § 9. Линейные операторы в вещественном евклидовом пространстве
- 2. Ортогональные операторы.
- ГЛАВА 6. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЛИНЕЙНЫХ СИСТЕМ И ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
- § 1. Итерационные методы решения линейных систем
- 2. Общий неявный метод простой итерации.
- 3. Модифицированный метод простой итерации.
- 4. Метод Зейделя.
- 5. Метод верхней релаксации.
- 6. Случай несимметричной матрицы А.
- 7. Итерационный метод П. Л. Чебышева.
- § 2. Решение полной проблемы собственных значений методом вращений
- ГЛАВА 7. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейные формы
- 2. Представление билинейной формы в конечномерном линейном пространстве.
- 3. Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы.
- § 2. Квадратичные формы
- § 3. Приведение квадратичной формы к сумме квадратов
- 2. Метод Якоби.
- § 4. Закон инерции квадратичных форм. Классификация квадратичных форм
- 2. Классификация квадратичных форм.
- 3. Критерий Сильвестра знакоопределенности квадратичной формы.
- § 5. Полилинейные формы
- § 6. Билинейные и квадратичные формы в евклидовом пространстве
- 2. Приведение квадратичной формы к сумме квадратов в ортогональном базисе.
- 3. Одновременное приведение двух квадратичных форм к сумме квадратов в линейном пространстве.
- 4. Экстремальные свойства квадратичной формы.
- § 7. Гиперповерхности второго порядка
- 2. Параллельные переносы в евклидовом пространстве. Преобразования ортонормированных базисов в ортонормированные.
- 3. Преобразование общего уравнения гиперповерхности второго порядка при параллельном переносе.
- 4. Преобразование общего уравнения гиперповерхности второго порядка при переходе от ортонормированного базиса к ортонормированиому.
- 5. Инварианты общего уравнения гиперповерхности второго порядка.
- 6. Центр гиперповерхности второго порядка.
- 7. Стандартное упрощение любого уравнения гиперповерхности второго порядка путем преобразования ортонормированного базиса.
- 8. Упрощение уравнения центральной гиперповерхности второго порядка. Классификация центральных гиперповерхностей.
- 9. Упрощение уравнения нецентральной гиперповерхности второго порядка. Классификация нецентральных гиперповерхностей.
- ГЛАВА 8. ТЕНЗОРЫ
- § 1. Преобразование базисов и координат
- 2. Взаимные базисы. Ковариантные и контравариантные координаты векторов.
- 3. Преобразования базиса и координат.
- § 2. Понятие тензора. Основные операции над тензорами
- 2. Примеры тензоров.
- 3. Основные операции над тензорами.
- § 3. Метрический тензор. Основные операции векторной алгебры в тензорных обозначениях
- 2. Операция поднятия и опускания индексов с помощью метрического тензора.
- 3. Ортонормированные базисы в E^n.
- 4. Дискриминантный тензор.
- 5. Ориентированный объем.
- 6. Векторное произведение.
- 7. Двойное векторное произведение.
- § 4. Метрический тензор псевдоевклидова пространства
- 2. Галилеевы координаты. Преобразования Лоренца.
- 3. Преобразования Лоренца пространства
- § 5. Тензор момента инерции
- ГЛАВА 9. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
- § 1. Понятие группы. Основные свойства групп
- 2. Понятие группы. Некоторые свойства групп.
- 3. Изоморфизм групп. Подгруппы.
- 4. Смежные классы. Нормальные делители.
- 5. Гомоморфизмы. Фактор-группы.
- § 2. Группы преобразований
- 2. Группа линейных преобразований.
- 3. Сходимость элементов в группе GL(n). Подгруппы группы GL(n).
- 4. Группа ортогональных преобразований.
- 5. Некоторые дискретные и конечные подгруппы ортогональной группы.
- 6. Группа Лоренца.
- 7. Унитарные группы.
- § 3. Представления групп
- 2. Матрицы линейных представлений. Эквивалентные представления.
- 3. Приводимые и неприводимые представления.
- 4. Характеры.
- 5. Примеры представлений групп.