§ 2. Определители

Целью настоящего параграфа является построение теории определителей любого порядка Хотя читатель (из курса аналитической геометрии) уже знаком с определителями второго и третьего порядков, мы будем вести изложение так, чтобы избегнуть каких-либо ссылок. Знакомство с определителями второго и третьего порядков разве лишь облегчит восприятие излагаемого ниже материала.

1. Понятие определителя.

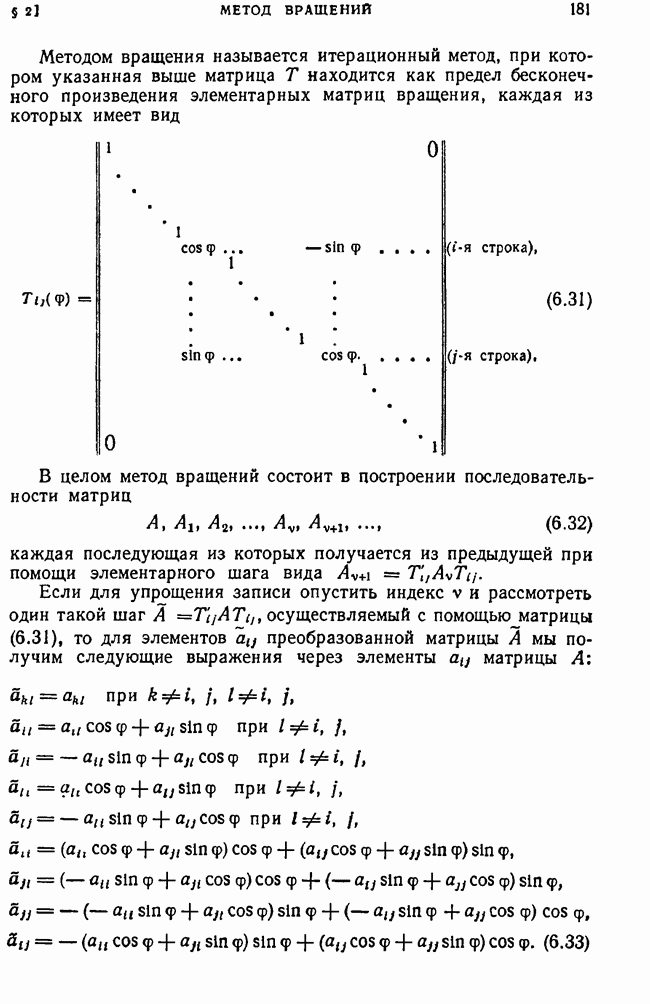
Рассмотрим произвольную квадратную матрицу любого порядка n:

С каждой такой матрицей свяжем вполне определенную численную характеристику, называемую определителем, соответствующим этой матрице.

Если порядок матрицы (1.8) равен единице, то эта матрица состоит из одного элемента и определителем первого порядка, соответствующим такой матрице, мы назовем величину этого элемента.

Если далее порядок матрицы (1.8) равен двум, т. е. если эта матрица имеет вид

то определителем второго порядка, соответствующим такой матрице, назовем число, равное обозначаемое одним из символов . Итак, по определению

Формула (1.10) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы. Словесная формулировка этого правила такова: определитель второго порядка, соответствующий матрице (1.9), равен разности произведения элементов, стоящих на главной диагонали этой матрицы, и произведения элементов, стоящих на побочной ее диагонали.

В дальнейшем изложении мы будем говорить об элементах, строках или столбцах определителя, подразумевая под этими терминами соответственно элементы, строки или столбцы отвечающей этому определителю матрицы.

Перейдем теперь к выяснению понятия определителя любого порядка , где . Понятие такого определителя мы введем индуктивно, считая, что нами уже введено понятие определителя порядка соответствующего произвольной квадратной матрице порядка

Договоримся называть минором любого элемента матрицы порядка (1.8) определитель порядка соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания строки и столбца (той строки и того столбца, на пересечении которых стоит элемент Минор элемента будем обозначать символом М). В этом обозначении верхний индекс обозначает номер строки, нижний — номер столбца, а черта над М означает, что указанные строка и столбец вычеркиваются.

Определителем порядка соответствующим матрице (1.8), назовем число, равное и обозначаемое символом

Итак, по определению

Формула (1.12) представляет собой правило составления определителя порядка по элементам первой строки соответствующей ему матрицы и по минорам М) элементов первой строки, являющимся определителями порядка

Заметим, что при правило (1.12) в точности совпадает с правилом (1.10), ибо в этом случае мииоры элементов первой строки имеют вид:

Естественно возникает вопрос, нельзя ли использовать для получения величины определителя (1.11) элементы и отвечающие им миноры не первой, а произвольной строки матрицы (1.8). Ответ на этот вопрос дает следующая основная теорема.

Теорема 1.1. Каков бы ни был номер строки для определителя порядка (1.11) справедлива формула

называемая разложением этого определителя по строке.

Замечание. Подчеркнем, что в этой формуле показатель степени, в которую возводится число равен сумме номеров строки и столбца, на пересечении которых стоит элемент

Доказательство теоремы 1.1, Формулу (1.13) нужно доказать лишь для номеров . При (т. е. для определителя второго порядка) эту формулу нужно доказать лишь для номера , т. е. при нужно доказать лишь формулу

Справедливость этой последней формулы сразу вытекает из выражений для миноров матрицы в силу которых правая часть этой формулы совпадает с правой частью (1.10). Итак, при теорема доказана.

Доказательство формулы (1.13) для произвольного проведем по индукции, т. е. предположим, что для определителя порядка справедлива формула вида разложения по любой строке, и, опираясь на это, убедимся в справедливости формулы (1.13) для определителя порядка

При доказательстве нам понадобится понятие миноров матрицы (1.8) порядка Определитель порядка соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания двух строк с номерами и двух столбцов с номерами называется минором порядка и обозначается символом

Определитель порядка вводится формулой (1.12), причем в этой формуле каждый минор М) является определителем порядка , для которого по предположению справедлива формула внда (1.13) разложения по любой строке.

Фиксировав любой номер разложим в формуле (1.12) каждый минор М) по строке основного определителя (1.11) (в самом миноре М) эта строка будет

В результате весь определитель окажется представленным в виде некоторой линейной комбинации миноров порядка с несовпадающими номерами , т. е. в виде

Для вычисления множителей заметим, что минор получается в результате разложения по строке только следующих двух миноров порядка, отвечающих элементам первой строки матрицы (1.8): минора и минора (ибо только эти два минора элементов первой строки содержат все столбцы минора

В разложениях миноров по указанной строке выпишем только слагаемые, содержащие минор (остальные не интересующие нас слагаемые обозначим многоточием). Учитывая при этом, что элемент минора М) стоит на пересечении строки и столбца этого минора , а элемент минора стоит на пересечении строки и столбца этого минора мы получим

Вставляя (1.15) и (1.16) в правую часть (1.12) и собирая коэффициент при М), мы получим, что множитель в равенстве (1.14) имеет вид

Для завершения доказательства теоремы покажем, что и правая часть (1.13) равна сумме, стоящей в правой части (1.14), с теми же самыми значениями (1.17) для

Для этого в правой части (1.13) разложим каждый минор порядка первой строке. В результате

вся правая часть (1.13) представится в виде линейной комбинации с некоторыми коэффициентами 0, тех же самых миноров

и нам остается вычислить множители и убедиться в справедливости для них формулы (1.17).

Для этого заметим, что минор получается в результате разложения по первой строке только следующих двух миноров порядка, отвечающих элементам строки матрицы (1.8): минора М) и минора (ибо только эти два минора элементов строки содержат все столбцы минора ).

В разложениях миноров и по первой строке выпишем только слагаемые, содержащие минор (остальные не интересующие нас слагаемые обозначим многоточием). Учитывая при этом, что элемент минора М) стоит на пересечении первой строки и столбца этого минора, а элемент минора стоит на пересечении первой строки и столбца этого минора, мы получим

Вставляя (1.19) и (1.20) в правую часть (1.13) и собирая коэффициент при мы получим, что в сумме (1.18) определяется той же самой формулой (1.17), что и в равенстве (1.14).

Теорема 1.1 доказана.

Теорема 1.1 установила возможность разложения определителя порядка по любой его строке. Естественно возникает вопрос о возможности разложения определителя порядка по любому его столбцу. Положительный ответ на этот вопрос дает следующая основная теорема.

Теорема 1.2. Каков бы ни был номер столбца для определителя порядка (1.11) справедлива формула

называемая разложением этого определителя столбцу.

Доказательство. Достаточно доказать теорему для , т. е. установить формулу разложения по первому столбцу

ибо если формула (1.22) будет установлена, то для доказательства формулы (1.21) для любого достаточно, поменяв ролями строки и столбцы, дословно повторить схему рассуждений теоремы 1.1.

Формулу (1.22) установим по индукции.

При эта формула проверяется элементарно (так как при миноры элементов первого столбца имеют вид то при правая часть (1.22) совпадает с правой частью

Предположим, что формула разложения по первому столбцу (1.22) верна для определителя порядка , опираясь на это, убедимся в справедливости этой формулы для определителя порядка

С этой целью выделим в правой части формулы (1.12) для определителя порядка первое слагаемое а в каждом из остальных слагаемых разложим минор порядка М) по первому столбцу.

В результате формула (1.12) будет иметь вид

где — некоторые подлежащие определению коэффициенты. Для вычисления заметим, что минор получается при разложении по первому столбцу только одного из миноров порядка, отвечающих первой строке — минора М). Запишем в разложении минора по первому столбцу только то слагаемое, которое содержит минор (остальные не интересующие нас слагаемые обозначим многоточием). Учитывая, что элемент минора М) (при стоит на пересечении строки и первого столбца этого минора, мы получим, что при

Вставляя (1.24) в правую часть (1.12) (из которой исключено первое слагаемое) и собирая коэффициент при мы получим, что коэффициент в формуле (1.23) имеет вид

Остается доказать, что и правая часть (1.22) равна сумме, стоящей в правой части (1.23) с теми же самыми значениями (1.25) для

Для этого в правой части (1.22) выделим первое слагаемое , а в каждом из остальных слагаемых разложим минор порядка по первой строке.

В результате правая часть (1.22) представится в виде суммы первого слагаемого и линейной комбинации с некоторыми коэффициентами миноров порядка , т. е. в виде

и нам остается вычислить множители и убедиться в справедливости для них формулы (1.25).

Для этого заметим, что минор получается в результате разложения по первой строке только одного из миноров порядка, отвечающих первому столбцу, — минора Запишем в разложении минора (при по первой строке только то слагаемое, которое содержит минор (остальные не интересующие нас слагаемые обозначим многоточием). Учитывая, что элемент минора стоит на пересечении первой строки и столбца этого минора, мы получим, что при

Вставляя (1.27) в правую часть (1.22), из которой исключено первое слагаемое, и собирая коэффициент при мы получим, что в сумме (1.26) определяется той же самой формулой (1.25), что и в равенстве (1.23). Теорема 1.2 доказана.