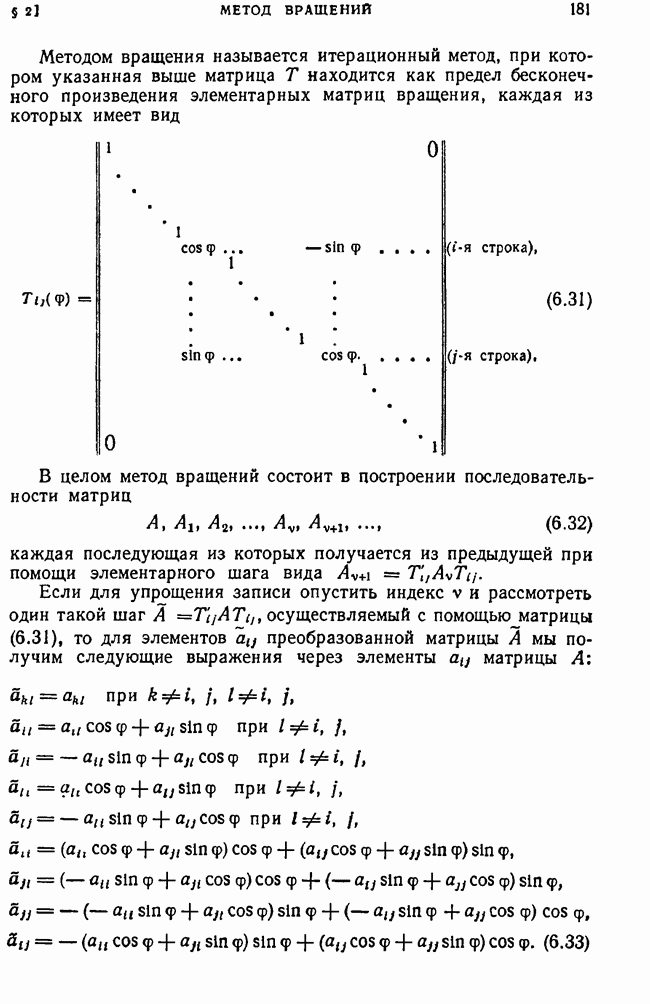
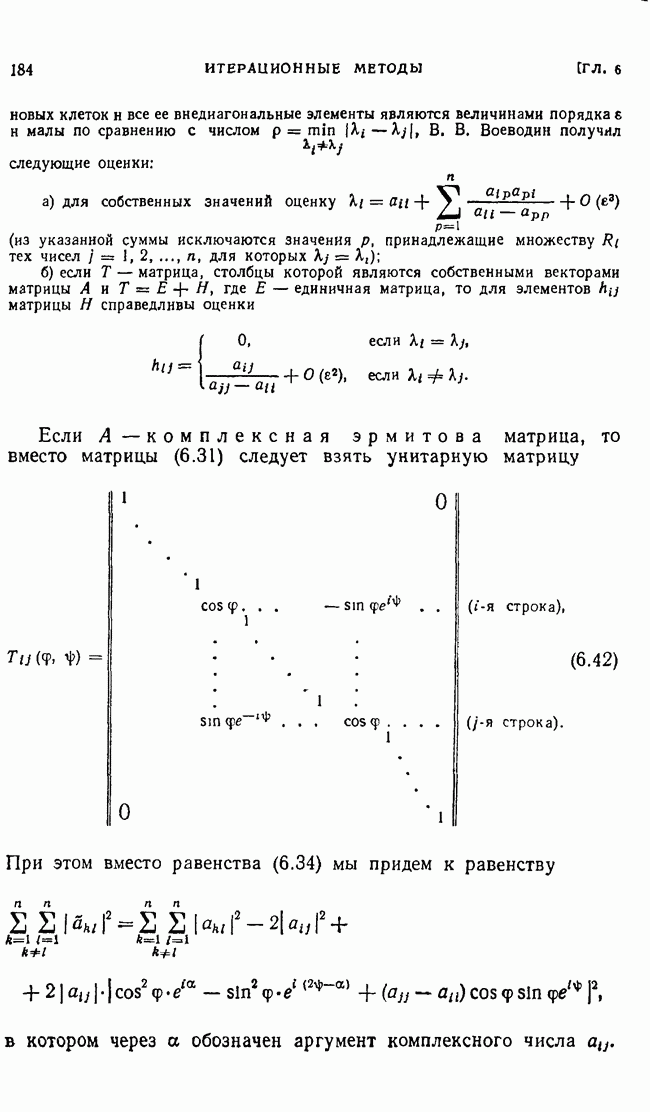
| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Нетривиальная совместность однородной системы.
Начнем с рассмотрения однородной линейной системы вида (3.1), т. е. системы

Сразу же отметим, что эта система всегда совместна, ибо она всегда обладает так называемым тривиальным (или нулевым) решением 
Возникает вопрос о том, при каких условиях однородная система (3.7) имеет, кроме указанного тривиального решения, еще и другие решения (т. е. является «нетривиально совместной»).
Этот вопрос решается довольно просто. Заметим, что существование нетривиального решения системы (3.7) эквивалентно линейной зависимости столбцов матрицы (3.2) (ибо линейная зависимость столбцов матрицы (3.2) означает, что существуют числа  не все равные нулю и такие, что справедливы равенства
не все равные нулю и такие, что справедливы равенства 
Но в силу теоремы 1.6 о базисном миноре линейная зависимость столбцов матрицы  будет иметь место тогда и только тогда, когда не все столбцы этой матрицы являются базисными, т. е. тогда и только тогда, когда порядок
будет иметь место тогда и только тогда, когда не все столбцы этой матрицы являются базисными, т. е. тогда и только тогда, когда порядок  базисного минора матрицы (3.2) меньше числа
базисного минора матрицы (3.2) меньше числа  ее столбцов.
ее столбцов.
Мы приходим к следующей теореме.
Теорема 3.1. Однородная система (3.7) имеет нетривиальные решения тогда и только тогда, когда ранг  матрицы (3.2) меньше числа
матрицы (3.2) меньше числа  ее столбцов.
ее столбцов.
Следствие. Квадратная однородная система имеет нетривиальные решения тогда и только тогда, когда определитель, составленный из коэффициентов при неизвестных, равен нулю.
В самом деле, в случае квадратной однородной системы (3.7), т. е. при  ранг
ранг  матрицы (3.2) будет меньше числа
матрицы (3.2) будет меньше числа  тогда и только тогда, когда определитель этой матрицы равен нулю.
тогда и только тогда, когда определитель этой матрицы равен нулю.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- 1. Понятие матрицы.
- 2. Основные операции над матрицами и их свойства.
- 3. Блочные матрицы.
- § 2. Определители
- 2. Выражение определителя непосредственно через его элементы.
- 3. Теорема Лапласа.
- 4. Свойства определителей.
- 5. Примеры вычисления определителей.
- 6. Определитель суммы и произведения матриц.
- 7. Понятие обратной матрицы.
- § 3. Теорема о базисном миноре матрицы
- 1. Понятие линейной зависимости строк.
- 2. Теорема о базисном мнноре.
- 3. Необходимое и достаточное условие равенства нулю определителя.
- ГЛАВА 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- § 1. Понятие линейного пространства
- 2. Некоторые свойства произвольных линейных пространств.
- § 2. Базис и размерность линейного пространства
- 1. Понятие линейной зависимости элементов линейного пространства.
- 2. Базис и координаты.
- 3. Размерность линейного пространства.
- 4. Понятие изоморфизма линейных пространств.
- § 3. Подпространства линейных пространств
- 1. Понятие подпространства и линейной оболочки.
- 2. Новое определение ранга матрицы.
- 3. Сумма и пересечение подпространств.
- 4. Разложение линейного пространства в прямую сумму подпространств.
- § 4. Преобразование координат при преобразовании базиса n-мерного линейного пространства
- 2. Связь между преобразованием базисов и преобразованием соответствующих координат.
- ГЛАВА 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Условие совместности линейной системы
- 2. Нетривиальная совместность однородной системы.
- 3. Условие совместности общей линейной системы.
- § 2. Отыскание решений линейной системы
- 2. Отыскание всех решений общей линейной системы.
- 3. Свойства совокупности решений однородной системы.
- 4. Заключительные замечания о решении линейных систем.
- ГЛАВА 4. ЕВКЛИДОВЫ ПРОСТРАНСТВА
- § 1. Вещественное евклидово пространство и его простейшие свойства
- 2. Простейшие свойства произвольного евклидова пространства.
- § 2. Ортонормированный базис конечномерного евклидова пространства
- 2. Свойства ортонормированного базиса.
- 3. Разложение n-мерного евклидова пространства на прямую сумму подпространства и его ортогонального дополнения.
- 4. Изоморфизм n-мерных евклидовых пространств.
- § 3. Комплексное евклидово пространство
- 2. Неравенство Коши — Буняковского. Понятие нормы.
- 3. Ортонормированный базис и его свойства.
- § 4. Метод регуляризации для отыскания нормального решения линейной системы
- ГЛАВА 5. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- § 1. Понятие линейного оператора. Основные свойства
- 2. Действия над линейными операторами. Пространство линейных операторов.
- 3. Свойства множества L(V, V) линейных операторов.
- § 2. Матричная запись линейных операторов
- 2. Преобразование матрицы линейного оператора при переходе к новому базису.
- 3. Характеристический многочлен линейного оператора.
- § 3. Собственные значения и собственные векторы линейных операторов
- § 4. Линейные и полуторалинейные формы в евклидовом пространстве
- 2. Полуторалинейные формы в евклидовом пространстве. Специальное представление таких форм.
- § 5. Линейные самосопряженные операторы в евклидовом пространстве
- 2. Самосопряженные операторы. Основные свойства.
- 3. Норма линейного оператора.
- 4. Дальнейшие свойства самосопряженных операторов.
- 5. Спектральное разложение самосопряженных операторов. Теорема Гамильтона—Кэли.
- 6. Положительные операторы. Корни m-й степени из оператора.
- § 6. Приведение квадратичной формы к сумме квадратов
- § 7. Унитарные и нормальные операторы
- § 8. Канонический вид линейных операторов
- § 9. Линейные операторы в вещественном евклидовом пространстве
- 2. Ортогональные операторы.
- ГЛАВА 6. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЛИНЕЙНЫХ СИСТЕМ И ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
- § 1. Итерационные методы решения линейных систем
- 2. Общий неявный метод простой итерации.
- 3. Модифицированный метод простой итерации.
- 4. Метод Зейделя.
- 5. Метод верхней релаксации.
- 6. Случай несимметричной матрицы А.
- 7. Итерационный метод П. Л. Чебышева.
- § 2. Решение полной проблемы собственных значений методом вращений
- ГЛАВА 7. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейные формы
- 2. Представление билинейной формы в конечномерном линейном пространстве.
- 3. Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы.
- § 2. Квадратичные формы
- § 3. Приведение квадратичной формы к сумме квадратов
- 2. Метод Якоби.
- § 4. Закон инерции квадратичных форм. Классификация квадратичных форм
- 2. Классификация квадратичных форм.
- 3. Критерий Сильвестра знакоопределенности квадратичной формы.
- § 5. Полилинейные формы
- § 6. Билинейные и квадратичные формы в евклидовом пространстве
- 2. Приведение квадратичной формы к сумме квадратов в ортогональном базисе.
- 3. Одновременное приведение двух квадратичных форм к сумме квадратов в линейном пространстве.
- 4. Экстремальные свойства квадратичной формы.
- § 7. Гиперповерхности второго порядка
- 2. Параллельные переносы в евклидовом пространстве. Преобразования ортонормированных базисов в ортонормированные.
- 3. Преобразование общего уравнения гиперповерхности второго порядка при параллельном переносе.
- 4. Преобразование общего уравнения гиперповерхности второго порядка при переходе от ортонормированного базиса к ортонормированиому.
- 5. Инварианты общего уравнения гиперповерхности второго порядка.
- 6. Центр гиперповерхности второго порядка.
- 7. Стандартное упрощение любого уравнения гиперповерхности второго порядка путем преобразования ортонормированного базиса.
- 8. Упрощение уравнения центральной гиперповерхности второго порядка. Классификация центральных гиперповерхностей.
- 9. Упрощение уравнения нецентральной гиперповерхности второго порядка. Классификация нецентральных гиперповерхностей.
- ГЛАВА 8. ТЕНЗОРЫ
- § 1. Преобразование базисов и координат
- 2. Взаимные базисы. Ковариантные и контравариантные координаты векторов.
- 3. Преобразования базиса и координат.
- § 2. Понятие тензора. Основные операции над тензорами
- 2. Примеры тензоров.
- 3. Основные операции над тензорами.
- § 3. Метрический тензор. Основные операции векторной алгебры в тензорных обозначениях
- 2. Операция поднятия и опускания индексов с помощью метрического тензора.
- 3. Ортонормированные базисы в E^n.
- 4. Дискриминантный тензор.
- 5. Ориентированный объем.
- 6. Векторное произведение.
- 7. Двойное векторное произведение.
- § 4. Метрический тензор псевдоевклидова пространства
- 2. Галилеевы координаты. Преобразования Лоренца.
- 3. Преобразования Лоренца пространства
- § 5. Тензор момента инерции
- ГЛАВА 9. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
- § 1. Понятие группы. Основные свойства групп
- 2. Понятие группы. Некоторые свойства групп.
- 3. Изоморфизм групп. Подгруппы.
- 4. Смежные классы. Нормальные делители.
- 5. Гомоморфизмы. Фактор-группы.
- § 2. Группы преобразований
- 2. Группа линейных преобразований.
- 3. Сходимость элементов в группе GL(n). Подгруппы группы GL(n).
- 4. Группа ортогональных преобразований.
- 5. Некоторые дискретные и конечные подгруппы ортогональной группы.
- 6. Группа Лоренца.
- 7. Унитарные группы.
- § 3. Представления групп
- 2. Матрицы линейных представлений. Эквивалентные представления.
- 3. Приводимые и неприводимые представления.
- 4. Характеры.
- 5. Примеры представлений групп.