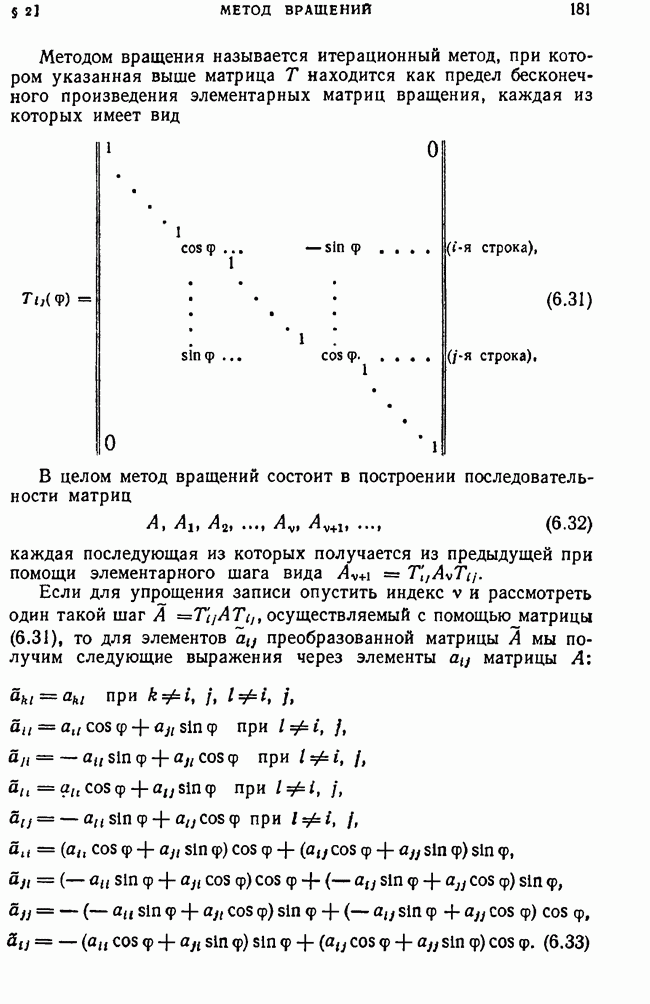
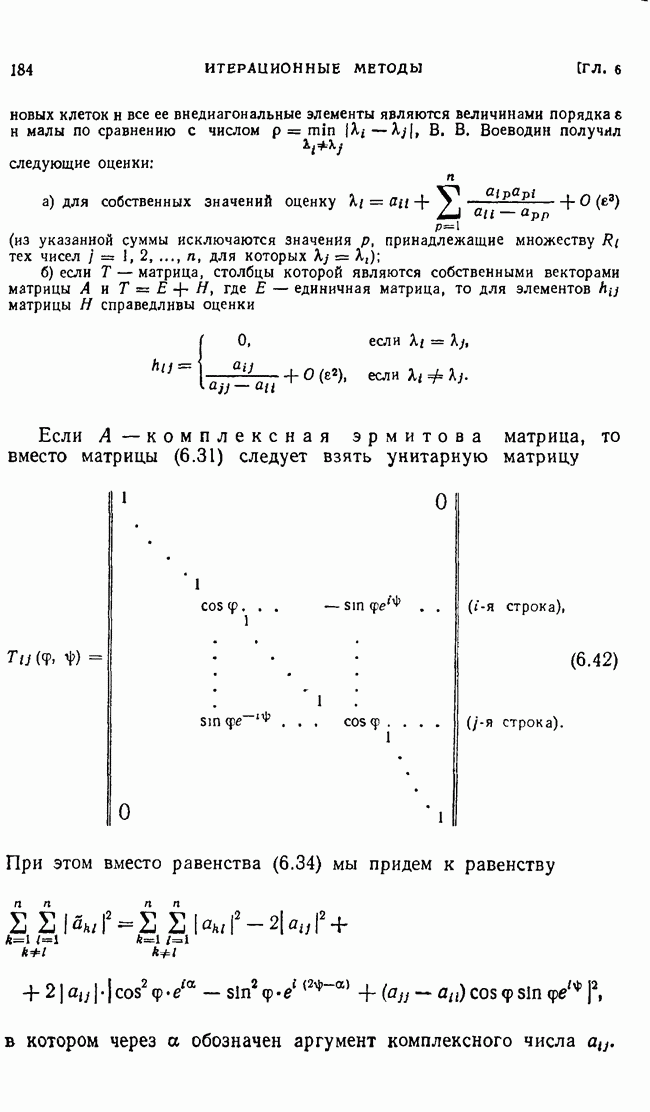
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6. Приведение квадратичной формы к сумме квадратов
В этом параграфе мы изучим вопрос о выборе такого базиса, в котором квадратичная форма (инвариантная квадратичная функция координат вектора; точно это понятие определяется ниже) имеет наиболее простой вид.
Квадратичные формы подробно изучаются в главе 7. Там будут, в частности, рассмотрены различные способы приведения таких форм к сумме квадратов.
Введем понятие так называемых эрмитовых форм.
Определение. Полуторалинейная форма  называется эрмитовой, если для любых х и у справедливо соотношение
называется эрмитовой, если для любых х и у справедливо соотношение

Согласно следствию из теоремы 5.11 любая полуторалинейная форма  (в том числе и эрмитова) может быть единственным образом представлена в виде
(в том числе и эрмитова) может быть единственным образом представлена в виде

где А — линейный оператор.
Докажем следующие два утверждения, в которых выясняются условия, при которых полуторалинейная форма является эрмитовой.
Теорема 5.25. Для того чтобы полуторалинейная форма  являлась эрмитовой, необходимо и достаточно, чтобы оператор А в представлении (5.80) этой формы был самосопряженным
являлась эрмитовой, необходимо и достаточно, чтобы оператор А в представлении (5.80) этой формы был самосопряженным 
Доказательство. Действительно, если А — самосопряженный оператор, то, используя свойства скалярного произведения, получим

Таким образом, выполнено соотношение (5.79), т. е. форма  является эрмитовой.
является эрмитовой.
Если же форма  эрмитова, то, опять обращаясь к свойствам скалярного произведения, получим равенства
эрмитова, то, опять обращаясь к свойствам скалярного произведения, получим равенства

Таким образом,  , т. е. оператор А является самосопряженным. Теорема доказана.
, т. е. оператор А является самосопряженным. Теорема доказана.
Теорема 5.26. Для того чтобы полуторалинейная форма  была эрмитовой, необходимо и достаточно, чтобы функция
была эрмитовой, необходимо и достаточно, чтобы функция  была вещественной.
была вещественной.
Доказательство. Форма  будет эрмитовой в том и только в том случае, когда линейный оператор А в представлении (5.80) этой формы является самосопряженным (см. теорему 5.25). Согласно же теореме 5.18, для того чтобы оператор А был самосопряженным, необходимо и достаточно, чтобы для любого х скалярное произведение
будет эрмитовой в том и только в том случае, когда линейный оператор А в представлении (5.80) этой формы является самосопряженным (см. теорему 5.25). Согласно же теореме 5.18, для того чтобы оператор А был самосопряженным, необходимо и достаточно, чтобы для любого х скалярное произведение  было вещественным. Теорема доказана.
было вещественным. Теорема доказана.
Введем теперь понятие квадратичной формы.
Пусть  — эрмитова форма.
— эрмитова форма.
Квадратичной формой, соответствующей форме  называется функция
называется функция 
Докажем следующую теорему о приведении квадратичной формы к сумме квадратов.
Теорема 5.27. Пусть  — эрмитова форма, определенная на всевозможных векторах х и у n-мерного евклидова пространства V. Тогда в этом пространстве существует такой ортонормированный базис
— эрмитова форма, определенная на всевозможных векторах х и у n-мерного евклидова пространства V. Тогда в этом пространстве существует такой ортонормированный базис  и можно указать такие вещественные числа
и можно указать такие вещественные числа  что для любого х, принадлежащего V, квадратичная форма
что для любого х, принадлежащего V, квадратичная форма  может быть представлена в виде следующей суммы квадратов координат вектора х в базисе
может быть представлена в виде следующей суммы квадратов координат вектора х в базисе 

Доказательство. Так как форма  эрмитова, то, согласно теореме 5.25, существует самосопряженный оператор А такой, что
эрмитова, то, согласно теореме 5.25, существует самосопряженный оператор А такой, что

Обратимся теперь к теореме 5.21. По этой теореме для оператора А можно указать ортонормированный базис  из собственных векторов этого оператора. Если
из собственных векторов этого оператора. Если  — собственные значения
— собственные значения  координаты вектора х в базисе
координаты вектора х в базисе  так что
так что

то, используя формулу (5.12) и соотношение  получим следующее выражение для
получим следующее выражение для 

Из (5.83), (5.84) и ортонормированности базиса  получим следующее выражение для
получим следующее выражение для 

Из этого выражения и из соотношения (5.82) получим (5.81). Теорема доказана.
Докажем теперь важную теорему об одновременном приведении двух квадратичных форм к сумме квадратов.
Теорема 5.28. Пусть  — эрмитовы формы, определенные на всевозможных векторах х и у n-мерного линейного пространства V. Допустим, далее что для всех ненулевых элементов х из V имеет место неравенство
— эрмитовы формы, определенные на всевозможных векторах х и у n-мерного линейного пространства V. Допустим, далее что для всех ненулевых элементов х из V имеет место неравенство  Тогда в пространстве V можно указать базис такой, что квадратичные формы
Тогда в пространстве V можно указать базис такой, что квадратичные формы  могут быть представлены в следующем виде:
могут быть представлены в следующем виде:

где  — вещественные числа,
— вещественные числа,  — координаты вектора х в базисе
— координаты вектора х в базисе
Доказательство. Так как свойства скалярного произведения и свойства эрмитовой формы  при дополнительном требовании о том, что
при дополнительном требовании о том, что  при
при  , формулируются одинаково, мы можем ввести в линейном пространстве V скалярное произведение
, формулируются одинаково, мы можем ввести в линейном пространстве V скалярное произведение  векторов, полагая
векторов, полагая

Таким образом, V представляет собой евклидово пространство со скалярным произведением (5.87).
По теореме 5.27 можно указать в V такой ортонормированный базис  и такие вещественные числа
и такие вещественные числа  что в этом базисе квадратичная форма
что в этом базисе квадратичная форма  будет представлена в виде (5.85).
будет представлена в виде (5.85).
С другой стороны, в любом ортонормированном базисе скалярное произведение  равное, согласно (5.87),
равное, согласно (5.87),  равно сумме квадратов модулей координат вектора х. Таким образом, представление
равно сумме квадратов модулей координат вектора х. Таким образом, представление  в виде (5.86) также обосновано. Теорема доказана.
в виде (5.86) также обосновано. Теорема доказана.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- ГЛАВА 1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- 1. Понятие матрицы.
- 2. Основные операции над матрицами и их свойства.
- 3. Блочные матрицы.
- § 2. Определители
- 2. Выражение определителя непосредственно через его элементы.
- 3. Теорема Лапласа.
- 4. Свойства определителей.
- 5. Примеры вычисления определителей.
- 6. Определитель суммы и произведения матриц.
- 7. Понятие обратной матрицы.
- § 3. Теорема о базисном миноре матрицы
- 1. Понятие линейной зависимости строк.
- 2. Теорема о базисном мнноре.
- 3. Необходимое и достаточное условие равенства нулю определителя.
- ГЛАВА 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- § 1. Понятие линейного пространства
- 2. Некоторые свойства произвольных линейных пространств.
- § 2. Базис и размерность линейного пространства
- 1. Понятие линейной зависимости элементов линейного пространства.
- 2. Базис и координаты.
- 3. Размерность линейного пространства.
- 4. Понятие изоморфизма линейных пространств.
- § 3. Подпространства линейных пространств
- 1. Понятие подпространства и линейной оболочки.
- 2. Новое определение ранга матрицы.
- 3. Сумма и пересечение подпространств.
- 4. Разложение линейного пространства в прямую сумму подпространств.
- § 4. Преобразование координат при преобразовании базиса n-мерного линейного пространства
- 2. Связь между преобразованием базисов и преобразованием соответствующих координат.
- ГЛАВА 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Условие совместности линейной системы
- 2. Нетривиальная совместность однородной системы.
- 3. Условие совместности общей линейной системы.
- § 2. Отыскание решений линейной системы
- 2. Отыскание всех решений общей линейной системы.
- 3. Свойства совокупности решений однородной системы.
- 4. Заключительные замечания о решении линейных систем.
- ГЛАВА 4. ЕВКЛИДОВЫ ПРОСТРАНСТВА
- § 1. Вещественное евклидово пространство и его простейшие свойства
- 2. Простейшие свойства произвольного евклидова пространства.
- § 2. Ортонормированный базис конечномерного евклидова пространства
- 2. Свойства ортонормированного базиса.
- 3. Разложение n-мерного евклидова пространства на прямую сумму подпространства и его ортогонального дополнения.
- 4. Изоморфизм n-мерных евклидовых пространств.
- § 3. Комплексное евклидово пространство
- 2. Неравенство Коши — Буняковского. Понятие нормы.
- 3. Ортонормированный базис и его свойства.
- § 4. Метод регуляризации для отыскания нормального решения линейной системы
- ГЛАВА 5. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- § 1. Понятие линейного оператора. Основные свойства
- 2. Действия над линейными операторами. Пространство линейных операторов.
- 3. Свойства множества L(V, V) линейных операторов.
- § 2. Матричная запись линейных операторов
- 2. Преобразование матрицы линейного оператора при переходе к новому базису.
- 3. Характеристический многочлен линейного оператора.
- § 3. Собственные значения и собственные векторы линейных операторов
- § 4. Линейные и полуторалинейные формы в евклидовом пространстве
- 2. Полуторалинейные формы в евклидовом пространстве. Специальное представление таких форм.
- § 5. Линейные самосопряженные операторы в евклидовом пространстве
- 2. Самосопряженные операторы. Основные свойства.
- 3. Норма линейного оператора.
- 4. Дальнейшие свойства самосопряженных операторов.
- 5. Спектральное разложение самосопряженных операторов. Теорема Гамильтона—Кэли.
- 6. Положительные операторы. Корни m-й степени из оператора.
- § 6. Приведение квадратичной формы к сумме квадратов
- § 7. Унитарные и нормальные операторы
- § 8. Канонический вид линейных операторов
- § 9. Линейные операторы в вещественном евклидовом пространстве
- 2. Ортогональные операторы.
- ГЛАВА 6. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЛИНЕЙНЫХ СИСТЕМ И ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
- § 1. Итерационные методы решения линейных систем
- 2. Общий неявный метод простой итерации.
- 3. Модифицированный метод простой итерации.
- 4. Метод Зейделя.
- 5. Метод верхней релаксации.
- 6. Случай несимметричной матрицы А.
- 7. Итерационный метод П. Л. Чебышева.
- § 2. Решение полной проблемы собственных значений методом вращений
- ГЛАВА 7. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейные формы
- 2. Представление билинейной формы в конечномерном линейном пространстве.
- 3. Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы.
- § 2. Квадратичные формы
- § 3. Приведение квадратичной формы к сумме квадратов
- 2. Метод Якоби.
- § 4. Закон инерции квадратичных форм. Классификация квадратичных форм
- 2. Классификация квадратичных форм.
- 3. Критерий Сильвестра знакоопределенности квадратичной формы.
- § 5. Полилинейные формы
- § 6. Билинейные и квадратичные формы в евклидовом пространстве
- 2. Приведение квадратичной формы к сумме квадратов в ортогональном базисе.
- 3. Одновременное приведение двух квадратичных форм к сумме квадратов в линейном пространстве.
- 4. Экстремальные свойства квадратичной формы.
- § 7. Гиперповерхности второго порядка
- 2. Параллельные переносы в евклидовом пространстве. Преобразования ортонормированных базисов в ортонормированные.
- 3. Преобразование общего уравнения гиперповерхности второго порядка при параллельном переносе.
- 4. Преобразование общего уравнения гиперповерхности второго порядка при переходе от ортонормированного базиса к ортонормированиому.
- 5. Инварианты общего уравнения гиперповерхности второго порядка.
- 6. Центр гиперповерхности второго порядка.
- 7. Стандартное упрощение любого уравнения гиперповерхности второго порядка путем преобразования ортонормированного базиса.
- 8. Упрощение уравнения центральной гиперповерхности второго порядка. Классификация центральных гиперповерхностей.
- 9. Упрощение уравнения нецентральной гиперповерхности второго порядка. Классификация нецентральных гиперповерхностей.
- ГЛАВА 8. ТЕНЗОРЫ
- § 1. Преобразование базисов и координат
- 2. Взаимные базисы. Ковариантные и контравариантные координаты векторов.
- 3. Преобразования базиса и координат.
- § 2. Понятие тензора. Основные операции над тензорами
- 2. Примеры тензоров.
- 3. Основные операции над тензорами.
- § 3. Метрический тензор. Основные операции векторной алгебры в тензорных обозначениях
- 2. Операция поднятия и опускания индексов с помощью метрического тензора.
- 3. Ортонормированные базисы в E^n.
- 4. Дискриминантный тензор.
- 5. Ориентированный объем.
- 6. Векторное произведение.
- 7. Двойное векторное произведение.
- § 4. Метрический тензор псевдоевклидова пространства
- 2. Галилеевы координаты. Преобразования Лоренца.
- 3. Преобразования Лоренца пространства
- § 5. Тензор момента инерции
- ГЛАВА 9. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
- § 1. Понятие группы. Основные свойства групп
- 2. Понятие группы. Некоторые свойства групп.
- 3. Изоморфизм групп. Подгруппы.
- 4. Смежные классы. Нормальные делители.
- 5. Гомоморфизмы. Фактор-группы.
- § 2. Группы преобразований
- 2. Группа линейных преобразований.
- 3. Сходимость элементов в группе GL(n). Подгруппы группы GL(n).
- 4. Группа ортогональных преобразований.
- 5. Некоторые дискретные и конечные подгруппы ортогональной группы.
- 6. Группа Лоренца.
- 7. Унитарные группы.
- § 3. Представления групп
- 2. Матрицы линейных представлений. Эквивалентные представления.
- 3. Приводимые и неприводимые представления.
- 4. Характеры.
- 5. Примеры представлений групп.