| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
IV. Многочастичные задачи
А. Малое число частиц
Задача 148. Две отталкивающиеся частицы на окружности
Две одинаковые точечные частицы находятся на гладкой окружности радиуса  и взаимодействуют по закону
и взаимодействуют по закону

это может, например, служить моделью кулоновского отталкивания электронов в основном состоянии атома гелия. Вывести закон сохранения момента количества движения и рассмотреть относительное движение частиц.
Решение. Уравнение Шредингера

допускает разделение переменных, если перейти к новым координатам

описывающим относительное и "абсолютное" движение частиц. Действительно, подставляя выражения

в уравнение (148.2), приходим к уравнению

решение которого можно искать в виде

Теперь мы имеем

и

причем

Абсолютное движение частиц определяется уравнением (148.6). Учитывая, что оператор проекции суммарного орбитального момента нашей двухчастичной системы на ось z дается выражением

мы можем переписать уравнение (148.6) в виде

где  - суммарный момент инерции обеих частиц. Последнее уравнение позволяет определить собственные значения оператора вращательной энергии. Так как решение уравнения (148.6) имеет вид
- суммарный момент инерции обеих частиц. Последнее уравнение позволяет определить собственные значения оператора вращательной энергии. Так как решение уравнения (148.6) имеет вид

то допустимые значения вращательной энергии будут равны

Гораздо сложнее вопрос об относительном движении частиц, так как оно определяется дифференциальным уравнением Матье (148.5). Чтобы упростить последующие рассуждения, преобразуем уравнение (148.5) к стандартной форме, положив

Таким образом, получим

Мы будем интересоваться периодическими решениями с периодом  по переменной а или, что то же самое, с периодом
по переменной а или, что то же самое, с периодом  по переменной
по переменной  Так как в уравнении (148.11) коэффициент при функции
Так как в уравнении (148.11) коэффициент при функции  четным образом зависит от угла
четным образом зависит от угла  то решения этого уравнения будут либо четными, либо нечетными функциями
то решения этого уравнения будут либо четными, либо нечетными функциями 
Периодичность решений позволяет разложить их в ряды Фурье, поэтому мы имеем

Обычно принято обозначать собственные значения X посредством  в случае четных решений и посредством
в случае четных решений и посредством  в случае нечетных решений. В теории уравнения Матье показывается, что собственные значения можно расположить в следующем порядке:
в случае нечетных решений. В теории уравнения Матье показывается, что собственные значения можно расположить в следующем порядке:

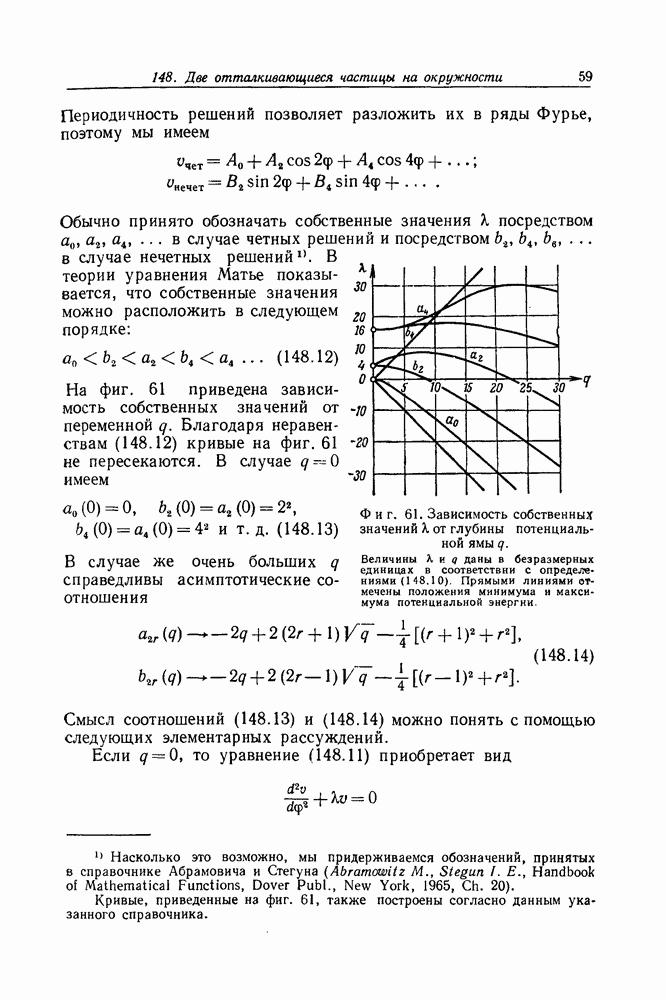
На фиг. 61 приведена зависимость собственных значений от переменной  Благодаря неравенствам (148.12) кривые на фиг. 61 не пересекаются. В случае
Благодаря неравенствам (148.12) кривые на фиг. 61 не пересекаются. В случае  имеем
имеем


Фиг. 61. Зависимость собственных значений X от глубины потенциальной ямы  Величины
Величины  даны в безразмерных единицах в соответствии с определениями (1 48.10). Прямыми линиями отмечены положения минимума и максимума потенциальной энергии.
даны в безразмерных единицах в соответствии с определениями (1 48.10). Прямыми линиями отмечены положения минимума и максимума потенциальной энергии.
В случае же очень больших  справедливы асимптотические соотношения
справедливы асимптотические соотношения

Смысл соотношений (148.13) и (148.14) можно понять с помощью следующих элементарных рассуждений.
Если  то уравнение (148.11) приобретает вид
то уравнение (148.11) приобретает вид

и оба его периодических решения

принадлежат одному и тому же собственному значению  Это полностью согласуется с соотношением (148.13).
Это полностью согласуется с соотношением (148.13).
Если, с другой стороны, значение  очень велико, то вблизи точки
очень велико, то вблизи точки  мы будем иметь очень глубокую потенциальную яму, что практически почти полностью зафиксирует наши частицы на противоположных концах диаметра. В этом случае вместо переменной
мы будем иметь очень глубокую потенциальную яму, что практически почти полностью зафиксирует наши частицы на противоположных концах диаметра. В этом случае вместо переменной  удобно ввести новую переменную
удобно ввести новую переменную

Из соотношений

следует, что функции ичет и онечет будут соответственно четными и нечетными функциями и по отношению к переменной  Если потенциальная яма очень глубока, то в уравнении (148.11) можно написать
Если потенциальная яма очень глубока, то в уравнении (148.11) можно написать

и оно приближенно перейдет в дифференциальное уравнение для гармонического осциллятора:

Как хорошо известно (см. задачу 30), собственные значения для этого уравнения равны

а собственные функции, относящиеся к четным (нечетным)  четны (нечетны) по переменной
четны (нечетны) по переменной  Соотношение (148.17) почти полностью совпадает с соотношением (148.14), если отождествить решения при малых
Соотношение (148.17) почти полностью совпадает с соотношением (148.14), если отождествить решения при малых  с решениями при больших
с решениями при больших  по схеме:
по схеме:
(см. скан)
Дополнительные постоянные, фигурирующие в формулах (148.14), можно получить, удержав в разложении  еще один член,
еще один член,
а затем воспользоваться теорией возмущений. В результате получим

Как оказывается, этот дополнительный член обеспечивает полное согласие между формулами (148.18) и (148.14).
Замечание 1. На фиг. 61 мы изобразили диагонали двух координатных углов: нижняя диагональ отмечает положение минимума потенциальной энергии  верхняя — положение ее максимума
верхняя — положение ее максимума  Собственные значения, разумеется, всегда располагаются выше линии минимума потенциальной энергии. Если они лежат ниже верхней диагонали, то соответствующие им состояния являются колебательными состояниями внутри потенциальной ямы. Так, например, при
Собственные значения, разумеется, всегда располагаются выше линии минимума потенциальной энергии. Если они лежат ниже верхней диагонали, то соответствующие им состояния являются колебательными состояниями внутри потенциальной ямы. Так, например, при  имеются четыре таких колебательных состояния, пятое же собственное значение
имеются четыре таких колебательных состояния, пятое же собственное значение  соответствует состоянию либрационного типа. При либрации движение частиц захватывает всю окружность, так что временами положения обеих частиц совпадают. Первые четыре состояния можно было бы назвать ангармоническими колебаниями. Начиная же с пятого состояния по мере роста энергии движение все более и более приближается к движению невзаимодействующих независимых частиц.
соответствует состоянию либрационного типа. При либрации движение частиц захватывает всю окружность, так что временами положения обеих частиц совпадают. Первые четыре состояния можно было бы назвать ангармоническими колебаниями. Начиная же с пятого состояния по мере роста энергии движение все более и более приближается к движению невзаимодействующих независимых частиц.
Замечание  Относительное движение двух частиц происходит в потенциальном поле того же вида
Относительное движение двух частиц происходит в потенциальном поле того же вида  что и в случае математического маятника. В классической механике эта задача сводится к эллиптическим интегралам, квантовая же задача требует для своего решения, как мы видели, функций Матье. Это снова показывает (см также задачу 40), насколько сложнее в математическом отношении ситуация в задачах квантовой механики по сравнению с аналогичными задачами классической механики.
что и в случае математического маятника. В классической механике эта задача сводится к эллиптическим интегралам, квантовая же задача требует для своего решения, как мы видели, функций Матье. Это снова показывает (см также задачу 40), насколько сложнее в математическом отношении ситуация в задачах квантовой механики по сравнению с аналогичными задачами классической механики.
| << Предыдущий параграф | Следующий параграф >> |
- III. Частицы со спином
- Задача 130. Собственные векторы матриц Паули
- Задача 131. Алгебра спиновых матриц
- Задача 132. Трансформационные свойства спиноров
- Задача 133. Электрон со спином в центральном поле
- Задача 134. Квадрупольный момент при наличии спина
- Задача 135. Среднее значение магнитного момента
- Задача 136. Тонкая структура
- Задача 137. Плоские волны для частиц со спином 1/2
- Задача 138. Спиновый резонанс для свободного электрона
- Б. Двух- и трехчастичные задачи
- Задача 139. Спиновые функции двух частиц
- Задача 140. Центральное взаимодействие между нуклонами, зависящее от спина
- Задача 141. Степени спиновых операторов
- Задача 142. Собственные функции оператора полного момента двух частиц, обладающих спином
- Задача 143. Тензорные силы
- Задача 144. Дейтрон с тензорным взаимодействием
- Задача 145. Электрический квадрупольный и магнитный днпольный моменты дейтрона
- Задача 146. Спиновые функции трех частиц
- Задача 147. Рассеяние нейтронов молекулярным водородом
- IV. Многочастичные задачи
- Задача 148. Две отталкивающиеся частицы на окружности
- Задача 149. Трехатомная линейная молекула
- Задача 150. Движение центра масс
- Задача 151. Теорема вириала
- Задача 152. Определитель Слэтера
- Задача 153. Определитель Слэтера и обменное взаимодействие
- Задача 154. Два атомных электрона в основном состоянии
- Задача 155. Возбужденные состояния атома гелия
- Задача 156. Возбужденные S-состояния атома гелия
- Задача 157. Основное состояние атома лития
- Задача 158. Обменные поправки к основному состоянию атома лития
- Задача 159. Электрическая восприимчивость
- Задача 160. Диамагнитная восприимчивость неона
- Задача 161. Силы Ван-дер-Ваальса
- Задача 162. Обменное вырождение при наличии возбуждения
- Задача 163. Нейтральная молекула водорода
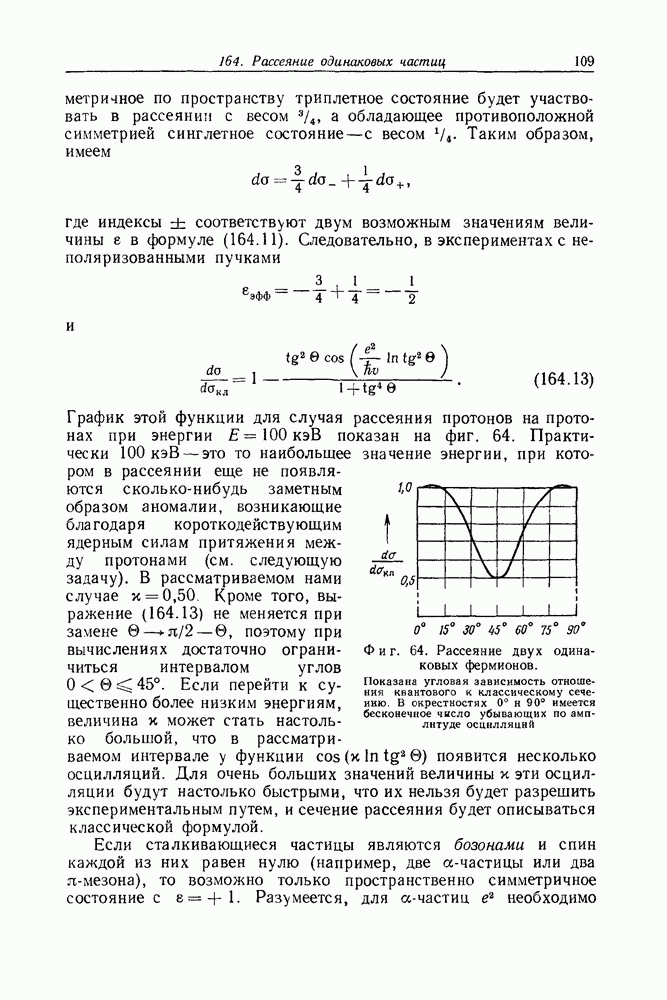
- Задача 164. Рассеяние одинаковых частиц
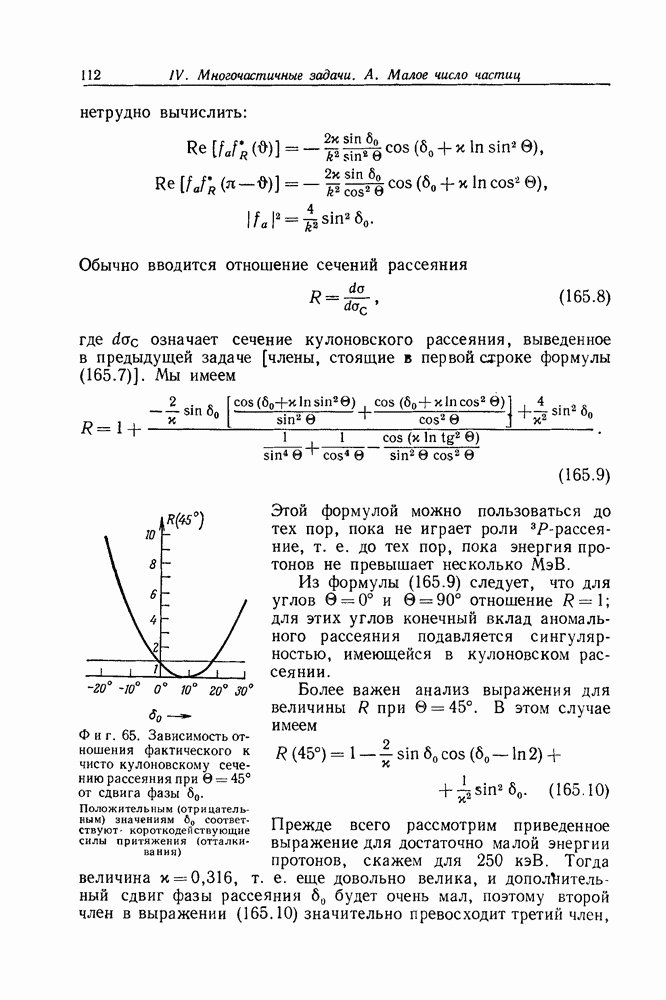
- Задача 165. Аномальное рассеяние протонов на протонах
- Задача 166. Неупругое рассеяние
- Б. Очень большое число частиц. Квантовая статистика
- Задача 167. Электронный газ в металле
- Задача 168. Парамагнитная восприимчивость металла
- Задача 169. Холодная эмиссия без учета сил электростатического изображения
- Задача 170. Холодная эмиссия с учетом сил электростатического изображения
- Задача 171. Белый карлик
- Задача 172. Приближение Томаса — Ферми
- Задача 173. Поправка Амальди для нейтрального атома
- Задача 174. Энергия атома в модели Томаса — Ферми
- Задача 175. Теорема вириала для модели атома Томаса-Ферми
- Задача 176. Приближение Тайтца для модели атома Томаса — Ферми
- Задача 177. Вариационный метод для модели атома Томаса — Ферми
- Задача 178. Влияние экранировки на K-электроны
- V. Нестационарные задачи
- Задача 179. Двухуровневая система под действием не зависящего от времени возмущения
- Задача 180. Действие периодического возмущения на двухуровневую систему
- Задача 181. Теория возмущений Дирака
- Задача 182. Периодическое возмущение и резонанс
- Задача 183. Золотое правило для рассеяния
- Задача 184. Борновское рассеяние в импульсном представлении
- Задача 185. Кулоновское возбуждение атома
- Задача 186. Фотоэффект
- Задача 187. Дисперсия света. Силы осцилляторов
- Задача 188. Спин-флип в магнитной резонансной системе
- VI. Релятивистское уравнение Дирака
- Задача 189. Квадрирование уравнения Дирака
- Задача 190. Плоские волны Дирака с положительной энергией
- Задача 191. Трансформационные свойства дираковских спиноров
- Задача 192. Лоренцевы коварианты
- Задача 193. Пространственная инверсия
- Задача 194. Зарядовое сопряжение
- Задача 195. Состояния со смешанной спиральностью
- Задача 196. Среднее значение спина
- Задача 197. Алгебраические свойства волнового спинора Дирака
- Задача 198. Плотность тока в алгебраической формулировке
- Задача 199. Ток проводимости и ток поляризации
- Задача 200. Уравнение Дирака в двухкомпонентной записи
- Задача 201. Центральные силы в теории Дирака
- Задача 202. Проблема Кеплера в теории Дирака
- Задача 203. Тонкая структура энергетических уровней атома водорода
- Задача 204. Проблема Кеплера. Радиальные функции при положительных энергиях
- Задача 205. Разложение дираковской плоской волны по состояниям с определенным моментом
- Задача 206. Рассеяние в поле центральных сил
- Задача 208. Наклонное падение плоской волны на прямоугольную потенциальную ступеньку
- Задача 209. Отражение от прямоугольной потенциальной ступеньки при наклонном падении
- VII. Теория излучения
- Задача 210. Квантование шредингеровского волнового поля
- Задача 211. Рассеяние в борновском приближении
- Задача 212. Квантование классического поля излучения
- Задача 213. Вероятность переходов с излучением одного фотона
- Задача 214. Угловое распределение излучения
- Задача 215. Полная вероятность перехода
- Задача 216. Правила отбора для дипольного излучения
- Задача 217. Интенсивности линий лаймановской серии
- Задача 218. Эффект Комптона
- Задача 219. Тормозное излучение
- Математическое приложение
- Криволинейные координаты
- Г-функция
- Функции Лежандра
- Сферические гармоники
- Гипергеометрическая функция
- Вырожденная гипергеометрическая функция
- Некоторые функции, определяемые интегралами