| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Задача 218. Эффект Комптона
Ограничившись нерелятивистской теорией, рассмотреть рассеяние фотона на свободном покоящемся электроне.
Решение. При наличии поля излучения плотность электрического тока шредингеровского поля электронов описывается формулой

а взаимодействие полей  и А имеет вид
и А имеет вид

Подставив в энергию взаимодействия вместо квантованного
шредингеровского поля  выражение
выражение

а вместо квантованного поля излучения выражение

легко заметить, что энергия  (она возникает из члена с
(она возникает из члена с  дает вклад в рассеяние уже в первом порядке теории возмущений, энергия же
дает вклад в рассеяние уже в первом порядке теории возмущений, энергия же  (она возникает из члена с
(она возникает из члена с  дает вклад в рассеяние лишь во втором порядке теории возмущений. По этой причине мы сосредоточим наше внимание на энергии взаимодействия
дает вклад в рассеяние лишь во втором порядке теории возмущений. По этой причине мы сосредоточим наше внимание на энергии взаимодействия

Возникновение этого члена в энергии взаимодействия легко объяснимо и с точки зрения классических представлений. Напряженность электрического поля световой волны

падающей на электрон, приводит его в движение, так что

и следовательно,

В результате возникает индуцированная плотность тока

где  плотность заряда. Согласно же теории Максвелла, взаимодействие тока и поля излучения имеет вид
плотность заряда. Согласно же теории Максвелла, взаимодействие тока и поля излучения имеет вид

Если сюда подставить выражение

то в результате мы придем к формуле (218.5).
При комптоновском рассеянии начальный фотон, находящийся в состоянии с квантовыми числами  и начальный электрон с импульсом
и начальный электрон с импульсом  уничтожаются и заменяются фотоном в состоянии
уничтожаются и заменяются фотоном в состоянии
с квантовыми числами к и X и электроном с импульсом  Такой процесс в первом порядке теории возмущений описывается тем членом гамильтониана, который содержит комбинацию операторов
Такой процесс в первом порядке теории возмущений описывается тем членом гамильтониана, который содержит комбинацию операторов

Матричный элемент интересующего нас члена энергии взаимодействия (218.5) имеет вид

Фигурирующий здесь интеграл не обращается в нуль лишь при условии

т. е. в том случае, если в рассматриваемом процессе выполняется закон сохранения импульса. С учетом закона сохранения импульса выражение (218.7) принимает вид

Для определения сечения рассеяния воспользуемся золотым правилом. Имеем

где плотность конечных состояний описывается выражением

а суммарная энергия фотона и электрона в конечном состоянии имеет вид

и

Перейдем теперь к рассмотрению поляризации. На фиг. 75 импульсы фотона  до и после рассеяния расположены в плоскости фигуры. Оба вектора
до и после рассеяния расположены в плоскости фигуры. Оба вектора  также лежат в этой плоскости, а векторы и и (на фигуре они не показаны) перпендикулярны к ней. Скалярные произведения, стоящие в выражении (218.9), как следует непосредственно из фиг. 75,
также лежат в этой плоскости, а векторы и и (на фигуре они не показаны) перпендикулярны к ней. Скалярные произведения, стоящие в выражении (218.9), как следует непосредственно из фиг. 75,
имеют вид

Поэтому в рассматриваемом процессе возможны лишь те переходы, при которых векторы, характеризующие поляризацию соответственно до и после рассеяния, либо оба лежат в плоскости векторов  либо оба перпендикулярны ей.
либо оба перпендикулярны ей.

Фиг. 75. Эффект Комптона. Векторы  характеризующие поляризацию в начальном состоянии
характеризующие поляризацию в начальном состоянии  и конечном состоянии
и конечном состоянии  расположены в плоскости векторов
расположены в плоскости векторов  и
и  векторы
векторы  перпендикулярны этой плоскости (на фигуре они не показаны).
перпендикулярны этой плоскости (на фигуре они не показаны).
В первом случае вероятность перехода пропорциональна  во втором случае она от угла рассеяния не зависит. Если вначале свет не поляризован, то необходимо вероятность перехода усреднить по поляризации А, и просуммировать по конечной поляризации
во втором случае она от угла рассеяния не зависит. Если вначале свет не поляризован, то необходимо вероятность перехода усреднить по поляризации А, и просуммировать по конечной поляризации  Таким образом, получаем
Таким образом, получаем

Ниже будем предполагать, что в начальном состоянии электрон покоился. Это означает, что

тогда с учетом формулы (218.12) закон сохранения энергии можно записать в виде

Так как

то предыдущее равенство представляет собой квадратное уравнение относительно  Его решение имеет вид
Его решение имеет вид

Поскольку, далее, в силу (218.16)

то выражение (218.11) для плотности конечных состояний  можно представить в виде
можно представить в виде

Таким образом, с учетом выражений (218.9), (218.10), (218.14) и (218.18) окончательно получаем

где величина А определяется соотношением (218.17).
До сих пор все наши формулы в рамках нерелятивистской теории были совершенно точными, но, разумеется, ими следует пользоваться только в том случае, если кинетическая энергия электронов мала по сравнению с 

поэтому в формулах (218.17) и (218.19) целесообразно прибегнуть к разложению в ряд по степеням отношения  Имеем
Имеем

и

Отсюда после элементарного интегрирования по угловым переменным получаем выражение для полного сечения рассеяния:

Как хорошо известно из классической электродинамики, в длинноволновом приближении сечение рассматриваемого процесса описывается формулой Томсона:

Фигурирующий в выражении (218.21) дополнительный множитель представляет собой первую квантовую поправку, благодаря
которой величина сечения уменьшается с ростом энергии фотона  Разумеется, мы можем ограничиться только этой поправкой лишь в том случае, если т.е. если длина волны падающего света велика по сравнению с комптоновской длиной волны
Разумеется, мы можем ограничиться только этой поправкой лишь в том случае, если т.е. если длина волны падающего света велика по сравнению с комптоновской длиной волны  или
или  мы имеем
мы имеем 
Замечание 1. Если  то вклад от члена
то вклад от члена  энергии взаимодействия (218.2) во втором порядке теории возмущений равен нулю. При релятивистском рассмотрении интересующего нас процесса обычно для плотности тока используется выражение (199.1), так что комптоновские переходы оказываются возможными лишь во втором порядке теории возмущений. Однако и в релятивистском случае решению можно придать форму, полностью аналогичную приведенной выше, если разбить выражение для плотности тока на две части, как это было сделано в задаче 199.
энергии взаимодействия (218.2) во втором порядке теории возмущений равен нулю. При релятивистском рассмотрении интересующего нас процесса обычно для плотности тока используется выражение (199.1), так что комптоновские переходы оказываются возможными лишь во втором порядке теории возмущений. Однако и в релятивистском случае решению можно придать форму, полностью аналогичную приведенной выше, если разбить выражение для плотности тока на две части, как это было сделано в задаче 199.
Замечание 2. Если энергия фотонов велика, то для описания электронов необходимо пользоваться уравнением Дирака. При этом вместо формулы (218.21) получается формула Клейна-Нишины. Следует, однако, заметить, что наше приближение оказывается хорошим в довольно широкой области энергий. Так, например, при  из (218.21) получаем
из (218.21) получаем  а точная формула Клейна — Нишины дает 0,737. Далее при
а точная формула Клейна — Нишины дает 0,737. Далее при  соответственно имеем 0,333 и 0,431. Фактическая величина сечения рассеяния уменьшается с ростом энергии значительно медленнее, чем это следует из нашей приближенной формулы. Так, например, при
соответственно имеем 0,333 и 0,431. Фактическая величина сечения рассеяния уменьшается с ростом энергии значительно медленнее, чем это следует из нашей приближенной формулы. Так, например, при  вместо точного значения 0,0215 получаем значение
вместо точного значения 0,0215 получаем значение 
| << Предыдущий параграф | Следующий параграф >> |
- III. Частицы со спином
- Задача 130. Собственные векторы матриц Паули
- Задача 131. Алгебра спиновых матриц
- Задача 132. Трансформационные свойства спиноров
- Задача 133. Электрон со спином в центральном поле
- Задача 134. Квадрупольный момент при наличии спина
- Задача 135. Среднее значение магнитного момента
- Задача 136. Тонкая структура
- Задача 137. Плоские волны для частиц со спином 1/2
- Задача 138. Спиновый резонанс для свободного электрона
- Б. Двух- и трехчастичные задачи
- Задача 139. Спиновые функции двух частиц
- Задача 140. Центральное взаимодействие между нуклонами, зависящее от спина
- Задача 141. Степени спиновых операторов
- Задача 142. Собственные функции оператора полного момента двух частиц, обладающих спином
- Задача 143. Тензорные силы
- Задача 144. Дейтрон с тензорным взаимодействием
- Задача 145. Электрический квадрупольный и магнитный днпольный моменты дейтрона
- Задача 146. Спиновые функции трех частиц
- Задача 147. Рассеяние нейтронов молекулярным водородом
- IV. Многочастичные задачи
- Задача 148. Две отталкивающиеся частицы на окружности
- Задача 149. Трехатомная линейная молекула
- Задача 150. Движение центра масс
- Задача 151. Теорема вириала
- Задача 152. Определитель Слэтера
- Задача 153. Определитель Слэтера и обменное взаимодействие
- Задача 154. Два атомных электрона в основном состоянии
- Задача 155. Возбужденные состояния атома гелия
- Задача 156. Возбужденные S-состояния атома гелия
- Задача 157. Основное состояние атома лития
- Задача 158. Обменные поправки к основному состоянию атома лития
- Задача 159. Электрическая восприимчивость
- Задача 160. Диамагнитная восприимчивость неона
- Задача 161. Силы Ван-дер-Ваальса
- Задача 162. Обменное вырождение при наличии возбуждения
- Задача 163. Нейтральная молекула водорода
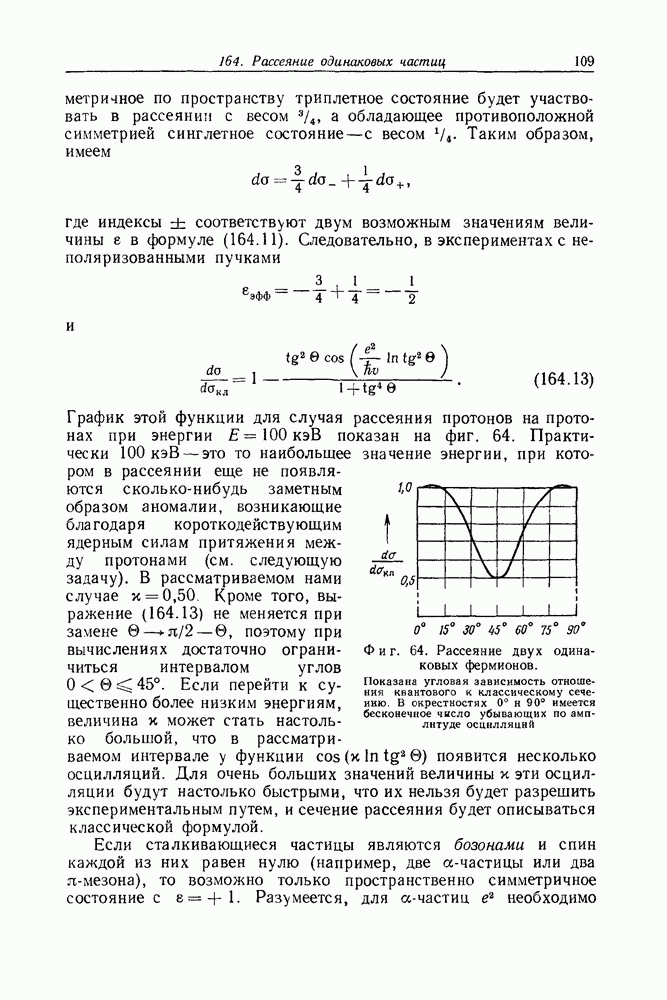
- Задача 164. Рассеяние одинаковых частиц
- Задача 165. Аномальное рассеяние протонов на протонах
- Задача 166. Неупругое рассеяние
- Б. Очень большое число частиц. Квантовая статистика
- Задача 167. Электронный газ в металле
- Задача 168. Парамагнитная восприимчивость металла
- Задача 169. Холодная эмиссия без учета сил электростатического изображения
- Задача 170. Холодная эмиссия с учетом сил электростатического изображения
- Задача 171. Белый карлик
- Задача 172. Приближение Томаса — Ферми
- Задача 173. Поправка Амальди для нейтрального атома
- Задача 174. Энергия атома в модели Томаса — Ферми
- Задача 175. Теорема вириала для модели атома Томаса-Ферми
- Задача 176. Приближение Тайтца для модели атома Томаса — Ферми
- Задача 177. Вариационный метод для модели атома Томаса — Ферми
- Задача 178. Влияние экранировки на K-электроны
- V. Нестационарные задачи
- Задача 179. Двухуровневая система под действием не зависящего от времени возмущения
- Задача 180. Действие периодического возмущения на двухуровневую систему
- Задача 181. Теория возмущений Дирака
- Задача 182. Периодическое возмущение и резонанс
- Задача 183. Золотое правило для рассеяния
- Задача 184. Борновское рассеяние в импульсном представлении
- Задача 185. Кулоновское возбуждение атома
- Задача 186. Фотоэффект
- Задача 187. Дисперсия света. Силы осцилляторов
- Задача 188. Спин-флип в магнитной резонансной системе
- VI. Релятивистское уравнение Дирака
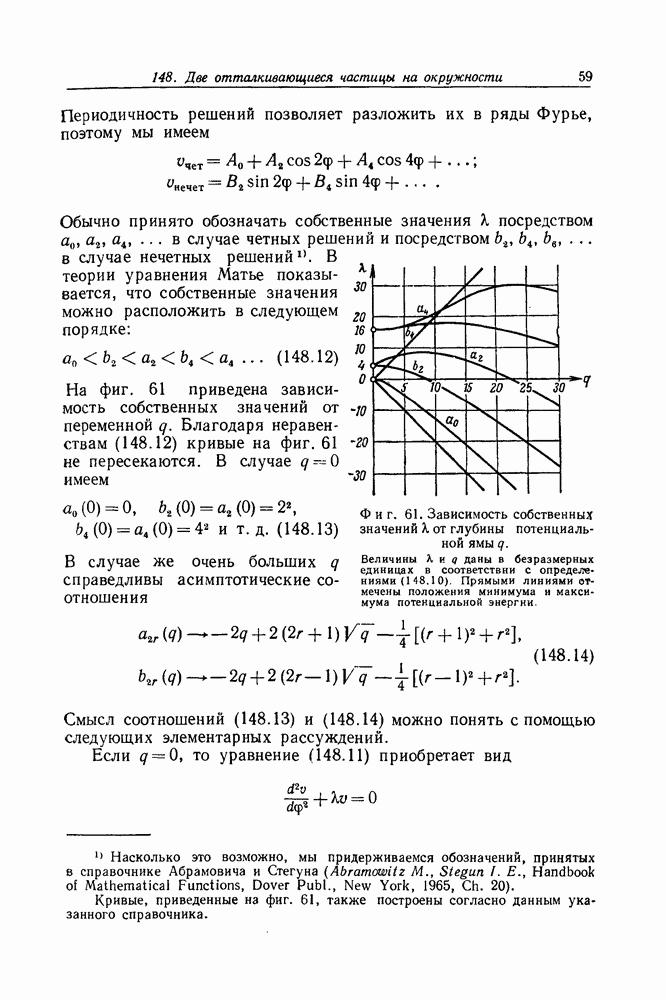
- Задача 189. Квадрирование уравнения Дирака
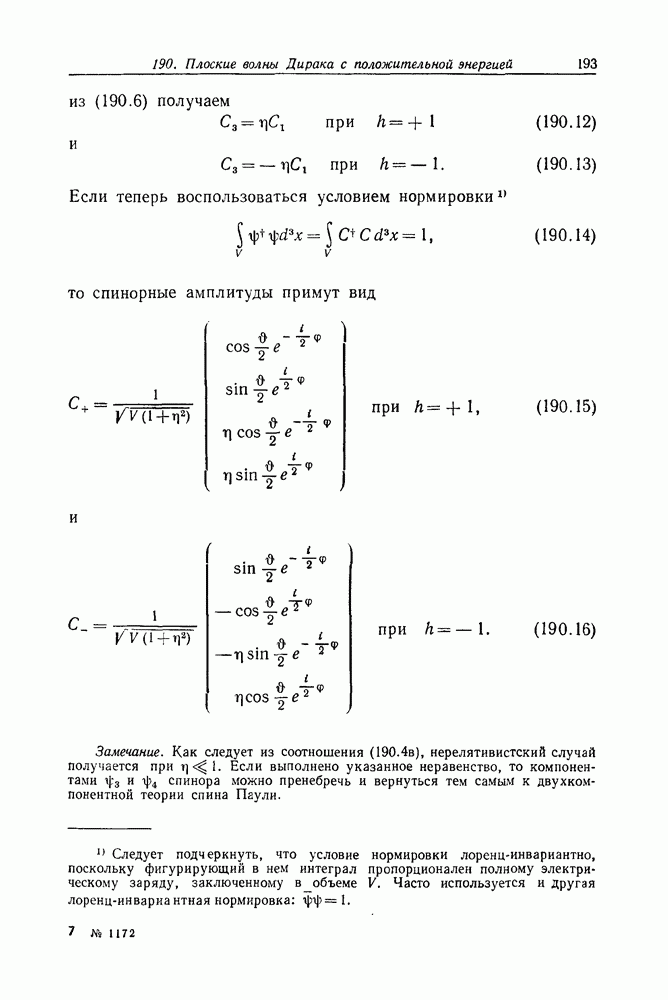
- Задача 190. Плоские волны Дирака с положительной энергией
- Задача 191. Трансформационные свойства дираковских спиноров
- Задача 192. Лоренцевы коварианты
- Задача 193. Пространственная инверсия
- Задача 194. Зарядовое сопряжение
- Задача 195. Состояния со смешанной спиральностью
- Задача 196. Среднее значение спина
- Задача 197. Алгебраические свойства волнового спинора Дирака
- Задача 198. Плотность тока в алгебраической формулировке
- Задача 199. Ток проводимости и ток поляризации
- Задача 200. Уравнение Дирака в двухкомпонентной записи
- Задача 201. Центральные силы в теории Дирака
- Задача 202. Проблема Кеплера в теории Дирака
- Задача 203. Тонкая структура энергетических уровней атома водорода
- Задача 204. Проблема Кеплера. Радиальные функции при положительных энергиях
- Задача 205. Разложение дираковской плоской волны по состояниям с определенным моментом
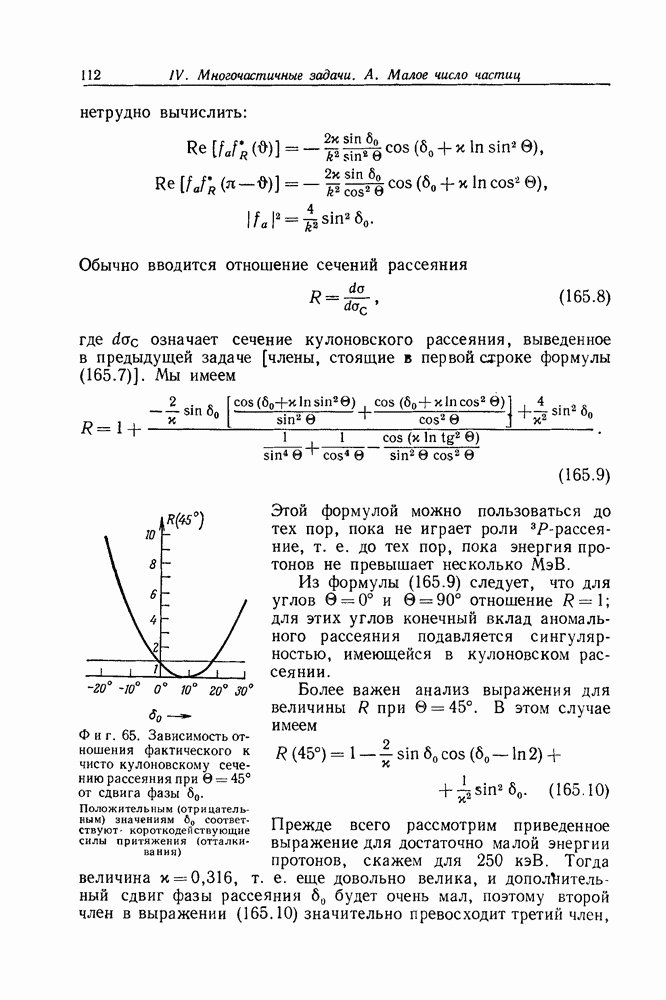
- Задача 206. Рассеяние в поле центральных сил
- Задача 208. Наклонное падение плоской волны на прямоугольную потенциальную ступеньку
- Задача 209. Отражение от прямоугольной потенциальной ступеньки при наклонном падении
- VII. Теория излучения
- Задача 210. Квантование шредингеровского волнового поля
- Задача 211. Рассеяние в борновском приближении
- Задача 212. Квантование классического поля излучения
- Задача 213. Вероятность переходов с излучением одного фотона
- Задача 214. Угловое распределение излучения
- Задача 215. Полная вероятность перехода
- Задача 216. Правила отбора для дипольного излучения
- Задача 217. Интенсивности линий лаймановской серии
- Задача 218. Эффект Комптона
- Задача 219. Тормозное излучение
- Математическое приложение
- Криволинейные координаты
- Г-функция
- Функции Лежандра
- Сферические гармоники
- Гипергеометрическая функция
- Вырожденная гипергеометрическая функция
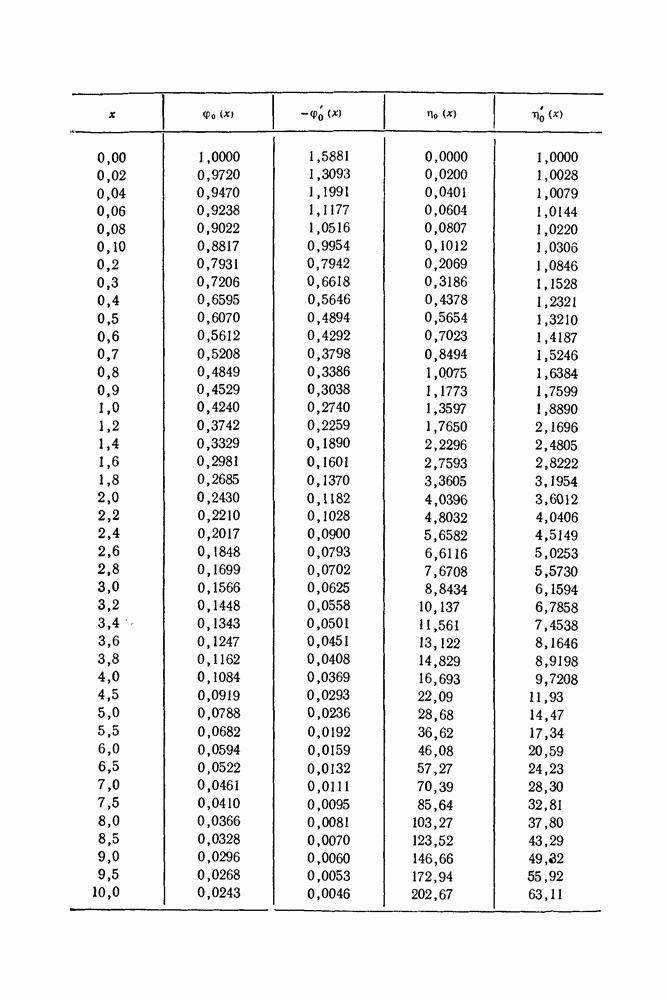
- Некоторые функции, определяемые интегралами