| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Задача 172. Приближение Томаса — Ферми
Рассчитать плотность электронов в атоме (или положительном ионе). Чтобы получить приемлемое приближение, предположите, что во всякой области, где электростатический потенциал можно считать практически постоянным, имеется достаточно большое число электронов, так что их допустимо рассматривать статистически.
Решение. В основу этой модели атома положено две идеи: одна заимствована из электростатики, другая — из квантовой статистики. Мы начнем с электростатической части нашей задачи. Если на расстоянии  от атомного ядра в единице объема содержится
от атомного ядра в единице объема содержится  электронов, то электростатический потенциал, создаваемый в пространстве совместным действием электронов и атомного ядра, удовлетворяет уравнению Пуассона. Таким образом, первое основное уравнение нашей задачи гласит:
электронов, то электростатический потенциал, создаваемый в пространстве совместным действием электронов и атомного ядра, удовлетворяет уравнению Пуассона. Таким образом, первое основное уравнение нашей задачи гласит:

где  - плотность заряда электронного облака. На решение этого уравнения необходимо наложить два граничных условия: в непосредственной близости от ядра с зарядом
- плотность заряда электронного облака. На решение этого уравнения необходимо наложить два граничных условия: в непосредственной близости от ядра с зарядом 

и, кроме того, если  радиус положительного иона с зарядом
радиус положительного иона с зарядом  то
то

Фактическое значение радиуса положительного иона нам предстоит определить в дальнейшем.
На границе иона, т. е. в точках  не должно быть никаких сингулярностей, поэтому здесь непрерывен не только потенциал, но и напряженность поля. В связи с этим граничное условие (172.3) можно переписать по-иному:
не должно быть никаких сингулярностей, поэтому здесь непрерывен не только потенциал, но и напряженность поля. В связи с этим граничное условие (172.3) можно переписать по-иному:

Перейдем теперь к квантовостатистической части нашей задачи. Рассматривая любой элементарный объем внутри атома (или иона), мы видим, что импульс  всякого находящегося в нем электрона связан с его энергией соотношением
всякого находящегося в нем электрона связан с его энергией соотношением

Чтобы электрон был в связанном состоянии, эта энергия во внутренних областях атома, очевидно, не должна превышать потенциальную энергию на его границе. Отсюда следует, что импульс электрона, находящегося на расстоянии  от ядра, не может быть больше рмакс, где
от ядра, не может быть больше рмакс, где

Согласно же квантовой статистике, величина рмакс связана с плотностью электронов  (см. задачу 167) соотношением
(см. задачу 167) соотношением

Сравнение соотношений (172.5) и (172.6) приводит к другому основному уравнению нашей задачи:

Уравнения (172.1) и (172.7) в принципе позволяют определить обе неизвестные функции  и
и  Исключая функцию
Исключая функцию  и пользуясь сферической симметрией задачи, получаем
и пользуясь сферической симметрией задачи, получаем

Вводя вместо  безразмерную функцию
безразмерную функцию

а вместо независимой переменной  безразмерную переменную
безразмерную переменную

где

приходим к универсальному дифференциальному уравнению

Граничные условия (172.2) и (172.4) теперь принимают вид

и

причем выше мы положили 
Необходимо подчеркнуть, что при таких граничных условиях все  электронов действительно заключены внутри сферы радиуса
электронов действительно заключены внутри сферы радиуса  . В этом можно убедиться следующим образом. Из уравнения (172.7) и соотношения (172.9) следует
. В этом можно убедиться следующим образом. Из уравнения (172.7) и соотношения (172.9) следует

С помощью уравнения (172.10) функцию  фигурирующую в последнем интеграле, можно выразить через производную
фигурирующую в последнем интеграле, можно выразить через производную  так что этот интеграл будет равен
так что этот интеграл будет равен

С учетом же граничных условий (172.11) и (172.12) последнее выражение попросту равно

Таким образом, число электронов, заключенных внутри сферы радиуса  действительно равно
действительно равно 
Мы свели нашу задачу к интегрированию универсального уравнения (172.10) при граничных условиях (172.11) и (172.12). Чтобы получить общее представление о разнообразии решений этого дифференциального уравнения, целесообразно проинтегрировать его при одном и том же начальном условии  и различном наклоне касательных в начальной точке
и различном наклоне касательных в начальной точке  . Четыре таких решения показаны на фиг. 69. Кривым
. Четыре таких решения показаны на фиг. 69. Кривым  и 2 соответствуют конечные радиусы X, и
и 2 соответствуют конечные радиусы X, и  так как в обоих случаях
так как в обоих случаях  Оба указанных решения, согласно условию (172.12), описывают положительные ионы. Для нейтрального атома из (172.12) следует, что
Оба указанных решения, согласно условию (172.12), описывают положительные ионы. Для нейтрального атома из (172.12) следует, что  Это условие не удовлетворяется ни при каком конечном значении
Это условие не удовлетворяется ни при каком конечном значении  На фиг. 69 такому случаю соответствует кривая 3 (радиус атома бесконечен). Что касается кривой 4, то для свободных атомов или ионов она не имеет непосредственного физического смысла, однако с ее помощью можно
На фиг. 69 такому случаю соответствует кривая 3 (радиус атома бесконечен). Что касается кривой 4, то для свободных атомов или ионов она не имеет непосредственного физического смысла, однако с ее помощью можно

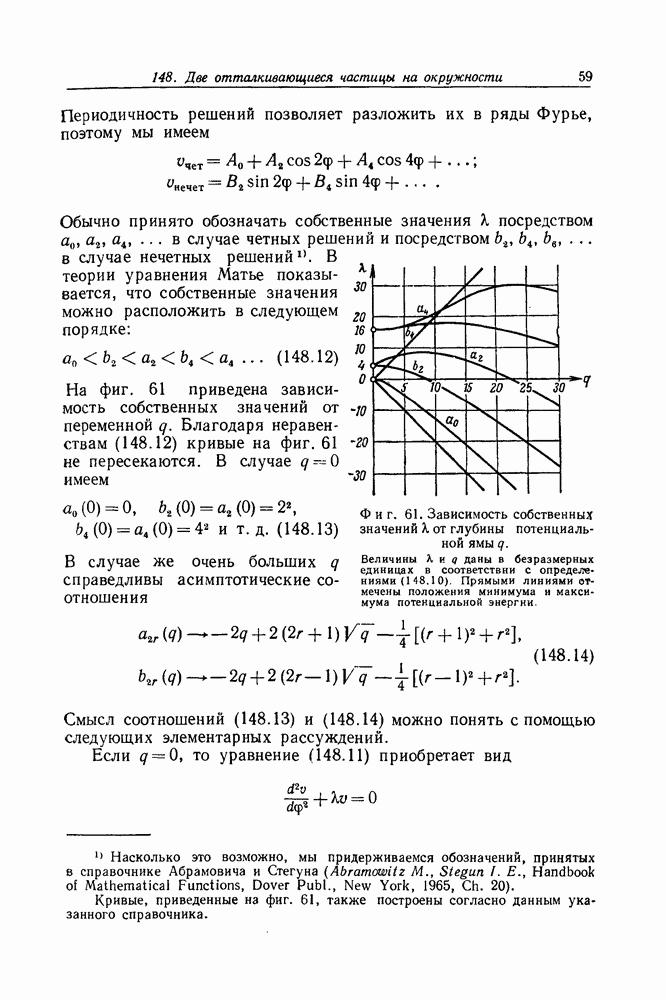
Фиг. 69. Решения уравнения Томаса — Ферми (172.10), отличающиеся наклоном касательной в начальной точке.
описывать атомы, связанные внутри кристаллической решетки (разумеется, граничные условия в этом случае будут совсем иными).
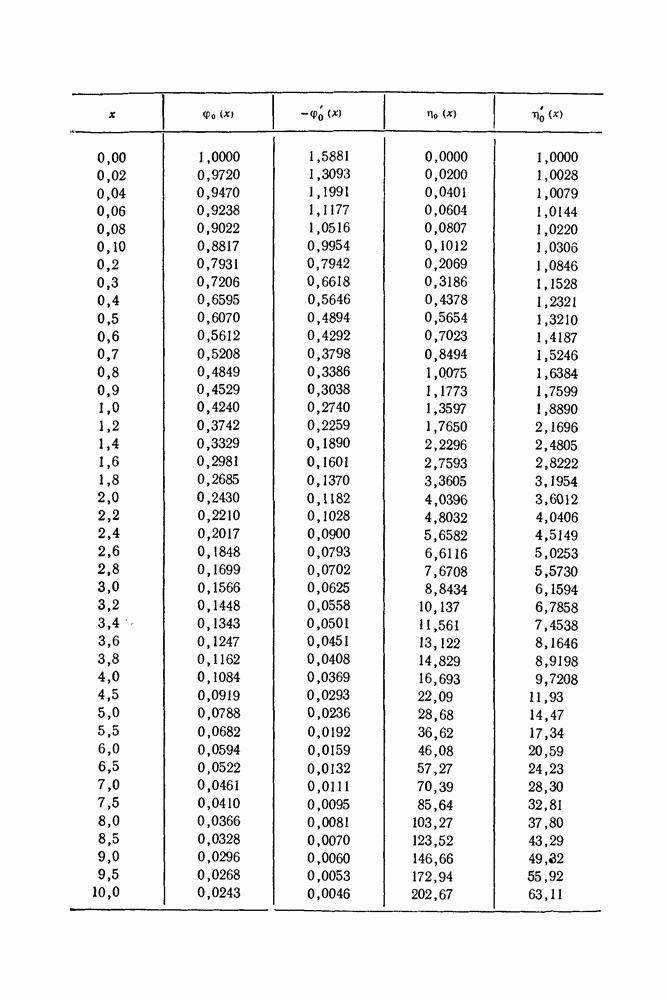
Ниже нас главным образом будет интересовать кривая 3, соответствующая нейтральному атому. Мы назовем полученное решение стандартным и будем обозначать его через  Числовые значения функции
Числовые значения функции  приведены в нижеследующей таблице. Наклон касательной в начальной точке в рассматриваемом случае характеризуется значением
приведены в нижеследующей таблице. Наклон касательной в начальной точке в рассматриваемом случае характеризуется значением  , а асимптотическое поведение имеет вид
, а асимптотическое поведение имеет вид  [заметим, кстати, что указанная асимптотика является точным решением дифференциального уравнения (172.10), однако при
[заметим, кстати, что указанная асимптотика является точным решением дифференциального уравнения (172.10), однако при  это решение имеет сингулярность]. Для практических целей приведенное асимптотическое выражение малопригодно, так как даже при
это решение имеет сингулярность]. Для практических целей приведенное асимптотическое выражение малопригодно, так как даже при  оно отличается от точного решения
оно отличается от точного решения  примерно на 40%. Надо, однако, иметь в виду, что истинный потенциал нейтрального атома
примерно на 40%. Надо, однако, иметь в виду, что истинный потенциал нейтрального атома  должен убывать по мере роста х значительно быстрее, во всяком случае убывание должно быть экспоненциальным. Ошибка, свойственная модели Томаса — Ферми, как и любой другой статистической модели, быстро возрастаете уменьшением числа частиц. На больших расстояниях число частиц становится сколь угодно малым, поэтому нельзя ожидать, что там наше приближение, каким бы хорошим оно ни было во внутренних областях атома, будет оставаться пригодным.
должен убывать по мере роста х значительно быстрее, во всяком случае убывание должно быть экспоненциальным. Ошибка, свойственная модели Томаса — Ферми, как и любой другой статистической модели, быстро возрастаете уменьшением числа частиц. На больших расстояниях число частиц становится сколь угодно малым, поэтому нельзя ожидать, что там наше приближение, каким бы хорошим оно ни было во внутренних областях атома, будет оставаться пригодным.
Чтобы получить решения, близкие к стандартному, можно положить

так что для малых отклонений  из (172.10) получается линеаризованное уравнение
из (172.10) получается линеаризованное уравнение

Кроме того, чтобы удовлетворить граничному условию (172.11), необходимо положить  В целях стандартизации можно также потребовать, чтобы выполнялось равенство
В целях стандартизации можно также потребовать, чтобы выполнялось равенство  а граничному условию (172.12) удовлетворить путем подходящего выбора параметра
а граничному условию (172.12) удовлетворить путем подходящего выбора параметра  Таким образом, имеем
Таким образом, имеем

Соотношение (172.15а) устанавливает простую связь между параметром  и радиусом положительного иона
и радиусом положительного иона  Значения функции
Значения функции  и ее производной
и ее производной  приведены в таблице.
приведены в таблице.
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- III. Частицы со спином
- Задача 130. Собственные векторы матриц Паули
- Задача 131. Алгебра спиновых матриц
- Задача 132. Трансформационные свойства спиноров
- Задача 133. Электрон со спином в центральном поле
- Задача 134. Квадрупольный момент при наличии спина
- Задача 135. Среднее значение магнитного момента
- Задача 136. Тонкая структура
- Задача 137. Плоские волны для частиц со спином 1/2
- Задача 138. Спиновый резонанс для свободного электрона
- Б. Двух- и трехчастичные задачи
- Задача 139. Спиновые функции двух частиц
- Задача 140. Центральное взаимодействие между нуклонами, зависящее от спина
- Задача 141. Степени спиновых операторов
- Задача 142. Собственные функции оператора полного момента двух частиц, обладающих спином
- Задача 143. Тензорные силы
- Задача 144. Дейтрон с тензорным взаимодействием
- Задача 145. Электрический квадрупольный и магнитный днпольный моменты дейтрона
- Задача 146. Спиновые функции трех частиц
- Задача 147. Рассеяние нейтронов молекулярным водородом
- IV. Многочастичные задачи
- Задача 148. Две отталкивающиеся частицы на окружности
- Задача 149. Трехатомная линейная молекула
- Задача 150. Движение центра масс
- Задача 151. Теорема вириала
- Задача 152. Определитель Слэтера
- Задача 153. Определитель Слэтера и обменное взаимодействие
- Задача 154. Два атомных электрона в основном состоянии
- Задача 155. Возбужденные состояния атома гелия
- Задача 156. Возбужденные S-состояния атома гелия
- Задача 157. Основное состояние атома лития
- Задача 158. Обменные поправки к основному состоянию атома лития
- Задача 159. Электрическая восприимчивость
- Задача 160. Диамагнитная восприимчивость неона
- Задача 161. Силы Ван-дер-Ваальса
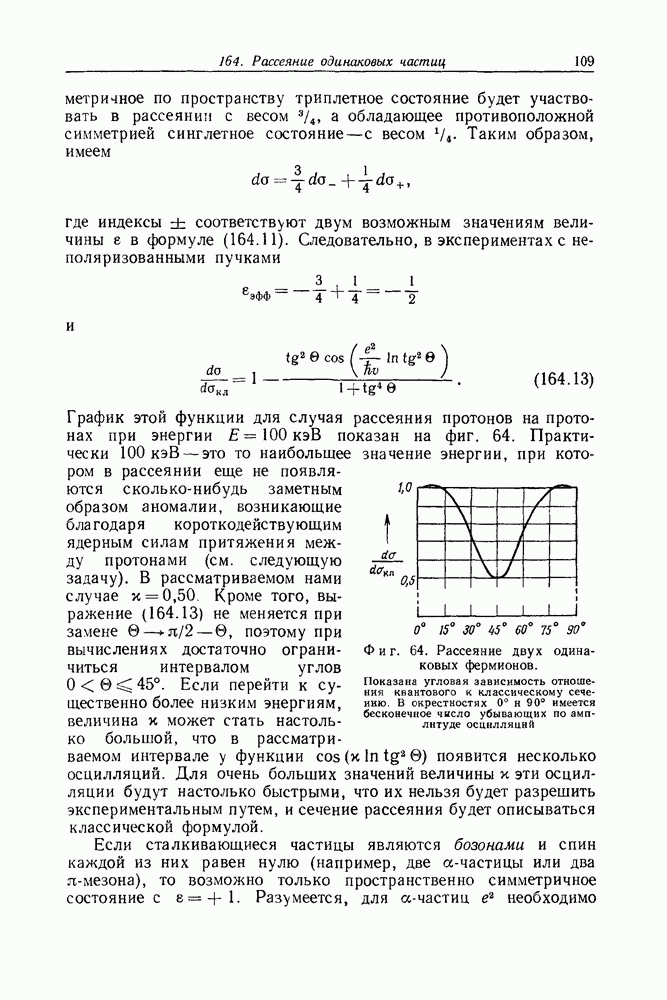
- Задача 162. Обменное вырождение при наличии возбуждения
- Задача 163. Нейтральная молекула водорода
- Задача 164. Рассеяние одинаковых частиц
- Задача 165. Аномальное рассеяние протонов на протонах
- Задача 166. Неупругое рассеяние
- Б. Очень большое число частиц. Квантовая статистика
- Задача 167. Электронный газ в металле
- Задача 168. Парамагнитная восприимчивость металла
- Задача 169. Холодная эмиссия без учета сил электростатического изображения
- Задача 170. Холодная эмиссия с учетом сил электростатического изображения
- Задача 171. Белый карлик
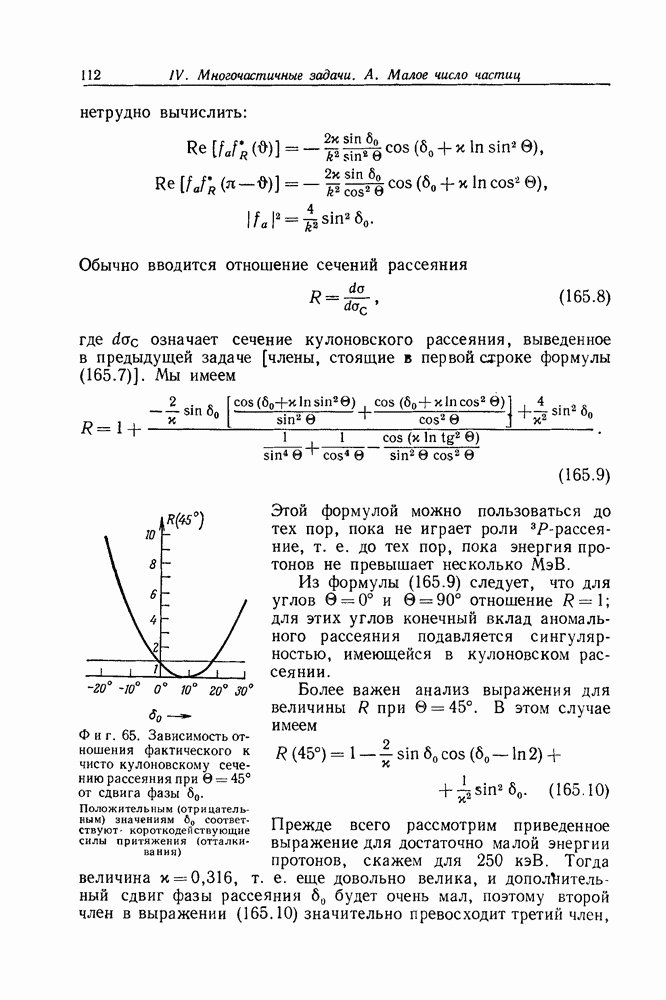
- Задача 172. Приближение Томаса — Ферми
- Задача 173. Поправка Амальди для нейтрального атома
- Задача 174. Энергия атома в модели Томаса — Ферми
- Задача 175. Теорема вириала для модели атома Томаса-Ферми
- Задача 176. Приближение Тайтца для модели атома Томаса — Ферми
- Задача 177. Вариационный метод для модели атома Томаса — Ферми
- Задача 178. Влияние экранировки на K-электроны
- V. Нестационарные задачи
- Задача 179. Двухуровневая система под действием не зависящего от времени возмущения
- Задача 180. Действие периодического возмущения на двухуровневую систему
- Задача 181. Теория возмущений Дирака
- Задача 182. Периодическое возмущение и резонанс
- Задача 183. Золотое правило для рассеяния
- Задача 184. Борновское рассеяние в импульсном представлении
- Задача 185. Кулоновское возбуждение атома
- Задача 186. Фотоэффект
- Задача 187. Дисперсия света. Силы осцилляторов
- Задача 188. Спин-флип в магнитной резонансной системе
- VI. Релятивистское уравнение Дирака
- Задача 189. Квадрирование уравнения Дирака
- Задача 190. Плоские волны Дирака с положительной энергией
- Задача 191. Трансформационные свойства дираковских спиноров
- Задача 192. Лоренцевы коварианты
- Задача 193. Пространственная инверсия
- Задача 194. Зарядовое сопряжение
- Задача 195. Состояния со смешанной спиральностью
- Задача 196. Среднее значение спина
- Задача 197. Алгебраические свойства волнового спинора Дирака
- Задача 198. Плотность тока в алгебраической формулировке
- Задача 199. Ток проводимости и ток поляризации
- Задача 200. Уравнение Дирака в двухкомпонентной записи
- Задача 201. Центральные силы в теории Дирака
- Задача 202. Проблема Кеплера в теории Дирака
- Задача 203. Тонкая структура энергетических уровней атома водорода
- Задача 204. Проблема Кеплера. Радиальные функции при положительных энергиях
- Задача 205. Разложение дираковской плоской волны по состояниям с определенным моментом
- Задача 206. Рассеяние в поле центральных сил
- Задача 208. Наклонное падение плоской волны на прямоугольную потенциальную ступеньку
- Задача 209. Отражение от прямоугольной потенциальной ступеньки при наклонном падении
- VII. Теория излучения
- Задача 210. Квантование шредингеровского волнового поля
- Задача 211. Рассеяние в борновском приближении
- Задача 212. Квантование классического поля излучения
- Задача 213. Вероятность переходов с излучением одного фотона
- Задача 214. Угловое распределение излучения
- Задача 215. Полная вероятность перехода
- Задача 216. Правила отбора для дипольного излучения
- Задача 217. Интенсивности линий лаймановской серии
- Задача 218. Эффект Комптона
- Задача 219. Тормозное излучение
- Математическое приложение
- Криволинейные координаты
- Г-функция
- Функции Лежандра
- Сферические гармоники
- Гипергеометрическая функция
- Вырожденная гипергеометрическая функция
- Некоторые функции, определяемые интегралами