| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Задача 171. Белый карлик
Предположим, что температура белого карлика достаточно высока и поэтому все атомы практически полностью ионизованы. Кроме того, будем считать, что эта температура все еще настолько мала, что можно пренебречь давлением газа и давлением излучения по сравнению с давлением вырожденного электронного газа при абсолютном нуле температур (это второе предположение не является вполне удовлетворительным). Считая, что давление, соответствующее абсолютному нулю температур, уравновешивается силами гравитационного притяжения, найти распределение плотности вещества по объему звезды. Масса звезды предполагается заданной.
Решение. В сферически симметричной массе газа градиент давления в направлении радиуса должен равняться плотности гравитационных сил (барометрическая формула):

Здесь  - гравитационная постоянная,
- гравитационная постоянная,  — масса вещества, заключенная внутри сферы радиуса
— масса вещества, заключенная внутри сферы радиуса 

и, наконец,  плотность вещества, т. е. масса всех ионов и всех свободных электронов, находящихся в
плотность вещества, т. е. масса всех ионов и всех свободных электронов, находящихся в  звездного вещества. При полной ионизации в
звездного вещества. При полной ионизации в  наряду с
наряду с  электронами содержится
электронами содержится  ионов (ядер), поэтому
ионов (ядер), поэтому

где  масса нейтрального атома. Если вещество звезды содержит различные элементы, то фигурирующие здесь
масса нейтрального атома. Если вещество звезды содержит различные элементы, то фигурирующие здесь  надо понимать как некие средние значения. В этой связи необходимо отметить, что отношение
надо понимать как некие средние значения. В этой связи необходимо отметить, что отношение

почти не зависит от химического состава: величина а меняется от 1,0 до 1,3 при переходе от легких элементов к тяжелым, и лишь водород, для которого  представляете этом отношении исключение. Таким образом, плотность вещества
представляете этом отношении исключение. Таким образом, плотность вещества

практически зависит лишь от плотности электронов.
Согласно результатам задачи 167, давление электронного газа при абсолютном нуле определяется формулой

Что касается давления газа ионов,  то при абсолютном нуле оно (будучи пропорциональным
то при абсолютном нуле оно (будучи пропорциональным  значительно меньше давления
значительно меньше давления 

Даже в случае водорода  мы имеем
мы имеем  ; для других элементов отношение
; для других элементов отношение  еще меньше. По этой причине мы пренебрежем величиной
еще меньше. По этой причине мы пренебрежем величиной  и отождествим давление электронного газа
и отождествим давление электронного газа  фигурирующее в формуле (171.5) с полным давлением
фигурирующее в формуле (171.5) с полным давлением 
Обойтись без рассмотрения температурных эффектов далеко не так просто. Газ можно считать сильно вырожденным только в том случае, когда 
При этом условии давление газа практически не отличается от давления при абсолютном нуле. Для электронов энергия Ферми определяется формулой

Вычисленные с помощью этой формулы значения  надо сравнить со значениями тепловой энергии. При температуре
надо сравнить со значениями тепловой энергии. При температуре  мы имеем
мы имеем  и даже для плотности
и даже для плотности  обе величины оказываются одного порядка. При этом газ ионов вообще будет невырожденным, а его вклад в полное давление будет сравним с вкладом электронного газа. Что же касается радиационного давления, то для него справедлива формула
обе величины оказываются одного порядка. При этом газ ионов вообще будет невырожденным, а его вклад в полное давление будет сравним с вкладом электронного газа. Что же касается радиационного давления, то для него справедлива формула

С другой стороны, согласно (171.6) и (171.4), имеем

При  радиационное давление по порядку величины равно
радиационное давление по порядку величины равно  , и для плотностей вещества, с которыми мы сталкиваемся в белых карликах, его действительно можно не учитывать.
, и для плотностей вещества, с которыми мы сталкиваемся в белых карликах, его действительно можно не учитывать.
Комбинируя формулы (171.5) и (171.4), получаем уравнение состояния

где

Когда функциональная связь между давлением и плотностью имеет вид

то говорят, что мы имеем политропу с показателем  Таким образом, можно сказать, что состояние вещества в белом карлике описывается политропой с показателем
Таким образом, можно сказать, что состояние вещества в белом карлике описывается политропой с показателем 
Подставляя выражение (171.6) в условие равновесия (171.1), получаем

Отсюда путем дифференцирования находим

Вместо плотности  удобно ввести безразмерную функцию
удобно ввести безразмерную функцию

где  - некоторая постоянная, а вместо радиуса
- некоторая постоянная, а вместо радиуса  -безразмерную переменную
-безразмерную переменную

где величина  используется в качестве единицы длины и определяется соотношением
используется в качестве единицы длины и определяется соотношением

В результате этих преобразований уравнение (171.7) приводится к виду, не зависящему ни от каких физических постоянных:

Если мы отождествим постоянную  с плотностью вещества в центре звезды, то к уравнению (171.11) надо присоединить начальные условия
с плотностью вещества в центре звезды, то к уравнению (171.11) надо присоединить начальные условия

Единственное решение нелинейного дифференциального уравнения (171.11), удовлетворяющее начальным условиям (171.12), находится путем численного интегрирования. Это решение монотонно убывает и в точке

обращается в нуль  В этой же точке
В этой же точке

Согласно соотношению (171.8), нуль функции  определяет радиус звезды
определяет радиус звезды  Зная радиус звезды, можно записать ее полную массу:
Зная радиус звезды, можно записать ее полную массу:

Последний интеграл можно вычислить, не зная всех числовых значений функции  Действительно, в силу уравнения (171.11) имеем
Действительно, в силу уравнения (171.11) имеем

поэтому

Когда масса звезды известна из опыта, между величинами  в силу (171.10) и (171.14) имеется два соотношения:
в силу (171.10) и (171.14) имеется два соотношения:

где

и

где

Отсюда

так что радиус звезды  можно записать теперь в виде
можно записать теперь в виде

Для средней плотности звездного вещества имеем

следовательно, она составляет примерно  плотности вещества в центре звезды.
плотности вещества в центре звезды.
Числовой пример. Наблюдения за движением Сириуса показывают, что Сириус В, входящий в состав этой двойной звезды, имеет массу, примерно равную массе Солнца, а именно  Таким образом, в данном случае
Таким образом, в данном случае

Известно также, что радиус Сириуса В составляет примерно  радиуса Солнца
радиуса Солнца  см); этому в нашей Модели соответствует значение
см); этому в нашей Модели соответствует значение  Найденное значение довольно близко к значению
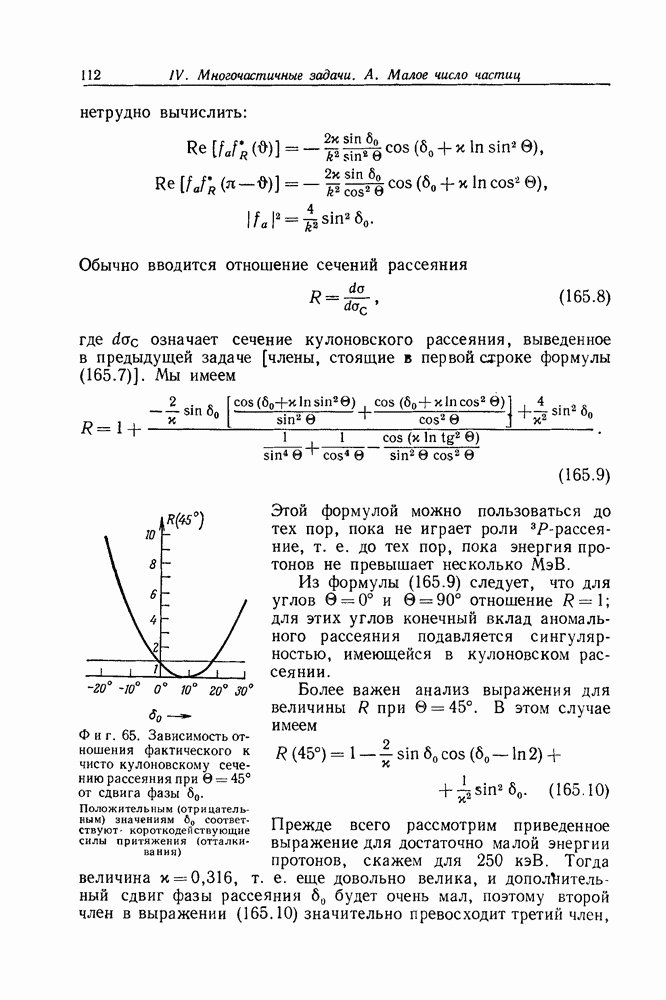
Найденное значение довольно близко к значению  для водородной звезды, хотя и располагается с неправильной стороны. Надо, однако, иметь в виду, что в нашей модели для радиуса звезды получается заниженное значение, так как при вычислениях мы не учитывали температурные эффекты и, следовательно, отбросили существенную часть давления. Фактически звезда должна раздуться до заметно больших размеров.
для водородной звезды, хотя и располагается с неправильной стороны. Надо, однако, иметь в виду, что в нашей модели для радиуса звезды получается заниженное значение, так как при вычислениях мы не учитывали температурные эффекты и, следовательно, отбросили существенную часть давления. Фактически звезда должна раздуться до заметно больших размеров.
| << Предыдущий параграф | Следующий параграф >> |
- III. Частицы со спином
- Задача 130. Собственные векторы матриц Паули
- Задача 131. Алгебра спиновых матриц
- Задача 132. Трансформационные свойства спиноров
- Задача 133. Электрон со спином в центральном поле
- Задача 134. Квадрупольный момент при наличии спина
- Задача 135. Среднее значение магнитного момента
- Задача 136. Тонкая структура
- Задача 137. Плоские волны для частиц со спином 1/2
- Задача 138. Спиновый резонанс для свободного электрона
- Б. Двух- и трехчастичные задачи
- Задача 139. Спиновые функции двух частиц
- Задача 140. Центральное взаимодействие между нуклонами, зависящее от спина
- Задача 141. Степени спиновых операторов
- Задача 142. Собственные функции оператора полного момента двух частиц, обладающих спином
- Задача 143. Тензорные силы
- Задача 144. Дейтрон с тензорным взаимодействием
- Задача 145. Электрический квадрупольный и магнитный днпольный моменты дейтрона
- Задача 146. Спиновые функции трех частиц
- Задача 147. Рассеяние нейтронов молекулярным водородом
- IV. Многочастичные задачи
- Задача 148. Две отталкивающиеся частицы на окружности
- Задача 149. Трехатомная линейная молекула
- Задача 150. Движение центра масс
- Задача 151. Теорема вириала
- Задача 152. Определитель Слэтера
- Задача 153. Определитель Слэтера и обменное взаимодействие
- Задача 154. Два атомных электрона в основном состоянии
- Задача 155. Возбужденные состояния атома гелия
- Задача 156. Возбужденные S-состояния атома гелия
- Задача 157. Основное состояние атома лития
- Задача 158. Обменные поправки к основному состоянию атома лития
- Задача 159. Электрическая восприимчивость
- Задача 160. Диамагнитная восприимчивость неона
- Задача 161. Силы Ван-дер-Ваальса
- Задача 162. Обменное вырождение при наличии возбуждения
- Задача 163. Нейтральная молекула водорода
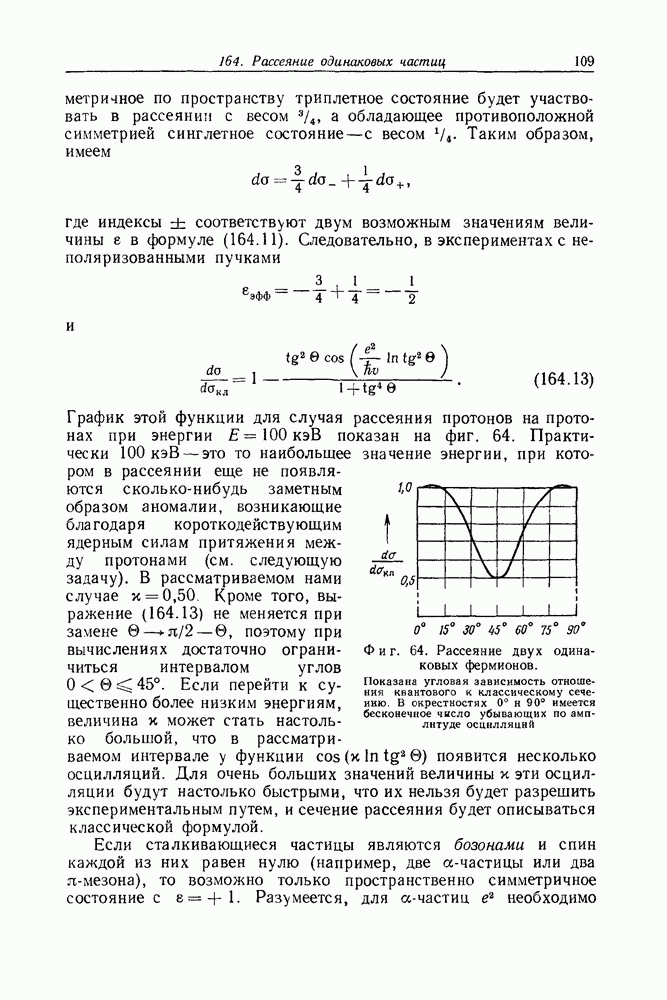
- Задача 164. Рассеяние одинаковых частиц
- Задача 165. Аномальное рассеяние протонов на протонах
- Задача 166. Неупругое рассеяние
- Б. Очень большое число частиц. Квантовая статистика
- Задача 167. Электронный газ в металле
- Задача 168. Парамагнитная восприимчивость металла
- Задача 169. Холодная эмиссия без учета сил электростатического изображения
- Задача 170. Холодная эмиссия с учетом сил электростатического изображения
- Задача 171. Белый карлик
- Задача 172. Приближение Томаса — Ферми
- Задача 173. Поправка Амальди для нейтрального атома
- Задача 174. Энергия атома в модели Томаса — Ферми
- Задача 175. Теорема вириала для модели атома Томаса-Ферми
- Задача 176. Приближение Тайтца для модели атома Томаса — Ферми
- Задача 177. Вариационный метод для модели атома Томаса — Ферми
- Задача 178. Влияние экранировки на K-электроны
- V. Нестационарные задачи
- Задача 179. Двухуровневая система под действием не зависящего от времени возмущения
- Задача 180. Действие периодического возмущения на двухуровневую систему
- Задача 181. Теория возмущений Дирака
- Задача 182. Периодическое возмущение и резонанс
- Задача 183. Золотое правило для рассеяния
- Задача 184. Борновское рассеяние в импульсном представлении
- Задача 185. Кулоновское возбуждение атома
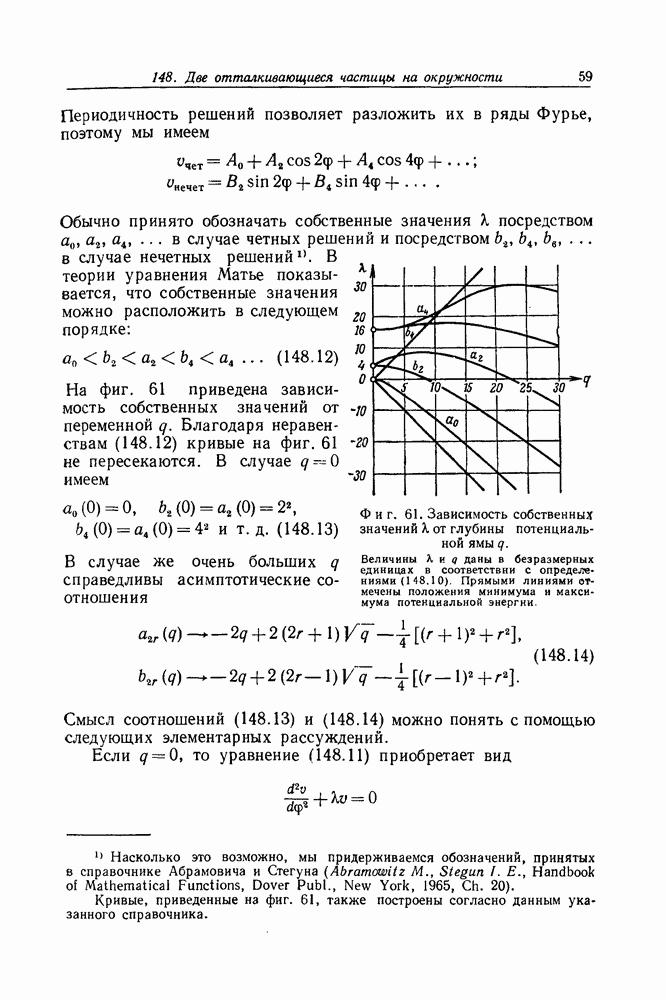
- Задача 186. Фотоэффект
- Задача 187. Дисперсия света. Силы осцилляторов
- Задача 188. Спин-флип в магнитной резонансной системе
- VI. Релятивистское уравнение Дирака
- Задача 189. Квадрирование уравнения Дирака
- Задача 190. Плоские волны Дирака с положительной энергией
- Задача 191. Трансформационные свойства дираковских спиноров
- Задача 192. Лоренцевы коварианты
- Задача 193. Пространственная инверсия
- Задача 194. Зарядовое сопряжение
- Задача 195. Состояния со смешанной спиральностью
- Задача 196. Среднее значение спина
- Задача 197. Алгебраические свойства волнового спинора Дирака
- Задача 198. Плотность тока в алгебраической формулировке
- Задача 199. Ток проводимости и ток поляризации
- Задача 200. Уравнение Дирака в двухкомпонентной записи
- Задача 201. Центральные силы в теории Дирака
- Задача 202. Проблема Кеплера в теории Дирака
- Задача 203. Тонкая структура энергетических уровней атома водорода
- Задача 204. Проблема Кеплера. Радиальные функции при положительных энергиях
- Задача 205. Разложение дираковской плоской волны по состояниям с определенным моментом
- Задача 206. Рассеяние в поле центральных сил
- Задача 208. Наклонное падение плоской волны на прямоугольную потенциальную ступеньку
- Задача 209. Отражение от прямоугольной потенциальной ступеньки при наклонном падении
- VII. Теория излучения
- Задача 210. Квантование шредингеровского волнового поля
- Задача 211. Рассеяние в борновском приближении
- Задача 212. Квантование классического поля излучения
- Задача 213. Вероятность переходов с излучением одного фотона
- Задача 214. Угловое распределение излучения
- Задача 215. Полная вероятность перехода
- Задача 216. Правила отбора для дипольного излучения
- Задача 217. Интенсивности линий лаймановской серии
- Задача 218. Эффект Комптона
- Задача 219. Тормозное излучение
- Математическое приложение
- Криволинейные координаты
- Г-функция
- Функции Лежандра
- Сферические гармоники
- Гипергеометрическая функция
- Вырожденная гипергеометрическая функция
- Некоторые функции, определяемые интегралами