Задача 154. Два атомных электрона в основном состоянии
К-оболочка атома образована двумя электронами в 
-состоянии. Оценить их энергию, воспользовавшись экранированными водородными волновыми функциями в поле бесконечно тяжелого ядра с зарядом 
Решение. Гамильтониан данной задачи, записанный в атомных единицах 
, выглядит следующим образом:
а приближенная волновая функция, согласно задаче 67, имеет вид
здесь
где 
-экранировочная постоянная. Следует ожидать, что 
поскольку действие ядерного заряда на каждый электрон лишь частично экранируется другим электроном. Отдельные сомножители из выражения (154.2) удовлетворяют волновым уравнениям
так что
а выражение для среднего значения энергии принимает вид
Подставляя сюда явное выражение (154.2) для функции 
и учитывая нормировку каждого сомножителя и, получаем 
Первый интеграл в формуле (154.5) вычисляется элементарно:
Чтобы вычислить двойной интеграл
разложим дробь 
по полиномам Лежандра:
где 
угол между векторами 
Вклад в интеграл 
дает только первый член разложения 
поэтому имеем
Так как
то все интегралы вычисляются элементарно, и мы получаем
После подстановки значений интегралов (154.6) и (154.7) среднее значение энергии (154.5) принимает вид
До сих пор мы не налагали на значения а никаких ограничений. Теперь же мы потребуем, чтобы значение а было оптимальным в смысле вариационного исчисления, для этого положим
Отсюда получаем
и
Отметим, что при таком значении а функция (154.2) становится точной собственной функцией гамильтониана
допускающего разделение переменных. Сравнивая выражения (154.12) и (154.1), находим
Если рассматривать теперь 
как энергию возмущения, а экранировочную постоянную 
выбрать в соответствии с равенством (154.10), то в первом порядке теории возмущений сдвиг рассматриваемого уровня
окажется равным нулю.
В заключение рассмотрим несколько числовых примеров. Развитая теория описывает атомы, у которых удалены все электроны, за исключением двух электронов, находящихся на К-оболочке. Мы располагаем экспериментальными данными для
Во всех этих случаях измеряется не сама энергия 
а энергия ионизации 
необходимая для отрыва от иона только одного из двух 
-электронов. Остающийся ион обладает всего одним электроном, поэтому его энергия равна
а для энергии ионизации получаем
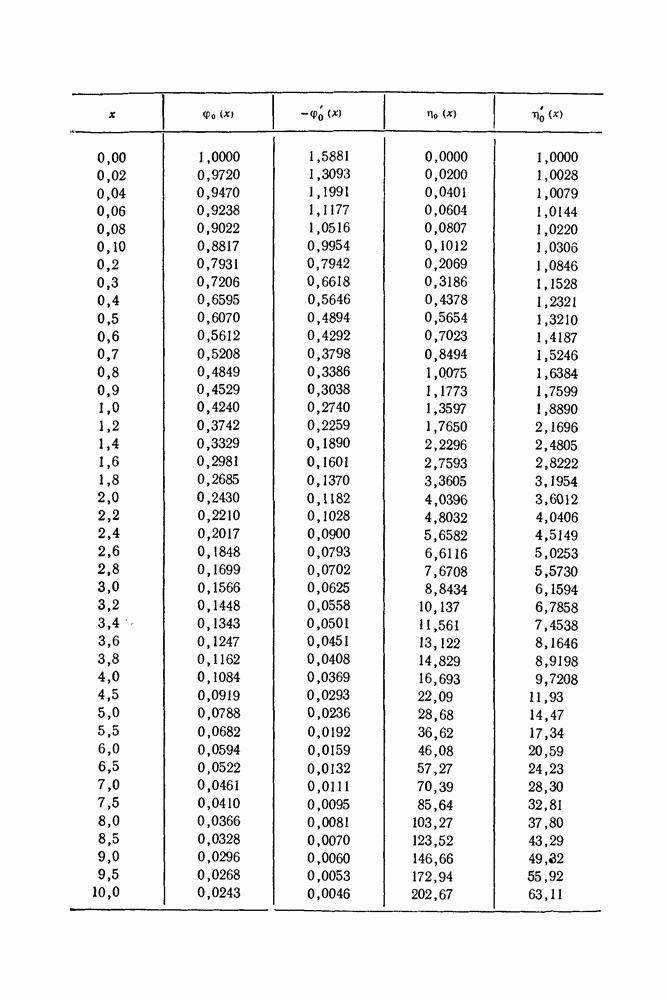
Из приводимой ниже таблицы ясно видно, что согласие экспериментальных данных с формулой (154.13) непрерывно улучшается по мере роста 
(см. скан)
Эта закономерность вполне разумна, так как член 
ответственный за взаимодействие электронов между собой, играет все меньшую роль по мере того, как с ростом 
увеличивается связь каждого электрона с ядром.
