| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Задача 178. Влияние экранировки на K-электроны
Найти поправку к энергии связи  -электрона, обусловленную экранировкой. При расчетах использовать приближение Тайтца для модели атома Томаса — Ферми.
-электрона, обусловленную экранировкой. При расчетах использовать приближение Тайтца для модели атома Томаса — Ферми.
Решение. Предположим, что из атома с зарядом ядра  удалены единичный ядерный заряд и один из двух
удалены единичный ядерный заряд и один из двух  -электронов. В результате такой операции у нас получился бы нейтральный атом с зарядом ядра
-электронов. В результате такой операции у нас получился бы нейтральный атом с зарядом ядра  Если теперь вернуть ядру удаленный ранее положительный заряд, но пренебречь его влиянием на движение оставшихся
Если теперь вернуть ядру удаленный ранее положительный заряд, но пренебречь его влиянием на движение оставшихся  электронов, то полученная таким образом система зарядов будет создавать в пространстве электростатический потенциал, описываемый формулой (ниже используются атомные единицы)
электронов, то полученная таким образом система зарядов будет создавать в пространстве электростатический потенциал, описываемый формулой (ниже используются атомные единицы)

где  - функция Томаса — Ферми от переменной
- функция Томаса — Ферми от переменной

Если теперь добавить к этой системе ранее удаленный  -электрон (заряд —1), то его потенциальная энергия будет равна
-электрон (заряд —1), то его потенциальная энергия будет равна

Для дальнейших расчетов воспользуемся теорией возмущений. Без учета экранировки выражение для потенциальной энергии  -электрона имело бы вид
-электрона имело бы вид

Таким образом, с учетом экранировки имеем

В пренебрежении экранировкой энергия  и соответствующая ей волновая функция
и соответствующая ей волновая функция  -электрона определяются выражениями
-электрона определяются выражениями

Благодаря экранировке энергетический уровень в первом порядке теории возмущений сдвигается на величину

Последнее выражение после подстановки в него функции  принимает вид
принимает вид

Теперь уже можно воспользоваться приближением Тайтца (см. вадачу 176):

Чтобы вычислить интеграл (178.6), перейдем к новой переменной

где

В результате получаем

Фигурирующий здесь интеграл

представляет собой хорошо известную функцию, асимптотическое поведение которой при больших значениях  описывается, рядом
описывается, рядом

Что же касается интеграла от последнего члена в формуле (178.10), то он также выражается через 

Таким образом, находим

Отсюда при  с учетом разложения (178.12) окончательно получаем
с учетом разложения (178.12) окончательно получаем

Переходя к числовым оценкам величины сдвига энергетического уровня  прежде всего заметим, что параметр
прежде всего заметим, что параметр  определяемый формулой (178.9), действительно велик (см. также приведенную ниже таблицу), поэтому приближение (178.15) является вполне разумным. В третьем столбце таблицы даны значения выражения, стоящего в круглых скобках в формуле (178.15) (начальные члены этого ряда быстро убывают). При изменении
определяемый формулой (178.9), действительно велик (см. также приведенную ниже таблицу), поэтому приближение (178.15) является вполне разумным. В третьем столбце таблицы даны значения выражения, стоящего в круглых скобках в формуле (178.15) (начальные члены этого ряда быстро убывают). При изменении  от 20 до 80 сдвиг энергетического уровня
от 20 до 80 сдвиг энергетического уровня  составляет 26—12% от величины
составляет 26—12% от величины  Следовательно, он действительно представляет собой всего лишь поправку, хотя и не настолько малую, чтобы учет второго порядка теории возмущений не мог изменить ее на несколько процентов. Надо, однако, иметь в виду, что уже сама по себе используемая модель Томаса — Ферми слишком груба, поэтому учет второго порядка теории возмущений физически нецелесообразен.
Следовательно, он действительно представляет собой всего лишь поправку, хотя и не настолько малую, чтобы учет второго порядка теории возмущений не мог изменить ее на несколько процентов. Надо, однако, иметь в виду, что уже сама по себе используемая модель Томаса — Ферми слишком груба, поэтому учет второго порядка теории возмущений физически нецелесообразен.
В рентгеноспектроскопии обычно принято характеризовать сдвиг энергетического уровня с помощью экранировочной постоянной  определяемой равенством
определяемой равенством

Из этого определения следует

Значения экранировочной постоянной, рассчитанные по этой формуле, также приведены в нашей таблице. Так как

то для грубой оценки квадратный корень можно заменить степенным разложением, и мы получаем

Таким образом, экранировочная постоянная примерно пропорциональна  Если для оценок воспользоваться грубой формулой вида
Если для оценок воспользоваться грубой формулой вида

то с ее помощью нетрудно получить следующие пары значений:

Однако определять коэффициент пропорциональности  с такой большой точностью не имеет смысла. Сравнение экспериментальных значений экранировочной постоянной
с такой большой точностью не имеет смысла. Сравнение экспериментальных значений экранировочной постоянной  с ее теоретическими значениями показывает, что вплоть до
с ее теоретическими значениями показывает, что вплоть до  согласие между теорией и экспериментом довольно хорошее, но по мере дальнейшего роста
согласие между теорией и экспериментом довольно хорошее, но по мере дальнейшего роста  согласие между ними нарушается. Вместо предсказываемого теорией медленного увеличения
согласие между ними нарушается. Вместо предсказываемого теорией медленного увеличения  фактические значения экранировочной постоянной, достигнув максимума 3,7, начинают сначала медленно, а после
фактические значения экранировочной постоянной, достигнув максимума 3,7, начинают сначала медленно, а после  быстро убывать. Вполне очевидно, что отмеченное противоречие между теорией и экспериментом при больших значениях
быстро убывать. Вполне очевидно, что отмеченное противоречие между теорией и экспериментом при больших значениях  следует приписать релятивистским эффектам. Такое заключение качественно подтверждается данными, приведенными в двух последних столбцах нашей таблицы.
следует приписать релятивистским эффектам. Такое заключение качественно подтверждается данными, приведенными в двух последних столбцах нашей таблицы.
(см. скан)
Согласно релятивистской квантовой механике (см. задачу 203), невозмущенная энергия  -электрона понижается на величину
-электрона понижается на величину

Этот сдвиг уровня надо добавить к сдвигу  обусловленному экранировкой, и лишь затем вычислять экранировочную постоянную. Результаты таких расчетов приведены в последнем столбце нашей таблицы. Так как суммарный сдвиг
обусловленному экранировкой, и лишь затем вычислять экранировочную постоянную. Результаты таких расчетов приведены в последнем столбце нашей таблицы. Так как суммарный сдвиг

по мере роста  делается все меньше и меньше по сравнению с первоначальным сдвигом
делается все меньше и меньше по сравнению с первоначальным сдвигом  то исправленное значение экранировочной постоянной
то исправленное значение экранировочной постоянной  характеризующее отклонение эффективного поля от неэкранированного поля ядра, также убывает все быстрее с ростом
характеризующее отклонение эффективного поля от неэкранированного поля ядра, также убывает все быстрее с ростом  что согласуется с данными эксперимента. Строго говоря, релятивистские эффекты следовало бы учесть не только при вычислении энергии
что согласуется с данными эксперимента. Строго говоря, релятивистские эффекты следовало бы учесть не только при вычислении энергии  но и при вычислении сдвига В этой связи наши результаты нужно рассматривать как сравнительно грубое приближение, однако допускаемая нами ошибка вряд ли выходит за рамки точности модели Томаса — Ферми, не учитывающей эффектов, обусловленных оболочечной структурой атома.
но и при вычислении сдвига В этой связи наши результаты нужно рассматривать как сравнительно грубое приближение, однако допускаемая нами ошибка вряд ли выходит за рамки точности модели Томаса — Ферми, не учитывающей эффектов, обусловленных оболочечной структурой атома.
| << Предыдущий параграф | Следующий параграф >> |
- III. Частицы со спином
- Задача 130. Собственные векторы матриц Паули
- Задача 131. Алгебра спиновых матриц
- Задача 132. Трансформационные свойства спиноров
- Задача 133. Электрон со спином в центральном поле
- Задача 134. Квадрупольный момент при наличии спина
- Задача 135. Среднее значение магнитного момента
- Задача 136. Тонкая структура
- Задача 137. Плоские волны для частиц со спином 1/2
- Задача 138. Спиновый резонанс для свободного электрона
- Б. Двух- и трехчастичные задачи
- Задача 139. Спиновые функции двух частиц
- Задача 140. Центральное взаимодействие между нуклонами, зависящее от спина
- Задача 141. Степени спиновых операторов
- Задача 142. Собственные функции оператора полного момента двух частиц, обладающих спином
- Задача 143. Тензорные силы
- Задача 144. Дейтрон с тензорным взаимодействием
- Задача 145. Электрический квадрупольный и магнитный днпольный моменты дейтрона
- Задача 146. Спиновые функции трех частиц
- Задача 147. Рассеяние нейтронов молекулярным водородом
- IV. Многочастичные задачи
- Задача 148. Две отталкивающиеся частицы на окружности
- Задача 149. Трехатомная линейная молекула
- Задача 150. Движение центра масс
- Задача 151. Теорема вириала
- Задача 152. Определитель Слэтера
- Задача 153. Определитель Слэтера и обменное взаимодействие
- Задача 154. Два атомных электрона в основном состоянии
- Задача 155. Возбужденные состояния атома гелия
- Задача 156. Возбужденные S-состояния атома гелия
- Задача 157. Основное состояние атома лития
- Задача 158. Обменные поправки к основному состоянию атома лития
- Задача 159. Электрическая восприимчивость
- Задача 160. Диамагнитная восприимчивость неона
- Задача 161. Силы Ван-дер-Ваальса
- Задача 162. Обменное вырождение при наличии возбуждения
- Задача 163. Нейтральная молекула водорода
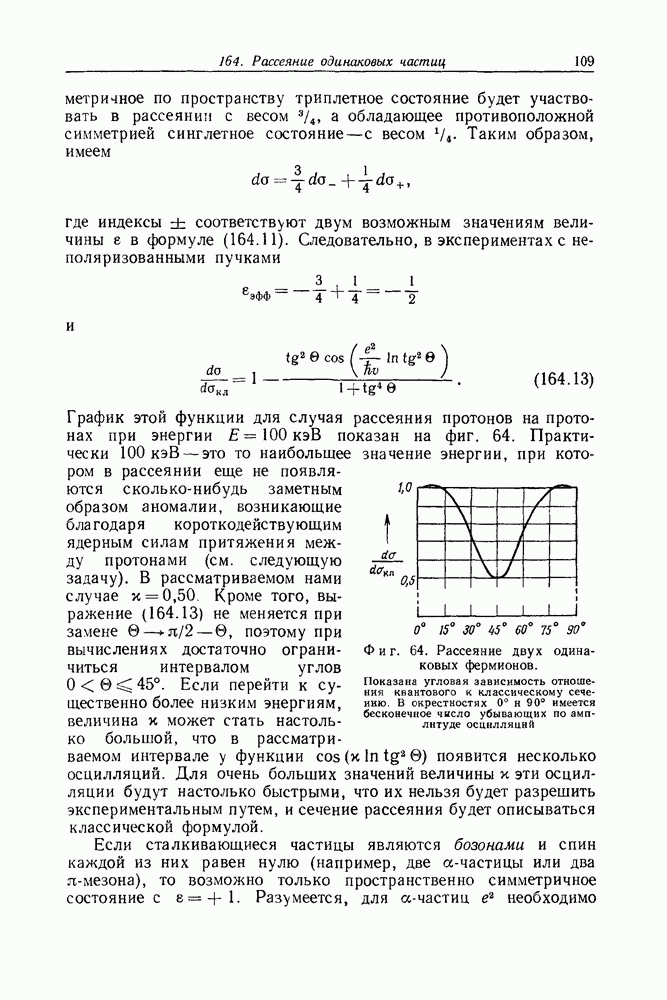
- Задача 164. Рассеяние одинаковых частиц
- Задача 165. Аномальное рассеяние протонов на протонах
- Задача 166. Неупругое рассеяние
- Б. Очень большое число частиц. Квантовая статистика
- Задача 167. Электронный газ в металле
- Задача 168. Парамагнитная восприимчивость металла
- Задача 169. Холодная эмиссия без учета сил электростатического изображения
- Задача 170. Холодная эмиссия с учетом сил электростатического изображения
- Задача 171. Белый карлик
- Задача 172. Приближение Томаса — Ферми
- Задача 173. Поправка Амальди для нейтрального атома
- Задача 174. Энергия атома в модели Томаса — Ферми
- Задача 175. Теорема вириала для модели атома Томаса-Ферми
- Задача 176. Приближение Тайтца для модели атома Томаса — Ферми
- Задача 177. Вариационный метод для модели атома Томаса — Ферми
- Задача 178. Влияние экранировки на K-электроны
- V. Нестационарные задачи
- Задача 179. Двухуровневая система под действием не зависящего от времени возмущения
- Задача 180. Действие периодического возмущения на двухуровневую систему
- Задача 181. Теория возмущений Дирака
- Задача 182. Периодическое возмущение и резонанс
- Задача 183. Золотое правило для рассеяния
- Задача 184. Борновское рассеяние в импульсном представлении
- Задача 185. Кулоновское возбуждение атома
- Задача 186. Фотоэффект
- Задача 187. Дисперсия света. Силы осцилляторов
- Задача 188. Спин-флип в магнитной резонансной системе
- VI. Релятивистское уравнение Дирака
- Задача 189. Квадрирование уравнения Дирака
- Задача 190. Плоские волны Дирака с положительной энергией
- Задача 191. Трансформационные свойства дираковских спиноров
- Задача 192. Лоренцевы коварианты
- Задача 193. Пространственная инверсия
- Задача 194. Зарядовое сопряжение
- Задача 195. Состояния со смешанной спиральностью
- Задача 196. Среднее значение спина
- Задача 197. Алгебраические свойства волнового спинора Дирака
- Задача 198. Плотность тока в алгебраической формулировке
- Задача 199. Ток проводимости и ток поляризации
- Задача 200. Уравнение Дирака в двухкомпонентной записи
- Задача 201. Центральные силы в теории Дирака
- Задача 202. Проблема Кеплера в теории Дирака
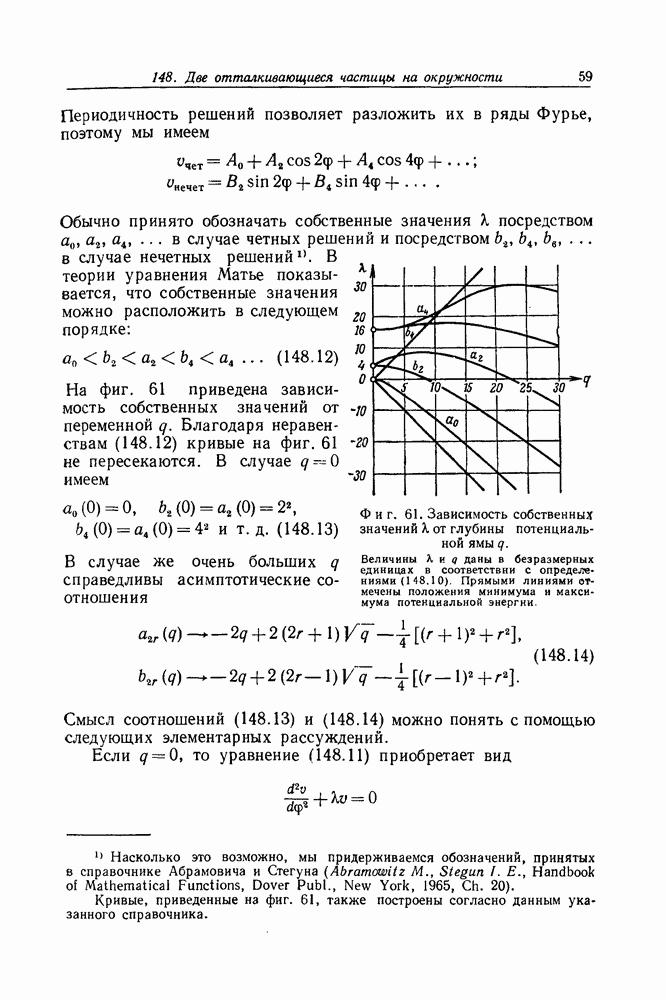
- Задача 203. Тонкая структура энергетических уровней атома водорода
- Задача 204. Проблема Кеплера. Радиальные функции при положительных энергиях
- Задача 205. Разложение дираковской плоской волны по состояниям с определенным моментом
- Задача 206. Рассеяние в поле центральных сил
- Задача 208. Наклонное падение плоской волны на прямоугольную потенциальную ступеньку
- Задача 209. Отражение от прямоугольной потенциальной ступеньки при наклонном падении
- VII. Теория излучения
- Задача 210. Квантование шредингеровского волнового поля
- Задача 211. Рассеяние в борновском приближении
- Задача 212. Квантование классического поля излучения
- Задача 213. Вероятность переходов с излучением одного фотона
- Задача 214. Угловое распределение излучения
- Задача 215. Полная вероятность перехода
- Задача 216. Правила отбора для дипольного излучения
- Задача 217. Интенсивности линий лаймановской серии
- Задача 218. Эффект Комптона
- Задача 219. Тормозное излучение
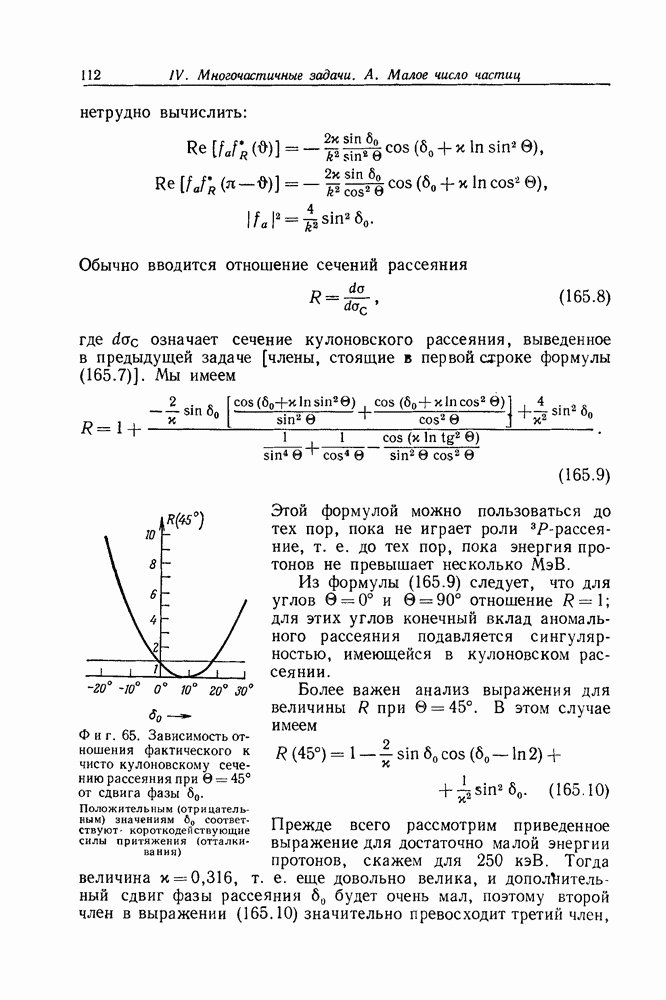
- Математическое приложение
- Криволинейные координаты
- Г-функция
- Функции Лежандра
- Сферические гармоники
- Гипергеометрическая функция
- Вырожденная гипергеометрическая функция
- Некоторые функции, определяемые интегралами