| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Функции Лежандра
Дифференциальное уравнение

принадлежит к уравнениям гипергеометрического типа с тремя особыми точками:  Общее решение уравнения
Общее решение уравнения
(1) можно записать в виде

где первое и второе слагаемые представляют  если отвлечься от нормировочных множителей, так называемые функции Лежандра первого и второго родов, которые обычно обозначают соответственно через
если отвлечься от нормировочных множителей, так называемые функции Лежандра первого и второго родов, которые обычно обозначают соответственно через 
Если  целое число
целое число  то функция Лежандра первого рода вырождается в полином. Когда
то функция Лежандра первого рода вырождается в полином. Когда  где действительное число и или
где действительное число и или  полиномы
полиномы
Лежандра, будучи связаны со сферическими гармониками  соотношением
соотношением

имеют простой геометрический смысл.
Свойства полиномов Лежандра. Эти полиномы образуют ортогональную систему: 

Первые пять полиномов имеют вид

Все они либо четные, либо нечетные функции переменной х. Четность полиномов Лежандра определяется четностью индекса I:

Полиномы с  можно получить с помощью рекуррентного соотношения
можно получить с помощью рекуррентного соотношения

Полиномы Лежандра и их производные связаны простым соотношением

из которого, в частности, следует

При  имеем
имеем

и

Если ввести новую переменную  то определение (2) полиномов Лежандра можно представить в иной форме:
то определение (2) полиномов Лежандра можно представить в иной форме:

Когда  а модуль
а модуль  по порядку величины равен
по порядку величины равен  , последний ряд упрощается и мы получаем
, последний ряд упрощается и мы получаем

причем ошибка этого приближения имеет порядок  Что же касается корней полиномов
Что же касается корней полиномов  то и при больших значениях угла
то и при больших значениях угла  они довольно хорошо описываются приближенной формулой (11). Для случая
они довольно хорошо описываются приближенной формулой (11). Для случая  полином Лежандра и соответствующая ему аппроксимирующая функция Бесселя показаны на фиг. 55 (том 1, стр. 284).
полином Лежандра и соответствующая ему аппроксимирующая функция Бесселя показаны на фиг. 55 (том 1, стр. 284).
О соотношениях, связанных с геометрической интерпретацией, см. раздел, посвященный сферическим гармоникам.
Функции Лежандра первого рода. Когда  не является целым числом, ряд (10) уже не обрывается на конечном члене, и
не является целым числом, ряд (10) уже не обрывается на конечном члене, и  становится трансцендентной функцией с особенностями в точках
становится трансцендентной функцией с особенностями в точках  Эту функцию можно разложить в ряд по полиномам Лежандра:
Эту функцию можно разложить в ряд по полиномам Лежандра:

Ряд (12) — частный случай разложения функции

с коэффициентами

Так как полиномы Лежандра образуют полную ортогональную систему, то такое разложение возможно для широкого класса функций.
Приведем примеры часто используемых разложений:

В физических приложениях обычно  так что
так что

Ряды (14) и (15) сходятся при всех действительных значениях переменной у. Другой важный пример:

Последнее разложение можно также использовать в качестве определения полиномов Лежандра.
Функции Лежандра второго рода. Рассмотрим разложение

где  произвольное комплексное число, не принадлежащее отрезку действительной оси
произвольное комплексное число, не принадлежащее отрезку действительной оси  . Функция
. Функция  определенная соотношением
определенная соотношением

называется функцией Лежандра второго рода. В силу симметрии разложения (16а) по отношению к переменным z их эти функции должны удовлетворять тому же самому дифференциальному уравнению (1), которому удовлетворяют полиномы Лежандра  Функции Лежандра второго рода имеют при
Функции Лежандра второго рода имеют при  логарифмические точки ветвления. Приведем явные выражения для трех
логарифмические точки ветвления. Приведем явные выражения для трех
первых функций Лежандра второго рода:

Выражения для функций более высокого порядка можно получить с помощью рекуррентного соотношения (7), которое справедливо для функций  так же как и для полиномов
так же как и для полиномов  . В общем случае функция
. В общем случае функция  имеет вид
имеет вид

где  полином
полином  степени. Этот полинбм является четным, если четен индекс
степени. Этот полинбм является четным, если четен индекс  и нечетным в противном случае.
и нечетным в противном случае.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- III. Частицы со спином
- Задача 130. Собственные векторы матриц Паули
- Задача 131. Алгебра спиновых матриц
- Задача 132. Трансформационные свойства спиноров
- Задача 133. Электрон со спином в центральном поле
- Задача 134. Квадрупольный момент при наличии спина
- Задача 135. Среднее значение магнитного момента
- Задача 136. Тонкая структура
- Задача 137. Плоские волны для частиц со спином 1/2
- Задача 138. Спиновый резонанс для свободного электрона
- Б. Двух- и трехчастичные задачи
- Задача 139. Спиновые функции двух частиц
- Задача 140. Центральное взаимодействие между нуклонами, зависящее от спина
- Задача 141. Степени спиновых операторов
- Задача 142. Собственные функции оператора полного момента двух частиц, обладающих спином
- Задача 143. Тензорные силы
- Задача 144. Дейтрон с тензорным взаимодействием
- Задача 145. Электрический квадрупольный и магнитный днпольный моменты дейтрона
- Задача 146. Спиновые функции трех частиц
- Задача 147. Рассеяние нейтронов молекулярным водородом
- IV. Многочастичные задачи
- Задача 148. Две отталкивающиеся частицы на окружности
- Задача 149. Трехатомная линейная молекула
- Задача 150. Движение центра масс
- Задача 151. Теорема вириала
- Задача 152. Определитель Слэтера
- Задача 153. Определитель Слэтера и обменное взаимодействие
- Задача 154. Два атомных электрона в основном состоянии
- Задача 155. Возбужденные состояния атома гелия
- Задача 156. Возбужденные S-состояния атома гелия
- Задача 157. Основное состояние атома лития
- Задача 158. Обменные поправки к основному состоянию атома лития
- Задача 159. Электрическая восприимчивость
- Задача 160. Диамагнитная восприимчивость неона
- Задача 161. Силы Ван-дер-Ваальса
- Задача 162. Обменное вырождение при наличии возбуждения
- Задача 163. Нейтральная молекула водорода
- Задача 164. Рассеяние одинаковых частиц
- Задача 165. Аномальное рассеяние протонов на протонах
- Задача 166. Неупругое рассеяние
- Б. Очень большое число частиц. Квантовая статистика
- Задача 167. Электронный газ в металле
- Задача 168. Парамагнитная восприимчивость металла
- Задача 169. Холодная эмиссия без учета сил электростатического изображения
- Задача 170. Холодная эмиссия с учетом сил электростатического изображения
- Задача 171. Белый карлик
- Задача 172. Приближение Томаса — Ферми
- Задача 173. Поправка Амальди для нейтрального атома
- Задача 174. Энергия атома в модели Томаса — Ферми
- Задача 175. Теорема вириала для модели атома Томаса-Ферми
- Задача 176. Приближение Тайтца для модели атома Томаса — Ферми
- Задача 177. Вариационный метод для модели атома Томаса — Ферми
- Задача 178. Влияние экранировки на K-электроны
- V. Нестационарные задачи
- Задача 179. Двухуровневая система под действием не зависящего от времени возмущения
- Задача 180. Действие периодического возмущения на двухуровневую систему
- Задача 181. Теория возмущений Дирака
- Задача 182. Периодическое возмущение и резонанс
- Задача 183. Золотое правило для рассеяния
- Задача 184. Борновское рассеяние в импульсном представлении
- Задача 185. Кулоновское возбуждение атома
- Задача 186. Фотоэффект
- Задача 187. Дисперсия света. Силы осцилляторов
- Задача 188. Спин-флип в магнитной резонансной системе
- VI. Релятивистское уравнение Дирака
- Задача 189. Квадрирование уравнения Дирака
- Задача 190. Плоские волны Дирака с положительной энергией
- Задача 191. Трансформационные свойства дираковских спиноров
- Задача 192. Лоренцевы коварианты
- Задача 193. Пространственная инверсия
- Задача 194. Зарядовое сопряжение
- Задача 195. Состояния со смешанной спиральностью
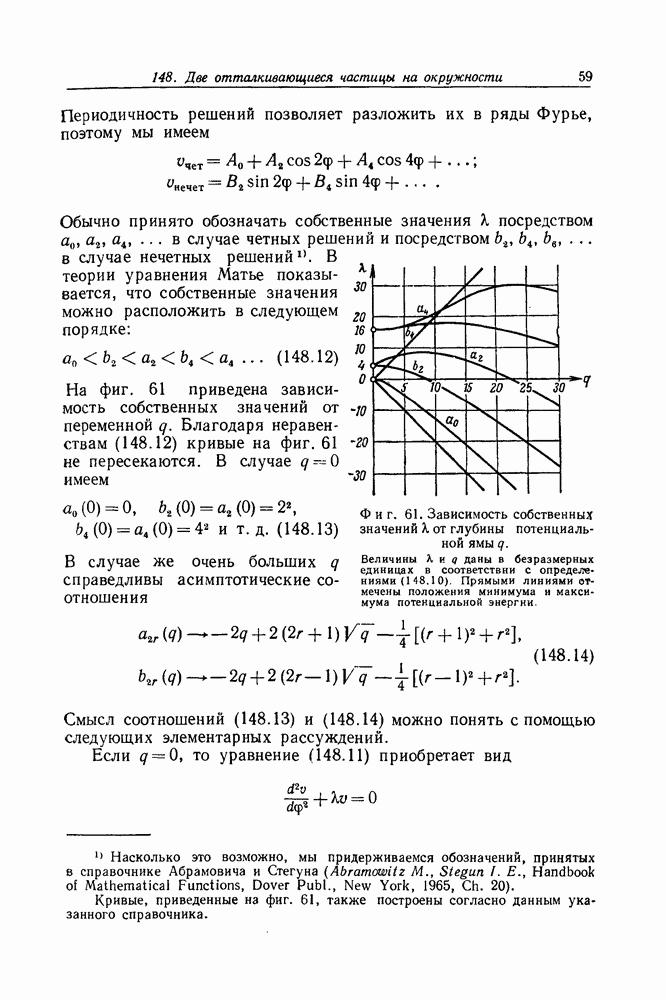
- Задача 196. Среднее значение спина
- Задача 197. Алгебраические свойства волнового спинора Дирака
- Задача 198. Плотность тока в алгебраической формулировке
- Задача 199. Ток проводимости и ток поляризации
- Задача 200. Уравнение Дирака в двухкомпонентной записи
- Задача 201. Центральные силы в теории Дирака
- Задача 202. Проблема Кеплера в теории Дирака
- Задача 203. Тонкая структура энергетических уровней атома водорода
- Задача 204. Проблема Кеплера. Радиальные функции при положительных энергиях
- Задача 205. Разложение дираковской плоской волны по состояниям с определенным моментом
- Задача 206. Рассеяние в поле центральных сил
- Задача 208. Наклонное падение плоской волны на прямоугольную потенциальную ступеньку
- Задача 209. Отражение от прямоугольной потенциальной ступеньки при наклонном падении
- VII. Теория излучения
- Задача 210. Квантование шредингеровского волнового поля
- Задача 211. Рассеяние в борновском приближении
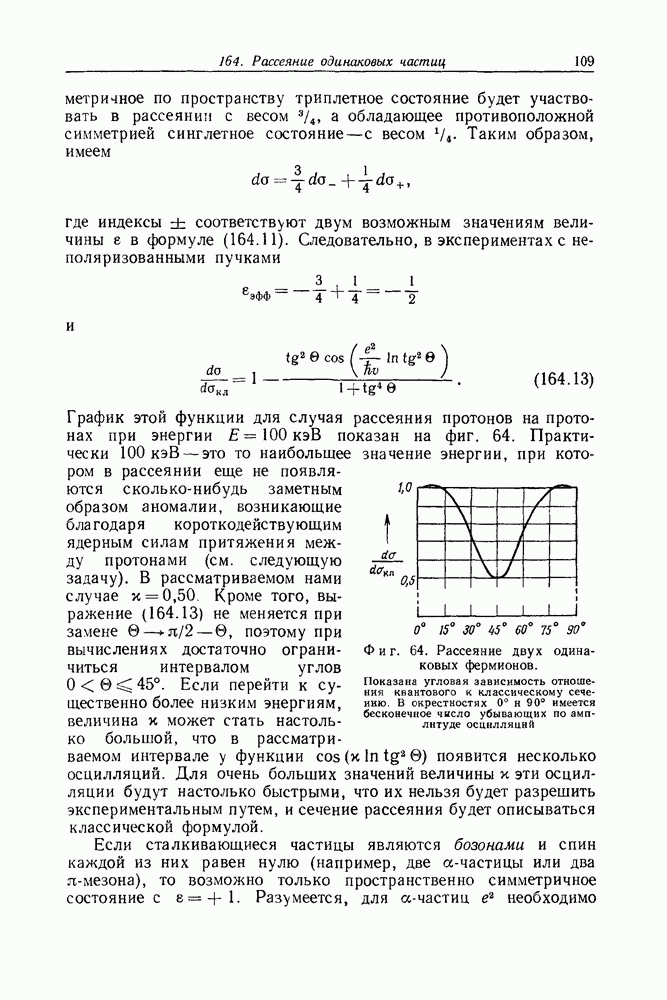
- Задача 212. Квантование классического поля излучения
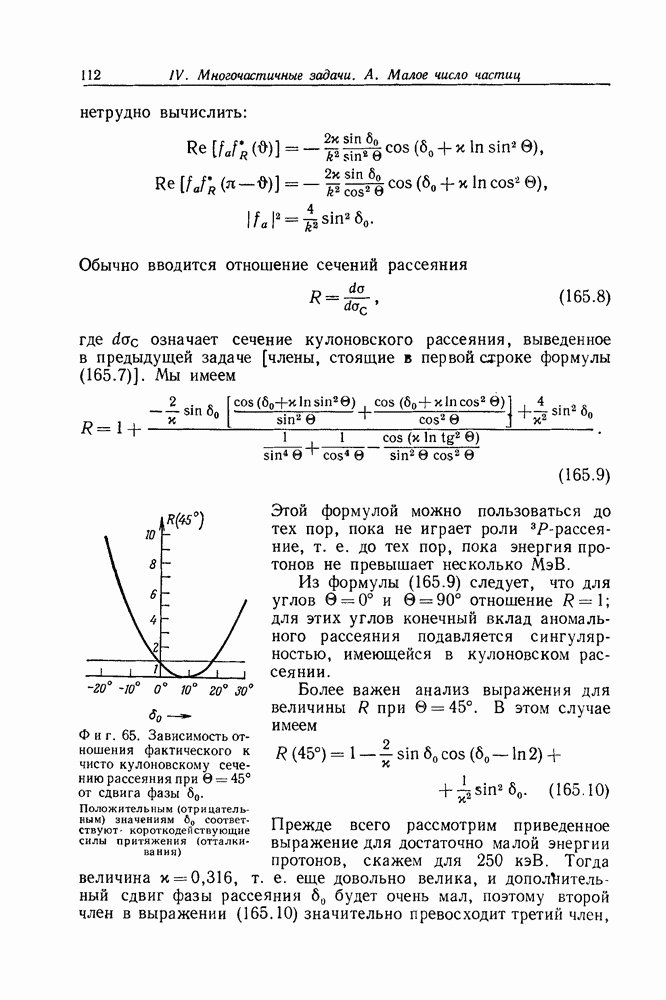
- Задача 213. Вероятность переходов с излучением одного фотона
- Задача 214. Угловое распределение излучения
- Задача 215. Полная вероятность перехода
- Задача 216. Правила отбора для дипольного излучения
- Задача 217. Интенсивности линий лаймановской серии
- Задача 218. Эффект Комптона
- Задача 219. Тормозное излучение
- Математическое приложение
- Криволинейные координаты
- Г-функция
- Функции Лежандра
- Сферические гармоники
- Гипергеометрическая функция
- Вырожденная гипергеометрическая функция
- Некоторые функции, определяемые интегралами