Задача 164. Рассеяние одинаковых частиц

Пучок частиц с зарядом сталкивается с покоящейся мишенью, состоящей из частиц того же сорта. Как сравнить угловое распределение сталкивающихся частиц, ожидаемое в классической физике, с угловым распределением, полученным с номощью квантовой механики, если при выводе последнего учитывалась симметрия волновой функции? Рассмотреть этот вопрос для столкновения неполяризованных частиц со спином

Решение. Амплитуда резерфордовского рассеяния в системе центра масс сталкивающихся частиц была получена в задаче 110. Она имеет следующий вид:

Величины относятся к системе центра масс, причем

где приведенная масса двух одинаковых частиц, Относительная скорость не зависит от выбора системы отсчета, поэтому для величин и относящихся к лабораторной системе, можно написать

Отсюда следует

Угол рассеяния в лабораторной системе в связан с углом рассеяния в системе центра масс соотношением

Следовательно, для элемента телесного угла можно написать

С учетом этих замечаний дифференциальное сечение резерфордовского рассеяния принимает в лабораторной системе вид

где

Даже с точки зрения классической механики эта формула нуждается в существенных исправлениях. Действительно, если обе сталкивающиеся частицы одинаковы, то рассеиваемую частицу нельзя отличить от частицы, выбитой из мишени: обе они дают равноценный вклад в сечение рассеяния. Так как, согласно соотношению (164.5), сталкивающиеся частицы разлетаются под прямым углом, то частица, выбитая из мишени, летит под углом к направлению падающего пучка, а вместо формулы (164.7) мы должны написать

Именно это классическое выражение следует сравнивать с квантовомеханическими результатами, которые будут получены ниже.

Согласно законам квантовой механики, мы должны складывать не интенсивности (т. е. эффективные сечения), а амплитуды. Пусть и -несимметризованная волновая функция в системе центра масс, радиус-вектор относительного положения частиц. Асимптотика волновой функции, если отвлечься от логарифмического искажения фазы, имеет вид

Фигурирующую в этом выражении плоскую волну можно записать в виде

Последнее выражение описывает две частицы, движущиеся вдоль оси одна движется со скоростью а другая — со скоростью Если ввести сюда множитель, описывающий движение центра масс

то у нас получится плоская волна

описывающая движение частицы 1 (налетающая частица), при этом частица 2 (частица-мишень) будет находиться в состоянии покоя. Приведенные рассуждения относились к несимметризованной волновой функции двухчастичной системы. Чтобы произвести симметризацию, мы должны заменить и на

где

Для сферической волны в асимптотическом выражении волновой функции это означает замену на

Отметим, что величина при переходе к симметризованному выражению остается неизменной. Таким образам, используя выражение (164.4), имеем

и следовательно, формула (164.8) для классического сечения рассеяния заменяется теперь формулой

которая после элементарных преобразований принимает вид

Мы видим, что от классического выражения полученная формула отличается наличием интерференционного числа. Чтобы сравнить классическую и квантовую формулы для дифференциального сечения рассеяния, удобно рассмотреть отношение

В заключение мы должны решить, какая часть первично неполяризованного пучка описывается симметричной амплитудой, а какая — антисимметричной. Если обе сталкивающиеся частицы являются фермионами со спином каждая (два протона или два электрона), то их полная волновая функция должна быть антисимметричной, и поэтому симметричное по спину и

антисимметричное по пространству триплетное состояние будет участвовать в рассеянин с весом 3/4, а обладающее противоположной симметрией синглетное состояние — с весом Таким образом, имеем

где индексы соответствуют двум возможным значениям величины в формуле (164.11). Следовательно, в экспериментах с неполяризованными пучками

и

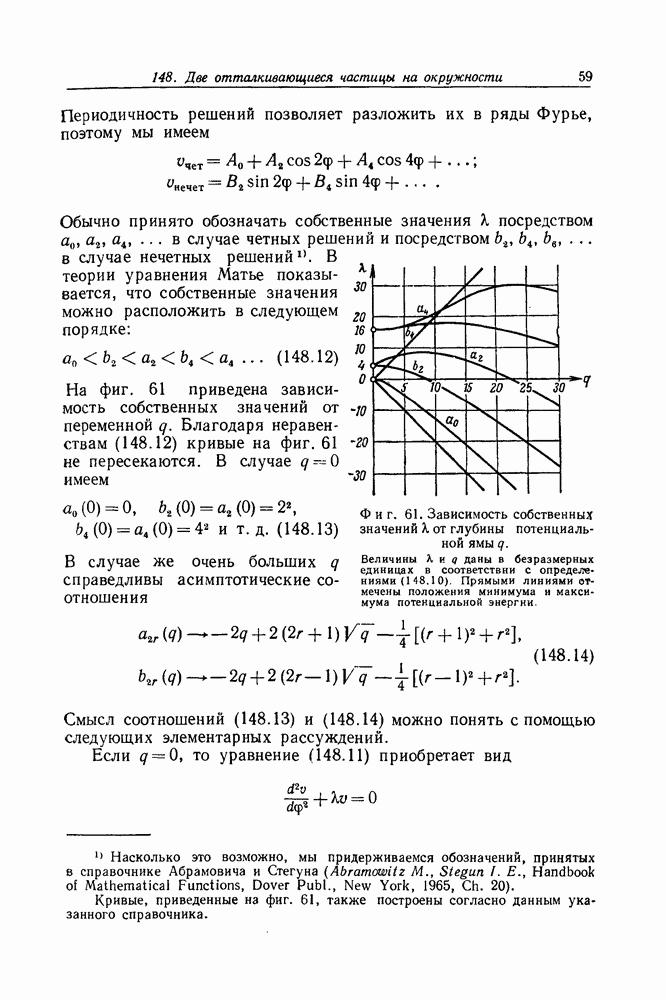
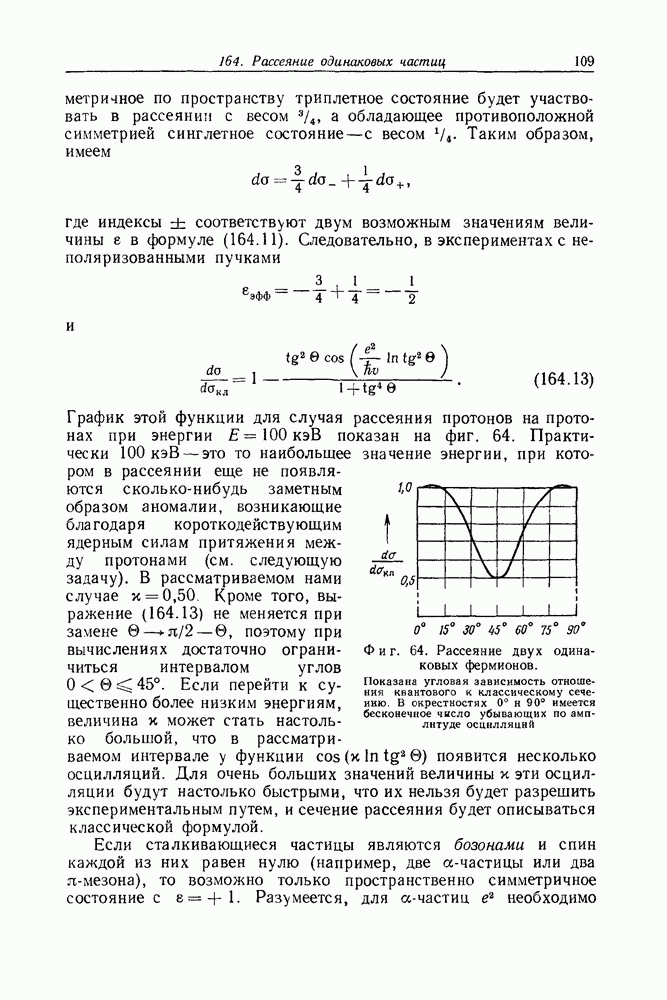
График этой функции для случая рассеяния протонов на протонах при энергии показан на фиг. 64. Практически это то наибольшее значение энергии, при котором в рассеянии еще не появляются сколько-нибудь заметным образом аномалии, возникающие благодаря короткодействующим ядерным силам притяжения между протонами (см. следующую задачу). В рассматриваемом нами случае Кроме того, выражение (164.13) не меняется при замене в, поэтому при вычислениях достаточно ограничиться интервалом углов Если перейти к существенно более низким энергиям, величина х может стать настолько большой, что в рассматриваемом интервале у функции появится несколько осцилляции. Для очень больших значений величины х эти осцилляции будут настолько быстрыми, что их нельзя будет разрешить экспериментальным путем, и сечение рассеяния будет описываться классической формулой.

Если сталкивающиеся частицы являются бозонами и спин каждой из них равен нулю (например, две -частицы или два -мезона), то возможно только пространственно симметричное состояние с Разумеется, для -частиц необходимо

Фиг. 64. Рассеяние двух одинаковых фермионов.

Показана угловая зависимость отношения квантового к классическому сечению. В окрестностях 0° и 90° имеется бесконечное число убывающих по амплитуде осцнлляцнй

заменить на Если же обе частицы являются бозонами и спин каждой из них равен 1 (например, два дейтрона), то возможны спиновые состояния с суммарным спином и причем в первом и в последнем случаях волновая функция должна быть пространственно симметричной. Таким образом, имеем

и

Замечание. Симметризованное классическое выражение (164.8) впервые было использовано в работе Дарвина [Darwin С. G., Proc.Roy. Soc., 120А, 631 (1928)]. Вывод квантовомеханической формулы принадлежит Мотту Mott N. F., Ргос. Roy. Soc., 126, 259 (1930)]. Экспериментальная проверка этой формулы применительно к рассеянию ос-частиц была осуществлена Чэдвиком [Chadwick J., Ргос. Roy. Soc., 128А, 114 (1930)], а также Блэкеттом и Чэмпиеном [Blackett P.M.S., Champion F.C., Ргос Roy. Soc., 130, 380 (1931)], а для протонов это сделал Гертзен [Gerthsen С., Ann. Phys., 9, 769 (1931)].