| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Задача 156. Возбужденные S-состояния атома гелия
Метод предыдущей задачи распространить на электронную конфигурацию  Для этого по-прежнему считать, что
Для этого по-прежнему считать, что  -электрон описывается невозмущенной водородной функцией, относительно же волновой функции
-электрон описывается невозмущенной водородной функцией, относительно же волновой функции  -электрона не делать никаких специальных предположений. Рассматривая далее обменный интеграл и интеграл перекрытия как малые поправки, показать, что можно построить эффективное потенциальное поле, в котором движется
-электрона не делать никаких специальных предположений. Рассматривая далее обменный интеграл и интеграл перекрытия как малые поправки, показать, что можно построить эффективное потенциальное поле, в котором движется  -электрон.
-электрон.
Решение. Мы запишем волновую функцию в виде симметризованного произведения волновых функций одноэлектронных состояний:

где  Для волновой функции
Для волновой функции  -электрона (в атомных единицах) имеем
-электрона (в атомных единицах) имеем

Относительно же волновой функции  -электрона мы знаем лишь, что она не зависит от углов и удовлетворяет условию нормировки:
-электрона мы знаем лишь, что она не зависит от углов и удовлетворяет условию нормировки:

Никаких иных требований к функции  не предъявляется.
не предъявляется.
Волновая функция  является приближенным решением уравнения Шредингера
является приближенным решением уравнения Шредингера

в котором гамильтониан имеет вид

Таковы основные уравнения нашей задачи. Прежде всего умножим уравнение (156.4) почленно на совектор 

затем найдем интегралы, содержащие оператор  , определяемый (156.5). До сих пор наши формулы очень похожи на формулы предыдущей задачи, хотя одно существенное отличие можно усмотреть немедленно. Оно обусловлено тем, что функции
, определяемый (156.5). До сих пор наши формулы очень похожи на формулы предыдущей задачи, хотя одно существенное отличие можно усмотреть немедленно. Оно обусловлено тем, что функции  в данном случае неортогональны, поскольку обе они принадлежат одному и тому же значению
в данном случае неортогональны, поскольку обе они принадлежат одному и тому же значению  но относятся к разным потенциальным полям. В этой связи мы введем интеграл перекрытия
но относятся к разным потенциальным полям. В этой связи мы введем интеграл перекрытия

и воспользуемся обозначениями

Теперь нам остается рассмотреть следующие интегралы:

Здесь при получении последнего равенства мы использовали тождество

С учетом этих соотношений уравнение (156.6) можно записать в виде

или

Так как  есть энергия основного состояния иона
есть энергия основного состояния иона  то энергия ионизации
то энергия ионизации  теперь равна
теперь равна

Чтобы определить величину  или величину
или величину  мы можем вычислить интегралы
мы можем вычислить интегралы  пользуясь каким-нибудь достаточно удобным набором функций
пользуясь каким-нибудь достаточно удобным набором функций  зависящих от некоторого числа параметров Ритца, а затем подходящим выбором этих параметров добиться экстремальности величины
зависящих от некоторого числа параметров Ритца, а затем подходящим выбором этих параметров добиться экстремальности величины  или величины
или величины 
Если интеграл перекрытия 5 и обменный интеграл  достаточно малы, то соотношения (156.10) и (156.11) упрощаются и принимают вид
достаточно малы, то соотношения (156.10) и (156.11) упрощаются и принимают вид

К соотношениям точно такого же вида мы пришли бы и в том случае, если бы сразу пренебрегли симметризацией, положив  именно в этом смысле можно говорить, что иногда волновые функции многочастичных задач не требуют симметризации.
именно в этом смысле можно говорить, что иногда волновые функции многочастичных задач не требуют симметризации.
Возвращаясь к определениям (156.8) и (156.9) для интегралов  можно записать первое из равенств (156.12) в виде
можно записать первое из равенств (156.12) в виде

где оператор  определяется формулой
определяется формулой

Чтобы найти нормированную функцию  минимизирующую энергию
минимизирующую энергию  мы должны рассмотреть вариацию:
мы должны рассмотреть вариацию:

где  — множитель Лагранжа. Так как
— множитель Лагранжа. Так как

то получаем

и ввиду произвольности вариации  волновая функция
волновая функция  должна удовлетворять уравнению
должна удовлетворять уравнению

Переписав теперь равенство (156.13) в виде

легко усмотреть, что  следовательно, функция
следовательно, функция  обязана удовлетворять одноэлектронному уравнению Шредингера
обязана удовлетворять одноэлектронному уравнению Шредингера

с эффективным потенциалом

Потенциал точно такого же вида мы могли бы получить, решая уравнение Пуассона

где  — плотность заряда, представляющего собой сумму отрицательного пространственного заряда
— плотность заряда, представляющего собой сумму отрицательного пространственного заряда  -электрона
-электрона  и точечного ядерного заряда
и точечного ядерного заряда  Подставляя в формулу (156.16) явное выражение (156.2) для функции
Подставляя в формулу (156.16) явное выражение (156.2) для функции  немедленно получаем
немедленно получаем

Найдя с помощью уравнения (156.15) функцию  мы можем затем вычислить приближенные значения всех интегралов, входящих в выражение для энергии (156.10). До тех пор пока величины
мы можем затем вычислить приближенные значения всех интегралов, входящих в выражение для энергии (156.10). До тех пор пока величины  и
и  удовлетворяют неравенствам
удовлетворяют неравенствам  следовательно, являются лишь малыми поправками, это приближение можно считать достаточным.
следовательно, являются лишь малыми поправками, это приближение можно считать достаточным.
Приложение. Числовые расчеты по обрисованной выше общей схеме могут оказаться довольно трудоемкими, и поэтому мы приведем для  -состоянии результаты, полученные с помощью более простой вариационной процедуры. Мы будем минимизировать выражение (156.12), используя пробные функции вида
-состоянии результаты, полученные с помощью более простой вариационной процедуры. Мы будем минимизировать выражение (156.12), используя пробные функции вида

где  — вариационный параметр Ритца и
— вариационный параметр Ритца и  Эти функции конечны при
Эти функции конечны при  и каждая из них имеет один нуль, что необходимо для
и каждая из них имеет один нуль, что необходимо для  -состоянии, кроме того, они обладают правильной асимптотикой, которая определяется вторым слагаемым. Первый член в выражении (156.18) описывает отклонения поведения наших функций от поведения водородоподобной волновой функции на малых расстояниях от ядра, где экранировка ядерного заряда становится все менее существенной. Так как волновая функция
-состоянии, кроме того, они обладают правильной асимптотикой, которая определяется вторым слагаемым. Первый член в выражении (156.18) описывает отклонения поведения наших функций от поведения водородоподобной волновой функции на малых расстояниях от ядра, где экранировка ядерного заряда становится все менее существенной. Так как волновая функция  -состояния ведет себя как
-состояния ведет себя как  то этот член должен вести себя примерно таким же образом.
то этот член должен вести себя примерно таким же образом.
Пробные функции (156.18) приводят к следующим результатам:


Энергия  определяемая выражением (156.12), будет иметь минимум при подходящем выборе параметра
определяемая выражением (156.12), будет иметь минимум при подходящем выборе параметра  он должен удовлетворять квадратному уравнению, у которого имеется один положительный корень
он должен удовлетворять квадратному уравнению, у которого имеется один положительный корень  Если не учитывать симметризацию, то отсюда для энергии ионизации получаем
Если не учитывать симметризацию, то отсюда для энергии ионизации получаем

Если же при том же значении параметра  использовать для энергии ионизации полное выражение (156.11), то будем иметь
использовать для энергии ионизации полное выражение (156.11), то будем иметь 

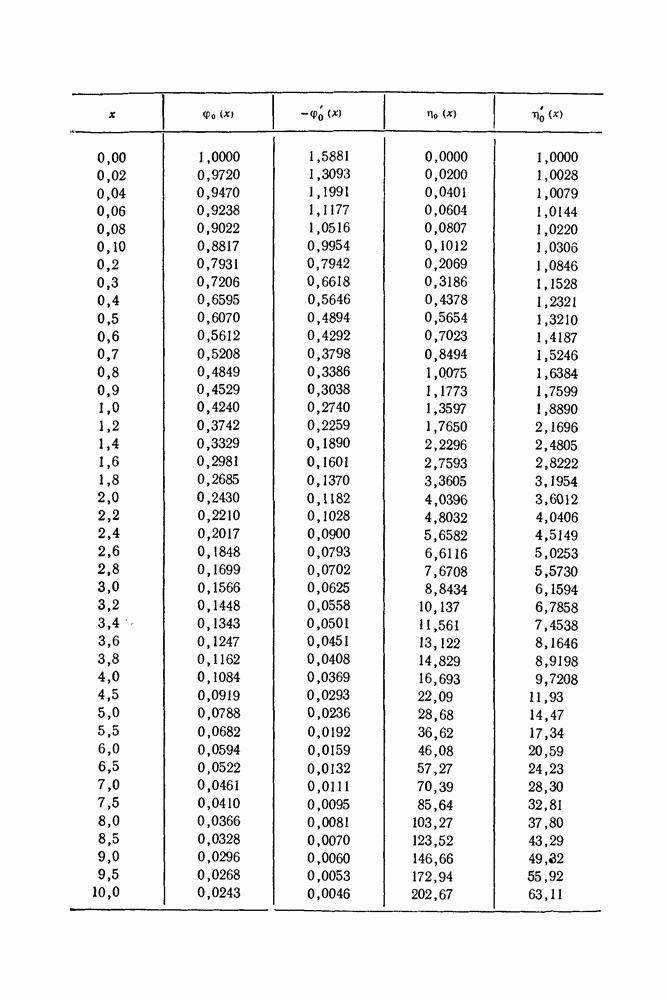
Полученные с помощью этой формулы результаты вместе с экспериментальными данными приводятся в нижеследующей таблице.
(см. скан)
Мы видим, что теоретические значения термов, как это всегда бывает при вариационных расчетах, несколько превышают их истинные значения. Довольно значительный сдвиг между орто- и парауровнями даже в этой очень простой приближенной теории получается с  -ной точностью.
-ной точностью.
| << Предыдущий параграф | Следующий параграф >> |
- III. Частицы со спином
- Задача 130. Собственные векторы матриц Паули
- Задача 131. Алгебра спиновых матриц
- Задача 132. Трансформационные свойства спиноров
- Задача 133. Электрон со спином в центральном поле
- Задача 134. Квадрупольный момент при наличии спина
- Задача 135. Среднее значение магнитного момента
- Задача 136. Тонкая структура
- Задача 137. Плоские волны для частиц со спином 1/2
- Задача 138. Спиновый резонанс для свободного электрона
- Б. Двух- и трехчастичные задачи
- Задача 139. Спиновые функции двух частиц
- Задача 140. Центральное взаимодействие между нуклонами, зависящее от спина
- Задача 141. Степени спиновых операторов
- Задача 142. Собственные функции оператора полного момента двух частиц, обладающих спином
- Задача 143. Тензорные силы
- Задача 144. Дейтрон с тензорным взаимодействием
- Задача 145. Электрический квадрупольный и магнитный днпольный моменты дейтрона
- Задача 146. Спиновые функции трех частиц
- Задача 147. Рассеяние нейтронов молекулярным водородом
- IV. Многочастичные задачи
- Задача 148. Две отталкивающиеся частицы на окружности
- Задача 149. Трехатомная линейная молекула
- Задача 150. Движение центра масс
- Задача 151. Теорема вириала
- Задача 152. Определитель Слэтера
- Задача 153. Определитель Слэтера и обменное взаимодействие
- Задача 154. Два атомных электрона в основном состоянии
- Задача 155. Возбужденные состояния атома гелия
- Задача 156. Возбужденные S-состояния атома гелия
- Задача 157. Основное состояние атома лития
- Задача 158. Обменные поправки к основному состоянию атома лития
- Задача 159. Электрическая восприимчивость
- Задача 160. Диамагнитная восприимчивость неона
- Задача 161. Силы Ван-дер-Ваальса
- Задача 162. Обменное вырождение при наличии возбуждения
- Задача 163. Нейтральная молекула водорода
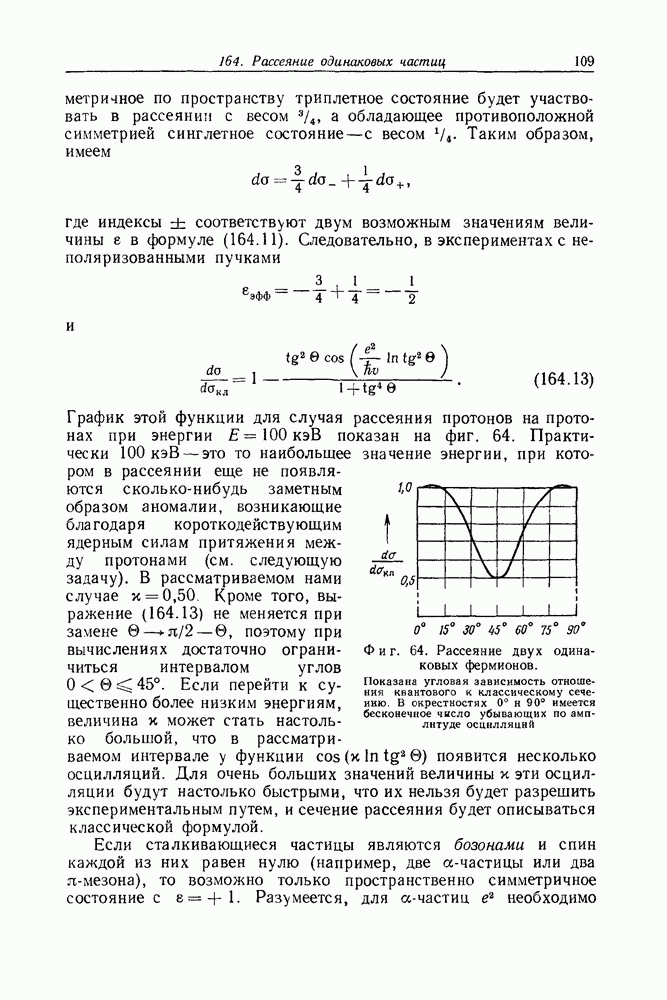
- Задача 164. Рассеяние одинаковых частиц
- Задача 165. Аномальное рассеяние протонов на протонах
- Задача 166. Неупругое рассеяние
- Б. Очень большое число частиц. Квантовая статистика
- Задача 167. Электронный газ в металле
- Задача 168. Парамагнитная восприимчивость металла
- Задача 169. Холодная эмиссия без учета сил электростатического изображения
- Задача 170. Холодная эмиссия с учетом сил электростатического изображения
- Задача 171. Белый карлик
- Задача 172. Приближение Томаса — Ферми
- Задача 173. Поправка Амальди для нейтрального атома
- Задача 174. Энергия атома в модели Томаса — Ферми
- Задача 175. Теорема вириала для модели атома Томаса-Ферми
- Задача 176. Приближение Тайтца для модели атома Томаса — Ферми
- Задача 177. Вариационный метод для модели атома Томаса — Ферми
- Задача 178. Влияние экранировки на K-электроны
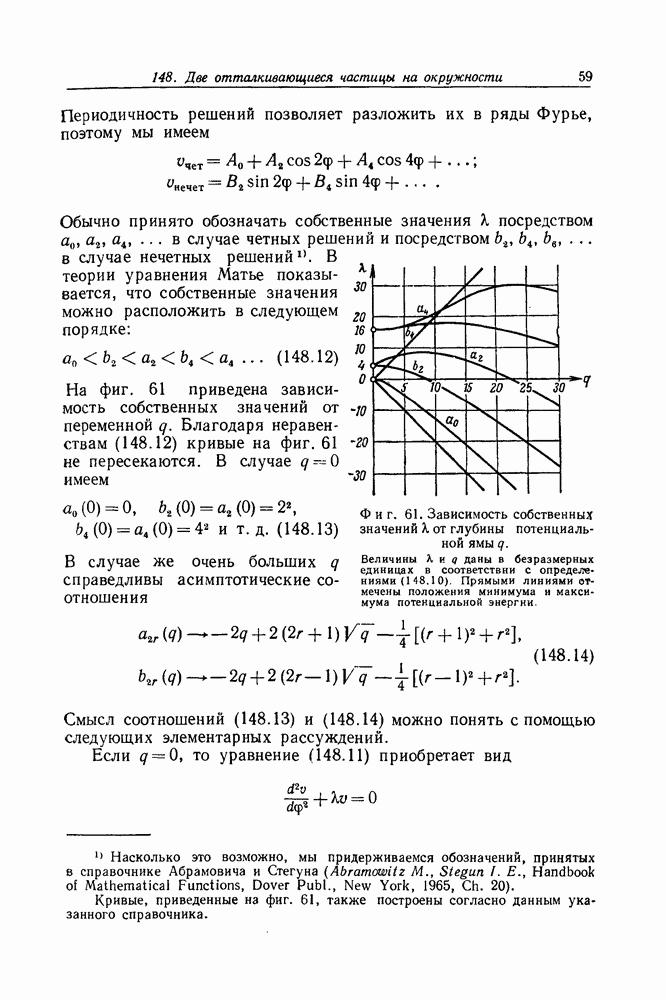
- V. Нестационарные задачи
- Задача 179. Двухуровневая система под действием не зависящего от времени возмущения
- Задача 180. Действие периодического возмущения на двухуровневую систему
- Задача 181. Теория возмущений Дирака
- Задача 182. Периодическое возмущение и резонанс
- Задача 183. Золотое правило для рассеяния
- Задача 184. Борновское рассеяние в импульсном представлении
- Задача 185. Кулоновское возбуждение атома
- Задача 186. Фотоэффект
- Задача 187. Дисперсия света. Силы осцилляторов
- Задача 188. Спин-флип в магнитной резонансной системе
- VI. Релятивистское уравнение Дирака
- Задача 189. Квадрирование уравнения Дирака
- Задача 190. Плоские волны Дирака с положительной энергией
- Задача 191. Трансформационные свойства дираковских спиноров
- Задача 192. Лоренцевы коварианты
- Задача 193. Пространственная инверсия
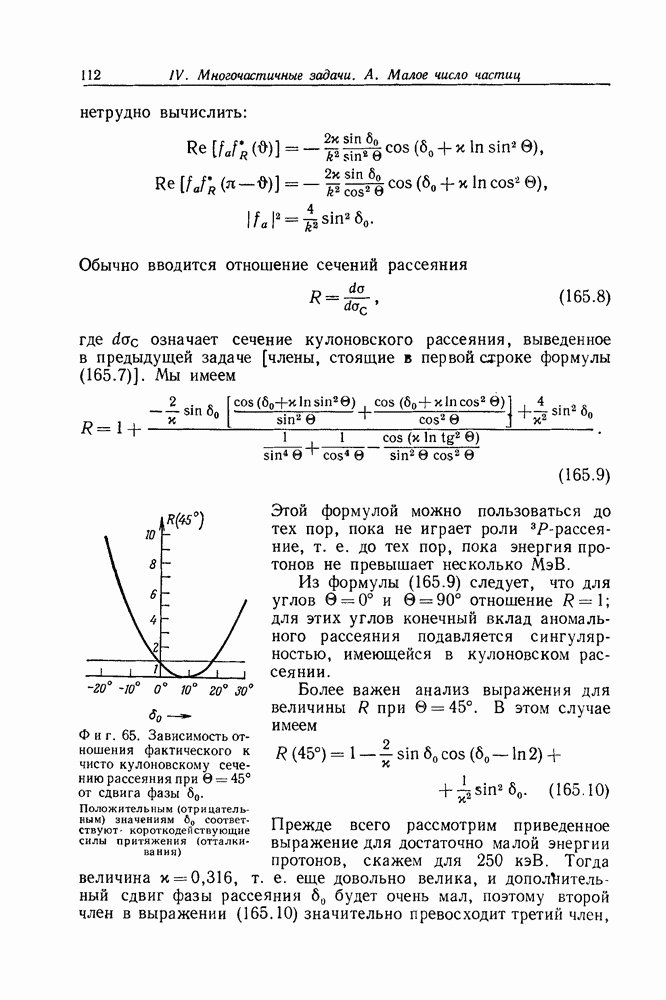
- Задача 194. Зарядовое сопряжение
- Задача 195. Состояния со смешанной спиральностью
- Задача 196. Среднее значение спина
- Задача 197. Алгебраические свойства волнового спинора Дирака
- Задача 198. Плотность тока в алгебраической формулировке
- Задача 199. Ток проводимости и ток поляризации
- Задача 200. Уравнение Дирака в двухкомпонентной записи
- Задача 201. Центральные силы в теории Дирака
- Задача 202. Проблема Кеплера в теории Дирака
- Задача 203. Тонкая структура энергетических уровней атома водорода
- Задача 204. Проблема Кеплера. Радиальные функции при положительных энергиях
- Задача 205. Разложение дираковской плоской волны по состояниям с определенным моментом
- Задача 206. Рассеяние в поле центральных сил
- Задача 208. Наклонное падение плоской волны на прямоугольную потенциальную ступеньку
- Задача 209. Отражение от прямоугольной потенциальной ступеньки при наклонном падении
- VII. Теория излучения
- Задача 210. Квантование шредингеровского волнового поля
- Задача 211. Рассеяние в борновском приближении
- Задача 212. Квантование классического поля излучения
- Задача 213. Вероятность переходов с излучением одного фотона
- Задача 214. Угловое распределение излучения
- Задача 215. Полная вероятность перехода
- Задача 216. Правила отбора для дипольного излучения
- Задача 217. Интенсивности линий лаймановской серии
- Задача 218. Эффект Комптона
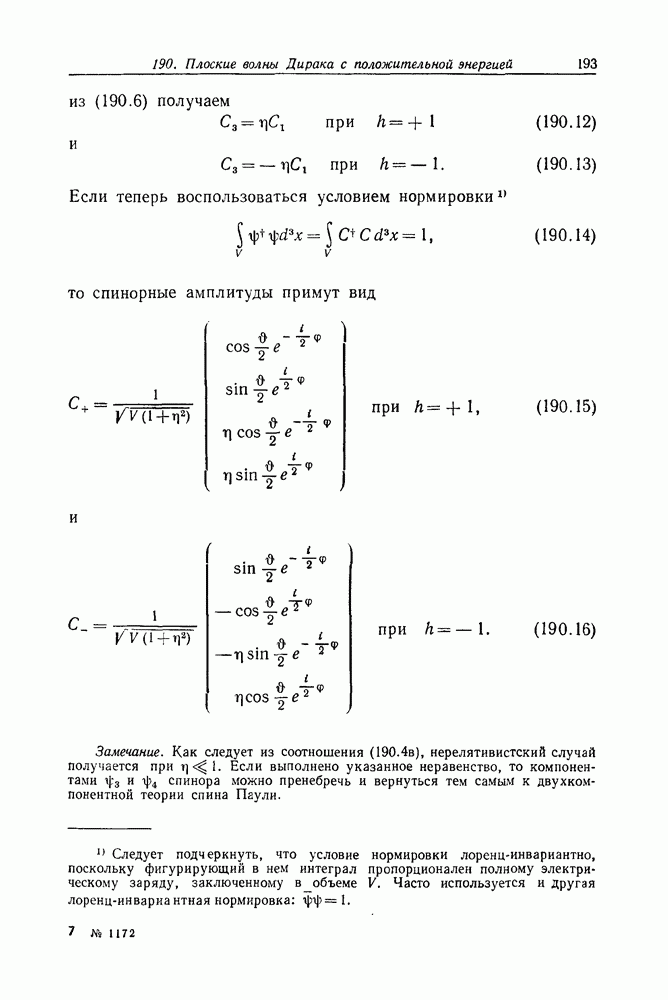
- Задача 219. Тормозное излучение
- Математическое приложение
- Криволинейные координаты
- Г-функция
- Функции Лежандра
- Сферические гармоники
- Гипергеометрическая функция
- Вырожденная гипергеометрическая функция
- Некоторые функции, определяемые интегралами