Задача 165. Аномальное рассеяние протонов на протонах

При энергиях, превышающих в рассеянии протонов на протонах начинают появляться аномалии, обусловленные наличием короткодействующих ядерных сил притяжения. Описать это аномальное рассеяние с помощью дополнительного сдвига фазы 80 парциальной волны с

Решение. Без учета симметризации вопрос об аномальном рассеянии заряженных частиц рассматривался нами в задаче 112. Согласно полученным там результатам [формула (112.5)], амплитуда рассеяния в системе центра масс сталкивающихся частиц имеет вид

Для дальнейшего удобно ввести обозначения

где первый член описывает резерфордовское рассеяние, вызванное кулоновским взаимодействием, а второй член

представляет собой амплитуду аномального рассеяния. Учитывая далее, что

и что, согласно результатам предыдущей задачи, симметризация приводит к соотношению

мы получаем

Так как амплитуда аномального рассеяния не зависит от угла то из первого члена формулы (165.5) она выпадает. Замечательно, что даже при более высоких энергиях, когда в амплитуду аномального рассеяния дают вклад состояния с высшими значениями момента и когда

ни одно из состояний с четным I не дает вклада в триплетный член и ни одно из состояний с нечетным I не дает вклада в синглетный член. Этот результат является прямым следствием соотношения

Таким образом, в сечение рассеяния дают вклад лишь те члены, которые соответствуют состояниям

Этот результат находится в полном согласии с принципом Паули, если его применять по отдельности к каждой из парциальных волн (состояния запрещены)

Выражение (165.6) нетрудно привести к виду

В первой строке здесь собраны члены, обусловленные кулоновским рассеянием; они подробно рассматривались нами в предыдущей задаче. Во второй строке имеются два члена, связанные с интерференцией кулоновского и аномального рассеяния, и член, обусловленный собственно аномальным рассеянием. Если вспомнить явный вид амплитуд то эти три последние члена

нетрудно вычислить:

Обычно вводится отношение сечений рассеяния

где означает сечение кулоновского рассеяния, выведенное в предыдущей задаче [члены, стоящие в пер вой строке формулы (165.7)]. Мы имеем

Этой формулой можно пользоваться до тех пор, пока не играет роли -рассеяние, т. е. до тех пор, пока энергия протонов не превышает несколько

Из формулы (165.9) следует, что для углов отношение для этих углов конечный вклад аномального рассеяния подавляется сингулярностью, имеющейся в кулоновском рассеянии.

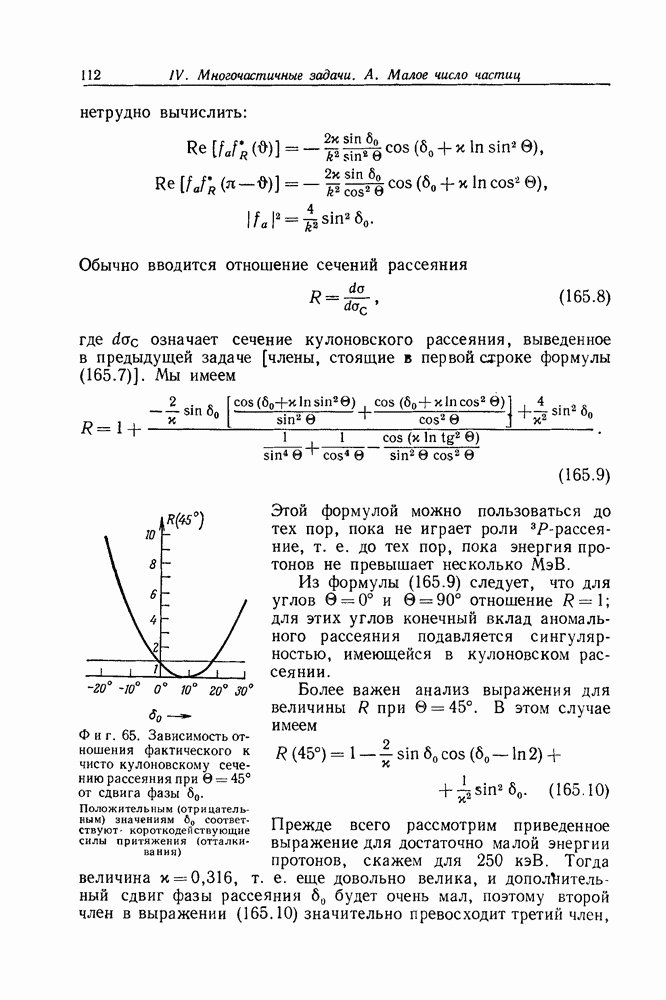
Фиг. 65. Зависимость отношения фактического к чисто кулоновскому сечению рассеяния при от сдвига фазы 80. Положительным (отрицательным) значениям 60 соответствуют короткодействующие силы притяжения (отталкивания)

Более важен анализ выражения для величины при В этом случае имеем

Прежде всего рассмотрим приведенное выражение для достаточно малой энергии протонов, скажем для Тогда величина т. е. еще довольно велика, и дополнительный сдвиг фазы рассеяния 80 будет очень мал, поэтому второй член в выражении (165.10) значительно превосходит третий член,

и, наблюдая рассеяние под углом 45°, мы легко можем решить вопрос о знаке дополнительных сил. Если мы имеем дело с силами притяжения, то если же мы имеем дело с силами отталкивания, то Эксперимент показывает, что ядерные силы являются силами притяжения.

Перейдем теперь к более высоким энергиям. Пусть, например, . Вычисленная по формуле (165.10) зависимость отношения от сдвига фазы 60 показана на фиг. 65. Так как мы уже решили, что (притяжение), то эта кривая однозначно определяет сдвиг фазы 80, если Именно так и обстоит дело в случае По данным эксперимента и, следовательно, Действуя таким образом, мы однозначно находим зависимость дополнительного сдвига фазы рассеяния 80 от энергии.

С помощью формулы (165.9) и найденных значений 60 мы можем теперь вычислить отношение для других углов рассеяния и полученные таким путем угловые распределения для каждого значения энергии сравнить с данными эксперимента. Тем самым теория подвергается более тщательной проверке. Как оказалось, теория и эксперимент прекрасно согласуются друг с другом.

Литература

(см. скан)