| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
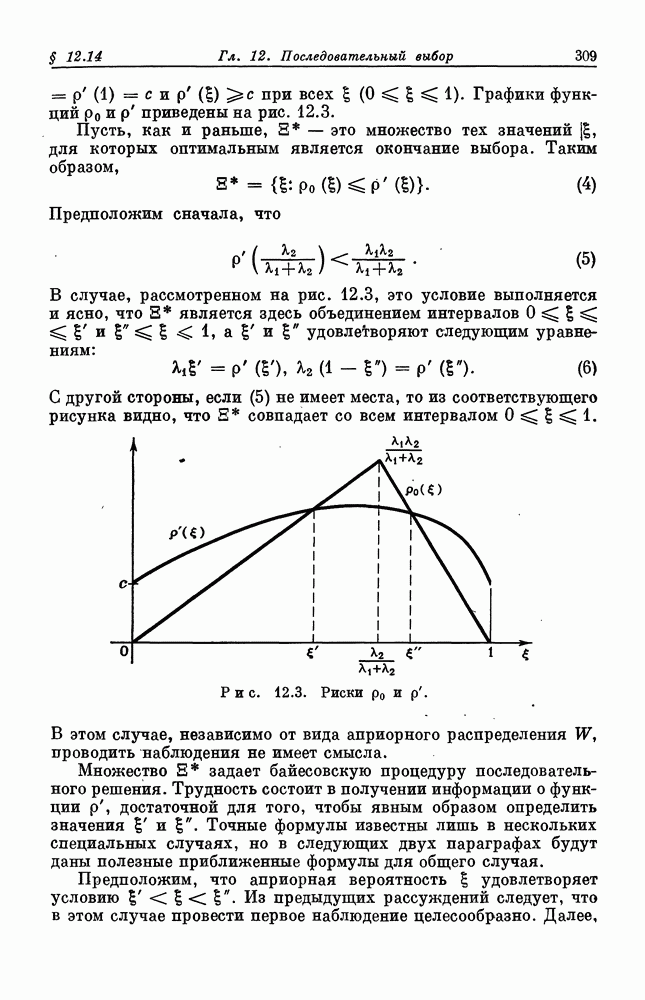
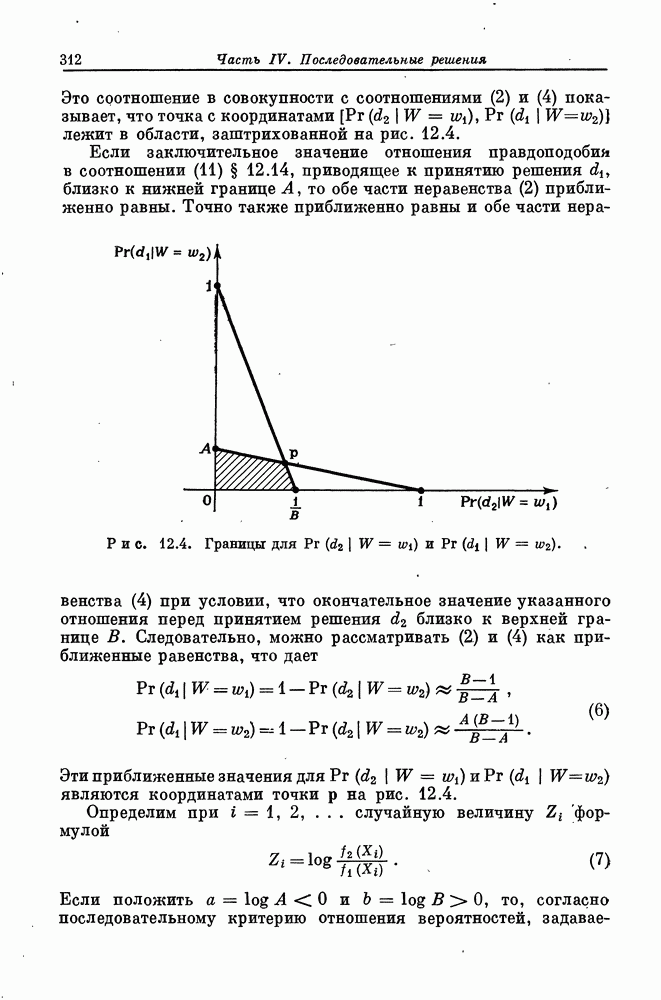
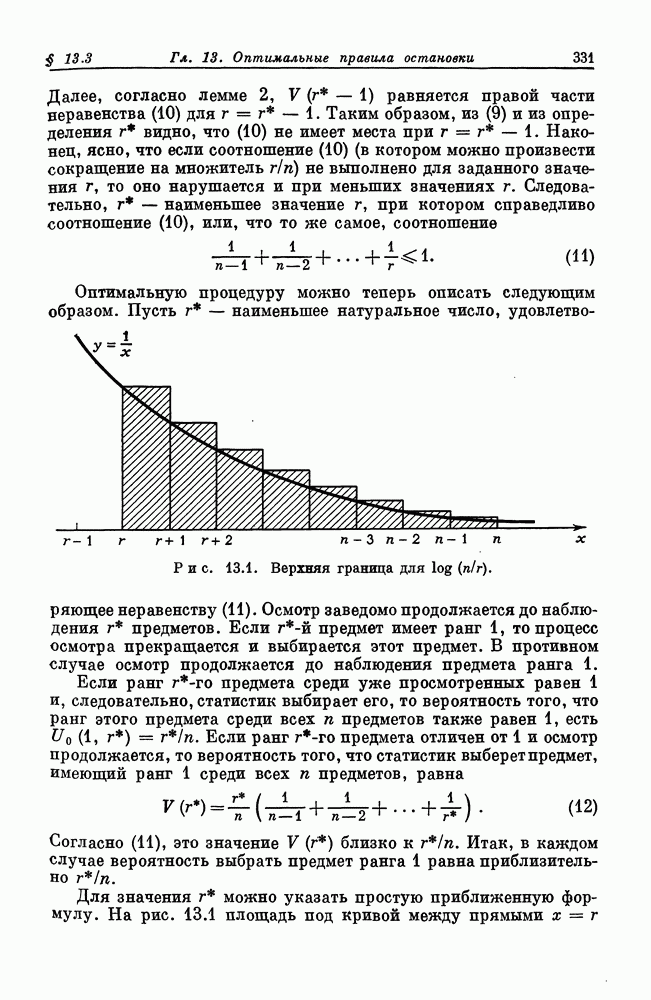
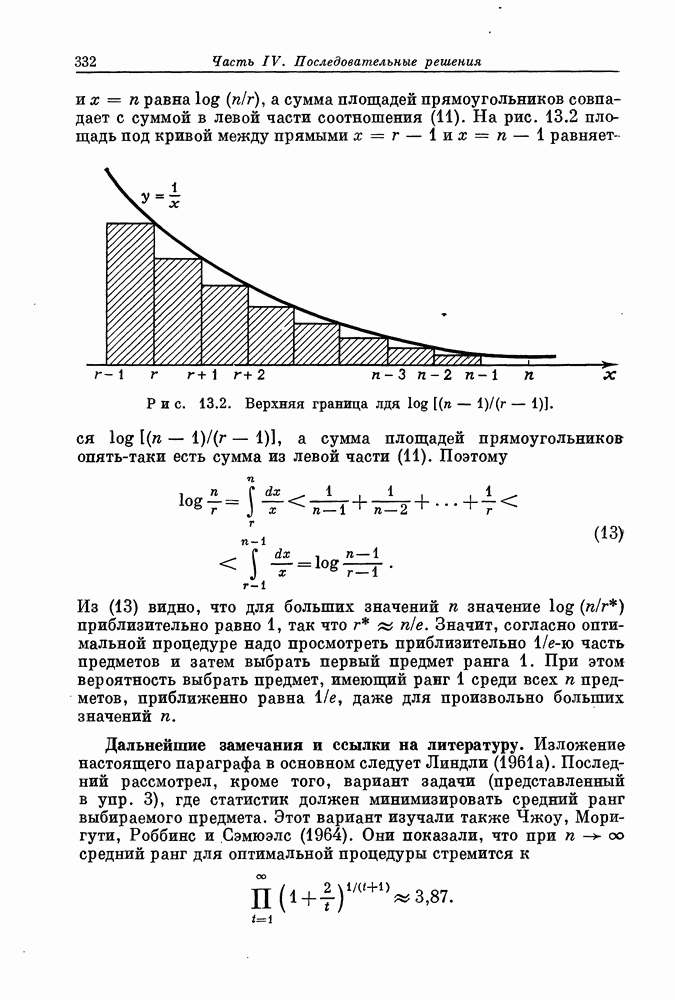
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
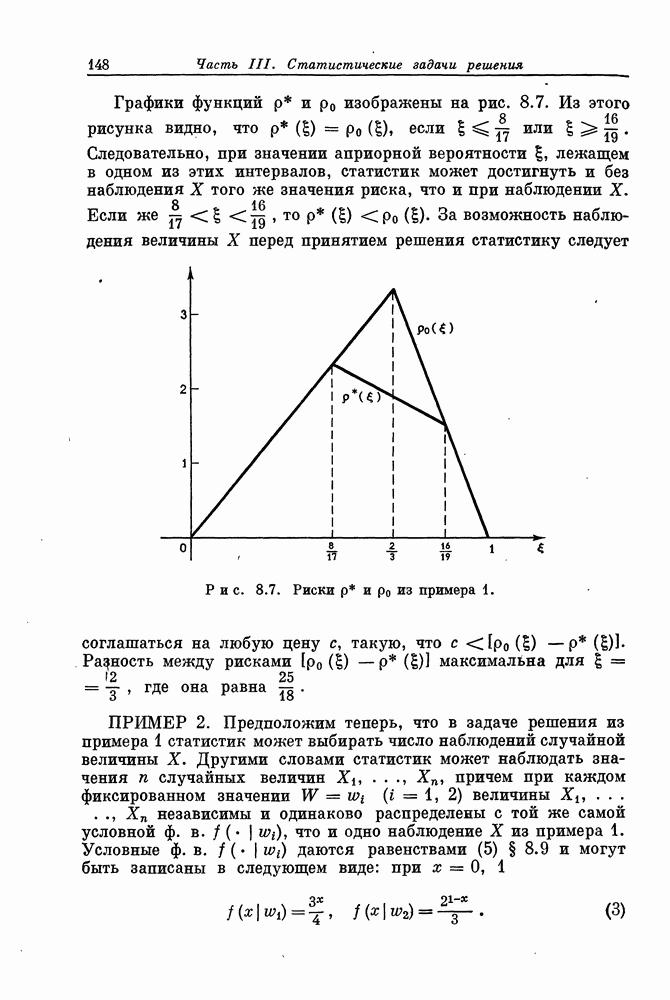
§ 13.4. Выбор с отбрасыванием
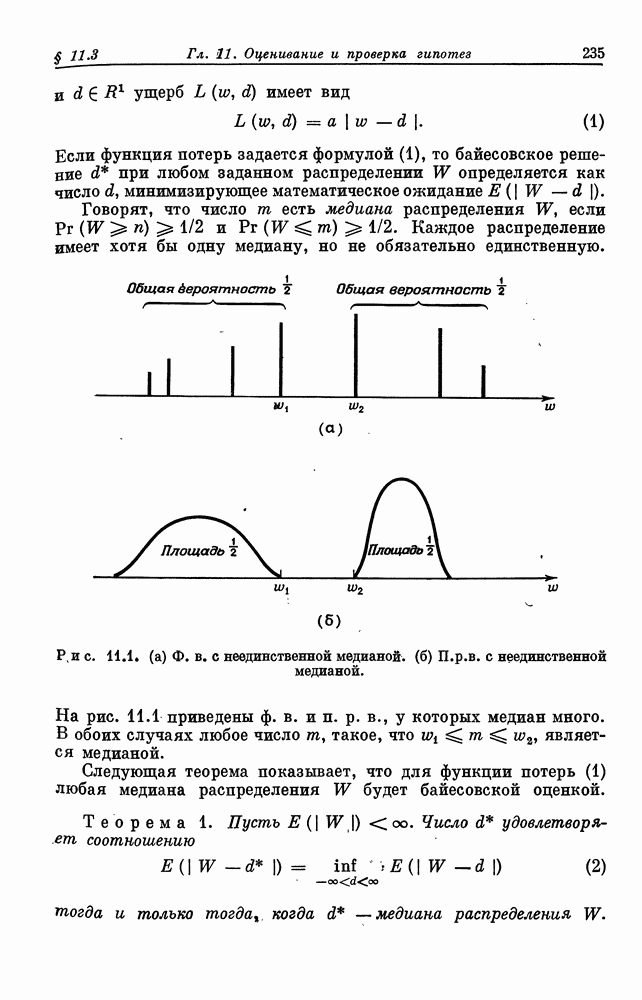
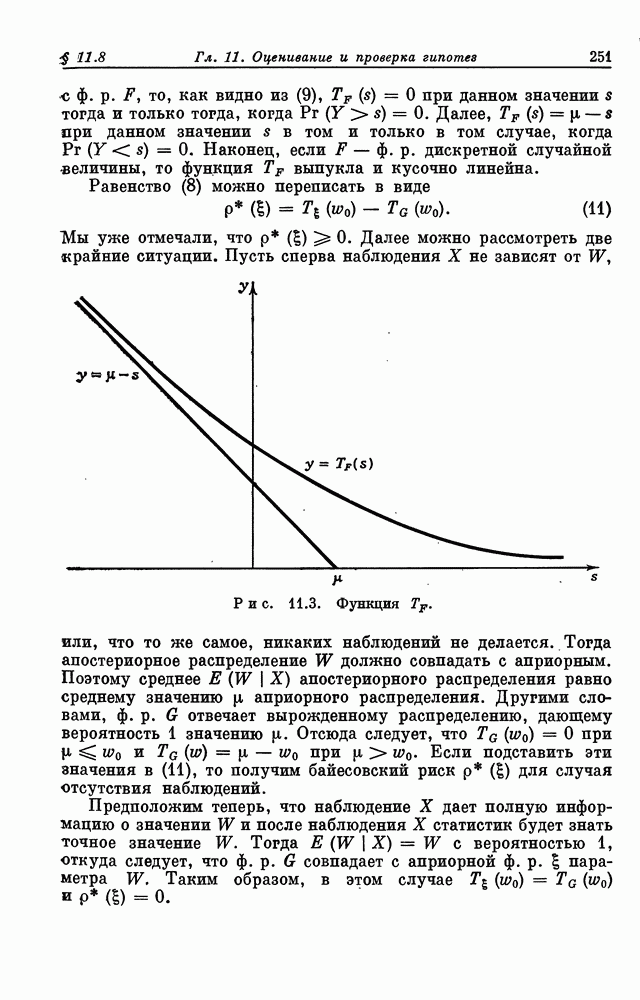
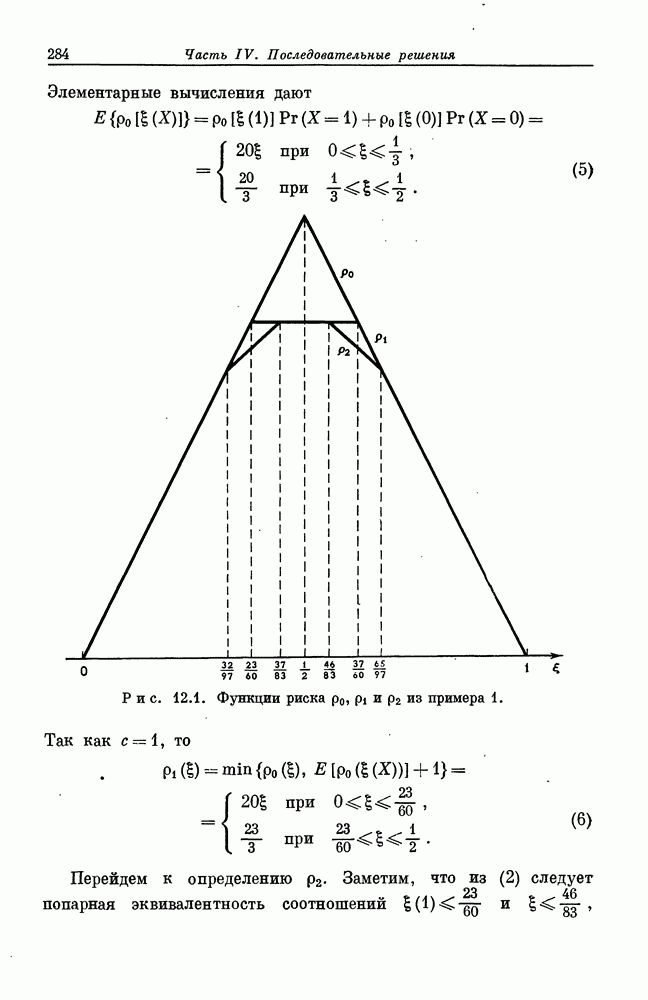
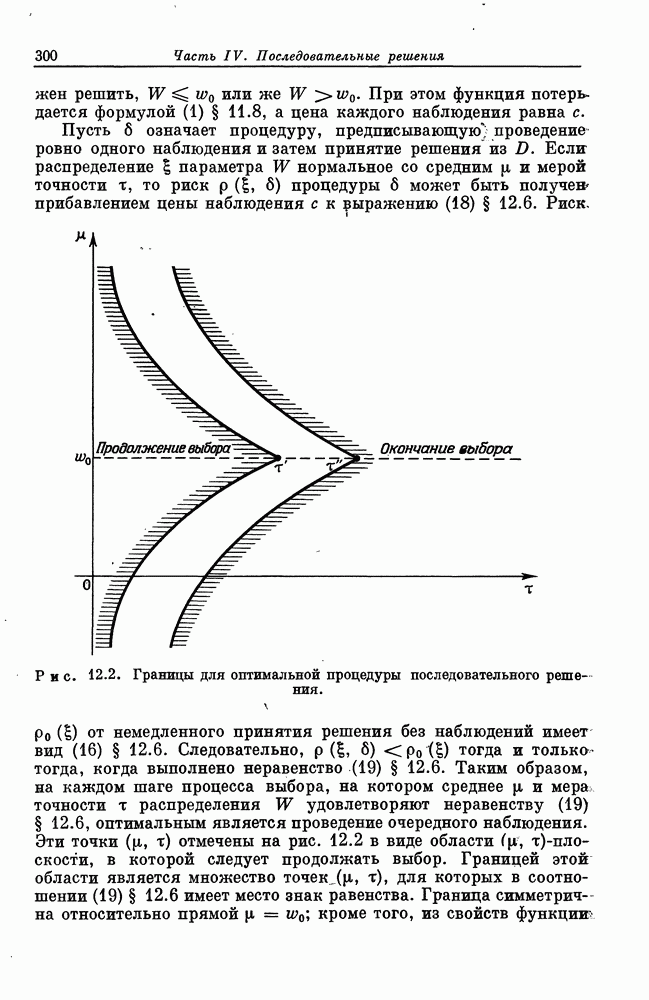
Задача, рассматривавшаяся в § 13.2 и 13.3, весьма специфична в тгом отношении, что единственной информацией, которую статистик получает в результате осмотра предмета, является его ранг среди всех уже просмотренных предметов. Тем самым предполагается, что в начале процесса осмотра статистик ничего не знает об общем уровне  обследуемых им произведений искусства. Таким образом, даже если статистик осознает чрезвычайную красоту и совершенство первого из них, то он должен считать равновероятным высокое и низкое качество этого произведения среди всех осматриваемых. В задачах, к которым мы сейчас перейдем, статистик располагает значительно более обширной информацией. Мы предположим, что каждому просмотренному предмету статистик сразу по осмотре может приписать численную полезность и самое важное, что статистику известно распределение этих полезностей во всей большой совокупности,
обследуемых им произведений искусства. Таким образом, даже если статистик осознает чрезвычайную красоту и совершенство первого из них, то он должен считать равновероятным высокое и низкое качество этого произведения среди всех осматриваемых. В задачах, к которым мы сейчас перейдем, статистик располагает значительно более обширной информацией. Мы предположим, что каждому просмотренному предмету статистик сразу по осмотре может приписать численную полезность и самое важное, что статистику известно распределение этих полезностей во всей большой совокупности,  предметов из которой могут рассматриваться как выборка.
предметов из которой могут рассматриваться как выборка.
Более точно, предположим, что  последовательная повторная выборка из распределения на вещественной прямой с известной
последовательная повторная выборка из распределения на вещественной прямой с известной  и конечным средним значением. Допустим, что для числа производимых наблюдений задана верхняя граница
и конечным средним значением. Допустим, что для числа производимых наблюдений задана верхняя граница  На
На  шаге процесса выбора
шаге процесса выбора  после наблюдения значений
после наблюдения значений  статистик может либо Остановиться, получив выигрыш
статистик может либо Остановиться, получив выигрыш  либо продолжать выбор, наблюдая Он заведомо должен остановиться с выигрышем, равным последнему наблюдению
либо продолжать выбор, наблюдая Он заведомо должен остановиться с выигрышем, равным последнему наблюдению  если не остановился нигде ранее. Как обычно, обозначим через
если не остановился нигде ранее. Как обычно, обозначим через  случайное число наблюдений, проводимых при некотором заданном правиле остановки. Задача состоит в отыскании правила остановки, максимизирующего средний выигрыш
случайное число наблюдений, проводимых при некотором заданном правиле остановки. Задача состоит в отыскании правила остановки, максимизирующего средний выигрыш  Это задача выбора с отбрасыванием, поскольку здесь, как и в задаче из § 13.2 и 13.3, если статистик решил не останавливаться на некотором наблюдении, то он «отбрасывает» его и уже не сможет позже принять это значение в качестве выигрыша.
Это задача выбора с отбрасыванием, поскольку здесь, как и в задаче из § 13.2 и 13.3, если статистик решил не останавливаться на некотором наблюдении, то он «отбрасывает» его и уже не сможет позже принять это значение в качестве выигрыша.
На всяком шаге процесса выбора после того, как сделано хотя бы одно наблюдение, состояние статистика задается значением х последнего наблюдения и числом  наблюдений, оставшихся да момента обязательного прекращения выбора. При
наблюдений, оставшихся да момента обязательного прекращения выбора. При  обозначим через
обозначим через  средний выигрыш от использования оптимальной процедуры при этих условиях. Итак, после наблюдения значений
средний выигрыш от использования оптимальной процедуры при этих условиях. Итак, после наблюдения значений  средний выигрыш, отвечающий оптимальной процедуре, равен
средний выигрыш, отвечающий оптимальной процедуре, равен  Так как статистик обязан остановиться и принять значение последнего из отведенных ему наблюдений в качестве выигрыша, в случае если он не остановился раньше, то
Так как статистик обязан остановиться и принять значение последнего из отведенных ему наблюдений в качестве выигрыша, в случае если он не остановился раньше, то  при
при 
Далее, для  обозначим через
обозначим через  максимальный средний выигрыш, который может быть получен, когда осталось провести
максимальный средний выигрыш, который может быть получен, когда осталось провести  наблюдений, причем хотя бы одно из них обязательна проводится до окончания выбора. Так как рассматриваемая задача есть задача выбора с отбрасыванием из известного распределения, то средний выигрыш
наблюдений, причем хотя бы одно из них обязательна проводится до окончания выбора. Так как рассматриваемая задача есть задача выбора с отбрасыванием из известного распределения, то средний выигрыш  от проведения хотя бы одного наблюдения и последующего оптимального продолжения есть постоянная, зависящая лишь от числа
от проведения хотя бы одного наблюдения и последующего оптимального продолжения есть постоянная, зависящая лишь от числа  оставшихся наблюдений и не зависящая от значений уже проведенных наблюдений. После одного дальнейшего наблюдения X средний выигрыш от продолжения оптимального на оставшихся
оставшихся наблюдений и не зависящая от значений уже проведенных наблюдений. После одного дальнейшего наблюдения X средний выигрыш от продолжения оптимального на оставшихся  шагах есть
шагах есть  Поэтому средний выигрыш
Поэтому средний выигрыш  равен
равен

При  средний выигрыш
средний выигрыш  от использования оптимальной процедуры должен быть равен максимуму
от использования оптимальной процедуры должен быть равен максимуму  двух выигрышей: выигрыша х от остановки и среднего выигрыша
двух выигрышей: выигрыша х от остановки и среднего выигрыша  от продолжения. Таким образом,
от продолжения. Таким образом,

Так как  то функции
то функции  и числа
и числа  можно найти последовательно из соотношений (1) и (2). Поскольку более
можно найти последовательно из соотношений (1) и (2). Поскольку более  наблюдений провести нельзя, а хотя бы одно наблюдение должно быть сделано, средний выигрыш от оптимальной процедуры равен
наблюдений провести нельзя, а хотя бы одно наблюдение должно быть сделано, средний выигрыш от оптимальной процедуры равен  Если в начале процесса выбора статистик может получить выигрыш
Если в начале процесса выбора статистик может получить выигрыш  без всяких наблюдений, то средний выигрыш от оптимальной процедуры равен
без всяких наблюдений, то средний выигрыш от оптимальной процедуры равен 
Пусть теперь  преобразование
преобразование  определенное формулой (9) § 11.8. Оно существует в силу предположения о конечности среднего
определенное формулой (9) § 11.8. Оно существует в силу предположения о конечности среднего  Можно показать (упр. 5), что преобразование
Можно показать (упр. 5), что преобразование  обладает следующим свойством:
обладает следующим свойством:

Из (1) и (2) видно, что при 

Согласно (1),  Следовательно, последовательность
Следовательно, последовательность  может быть найдена с помощью рекуррентного соотношения (4). Так как число наблюдений не может превосходить
может быть найдена с помощью рекуррентного соотношения (4). Так как число наблюдений не может превосходить  то, согласно оптимальной процедуре надо продолжать наблюдения, если наблюденное значение
то, согласно оптимальной процедуре надо продолжать наблюдения, если наблюденное значение  надо окончить выборг если
надо окончить выборг если  Средний выигрыш при такой процедуре равен
Средний выигрыш при такой процедуре равен 
Некоторые примеры представлены ниже в упр. 6—9.
Аналогичные задачи рассматривали Гилберт и Мостеллер (1966), Гутмэн (1960) и Мозер (1956), а также Кэли (1875) боле чем на 80 лет раньше всех других.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- Глава 2. ЭКСПЕРИМЕНТЫ, ВЫБОРОЧНЫЕ ПРОСТРАНСТВА И ВЕРОЯТНОСТЬ
- § 2.1. Эксперименты и выборочные пространства
- § 2.2. Теория множеств
- § 2.3. События и вероятность
- § 2.4. Условная вероятность
- § 2.5. Биномиальные коэффициенты
- Глава 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, СЛУЧАЙНЫЕ ВЕКТОРЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- § 3.1. Случайные величины и их распределения
- § 3.2. Многомерные распределения
- § 3.3. Суммы и интегралы
- § 3.4. Маргинальные распределения и независимость
- § 3.5. Векторы и матрицы
- § 3.6. Математические ожидания, моменты и характеристические функции
- § 3.7. Преобразования случайных величин
- § 3.8. Условные распределения
- Глава 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 4.2. Распределение Бернулли
- § 4.3. Биномиальное распределение
- § 4.4. Распределение Пуассона
- § 4.5. Отрицательное биномиальное распределение
- § 4.6. Гипергеометрическое распределение
- § 4.7. Нормальное распределение
- § 4.8. Гамма-распределение
- § 4.9. Бета-распределение
- § 4.10. Равномерное распределение
- § 4.11. Распределение Парето
- § 4.12. Распределение Стьюдента
- Глава 5. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 5.2. Мультиномиальное распределение
- § 5.3. Распределение Дирихле
- § 5.4. Многомерное нормальное распределение
- § 5.5. Распределение Уишарта
- § 5.6. Многомерное t-распределение
- § 5.7. Двустороннее двумерное распределение Парето
- ЧАСТЬ II. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ И ПОЛЕЗНОСТЬ
- Глава 6. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ
- § 6.2. Относительное правдоподобие
- § 6.3. Вспомогательный эксперимент
- § 6.4. Построение вероятностного распределения
- § 6.5. Проверка выполнения свойств вероятностного распределения
- § 6.6. Условные правдоподобия
- Глава 7. ПОЛЕЗНОСТЬ
- § 7.2. Предпочтения в множестве вероятностных распределений
- § 7.3. Определение функции полезности
- § 7.4. Некоторые свойства функций полезности
- § 7.5. Полезность в случае денежных доходов
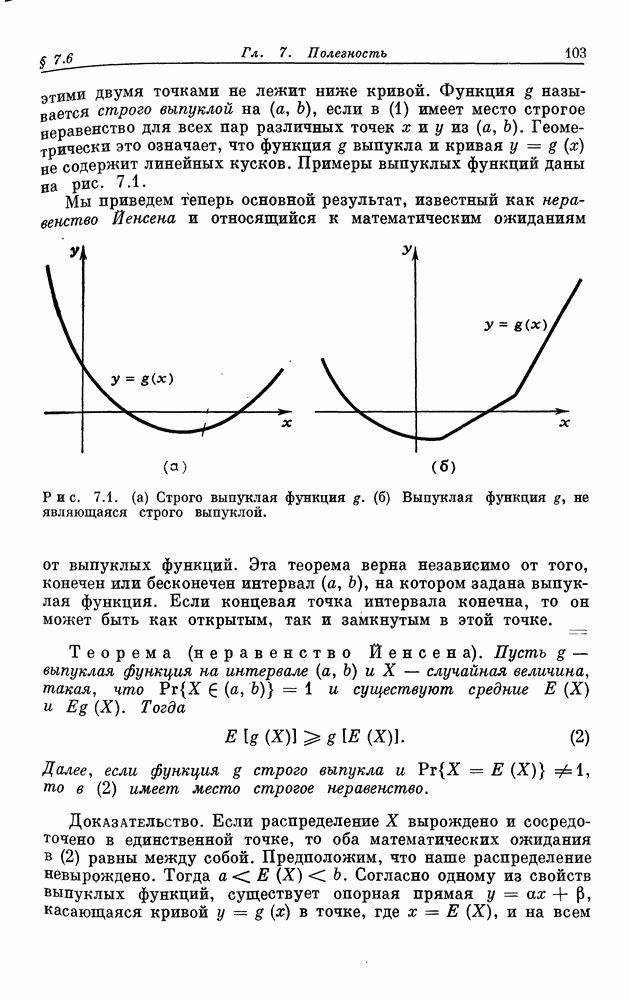
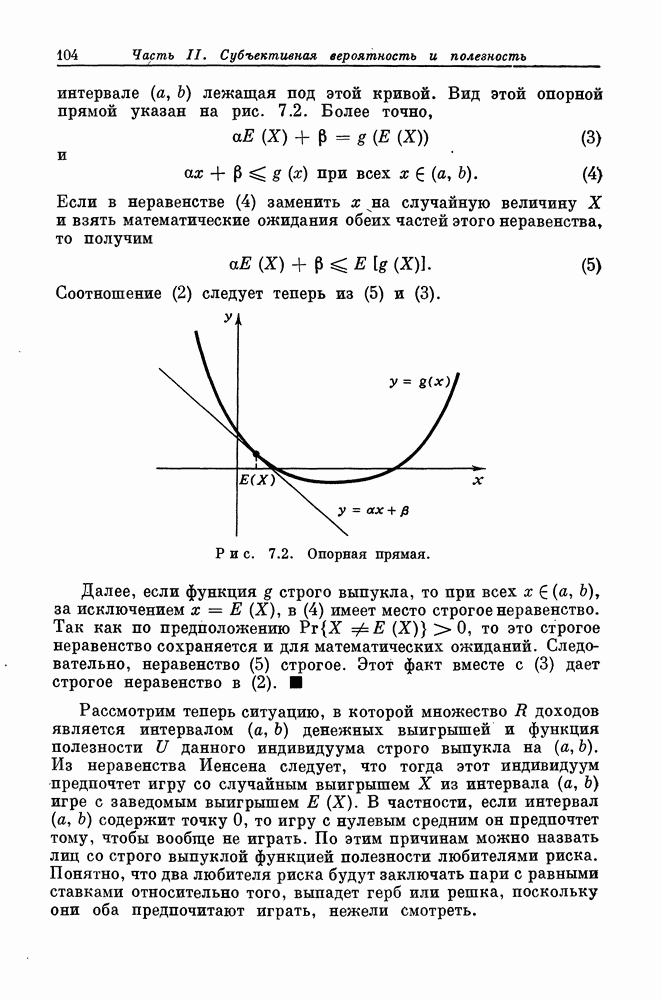
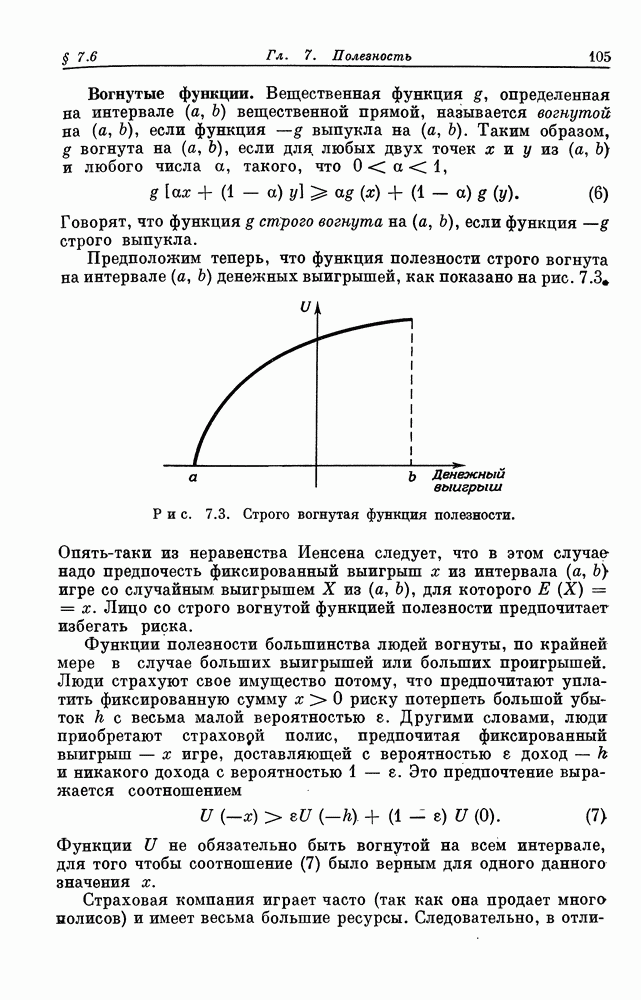
- § 7.6. Выпуклые и вогнутые функции полезности
- § 7.7. Аксиоматический подход к полезности
- § 7.8. Построение функции полезности
- § 7.9. Проверка свойств функции полезности
- § 7.10. Распространение свойств функции полезности на класс
- ЧАСТЬ III. СТАТИСТИЧЕСКИЕ ЗАДАЧИ РЕШЕНИЯ
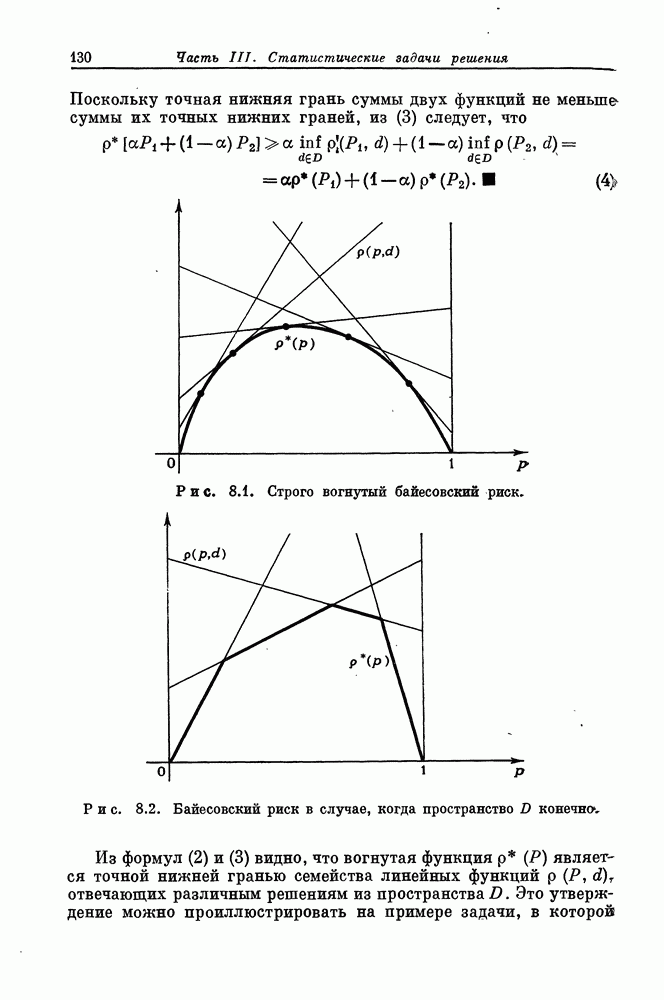
- § 8.2. Байесовский риск и байесовские решения
- § 8.3. Неотрицательные функции потерь
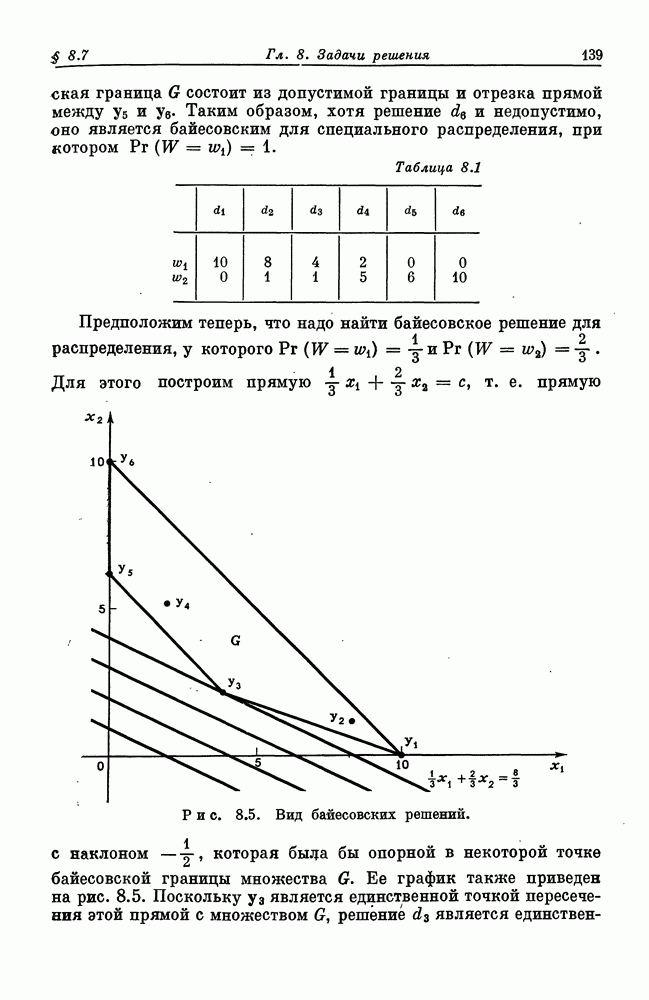
- § 8.4. Вогнутость байесовского риска
- § 8.5. Рандомизация и смешанные решения
- § 8.6. Выпуклые множества
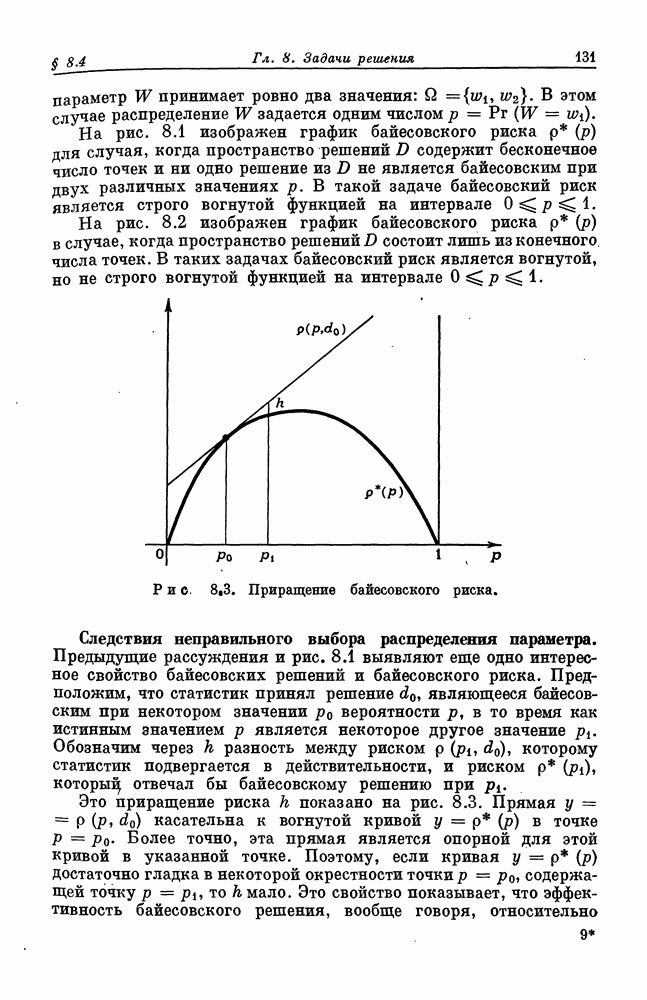
- § 8.7. Задачи решения с конечными …
- § 8.8. Задачи решения с наблюдениями
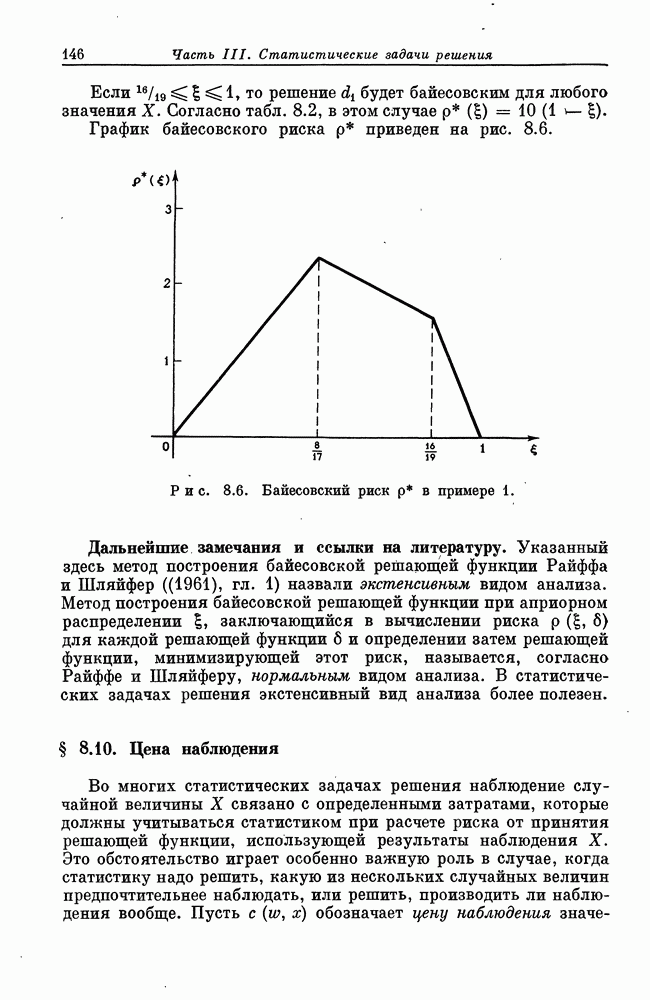
- § 8.9. Построение байесовских решающих функций
- § 8.10. Цена наблюдения
- § 8.11. Статистические задачи решения, в которых … состоят из двух точек
- § 8.12. Вычисление апостериорного распределения в случае, когда наблюдения производятся в несколько этапов
- Глава 9. СОПРЯЖЕННЫЕ АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 9.1. Достаточные статистики
- § 9.2. Сопряженные семейства распределений
- § 9.3. Построение сопряженного семейства
- § 9.4. Сопряженные семейства для выборок из различных стандартных распределений
- § 9.5. Сопряженные семейства для выборок из нормального распределения
- § 9.6. Выборка из нормального распределения с неизвестным средним и неизвестной мерой точности
- § 9.7. Выборка из равномерного распределения
- § 9.8. Сопряженное семейство для мультиномиальных наблюдений
- § 9.9. Сопряженные семейства для выборок из многомерного нормального распределения
- § 9.10. Многомерное нормальное распределение с неизвестным вектором средних и неизвестной матрицей точности
- § 9.11. Маргинальное распределение вектора средних
- § 9.12. Распределение коэффициента корреляции
- § 9.13. Матрицы точности с неизвестным множителем
- Глава 10. ПРЕДЕЛЬНЫЕ АПОСТЕРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
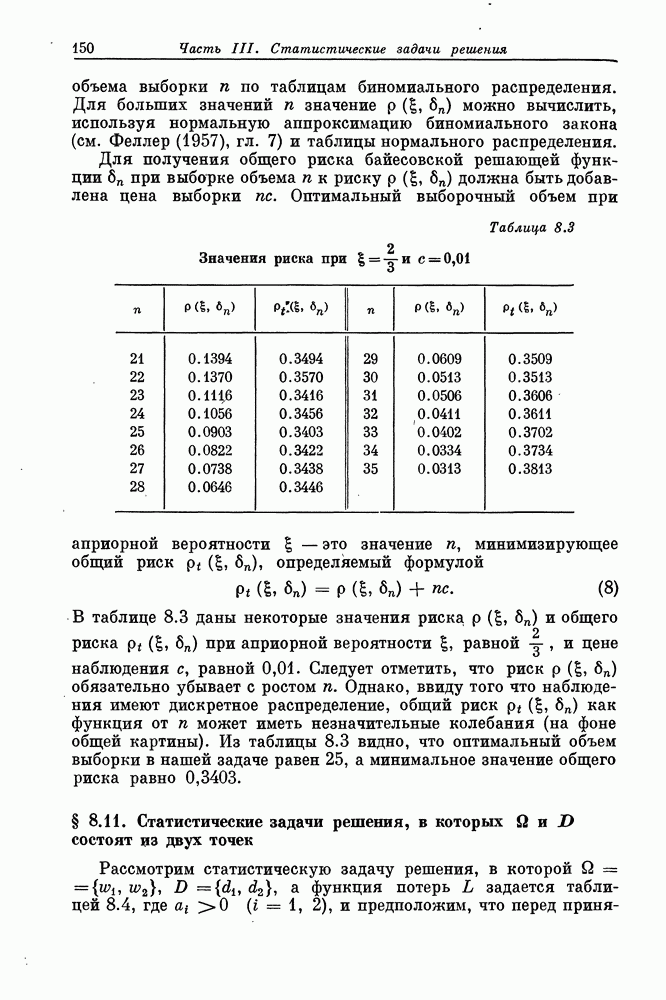
- § 10.1. Несобственные априорные распределения
- § 10.2. Несобственные априорные распределения для выборок из нормального распределения
- § 10.3. Несобственные априорные распределения для выборок из многомерного нормального распределения
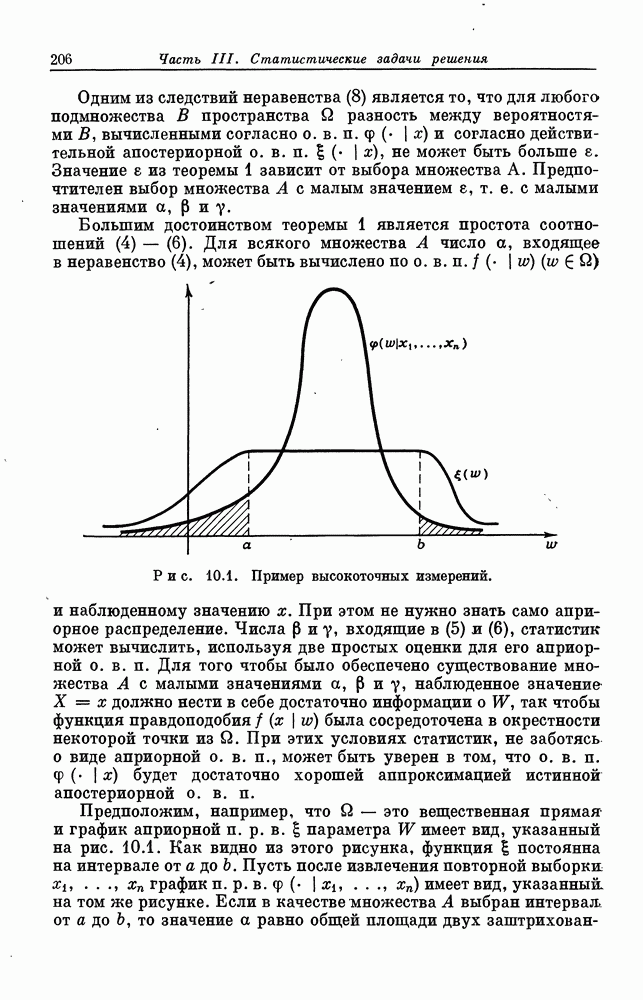
- § 10.4. Высокоточные измерения
- § 10.5. Сходимость апостериорных распределений
- § 10.6. Супер непрерывность
- § 10.7. Решения уравнения правдоподобия
- § 10.8. Сходимость супернепрерывных функций
- § 10.9. Предельные свойства функции правдоподобия
- § 10.10. Нормальная аппроксимация апостериорного распределения
- § 10.11. Аппроксимации в случае векторных параметров
- § 10.12. Апостериорные отношения
- Глава 11. ОЦЕНИВАНИЕ, ПРОВЕРКА ГИПОТЕЗ И ЛИНЕЙНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ
- § 11.2. Квадратическая функция потерь
- § 11.3. Ущерб пропорциональный абсолютной величине погрешности
- § 11.4. Оценивание векторного параметра
- § 11.5. Задачи проверки гипотез
- § 11.6. Проверка простой гипотезы о среднем значении нормального распределения
- § 11.7. Проверка гипотез о среднем значении нормального распределения с неизвестной мерой точности
- § 11.8. Решение вопроса о том, будет ли параметр меньше или больше предписанного значения
- § 11.9. Проверка гипотезы о том, превосходит или нет среднее нормального распределения заданное значение
- § 11.10. Линейные модели
- § 11.11. Проверка гипотез в линейных моделях
- § 11.12. Проверка гипотезы о равенстве нулю некоторых коэффициентов регрессии
- § 11.13. Дисперсионный анализ по одному признаку
- ЧАСТЬ IV. ПОСЛЕДОВАТЕЛЬНЫЕ РЕШЕНИЯ
- § 12.1. Эффект последовательного выбора
- § 12.2. Процедуры последовательного решения
- § 12.3. Риск процедуры последовательного решения
- § 12.4. Индукция назад
- § 12.5. Оптимальные ограниченные процедуры последовательного решения
- § 12.6. Примеры
- § 12.7. Неограниченные процедуры последовательного решения
- § 12.8. Регулярные процедуры последовательного решения
- § 12.9. Существование оптимальной процедуры
- § 12.10. Приближение оптимальной прцоедуры ограниченными процедурами
- § 12.11. Области продолжения и окончания выбора
- § 12.12. Функциональное уравнение
- § 12.13 Приближения и границы для байесовского риска
- § 12.14. Последовательный критерий отношения вероятностей
- § 12.15. Характеристики последовательных критериев отношения вероятностей
- § 12.16. Аппроксимации для среднего числа наблюдений
- Глава 13. ОПТИМАЛЬНЫЕ ПРАВИЛА ОСТАНОВКИ
- § 13.2. Вознаграждение статистика
- § 13.3. Выбор функции полезности
- § 13.4. Выбор с отбрасыванием
- § 13.5. Дальнейшие задачи выбора с отбрасыванием и выбора без отбрасывания
- § 13.6. Выбор с отбрасыванием из нормального распределения с неизвестным средним
- § 13.7. Выбор без отбрасывания из нормального распределения с неизвестным средним
- § 13.8. Существование оптимальных правил остановки
- § 13.9. Существование оптимальных правил остановки в задачах выбора без отбрасывания и с отбрасыванием
- § 13.10. Мартингалы
- § 13.11. Правила остановки для мартингалов
- § 13.12. Равномерно интегрируемые последовательности случайных величин
- § 13.13. Мартингалы, получаемые из сумм и произведений случайных величин
- § 13.14. Регулярные супермартингалы
- § 13.15. Супермартингалы и общие задачи об оптимальной остановке
- § 13.16. Марковские процессы
- § 13.17. Стационарные правила остановки для марковских процессов
- § 13.18. Задачи с входной платой
- § 13.19. Функциональное уравнение для марковского процесса
- Глава 14. ПОСЛЕДОВАТЕЛЬНОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
- § 14.2. Марковские процессы решения с конечным числом шагов
- § 14.3. Марковские процессы решения с бесконечным числом шагов
- § 14.4. Некоторые задачи о пари
- § 14.5. Задачи о «двуруком бандите»
- § 14.6. Задачи о «двуруком бандите» с известным значением одного из параметров
- § 14.7. Задачи о «двуруком бандите» в случае зависимых параметров
- § 14.8. Задачи оптимального управления запасами
- § 14.9. Задачи управления запасами с бесконечным числом шагов
- § 14.10. Задачи управления
- § 14.11. Оптимальное управление в случае, когда процесс наблюдается с ошибками
- § 14.12. Многомерные задачи управления
- § 14.13. Задачи управления с погрешностями, вносимыми статистиком
- § 14.14. Задачи поиска
- § 14.15. Задачи поиска с равными стоимостями
- § 14.16. Функции неопределенности и задачи статистического решения
- § 14.17. Достаточные эксперименты
- § 14.18. Примеры достаточных экспериментов
- СПИСОК ЛИТЕРАТУРЫ