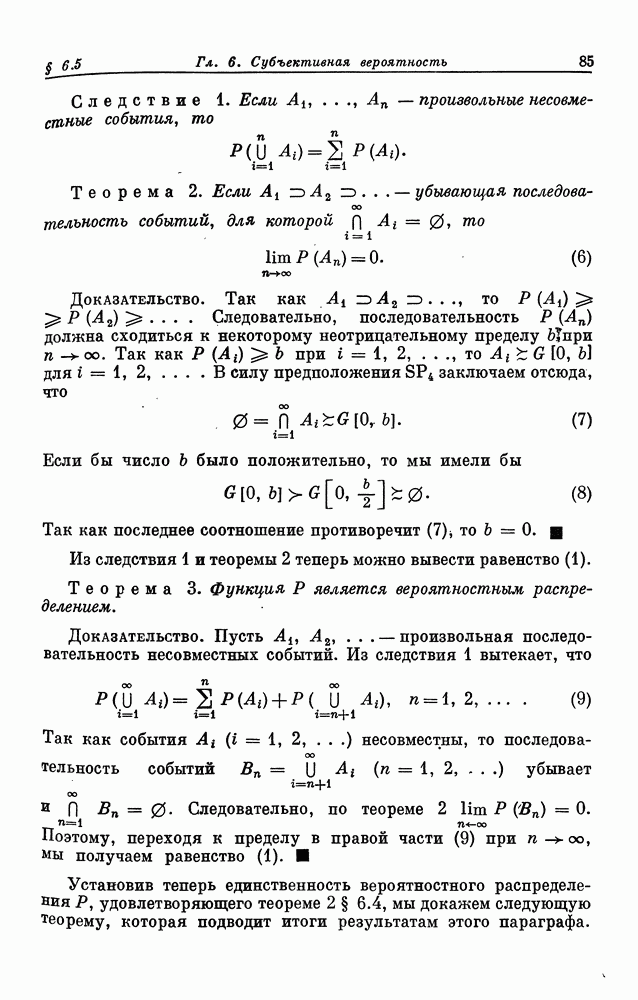| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
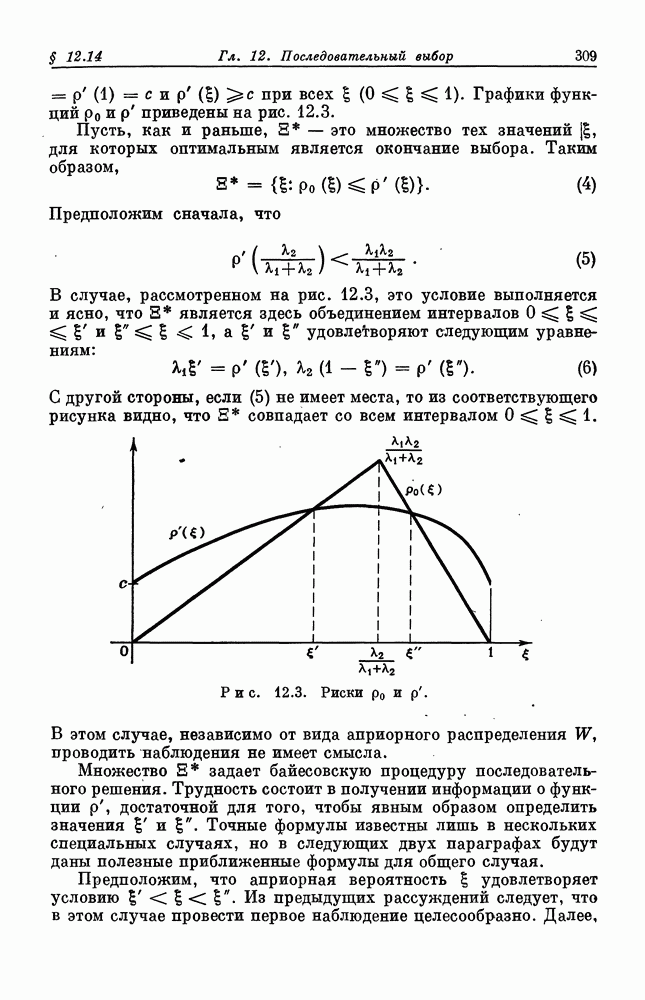
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 7.6. Выпуклые и вогнутые функции полезности
Выпуклые функции. Говорят, что вещественная функция  определенная на интервале
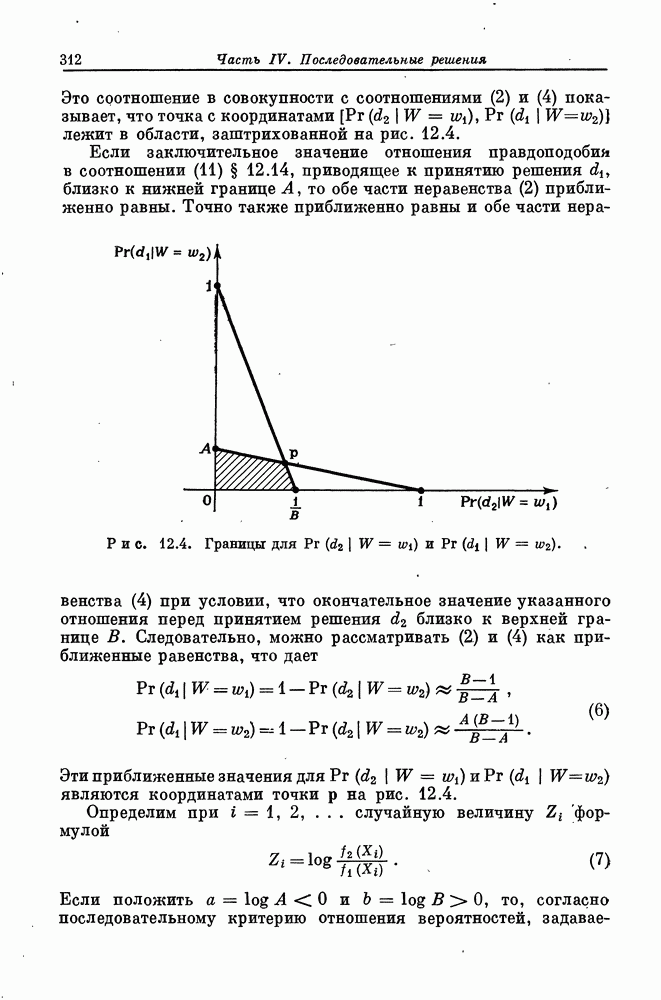
определенная на интервале  вещественной прямой, выпукла на
вещественной прямой, выпукла на  если для любых двух точек х и у из
если для любых двух точек х и у из  и любого числа а, такого, что
и любого числа а, такого, что  выполнено неравенство
выполнено неравенство

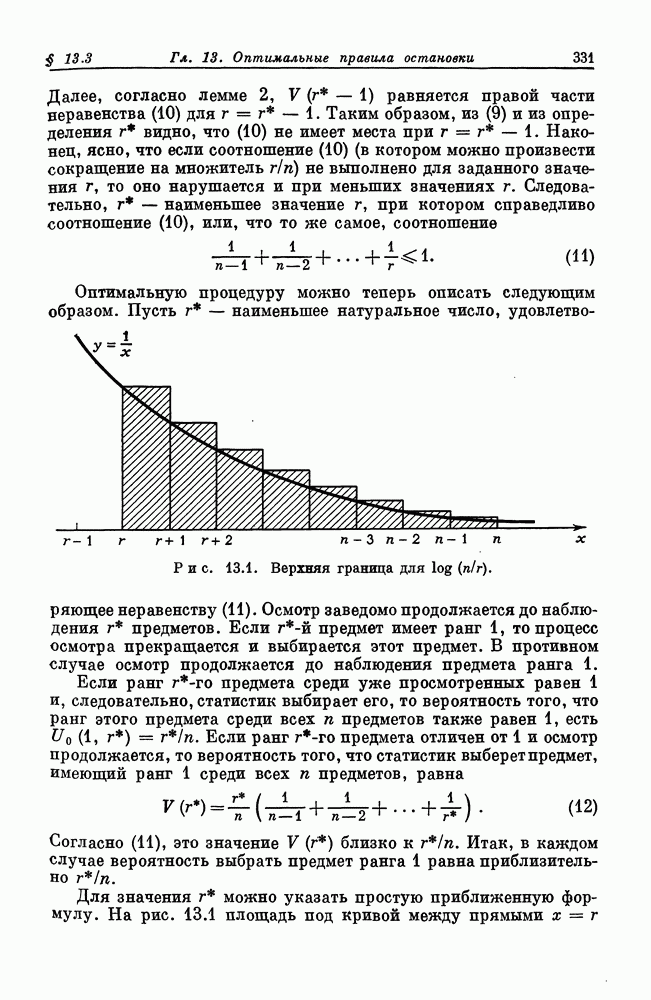
Геометрически соотношение (1) означает, что отрезок прямой, соединяющей любые две точки кривой  нигде между
нигде между
этими двумя точками не лежит ниже кривой. Функция  называется строго выпуклой на
называется строго выпуклой на  если в (1) имеет место строгое неравенство для всех пар различных точек х и у из
если в (1) имеет место строгое неравенство для всех пар различных точек х и у из  Геометрически это означает, что функция
Геометрически это означает, что функция  выпукла и кривая
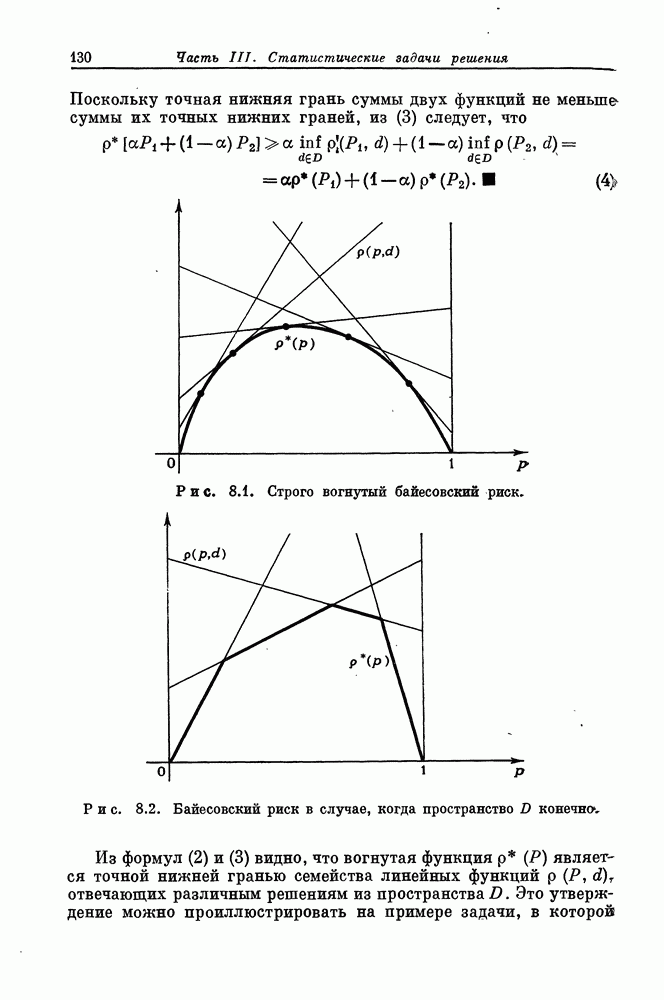
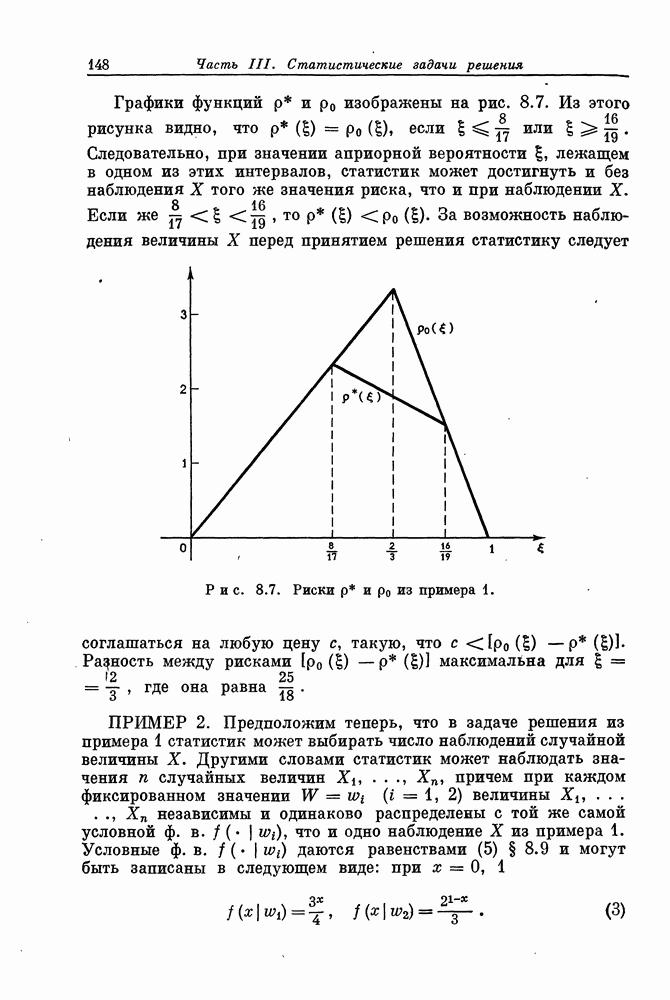
выпукла и кривая  не содержит линейных кусков. Примеры выпуклых функций даны на рис. 7.1.
не содержит линейных кусков. Примеры выпуклых функций даны на рис. 7.1.
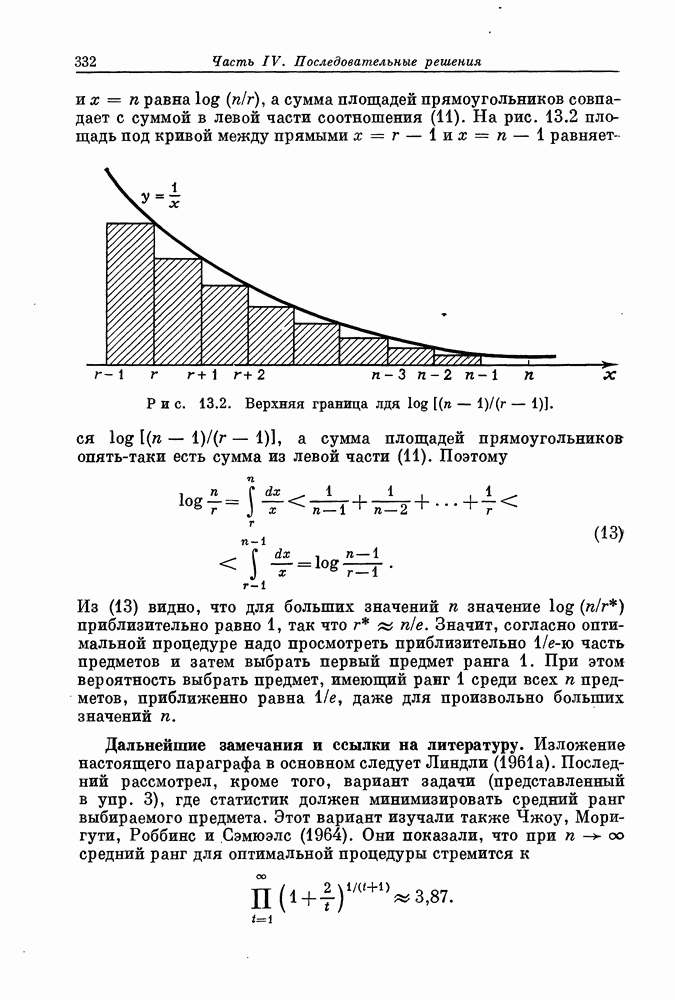
Мы приведем теперь основной результат, известный как неравенство Йенсена и относящийся к математическим ожиданиям от выпуклых функций.

Рис. 7.1. (а) Строго выпуклая функция g. (б) Выпуклая функция g, не являющаяся строго выпуклой.
Эта теорема верна независимо от того, конечен или бесконечен интервал  на котором задана выпуклая функция. Если концевая точка интервала конечна, то он может быть как открытым, так и замкнутым в этой точке.
на котором задана выпуклая функция. Если концевая точка интервала конечна, то он может быть как открытым, так и замкнутым в этой точке. 
Теорема (неравенство Йенсена). Пусть  выпуклая функция на интервале
выпуклая функция на интервале  и X — случайная величина, такая, что
и X — случайная величина, такая, что  и существуют средние
и существуют средние  и
и  Тогда
Тогда

Далее, если функция  строго выпукла и
строго выпукла и  то в (2) имеет место строгое неравенство.
то в (2) имеет место строгое неравенство.
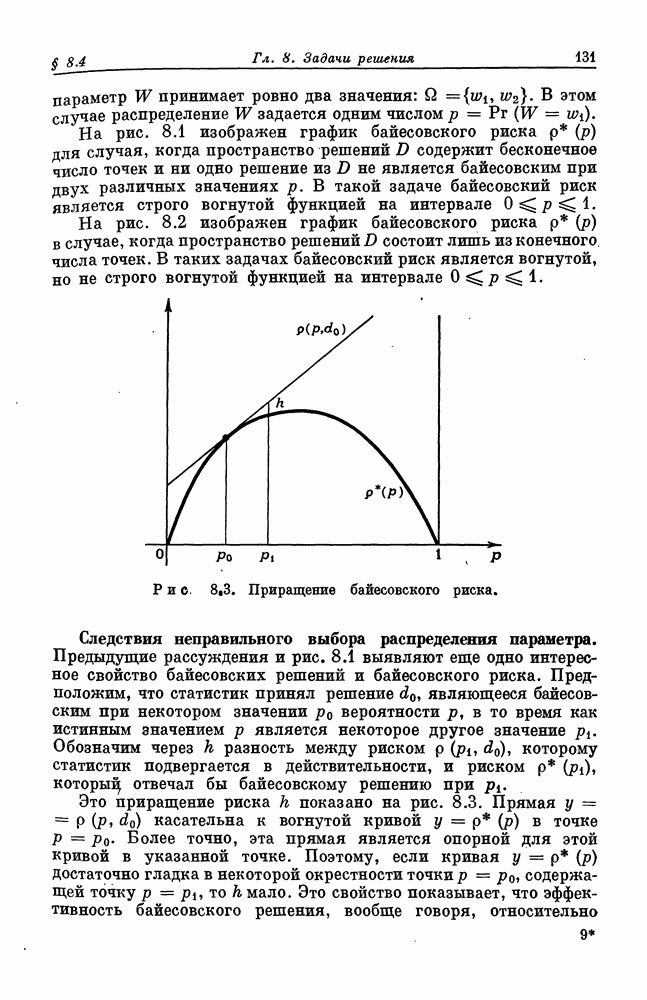
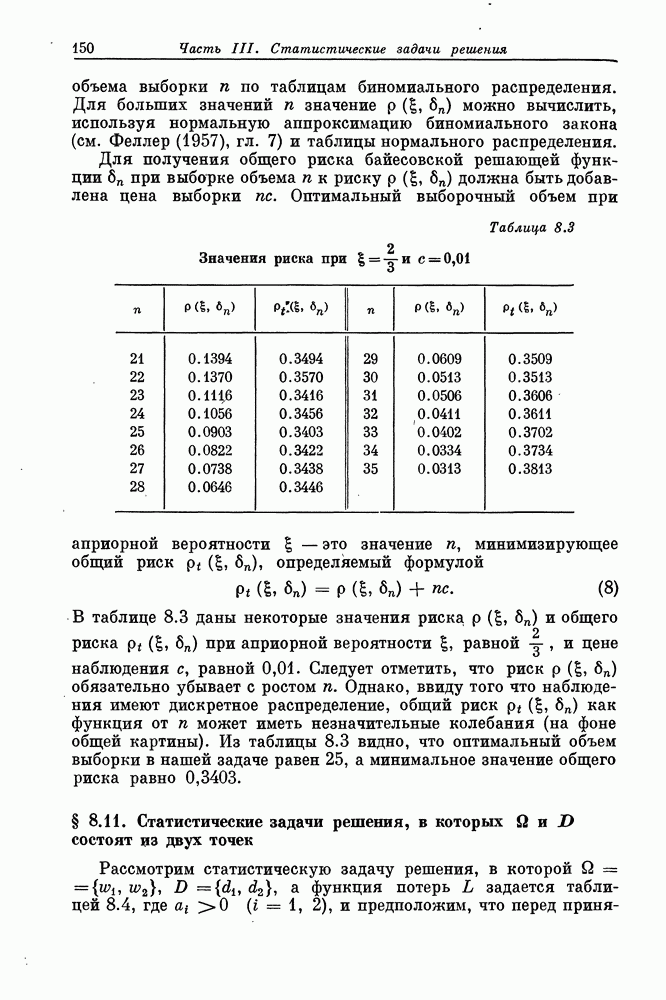
Доказательство. Если распределение X вырождено и сосредоточено в единственной точке, то оба математических ожидания в (2) равны между собой. Предположим, что наше распределение невырождено. Тогда  Согласно одному из свойств выпуклых функций, существует опорная прямая
Согласно одному из свойств выпуклых функций, существует опорная прямая  касающаяся кривой
касающаяся кривой  в точке, где
в точке, где  и на всем
и на всем
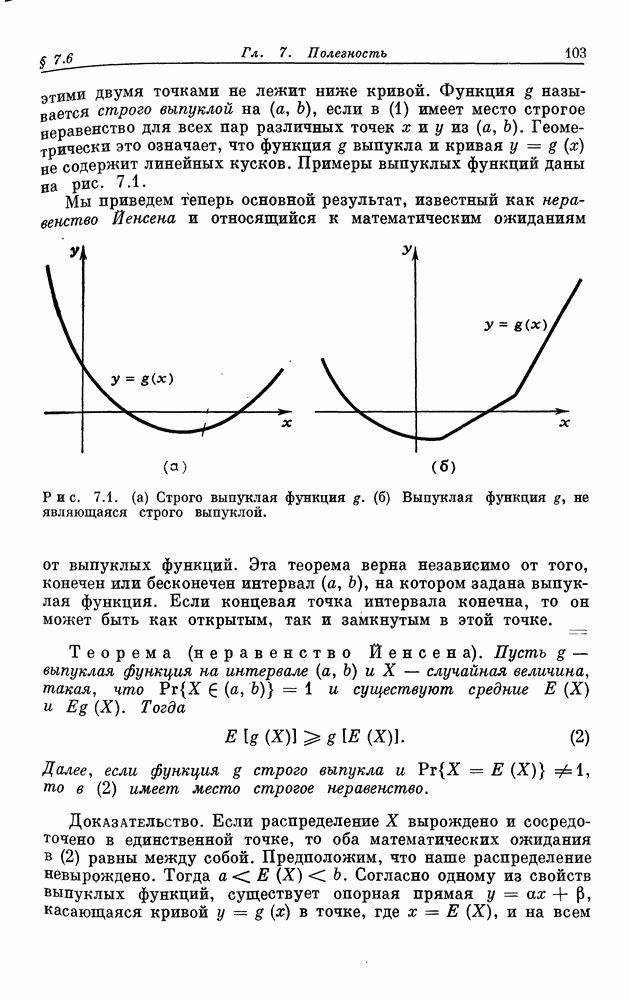
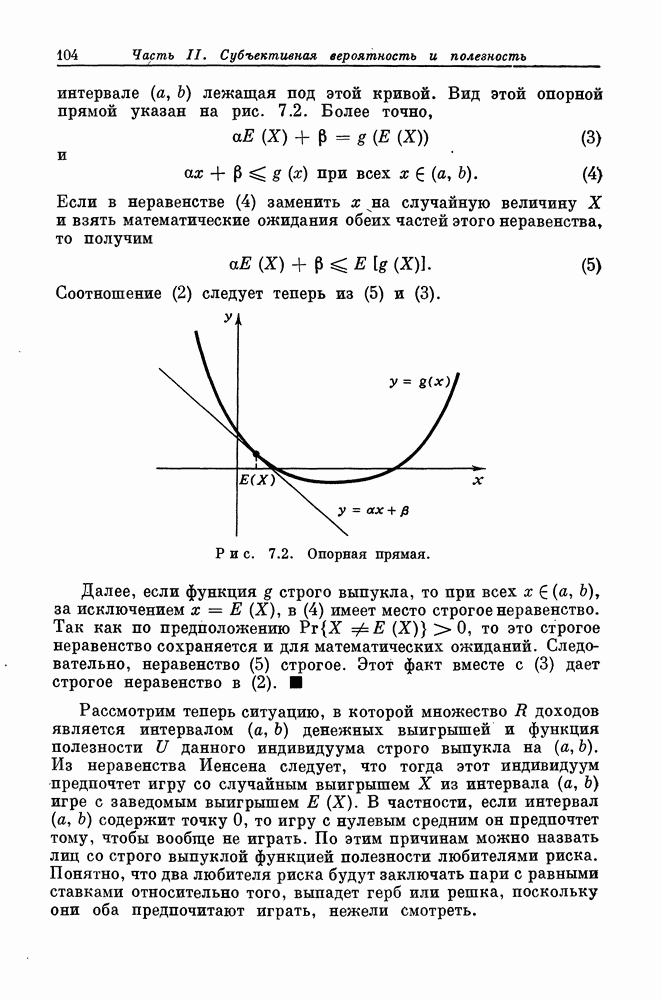
интервале  лежащая под этой кривой. Вид этой опорной прямой указан на рис. 7.2. Более точно,
лежащая под этой кривой. Вид этой опорной прямой указан на рис. 7.2. Более точно,

и

Если в неравенстве (4) заменить х на случайную величину X и взять математические ожидания обеих частей этого неравенства, то получим

Соотношение (2) следует теперь из (5) и (3).

Рис. 7.2. Опорная прямая.
Далее, если функция  строго выпукла, то при всех
строго выпукла, то при всех  за исключением
за исключением  в (4) имеет место строгое неравенство. Так как по предположению
в (4) имеет место строгое неравенство. Так как по предположению  то это строгое неравенство сохраняется и для математических ожиданий. Следовательно, неравенство (5) строгое. Этот факт вместе с (3) дает строгое неравенство в (2).
то это строгое неравенство сохраняется и для математических ожиданий. Следовательно, неравенство (5) строгое. Этот факт вместе с (3) дает строгое неравенство в (2).
Рассмотрим теперь ситуацию, в которой множество R доходов является интервалом  денежных выигрышей и функция полезности
денежных выигрышей и функция полезности  данного индивидуума строго выпукла на
данного индивидуума строго выпукла на  Из неравенства Иенсена следует, что тогда этот индивидуум предпочтет игру со случайным выигрышем X из интервала
Из неравенства Иенсена следует, что тогда этот индивидуум предпочтет игру со случайным выигрышем X из интервала  игре с заведомым выигрышем
игре с заведомым выигрышем  . В частности, если интервал
. В частности, если интервал  содержит точку 0, то игру с нулевым средним он предпочтет тому, чтобы вообще не играть. По этим причинам можно назвать лиц со строго выпуклой функцией полезности любителями риска. Понятно, что два любителя риска будут заключать пари с равными ставками относительно того, выпадет герб или решка, поскольку они оба предпочитают играть, нежели смотреть.
содержит точку 0, то игру с нулевым средним он предпочтет тому, чтобы вообще не играть. По этим причинам можно назвать лиц со строго выпуклой функцией полезности любителями риска. Понятно, что два любителя риска будут заключать пари с равными ставками относительно того, выпадет герб или решка, поскольку они оба предпочитают играть, нежели смотреть.
Вогнутые функции. Вещественная функция  определенная на интервале
определенная на интервале  вещественной прямой, называется вогнутой на
вещественной прямой, называется вогнутой на  если функция
если функция  выпукла на
выпукла на  Таким образом,
Таким образом,  вогнута на
вогнута на  если для любых двух точек х и у из
если для любых двух точек х и у из  и любого числа а, такого, что
и любого числа а, такого, что 

Говорят, что функция  строго вогнута на
строго вогнута на  если функция —
если функция —  строго выпукла.
строго выпукла.
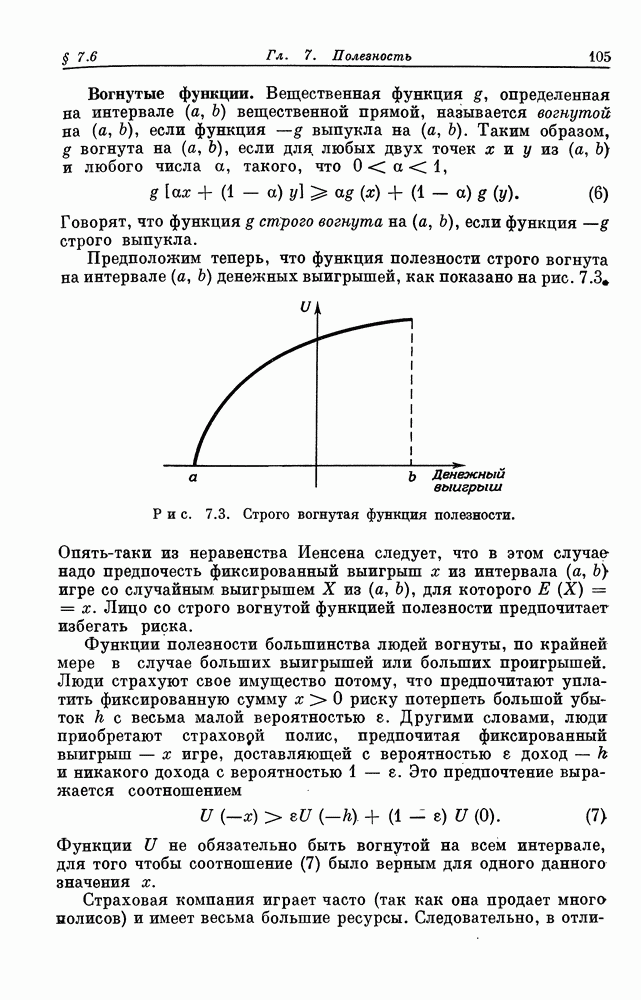
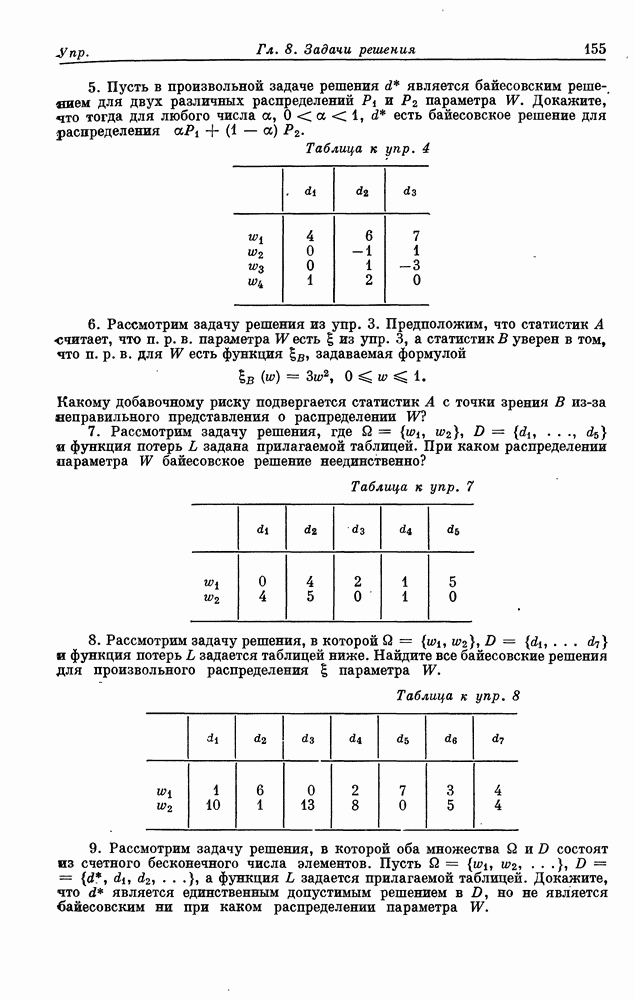
Предположим теперь, что функция полезности строго вогнута на интервале  денежных выигрышей, как показано на рис. 7.3
денежных выигрышей, как показано на рис. 7.3

Рис. 7.3. Строго вогнутая функция полезности.
Опять-таки из неравенства Иенсена следует, что в этом случае надо предпочесть фиксированный выигрыш х из интервала  игре со случайным выигрышем X из
игре со случайным выигрышем X из  для которого
для которого  Лицо со строго вогнутой функцией полезности предпочитает избегать риска.
Лицо со строго вогнутой функцией полезности предпочитает избегать риска.
Функции полезности большинства людей вогнуты, по крайней мере в случае больших выигрышей или больших проигрышей. Люди страхуют свое имущество потому, что предпочитают уплатить фиксированную сумму  риску потерпеть большой убыток
риску потерпеть большой убыток  с весьма малой вероятностью
с весьма малой вероятностью  Другими словами, люди приобретают страховрй полис, предпочитая фиксированный выигрыш — х игре, доставляющей с вероятностью
Другими словами, люди приобретают страховрй полис, предпочитая фиксированный выигрыш — х игре, доставляющей с вероятностью  доход —
доход —  и никакого дохода с вероятностью
и никакого дохода с вероятностью  . Это предпочтение выражается соотношением
. Это предпочтение выражается соотношением

Функции  не обязательно быть вогнутой на всем интервале, для того чтобы соотношение (7) было верным для одного данного значения х.
не обязательно быть вогнутой на всем интервале, для того чтобы соотношение (7) было верным для одного данного значения х.
Страховая компания играет часто (так как она продает много полисов) и имеет весьма большие ресурсы. Следовательно, в
отличие от случая отдельного полиса функция полезности  страховой компании есть приблизительно линейная функция от денежного выигрыша. Поэтому
страховой компании есть приблизительно линейная функция от денежного выигрыша. Поэтому  можно выбрать так, чтобы
можно выбрать так, чтобы  на соответствующем интервале. При продаже страхового полиса ожидаемый выигрыш компании должен быть больше нуля — ее выигрыша при несостоявшейся сделке. Поскольку ожидаемый выигрыш компании от продажи полиса равен получаемой сумме х минус средняя сумма
на соответствующем интервале. При продаже страхового полиса ожидаемый выигрыш компании должен быть больше нуля — ее выигрыша при несостоявшейся сделке. Поскольку ожидаемый выигрыш компании от продажи полиса равен получаемой сумме х минус средняя сумма  выплачиваемая по полису, то страховая компания выбирает сумму х такой, чтобы
выплачиваемая по полису, то страховая компания выбирает сумму х такой, чтобы

Страховой полис продается при выполнении обоих неравенств (7) и (8).
Дальнейшие замечания и ссылки на литературу. Обсуждение некоторых задач, связанных с выпуклыми и вогнутыми функциями лолезности, имеется у Фридмэна и Сэвиджа (1948, 1952) и у Прэтта (1964). Чтобы учесть изменчивость в индивидуальных предпочтениях, часто наблюдаемую в реальных ситуациях, были предложены различные стохастические модели выбора поведения и полезности (см. Льюс (1959), Саппс и Уолш (1959) и Беккер, Де Гроот и Маршак (1963)). Льюс и Саппс (1965) приводят превосходный обзор работ по теории полезности, включая статьи по экспериментальному измерению полезности, стохастическим моделям и аксиоматическому подходу к полезности, который будет обсуждаться в следующем параграфе.
Прежде чем перейти к изложению аксиоматического подхода к полезности, сделаем одно заключительное замечание. В рамках настоящей теории при выборе одной из нескольких игр, в особенности если такой выбор может производиться только один раз, следует выбирать игру с максимальной средней Полезностью. Выбор здесь не связан ни с какими соображениями о «большой серии испытаний», которые иногда привлекаются при рассмотрении математических ожиданий, но является просто следствием определения полезности. В случае когда игры выбираются неоднократно, общий выигрыш от всей последовательности игр следует рассматривать как доход от одной составной игры и наиболее предпочтительная последовательность игр должна быть той, которая приводит к наибольшей средней полезности общего выигрыша. Как правило, такая последовательность игр отлична от последовательности, в которой на каждом шагу выбирается игра с наибольшей средней полезностью выигрыша на этом шагу. Задачи такого типа относятся к проблематике последовательных решений, которые систематически будут изучаться в гл. 12—14.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- Глава 2. ЭКСПЕРИМЕНТЫ, ВЫБОРОЧНЫЕ ПРОСТРАНСТВА И ВЕРОЯТНОСТЬ
- § 2.1. Эксперименты и выборочные пространства
- § 2.2. Теория множеств
- § 2.3. События и вероятность
- § 2.4. Условная вероятность
- § 2.5. Биномиальные коэффициенты
- Глава 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, СЛУЧАЙНЫЕ ВЕКТОРЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- § 3.1. Случайные величины и их распределения
- § 3.2. Многомерные распределения
- § 3.3. Суммы и интегралы
- § 3.4. Маргинальные распределения и независимость
- § 3.5. Векторы и матрицы
- § 3.6. Математические ожидания, моменты и характеристические функции
- § 3.7. Преобразования случайных величин
- § 3.8. Условные распределения
- Глава 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 4.2. Распределение Бернулли
- § 4.3. Биномиальное распределение
- § 4.4. Распределение Пуассона
- § 4.5. Отрицательное биномиальное распределение
- § 4.6. Гипергеометрическое распределение
- § 4.7. Нормальное распределение
- § 4.8. Гамма-распределение
- § 4.9. Бета-распределение
- § 4.10. Равномерное распределение
- § 4.11. Распределение Парето
- § 4.12. Распределение Стьюдента
- Глава 5. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 5.2. Мультиномиальное распределение
- § 5.3. Распределение Дирихле
- § 5.4. Многомерное нормальное распределение
- § 5.5. Распределение Уишарта
- § 5.6. Многомерное t-распределение
- § 5.7. Двустороннее двумерное распределение Парето
- ЧАСТЬ II. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ И ПОЛЕЗНОСТЬ
- Глава 6. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ
- § 6.2. Относительное правдоподобие
- § 6.3. Вспомогательный эксперимент
- § 6.4. Построение вероятностного распределения
- § 6.5. Проверка выполнения свойств вероятностного распределения
- § 6.6. Условные правдоподобия
- Глава 7. ПОЛЕЗНОСТЬ
- § 7.2. Предпочтения в множестве вероятностных распределений
- § 7.3. Определение функции полезности
- § 7.4. Некоторые свойства функций полезности
- § 7.5. Полезность в случае денежных доходов
- § 7.6. Выпуклые и вогнутые функции полезности
- § 7.7. Аксиоматический подход к полезности
- § 7.8. Построение функции полезности
- § 7.9. Проверка свойств функции полезности
- § 7.10. Распространение свойств функции полезности на класс
- ЧАСТЬ III. СТАТИСТИЧЕСКИЕ ЗАДАЧИ РЕШЕНИЯ
- § 8.2. Байесовский риск и байесовские решения
- § 8.3. Неотрицательные функции потерь
- § 8.4. Вогнутость байесовского риска
- § 8.5. Рандомизация и смешанные решения
- § 8.6. Выпуклые множества
- § 8.7. Задачи решения с конечными …
- § 8.8. Задачи решения с наблюдениями
- § 8.9. Построение байесовских решающих функций
- § 8.10. Цена наблюдения
- § 8.11. Статистические задачи решения, в которых … состоят из двух точек
- § 8.12. Вычисление апостериорного распределения в случае, когда наблюдения производятся в несколько этапов
- Глава 9. СОПРЯЖЕННЫЕ АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 9.1. Достаточные статистики
- § 9.2. Сопряженные семейства распределений
- § 9.3. Построение сопряженного семейства
- § 9.4. Сопряженные семейства для выборок из различных стандартных распределений
- § 9.5. Сопряженные семейства для выборок из нормального распределения
- § 9.6. Выборка из нормального распределения с неизвестным средним и неизвестной мерой точности
- § 9.7. Выборка из равномерного распределения
- § 9.8. Сопряженное семейство для мультиномиальных наблюдений
- § 9.9. Сопряженные семейства для выборок из многомерного нормального распределения
- § 9.10. Многомерное нормальное распределение с неизвестным вектором средних и неизвестной матрицей точности
- § 9.11. Маргинальное распределение вектора средних
- § 9.12. Распределение коэффициента корреляции
- § 9.13. Матрицы точности с неизвестным множителем
- Глава 10. ПРЕДЕЛЬНЫЕ АПОСТЕРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 10.1. Несобственные априорные распределения
- § 10.2. Несобственные априорные распределения для выборок из нормального распределения
- § 10.3. Несобственные априорные распределения для выборок из многомерного нормального распределения
- § 10.4. Высокоточные измерения
- § 10.5. Сходимость апостериорных распределений
- § 10.6. Супер непрерывность
- § 10.7. Решения уравнения правдоподобия
- § 10.8. Сходимость супернепрерывных функций
- § 10.9. Предельные свойства функции правдоподобия
- § 10.10. Нормальная аппроксимация апостериорного распределения
- § 10.11. Аппроксимации в случае векторных параметров
- § 10.12. Апостериорные отношения
- Глава 11. ОЦЕНИВАНИЕ, ПРОВЕРКА ГИПОТЕЗ И ЛИНЕЙНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ
- § 11.2. Квадратическая функция потерь
- § 11.3. Ущерб пропорциональный абсолютной величине погрешности
- § 11.4. Оценивание векторного параметра
- § 11.5. Задачи проверки гипотез
- § 11.6. Проверка простой гипотезы о среднем значении нормального распределения
- § 11.7. Проверка гипотез о среднем значении нормального распределения с неизвестной мерой точности
- § 11.8. Решение вопроса о том, будет ли параметр меньше или больше предписанного значения
- § 11.9. Проверка гипотезы о том, превосходит или нет среднее нормального распределения заданное значение
- § 11.10. Линейные модели
- § 11.11. Проверка гипотез в линейных моделях
- § 11.12. Проверка гипотезы о равенстве нулю некоторых коэффициентов регрессии
- § 11.13. Дисперсионный анализ по одному признаку
- ЧАСТЬ IV. ПОСЛЕДОВАТЕЛЬНЫЕ РЕШЕНИЯ
- § 12.1. Эффект последовательного выбора
- § 12.2. Процедуры последовательного решения
- § 12.3. Риск процедуры последовательного решения
- § 12.4. Индукция назад
- § 12.5. Оптимальные ограниченные процедуры последовательного решения
- § 12.6. Примеры
- § 12.7. Неограниченные процедуры последовательного решения
- § 12.8. Регулярные процедуры последовательного решения
- § 12.9. Существование оптимальной процедуры
- § 12.10. Приближение оптимальной прцоедуры ограниченными процедурами
- § 12.11. Области продолжения и окончания выбора
- § 12.12. Функциональное уравнение
- § 12.13 Приближения и границы для байесовского риска
- § 12.14. Последовательный критерий отношения вероятностей
- § 12.15. Характеристики последовательных критериев отношения вероятностей
- § 12.16. Аппроксимации для среднего числа наблюдений
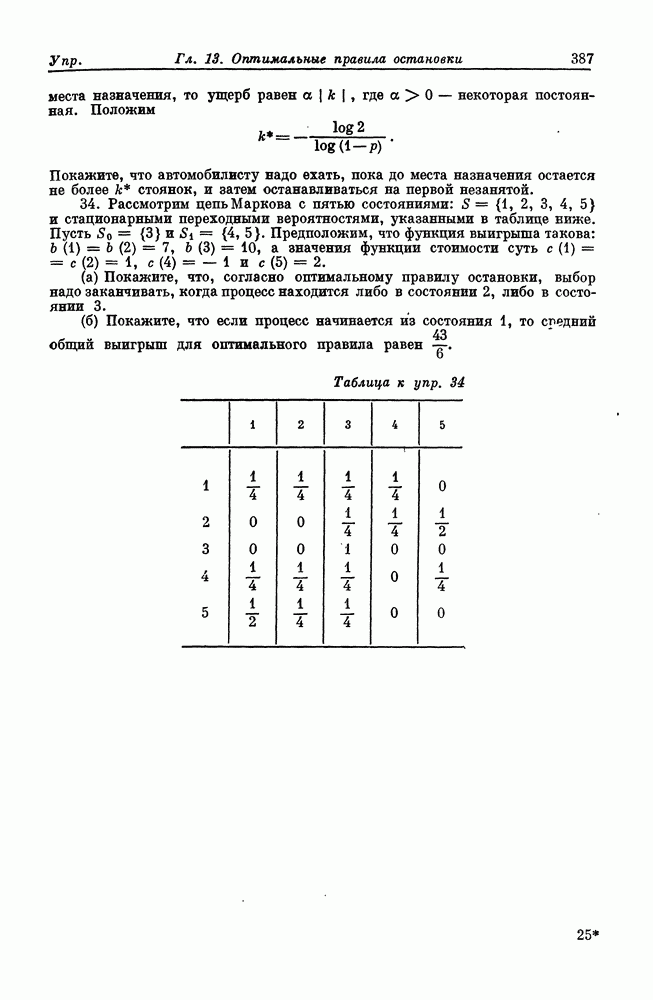
- Глава 13. ОПТИМАЛЬНЫЕ ПРАВИЛА ОСТАНОВКИ
- § 13.2. Вознаграждение статистика
- § 13.3. Выбор функции полезности
- § 13.4. Выбор с отбрасыванием
- § 13.5. Дальнейшие задачи выбора с отбрасыванием и выбора без отбрасывания
- § 13.6. Выбор с отбрасыванием из нормального распределения с неизвестным средним
- § 13.7. Выбор без отбрасывания из нормального распределения с неизвестным средним
- § 13.8. Существование оптимальных правил остановки
- § 13.9. Существование оптимальных правил остановки в задачах выбора без отбрасывания и с отбрасыванием
- § 13.10. Мартингалы
- § 13.11. Правила остановки для мартингалов
- § 13.12. Равномерно интегрируемые последовательности случайных величин
- § 13.13. Мартингалы, получаемые из сумм и произведений случайных величин
- § 13.14. Регулярные супермартингалы
- § 13.15. Супермартингалы и общие задачи об оптимальной остановке
- § 13.16. Марковские процессы
- § 13.17. Стационарные правила остановки для марковских процессов
- § 13.18. Задачи с входной платой
- § 13.19. Функциональное уравнение для марковского процесса
- Глава 14. ПОСЛЕДОВАТЕЛЬНОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
- § 14.2. Марковские процессы решения с конечным числом шагов
- § 14.3. Марковские процессы решения с бесконечным числом шагов
- § 14.4. Некоторые задачи о пари
- § 14.5. Задачи о «двуруком бандите»
- § 14.6. Задачи о «двуруком бандите» с известным значением одного из параметров
- § 14.7. Задачи о «двуруком бандите» в случае зависимых параметров
- § 14.8. Задачи оптимального управления запасами
- § 14.9. Задачи управления запасами с бесконечным числом шагов
- § 14.10. Задачи управления
- § 14.11. Оптимальное управление в случае, когда процесс наблюдается с ошибками
- § 14.12. Многомерные задачи управления
- § 14.13. Задачи управления с погрешностями, вносимыми статистиком
- § 14.14. Задачи поиска
- § 14.15. Задачи поиска с равными стоимостями
- § 14.16. Функции неопределенности и задачи статистического решения
- § 14.17. Достаточные эксперименты
- § 14.18. Примеры достаточных экспериментов
- СПИСОК ЛИТЕРАТУРЫ