| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 10.9. Предельные свойства функции правдоподобия
Пусть выполняются предположения  . В этом параграфе мы покажем, что при большом числе
. В этом параграфе мы покажем, что при большом числе  наблюдений функция правдоподобия и апостериорное распределение могут быть аппроксимированы некоторым нормальным распределением. Для доказательства этого факта мы формализуем следующие эвристические соображения.
наблюдений функция правдоподобия и апостериорное распределение могут быть аппроксимированы некоторым нормальным распределением. Для доказательства этого факта мы формализуем следующие эвристические соображения.
Пусть для достаточно больших значений 

суть решения уравнения правдоподобия, которые, согласно теореме 1 § 10.7, образуют состоятельную последовательность. Для упрощения обозначений пусть для любых значений наблюдений

Разлагая функцию  в ряд Тейлора в точке
в ряд Тейлора в точке  получаем
получаем

Из определения  следует, что
следует, что  Далее, из соотношения (7) § 10.7 и усиленного закона больших чисел заключаем, что при больших значениях
Далее, из соотношения (7) § 10.7 и усиленного закона больших чисел заключаем, что при больших значениях  верна следующая приближенная формула
верна следующая приближенная формула

Первый член в правой части равенства (2) не зависит от  Поэтому, пренебрегая слагаемыми более высокого порядка малости в (2), мы можем записать следующее выражение для функции правдоподобия при принадлежащих некоторой малой окрестности
Поэтому, пренебрегая слагаемыми более высокого порядка малости в (2), мы можем записать следующее выражение для функции правдоподобия при принадлежащих некоторой малой окрестности 

Соотношение (4) можно интерпретировать как приближение к функции правдоподобия посредством п. р. в. нормального закона со средним  и мерой точности
и мерой точности  Из этого соотношения видно, что если априорное распределение параметра
Из этого соотношения видно, что если априорное распределение параметра  задается в некоторой окрестности точки
задается в некоторой окрестности точки  гладкой положительной плотностью, то апостериорное распределение
гладкой положительной плотностью, то апостериорное распределение  сконцентрировано
сконцентрировано
в окрестности точки  и в этой окрестности может быть приближено нормальным распределением со средним
и в этой окрестности может быть приближено нормальным распределением со средним  и мерой точности
и мерой точности  . В оставшейся части этого параграфа мы дадим строгое обоснование этих рассуждений.
. В оставшейся части этого параграфа мы дадим строгое обоснование этих рассуждений.
Пусть  обозначает окрестность точки
обозначает окрестность точки  в которой выполнены предположения
в которой выполнены предположения  Так как с вероятностью
Так как с вероятностью  то
то  лежит в окрестности
лежит в окрестности  для достаточно больших значений
для достаточно больших значений  Для произвольных значений наблюдений
Для произвольных значений наблюдений  и для
и для  пусть
пусть

С помощью элементарного дифференцирования легко проверяется, что

Кроме того,  Поэтому, разлагая функцию
Поэтому, разлагая функцию  в ряд Тейлора в точке
в ряд Тейлора в точке  и учитывая члены до второго порядка малости, получаем
и учитывая члены до второго порядка малости, получаем

где  лежит между
лежит между 
Пусть теперь  — произвольное фиксированное число и
— произвольное фиксированное число и  определено равенством
определено равенством

Если положить

то из (7) — (9) вытекает, что

Покажем теперь, что  с вероятностью 1. По предположению
с вероятностью 1. По предположению  функция
функция  супернепрерывна в точке
супернепрерывна в точке  Поэтому из теоремы 1 § 10.8 следует, что с вероятностью 1
Поэтому из теоремы 1 § 10.8 следует, что с вероятностью 1

Далее, в силу предположения 

Поскольку  лежит между
лежит между  из (8) видно, что
из (8) видно, что  с вероятностью 1 для любого фиксированного значения 0. Мы можем снова применить теорему 1 § 10.8 и получить результат, аналогичный соотношению
с вероятностью 1 для любого фиксированного значения 0. Мы можем снова применить теорему 1 § 10.8 и получить результат, аналогичный соотношению  в котором
в котором  заменено на
заменено на  Так как
Так как  то
то

Кроме того, по предположению  функции
функции  супернепрерывны в точке
супернепрерывны в точке  Следовательно, с вероятностью 1 верны следующие два соотношения:
Следовательно, с вероятностью 1 верны следующие два соотношения:

Искомое соотношение  следует теперь из формулы (9), определяющей
следует теперь из формулы (9), определяющей  и из соотношений (6) и (12) — (14). Следующая теорема непосредственно вытекает из равенства (10).
и из соотношений (6) и (12) — (14). Следующая теорема непосредственно вытекает из равенства (10).
Теорема 1. Пусть выполнены предположения  и для произвольного фиксированного значения 8 пусть
и для произвольного фиксированного значения 8 пусть  задано формулой (8). Тогда с вероятностью 1
задано формулой (8). Тогда с вероятностью 1

Из (8) и (15) следует, что соотношение (4) обеспечивает хорошую аппроксимацию функции правдоподобия при больших значениях  и значениях
и значениях  из малой окрестности
из малой окрестности 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- Глава 2. ЭКСПЕРИМЕНТЫ, ВЫБОРОЧНЫЕ ПРОСТРАНСТВА И ВЕРОЯТНОСТЬ
- § 2.1. Эксперименты и выборочные пространства
- § 2.2. Теория множеств
- § 2.3. События и вероятность
- § 2.4. Условная вероятность
- § 2.5. Биномиальные коэффициенты
- Глава 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, СЛУЧАЙНЫЕ ВЕКТОРЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- § 3.1. Случайные величины и их распределения
- § 3.2. Многомерные распределения
- § 3.3. Суммы и интегралы
- § 3.4. Маргинальные распределения и независимость
- § 3.5. Векторы и матрицы
- § 3.6. Математические ожидания, моменты и характеристические функции
- § 3.7. Преобразования случайных величин
- § 3.8. Условные распределения
- Глава 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 4.2. Распределение Бернулли
- § 4.3. Биномиальное распределение
- § 4.4. Распределение Пуассона
- § 4.5. Отрицательное биномиальное распределение
- § 4.6. Гипергеометрическое распределение
- § 4.7. Нормальное распределение
- § 4.8. Гамма-распределение
- § 4.9. Бета-распределение
- § 4.10. Равномерное распределение
- § 4.11. Распределение Парето
- § 4.12. Распределение Стьюдента
- Глава 5. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 5.2. Мультиномиальное распределение
- § 5.3. Распределение Дирихле
- § 5.4. Многомерное нормальное распределение
- § 5.5. Распределение Уишарта
- § 5.6. Многомерное t-распределение
- § 5.7. Двустороннее двумерное распределение Парето
- ЧАСТЬ II. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ И ПОЛЕЗНОСТЬ
- Глава 6. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ
- § 6.2. Относительное правдоподобие
- § 6.3. Вспомогательный эксперимент
- § 6.4. Построение вероятностного распределения
- § 6.5. Проверка выполнения свойств вероятностного распределения
- § 6.6. Условные правдоподобия
- Глава 7. ПОЛЕЗНОСТЬ
- § 7.2. Предпочтения в множестве вероятностных распределений
- § 7.3. Определение функции полезности
- § 7.4. Некоторые свойства функций полезности
- § 7.5. Полезность в случае денежных доходов
- § 7.6. Выпуклые и вогнутые функции полезности
- § 7.7. Аксиоматический подход к полезности
- § 7.8. Построение функции полезности
- § 7.9. Проверка свойств функции полезности
- § 7.10. Распространение свойств функции полезности на класс
- ЧАСТЬ III. СТАТИСТИЧЕСКИЕ ЗАДАЧИ РЕШЕНИЯ
- § 8.2. Байесовский риск и байесовские решения
- § 8.3. Неотрицательные функции потерь
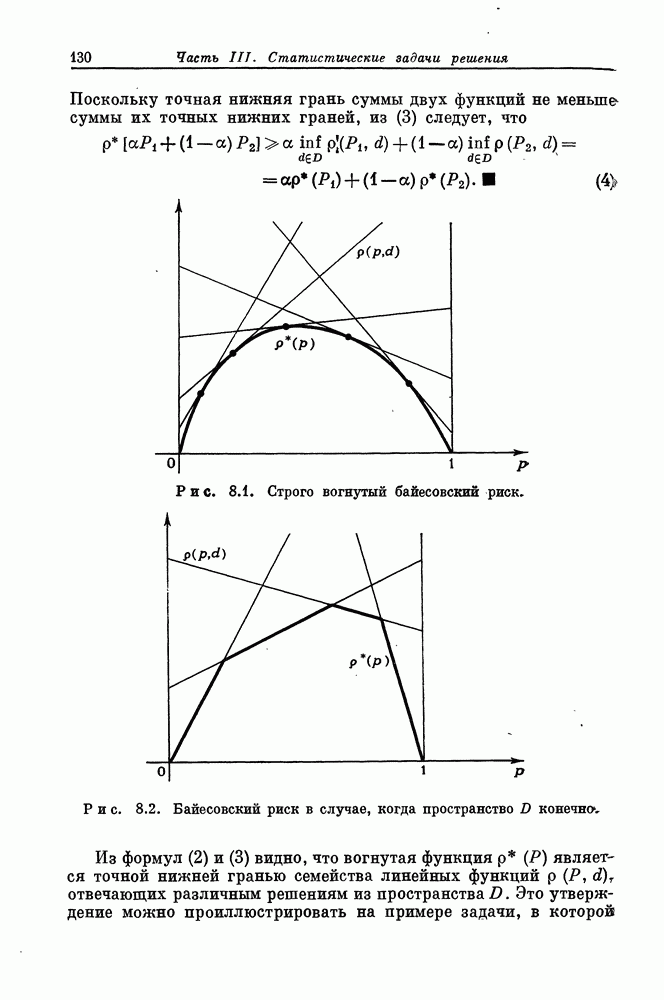
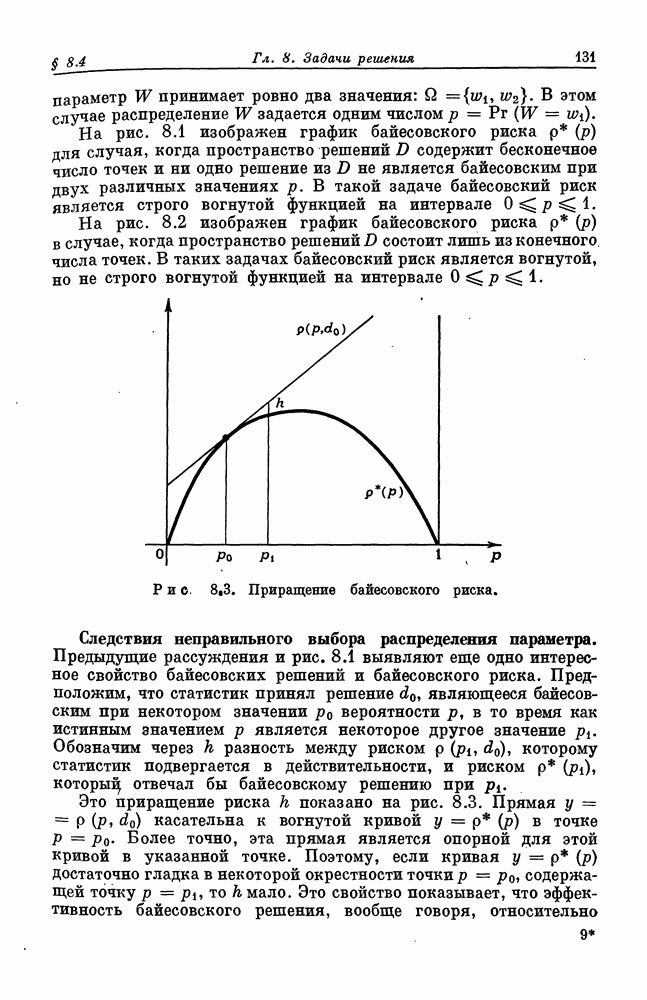
- § 8.4. Вогнутость байесовского риска
- § 8.5. Рандомизация и смешанные решения
- § 8.6. Выпуклые множества
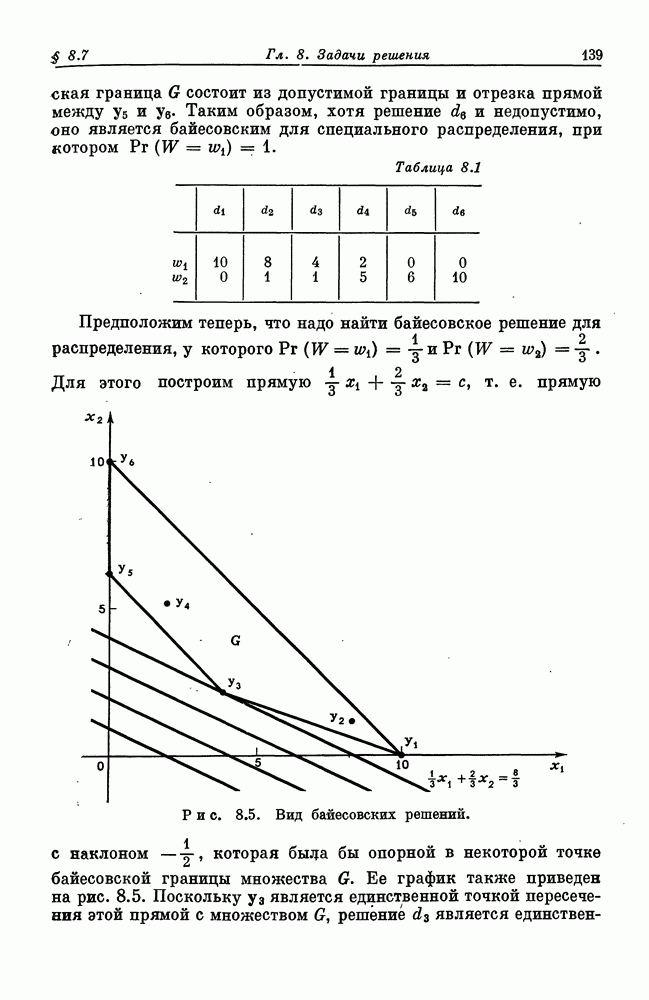
- § 8.7. Задачи решения с конечными …
- § 8.8. Задачи решения с наблюдениями
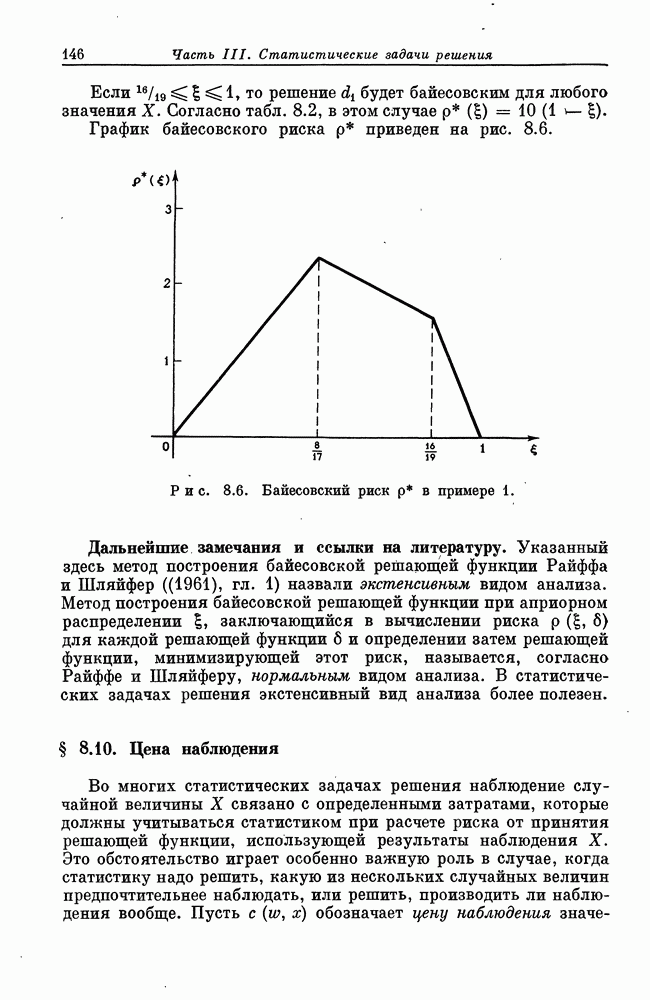
- § 8.9. Построение байесовских решающих функций
- § 8.10. Цена наблюдения
- § 8.11. Статистические задачи решения, в которых … состоят из двух точек
- § 8.12. Вычисление апостериорного распределения в случае, когда наблюдения производятся в несколько этапов
- Глава 9. СОПРЯЖЕННЫЕ АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 9.1. Достаточные статистики
- § 9.2. Сопряженные семейства распределений
- § 9.3. Построение сопряженного семейства
- § 9.4. Сопряженные семейства для выборок из различных стандартных распределений
- § 9.5. Сопряженные семейства для выборок из нормального распределения
- § 9.6. Выборка из нормального распределения с неизвестным средним и неизвестной мерой точности
- § 9.7. Выборка из равномерного распределения
- § 9.8. Сопряженное семейство для мультиномиальных наблюдений
- § 9.9. Сопряженные семейства для выборок из многомерного нормального распределения
- § 9.10. Многомерное нормальное распределение с неизвестным вектором средних и неизвестной матрицей точности
- § 9.11. Маргинальное распределение вектора средних
- § 9.12. Распределение коэффициента корреляции
- § 9.13. Матрицы точности с неизвестным множителем
- Глава 10. ПРЕДЕЛЬНЫЕ АПОСТЕРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 10.1. Несобственные априорные распределения
- § 10.2. Несобственные априорные распределения для выборок из нормального распределения
- § 10.3. Несобственные априорные распределения для выборок из многомерного нормального распределения
- § 10.4. Высокоточные измерения
- § 10.5. Сходимость апостериорных распределений
- § 10.6. Супер непрерывность
- § 10.7. Решения уравнения правдоподобия
- § 10.8. Сходимость супернепрерывных функций
- § 10.9. Предельные свойства функции правдоподобия
- § 10.10. Нормальная аппроксимация апостериорного распределения
- § 10.11. Аппроксимации в случае векторных параметров
- § 10.12. Апостериорные отношения
- Глава 11. ОЦЕНИВАНИЕ, ПРОВЕРКА ГИПОТЕЗ И ЛИНЕЙНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ
- § 11.2. Квадратическая функция потерь
- § 11.3. Ущерб пропорциональный абсолютной величине погрешности
- § 11.4. Оценивание векторного параметра
- § 11.5. Задачи проверки гипотез
- § 11.6. Проверка простой гипотезы о среднем значении нормального распределения
- § 11.7. Проверка гипотез о среднем значении нормального распределения с неизвестной мерой точности
- § 11.8. Решение вопроса о том, будет ли параметр меньше или больше предписанного значения
- § 11.9. Проверка гипотезы о том, превосходит или нет среднее нормального распределения заданное значение
- § 11.10. Линейные модели
- § 11.11. Проверка гипотез в линейных моделях
- § 11.12. Проверка гипотезы о равенстве нулю некоторых коэффициентов регрессии
- § 11.13. Дисперсионный анализ по одному признаку
- ЧАСТЬ IV. ПОСЛЕДОВАТЕЛЬНЫЕ РЕШЕНИЯ
- § 12.1. Эффект последовательного выбора
- § 12.2. Процедуры последовательного решения
- § 12.3. Риск процедуры последовательного решения
- § 12.4. Индукция назад
- § 12.5. Оптимальные ограниченные процедуры последовательного решения
- § 12.6. Примеры
- § 12.7. Неограниченные процедуры последовательного решения
- § 12.8. Регулярные процедуры последовательного решения
- § 12.9. Существование оптимальной процедуры
- § 12.10. Приближение оптимальной прцоедуры ограниченными процедурами
- § 12.11. Области продолжения и окончания выбора
- § 12.12. Функциональное уравнение
- § 12.13 Приближения и границы для байесовского риска
- § 12.14. Последовательный критерий отношения вероятностей
- § 12.15. Характеристики последовательных критериев отношения вероятностей
- § 12.16. Аппроксимации для среднего числа наблюдений
- Глава 13. ОПТИМАЛЬНЫЕ ПРАВИЛА ОСТАНОВКИ
- § 13.2. Вознаграждение статистика
- § 13.3. Выбор функции полезности
- § 13.4. Выбор с отбрасыванием
- § 13.5. Дальнейшие задачи выбора с отбрасыванием и выбора без отбрасывания
- § 13.6. Выбор с отбрасыванием из нормального распределения с неизвестным средним
- § 13.7. Выбор без отбрасывания из нормального распределения с неизвестным средним
- § 13.8. Существование оптимальных правил остановки
- § 13.9. Существование оптимальных правил остановки в задачах выбора без отбрасывания и с отбрасыванием
- § 13.10. Мартингалы
- § 13.11. Правила остановки для мартингалов
- § 13.12. Равномерно интегрируемые последовательности случайных величин
- § 13.13. Мартингалы, получаемые из сумм и произведений случайных величин
- § 13.14. Регулярные супермартингалы
- § 13.15. Супермартингалы и общие задачи об оптимальной остановке
- § 13.16. Марковские процессы
- § 13.17. Стационарные правила остановки для марковских процессов
- § 13.18. Задачи с входной платой
- § 13.19. Функциональное уравнение для марковского процесса
- Глава 14. ПОСЛЕДОВАТЕЛЬНОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
- § 14.2. Марковские процессы решения с конечным числом шагов
- § 14.3. Марковские процессы решения с бесконечным числом шагов
- § 14.4. Некоторые задачи о пари
- § 14.5. Задачи о «двуруком бандите»
- § 14.6. Задачи о «двуруком бандите» с известным значением одного из параметров
- § 14.7. Задачи о «двуруком бандите» в случае зависимых параметров
- § 14.8. Задачи оптимального управления запасами
- § 14.9. Задачи управления запасами с бесконечным числом шагов
- § 14.10. Задачи управления
- § 14.11. Оптимальное управление в случае, когда процесс наблюдается с ошибками
- § 14.12. Многомерные задачи управления
- § 14.13. Задачи управления с погрешностями, вносимыми статистиком
- § 14.14. Задачи поиска
- § 14.15. Задачи поиска с равными стоимостями
- § 14.16. Функции неопределенности и задачи статистического решения
- § 14.17. Достаточные эксперименты
- § 14.18. Примеры достаточных экспериментов
- СПИСОК ЛИТЕРАТУРЫ