| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 7.5. Полезность в случае денежных доходов
В предыдущем параграфе была сделана попытка отметить некоторые трудности, связанные с понятием полезности денежного выигрыша и с ее измерением. Однако если возможные
денежяые выигрыши и проигрыши в данной ситуации не слишком велики и действие других факторов незначительно, то кажется достаточно естественным рассматривать функции полезности, определенные на множестве денежных доходов. Такие функции полезности широко используются, и мы обсудим их в настоящем параграфе и в следующих за ним.
Петербургский парадокс. Приводимый здесь пример был одной из первых иллюстраций того обстоятельства, что функция полезности, рассматриваемая как функция от возможных денежных доходов, не является линейной. Предположим, что некто имеет возможность сыграть в следующую игру. Правильная монета, т. е. монета, для которой выпадение герба или решетки равновероятно, подбрасывается до тех пор, пока не выпадет герб. Если первый герб показался при  бросании, то выигрышем играющего будет
бросании, то выигрышем играющего будет  долларов
долларов  На какую плату за участие в этой игре следует согласиться?
На какую плату за участие в этой игре следует согласиться?
Поскольку вероятность появления первого герба при  бросании равна
бросании равна  то средний выигрыш может быть представлен в виде бесконечного ряда
то средний выигрыш может быть представлен в виде бесконечного ряда  Таким образом, ожидаемый выигрыш бесконечен. Если бы функция полезности игрока была линейной, то ему стоило бы заплатить любую произвольно большую сумму за участие в игре. На деле, однако, каждый хочет заплатить только некоторую вполне конкретную конечную сумму, зависящую от его функции полезности. Этот факт был назван петербургским парадоксом, хотя понятие полезности показывает, что никакого парадокса здесь нет.
Таким образом, ожидаемый выигрыш бесконечен. Если бы функция полезности игрока была линейной, то ему стоило бы заплатить любую произвольно большую сумму за участие в игре. На деле, однако, каждый хочет заплатить только некоторую вполне конкретную конечную сумму, зависящую от его функции полезности. Этот факт был назван петербургским парадоксом, хотя понятие полезности показывает, что никакого парадокса здесь нет.
Эта игра обсуждалась Даниилом Бернулли, который в начале восемнадцатого столетия одним из первых рассмотрел гипотезу средней полезности.
Экспериментальное измерение полезности. Рассмотрим теперь задачу об определении функции полезности данного конкретного лица. Мы приведем простой метод, с помощью которого можно определить эту функцию на некотором интервале возможных денежных доходов, в качестве которого мы выберем здесь промежуток от 0 до 1000 долларов. Пусть  обозначает для любых вещественных
обозначает для любых вещественных  лотерейный билет, дающий выигрыш в а долларов с вероятностью 1/2 и выигрыш в
лотерейный билет, дающий выигрыш в а долларов с вероятностью 1/2 и выигрыш в  долларов с той же вероятностью. Рассмотрим следующую четырехшаговую последовательность:
долларов с той же вероятностью. Рассмотрим следующую четырехшаговую последовательность:
Шаг. 1 состоит в определении числа  такого, что заведомый выигрыш
такого, что заведомый выигрыш  долларов рассматривается как эквивалентный получению дохода по лотерейному билету (0, 1000).
долларов рассматривается как эквивалентный получению дохода по лотерейному билету (0, 1000).
Шаг 2 заключается в нахождении такого числа  что достоверное получение
что достоверное получение  долларов считается равносильным выигрышу по лотерейному билету
долларов считается равносильным выигрышу по лотерейному билету 
Шаг 3 состоит в определении числа  такого, что заведомый выигрыш
такого, что заведомый выигрыш  долларов представляется эквивалентным получению дохода по лотерейному билету
долларов представляется эквивалентным получению дохода по лотерейному билету 
Шаг 4 заключается в нахождении числа  для которого заведомый выигрыш долларов равносилен выигрышу по билету
для которого заведомый выигрыш долларов равносилен выигрышу по билету 
Один экспериментальный метод определения этих четырех чисел указан в упр. 2 в конце настоящей главы.
Предположим, что функция полезности  является строго возрастающей функцией денежного дохода. Тогда без потери общности можно считать, что
является строго возрастающей функцией денежного дохода. Тогда без потери общности можно считать, что  Отсюда следует, что
Отсюда следует, что  Следовательно,
Следовательно,  Строго говоря, это равенство означает, что если числа, полученные на шагах 1 и 4, не совпадают, то не выполнены предположения, налагаемые на функцию полезности. На практике эти два числа редко оказываются равными
Строго говоря, это равенство означает, что если числа, полученные на шагах 1 и 4, не совпадают, то не выполнены предположения, налагаемые на функцию полезности. На практике эти два числа редко оказываются равными  первого раза. Однако, учитывая расхождение между
первого раза. Однако, учитывая расхождение между  и повторяя указанные четыре шага необходимое число раз, возможно в конце концов определить «предельное» значение
и повторяя указанные четыре шага необходимое число раз, возможно в конце концов определить «предельное» значение  , для которого
, для которого  Эту процедуру можно использовать для изучения решений, основанных на использовании лотерейных билетов с различными выигрышами и вероятностями, отличными от
Эту процедуру можно использовать для изучения решений, основанных на использовании лотерейных билетов с различными выигрышами и вероятностями, отличными от  при определении выигрщпа х, такого, что
при определении выигрщпа х, такого, что  и для некоторого фиксированного значения и
и для некоторого фиксированного значения и  Следовательно, эта процедура дает метод приближенного определения функции полезности.
Следовательно, эта процедура дает метод приближенного определения функции полезности.
Дальнейшие замечания и ссылки на литературу. Процедура, описанная в этом параграфе, предложена в работе Беккер, Де Гроот и Маршак (1964). Из других работ, посвященных экспериментальному измерению полезности, отметим статьи Мостеллер и Ноджи (1951) и Дэвидсон, Саппс и Сигел (1957).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- Глава 2. ЭКСПЕРИМЕНТЫ, ВЫБОРОЧНЫЕ ПРОСТРАНСТВА И ВЕРОЯТНОСТЬ
- § 2.1. Эксперименты и выборочные пространства
- § 2.2. Теория множеств
- § 2.3. События и вероятность
- § 2.4. Условная вероятность
- § 2.5. Биномиальные коэффициенты
- Глава 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, СЛУЧАЙНЫЕ ВЕКТОРЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- § 3.1. Случайные величины и их распределения
- § 3.2. Многомерные распределения
- § 3.3. Суммы и интегралы
- § 3.4. Маргинальные распределения и независимость
- § 3.5. Векторы и матрицы
- § 3.6. Математические ожидания, моменты и характеристические функции
- § 3.7. Преобразования случайных величин
- § 3.8. Условные распределения
- Глава 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 4.2. Распределение Бернулли
- § 4.3. Биномиальное распределение
- § 4.4. Распределение Пуассона
- § 4.5. Отрицательное биномиальное распределение
- § 4.6. Гипергеометрическое распределение
- § 4.7. Нормальное распределение
- § 4.8. Гамма-распределение
- § 4.9. Бета-распределение
- § 4.10. Равномерное распределение
- § 4.11. Распределение Парето
- § 4.12. Распределение Стьюдента
- Глава 5. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 5.2. Мультиномиальное распределение
- § 5.3. Распределение Дирихле
- § 5.4. Многомерное нормальное распределение
- § 5.5. Распределение Уишарта
- § 5.6. Многомерное t-распределение
- § 5.7. Двустороннее двумерное распределение Парето
- ЧАСТЬ II. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ И ПОЛЕЗНОСТЬ
- Глава 6. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ
- § 6.2. Относительное правдоподобие
- § 6.3. Вспомогательный эксперимент
- § 6.4. Построение вероятностного распределения
- § 6.5. Проверка выполнения свойств вероятностного распределения
- § 6.6. Условные правдоподобия
- Глава 7. ПОЛЕЗНОСТЬ
- § 7.2. Предпочтения в множестве вероятностных распределений
- § 7.3. Определение функции полезности
- § 7.4. Некоторые свойства функций полезности
- § 7.5. Полезность в случае денежных доходов
- § 7.6. Выпуклые и вогнутые функции полезности
- § 7.7. Аксиоматический подход к полезности
- § 7.8. Построение функции полезности
- § 7.9. Проверка свойств функции полезности
- § 7.10. Распространение свойств функции полезности на класс
- ЧАСТЬ III. СТАТИСТИЧЕСКИЕ ЗАДАЧИ РЕШЕНИЯ
- § 8.2. Байесовский риск и байесовские решения
- § 8.3. Неотрицательные функции потерь
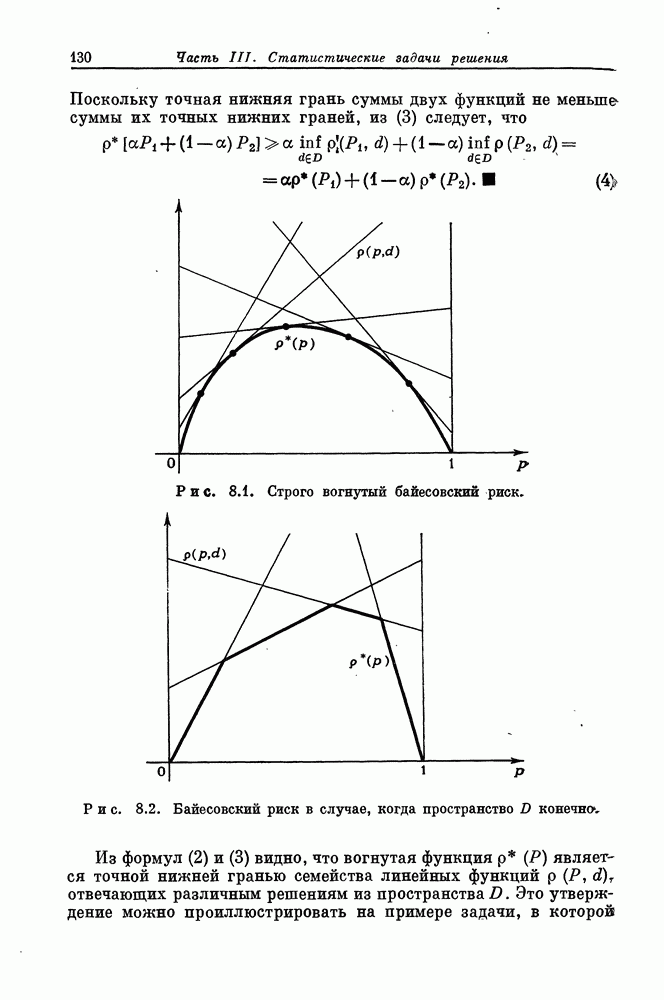
- § 8.4. Вогнутость байесовского риска
- § 8.5. Рандомизация и смешанные решения
- § 8.6. Выпуклые множества
- § 8.7. Задачи решения с конечными …
- § 8.8. Задачи решения с наблюдениями
- § 8.9. Построение байесовских решающих функций
- § 8.10. Цена наблюдения
- § 8.11. Статистические задачи решения, в которых … состоят из двух точек
- § 8.12. Вычисление апостериорного распределения в случае, когда наблюдения производятся в несколько этапов
- Глава 9. СОПРЯЖЕННЫЕ АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 9.1. Достаточные статистики
- § 9.2. Сопряженные семейства распределений
- § 9.3. Построение сопряженного семейства
- § 9.4. Сопряженные семейства для выборок из различных стандартных распределений
- § 9.5. Сопряженные семейства для выборок из нормального распределения
- § 9.6. Выборка из нормального распределения с неизвестным средним и неизвестной мерой точности
- § 9.7. Выборка из равномерного распределения
- § 9.8. Сопряженное семейство для мультиномиальных наблюдений
- § 9.9. Сопряженные семейства для выборок из многомерного нормального распределения
- § 9.10. Многомерное нормальное распределение с неизвестным вектором средних и неизвестной матрицей точности
- § 9.11. Маргинальное распределение вектора средних
- § 9.12. Распределение коэффициента корреляции
- § 9.13. Матрицы точности с неизвестным множителем
- Глава 10. ПРЕДЕЛЬНЫЕ АПОСТЕРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 10.1. Несобственные априорные распределения
- § 10.2. Несобственные априорные распределения для выборок из нормального распределения
- § 10.3. Несобственные априорные распределения для выборок из многомерного нормального распределения
- § 10.4. Высокоточные измерения
- § 10.5. Сходимость апостериорных распределений
- § 10.6. Супер непрерывность
- § 10.7. Решения уравнения правдоподобия
- § 10.8. Сходимость супернепрерывных функций
- § 10.9. Предельные свойства функции правдоподобия
- § 10.10. Нормальная аппроксимация апостериорного распределения
- § 10.11. Аппроксимации в случае векторных параметров
- § 10.12. Апостериорные отношения
- Глава 11. ОЦЕНИВАНИЕ, ПРОВЕРКА ГИПОТЕЗ И ЛИНЕЙНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ
- § 11.2. Квадратическая функция потерь
- § 11.3. Ущерб пропорциональный абсолютной величине погрешности
- § 11.4. Оценивание векторного параметра
- § 11.5. Задачи проверки гипотез
- § 11.6. Проверка простой гипотезы о среднем значении нормального распределения
- § 11.7. Проверка гипотез о среднем значении нормального распределения с неизвестной мерой точности
- § 11.8. Решение вопроса о том, будет ли параметр меньше или больше предписанного значения
- § 11.9. Проверка гипотезы о том, превосходит или нет среднее нормального распределения заданное значение
- § 11.10. Линейные модели
- § 11.11. Проверка гипотез в линейных моделях
- § 11.12. Проверка гипотезы о равенстве нулю некоторых коэффициентов регрессии
- § 11.13. Дисперсионный анализ по одному признаку
- ЧАСТЬ IV. ПОСЛЕДОВАТЕЛЬНЫЕ РЕШЕНИЯ
- § 12.1. Эффект последовательного выбора
- § 12.2. Процедуры последовательного решения
- § 12.3. Риск процедуры последовательного решения
- § 12.4. Индукция назад
- § 12.5. Оптимальные ограниченные процедуры последовательного решения
- § 12.6. Примеры
- § 12.7. Неограниченные процедуры последовательного решения
- § 12.8. Регулярные процедуры последовательного решения
- § 12.9. Существование оптимальной процедуры
- § 12.10. Приближение оптимальной прцоедуры ограниченными процедурами
- § 12.11. Области продолжения и окончания выбора
- § 12.12. Функциональное уравнение
- § 12.13 Приближения и границы для байесовского риска
- § 12.14. Последовательный критерий отношения вероятностей
- § 12.15. Характеристики последовательных критериев отношения вероятностей
- § 12.16. Аппроксимации для среднего числа наблюдений
- Глава 13. ОПТИМАЛЬНЫЕ ПРАВИЛА ОСТАНОВКИ
- § 13.2. Вознаграждение статистика
- § 13.3. Выбор функции полезности
- § 13.4. Выбор с отбрасыванием
- § 13.5. Дальнейшие задачи выбора с отбрасыванием и выбора без отбрасывания
- § 13.6. Выбор с отбрасыванием из нормального распределения с неизвестным средним
- § 13.7. Выбор без отбрасывания из нормального распределения с неизвестным средним
- § 13.8. Существование оптимальных правил остановки
- § 13.9. Существование оптимальных правил остановки в задачах выбора без отбрасывания и с отбрасыванием
- § 13.10. Мартингалы
- § 13.11. Правила остановки для мартингалов
- § 13.12. Равномерно интегрируемые последовательности случайных величин
- § 13.13. Мартингалы, получаемые из сумм и произведений случайных величин
- § 13.14. Регулярные супермартингалы
- § 13.15. Супермартингалы и общие задачи об оптимальной остановке
- § 13.16. Марковские процессы
- § 13.17. Стационарные правила остановки для марковских процессов
- § 13.18. Задачи с входной платой
- § 13.19. Функциональное уравнение для марковского процесса
- Глава 14. ПОСЛЕДОВАТЕЛЬНОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
- § 14.2. Марковские процессы решения с конечным числом шагов
- § 14.3. Марковские процессы решения с бесконечным числом шагов
- § 14.4. Некоторые задачи о пари
- § 14.5. Задачи о «двуруком бандите»
- § 14.6. Задачи о «двуруком бандите» с известным значением одного из параметров
- § 14.7. Задачи о «двуруком бандите» в случае зависимых параметров
- § 14.8. Задачи оптимального управления запасами
- § 14.9. Задачи управления запасами с бесконечным числом шагов
- § 14.10. Задачи управления
- § 14.11. Оптимальное управление в случае, когда процесс наблюдается с ошибками
- § 14.12. Многомерные задачи управления
- § 14.13. Задачи управления с погрешностями, вносимыми статистиком
- § 14.14. Задачи поиска
- § 14.15. Задачи поиска с равными стоимостями
- § 14.16. Функции неопределенности и задачи статистического решения
- § 14.17. Достаточные эксперименты
- § 14.18. Примеры достаточных экспериментов
- СПИСОК ЛИТЕРАТУРЫ