§ 7.10. Распространение свойств функции полезности на класс

В этом параграфе мы распространим свойство функции указанное в теореме 1 § 7.9, на класс всех распределений для которых конечно. Для этого нам придется усилить наши предположения об отношении а именно предположить, что они справедливы не только для распределений из класса но и для всех распределений из более широкого класса

В частности мы предполагаем, что на основе своих предпочтений среди распределений из класса статистик может задать полное упорядочение этого класса. Другими словами, предполагается, что для всех распределений из класса отношение удовлетворяет свойствам 1 и 2, приведенным в конце § 7.2. Кроме того, для всех распределений из класса будут считаться справедливыми предположения § 7.7.

Нам понадобятся также два дальнейших предположения. По аналогии со случаем вещественных чисел определим для любого дохода следующие подмножества

Из предположения следует, что для любого дохода оба множества и принадлежат -алгебре Поскольку ни один доход из не предпочтительнее никакого дохода из то следующее предположение представляется весьма естественным.

Предположение Пусть два распределения из класса таких, что для некоторого Тогда

Справедливость предположения для финитных распределений можно доказать, исходя из предположения и леммы 3 § 7.7. Здесь мы считаем, таким образом, что оно выполнено и для нефинитных распределений из

Для любого распределения и любого множества такого, что обозначим через условное распределение, получаемое сужением на множество В, т. е. положим для всех

Всякое такое распределение опять-таки принадлежит классу

Всюду в оставшейся части этого параграфа обозначают две последовательности доходов, обладающие следующим свойством. Для всякого дохода существуют доход из первой последовательности, такой, что и доход из второй последовательности, такой, что Последовательности, удовлетворяющие этому условию, называются кофинальными с Мы предполагаем, что такие последовательности существуют. Следует заметить, что существуют вполне упорядоченные множества, в которых нет кофинальных последовательностей (см. Уилдер (1965), стр. 134). Стандартными примерами являются соответствующие множества трансфинитных чисел.

Для любых доходов из наших кофинальных последовательностей рассмотрим множества и Если распределение из для которого будут обозначать условные распределения, определяемые формулой (2). Поскольку эти распределения будут многократно использоваться в дальнейшем изложении, то для удобства мы обозначим распределение через и распределение через

Лемма 1. Для всякого распределения

Доказательство. Пусть для Тогда из свойств кофинальных последовательностей следует, что Отсюда заключаем, что и

Доказательство для распределения аналогично.

Лемма 2. Пусть распределение из а натуральные числа, такие, Пусть, далее, также натуральные числа, причем Тогда

Доказательство. Покажем сначала, что Пусть Если то Предположим, что Тогда распределение представимо в следующем виде:

Так как из предположения следует, что Поэтому по лемме 1 § 7.7 .

Заменяя на видим, что Заменяя на точно так же получаем

Доказательство остальных соотношений в (4) вполне аналогично.

Сделаем теперь наше последнее предположение, которое будет гарантировать непрерывность отношения предпочтения при аппроксимации нефинитных распределений финитными.

Предположение Пусть два произвольных распределения из Если существует натуральное число такое, что при всех то Если существует натуральное число такое, что для всех то

В следующей лемме устанавливается справедливость свойства для функции по крайней мере для тех распределений из которые ограничены снизу, но могут быть неограничены сверху.

Лемма 3. Пусть два распределения из для которых существуют доходы такие, что

Тогда соотношения равносильны.

Доказательство. Распределения определены для всех достаточно больших значений Опустив конечное число элементов последовательности и перенумеровав оставшиеся элементы, мы можем без ограничения общности считать, что эти распределения определены для всех значений

Для пусть Из равенства (6) следует, что распределения финитны. Следовательно, из леммы 2 и известных свойств функции для финитных распределений вытекает, что

Предположим теперь, что . В силу предположения должно существовать натуральное число со свойством По лемме Из предположения вытекает существование числа а такого, что

Из леммы 2 следует, что при

Так как распределения, входящие в (7), финитны, то из известных свойств функции выводим, что

Переходя в (8) к пределу при в силу леммы 1 получаем

Далее, так как и оба эти распределения финитны, то Следовательно,

Поскольку последовательность не убывает, то, согласно лемме 1,

Из (9) и (11) вытекает теперь неравенство

Для завершения доказательства леммы осталось показать, что если то Итак, пусть Тогда найдется натуральное число такое, что значит, Отсюда следует существование числа а такого, что при

В силу финитности распределений из соотношения (12) и известных свойств функции для финитных распределений вытекает, что при

Из предположения и леммы 2 теперь следует, что

Итак,

Для завершения доказательства того, что является функцией полезности, нам осталось установить справедливость свойства для всех распределений из класса Это и составляет предмет следующей теоремы.

Теорема 1. Пусть два распределения из класса Тогда в том и только в том случае, когда

Доказательство. Распределения определены для всех достаточно больших значений Следовательно, как и в лемме 3, мы можем считать, что эти распределения определены для всех значений Положим Тогда Далее, так как распределения и ограничены снизу, то для них верна лемма 3.

Предположим сначала, что . В силу предположения найдется натуральное число такое, что По лемме Поэтому предположение и лемма 2 влекут за собой существование числа а такого, что при

Из леммы 3 следует, что при

Из леммы 1 и 2 вытекают теперь неравенства

откуда видно, что

Обратно, предположим, что Тогда найдется число для которого значит, должно существовать число а такое, что при

Из леммы 3 выводим, что для

В силу предположения и леммы 2 получаем теперь следующее соотношение

Итак,

Как было показано в теореме 2 § 7.9, единственными функциями, обладающими свойством, указанным в теореме 1, являются построенная в этой главе функция и ее возрастающие линейные преобразования.

Дальнейшие замечания и ссылки на литературу. Следует отметить, что на распределения из класса не принадлежащие не было наложено никаких условий. Для некоторых распределений величине можно приписать значение Для таких распределений естественно считать, что при всех однако непонятно, как сравнивать такие распределения между собой. Аналогичное замечание относится и к распределениям для которых значение можно рассматривать как равное Основные неприятности связаны с распределениями для которых не существует ни как конечное, ни как бесконечное число. Хотя и можно было бы предположить, что отношение вполне упорядочивает все распределения из и ввести дальнейшие предположения о том, как именно определяется «место» при этом упорядочении каждого распределения, не принадлежащего но все это представляется нецелесообразным, и мы не будем этим заниматься. Подчеркнем, что в случае ограниченной функции классы и совпадают и указанные вопросы не возникают.

Первый аксиоматический подход к полезности был предложен фон Нейманом и Моргенштерном (1947). Некоторые другие даны в работах Маршака (1950), Херстейна и Милнора (1953) и Дебрё (1960). Такие подходы рассмотрены также в книгах Блекуэлла и Гиршика (1958) и Чернова и Мозеса (1962). Интересные

обсуждения и результаты имеются в работах Фишбэрна (1964, 1967а), Льюса и Райффы (1957), Льюса и Саппса (1965), Прэтта, Райффы и Шляйфера (1964) и Сэвиджа (1954). Другие направления исследований по теории полезности, трактующие различные не затронутые нами вопросы, освещены в статьях сборника, изданного Троллом, Кумбсом и Дэвисом [1], и в статьях Ауманна [1], Купмэнса, Даймонда и Уильямсона (1964) и Раднера (1964).

Фишбэрном [3] опубликована библиография по теории полезности, содержащая 315 названий.

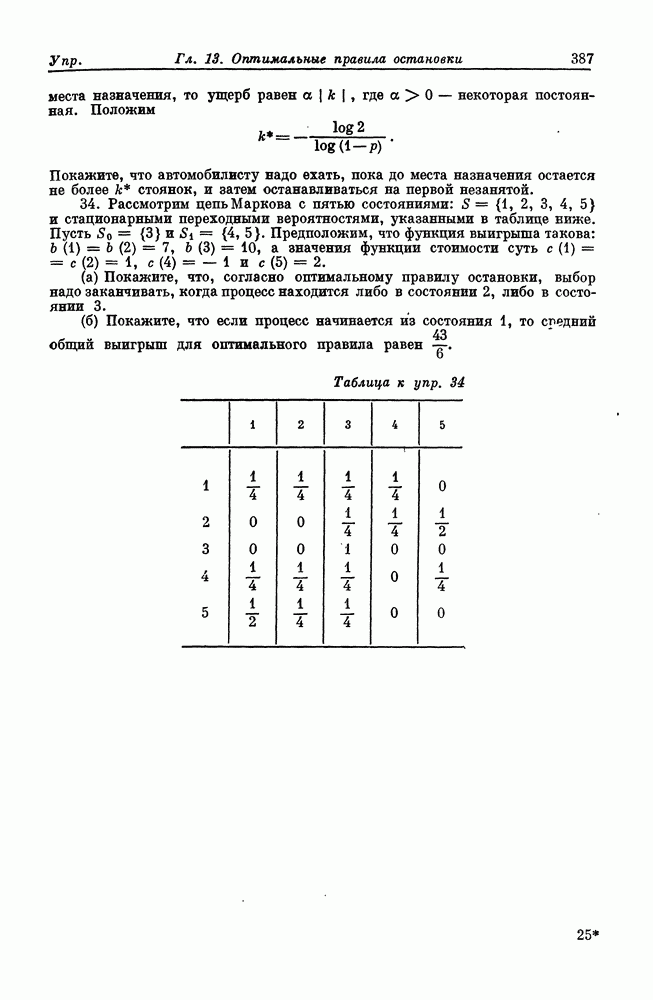
УПРАЖНЕНИЯ

(см. скан)

(см. скан)

(см. скан)

(см. скан)