| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 7.9. Проверка свойств функции полезности
В этом параграфе будут сделаны два дальнейших предположения, гарантирующих выполнение для функции  свойства
свойства  приведенного в начале § 7.7. В этом свойстве фигурируют математические ожидания
приведенного в начале § 7.7. В этом свойстве фигурируют математические ожидания  для всех распределений
для всех распределений  в, и наше первое предположение обеспечивает измеримость функции
в, и наше первое предположение обеспечивает измеримость функции  относительно
относительно  -алгебры А подмножеств множества
-алгебры А подмножеств множества  Это свойство измеримости необходимо для того, чтобы
Это свойство измеримости необходимо для того, чтобы  имело смысл для всех
имело смысл для всех  Второе предположение, которое мы сделаем, будет гарантировать выполнение некоторых простых соотношений эквивалентности для
Второе предположение, которое мы сделаем, будет гарантировать выполнение некоторых простых соотношений эквивалентности для 
Измеримость. В § 7.2 было предположено, что если  - два дохода из R, таких, что к
- два дохода из R, таких, что к  то и интервал
то и интервал  Сейчас мы сделаем более сильное
Сейчас мы сделаем более сильное
Предположение  Для любых трех доходов
Для любых трех доходов  из R и любых двух чисел
из R и любых двух чисел  имеет место соотношение
имеет место соотношение

Лемма 1. Функция  измерима относительно А.
измерима относительно А.
Доказательство. Нам надо показать, что для любого вещественного х

Предположим сначала, что  Если
Если  для некоторого дохода
для некоторого дохода  то
то  Следовательно, из соотношений (2) и
Следовательно, из соотношений (2) и  и леммы 3 § 7.7 мы видим, что
и леммы 3 § 7.7 мы видим, что  тогда и только тогда, когда
тогда и только тогда, когда

Но в силу предположения  множество доходов
множество доходов  удовлетворяющих (3), принадлежит А, и тем самым (2) верно.
удовлетворяющих (3), принадлежит А, и тем самым (2) верно.
Пусть верно  Тогда
Тогда  в том и только в том случае, когда
в том и только в том случае, когда

и соотношение (2) справедливо по предположению 
Пусть, наконец,  Тогда в силу формул (5) и (7) § 7.8 соотношения
Тогда в силу формул (5) и (7) § 7.8 соотношения  и
и

равносильны и из предположения  следует справедливость соотношения (2).
следует справедливость соотношения (2).
Отношения эквивалентности для финитных распределений. Пусть  два дохода из R, для которых
два дохода из R, для которых  интервал, определяемый формулой (2) § 7.2. В силу теоремы 1 § 7.7 для любого дохода
интервал, определяемый формулой (2) § 7.2. В силу теоремы 1 § 7.7 для любого дохода  найдется число
найдется число  такое, что
такое, что

Фактически для  можно указать явный вид. По теореме 1 § 7.8.
можно указать явный вид. По теореме 1 § 7.8.

и, значит,

Вводимое нами теперь предположение может быть пояснено следующим образом. Рассмотрим произвольное распределение  для которого
для которого  Поскольку каждый доход
Поскольку каждый доход  эквивалентен лотерее, в которой выигрыш
эквивалентен лотерее, в которой выигрыш  случается с вероятностью
случается с вероятностью  и выигрыш
и выигрыш  с вероятностью
с вероятностью  то само
то само  эквивалентно лотерее с выигрышами
эквивалентно лотерее с выигрышами  или
или  получаемыми с некоторыми вероятностями. В самом деле, рассмотрим двухшаговую лотерею, в которой сначала, согласно распределению
получаемыми с некоторыми вероятностями. В самом деле, рассмотрим двухшаговую лотерею, в которой сначала, согласно распределению  на интервале
на интервале  извлекается лотерея вида
извлекается лотерея вида  а затем по этой лотерее извлекается один из выигрышей
а затем по этой лотерее извлекается один из выигрышей  или
или  Полная вероятность
Полная вероятность  получения дохода
получения дохода  в этой составной лотерее равна
в этой составной лотерее равна

Вероятность же получения дохода равна  Отметим, что интеграл в (9) существует, так как, согласно (8), функция
Отметим, что интеграл в (9) существует, так как, согласно (8), функция  линейно зависит от измеримой функции
линейно зависит от измеримой функции  значит, ее значения на интервале
значит, ее значения на интервале  ограничены.
ограничены.
Предположение  Пусть
Пусть  любое распределение, для которого
любое распределение, для которого  некоторых доходах
некоторых доходах  Для любого дохода
Для любого дохода  пусть
пусть  определено соотношением (6), а значение
определено соотношением (6), а значение  формулой (9). Тогда
формулой (9). Тогда 
Из соотношений (8) и (9) видно, что условие эквивалентности из предположения  можно записать в виде
можно записать в виде

Мы в состоянии теперь доказать два основных результата. Наша первая теорема утверждает, что функция  удовлетворяет
удовлетворяет
буемому свойству  Согласно второй теореме, все функции удовлетворяющие этому свойству, являются возрастающими линейными функциями от
Согласно второй теореме, все функции удовлетворяющие этому свойству, являются возрастающими линейными функциями от 
Теорема 1. Пусть  два распределения из класса Тогда соотношения
два распределения из класса Тогда соотношения  равносильны.
равносильны.
Доказательство. Поскольку распределения и  финитны, то найдутся доходы
финитны, то найдутся доходы  для которых
для которых  и
и

Следовательно, как  так и
так и  эквивалентны распределениям вида (10). Теперь из леммы 3 § 7.7 следует, что
эквивалентны распределениям вида (10). Теперь из леммы 3 § 7.7 следует, что  тогда и только тогда, когда
тогда и только тогда, когда 
Теорема 2. Предположим, чттго  вещественные функции на R, каждая из которых обладает свойством, указанным в теореме 1. Тогда найдутся постоянные
вещественные функции на R, каждая из которых обладает свойством, указанным в теореме 1. Тогда найдутся постоянные  такие,
такие,  при всех
при всех 
Доказательство. Так как  то из предположенных свойств функций
то из предположенных свойств функций  вытекает, что
вытекает, что  Поэтому существует линейное преобразование указанного в теореме вида, после применения которого к
Поэтому существует линейное преобразование указанного в теореме вида, после применения которого к  функции
функции  совпадут в точках
совпадут в точках  . Таким образом, достаточно установить, что равенство
. Таким образом, достаточно установить, что равенство  справедливо при всех
справедливо при всех  если
если 
Рассмотрим сначала произвольный доход  такой, ччто
такой, ччто  Тогда найдется число
Тогда найдется число  для которого
для которого  . В силу свойств функций
. В силу свойств функций  получаем следующее равенство:
получаем следующее равенство:

Рассмотрим, далее, любой доход  для которого
для которого  Тогда найдется число
Тогда найдется число  такое, что
такое, что  Аналогичные вычисления дают
Аналогичные вычисления дают 
Наконец, если  то равенство
то равенство  выводится аналогично.
выводится аналогично.
Ограниченные функции полезности. При других аксиоматических подходах к теории полезности (см. ссылки в конце § 7.10) делаются предположения, в некоторых отношениях более сильные, нежели наши. Из этих усиленных предположений следует, что функция полезности  ограничена на множестве
ограничена на множестве 
В частности, при этих подходах предполагается, что соотношение к задает полное упорядочение всех распределений из Так как функция полезности  оказывается ограниченной, то математическое ожидание
оказывается ограниченной, то математическое ожидание  конечно для любого распределения
конечно для любого распределения  Следовательно, для любых двух распределений
Следовательно, для любых двух распределений  соотношения
соотношения  равносильны.
равносильны.
В этой главе мы не придерживались подхода, приводящего к ограниченным функциям полезности, по той причине, что во многих статистических задачах принято и чрезвычайно удобно работать с неограниченными функциями полезности. Например, в большом числе задач, некоторые из которых будут рассмотрены в книге дальше, в качестве множества R удобно брать вещественную прямую, а в качестве функции полезности — линейную или квадратическую функцию.
Пока что в этой главе были выведены свойства функции  лишь для распределений из класса Часто, однако, приходится вычислять среднюю полезность
лишь для распределений из класса Часто, однако, приходится вычислять среднюю полезность  для нефинитных распределений
для нефинитных распределений  . В следующем параграфе мы распространим основное свойство
. В следующем параграфе мы распространим основное свойство  функции
функции  на класс всех распределений
на класс всех распределений  для которых
для которых  конечно.
конечно.
Важно отметить, что если множество R содержит как наиболее предпочитаемый, так и наименее предпочитаемый доходы, то каждое распределение из  финитно и теория, развиваемая в следующем параграфе, не нужна. Даже если наше множество R не содержит наиболее предпочитаемого или наименее предпочитаемого дохода, то возможно иногда присоединить к R фиктивные доходы, которые служат той же цели. Трудность состоит в том, чтобы присоединить такие доходы, не нарушив сделанных предположений. Для того чтобы быть уверенными, что ни одно из предположений не нарушено, мы должны приписать конечную полезность наиболее предпочитаемому и наименее предпочитаемому доходам. Другими словами, для выполнения этого требования функция полезности
финитно и теория, развиваемая в следующем параграфе, не нужна. Даже если наше множество R не содержит наиболее предпочитаемого или наименее предпочитаемого дохода, то возможно иногда присоединить к R фиктивные доходы, которые служат той же цели. Трудность состоит в том, чтобы присоединить такие доходы, не нарушив сделанных предположений. Для того чтобы быть уверенными, что ни одно из предположений не нарушено, мы должны приписать конечную полезность наиболее предпочитаемому и наименее предпочитаемому доходам. Другими словами, для выполнения этого требования функция полезности  должна быть ограничена на множестве
должна быть ограничена на множестве  Однако, как мы уже упоминали, функция
Однако, как мы уже упоминали, функция  может быть и неограничена. В таких задачах необходим переход к нефинитным распределениям, который и развивается в § 7.10.
может быть и неограничена. В таких задачах необходим переход к нефинитным распределениям, который и развивается в § 7.10.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- Глава 2. ЭКСПЕРИМЕНТЫ, ВЫБОРОЧНЫЕ ПРОСТРАНСТВА И ВЕРОЯТНОСТЬ
- § 2.1. Эксперименты и выборочные пространства
- § 2.2. Теория множеств
- § 2.3. События и вероятность
- § 2.4. Условная вероятность
- § 2.5. Биномиальные коэффициенты
- Глава 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, СЛУЧАЙНЫЕ ВЕКТОРЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- § 3.1. Случайные величины и их распределения
- § 3.2. Многомерные распределения
- § 3.3. Суммы и интегралы
- § 3.4. Маргинальные распределения и независимость
- § 3.5. Векторы и матрицы
- § 3.6. Математические ожидания, моменты и характеристические функции
- § 3.7. Преобразования случайных величин
- § 3.8. Условные распределения
- Глава 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 4.2. Распределение Бернулли
- § 4.3. Биномиальное распределение
- § 4.4. Распределение Пуассона
- § 4.5. Отрицательное биномиальное распределение
- § 4.6. Гипергеометрическое распределение
- § 4.7. Нормальное распределение
- § 4.8. Гамма-распределение
- § 4.9. Бета-распределение
- § 4.10. Равномерное распределение
- § 4.11. Распределение Парето
- § 4.12. Распределение Стьюдента
- Глава 5. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 5.2. Мультиномиальное распределение
- § 5.3. Распределение Дирихле
- § 5.4. Многомерное нормальное распределение
- § 5.5. Распределение Уишарта
- § 5.6. Многомерное t-распределение
- § 5.7. Двустороннее двумерное распределение Парето
- ЧАСТЬ II. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ И ПОЛЕЗНОСТЬ
- Глава 6. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ
- § 6.2. Относительное правдоподобие
- § 6.3. Вспомогательный эксперимент
- § 6.4. Построение вероятностного распределения
- § 6.5. Проверка выполнения свойств вероятностного распределения
- § 6.6. Условные правдоподобия
- Глава 7. ПОЛЕЗНОСТЬ
- § 7.2. Предпочтения в множестве вероятностных распределений
- § 7.3. Определение функции полезности
- § 7.4. Некоторые свойства функций полезности
- § 7.5. Полезность в случае денежных доходов
- § 7.6. Выпуклые и вогнутые функции полезности
- § 7.7. Аксиоматический подход к полезности
- § 7.8. Построение функции полезности
- § 7.9. Проверка свойств функции полезности
- § 7.10. Распространение свойств функции полезности на класс
- ЧАСТЬ III. СТАТИСТИЧЕСКИЕ ЗАДАЧИ РЕШЕНИЯ
- § 8.2. Байесовский риск и байесовские решения
- § 8.3. Неотрицательные функции потерь
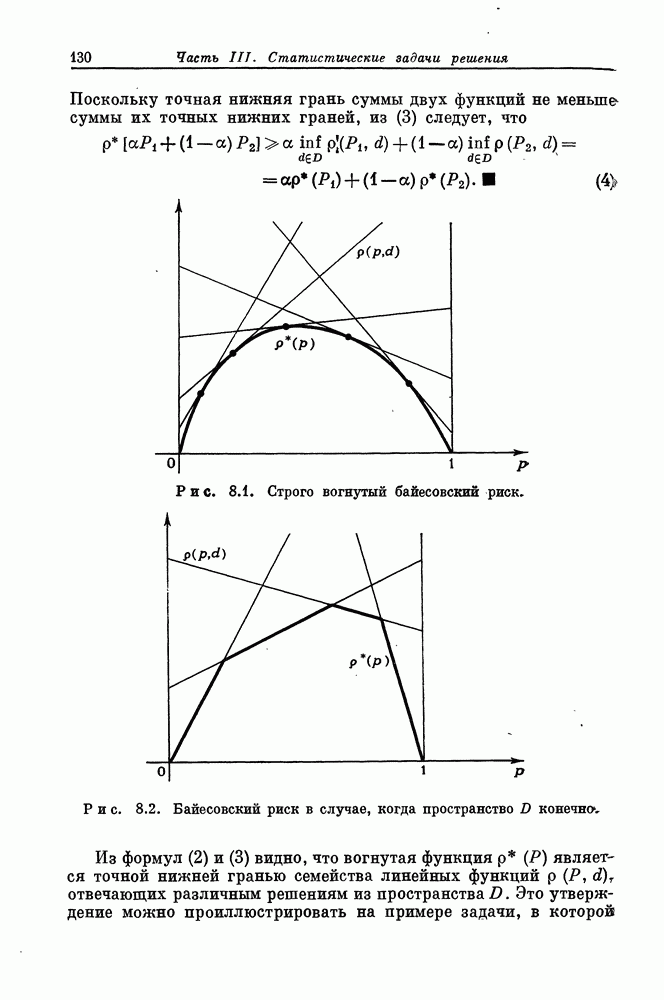
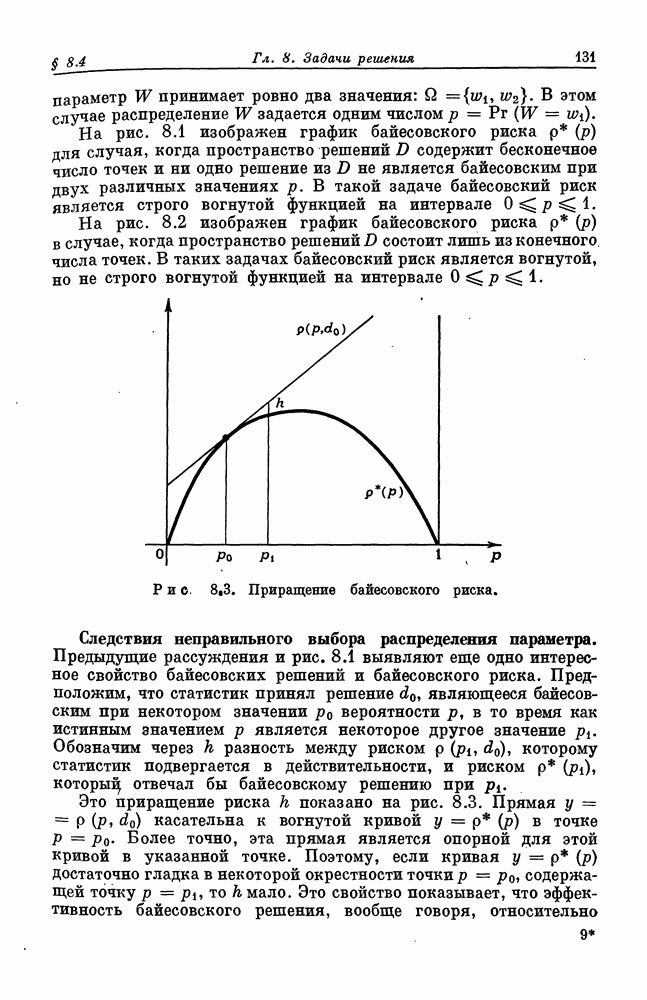
- § 8.4. Вогнутость байесовского риска
- § 8.5. Рандомизация и смешанные решения
- § 8.6. Выпуклые множества
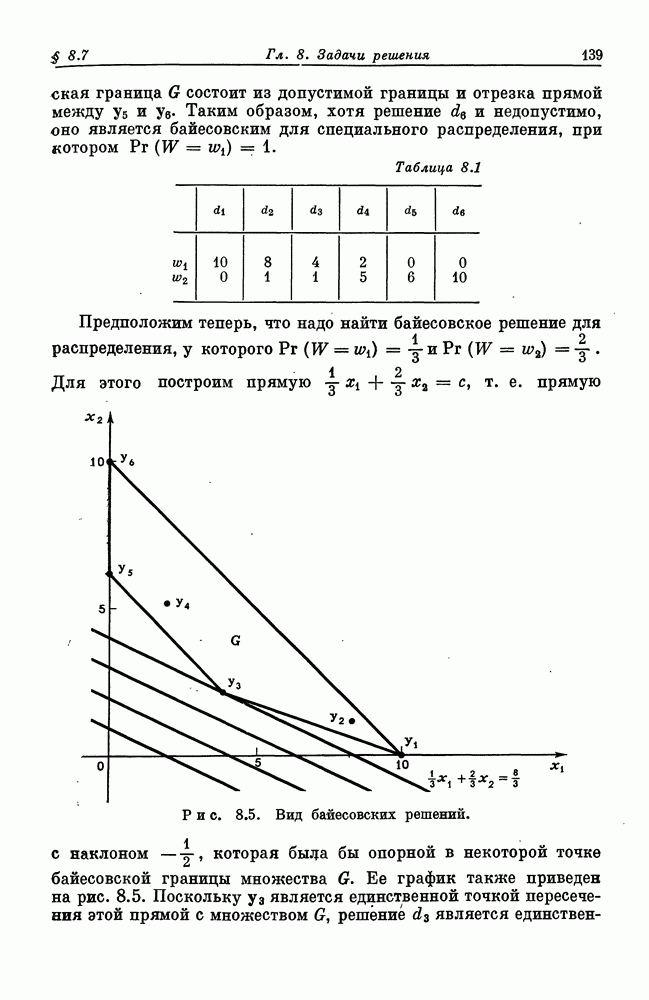
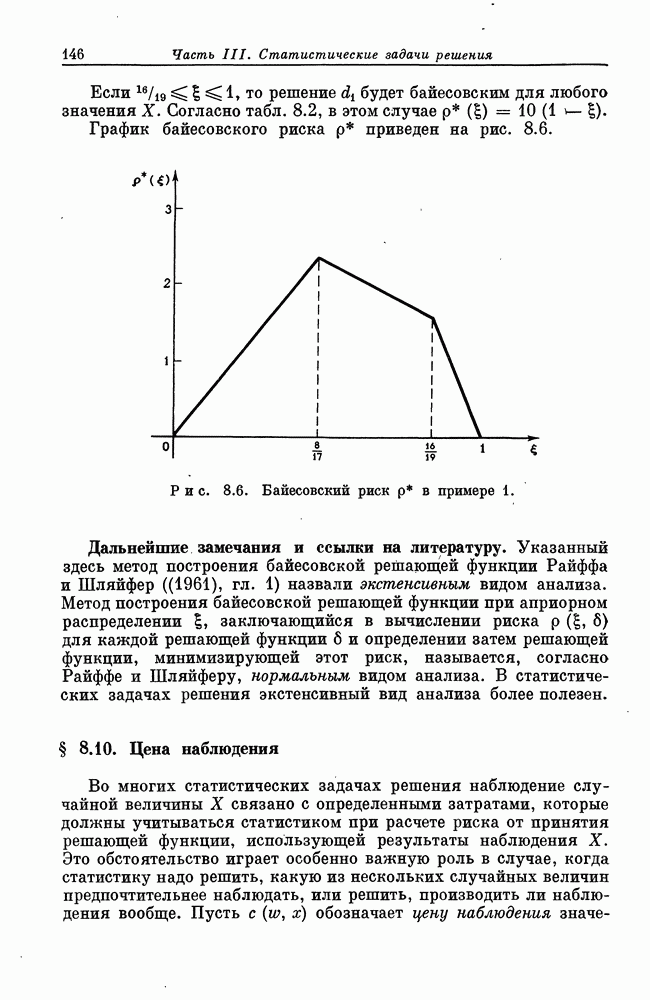
- § 8.7. Задачи решения с конечными …
- § 8.8. Задачи решения с наблюдениями
- § 8.9. Построение байесовских решающих функций
- § 8.10. Цена наблюдения
- § 8.11. Статистические задачи решения, в которых … состоят из двух точек
- § 8.12. Вычисление апостериорного распределения в случае, когда наблюдения производятся в несколько этапов
- Глава 9. СОПРЯЖЕННЫЕ АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 9.1. Достаточные статистики
- § 9.2. Сопряженные семейства распределений
- § 9.3. Построение сопряженного семейства
- § 9.4. Сопряженные семейства для выборок из различных стандартных распределений
- § 9.5. Сопряженные семейства для выборок из нормального распределения
- § 9.6. Выборка из нормального распределения с неизвестным средним и неизвестной мерой точности
- § 9.7. Выборка из равномерного распределения
- § 9.8. Сопряженное семейство для мультиномиальных наблюдений
- § 9.9. Сопряженные семейства для выборок из многомерного нормального распределения
- § 9.10. Многомерное нормальное распределение с неизвестным вектором средних и неизвестной матрицей точности
- § 9.11. Маргинальное распределение вектора средних
- § 9.12. Распределение коэффициента корреляции
- § 9.13. Матрицы точности с неизвестным множителем
- Глава 10. ПРЕДЕЛЬНЫЕ АПОСТЕРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 10.1. Несобственные априорные распределения
- § 10.2. Несобственные априорные распределения для выборок из нормального распределения
- § 10.3. Несобственные априорные распределения для выборок из многомерного нормального распределения
- § 10.4. Высокоточные измерения
- § 10.5. Сходимость апостериорных распределений
- § 10.6. Супер непрерывность
- § 10.7. Решения уравнения правдоподобия
- § 10.8. Сходимость супернепрерывных функций
- § 10.9. Предельные свойства функции правдоподобия
- § 10.10. Нормальная аппроксимация апостериорного распределения
- § 10.11. Аппроксимации в случае векторных параметров
- § 10.12. Апостериорные отношения
- Глава 11. ОЦЕНИВАНИЕ, ПРОВЕРКА ГИПОТЕЗ И ЛИНЕЙНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ
- § 11.2. Квадратическая функция потерь
- § 11.3. Ущерб пропорциональный абсолютной величине погрешности
- § 11.4. Оценивание векторного параметра
- § 11.5. Задачи проверки гипотез
- § 11.6. Проверка простой гипотезы о среднем значении нормального распределения
- § 11.7. Проверка гипотез о среднем значении нормального распределения с неизвестной мерой точности
- § 11.8. Решение вопроса о том, будет ли параметр меньше или больше предписанного значения
- § 11.9. Проверка гипотезы о том, превосходит или нет среднее нормального распределения заданное значение
- § 11.10. Линейные модели
- § 11.11. Проверка гипотез в линейных моделях
- § 11.12. Проверка гипотезы о равенстве нулю некоторых коэффициентов регрессии
- § 11.13. Дисперсионный анализ по одному признаку
- ЧАСТЬ IV. ПОСЛЕДОВАТЕЛЬНЫЕ РЕШЕНИЯ
- § 12.1. Эффект последовательного выбора
- § 12.2. Процедуры последовательного решения
- § 12.3. Риск процедуры последовательного решения
- § 12.4. Индукция назад
- § 12.5. Оптимальные ограниченные процедуры последовательного решения
- § 12.6. Примеры
- § 12.7. Неограниченные процедуры последовательного решения
- § 12.8. Регулярные процедуры последовательного решения
- § 12.9. Существование оптимальной процедуры
- § 12.10. Приближение оптимальной прцоедуры ограниченными процедурами
- § 12.11. Области продолжения и окончания выбора
- § 12.12. Функциональное уравнение
- § 12.13 Приближения и границы для байесовского риска
- § 12.14. Последовательный критерий отношения вероятностей
- § 12.15. Характеристики последовательных критериев отношения вероятностей
- § 12.16. Аппроксимации для среднего числа наблюдений
- Глава 13. ОПТИМАЛЬНЫЕ ПРАВИЛА ОСТАНОВКИ
- § 13.2. Вознаграждение статистика
- § 13.3. Выбор функции полезности
- § 13.4. Выбор с отбрасыванием
- § 13.5. Дальнейшие задачи выбора с отбрасыванием и выбора без отбрасывания
- § 13.6. Выбор с отбрасыванием из нормального распределения с неизвестным средним
- § 13.7. Выбор без отбрасывания из нормального распределения с неизвестным средним
- § 13.8. Существование оптимальных правил остановки
- § 13.9. Существование оптимальных правил остановки в задачах выбора без отбрасывания и с отбрасыванием
- § 13.10. Мартингалы
- § 13.11. Правила остановки для мартингалов
- § 13.12. Равномерно интегрируемые последовательности случайных величин
- § 13.13. Мартингалы, получаемые из сумм и произведений случайных величин
- § 13.14. Регулярные супермартингалы
- § 13.15. Супермартингалы и общие задачи об оптимальной остановке
- § 13.16. Марковские процессы
- § 13.17. Стационарные правила остановки для марковских процессов
- § 13.18. Задачи с входной платой
- § 13.19. Функциональное уравнение для марковского процесса
- Глава 14. ПОСЛЕДОВАТЕЛЬНОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
- § 14.2. Марковские процессы решения с конечным числом шагов
- § 14.3. Марковские процессы решения с бесконечным числом шагов
- § 14.4. Некоторые задачи о пари
- § 14.5. Задачи о «двуруком бандите»
- § 14.6. Задачи о «двуруком бандите» с известным значением одного из параметров
- § 14.7. Задачи о «двуруком бандите» в случае зависимых параметров
- § 14.8. Задачи оптимального управления запасами
- § 14.9. Задачи управления запасами с бесконечным числом шагов
- § 14.10. Задачи управления
- § 14.11. Оптимальное управление в случае, когда процесс наблюдается с ошибками
- § 14.12. Многомерные задачи управления
- § 14.13. Задачи управления с погрешностями, вносимыми статистиком
- § 14.14. Задачи поиска
- § 14.15. Задачи поиска с равными стоимостями
- § 14.16. Функции неопределенности и задачи статистического решения
- § 14.17. Достаточные эксперименты
- § 14.18. Примеры достаточных экспериментов
- СПИСОК ЛИТЕРАТУРЫ