§ 6.2. Относительное правдоподобие

Пусть выборочное пространство с -алгеброй событий и мы хотим определить вероятность каждого события из Основным понятием, которое считается первоначальным и не определяется, будет понятие относительного правдоподобия одного события сравнительно с другим. Более точно, принимается, что для любых двух событий из можно сказать, является ли одно из них (какое именно) более правдоподобным (т. е. имеющим больше шансов наступить) или же оба они одинаково правдоподобны.

При сравнении двух событий мы будем писать в случае, когда событие В более правдоподобно, чем А, и в случае, когда одинаково правдоподобны. По аналогии с отношением порядка среди вещественных чисел мы будем писать для указания того обстоятельства, что событие В по крайней мере так же правдоподобно, как и или, что то же самое, что А не более правдоподобно, чем В. Таким образом, если то либо либо Далее, по определению обозначает то же самое, что и — то же самое, что

Поскольку считается, что вероятность события есть численная характеристика его правдоподобия, то для всякого вероятностного распределения заданного на -алгебре событий естественно требовать, чтобы тогда и только тогда, когда Вероятностное распределение обладающее этим свойством, называется согласованным с отношением Мы выясним сейчас условия, которым должно удовлетворять отношение для того, чтобы существовало единственное вероятностное распределение, согласованное с ним. Об отношении будут сделаны некоторые предположения, основывающиеся как на интуитивном понимании понятия относительного правдоподобия двух событий, так и на математических свойствах вероятностных распределений, указанных в гл. 2.

Вот основное предположение.

Предположение SP. Для любых двух событий имеет место одно и только одно из следующих соотношений:

Следующее предположение допускает простую интерпретацию, делающую его интуитивно понятным.

Предположение SP. Если четыре события, причем то Если при этом или

Это предположение может быть истолковано так. Допустим, что каждое из событий может произойти одним из двух взаимно исключающих друг друга способов. Если каждый из двух способов осуществления события А не более правдоподобен, нежели соответствующий способ осуществления события В, то . Далее, если хотя бы один из способов осуществления А на самом деле менее правдоподобен, чем соответствующий способ для В, то

Из этих двух предположений уже можно получить несколько следствий. Одним из интересных и важных результатов является транзитивность отношения устанавливаемая ниже в теореме 1. Перед ее доказательством мы приведем следующую простую лемму.

Лемма 1. Пусть такие события, что Соотношение справедливо тогда и только тогда, когда

Доказательство. Если то утверждение леммы следует из предположения . Если же то в силу предположения имеем

Теорема 1. Если события, для которых то

Доказательство. Рассмотрим семь непересекающихся событий, указанных на рис. 6.1 и дающих в объединении

Рис. 6.1. Разбиение множества

В силу того что из леммы 1 выводим

Аналогично, так как то по той же лемме 1

Поскольку события как в левых, так и в правых частях соотношений (1) и (2) несовместны, то из предположения SP2 следует, что

Удаляя событие из обеих частей этого соотношения с помощью леммы 1, заключаем

Из рис. 6.1 и леммы 1 теперь видно, что

Из предположения и установленной в теореме 1 транзитивности следует, что отношение задает полное упорядочение событий из Конечно, вполне может быть, что различные события эквивалентны между собой относительно этого упорядочения, т. е.

Следующий результат является распространением предположения на случай объединения конечного числа несовместных событий.

Теорема 2. Если суть несовместных событий и также несовместных событий, причем то Если, кроме того, по крайней мере для одного значения то

Эта теорема легко доказывается по индукции. Следующая теорема отражает основное свойство относительного правдоподобия, которое было отмечено в гл. 2 для вероятностей.

Теорема 3. Для любых событий тогда и только тогда когда

Доказательство этой теоремы составляет предмет упр. 16 в конце настоящей главы.

Теперь мы сделаем естественное предположение о том, что ни одно событие не является менее правдоподобным, чем невозможное событие 0, и исключим из рассмотрения тривиальный случай, условившись считать, что все выборочное пространство S более правдоподобно, чем 0.

Предположение SP3. Каково бы ни было событие . Кроме того,

Это предположение приводит к следующему основному свойству относительного правдоподобия, аналог которого для вероятностей уже был отмечен (см. упр. 1в ниже).

Теорема 4. Если такие события., что А а В, то . В частности, для каждого события А.

Наконец, мы сделаем предположение, касающееся поведения бесконечной последовательности событий.

Предположение SP4. Если убывающая последовательность событий, причем где В — некоторое фиксированное событие, то

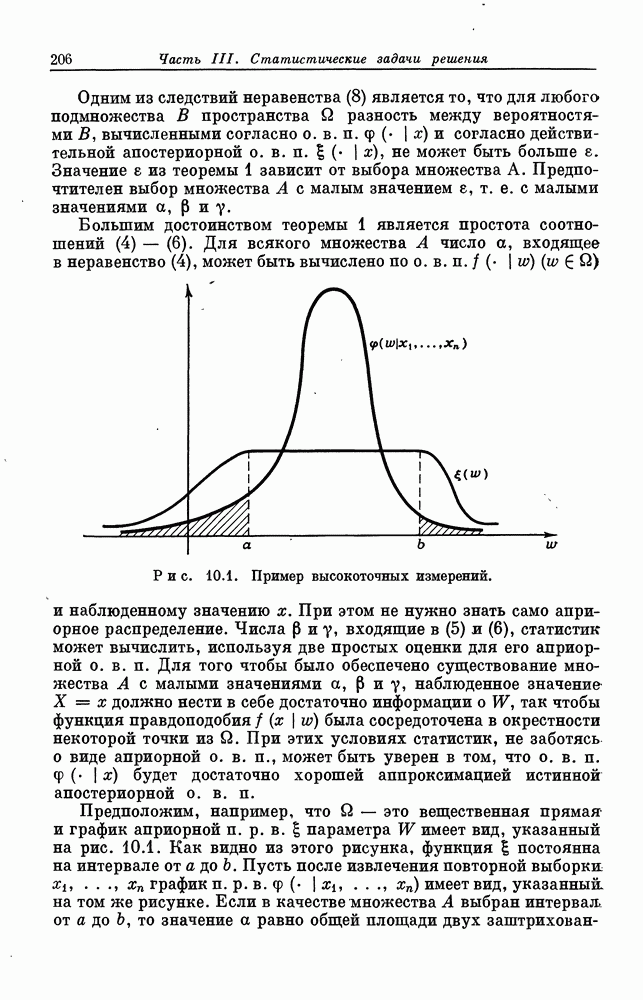
Для пояснения смысла предположения рассмотрим пример, в котором событиями являются подмножества вещественной прямой. Пусть каждый бесконечный интервал вида считается более правдоподобным, нежели некоторое фиксированное подмножество В прямой. Поскольку пересечение всех указанных бесконечных интервалов есть пустое множество 0, то из предположения следует, что множество В должно быть эквивалентно 0. Другими словами, если В — некоторое множество, для которого то независимо от «малости» В никакой бесконечный интервал не может быть правдоподобнее В или хотя бы столь же правдоподобным. Свойство такого типа, выделяет счетно аддитивные вероятностные распределения (т. е. удовлетворяющие свойству 2 определения вероятностного распределения из § 2.3) среди множества всех конечно аддитивных распределений.

Следующая теорема является двойственной к предположению Можно было бы взять ее в качестве предположения а старое предположение вывести из него как теорему.

Теорема 5. Если возрастающая последовательность событий и В — некоторое фиксированное событие, причем при всех то

Доказательство. Из условий данной теоремы и из теоремы 3 следует, что является убывающей последовательностью Следовательно, по предположению имеем Доказательство завершается теперь применением теоремы 3.

Приводимый далее результат обобщает теорему 2 на случай бесконечных последовательностей несовместных событий.

Теорема 6. Если - бесконечная последовательность несовместных событий и - другая бесконечная последовательность несовместных событий, причем то Если, кролее того, хотя бы при одном значении то

Доказательство. Из теоремы 2 вытекает, что при всех Теорема 4 дает

Так как события в левой части соотношения (5) образуют возрастающую последовательность то: из теоремы 5 выводим, что и

Если для какого-нибудь значения то применяя теорему 3, заключаем, что при

Далее, из уже доказанной первой части теоремы 6 следует, что

Поэтому из соотношений (6) и (7) и предположения SP2 получаем

Понятно, что отношение должно удовлетворять предположениям SP1 - SP4, для того чтобы существовало вероятностное распределение, согласованное с ним. Однако этих четырех предположений недостаточно, чтобы гарантировать существование такого вероятностного распределения. В следующем параграфе мы введем пятое предположение, после чего уже окажется возможным построить единственное вероятностное распределение, согласованное с отношением

Дальнейшие замечания и ссылки на литературу. Иногда при решении вопроса о том, какое из событий следует признать более правдоподобным, статистику могут помочь вспомогательные соображения. Например, етатистик может спросить себя,

что бы он предпочел: участвовать в пари, в котором получит ценный приз, если произойдет событие А, и ничего не получит, если А не произойдет, или в пари, в котором он получит ту же награду в случае осуществления события В и ничего, если В не произойдет. Хотя, естественно, статистик предпочтет участвовать в пари, в котором его выигрыш представляется более правдоподобным, у этого рассуждения есть свои слабые места. Рядовой гражданин Соединенных Штатов сочтет более правдоподобным свою гибель в атомной войне в течение ближайших десяти лет, нежели избрание в президенты в течение того же времени. Однако, если бы ему предложили выбор, он, разумеется, предпочел бы получить приз при вступлении в должность президента, чем тот же приз в случае своей гибели. Этот пример, конечно, несколько утрирован, но он иллюстрирует трудности, которые возникают при сравнении событий, не являющихся этически нейтральными по Рамсею (1926). Эти трудности показывают, почему, когда это возможно, лучше непосредственно сравнивать относительное правдоподобие двух событий, без рассмотрения последствий, связанных с их наступлением.

Вопрос о существовании по крайней мере одного вероятностного распределения, согласованного с отношением в случае, когда это отношение удовлетворяет предположениям SP1 - SP4, был поставлен де Финетти и Сэвиджем (см. Сэвидж (1954), стр. 40). Отрицательный ответ на него был дан Крафтом, Прэттом и Сейденбергом (1959), которые построили соответствующий пример, используя выборочное пространство состоящее из конечного числа точек.