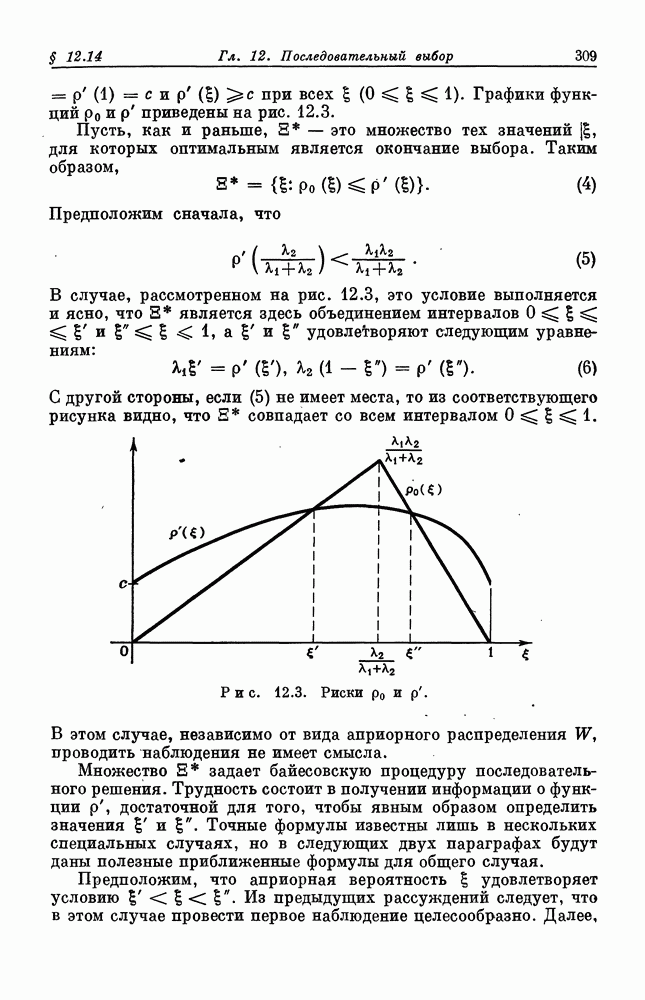
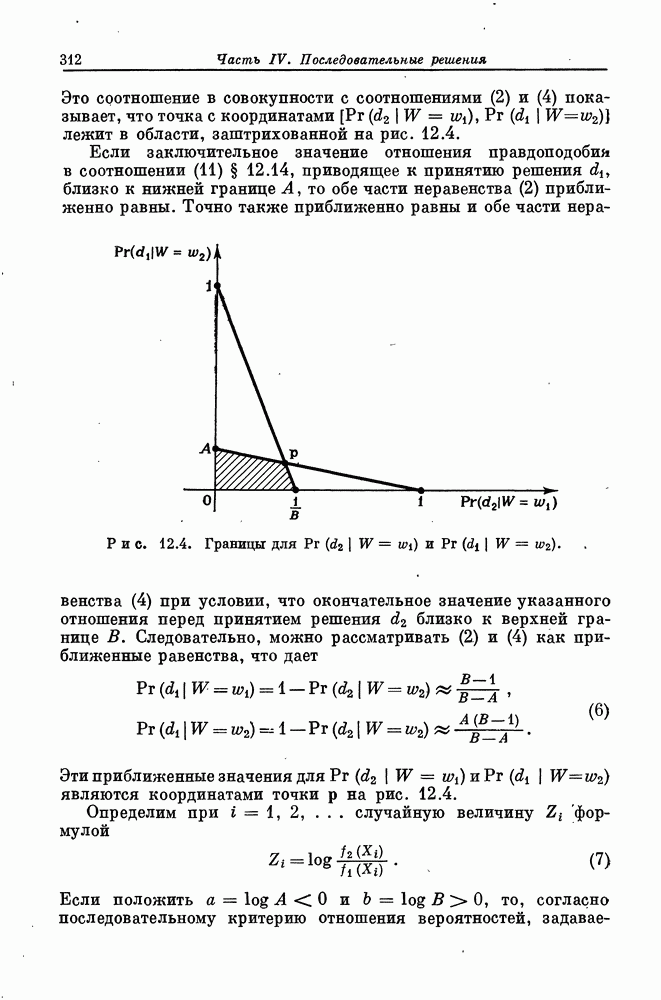
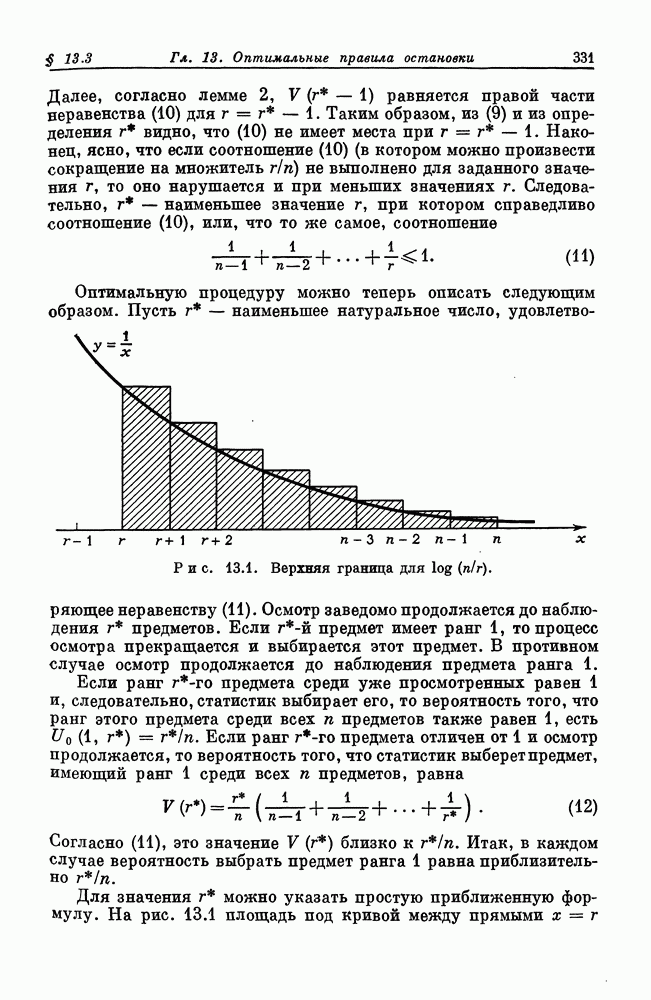
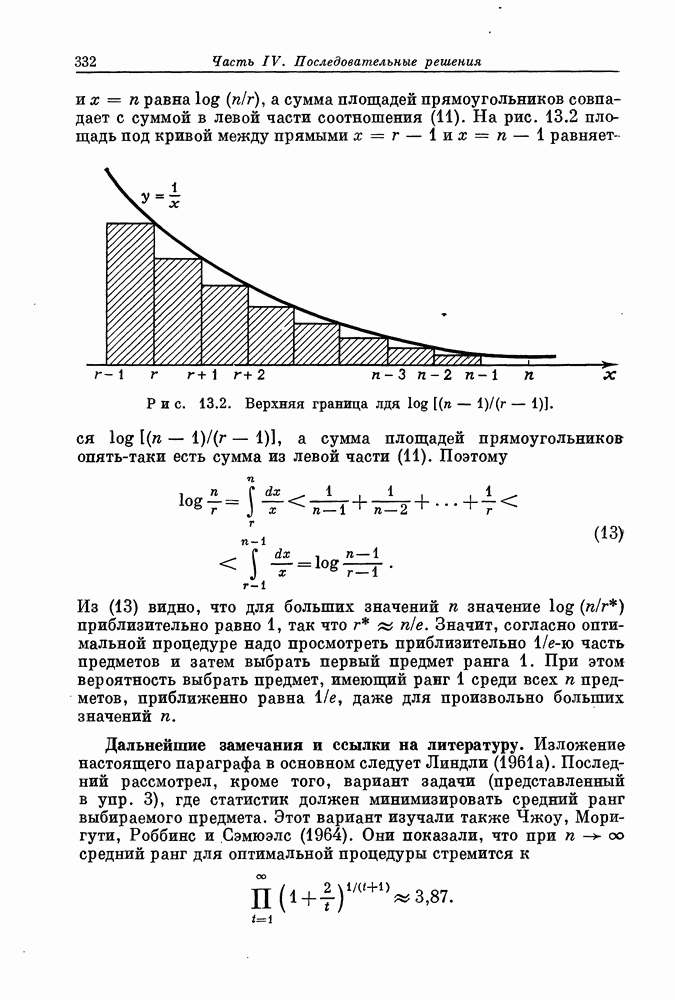
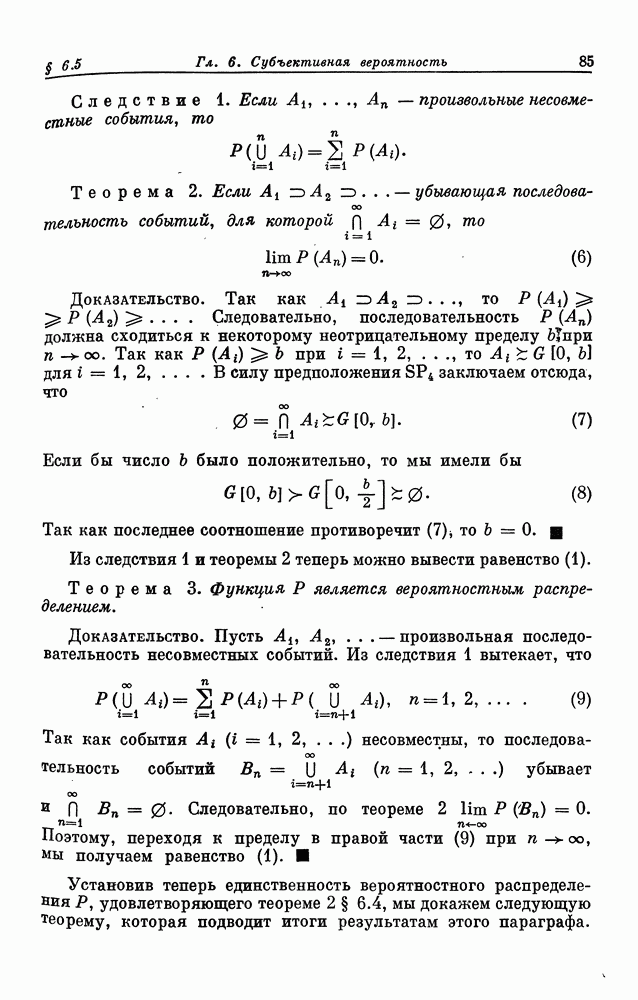| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 8.5. Рандомизация и смешанные решения
В задачах решения часто является довольно полезным (и безусловно реалистическим) допущение о том, что статистик может выбирать решение из  с помощью той или иной вспомогательной процедуры рандомизации, например подбрасывания монеты. Другими словами, статистик может принимать смешанное или ранд
с помощью той или иной вспомогательной процедуры рандомизации, например подбрасывания монеты. Другими словами, статистик может принимать смешанное или ранд  -мизованное решение
-мизованное решение  заключающееся в том, что сначала он приписывает вероятности
заключающееся в том, что сначала он приписывает вероятности  элементам некоторой последовательности
элементам некоторой последовательности  решений из
решений из  а затем выбирает одно из решений
а затем выбирает одно из решений  согласно этим вероятностям. Если ущерб
согласно этим вероятностям. Если ущерб  отвечающий смешанному решению
отвечающий смешанному решению  существует при
существует при  то, согласно предположению о средней полезности, его значение равно
то, согласно предположению о средней полезности, его значение равно

Для каждого распределения  параметра
параметра  и всякого смешанного решения
и всякого смешанного решения  риск
риск  в случае его существования может быть определен той же формулой (4) § 8.1.
в случае его существования может быть определен той же формулой (4) § 8.1.
В задачах, где пространство решений  содержит несчетное число элементов, рандомизованное решение можно определить более общим образом при помощи произвольного вероятностного распределения на некоторой
содержит несчетное число элементов, рандомизованное решение можно определить более общим образом при помощи произвольного вероятностного распределения на некоторой  -алгебре подмножеств множества
-алгебре подмножеств множества 
Пусть  обозначает множество всех смешанных решений данной задачи. В отличие от смешанных решений, решения из
обозначает множество всех смешанных решений данной задачи. В отличие от смешанных решений, решения из  называются чистыми. Всякое чистое решение
называются чистыми. Всякое чистое решение  можно рассматривать как рандомизованное посредством тривиальной рандомизации, при которой чистое решение
можно рассматривать как рандомизованное посредством тривиальной рандомизации, при которой чистое решение  выбирается с вероятностью 1. При таком соглашении
выбирается с вероятностью 1. При таком соглашении  а
а  Вводя смешанные решения, мы заменяем, таким образом, пространство решений
Вводя смешанные решения, мы заменяем, таким образом, пространство решений  более широким пространством
более широким пространством  Однако, как мы сейчас увидим, это расширение пространства решений никак не позволяет уменьшить риск статистика, так что нет особой нужды рассматривать решения, не входящие в исходное пространство
Однако, как мы сейчас увидим, это расширение пространства решений никак не позволяет уменьшить риск статистика, так что нет особой нужды рассматривать решения, не входящие в исходное пространство 
Для всякого распределения  параметра
параметра  статистику следует выбирать, если это возможно, решение
статистику следует выбирать, если это возможно, решение  минимизирующее риск
минимизирующее риск  Согласно формуле (1), функция потерь для всякого смешанного решения
Согласно формуле (1), функция потерь для всякого смешанного решения  является смесью (взвешенным средним) функций потерь, отвечающих чистым решениям
является смесью (взвешенным средним) функций потерь, отвечающих чистым решениям  Поэтому если риск
Поэтому если риск  смешанного решения существует, то его значение равно смеси рисков
смешанного решения существует, то его значение равно смеси рисков  чистых решений
чистых решений  Отсюда следует, что
Отсюда следует, что

Из соотношения (2) видно, что никакому смешанному решению из  не отвечает риск, меньший, чем минимальное значение
не отвечает риск, меньший, чем минимальное значение  получаемое при чистых решениях из
получаемое при чистых решениях из  Далее, соотношение (2) верно безотносительно к конечности или бесконечности байесовского риска
Далее, соотношение (2) верно безотносительно к конечности или бесконечности байесовского риска  и независимо от того, достигается ли это значение на каком-нибудь элементе
и независимо от того, достигается ли это значение на каком-нибудь элементе  или нет. Если байесовский риск
или нет. Если байесовский риск  конечен и достигается при некотором смешанном решении из
конечен и достигается при некотором смешанном решении из  то из предыдущих замечаний следует, что это же значение достигается и при некотором чистом решении из
то из предыдущих замечаний следует, что это же значение достигается и при некотором чистом решении из 
Эти рассуждения подтверждают интуитивное представление о том, что статистику не следует принимать важные решения с помощью подбрасывания монеты. Если два или более чистых решений обладают одинаковым байесовским риском, то, вводя добавочную рандомизацию, мы можем выбрать одно из этих решений. Однако поскольку здесь приемлемо любое из этих байесовских решений, метод рандомизации по существу излишен. Во всех других ситуациях использование рандомизации может привести к тому, что окончательное решение окажется не байесовским.
Тем не менее рандомизация играет чрезвычайно важную роль в статистике. Понятия случайного выбора и случайного распределения различных методов обработки по объектам эксперимента являются основными при выполнении эффективных экспериментов. Эти замечания на самом деле не противоречат предыдущим, согласно которым статистику не следует пользоваться рандомизованными решениями, и вот почему.
Утверждение о том, что статистику не следует использовать рандомизованные решения, справедливо в специальных задачах решения с фиксированными пространством доходов и функцией потерь. Утверждение о полезности рандомизации как статистического приема предполагает возможность того, что результаты эксперимента со случайной выборкой могут значительно отличаться от результатов эксперимента с выборкой, осуществляемой неслучайным образом. Независимо от метода получения выборки, статистик должен строить вероятностную модель, отвечающую
эксперименту, для того чтобы дать формальное обоснование дальнейшего статистического анализа.
Для случайных выборок эта модель относительно проста. Следовательно, у проводящих эксперимент статистиков вряд ли возникнут значительные расхождения во мнениях о пригодности данной модели для данного эксперимента и использовании модели в дальнейшем статистическом анализе, так что чисто субъективные аспекты удается отделить от тех, по которым есть общее согласие. По этой причине анализ данных по большой случайной выборке на основе такой общепризнанной модели обычно приводит к резкому уменьшению различий в отдельных взглядах.
С другой стороны, при неслучайном выборе вероятностная модель статистика обычно оказывается в высшей степени субъективной. Поэтому субъективен и весь последующий анализ, и статистику трудно убедить других в справедливости его результатов. Далее, если исходные представления статистика были ошибочными, то его заблуждения могут еще усугубиться при использовании неправильной субъективной модели. Как пишет Нейман (1967), «без рандомизации нет гарантии того, что в экспериментальных данных нет необъективности, которую не обнаружит ни один критерий значимости».
После небольшого отступления, посвященного выпуклым множествам, мы продолжим обсуждение некоторых специальных задач решения. Хотя, как мы убедились, статистик и может в таких задачах ограничиться пространством чистых решений  однако в § 8.7 будет показано, что рассмотрение пространства
однако в § 8.7 будет показано, что рассмотрение пространства  всех смешанных решений более глубоко вскрывает структуру оптимальных чистых решений.
всех смешанных решений более глубоко вскрывает структуру оптимальных чистых решений.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- Глава 2. ЭКСПЕРИМЕНТЫ, ВЫБОРОЧНЫЕ ПРОСТРАНСТВА И ВЕРОЯТНОСТЬ
- § 2.1. Эксперименты и выборочные пространства
- § 2.2. Теория множеств
- § 2.3. События и вероятность
- § 2.4. Условная вероятность
- § 2.5. Биномиальные коэффициенты
- Глава 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, СЛУЧАЙНЫЕ ВЕКТОРЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- § 3.1. Случайные величины и их распределения
- § 3.2. Многомерные распределения
- § 3.3. Суммы и интегралы
- § 3.4. Маргинальные распределения и независимость
- § 3.5. Векторы и матрицы
- § 3.6. Математические ожидания, моменты и характеристические функции
- § 3.7. Преобразования случайных величин
- § 3.8. Условные распределения
- Глава 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 4.2. Распределение Бернулли
- § 4.3. Биномиальное распределение
- § 4.4. Распределение Пуассона
- § 4.5. Отрицательное биномиальное распределение
- § 4.6. Гипергеометрическое распределение
- § 4.7. Нормальное распределение
- § 4.8. Гамма-распределение
- § 4.9. Бета-распределение
- § 4.10. Равномерное распределение
- § 4.11. Распределение Парето
- § 4.12. Распределение Стьюдента
- Глава 5. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 5.2. Мультиномиальное распределение
- § 5.3. Распределение Дирихле
- § 5.4. Многомерное нормальное распределение
- § 5.5. Распределение Уишарта
- § 5.6. Многомерное t-распределение
- § 5.7. Двустороннее двумерное распределение Парето
- ЧАСТЬ II. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ И ПОЛЕЗНОСТЬ
- Глава 6. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ
- § 6.2. Относительное правдоподобие
- § 6.3. Вспомогательный эксперимент
- § 6.4. Построение вероятностного распределения
- § 6.5. Проверка выполнения свойств вероятностного распределения
- § 6.6. Условные правдоподобия
- Глава 7. ПОЛЕЗНОСТЬ
- § 7.2. Предпочтения в множестве вероятностных распределений
- § 7.3. Определение функции полезности
- § 7.4. Некоторые свойства функций полезности
- § 7.5. Полезность в случае денежных доходов
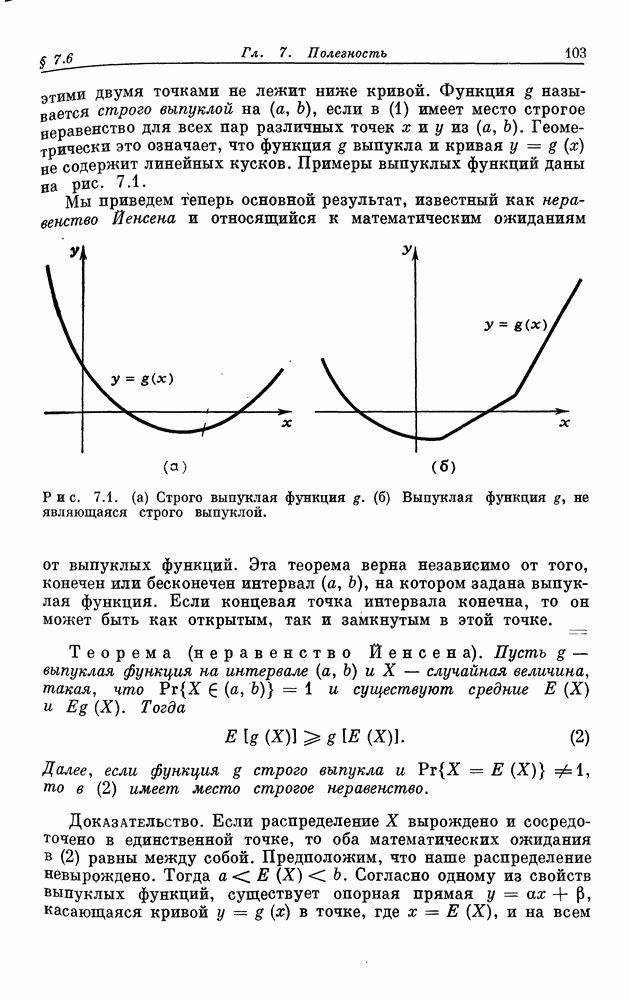
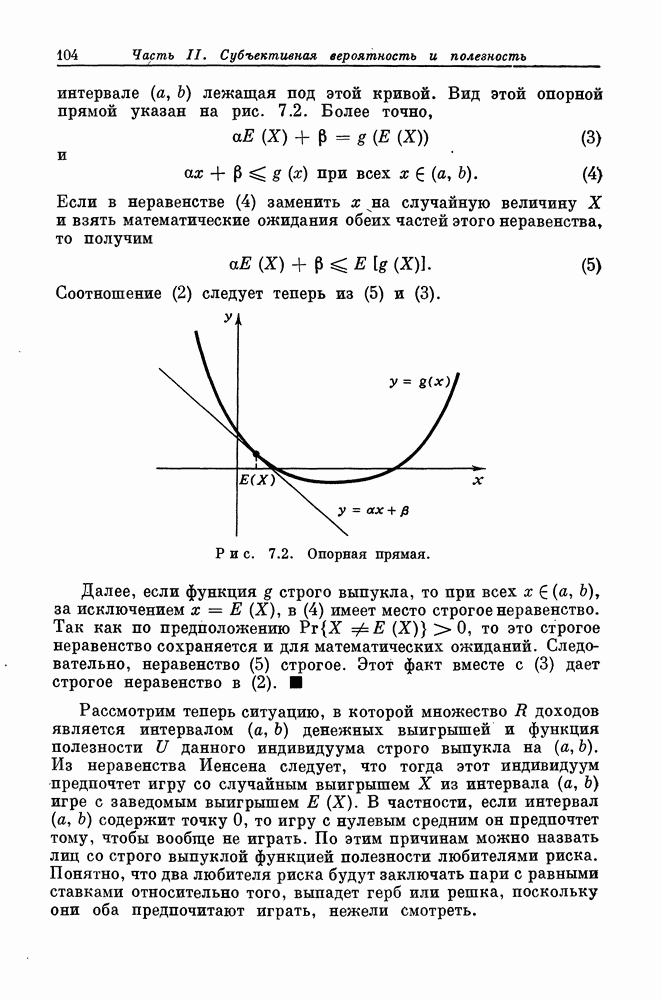
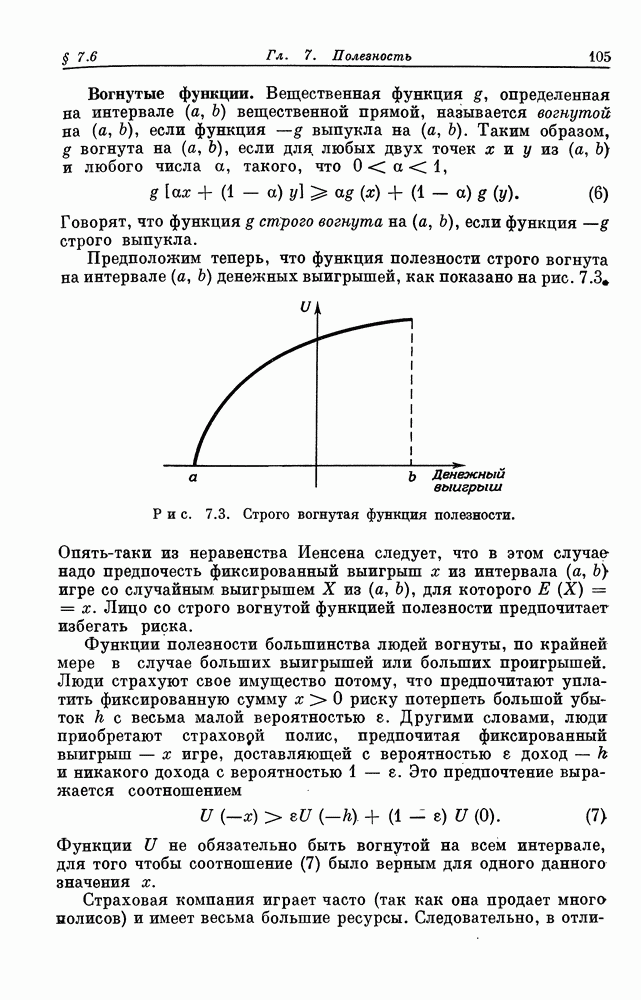
- § 7.6. Выпуклые и вогнутые функции полезности
- § 7.7. Аксиоматический подход к полезности
- § 7.8. Построение функции полезности
- § 7.9. Проверка свойств функции полезности
- § 7.10. Распространение свойств функции полезности на класс
- ЧАСТЬ III. СТАТИСТИЧЕСКИЕ ЗАДАЧИ РЕШЕНИЯ
- § 8.2. Байесовский риск и байесовские решения
- § 8.3. Неотрицательные функции потерь
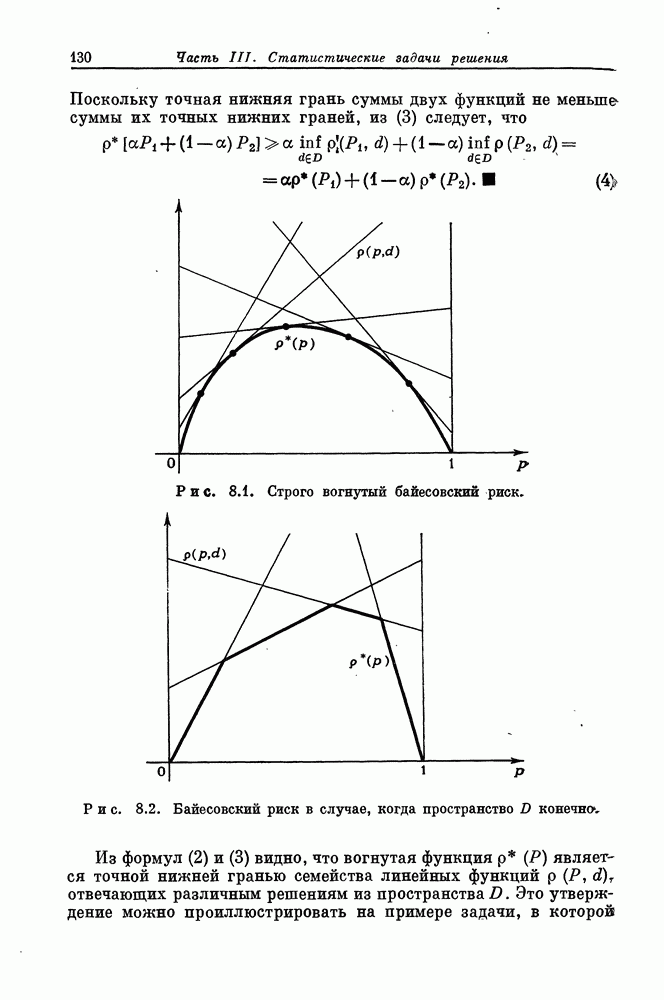
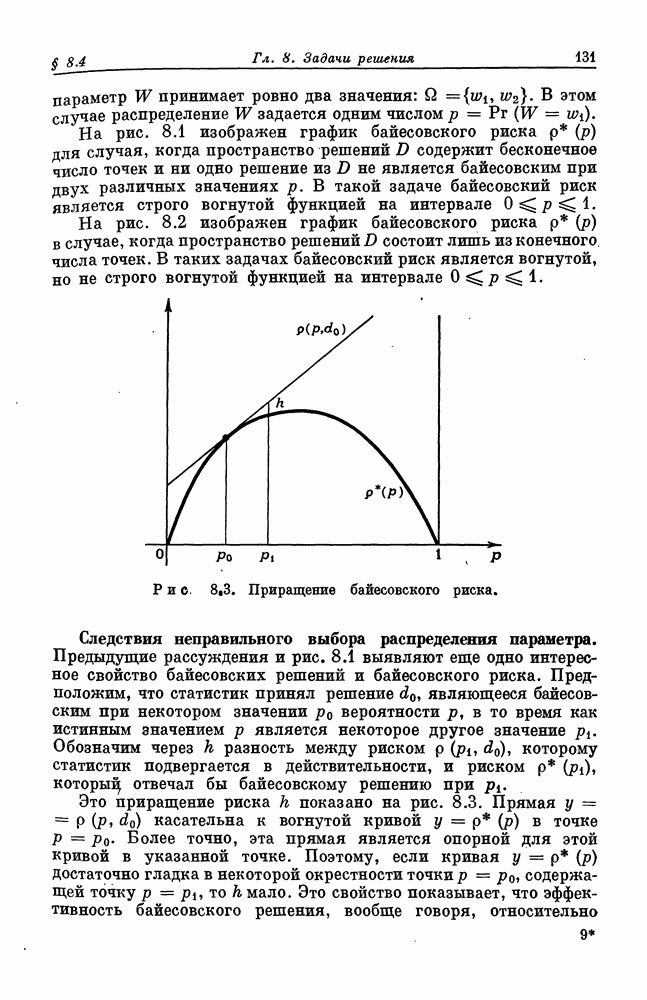
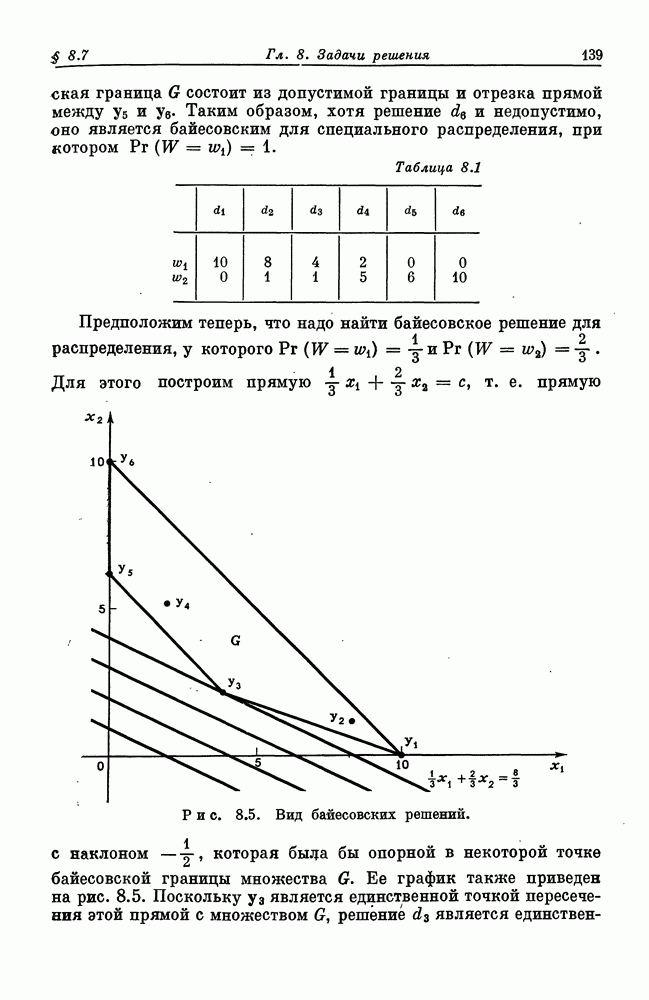
- § 8.4. Вогнутость байесовского риска
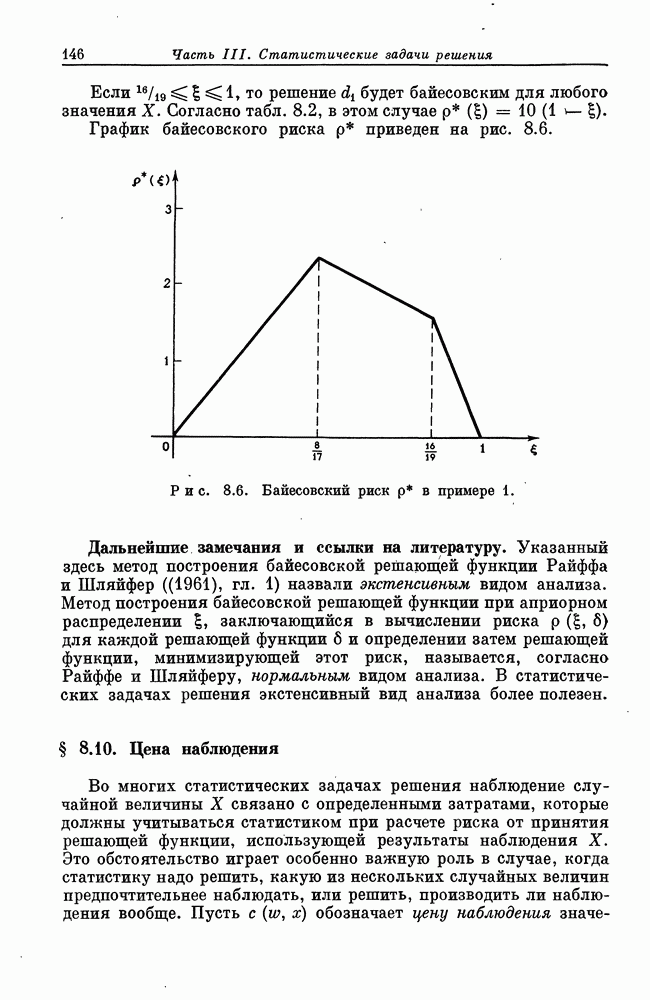
- § 8.5. Рандомизация и смешанные решения
- § 8.6. Выпуклые множества
- § 8.7. Задачи решения с конечными …
- § 8.8. Задачи решения с наблюдениями
- § 8.9. Построение байесовских решающих функций
- § 8.10. Цена наблюдения
- § 8.11. Статистические задачи решения, в которых … состоят из двух точек
- § 8.12. Вычисление апостериорного распределения в случае, когда наблюдения производятся в несколько этапов
- Глава 9. СОПРЯЖЕННЫЕ АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 9.1. Достаточные статистики
- § 9.2. Сопряженные семейства распределений
- § 9.3. Построение сопряженного семейства
- § 9.4. Сопряженные семейства для выборок из различных стандартных распределений
- § 9.5. Сопряженные семейства для выборок из нормального распределения
- § 9.6. Выборка из нормального распределения с неизвестным средним и неизвестной мерой точности
- § 9.7. Выборка из равномерного распределения
- § 9.8. Сопряженное семейство для мультиномиальных наблюдений
- § 9.9. Сопряженные семейства для выборок из многомерного нормального распределения
- § 9.10. Многомерное нормальное распределение с неизвестным вектором средних и неизвестной матрицей точности
- § 9.11. Маргинальное распределение вектора средних
- § 9.12. Распределение коэффициента корреляции
- § 9.13. Матрицы точности с неизвестным множителем
- Глава 10. ПРЕДЕЛЬНЫЕ АПОСТЕРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 10.1. Несобственные априорные распределения
- § 10.2. Несобственные априорные распределения для выборок из нормального распределения
- § 10.3. Несобственные априорные распределения для выборок из многомерного нормального распределения
- § 10.4. Высокоточные измерения
- § 10.5. Сходимость апостериорных распределений
- § 10.6. Супер непрерывность
- § 10.7. Решения уравнения правдоподобия
- § 10.8. Сходимость супернепрерывных функций
- § 10.9. Предельные свойства функции правдоподобия
- § 10.10. Нормальная аппроксимация апостериорного распределения
- § 10.11. Аппроксимации в случае векторных параметров
- § 10.12. Апостериорные отношения
- Глава 11. ОЦЕНИВАНИЕ, ПРОВЕРКА ГИПОТЕЗ И ЛИНЕЙНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ
- § 11.2. Квадратическая функция потерь
- § 11.3. Ущерб пропорциональный абсолютной величине погрешности
- § 11.4. Оценивание векторного параметра
- § 11.5. Задачи проверки гипотез
- § 11.6. Проверка простой гипотезы о среднем значении нормального распределения
- § 11.7. Проверка гипотез о среднем значении нормального распределения с неизвестной мерой точности
- § 11.8. Решение вопроса о том, будет ли параметр меньше или больше предписанного значения
- § 11.9. Проверка гипотезы о том, превосходит или нет среднее нормального распределения заданное значение
- § 11.10. Линейные модели
- § 11.11. Проверка гипотез в линейных моделях
- § 11.12. Проверка гипотезы о равенстве нулю некоторых коэффициентов регрессии
- § 11.13. Дисперсионный анализ по одному признаку
- ЧАСТЬ IV. ПОСЛЕДОВАТЕЛЬНЫЕ РЕШЕНИЯ
- § 12.1. Эффект последовательного выбора
- § 12.2. Процедуры последовательного решения
- § 12.3. Риск процедуры последовательного решения
- § 12.4. Индукция назад
- § 12.5. Оптимальные ограниченные процедуры последовательного решения
- § 12.6. Примеры
- § 12.7. Неограниченные процедуры последовательного решения
- § 12.8. Регулярные процедуры последовательного решения
- § 12.9. Существование оптимальной процедуры
- § 12.10. Приближение оптимальной прцоедуры ограниченными процедурами
- § 12.11. Области продолжения и окончания выбора
- § 12.12. Функциональное уравнение
- § 12.13 Приближения и границы для байесовского риска
- § 12.14. Последовательный критерий отношения вероятностей
- § 12.15. Характеристики последовательных критериев отношения вероятностей
- § 12.16. Аппроксимации для среднего числа наблюдений
- Глава 13. ОПТИМАЛЬНЫЕ ПРАВИЛА ОСТАНОВКИ
- § 13.2. Вознаграждение статистика
- § 13.3. Выбор функции полезности
- § 13.4. Выбор с отбрасыванием
- § 13.5. Дальнейшие задачи выбора с отбрасыванием и выбора без отбрасывания
- § 13.6. Выбор с отбрасыванием из нормального распределения с неизвестным средним
- § 13.7. Выбор без отбрасывания из нормального распределения с неизвестным средним
- § 13.8. Существование оптимальных правил остановки
- § 13.9. Существование оптимальных правил остановки в задачах выбора без отбрасывания и с отбрасыванием
- § 13.10. Мартингалы
- § 13.11. Правила остановки для мартингалов
- § 13.12. Равномерно интегрируемые последовательности случайных величин
- § 13.13. Мартингалы, получаемые из сумм и произведений случайных величин
- § 13.14. Регулярные супермартингалы
- § 13.15. Супермартингалы и общие задачи об оптимальной остановке
- § 13.16. Марковские процессы
- § 13.17. Стационарные правила остановки для марковских процессов
- § 13.18. Задачи с входной платой
- § 13.19. Функциональное уравнение для марковского процесса
- Глава 14. ПОСЛЕДОВАТЕЛЬНОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
- § 14.2. Марковские процессы решения с конечным числом шагов
- § 14.3. Марковские процессы решения с бесконечным числом шагов
- § 14.4. Некоторые задачи о пари
- § 14.5. Задачи о «двуруком бандите»
- § 14.6. Задачи о «двуруком бандите» с известным значением одного из параметров
- § 14.7. Задачи о «двуруком бандите» в случае зависимых параметров
- § 14.8. Задачи оптимального управления запасами
- § 14.9. Задачи управления запасами с бесконечным числом шагов
- § 14.10. Задачи управления
- § 14.11. Оптимальное управление в случае, когда процесс наблюдается с ошибками
- § 14.12. Многомерные задачи управления
- § 14.13. Задачи управления с погрешностями, вносимыми статистиком
- § 14.14. Задачи поиска
- § 14.15. Задачи поиска с равными стоимостями
- § 14.16. Функции неопределенности и задачи статистического решения
- § 14.17. Достаточные эксперименты
- § 14.18. Примеры достаточных экспериментов
- СПИСОК ЛИТЕРАТУРЫ