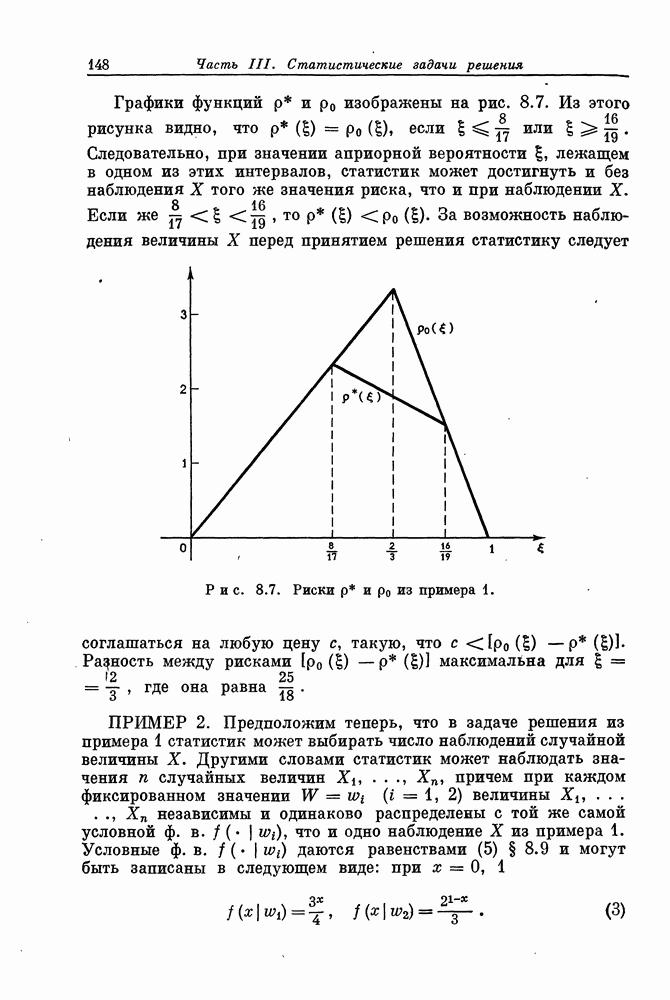
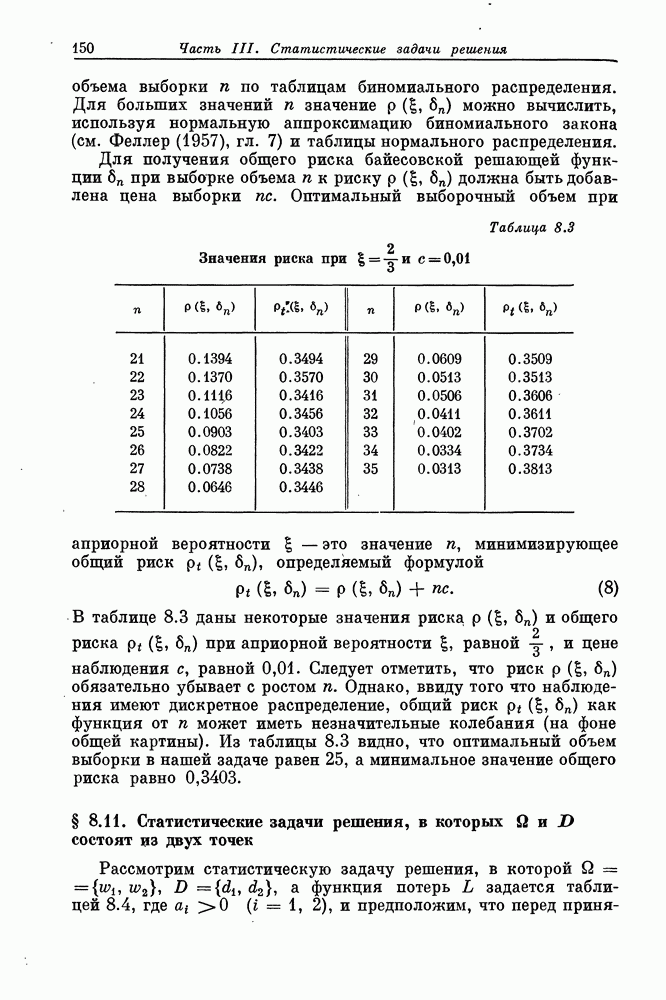
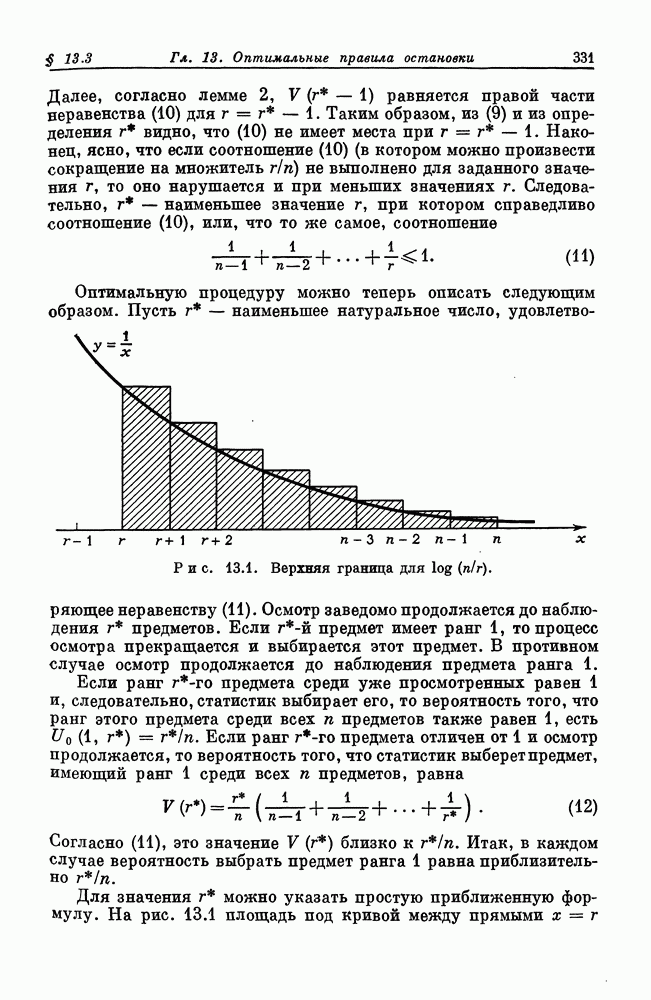
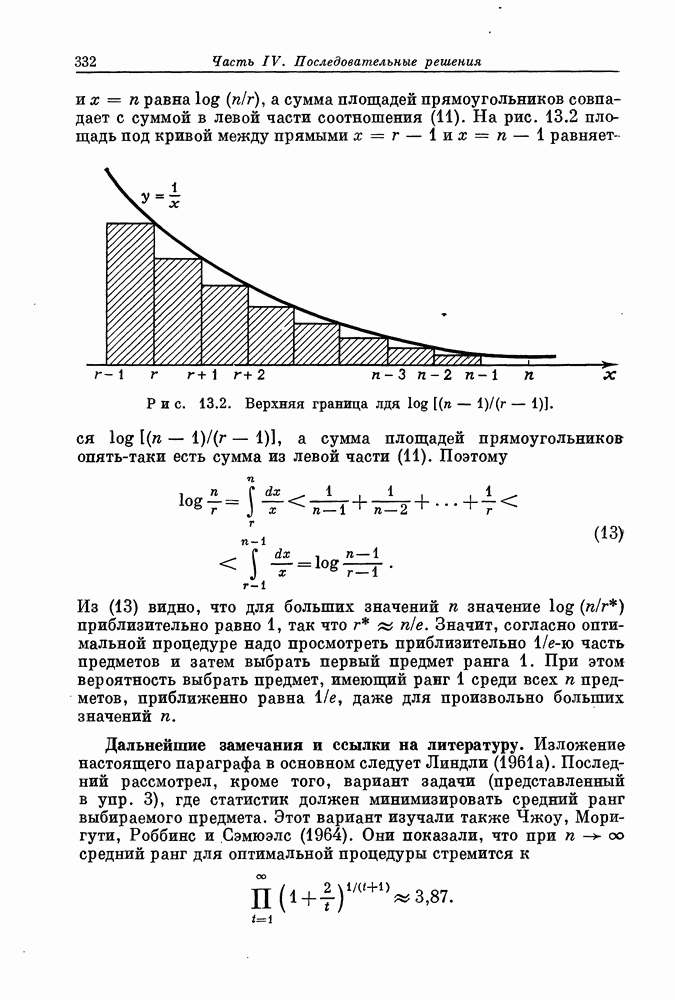
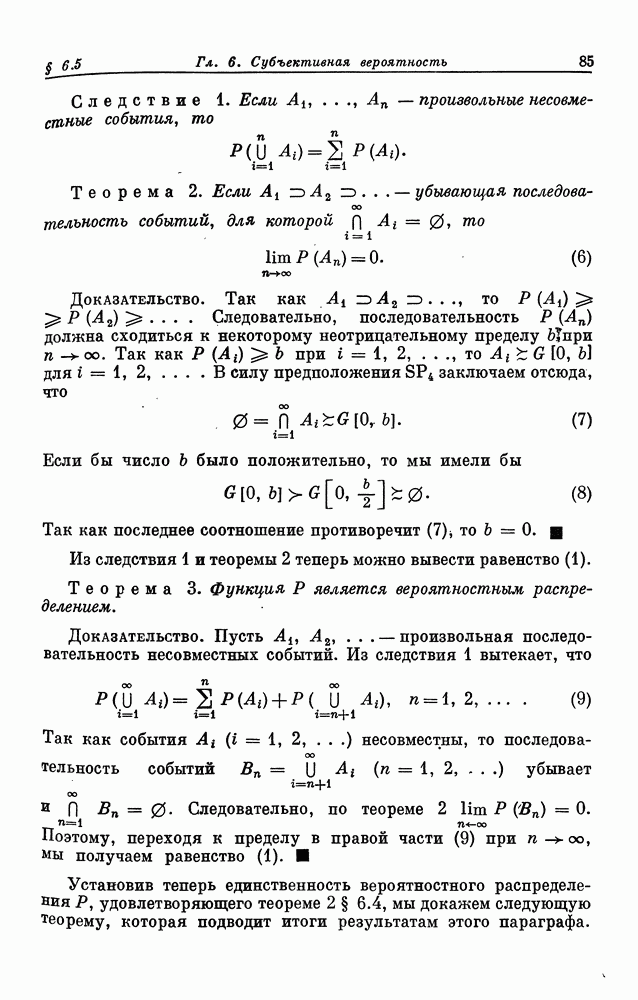| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 10. ПРЕДЕЛЬНЫЕ АПОСТЕРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
§ 10.1. Несобственные априорные распределения
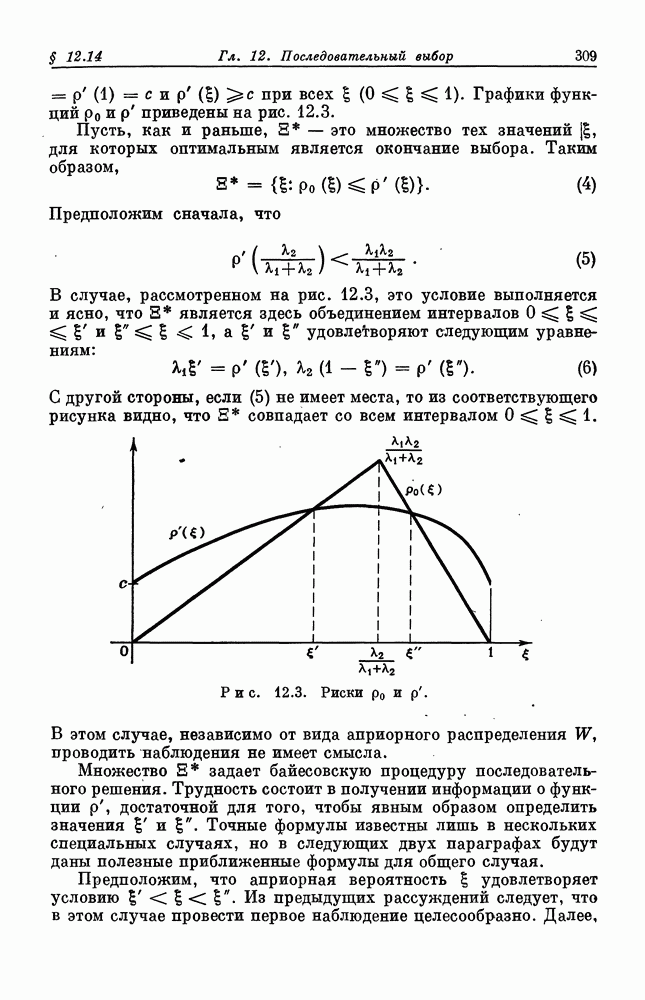
В ряде задач априорная информация статистика о некотором параметре  является совсем незначительной и неопределенной по сравнению с тем, что он предполагает узнать о
является совсем незначительной и неопределенной по сравнению с тем, что он предполагает узнать о  из доступных ему наблюдений. В таких задачах, даже если статистик и может найти подходящее сопряженное семейство распределений
из доступных ему наблюдений. В таких задачах, даже если статистик и может найти подходящее сопряженное семейство распределений  выбрать из него подходящее априорное распределение может оставаться делом отнюдь не легким. В силу неопределенности априорной информации по сравнению с информацией, которой он будет скоро располагать после наблюдений, статистику не стоит тратить много времени и сил на поиски наилучшего в данной ситуации априорного распределения. Вместо этого удобно использовать некоторое стандартное априорное распределение, которое было бы употребительным сразу во многих ситуациях, где априорная информация достаточно неопределенна.
выбрать из него подходящее априорное распределение может оставаться делом отнюдь не легким. В силу неопределенности априорной информации по сравнению с информацией, которой он будет скоро располагать после наблюдений, статистику не стоит тратить много времени и сил на поиски наилучшего в данной ситуации априорного распределения. Вместо этого удобно использовать некоторое стандартное априорное распределение, которое было бы употребительным сразу во многих ситуациях, где априорная информация достаточно неопределенна.
Часто в качестве такого стандартного априорного распределения выбирается несобственное распределение, задаваемое неотрицательной плотностью, интеграл от которой по всему параметрическому пространству и бесконечен (в то время как для всякого собственного вероятностного распределения этот интеграл равен единице). Например, если  это вещественная прямая и из-за незначительности информации априорная п. р. в. W весьма сильно «размазана» по всей прямой, то статистик может счесть удобным выбрать для своего априорного распределения плотность, постоянную на всей прямой. Такая равномерная плотность не является п. р. в. никакого собственного вероятностного распределения на вещественной прямой. Однако часто статистик может получить апостериорное распределение, являющееся уже собственным, выбирая в качестве априорной равномерную плотность и проводя формально все вычисления по теореме Байеса с некоторыми наблюдениями
это вещественная прямая и из-за незначительности информации априорная п. р. в. W весьма сильно «размазана» по всей прямой, то статистик может счесть удобным выбрать для своего априорного распределения плотность, постоянную на всей прямой. Такая равномерная плотность не является п. р. в. никакого собственного вероятностного распределения на вещественной прямой. Однако часто статистик может получить апостериорное распределение, являющееся уже собственным, выбирая в качестве априорной равномерную плотность и проводя формально все вычисления по теореме Байеса с некоторыми наблюдениями  Таким образом, если
Таким образом, если  функция правдоподобия для этих наблюдений и
функция правдоподобия для этих наблюдений и

то апостериорная п. р. в.  параметра
параметра  удовле творяет соотношению
удовле творяет соотношению

В качестве иллюстрации соотношения (2) предположим, что  повторная выборка из нормального распределения с неизвестным значением среднего
повторная выборка из нормального распределения с неизвестным значением среднего  и заданной мерой точности
и заданной мерой точности  Если априорное распределение для
Если априорное распределение для  определяется равномерной плотностью на вещественной прямой, то из соотношения (4) § 9.5 следует, что
определяется равномерной плотностью на вещественной прямой, то из соотношения (4) § 9.5 следует, что

Поэтому апостериорное распределение  при
при  является нормальным со средним х и мерой точности
является нормальным со средним х и мерой точности  Хотя априорное распределение — несобственное, апостериорное будет обычным нормальным распределением, если сделано хотя бы одно наблюдение.
Хотя априорное распределение — несобственное, апостериорное будет обычным нормальным распределением, если сделано хотя бы одно наблюдение.
Другой возможный способ действий в условиях априорной неопределенности заключается в том, что используют собственные априорные распределения  из некоторого подходящего сопряженного семейства, заиндексированного параметром а, вычисляют апостериорные распределения по наблюденным значениям
из некоторого подходящего сопряженного семейства, заиндексированного параметром а, вычисляют апостериорные распределения по наблюденным значениям  и затем находят предельное апостериорное распределение при стремлении параметра а к некоторому предельному значению. Часто это предельное апостериорное распределение параметра
и затем находят предельное апостериорное распределение при стремлении параметра а к некоторому предельному значению. Часто это предельное апостериорное распределение параметра  оказывается собственным вероятностным распределением, даже если оно не отвечает никакому собственному априорному распределению.
оказывается собственным вероятностным распределением, даже если оно не отвечает никакому собственному априорному распределению.
В качестве примера применения предельных апостериорных распределений рассмотрим опять-таки задачу выбора из нормальной совокупности с неизвестным значением среднего  и заданной мерой точности
и заданной мерой точности  Сопряженное семейство распределений для этой задачи было описано в теореме 1 § 9.5. Если в апостериорном нормальном распределении
Сопряженное семейство распределений для этой задачи было описано в теореме 1 § 9.5. Если в апостериорном нормальном распределении  указанном в этой теореме,
указанном в этой теореме,  то предельным распределением будет нормальное со средним х и мерой точности
то предельным распределением будет нормальное со средним х и мерой точности  Это распределение может служить в качестве апостериорного для
Это распределение может служить в качестве апостериорного для  но его нельзя получить ни из какого собственного априорного распределения. В этом примере предельное апостериорное распределение совпадает с апостериорным распределением (3), которое мы получили исходя из несобственной равномерной априорной плотности для
но его нельзя получить ни из какого собственного априорного распределения. В этом примере предельное апостериорное распределение совпадает с апостериорным распределением (3), которое мы получили исходя из несобственной равномерной априорной плотности для  Это совпадение результатов можно было ожидать: если в априорном нормальном распределении
Это совпадение результатов можно было ожидать: если в априорном нормальном распределении  мера точности
мера точности  то дисперсия становится все больше и больше и распределение все более «размазывается» по всей прямой.
то дисперсия становится все больше и больше и распределение все более «размазывается» по всей прямой.
Апостериорное распределение (3) обладает некоторыми интересными свойствами. Пусть случайная величина  определена соотношением
определена соотношением

Тогда для рассматриваемого апостериорного распределения  условное распределение
условное распределение  при каждом фиксированном значении х величины X является стандартным нормальным (т. е. нормальным распределением со средним 0 и мерой точности 1). Поскольку условное распределение
при каждом фиксированном значении х величины X является стандартным нормальным (т. е. нормальным распределением со средним 0 и мерой точности 1). Поскольку условное распределение  одинаково для всех значений X, случайные величины
одинаково для всех значений X, случайные величины  независимы. Далее, обычная теория выбора из нормального распределения, изложенная в § 4.7, показывает, что условное распределение
независимы. Далее, обычная теория выбора из нормального распределения, изложенная в § 4.7, показывает, что условное распределение  при заданном значении
при заданном значении  параметра
параметра  также является стандартным нормальным. Поэтому независимы и величины
также является стандартным нормальным. Поэтому независимы и величины 
Строго говоря, два предыдущих заключения несовместимы. Для любого собственного двумерного распределения  при котором случайные величины
при котором случайные величины  независимы, случайные величины
независимы, случайные величины  зависимы, если только случайная величина
зависимы, если только случайная величина  не равна с вероятностью 1 постоянной (см. упр. 1). Случайная величина
не равна с вероятностью 1 постоянной (см. упр. 1). Случайная величина  не равна здесь постоянной потому, что мы использовали несобственное априорное распределение. Эти замечания показывают, что статистик должен быть чрезвычайно осторожен при обращении с несобственными распределениями.
не равна здесь постоянной потому, что мы использовали несобственное априорное распределение. Эти замечания показывают, что статистик должен быть чрезвычайно осторожен при обращении с несобственными распределениями.
Доверительные интервалы. Мы уже отмечали, что условное распределение  при любом заданном значении X совпадает с условным распределением
при любом заданном значении X совпадает с условным распределением  при всяком фиксированном значении
при всяком фиксированном значении  Вследствие этого выводы о
Вследствие этого выводы о  основанные на апостериорном распределении, вообще говоря, согласуются с выводами
основанные на апостериорном распределении, вообще говоря, согласуются с выводами  основанными на обычном методе доверительных интервалов. Этот метод можно описать следующим образом.
основанными на обычном методе доверительных интервалов. Этот метод можно описать следующим образом.
Пусть  случайные величины, такие, что для всякого значения
случайные величины, такие, что для всякого значения  выполнено соотношение
выполнено соотношение

где  — фиксированное число
— фиксированное число  Тогда при наблюдениях
Тогда при наблюдениях  можно рассмотреть следующий интервал для
можно рассмотреть следующий интервал для 

Этот интервал называется доверительным интервалом для  а число у называется доверительным коэффициентом этого интервала.
а число у называется доверительным коэффициентом этого интервала.
Для любого  обозначим через
обозначим через  такое число, что
такое число, что

где  стандартного нормального закона. Из полученного ранее вида условного распределения
стандартного нормального закона. Из полученного ранее вида условного распределения  следует, что доверительный интервал для
следует, что доверительный интервал для  с доверительным коэффициентом у
с доверительным коэффициентом у
может быть определен соотношением

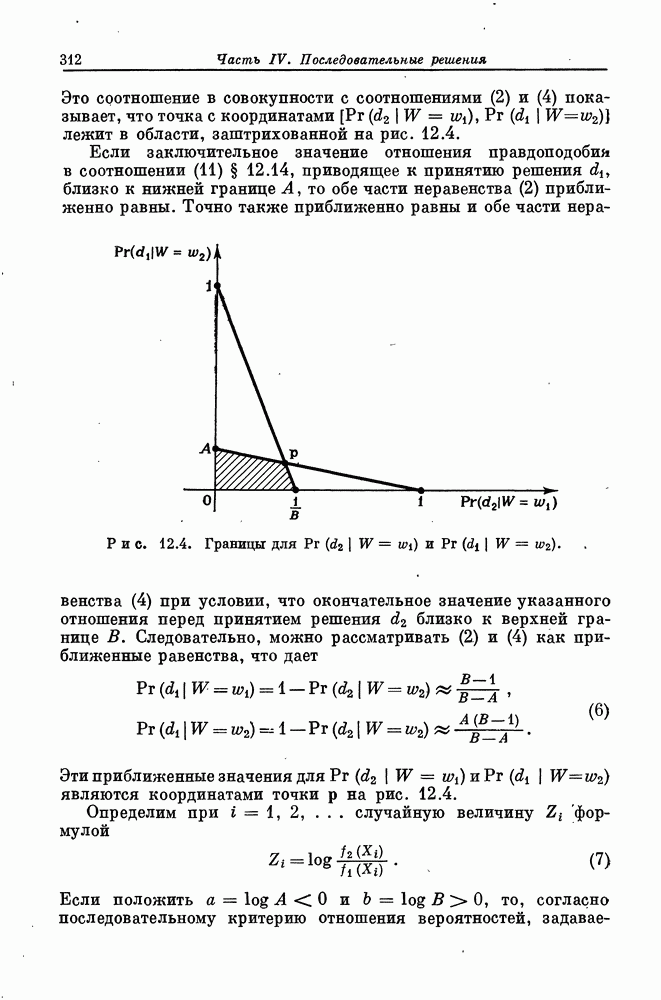
Но при указанном апостериорном распределении  вероятность того, что
вероятность того, что  лежит в интервале (8), равна у. Поэтому, согласно обычной теории, доверительный коэффициент этого интервала равен 7, а согласно байесовской или субъективистской теории, вероятность попадания в этот интервал равна 7. Поскольку оперативная интерпретация этих двух свойств по существу одна и та же, то, как уже отмечалось, выводы
лежит в интервале (8), равна у. Поэтому, согласно обычной теории, доверительный коэффициент этого интервала равен 7, а согласно байесовской или субъективистской теории, вероятность попадания в этот интервал равна 7. Поскольку оперативная интерпретация этих двух свойств по существу одна и та же, то, как уже отмечалось, выводы  основывающиеся на указанных двух, точках зрения, вообще говоря, совпадают.
основывающиеся на указанных двух, точках зрения, вообще говоря, совпадают.
Дальнейшие замечания и ссылки на литературу. Несобственные априорные распределения играют важную роль в статистических методах, развитых Джеффрисом (1961) и Линдли (1965). В последующих двух параграфах этой главы мы будем рассматривать апостериорные распределения, либо получающиеся из несобственных априорных распределений, либо являющиеся предельными в задачах выбора из одномерного или многомерного нормального распределения. Задачи с выборками из других совокупностей будут рассмотрены в упражнениях в конце главы.
Мы покажем, что во многих задачах, в которых апостериорное распределение параметра получается указанным образом, доверительные интервалы — или, в случае больших размерностей, доверительные множества — с заданным доверительным коэффициентом 7 являются интервалами или множествами, имеющими апостериорную вероятность 7.
Трудности представления неполной априорной информации о векторе  высоких размерностей и другие аспекты использования несобственных распределений обсуждаются в работах Стейна (1962а, 1965).
высоких размерностей и другие аспекты использования несобственных распределений обсуждаются в работах Стейна (1962а, 1965).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- Глава 2. ЭКСПЕРИМЕНТЫ, ВЫБОРОЧНЫЕ ПРОСТРАНСТВА И ВЕРОЯТНОСТЬ
- § 2.1. Эксперименты и выборочные пространства
- § 2.2. Теория множеств
- § 2.3. События и вероятность
- § 2.4. Условная вероятность
- § 2.5. Биномиальные коэффициенты
- Глава 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, СЛУЧАЙНЫЕ ВЕКТОРЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- § 3.1. Случайные величины и их распределения
- § 3.2. Многомерные распределения
- § 3.3. Суммы и интегралы
- § 3.4. Маргинальные распределения и независимость
- § 3.5. Векторы и матрицы
- § 3.6. Математические ожидания, моменты и характеристические функции
- § 3.7. Преобразования случайных величин
- § 3.8. Условные распределения
- Глава 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 4.2. Распределение Бернулли
- § 4.3. Биномиальное распределение
- § 4.4. Распределение Пуассона
- § 4.5. Отрицательное биномиальное распределение
- § 4.6. Гипергеометрическое распределение
- § 4.7. Нормальное распределение
- § 4.8. Гамма-распределение
- § 4.9. Бета-распределение
- § 4.10. Равномерное распределение
- § 4.11. Распределение Парето
- § 4.12. Распределение Стьюдента
- Глава 5. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 5.2. Мультиномиальное распределение
- § 5.3. Распределение Дирихле
- § 5.4. Многомерное нормальное распределение
- § 5.5. Распределение Уишарта
- § 5.6. Многомерное t-распределение
- § 5.7. Двустороннее двумерное распределение Парето
- ЧАСТЬ II. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ И ПОЛЕЗНОСТЬ
- Глава 6. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ
- § 6.2. Относительное правдоподобие
- § 6.3. Вспомогательный эксперимент
- § 6.4. Построение вероятностного распределения
- § 6.5. Проверка выполнения свойств вероятностного распределения
- § 6.6. Условные правдоподобия
- Глава 7. ПОЛЕЗНОСТЬ
- § 7.2. Предпочтения в множестве вероятностных распределений
- § 7.3. Определение функции полезности
- § 7.4. Некоторые свойства функций полезности
- § 7.5. Полезность в случае денежных доходов
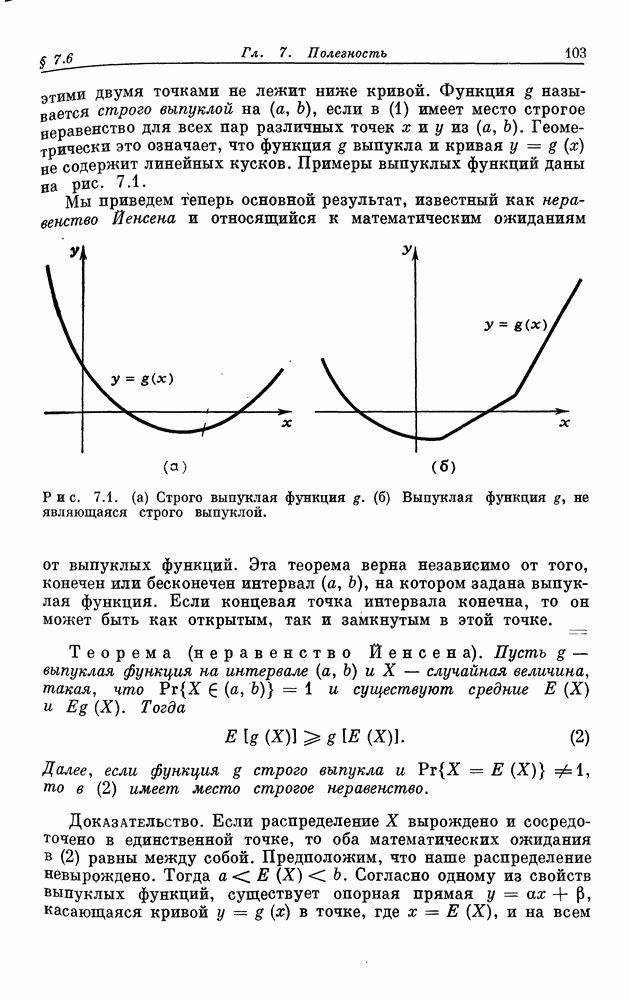
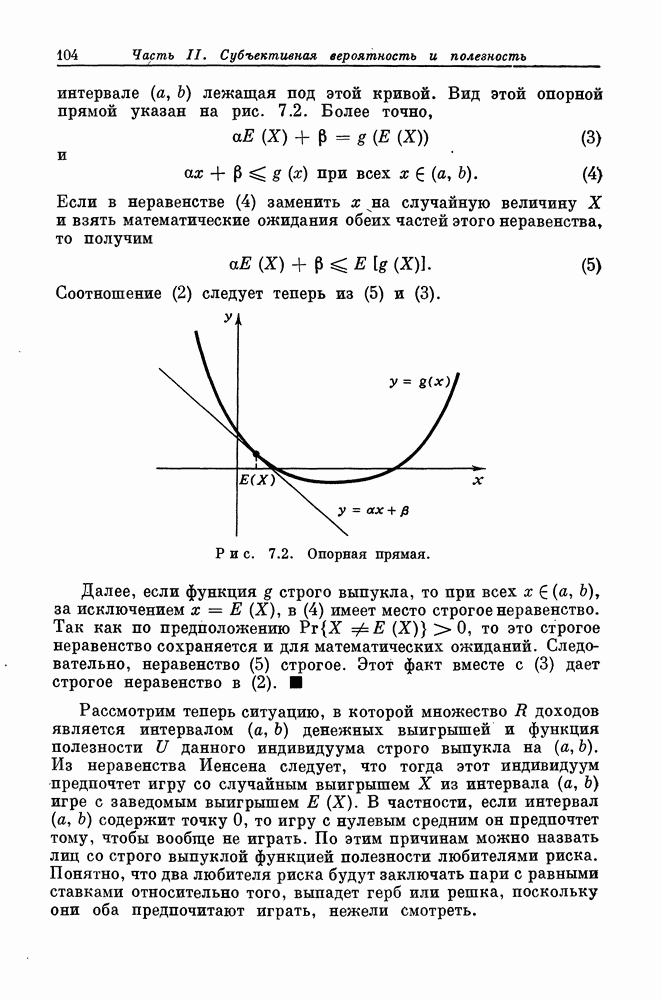
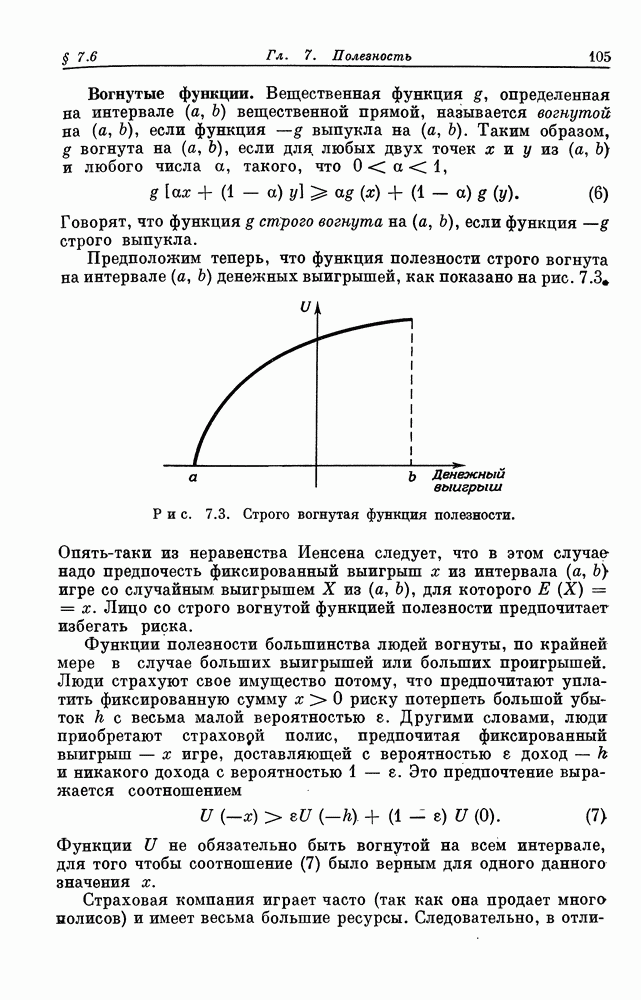
- § 7.6. Выпуклые и вогнутые функции полезности
- § 7.7. Аксиоматический подход к полезности
- § 7.8. Построение функции полезности
- § 7.9. Проверка свойств функции полезности
- § 7.10. Распространение свойств функции полезности на класс
- ЧАСТЬ III. СТАТИСТИЧЕСКИЕ ЗАДАЧИ РЕШЕНИЯ
- § 8.2. Байесовский риск и байесовские решения
- § 8.3. Неотрицательные функции потерь
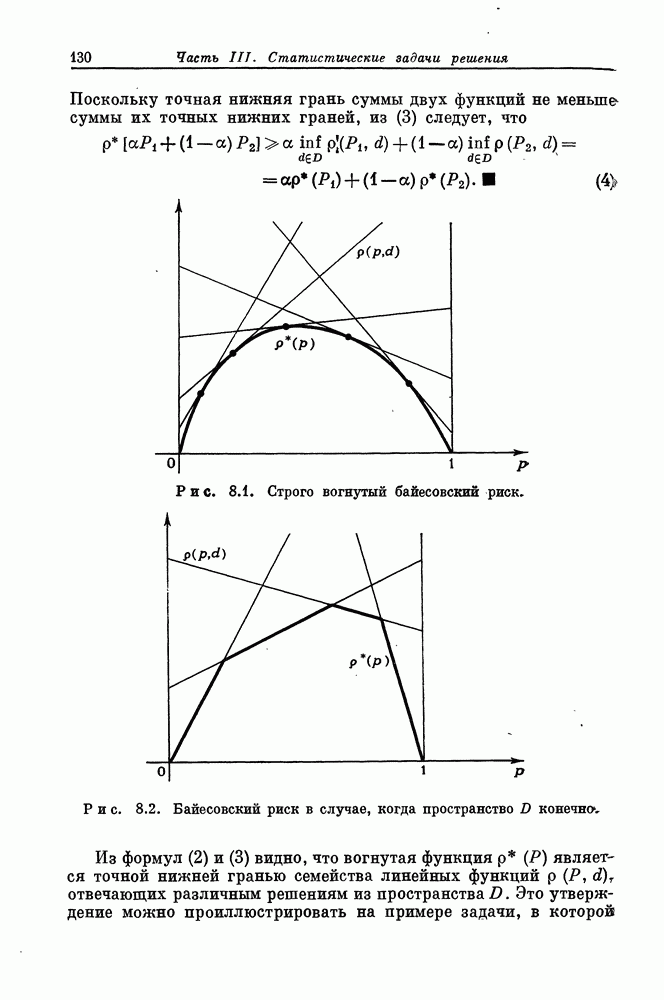
- § 8.4. Вогнутость байесовского риска
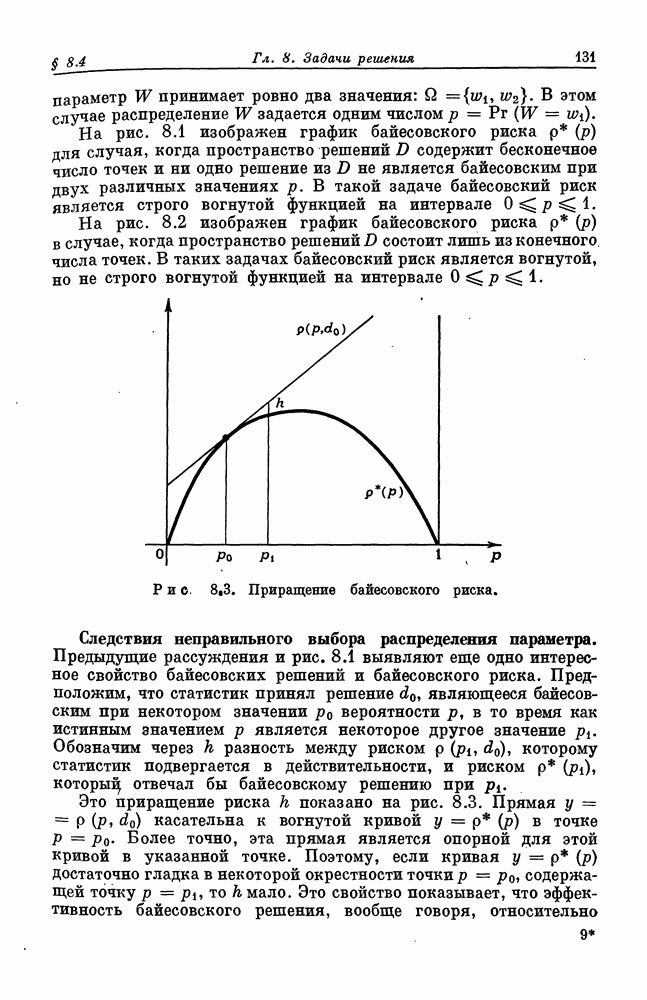
- § 8.5. Рандомизация и смешанные решения
- § 8.6. Выпуклые множества
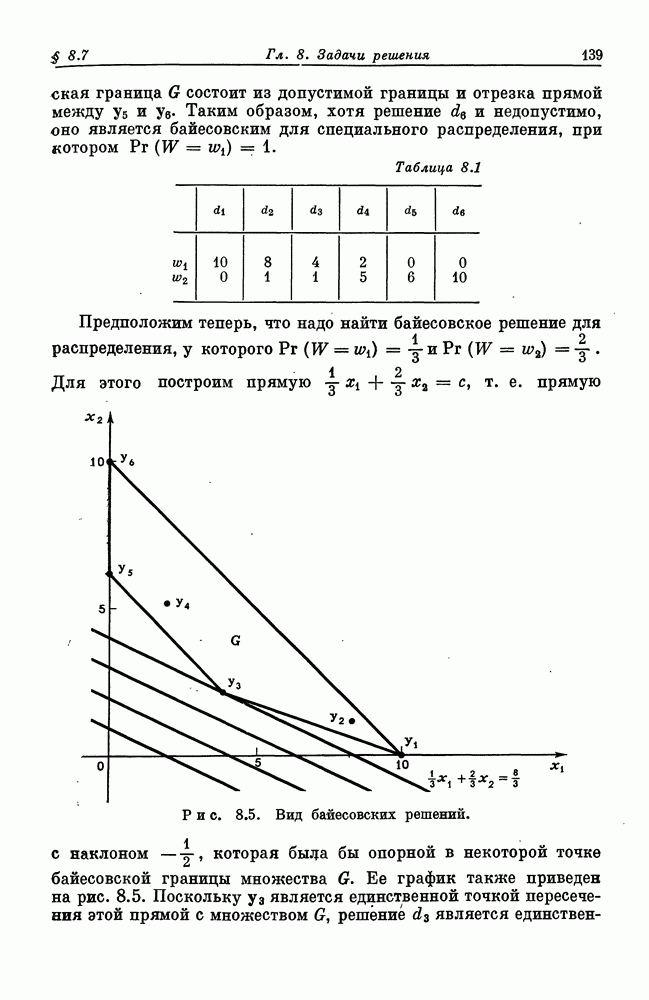
- § 8.7. Задачи решения с конечными …
- § 8.8. Задачи решения с наблюдениями
- § 8.9. Построение байесовских решающих функций
- § 8.10. Цена наблюдения
- § 8.11. Статистические задачи решения, в которых … состоят из двух точек
- § 8.12. Вычисление апостериорного распределения в случае, когда наблюдения производятся в несколько этапов
- Глава 9. СОПРЯЖЕННЫЕ АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 9.1. Достаточные статистики
- § 9.2. Сопряженные семейства распределений
- § 9.3. Построение сопряженного семейства
- § 9.4. Сопряженные семейства для выборок из различных стандартных распределений
- § 9.5. Сопряженные семейства для выборок из нормального распределения
- § 9.6. Выборка из нормального распределения с неизвестным средним и неизвестной мерой точности
- § 9.7. Выборка из равномерного распределения
- § 9.8. Сопряженное семейство для мультиномиальных наблюдений
- § 9.9. Сопряженные семейства для выборок из многомерного нормального распределения
- § 9.10. Многомерное нормальное распределение с неизвестным вектором средних и неизвестной матрицей точности
- § 9.11. Маргинальное распределение вектора средних
- § 9.12. Распределение коэффициента корреляции
- § 9.13. Матрицы точности с неизвестным множителем
- Глава 10. ПРЕДЕЛЬНЫЕ АПОСТЕРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 10.1. Несобственные априорные распределения
- § 10.2. Несобственные априорные распределения для выборок из нормального распределения
- § 10.3. Несобственные априорные распределения для выборок из многомерного нормального распределения
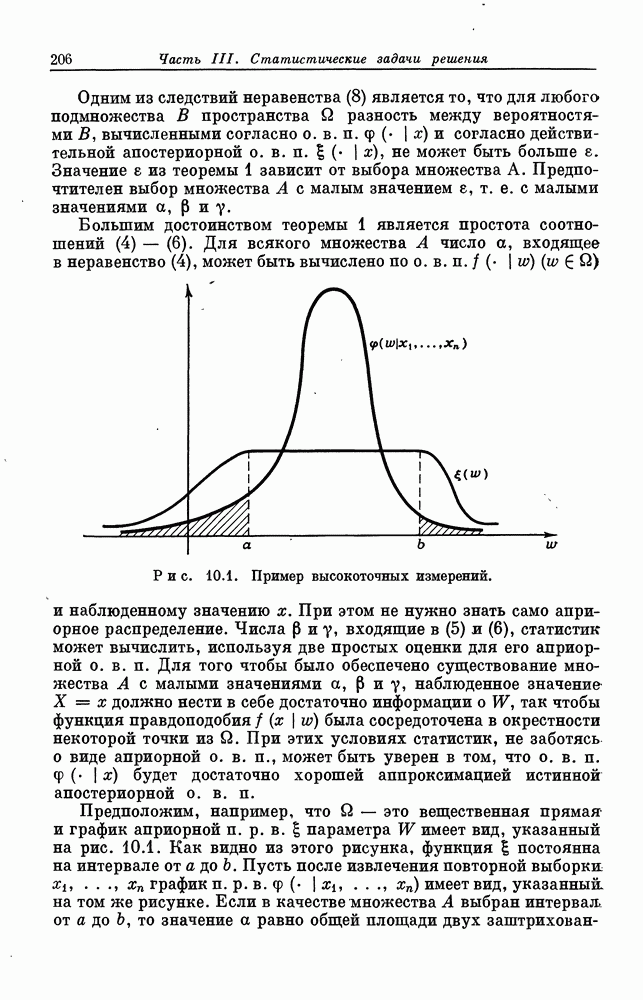
- § 10.4. Высокоточные измерения
- § 10.5. Сходимость апостериорных распределений
- § 10.6. Супер непрерывность
- § 10.7. Решения уравнения правдоподобия
- § 10.8. Сходимость супернепрерывных функций
- § 10.9. Предельные свойства функции правдоподобия
- § 10.10. Нормальная аппроксимация апостериорного распределения
- § 10.11. Аппроксимации в случае векторных параметров
- § 10.12. Апостериорные отношения
- Глава 11. ОЦЕНИВАНИЕ, ПРОВЕРКА ГИПОТЕЗ И ЛИНЕЙНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ
- § 11.2. Квадратическая функция потерь
- § 11.3. Ущерб пропорциональный абсолютной величине погрешности
- § 11.4. Оценивание векторного параметра
- § 11.5. Задачи проверки гипотез
- § 11.6. Проверка простой гипотезы о среднем значении нормального распределения
- § 11.7. Проверка гипотез о среднем значении нормального распределения с неизвестной мерой точности
- § 11.8. Решение вопроса о том, будет ли параметр меньше или больше предписанного значения
- § 11.9. Проверка гипотезы о том, превосходит или нет среднее нормального распределения заданное значение
- § 11.10. Линейные модели
- § 11.11. Проверка гипотез в линейных моделях
- § 11.12. Проверка гипотезы о равенстве нулю некоторых коэффициентов регрессии
- § 11.13. Дисперсионный анализ по одному признаку
- ЧАСТЬ IV. ПОСЛЕДОВАТЕЛЬНЫЕ РЕШЕНИЯ
- § 12.1. Эффект последовательного выбора
- § 12.2. Процедуры последовательного решения
- § 12.3. Риск процедуры последовательного решения
- § 12.4. Индукция назад
- § 12.5. Оптимальные ограниченные процедуры последовательного решения
- § 12.6. Примеры
- § 12.7. Неограниченные процедуры последовательного решения
- § 12.8. Регулярные процедуры последовательного решения
- § 12.9. Существование оптимальной процедуры
- § 12.10. Приближение оптимальной прцоедуры ограниченными процедурами
- § 12.11. Области продолжения и окончания выбора
- § 12.12. Функциональное уравнение
- § 12.13 Приближения и границы для байесовского риска
- § 12.14. Последовательный критерий отношения вероятностей
- § 12.15. Характеристики последовательных критериев отношения вероятностей
- § 12.16. Аппроксимации для среднего числа наблюдений
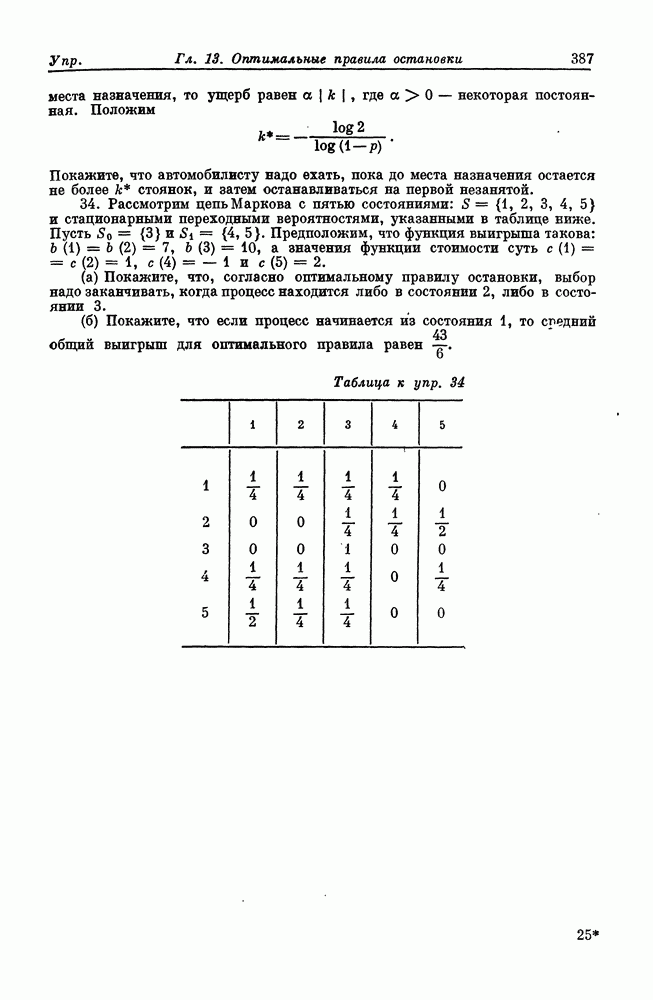
- Глава 13. ОПТИМАЛЬНЫЕ ПРАВИЛА ОСТАНОВКИ
- § 13.2. Вознаграждение статистика
- § 13.3. Выбор функции полезности
- § 13.4. Выбор с отбрасыванием
- § 13.5. Дальнейшие задачи выбора с отбрасыванием и выбора без отбрасывания
- § 13.6. Выбор с отбрасыванием из нормального распределения с неизвестным средним
- § 13.7. Выбор без отбрасывания из нормального распределения с неизвестным средним
- § 13.8. Существование оптимальных правил остановки
- § 13.9. Существование оптимальных правил остановки в задачах выбора без отбрасывания и с отбрасыванием
- § 13.10. Мартингалы
- § 13.11. Правила остановки для мартингалов
- § 13.12. Равномерно интегрируемые последовательности случайных величин
- § 13.13. Мартингалы, получаемые из сумм и произведений случайных величин
- § 13.14. Регулярные супермартингалы
- § 13.15. Супермартингалы и общие задачи об оптимальной остановке
- § 13.16. Марковские процессы
- § 13.17. Стационарные правила остановки для марковских процессов
- § 13.18. Задачи с входной платой
- § 13.19. Функциональное уравнение для марковского процесса
- Глава 14. ПОСЛЕДОВАТЕЛЬНОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
- § 14.2. Марковские процессы решения с конечным числом шагов
- § 14.3. Марковские процессы решения с бесконечным числом шагов
- § 14.4. Некоторые задачи о пари
- § 14.5. Задачи о «двуруком бандите»
- § 14.6. Задачи о «двуруком бандите» с известным значением одного из параметров
- § 14.7. Задачи о «двуруком бандите» в случае зависимых параметров
- § 14.8. Задачи оптимального управления запасами
- § 14.9. Задачи управления запасами с бесконечным числом шагов
- § 14.10. Задачи управления
- § 14.11. Оптимальное управление в случае, когда процесс наблюдается с ошибками
- § 14.12. Многомерные задачи управления
- § 14.13. Задачи управления с погрешностями, вносимыми статистиком
- § 14.14. Задачи поиска
- § 14.15. Задачи поиска с равными стоимостями
- § 14.16. Функции неопределенности и задачи статистического решения
- § 14.17. Достаточные эксперименты
- § 14.18. Примеры достаточных экспериментов
- СПИСОК ЛИТЕРАТУРЫ