| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ЧАСТЬ I. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Глава 1 ВВЕДЕНИЕ
Статистика как наука занимается теориями и методами, используемыми для принятия решений в условиях неопределенности и неполной информации, которые неизбежны в самых широких сферах человеческой деятельности. Современная статистическая практика связана главным образом с выбором вероятностных моделей для различных физических систем, с методами сбора и анализа численных данных и с планированием эффективных и информативных экспериментов. Термин теория решений относится к классу статистических задач, в которых статистик должен получить информацию о некоторых важных параметрах, для того чтобы иметь возможность принять эффективные решения в ситуациях, где последствия его решений зависят от истинных значений этих параметров. Теория оптимальных статистических решений, развиваемая в этой книге, может быть полезна в самых различных областях и уже была с успехом применена для решения широкого круга задач. Ее обычно называют теорией субъективных или байесовских статистических решений.
В большей части книги для каждой задачи те ее аспекты, от которых зависит принятие решения, можно формализовать с помощью явного задания возможных решений, величины выигрыша или проигрыша, связанного с принятием того или иного решения, и соответствующих вероятностных распределений. Теория и методы, на которых основывается такое задание, будут обсуждены во всех подробностях. При этом большое внимание будет уделено как математическим методам описания информированности статистика и неопределенности в значениях параметров, так и методам изменения этого описания после получения добавочной информации о параметрах.
Субъективная, или байесовская, теория статистических решений применима в тех задачах, в которых неопределенность или информация относительно параметров в любой момент времени может быть задана посредством вероятностного распределения на множестве ее возможных значений. Поэтому в этой книге мы
занимаемся только теми задачами принятия решения, которые удовлетворяют следующим двум требованиям. (1) Условия задачи могут быть описаны с помощью поддающегося учету числа параметров. (2) Хотя значения этих параметров не предполагаются известными с полной точностью, однако степень неопределенности этих значений может быть описана посредством подходящего распределения вероятностей.
В связи с этими требованиями следует иметь в виду следующие два обстоятельства. Во-первых, число параметров, поддающееся учету в данной ситуации, зависит в существенной степени от текущего состояния вычислительной техники и технологии (очевидно, сегодня это число больше, чем когда бы то ни было). Во-вторых, среди статистиков и других специалистов, изучающих основания теории вероятностей, имеются значительные разногласия по поводу того, можно ли охарактеризовать неопределенность в значениях того или иного данного параметра с помощью распределения вероятностей. Одни полагают, что о таком распределении можно говорить лишь в том случае, когда явно наблюдаются относительные частоты появления исследуемых значений параметров. Другие придерживаются той точки зрения, что вероятность является логическим понятием, которое может быть соотнесено параметрам в гораздо более широком классе случаев. Более того, эти ученые считают, что в каждой такой задаче существует единственное распределение, отвечающее данному определенному параметру, которое и должно быть ему приписано. Наконец, третьи полагают, что по существу все вероятностные распределения являются субъективными и что в статистических исследованиях о значениях параметров статистик всегда может характеризовать степень своего незнания истинного значения вероятностным распределением. Существуют также различные другие мнения и разнообразные модификации трех упомянутых выше. Вот авторы некоторых известных книг, посвященных этим вопросам, в алфавитном порядке: Гуд (1950), Джеффрис (1961), Карнап (1962), Кейнс (1921), фон Мизес (1957), Нагель (1937), Рейхенбах (1949), Сэвидж (1949) и Фишер (1959).
Во всех задачах, рассматриваемых в этой книге, предполагается, что каждому параметру может быть приписано определенное вероятностное распределение. Доводы типа приводимых в гл. 6 фактически применимы к весьма широкому классу задач, решения, и эти рассуждения показывают также, как находить подходящее распределение в таких задачах. Хотя в отношении некоторых аспектов оснований теории вероятностей и статистики налицо много разногласий, разница во мнениях не простирается до того, чтобы отрицать возможность задания вероятностных распределений параметров во многих конкретных задачах, рассматриваемых здесь. Более того, существует общее согласие, что в задачах, где
параметры заведомо обладают соответствующим вероятностным распределением, в том числе во многих важных практических задачах, теория и методы принятия статистических решений, излагаемые в этой книге, являются вполне применимыми, правильными и полезными.
Поскольку современная математическая теория вероятностей является основным рабочим инструментом при развитии статистических методов, последующие четыре главы посвящены обзору тех разделов теории вероятностей, которые понадобятся нам в дальнейшем. Для того чтобы этот обзор был по возможности компактен и в то же время достаточно полон, доказательства и поясняющие обсуждения по большей части не приводятся. Читателю, которого этот краткий обзор не удовлетворит, следует обратиться к любому из стандартных учебников по. теории вероятностей или математической статистике. Вот некоторые из недавно вышедших курсов вводного плана: Бранк (1965), Линдгрен (1962), Маккорд и Морони (1964), Муд и Грейбилл (1963), Папулис (1963), Парзен (1960), Пфейффер (1965), Таккер (1968), Феллер (1964), Фримэн (1963), Харрис Б. (1966), Хогг и Крейг (1965). А вот ряд менее элементарных книг: Гнеденко (1965), Крамер (1947), Крикеберг (1965), Лоэв (1965), Рао (1965), Уилкс (1967), Феллер (1967), Фиш (1963).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- Глава 2. ЭКСПЕРИМЕНТЫ, ВЫБОРОЧНЫЕ ПРОСТРАНСТВА И ВЕРОЯТНОСТЬ
- § 2.1. Эксперименты и выборочные пространства
- § 2.2. Теория множеств
- § 2.3. События и вероятность
- § 2.4. Условная вероятность
- § 2.5. Биномиальные коэффициенты
- Глава 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, СЛУЧАЙНЫЕ ВЕКТОРЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
- § 3.1. Случайные величины и их распределения
- § 3.2. Многомерные распределения
- § 3.3. Суммы и интегралы
- § 3.4. Маргинальные распределения и независимость
- § 3.5. Векторы и матрицы
- § 3.6. Математические ожидания, моменты и характеристические функции
- § 3.7. Преобразования случайных величин
- § 3.8. Условные распределения
- Глава 4. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 4.2. Распределение Бернулли
- § 4.3. Биномиальное распределение
- § 4.4. Распределение Пуассона
- § 4.5. Отрицательное биномиальное распределение
- § 4.6. Гипергеометрическое распределение
- § 4.7. Нормальное распределение
- § 4.8. Гамма-распределение
- § 4.9. Бета-распределение
- § 4.10. Равномерное распределение
- § 4.11. Распределение Парето
- § 4.12. Распределение Стьюдента
- Глава 5. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ МНОГОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 5.2. Мультиномиальное распределение
- § 5.3. Распределение Дирихле
- § 5.4. Многомерное нормальное распределение
- § 5.5. Распределение Уишарта
- § 5.6. Многомерное t-распределение
- § 5.7. Двустороннее двумерное распределение Парето
- ЧАСТЬ II. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ И ПОЛЕЗНОСТЬ
- Глава 6. СУБЪЕКТИВНАЯ ВЕРОЯТНОСТЬ
- § 6.2. Относительное правдоподобие
- § 6.3. Вспомогательный эксперимент
- § 6.4. Построение вероятностного распределения
- § 6.5. Проверка выполнения свойств вероятностного распределения
- § 6.6. Условные правдоподобия
- Глава 7. ПОЛЕЗНОСТЬ
- § 7.2. Предпочтения в множестве вероятностных распределений
- § 7.3. Определение функции полезности
- § 7.4. Некоторые свойства функций полезности
- § 7.5. Полезность в случае денежных доходов
- § 7.6. Выпуклые и вогнутые функции полезности
- § 7.7. Аксиоматический подход к полезности
- § 7.8. Построение функции полезности
- § 7.9. Проверка свойств функции полезности
- § 7.10. Распространение свойств функции полезности на класс
- ЧАСТЬ III. СТАТИСТИЧЕСКИЕ ЗАДАЧИ РЕШЕНИЯ
- § 8.2. Байесовский риск и байесовские решения
- § 8.3. Неотрицательные функции потерь
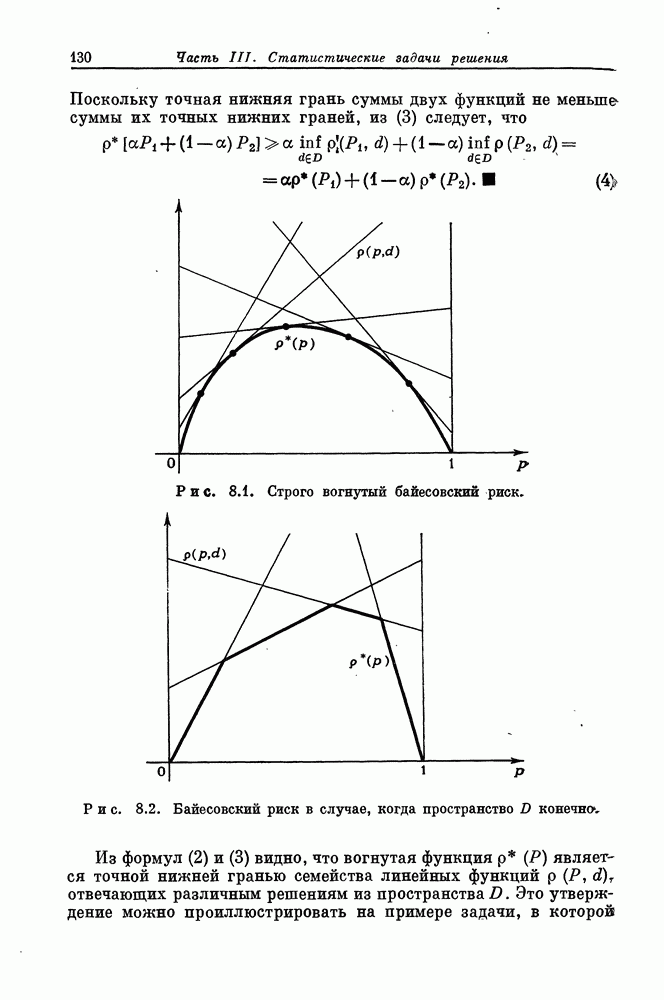
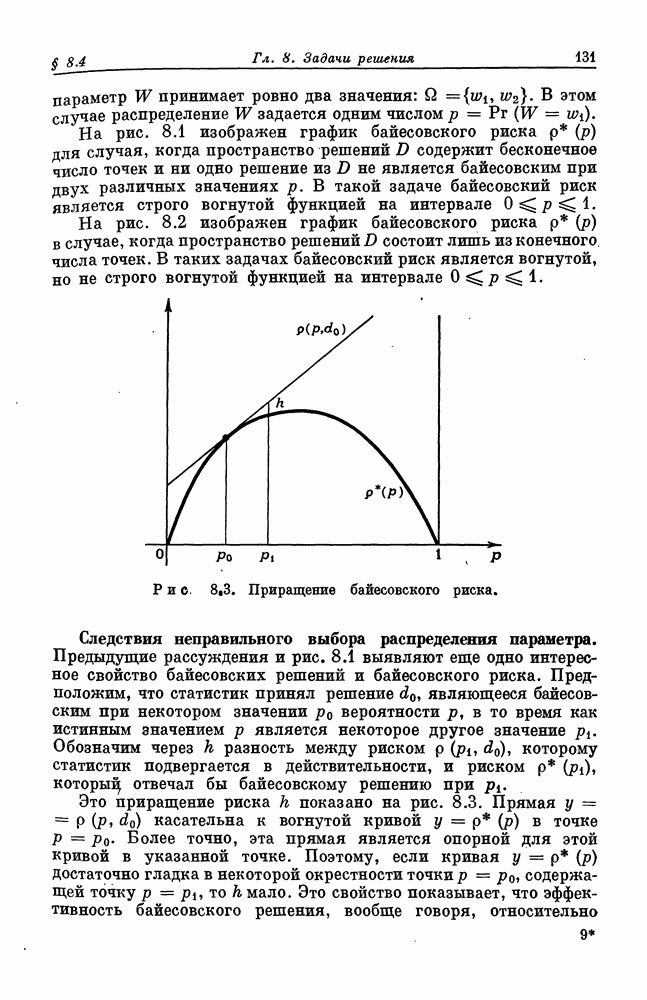
- § 8.4. Вогнутость байесовского риска
- § 8.5. Рандомизация и смешанные решения
- § 8.6. Выпуклые множества
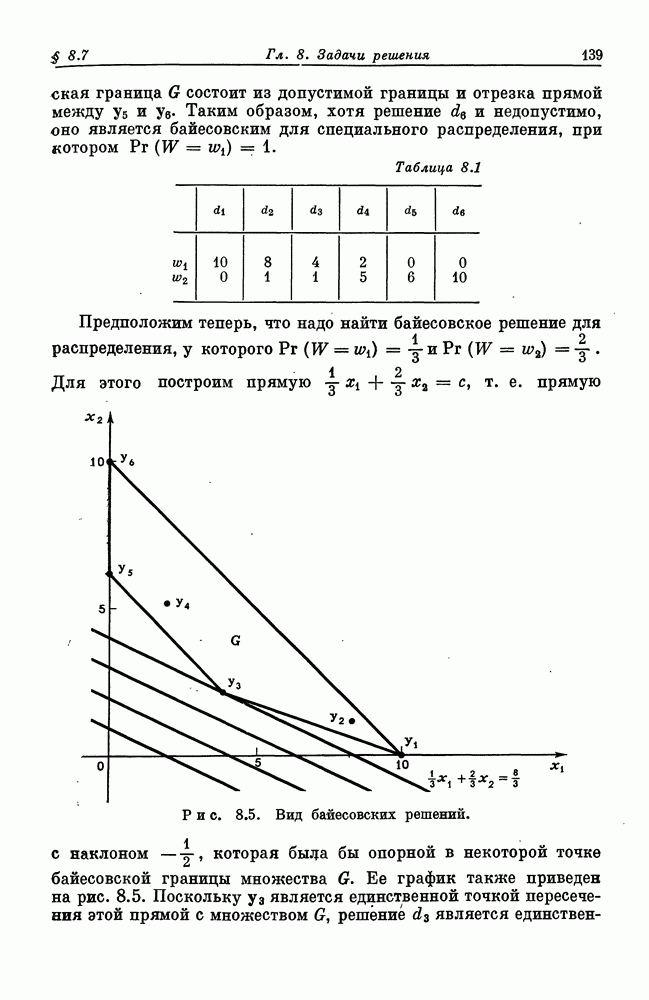
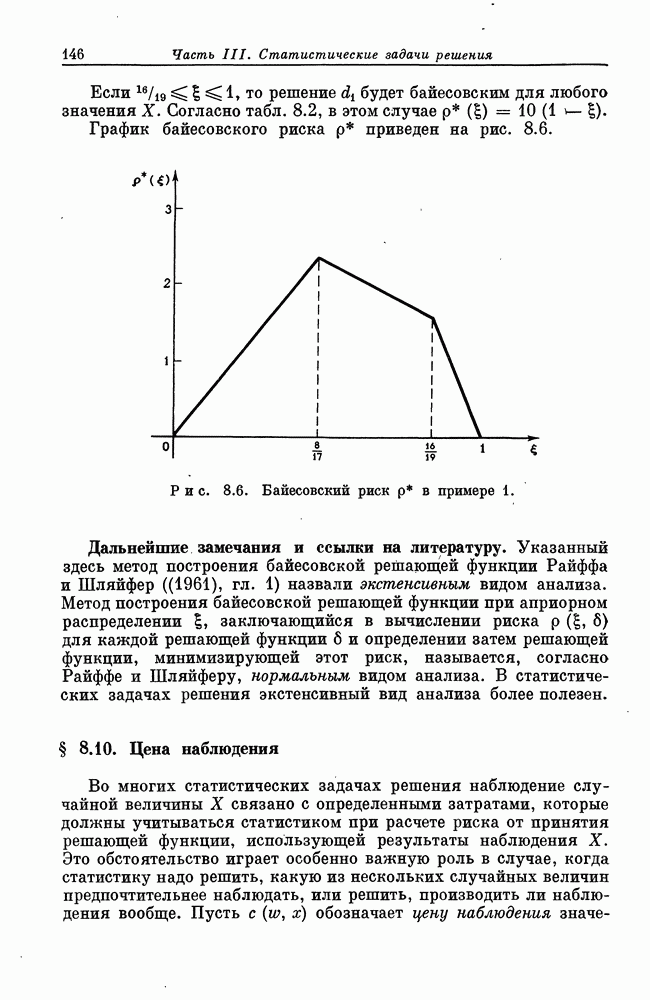
- § 8.7. Задачи решения с конечными …
- § 8.8. Задачи решения с наблюдениями
- § 8.9. Построение байесовских решающих функций
- § 8.10. Цена наблюдения
- § 8.11. Статистические задачи решения, в которых … состоят из двух точек
- § 8.12. Вычисление апостериорного распределения в случае, когда наблюдения производятся в несколько этапов
- Глава 9. СОПРЯЖЕННЫЕ АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 9.1. Достаточные статистики
- § 9.2. Сопряженные семейства распределений
- § 9.3. Построение сопряженного семейства
- § 9.4. Сопряженные семейства для выборок из различных стандартных распределений
- § 9.5. Сопряженные семейства для выборок из нормального распределения
- § 9.6. Выборка из нормального распределения с неизвестным средним и неизвестной мерой точности
- § 9.7. Выборка из равномерного распределения
- § 9.8. Сопряженное семейство для мультиномиальных наблюдений
- § 9.9. Сопряженные семейства для выборок из многомерного нормального распределения
- § 9.10. Многомерное нормальное распределение с неизвестным вектором средних и неизвестной матрицей точности
- § 9.11. Маргинальное распределение вектора средних
- § 9.12. Распределение коэффициента корреляции
- § 9.13. Матрицы точности с неизвестным множителем
- Глава 10. ПРЕДЕЛЬНЫЕ АПОСТЕРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
- § 10.1. Несобственные априорные распределения
- § 10.2. Несобственные априорные распределения для выборок из нормального распределения
- § 10.3. Несобственные априорные распределения для выборок из многомерного нормального распределения
- § 10.4. Высокоточные измерения
- § 10.5. Сходимость апостериорных распределений
- § 10.6. Супер непрерывность
- § 10.7. Решения уравнения правдоподобия
- § 10.8. Сходимость супернепрерывных функций
- § 10.9. Предельные свойства функции правдоподобия
- § 10.10. Нормальная аппроксимация апостериорного распределения
- § 10.11. Аппроксимации в случае векторных параметров
- § 10.12. Апостериорные отношения
- Глава 11. ОЦЕНИВАНИЕ, ПРОВЕРКА ГИПОТЕЗ И ЛИНЕЙНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ
- § 11.2. Квадратическая функция потерь
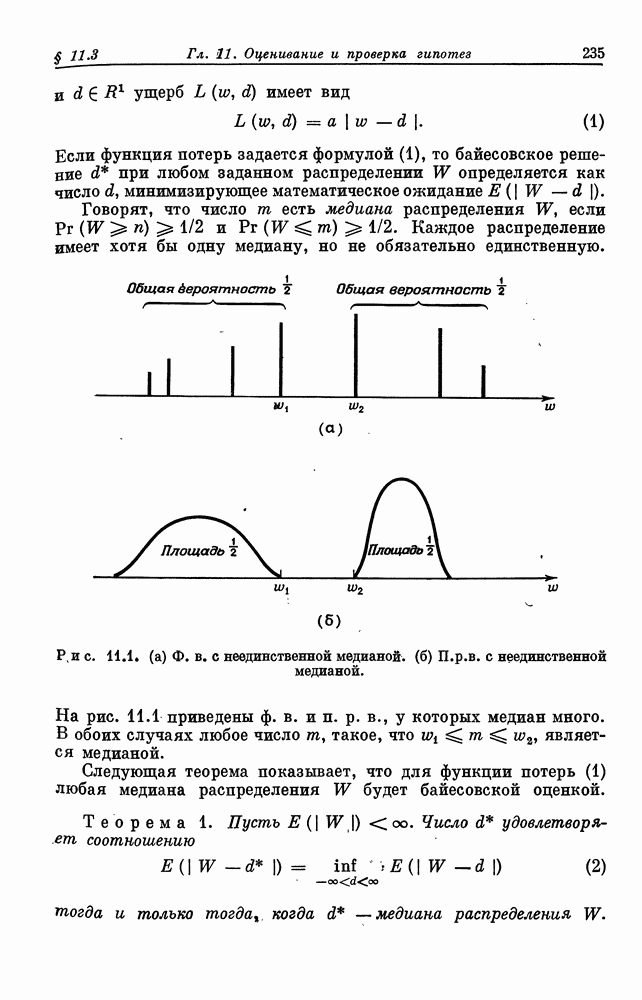
- § 11.3. Ущерб пропорциональный абсолютной величине погрешности
- § 11.4. Оценивание векторного параметра
- § 11.5. Задачи проверки гипотез
- § 11.6. Проверка простой гипотезы о среднем значении нормального распределения
- § 11.7. Проверка гипотез о среднем значении нормального распределения с неизвестной мерой точности
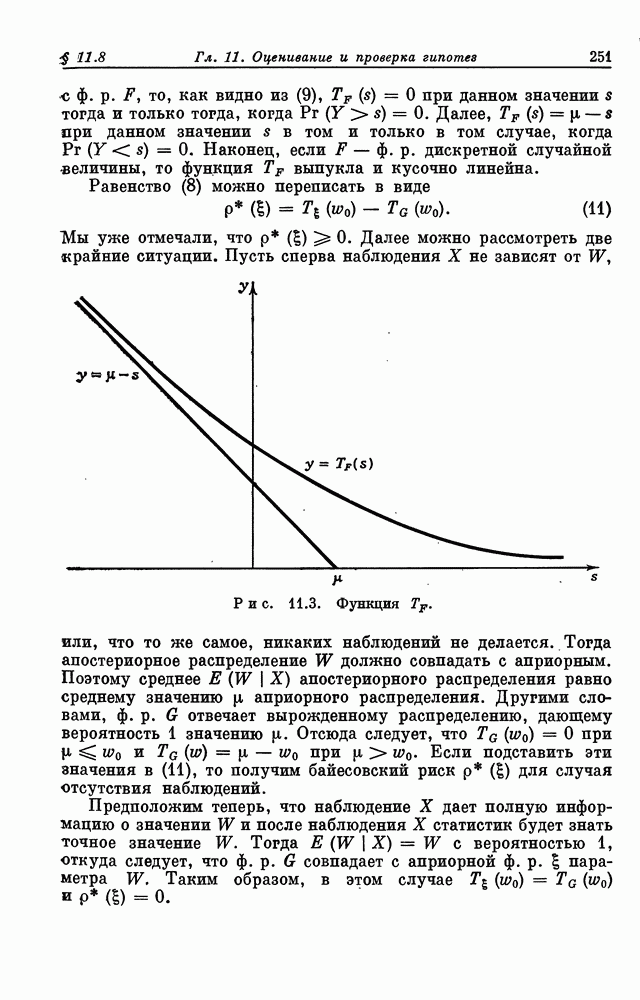
- § 11.8. Решение вопроса о том, будет ли параметр меньше или больше предписанного значения
- § 11.9. Проверка гипотезы о том, превосходит или нет среднее нормального распределения заданное значение
- § 11.10. Линейные модели
- § 11.11. Проверка гипотез в линейных моделях
- § 11.12. Проверка гипотезы о равенстве нулю некоторых коэффициентов регрессии
- § 11.13. Дисперсионный анализ по одному признаку
- ЧАСТЬ IV. ПОСЛЕДОВАТЕЛЬНЫЕ РЕШЕНИЯ
- § 12.1. Эффект последовательного выбора
- § 12.2. Процедуры последовательного решения
- § 12.3. Риск процедуры последовательного решения
- § 12.4. Индукция назад
- § 12.5. Оптимальные ограниченные процедуры последовательного решения
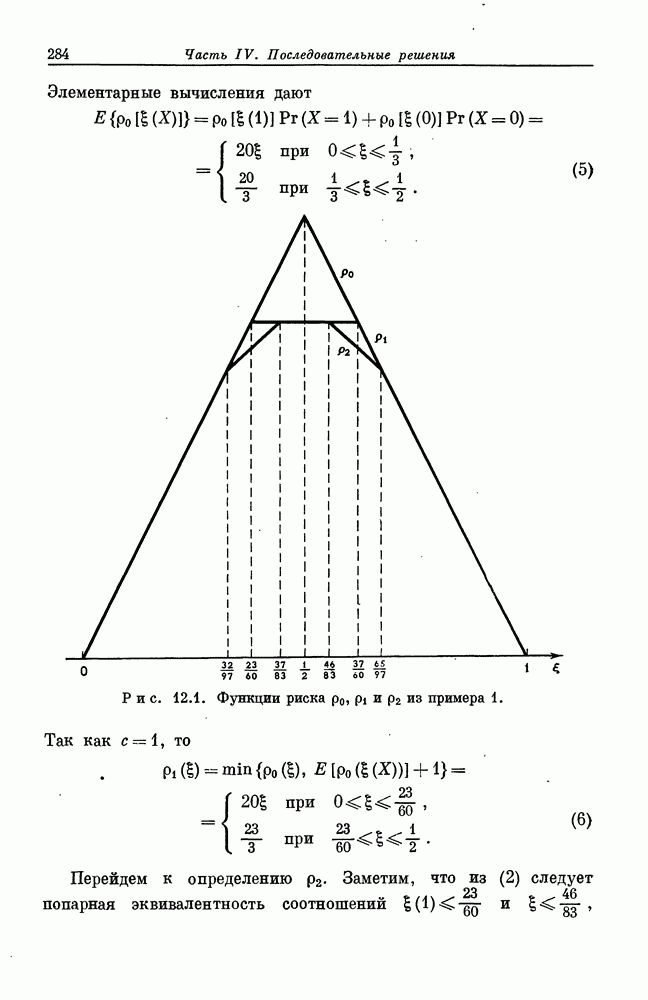
- § 12.6. Примеры
- § 12.7. Неограниченные процедуры последовательного решения
- § 12.8. Регулярные процедуры последовательного решения
- § 12.9. Существование оптимальной процедуры
- § 12.10. Приближение оптимальной прцоедуры ограниченными процедурами
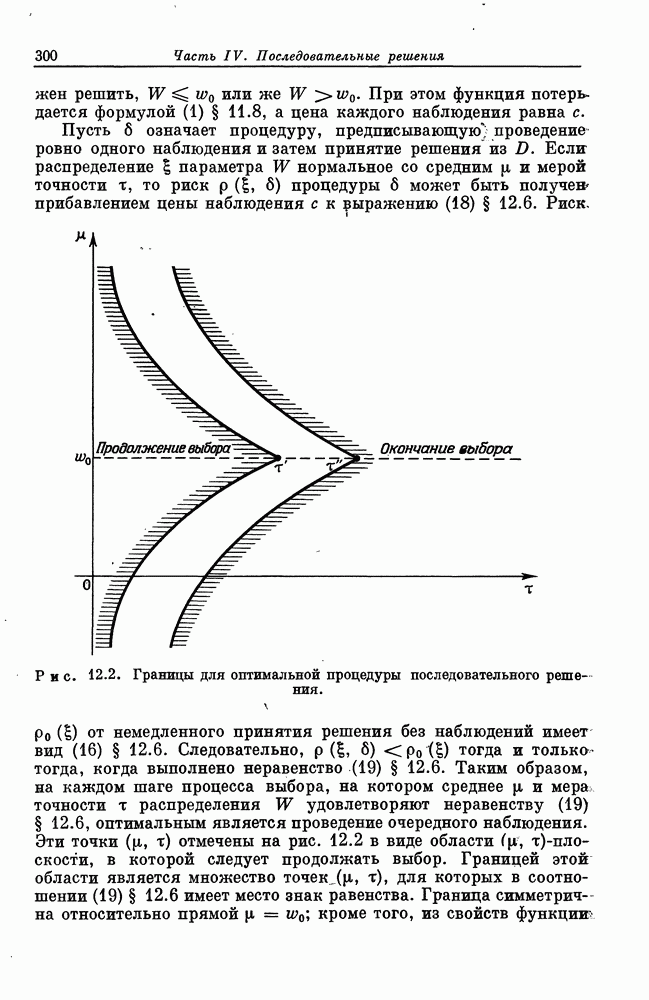
- § 12.11. Области продолжения и окончания выбора
- § 12.12. Функциональное уравнение
- § 12.13 Приближения и границы для байесовского риска
- § 12.14. Последовательный критерий отношения вероятностей
- § 12.15. Характеристики последовательных критериев отношения вероятностей
- § 12.16. Аппроксимации для среднего числа наблюдений
- Глава 13. ОПТИМАЛЬНЫЕ ПРАВИЛА ОСТАНОВКИ
- § 13.2. Вознаграждение статистика
- § 13.3. Выбор функции полезности
- § 13.4. Выбор с отбрасыванием
- § 13.5. Дальнейшие задачи выбора с отбрасыванием и выбора без отбрасывания
- § 13.6. Выбор с отбрасыванием из нормального распределения с неизвестным средним
- § 13.7. Выбор без отбрасывания из нормального распределения с неизвестным средним
- § 13.8. Существование оптимальных правил остановки
- § 13.9. Существование оптимальных правил остановки в задачах выбора без отбрасывания и с отбрасыванием
- § 13.10. Мартингалы
- § 13.11. Правила остановки для мартингалов
- § 13.12. Равномерно интегрируемые последовательности случайных величин
- § 13.13. Мартингалы, получаемые из сумм и произведений случайных величин
- § 13.14. Регулярные супермартингалы
- § 13.15. Супермартингалы и общие задачи об оптимальной остановке
- § 13.16. Марковские процессы
- § 13.17. Стационарные правила остановки для марковских процессов
- § 13.18. Задачи с входной платой
- § 13.19. Функциональное уравнение для марковского процесса
- Глава 14. ПОСЛЕДОВАТЕЛЬНОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
- § 14.2. Марковские процессы решения с конечным числом шагов
- § 14.3. Марковские процессы решения с бесконечным числом шагов
- § 14.4. Некоторые задачи о пари
- § 14.5. Задачи о «двуруком бандите»
- § 14.6. Задачи о «двуруком бандите» с известным значением одного из параметров
- § 14.7. Задачи о «двуруком бандите» в случае зависимых параметров
- § 14.8. Задачи оптимального управления запасами
- § 14.9. Задачи управления запасами с бесконечным числом шагов
- § 14.10. Задачи управления
- § 14.11. Оптимальное управление в случае, когда процесс наблюдается с ошибками
- § 14.12. Многомерные задачи управления
- § 14.13. Задачи управления с погрешностями, вносимыми статистиком
- § 14.14. Задачи поиска
- § 14.15. Задачи поиска с равными стоимостями
- § 14.16. Функции неопределенности и задачи статистического решения
- § 14.17. Достаточные эксперименты
- § 14.18. Примеры достаточных экспериментов
- СПИСОК ЛИТЕРАТУРЫ