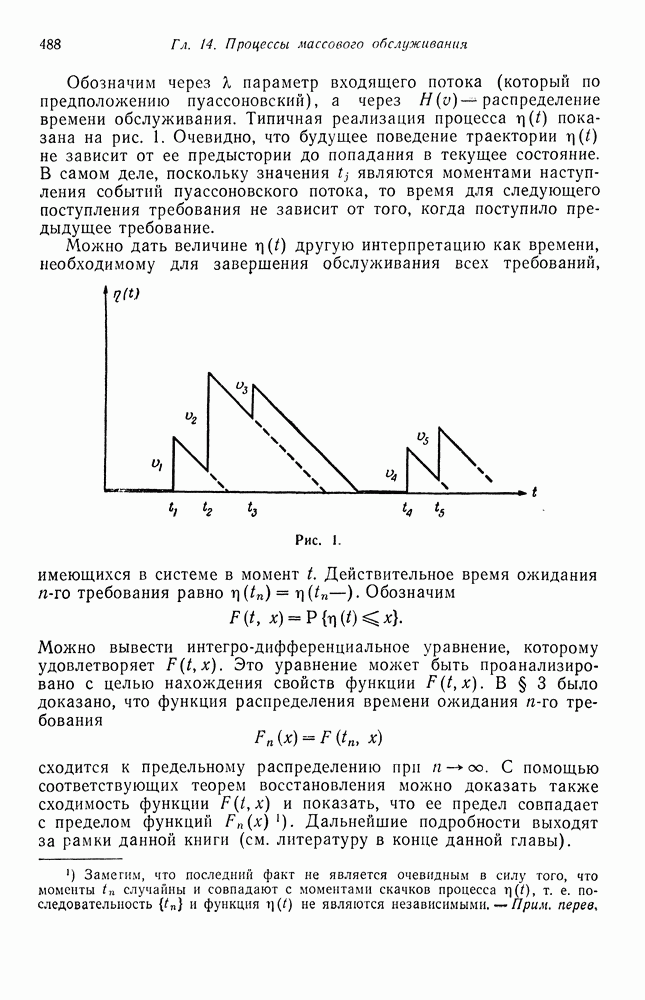
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
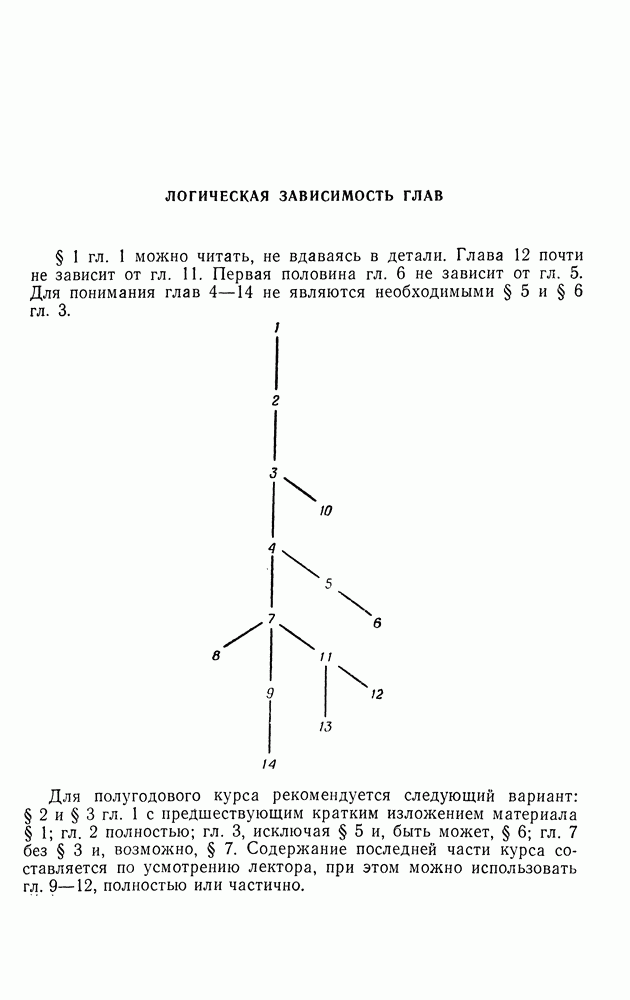
§ 7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МОДЕЛИ МУТАЦИИ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
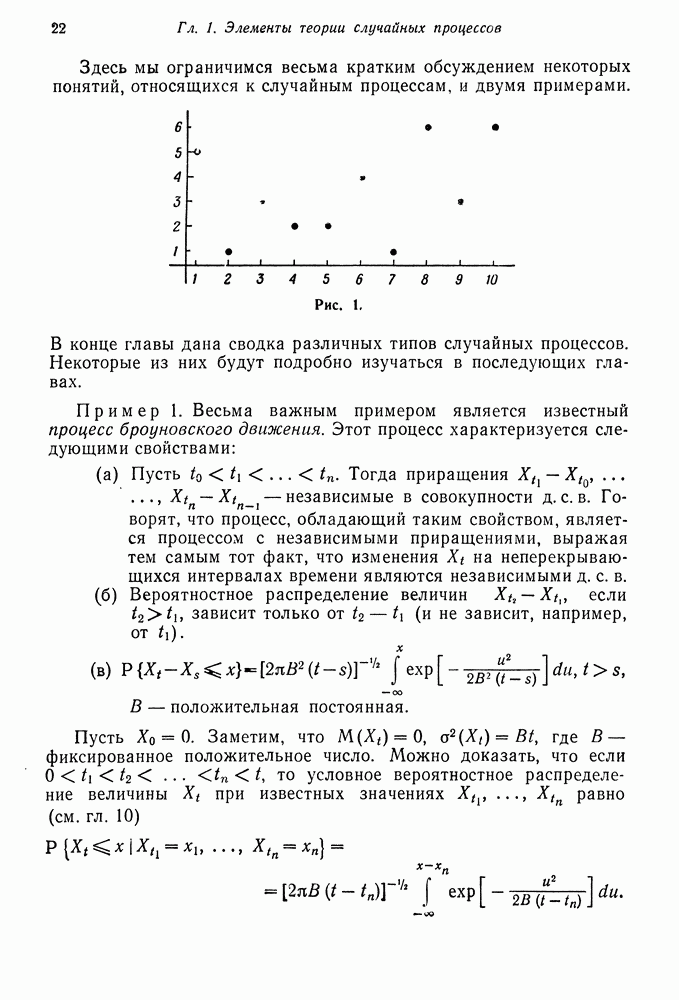
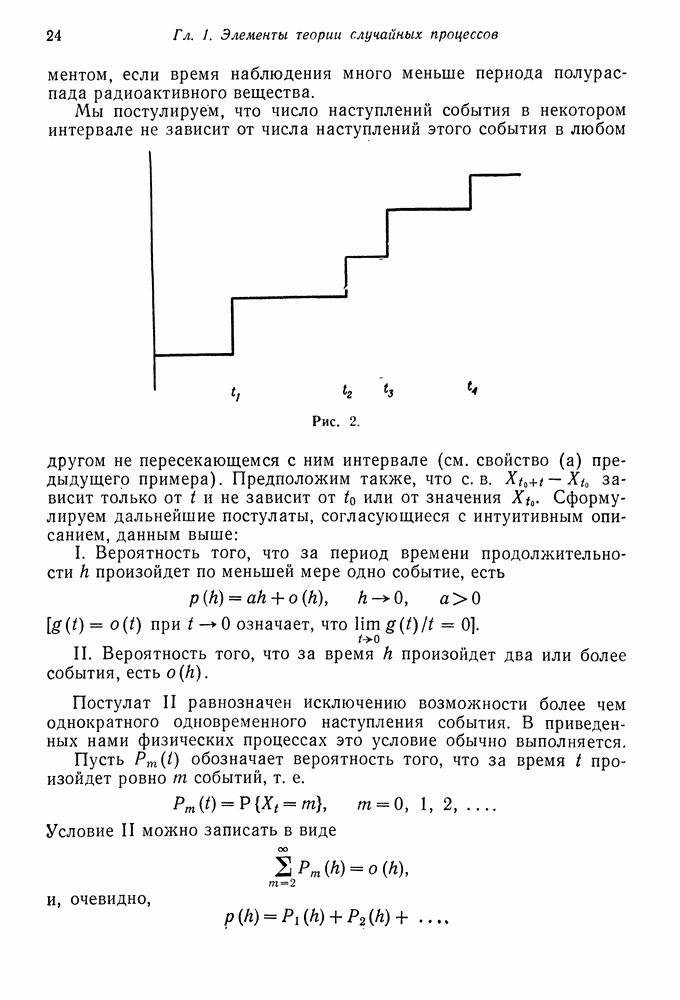
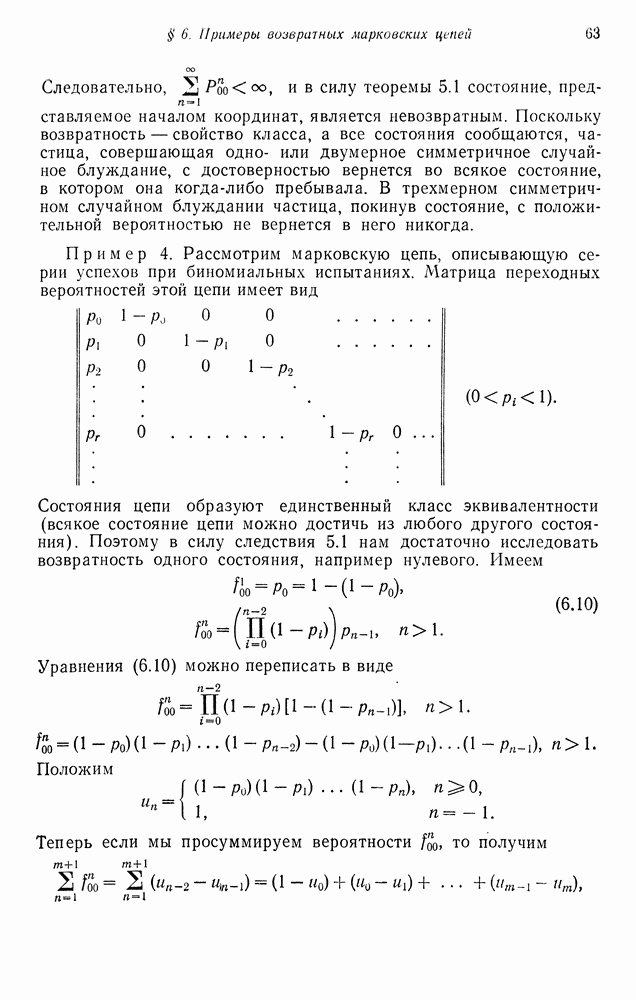
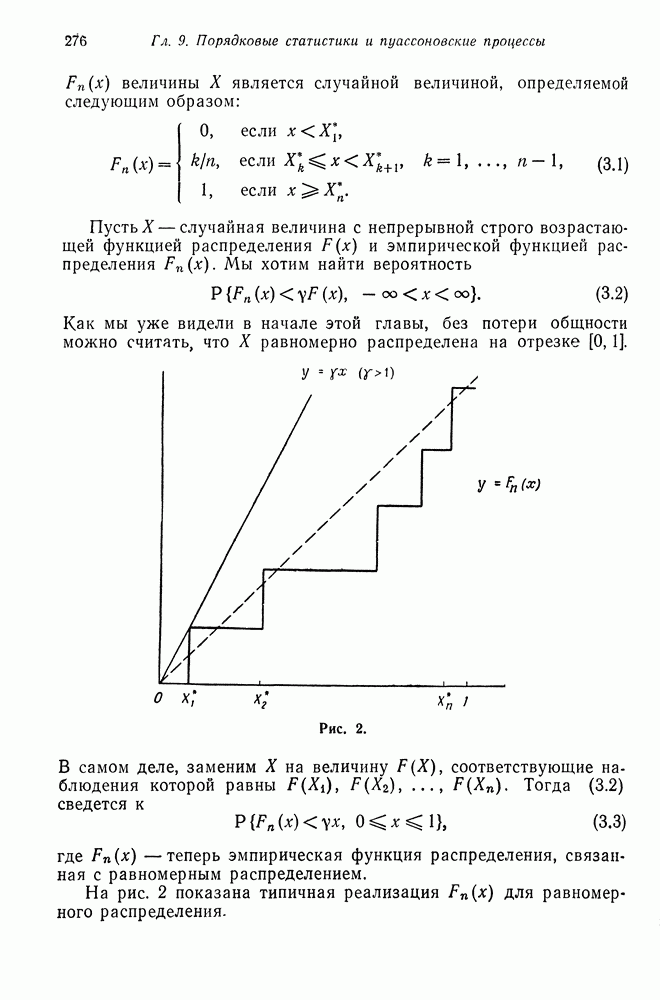
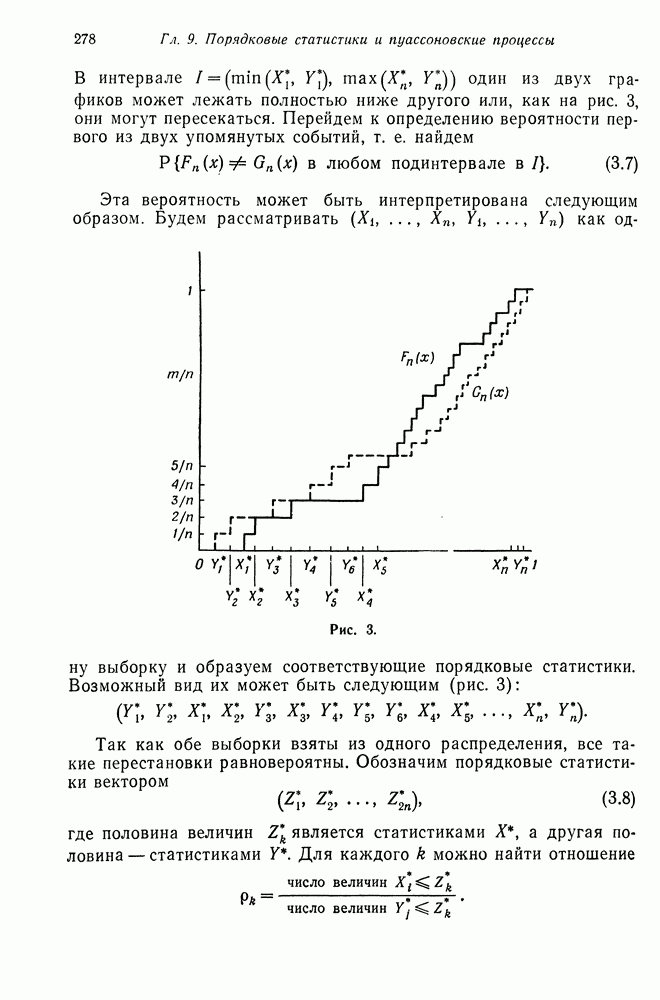
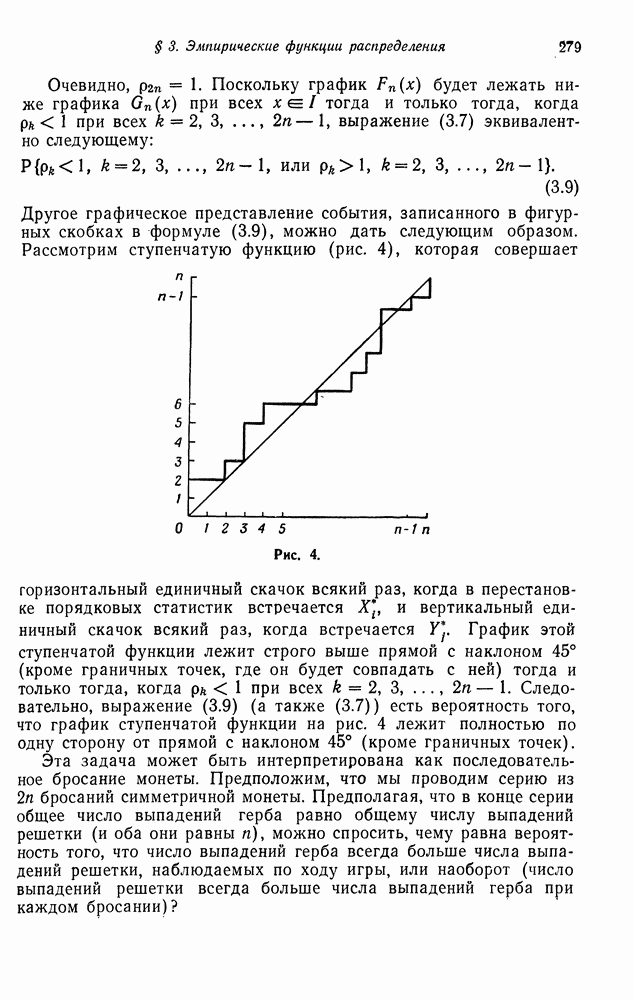
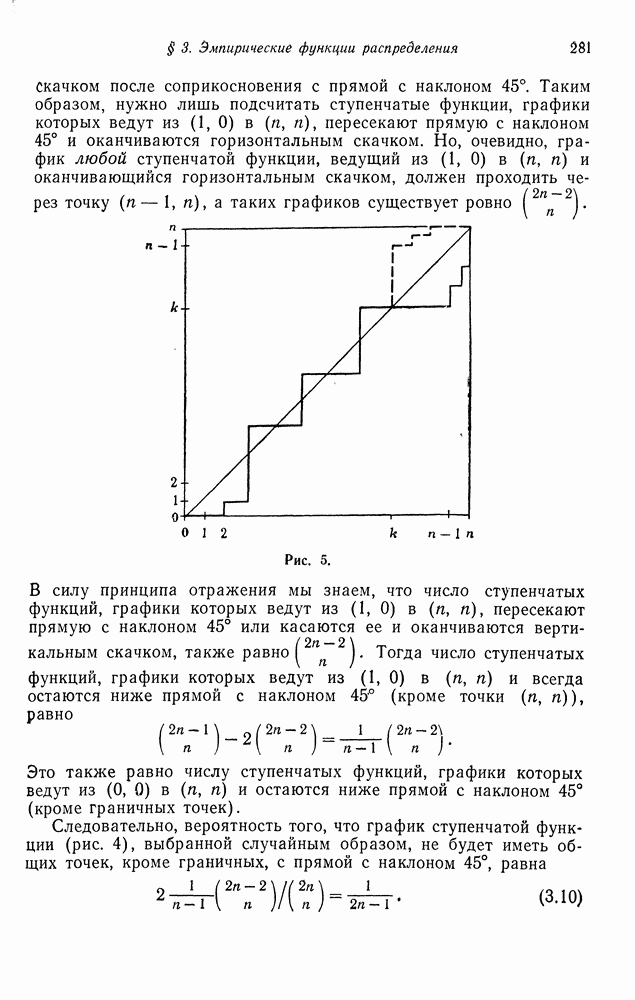
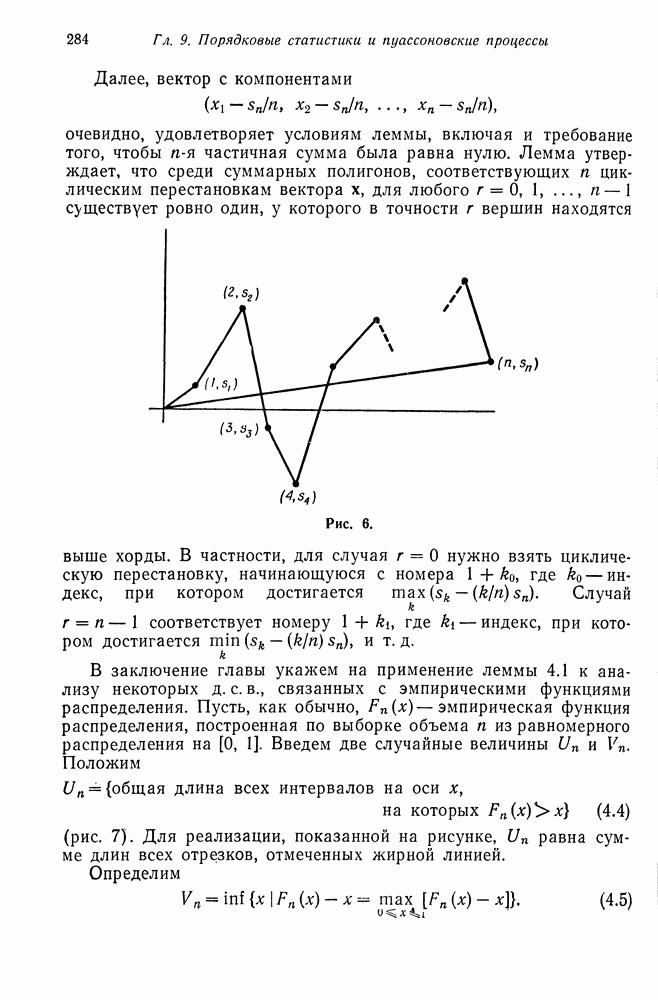
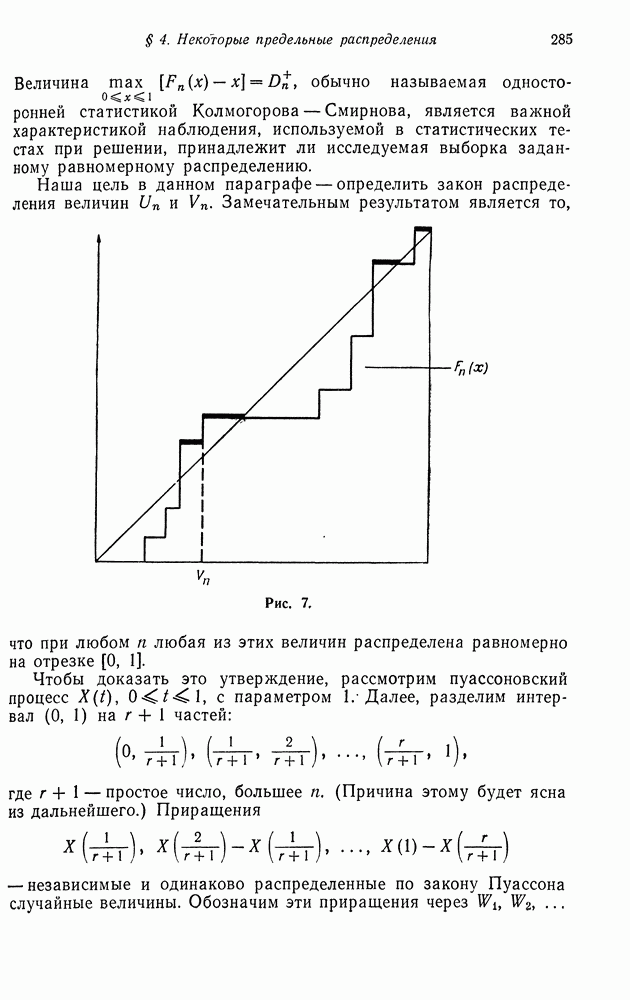
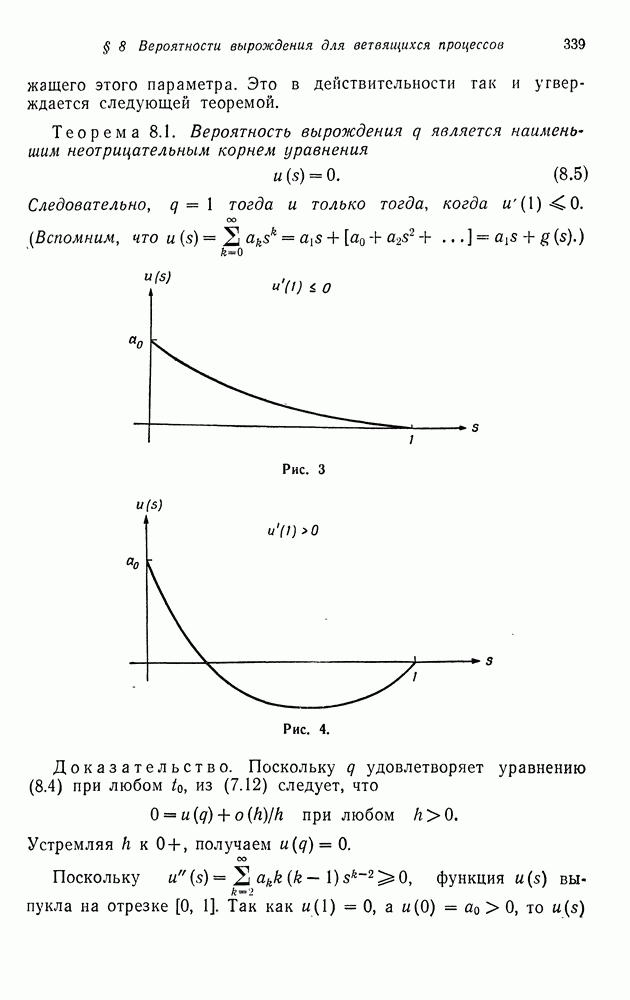
В предыдущем параграфе мы нашли вид собственных значений и собственных векторов матрицы перехода порожденной цепи Маркова (6.2). В этом параграфе мы будем изучать порожденную марковскую цепь для  типов
типов  индивидуумов при общих предположениях относительно мутации. В частности, будет найден вид собственных значений и собственных векторов цепи Маркова с переходными вероятностями
индивидуумов при общих предположениях относительно мутации. В частности, будет найден вид собственных значений и собственных векторов цепи Маркова с переходными вероятностями

где  при всех
при всех  задают условные (при условии, что
задают условные (при условии, что
общее число потомков равно  частоты
частоты  типов индивидуумов, когда
типов индивидуумов, когда  тип производит потомство с производящей функцией
тип производит потомство с производящей функцией  после чего каждый из потомков мутирует в тип
после чего каждый из потомков мутирует в тип  с вероятностью
с вероятностью 
В силу определения матрица  является стохастической, т. е.
является стохастической, т. е.  Мы предположим, что матрица
Мы предположим, что матрица  диагонализируема (см. приложение). Это означает, что ее
диагонализируема (см. приложение). Это означает, что ее  собственным значениям соответствуют
собственным значениям соответствуют  линейно независимых собственных векторов. Пусть
линейно независимых собственных векторов. Пусть  полное семейство правых собственных векторов, причем можно взять
полное семейство правых собственных векторов, причем можно взять  , поскольку сумма элементов любой строки матрицы
, поскольку сумма элементов любой строки матрицы  равна 1.
равна 1.
Выражение (7.1) можно переписать в следующем виде:

Производящая функция, соответствующая вероятностям  к» равна
к» равна

Прежде чем находить все собственные значения матрицы  мы рассмотрим два частных случая, которые помогут пояснить общий метод нахождения собственных значений матрицы (7.1).
мы рассмотрим два частных случая, которые помогут пояснить общий метод нахождения собственных значений матрицы (7.1).
Случай 1. Дифференцируя уравнение (7.3) по и полагая затем  получим
получим

Равенство (7.4) выполнено при всех  Положим
Положим

коэффициент при  в разложении
в разложении 
Тогда равенство (7.4) можно записать в виде (справедливом при всех 

Далее, умножим обе части равенства (7.5) на и просуммируем по  где
где  собственный вектор матрицы
собственный вектор матрицы  Получим
Получим

или, меняя порядок суммирования,

Так как  собственный вектор матрицы
собственный вектор матрицы  соответствующий собственному значению
соответствующий собственному значению  то
то

Отсюда

Для дальнейшего удобно ввести вектор  компонента которого равна
компонента которого равна

(Заметим, что  линейная функция от к, в частности
линейная функция от к, в частности  Равенство (7.6) примет вид
Равенство (7.6) примет вид

откуда следует, что  является собственным значением матрицы
является собственным значением матрицы  а
а  соответствующим ему собственным вектором.
соответствующим ему собственным вектором.
Заметим, что  (константа, не зависящая от
(константа, не зависящая от  Мы будем в какой-то мере выделять вектор
Мы будем в какой-то мере выделять вектор  из остальных векторов
из остальных векторов
 которые являются (не постоянными) линейными функциями от
которые являются (не постоянными) линейными функциями от  Собственные векторы
Собственные векторы  соответствующие собственным значениям
соответствующие собственным значениям  линейно независимы. Это следствие линейной независимости собственных векторов
линейно независимы. Это следствие линейной независимости собственных векторов  матрицы
матрицы  . В самом деле, если бы векторы
. В самом деле, если бы векторы  были линейно зависимы, то для некоторых действительных постоянных
были линейно зависимы, то для некоторых действительных постоянных  не всех равных нулю, было бы
не всех равных нулю, было бы  Но тогда
Но тогда

Так как это выполняется при всех  то отсюда следует
то отсюда следует

что противоречит линейной независимости векторов 
Поскольку  линейно независимы, то легко показать, что любая линейная функция
линейно независимы, то легко показать, что любая линейная функция  может быть представлена в виде линейной комбинации векторов
может быть представлена в виде линейной комбинации векторов  т. е. существуют постоянные
т. е. существуют постоянные  такие, что
такие, что

Из (7.7) и (7.8) вытекает, что матрица  переводит линейные функции в линейные, т. е. если
переводит линейные функции в линейные, т. е. если  линейна, то функция
линейна, то функция

также линейна по  Мы используем это свойство ниже.
Мы используем это свойство ниже.
Случай 2. Он аналогичен случаю 1, но требует для своего доказательства несколько более сложных выкладок и в некотором смысле более общих рассуждений.
Дифференцируя равенство (7.3) по любым двум аргументам  (они могут и совпадать) и полагая затем
(они могут и совпадать) и полагая затем  получим в левой части равенства
получим в левой части равенства

где

После дифференцирования правой части равенства (7.3) получим выражение

Введем в соответствии с предыдущим величину

Далее, умножим выражение (7.10) на  и просуммируем по всем
и просуммируем по всем  Получим
Получим

или, меняя порядок суммирования,

Выполняя аналогичные операции над выражением (7.11), получим

где  при всех
при всех  и
и  — линейная функция от
— линейная функция от  Мы снова воспользуемся тем фактом, что
Мы снова воспользуемся тем фактом, что  определению собственных векторов матрицы
определению собственных векторов матрицы  Выражение (7.13) тогда примет вид
Выражение (7.13) тогда примет вид

где  есть линейная функция от
есть линейная функция от 
Результатом этих вычислений является равенство

Перенося  в правую часть, получим к
в правую часть, получим к

где  линейная функция от
линейная функция от  (в силу (7.9)).
(в силу (7.9)).
Для простоты предположим (на самом деле это не существенно), что  при всех
при всех  Мы не будем рассматривать случай
Мы не будем рассматривать случай  так что
так что  квадратичные функции переменных
квадратичные функции переменных 
Если бы в равенстве (7.14) не было линейного члена  то это было бы соотношение, определяющее собственное значение.
то это было бы соотношение, определяющее собственное значение.
Мы утверждаем, что  собственное значение матрицы (7.1). Покажем, как построить собственный вектор, соответствующий значению
собственное значение матрицы (7.1). Покажем, как построить собственный вектор, соответствующий значению 
Предположим, что существует собственный вектор следующего вида:

где форма  линейна по
линейна по  и пока произвольна. Вектор
и пока произвольна. Вектор  нетривиальный, поскольку квадратичный член не может быть тождественно равным линейному члену. Представим
нетривиальный, поскольку квадратичный член не может быть тождественно равным линейному члену. Представим  в виде
в виде  что может быть сделано, поскольку
что может быть сделано, поскольку  образуют полную систему линейно независимых линейных собственных векторов (см. также (7.8)).
образуют полную систему линейно независимых линейных собственных векторов (см. также (7.8)).
Следующий метод построения собственных векторов аналогичен методу, использованному при нахождении собственных векторов матрицы перехода для модели с двумя типами индивидуумов при отсутствии мутации (см. § 6). В вышеприведенное выражение для собственных векторов входят неизвестные коэффициенты  Для того чтобы
Для того чтобы  был собственным вектором, нужно, чтобы удовлетворялось равенство
был собственным вектором, нужно, чтобы удовлетворялось равенство

Из равенств (7.7) и (7.14) следует, что левая часть (7.15) равна

Приравняем это выражение правой части (7.15). Приведя подобные члены, получим

Так как  линейна
линейна  можно записать
можно записать

где коэффициенты определяются единственным образом из вида  и являются известными величинами. Таким образом,
и являются известными величинами. Таким образом, 

поскольку  линейно независимы, то
линейно независимы, то

откуда

Собственный вектор может быть теперь записан в виде

где 
Мы доказали, что каждому собственному значению  ответствует собственный вектор
ответствует собственный вектор  Все собственные векторы
Все собственные векторы  линейно независимы, поскольку квадратичные части
линейно независимы, поскольку квадратичные части  очевидно, линейно независимы.
очевидно, линейно независимы.
Общий случай. Рассмотрим теперь общий случай. Дифференцируя равенство  раз по
раз по  и полагая затем
и полагая затем  получим
получим

где

 определяется так:
определяется так:

Первый член в правой части равенства (7.18) является однородным полиномом от  степени
степени  Он получен при однократном дифференцировании правой части (7.3). Как только при дифференцировании появляется член
Он получен при однократном дифференцировании правой части (7.3). Как только при дифференцировании появляется член  степень коэффициента при нем относительно
степень коэффициента при нем относительно  обязана быть меньше
обязана быть меньше  поскольку для того, чтобы получить
поскольку для того, чтобы получить  нужно продифференцировать
нужно продифференцировать  не возведено в степень
не возведено в степень  Используя равенство (7.18), можно найти собственные значения матрицы переходных вероятностей (7.1).
Используя равенство (7.18), можно найти собственные значения матрицы переходных вероятностей (7.1).
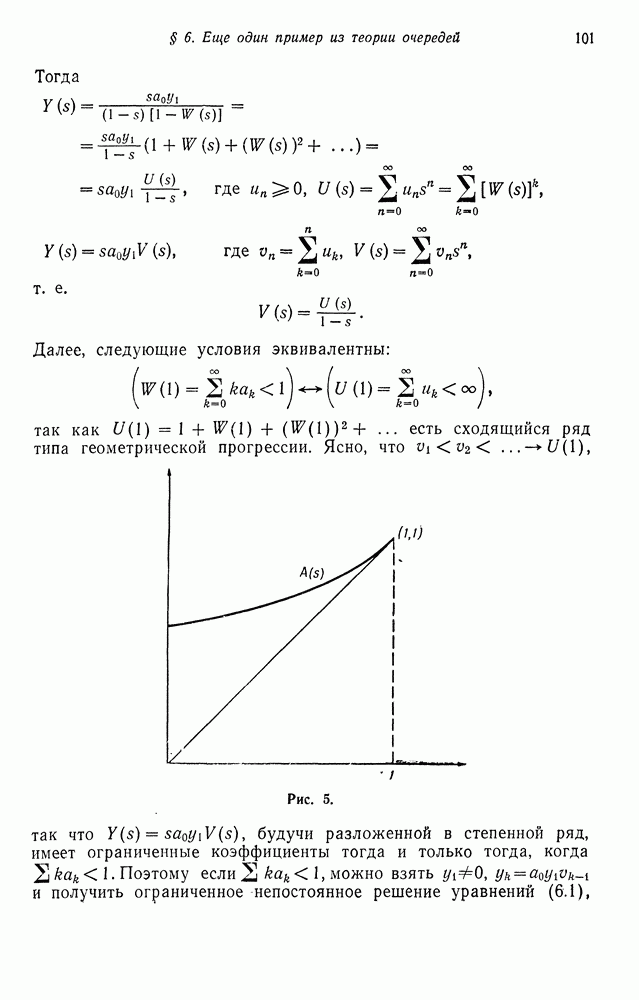
Первое собственное значение равно 1 и соответствующий ему собственный вектор имеет равные между собой компоненты. Причиной этому служит то, что сумма элементов строк матрицы переходных вероятностей равна 1. При  мы имеем случай 1, а при
мы имеем случай 1, а при  случай 2, рассмотренные выше. В случае 1 мы получили
случай 2, рассмотренные выше. В случае 1 мы получили  независимых собственных векторов. Член
независимых собственных векторов. Член  отвечает собственному значению 1, Член
отвечает собственному значению 1, Член  отвечает собственным значениям
отвечает собственным значениям  . В случае 2 было
. В случае 2 было  линейно независимых собственных векторов, соответствующих
линейно независимых собственных векторов, соответствующих  собственным значениям вида
собственным значениям вида 
Процедура, аналогичная использованной в случаях 1 и 2, может быть применена для построения  линеино независимых собственных векторов, которые являются полиномами степени
линеино независимых собственных векторов, которые являются полиномами степени  от переменных
от переменных

и соответствуют собственным значениям

Точное выражение для собственных векторов имеет вид

Число собственных значений вида  можно найти, рассматривая соответствующую задачу о размещении, где
можно найти, рассматривая соответствующую задачу о размещении, где  шаров нужно разместить в
шаров нужно разместить в  ячеек. В нашем случае
ячеек. В нашем случае  равно степени
равно степени  соответствующего собственного вектора, а
соответствующего собственного вектора, а  равно числу различных чисел
равно числу различных чисел  т. е.
т. е.  При такой интерпретации число различных собственных значений равно числу сочетаний из
При такой интерпретации число различных собственных значений равно числу сочетаний из  по
по  Поэтому число различных собственных векторов вида
Поэтому число различных собственных векторов вида

Равно 
Общее число линейно независимых собственных векторов равно

что в точности совпадает с числом состояний цепи Маркова (7.1). Подытожим полученные результаты в следующей теореме.
Теорема 7.1. Пусть  стохастическая матрица [т. е.
стохастическая матрица [т. е.  соответствующая неприводимой цепи Маркова. Пусть
соответствующая неприводимой цепи Маркова. Пусть  ее собственные значения, и предположим, что
ее собственные значения, и предположим, что  образуют полное семейство соответствующих им собственных векторов, т. е.
образуют полное семейство соответствующих им собственных векторов, т. е.  диагонализируема. Более того, предположим,
диагонализируема. Более того, предположим,  любых
любых  где
где

Рассмотрим цепь Маркова для  типов индивидуумов с матрицей переходных вероятностей, задаваемой равенством (7.1). При
типов индивидуумов с матрицей переходных вероятностей, задаваемой равенством (7.1). При  существует
существует  линейно независимых собственных векторов, которые получаются из полиномов степени
линейно независимых собственных векторов, которые получаются из полиномов степени  от переменных
от переменных

Вид собственных значений дается формулой (7.21), а правые собственные векторы имеют вид (7.20). На эти собственные векторы
и постоянный вектор натянуто пространство размерности  равной порядку матрицы
равной порядку матрицы 
В качестве примера применим теорему 7.1 к случаю, когда  единичная матрица. Другими словами, нет мутационного давления. В этом случае цепь Маркова (7.1) является непосредственным обобщением модели с двумя типами индивидуумов на случай
единичная матрица. Другими словами, нет мутационного давления. В этом случае цепь Маркова (7.1) является непосредственным обобщением модели с двумя типами индивидуумов на случай  типов
типов  Каждый из них размножается независимо в соответствии с законами развития ветвящегося процесса, характеризуемого вероятностной производящей функцией
Каждый из них размножается независимо в соответствии с законами развития ветвящегося процесса, характеризуемого вероятностной производящей функцией  Порожденная цепь Маркова имеет следующие вероятности перехода:
Порожденная цепь Маркова имеет следующие вероятности перехода:

В этом случае  Пусть константа
Пусть константа  определена равенством (7.22). Теорема 7.1 утверждает, что
определена равенством (7.22). Теорема 7.1 утверждает, что  является собственным значением кратности
является собственным значением кратности  т. е. существуют
т. е. существуют  линейно независимых собственных векторов, соответствующих собственному значению
линейно независимых собственных векторов, соответствующих собственному значению  Кратность возникает из-за того, что
Кратность возникает из-за того, что  и не зависит от выбора
и не зависит от выбора  Правые собственные векторы, соответствующие
Правые собственные векторы, соответствующие  являются полиномами степени
являются полиномами степени  от переменных
от переменных

поскольку можно выбрать 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 1. СВОДКА ОСНОВНЫХ ТЕРМИНОВ И СВОЙСТВ СЛУЧАЙНЫХ ВЕЛИЧИН И ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
- А. Совместные функции распределения
- Б. Условные распределения и плотности
- В. Бесконечные семейства случайных величин
- Г. Характеристические функции
- Д. Производящие функции
- Е. Примеры функций распределения
- Ж. Предельные теоремы
- § 2. ДВА ПРОСТЫХ ПРИМЕРА СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 3. КЛАССИФИКАЦИЯ ОБЩИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- ЗАМЕЧАНИЯ
- Глава 2. МАРКОВСКИЕ ЦЕПИ
- § 2. ПРИМЕРЫ МАРКОВСКИХ ЦЕПЕЙ
- Б. Одномерные случайные блуждания
- В. Дискретная марковская цепь, описывающая очередь
- Г. Модель из теории запасов
- Д. Серии успехов
- Е. Ветвящиеся процессы
- Ж. Марковские цепи в генетике
- 3. Генетическая модель II
- § 3. МАТРИЦЫ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ МАРКОВСКОЙ ЦЕПИ
- § 4. КЛАССИФИКАЦИЯ СОСТОЯНИЙ МАРКОВСКОЙ ЦЕПИ
- § 5. ВОЗВРАТНОСТЬ
- § 6. ПРИМЕРЫ ВОЗВРАТНЫХ МАРКОВСКИХ ЦЕПЕЙ
- § 7. ЕЩЕ О ВОЗВРАТНОСТИ
- Глава 3. ОСНОВНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ МАРКОВСКИХ ЦЕПЕЙ И ИХ ПРИЛОЖЕНИЯ
- § 2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 1.1
- § 3. ВЕРОЯТНОСТИ ПОГЛОЩЕНИЯ
- § 4. КРИТЕРИИ ВОЗВРАТНОСТИ
- § 5. ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
- § 6. ЕЩЕ ОДИН ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
- § 7. СЛУЧАЙНОЕ БЛУЖДАНИЕ
- Глава 4. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ МАРКОВСКИХ ЦЕПЕЙ
- § 2. СВЯЗЬ МЕЖДУ СОБСТВЕННЫМИ ЗНАЧЕНИЯМИ И КЛАССАМИ ВОЗВРАТНЫХ СОСТОЯНИЙ
- § 3. ПЕРИОДИЧЕСКИЕ КЛАССЫ
- § 4. СПЕЦИАЛЬНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ ДЛЯ МАРКОВСКИХ ЦЕПЕЙ
- § 5. ПРИМЕРЫ
- § 6. ПРИЛОЖЕНИЯ К БРОСАНИЯМ МОНЕТЫ
- Глава 5. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ И ИХ ПРИЛОЖЕНИЯ
- § 1. ВЕРОЯТНОСТИ ПЕРЕХОДА С ЗАПРЕЩЕНИЕМ
- § 2. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ
- § 3. СУЩЕСТВОВАНИЕ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ РАСПРЕДЕЛЕНИЙ
- § 4. ИНТЕРПРЕТАЦИЯ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ РАСПРЕДЕЛЕНИЙ
- § 5. РЕГУЛЯРНЫЕ, СУПЕРРЕГУЛЯРНЫЕ И СУБРЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТЬ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН КАК МАРКОВСКАЯ ЦЕПЬ
- § 1. СВОЙСТВА ВОЗВРАТНОСТИ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- § 2. ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
- § 3. ПРАВЫЕ РЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
- Глава 7. КЛАССИЧЕСКИЕ ПРИМЕРЫ ЦЕПЕЙ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 1. ОБЩИЕ ПРОЦЕССЫ ЧИСТОГО РОЖДЕНИЯ (РАЗМНОЖЕНИЯ) И ПУАССОНОВСКИЕ ПРОЦЕССЫ
- Б. Примеры пуассоновских процессов
- В. Процесс чистого рождения
- Г. Процесс Юла
- § 2. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О ПУАССОНОВСКИХ ПРОЦЕССАХ
- § 3. МОДЕЛЬ СЧЕТЧИКА
- § 4. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛИ
- § 5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
- § 6. ПРИМЕРЫ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
- § 7. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛЙ С ПОГЛОЩАЮЩИМИ СОСТОЯНИЯМИ
- § 8. ЦЕПИ МАРКОВА С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ И НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- Глава 8. ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 1. СВОЙСТВА ДИФФЕРЕНЦИРУЕМОСТИ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ
- § 2. КОНСЕРВАТИВНЫЕ ПРОЦЕССЫ. ПРЯМЫЕ И ОБРАТНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПОСТРОЕНИЕ ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ С ПОМОЩЬЮ ЕЕ ИНФИНИТЕЗИМАЛЬНЫХ ПАРАМЕТРОВ
- § 4. СТРОГО МАРКОВСКОЕ СВОЙСТВО
- Глава 9. ПОРЯДКОВЫЕ СТАТИСТИКИ, ПУАССОНОВСКИЕ ПРОЦЕССЫ И ИХ ПРИЛОЖЕНИЯ
- § 1. ПОРЯДКОВЫЕ СТАТИСТИКИ И ИХ СВЯЗЬ С ПУАССОНОВСКИМИ ПРОЦЕССАМИ
- § 2. ЗАДАЧА О БАЛЛОТИРОВКЕ
- § 3. ЭМПИРИЧЕСКИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПОРЯДКОВЫЕ СТАТИСТИКИ
- § 4. НЕКОТОРЫЕ ПРЕДЕЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ДЛЯ ЭМПИРИЧЕСКИХ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
- Глава 10. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 2. СОВМЕСТНЫЕ ВЕРОЯТНОСТИ ДЛЯ БРОУНОВСКОГО ДВИЖЕНИЯ
- § 3. НЕПРЕРЫВНОСТЬ ТРАЕКТОРИЙ И ИХ МАКСИМАЛЬНЫЕ ЗНАЧЕНИЯ
- Глава 11. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ
- § 1. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
- § 2. СООТНОШЕНИЯ ДЛЯ ПРОИЗВОДЯЩЕЙ ФУНКЦИИ, ОПИСЫВАЮЩЕЙ ВЕТВЯЩИЙСЯ ПРОЦЕСС
- § 3. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ
- § 4. ПРИМЕРЫ
- § 5. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДВУМЯ ТИПАМИ ЧАСТИЦ
- § 6. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕСКОЛЬКИМИ ТИПАМИ ЧАСТИЦ
- § 7. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 8. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 10. ВЕТВЯЩИЙСЯ ПРОЦЕСС С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ И ДВУМЯ ТИПАМИ ЧАСТИЦ
- § 11. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ, ЗАВИСЯЩИЕ ОТ ВОЗРАСТА
- Глава 12. СОСТАВНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- § 1. МНОГОМЕРНЫЕ ОДНОРОДНЫЕ ПУЛССОНОВСКИЕ ПРОЦЕССЫ
- § 2. ПРИМЕНЕНИЕ МНОГОМЕРНЫХ ПУАССОНОВСКИХ ПРОЦЕССОВ В АСТРОНОМИИ
- § 3. ИММИГРАЦИЯ И РОСТ ПОПУЛЯЦИЙ
- § 4. ВЕРОЯТНОСТНЫЕ МОДЕЛИ МУТАЦИИ И РОСТА
- § 5. ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ ОДНОМЕРНОЙ ПОПУЛЯЦИИ
- § 6. ВЕРОЯТНОСТНАЯ МОДЕЛЬ РОСТА ПОПУЛЯЦИИ В ПРОСТРАНСТВЕ И ВРЕМЕНИ
- § 7. ДЕТЕРМИНИРОВАННЫЙ РОСТ ПОПУЛЯЦИИ С РАСПРЕДЕЛЕНИЕМ ПО ВОЗРАСТАМ
- § 8. ДИСКРЕТНАЯ ВОЗРАСТНАЯ МОДЕЛЬ
- Глава 13. ДЕТЕРМИНИРОВАННЫЕ И СЛУЧАЙНЫЕ ГЕНЕТИЧЕСКИЕ И ЭКОЛОГИЧЕСКИЕ ПРОЦЕССЫ
- § 1. ГЕНЕТИЧЕСКИЕ МОДЕЛИ. ОПИСАНИЕ ГЕНЕТИЧЕСКОГО МЕХАНИЗМА
- § 2. ИНБРИДИНГ
- Б. Спаривание сибсов
- В. Гены, идентичные по происхождению
- Г. Бесконечная диплоидная популяция и коэффициент инбридинга
- Д. Популяция с самооплодотворением и случайным спариванием
- § 3. ПОЛИПЛОИДЫ
- § 4. МАРКОВСКИЕ ПРОЦЕССЫ, ПОРОЖДАЕМЫЕ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
- § 5. МОДЕЛИ РОСТА ПОПУЛЯЦИЙ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
- § 6. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЦЕПЕЙ МАРКОВА, ПОРОЖДЕННЫХ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
- § 7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МОДЕЛИ МУТАЦИИ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
- § 8. ВЕРОЯТНОСТНЫЙ СМЫСЛ СОБСТВЕННЫХ ЗНАЧЕНИЙ
- Глава 14. ПРОЦЕССЫ МАССОВОГО ОБСЛУЖИВАНИЯ
- § 2. ПРОСТЕЙШИЕ ПРОЦЕССЫ ОБСЛУЖИВАНИЯ (М/М/1)
- § 3. НЕКОТОРЫЕ ОБЩИЕ МОДЕЛИ ОБСЛУЖИВАНИЯ ОДНИМ ПРИБОРОМ
- § 4. МЕТОД ВЛОЖЕННЫХ ЦЕПЕЙ МАРКОВА ПРИМЕНИТЕЛЬНО К МОДЕЛИ ОБСЛУЖИВАНИЯ (M/G/1)
- § 5. ЭКСПОНЕНЦИАЛЬНО РАСПРЕДЕЛЕННОЕ ВРЕМЯ ОБСЛУЖИВАНИЯ (G/М/1)
- § 6. ГАММА-РАСПРЕДЕЛЕНИЕ ИНТЕРВАЛОВ МЕЖДУ ПОСТУПЛЕНИЯМИ И ОБОБЩЕНИЯ (Ek/М/1)
- § 7. ЭКСПОНЕНЦИАЛЬНОЕ ОБСЛУЖИВАНИЕ s ПРИБОРОВ (GI/M/s)
- § 8. ВИРТУАЛЬНОЕ ВРЕМЯ ОЖИДАНИЯ И ПЕРИОД ЗАНЯТОСТИ
- ПРИЛОЖЕНИЕ § 1. СПЕКТРАЛЬНАЯ ТЕОРЕМА
- § 2. ТЕОРИЯ ФРОБЕНИУСА ПОЛОЖИТЕЛЬНЫХ МАТРИЦ
- РАЗЛИЧНЫЕ ЗАДАЧИ